Матричный осветитель на основе дифракции Фраунгофера.

А.Н. Малов*, В.С. Фещенко**, Л.В. Фещенко**, Н.Ю. Выговская***

*Иркутский Филиал Института Лазерной Физики СО РАН

**Приднестровский Государственный Университет им. Т.Г. Шевченко

***Академия Печати, г. Москва

Для многих современных областей оптических исследований требуются средства эффективного снабжения матрицы микроэлементов световой энергией. Этим свойствам удовлетворяет матричный осветитель (МОС), который является оптическим элементом, осуществляющим преобразование однородной световой волны в заданное множество точечных областей с малой потерей либо без потери энергии при преобразовании. Такие элементы применяются при мультиплицировании изображения [1], в оптических преобразованиях [2] и в цифровых растровых оптических процессорах различной архитектуры [3]. Сегодня разрабатываются и проверяются различные методы для осуществления МОС [4-8].

В данной работе представлены экспериментальные результаты для МОС, полученных с использованием явления дифракции Фраунгофера на фазовом периодическом объекте. Мы использовали эффект оптического самопреобразования Фурье, т.е. явление преобразования Фурье, происходящее при освещении периодических структур плоской когерентной волной, без использования линз [9]. Использование фазового объекта на входе гарантирует низкое поглощение и высокую энергетическую эффективность. Более того, периодический фазовый объект позволяет получить множество фокусов с распределением интенсивности излучения в плоскости наблюдения, задаваемым Фурье образом изображения этого объекта.

1. Оптическая схема осветителя.

При освещении когерентной плоской волной периодического объекта, дифракция Фраунгофера наступает существенно раньше, чем для не периодического. Расстояние на котором это происходит [9] равно:

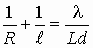, (1)

где R - расстояние от источника света до периодического объекта, l - фокусное расстояние оптической системы с периодической структурой, L - полный поперечный размер объекта, d - период структуры рисунка на объекте, l - длина волны падающего излучения.

Фокусное расстояние системы с периодическим объектом, а значит и расстояние от плоскости объекта до плоскости его Фурье-образа будет тем меньше, чем меньше период периодического объекта.

Отношение расстояний, на котором будет наблюдаться Фурье-спектр для периодического предмета и непериодического предмета таких же размеров, равно [9]:

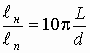(2)

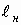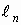где - расстояние до плоскости преобразования Фурье для изображения непериодического объекта, - расстояние до плоскости преобразования Фурье для изображения периодического объекта, L - полный поперечный размер предмета, d - период периодического предмета. Из соотношения (2) видно, что расстояние на котором будет наблюдаться Фурье-спектр периодического предмета в 10p L/d раз меньше, чем для непериодического предмета таких же размеров.

На рис.1. показана зависимость отношения расстояний, на которых начинает проявляться Фурье-спектр для изображений периодического и непериодического предметов. Видно, что расстояние, на котором наблюдается Фурье-спектр, в случае непериодического предмета таких же размеров, как и периодический, с увеличением относительных размеров растет, и в среднем на три порядка больше чем для периодического предмета.

Кроме того, из графика 2 на рис. 1, видно, что для периодического предмета существует область, где преобразование Фурье наступает раньше, чем даже для его отдельного элемента (участок кривой 2, где lg[l /l_п] <1).

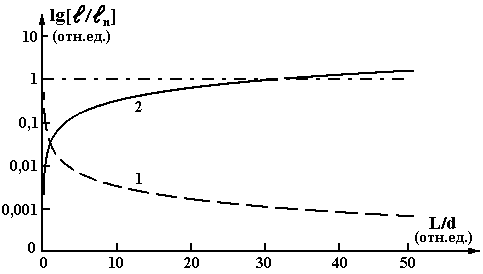
Рис.1. Зависимость отношения расстояний до зоны дифракции Фраунгофера для излучения дифрагировавшего на периодическом и непериодическом объекте от приведенной величины предмета.

1 - непериодический предмет имеет те же размеры, что и периодический; 2 - непериодический предмет имеет размеры равные размерам элементарной ячейки периодического предмета.

В такой оптической схеме преобразование Фурье осуществляется без линз в свободном пространстве. Интересным отличием рассматриваемой схемы от схемы, классического в оптике, преобразования Фурье с помощью линз является то, что согласно [9,10], Фурье-спектр не локализуется в одной плоскости. При распространении света вдоль оси z, однажды возникнув изображение Фурье-спектра, увеличивается в размерах, т.е. масштаб преобразования Фурье плавно меняется при изменении расстояния между плоскостями объекта и наблюдения.

Фурье-спектр периодического предмета так же как и само изображение обладает свойством самореставрации [11], которое заключается в том, что изображение периодического объекта полученного в плоскости Тальбота более совершенно, чем сам объект [12,13].

Все вышеперечисленные свойства Фурье-спектра периодического объекта, позволяют изготовить матричный осветитель, использующий для преобразования волнового фронта дифракцию Фраунгофера.

2. Экспериментальные результаты.

В качестве источника излучения использовался He-Ne лазер типа ЛГН-222, с длиной волны излучения l =0,63 мкм, мощностью до 50 мВт при диаметре пучка 2 мм и длиной когерентности 12 см. Регистрация изображений производилось на фотопленке “Микрат - Изопан”. Поскольку исследовалась структура электромагнитных полей, то нелинейность регистрации изображений, присущая фотопленке “Микрат-Изопан” способствовала выявлению тонкой структуры изображений. Периодический, чисто фазовый транспарант, изготовлялся так же на пленке “Микрат-Изопан” по методике предложенной в [14].

Оптическая схема установки изображена на рис.2. Периодический объект помещался в луч He-Ne лазера. Диаметр этого луча был примерно 2 мм.

На рисунках 3а и 4а изображены рисунки различных исходных транспарантов. А на рисунках. 3б и 4б соответственно изображены их Фурье - спектры, полученные вследствие дифракции Фраунгофера.

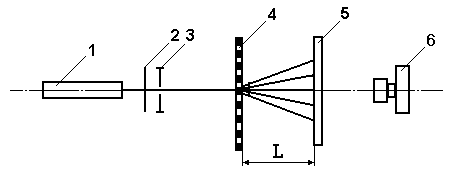
Рис.2. Оптическая схема эксперимента 1 - лазер; 2 - ослабитель; 3 - ирисовая диафрагма; 4 - периодический объект; 5 - матовый экран; 6 - фотоаппарат.

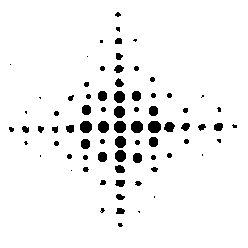
Рис.3а. Рисунок исходного транспаранта.	Рис.3б. Фотография его Фурье-спектра полученного по схеме показанной на рис.2.

Рис.4а. Рисунок транспаранта попавшего в зону освещения лазерным лучом.	Рис.4б. Фотография его Фурье-спектра полученного по схеме показанной на рис.2.

 

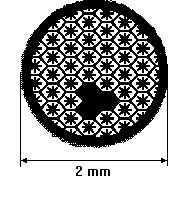
Одним из преимуществ использования в оптических схемах периодических объектов, является то, что их Фурье-спектр самореставрируется. На рис.5а показан периодический объект с повреждением, которое моделировалось посредством закрашивания разного количества единичных объектов черными чернилами, абсолютно непрозрачными в свете гелий неонового лазера.

Рис.5а. Рисунок области транспаранта попавшего в зону освещения лазерным лучом. Испорчено 7% элементарных транспарантов.	Рис.5б. Фотография Фурье-спектра транспаранта изображенного на рис.5а.

Рис.5б полностью идентичен рис.4б. Единственное отличие в том что интенсивность изображения несколько упала, при полном сохранении структуры изображения.

3. Обсуждение результатов.

Предложенные в данной работе МОС на основе явления дифракции Фраунгофера когерентного излучения на фазовых периодических структурах позволяют формировать заданное распределение интенсивности света в плоскости наблюдения. Причем в отличие от МОС, предложенных в [8], интенсивность излучения в пределах каждого отдельного фокуса можно менять, изменяя фазовый рисунок на периодическом транспаранте, что позволяет регулировать энергопотребление каждого отдельного элемента в оптической микросхеме. Некоторые энергетические потери, связанные с дифракцией света за приделы области освещения, можно так же минимизировать с помощью подбора оптимального фазового рисунка. Преимуществом данных МОС также является плавное изменение масштаба Фурье-преобразования, а значит, и размеров наблюдаемого Фурье-спектра, в процессе передвижения плоскости наблюдения вдоль оси z, что позволяет компенсировать погрешности изготовления МОС простым изменением расстояния между плоскостью МОС и плоскостью наблюдения. Эффект самореставрации Фурье-спектра позволяет повысить помехозащищенность оптических систем с такими МОС.

Литература

1. Damman H. and Gortler K. High-Efficiency In-Line Multiply Imaging by Means of Multiply Phase Holograms. / Opt. Commun. 3, p. 312-315 (1971).
2. . Lohman G.E and Lohmann A.W. Optical Interconnection Network Utilizing Diffraction Gratings. / Opt. Eng. 27, p.893-900 (1988).
3. Streibl N., Prise M.E. Digital Optics: Architectures and System Requirements. /Phys. Status Solidi, 150, p.447-454 (1988).
4. Damman H. and Klotz E. Coherent Optical Generation and Inspection of Two-Dimensional Periodic Structures. / Opt. Acta, 24, p.505-515 (1977)
5. Lohmann A. W., Schwider J., Streibl N. and Thomas J. An Array Illuminator based on Phase Contrast. / Appl. Opt. 27, p. 2915-2921 (1988)
6. Lohmann A. W. and Sauer F. Holographic Telescope Arrays. / Appl. Opt. 27, p.3003-3007 (1988)
7. Kubota T. and Takeda M. Array Illuminator Using Grating Couplers. / Opt. Lett. 14, p. 651-652 (1989)
8. Lohmann A. W. and Thomas J.A. Making an array illuminator based on the Talbot effect. / Appl. Opt., 29, № 29, p.4337-4340 (1990).
9. Корфуненко О.А., Фещенко В.С., Фещенко Л.В. Оптическая обработка изображений периодических объектов. / В кн.: “Люминесценция и сопутствующие явления. Труды IV всероссийской школы-семинара (Иркутск, октябрь 1998 г.)”. - Иркутск: Изд-во Иркутского университета, с.197-204 (1999).
10. Смирнов А.П. О безлинзовом преобразовании Фурье с помощью дырчатой маски и методе анализа интерферограмм на его основе в модифицированном интерферометре Тальбота. / “Оптика и спектроскопия”, 62, в.3, с.636-643 (1987).
11. Малов А.Н., Фещенко В.С. Фещенко Л.В. Самопреобразование Фурье транспарантов периодических объектов. / В кн. Применение лазеров в науке и технике" Иркутск: ИФ ИЛФ СО РАН, IX, с. 98-109 (1997).
12. Kalestynski A. and Smolinska B., Self-restoration of the autoidolon of defective periodic objects. / Optica Acta 9, p.125-134. (1978)
13. Patorski K. The self-imaging phenomenon and its application. / “Progress in optics”, XXVII, p.3-108 (1989).
14. Выговский Ю.Н, Малов А.Н., Фещенко В.С. Управление формированием фазового рельефа в слоях дихромированного желатина. / “Компьютерная оптика”, 17, ИСОИ РАН: Самара-Москва, с.75 - 85 (1997).