|
|
 |
 |

|
| |
ОСОБЕННОСТИ ГОЛОГРАФИЧЕСКОЙ ЗАПИСИ В ДВУПРЕЛОМЛЯЮЩИХ ЭЛЕКТРООПТИЧЕСКИХ КРИСТАЛЛАХ
С.И.Степанов, А.А.Камишлин, М.П.Петров
Рассмотрены особенности объемной голографической записи в двупреломляющих кристаллах. Приведен вывод общего выражения для дифракционной эффективности объемной фазовой голограммы, представляющего собой обобщение известных формул Когельника на случай решетки тензора диэлектрической проницаемости в анизотропном кристалле. Применение полученного соотношения к одноосному фоторефрактивному сегнетоэлектрику LiNbO3 приводит к выводу о возможности наблюдения в указанном кристалле эффективной дифракции света с поворотом плоскости поляризации. На примере LiNbO3 также рассмотрены некоторые нетривиальные случаи выполнения условий Брэгга для дифракции света на объемных голограммах в анизотропных кристаллах, а также возможность записи в них голограмм, при считывании которых воспроизводится не только фаза и амплитуда, но и поляризация исходной предметной световой волны.
В в е д е н и е
Сегнетоэлектрики, обладающие фоторефрактивным эффектом (то есть изменяющие показатель преломления под действием светового излучения) такие, как LiNbO3 /1,2/, Sr0,75Ba0,25Nb2O6SBN /3/ и другие, широко исследуются в последнее время как один из наиболее перспективных классов материалов для голографических запоминающих устройств. Однако, несмотря на их ярко выраженные двупреломлящие и электрооптические свойства, практически во всех работах, имеющихся к настоящему времени, указанные материалы, по существу, рассматривались как оптически изотропные и к ним применялась теория
Когельника, развитая для голографических решеток показателя преломления в изотропных средах /4/. Однако в /5/ к предыдущих работах авторов /6,7/ показано, что указанные свойства фоторефрактивных сегнетоэлектриков не только необходимо учитывать при интерпретации голографических экспериментов по исследованию природы явления фоторефракции, но они предполагают также ряд принципиально новых применений указанных материалов в устройствах оптоэлектроники в оптической обработки изображений. Данная работа посвящена последовательному теоретическому анализу основных особенностей объемной голографической записи в двупреломляющих электрооптических кристаллах, основные результаты которого иллюстрируются на конкретном примере одноосного LiNbО3.
1. Дифракционная эффективность объемных фазовых голограмм в фоторефрактивных кристаллах
Запись голограмм в фоточувствительных электрооптических кристаллах типа LiNbO3 осуществляется благодаря наличию в них так называемого фоторефрактивного эффекта - т.е. локального изменения тензора диэлектрической проницаемости среды под действием светового излучения. Не останавливаясь на микроскопических причинах явления фоторефракции (см.,например /1,2/),рассмотрим наиболее существенные особенности дифракции света на объемных фазовых голограммах, записанных в указанных кристаллах.
В настоящее время при интерпретации экспериментальных результатов по голографической записи в фоторефрактивных кристаллах используются следующим выражением для дифракционной эффективности η фазовой объемной голограммы в изотропной среде:
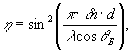 (1) (1)
где d - толщина кристалла, λ - длина волны света в вакууме, а θБ - брэгговский угол в объеме среды. Выражение ( 1) было получено для случая голографической решетки показателя преломления
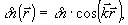 (2) (2)
где 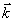 - волновой вектор, а σn - амплитуда решетки, и поэтому его применение является, вообще говоря, некорректным уже даже для оптически изотропных фоторефрактивных кристаллов кубической сингонии (например, Bi12SiO20 /8/. Последнее вызвано тем, что единственного параметра σn, характеризующего амплитуду дифракционной решетки, оказывается уже недостаточно для описания в общем случае сложной деформации, оптической индикатрисы среды под действием периодического в пространстве электрического поля - волновой вектор, а σn - амплитуда решетки, и поэтому его применение является, вообще говоря, некорректным уже даже для оптически изотропных фоторефрактивных кристаллов кубической сингонии (например, Bi12SiO20 /8/. Последнее вызвано тем, что единственного параметра σn, характеризующего амплитуду дифракционной решетки, оказывается уже недостаточно для описания в общем случае сложной деформации, оптической индикатрисы среды под действием периодического в пространстве электрического поля 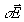 , решетки /1,2/. Обобщение соотношения (1) необходимо также и потому, что указанный случай описывает дифракционный процесс с сохранением плоскости поляризации световых волн в то время, как в фоторефрактивных кристаллах (как оптически изотропных, так и двупреломляющих) возможно наблюдение дифракции с поворотом плоскости поляризации. , решетки /1,2/. Обобщение соотношения (1) необходимо также и потому, что указанный случай описывает дифракционный процесс с сохранением плоскости поляризации световых волн в то время, как в фоторефрактивных кристаллах (как оптически изотропных, так и двупреломляющих) возможно наблюдение дифракции с поворотом плоскости поляризации.
Наиболее общим случаем пространственно-периодического возмущения оптических свойств прозрачной среды является решетка тензора диэлектрической проницаемости
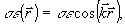 (3) (3)
здесь 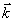 , как и в (2), - волновой вектор решетки, а σε - симметричный тензор произвольного вида. При дифракции света на периодической структуре в анизотропной среде, как и в изотропной, должны выполняться общие правила: закон сохранения энергии, выражающийся в равенстве частот считывающей и рассеянной световых волн и импульса, записываемых в векторной форме условий Брэгга /4/: , как и в (2), - волновой вектор решетки, а σε - симметричный тензор произвольного вида. При дифракции света на периодической структуре в анизотропной среде, как и в изотропной, должны выполняться общие правила: закон сохранения энергии, выражающийся в равенстве частот считывающей и рассеянной световых волн и импульса, записываемых в векторной форме условий Брэгга /4/:
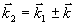 , (4) , (4)
здесь 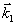 и и 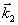 - волновые векторы считывающей и восстановленной плоских световых волн в кристалле. Поскольку брегговские условия дифракции заранее не накладывают каких-либо ограничений на поляризацию световых волн - волновые векторы считывающей и восстановленной плоских световых волн в кристалле. Поскольку брегговские условия дифракции заранее не накладывают каких-либо ограничений на поляризацию световых волн 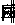 и и 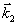 , дифракция на решетке , дифракция на решетке 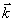 может происходить между любой парой световых волн, соответствующих двум произвольным точкам двухоболочечной поверхности показателя преломления анизотропной среды /9/ (рис.1а). При этом амплитуда рассеянной волны будет зависеть не только от взаимной ориентации векторов может происходить между любой парой световых волн, соответствующих двум произвольным точкам двухоболочечной поверхности показателя преломления анизотропной среды /9/ (рис.1а). При этом амплитуда рассеянной волны будет зависеть не только от взаимной ориентации векторов
электрического поля в соответствующих световых волнах, во также и от конкретного вида дифракционной решетки σε (3).
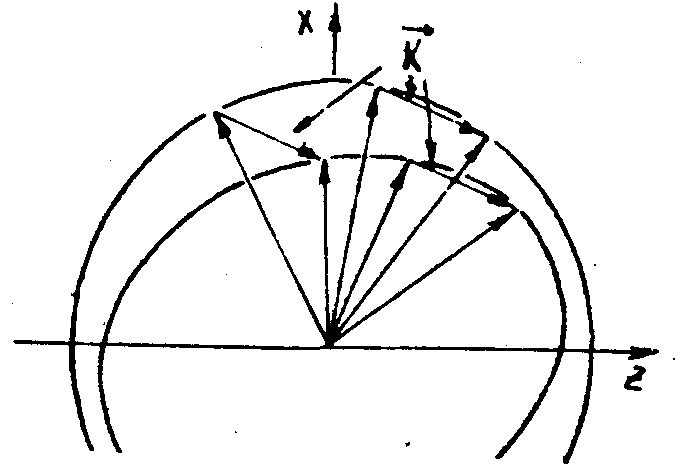
а)
б)
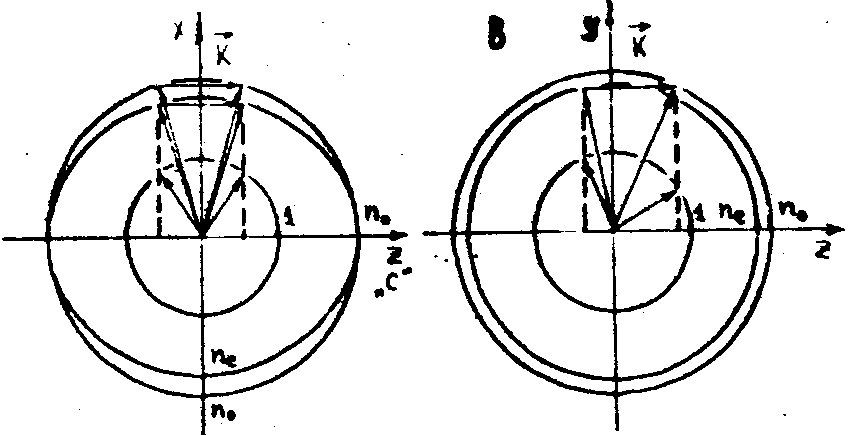
Рис.1. а) Различные случаи выполнения брэгговских условия для дифракции света на решетке с волновым вектором 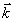 в анизотропном кристалле; в анизотропном кристалле;
б) традиционная симметричная схема записи-считывания объемных голограмм в LiNbO3 (ось "С" параллельна линии пересечения плоскости падения и границы раздела кристалл-воздух);
в) схема голографического эксперимента для наблюдения в LiNbO3 дифракции с поворотом плоскости поляризации на 90°.
Вычисление дифракционной эффективности голограммы в рассматриваемом случае можно произвести методом связанных волн, использованным в /4/ для получения соотношения (1) для изотропной среды. Следует иметь в виду, что в анизотропном кристалле с тензором диэлектрической проницаемости ε при заданном значении частоты света ω поляризация световой волны (за исключением точек пересечения оболочек поверхности показателя преломления) однозначно определяется ее волновым вектором. Поэтому световые волны, связанные брэгговским соотношением (4), могут быть записаны в виде:
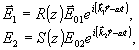 (5) (5)
здесь R(z) и S(z) - медленно меняющиеся вдоль оси Z амплитуда связанных волн, а 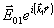 и и 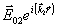 - точные решения волнового уравнения - точные решения волнового уравнения
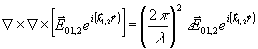 (6) (6)
в анизотропной среде без дифракционной решетки, нормированные так, что 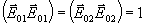 . Предполагая общее решение уравнения для среды с дифракционной решеткой . Предполагая общее решение уравнения для среды с дифракционной решеткой
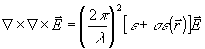 (7) (7)
в виде 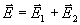 и пренебрегая вторыми производными и пренебрегая вторыми производными 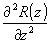 , а также небольшой непоперечностью световых волн , а также небольшой непоперечностью световых волн 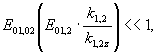 следующую систему уравнений для связанных волн: следующую систему уравнений для связанных волн:
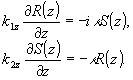 (8) (8)
Здесь k1z, k2z, - z-компоненты волновых векторов, а константа взаимодействия κ в силу симметричности тензора σε
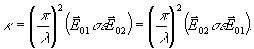 . (9) . (9)
Система уравнений (8) с точностью до константа κ совпадает с соответствующей системой уравнений для изотропной среды /4/, поэтому не проводя повторных математических выкладок, сразу можно записать общее выражение для дифракционной эффективности голографической решетки в анизотропном кристалле, толщиной d:
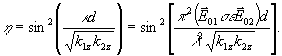 (10) (10)
В случае дифракционной решетки показателя преломления (2) в изотропной среде
σε=2nσnσ ij, (11)
где σij - символ Кронекера,
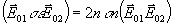 (12) (12)
и соотношение (10) сводится к хорошо известным формулам Когельника /4/, в частности, к ( 1), когда 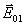 и и 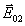 перпендикулярны плоскости падения (случай Н-поляризации). перпендикулярны плоскости падения (случай Н-поляризации).
В качестве примера рассмотрим два частных случая дифракции света на объемных фазовых решетках, записанных в типичном фоторефрактивном сегнетоэлектрике LiNbО3 при двух различных ориентациях кристалла. Поскольку в указанных кристаллах образование фазовой дифракционной решетки (3) происходит под действием пространственно-периодического электрического поля 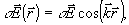 /1,2/ /1,2/
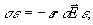 (13) (13)
здесь r - тензор электрооптических коэффициентов третьего ранга (см.,например /10/).
1 . При традиционной симметричной схеме голографического эксперимента (рис.10), когда оптическая ось "С" кристалла LiNbO3 лежит в плоскости падания записывающих лучей, электрическое поле дифракционной решетки направлено вдоль оси "С" и тензор
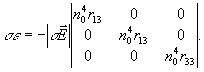 (14) (14)
Поскольку при рассматриваемой геометрии "необыкновенные" световые волны поляризованы в плоскости zx, а "обыкновенные" вдоль оси у, из (10) и (14) следует, что наблюдение дифракции с поворотом плоскости поляризации невозможно. В этом случае наблюдается характерная для решеток показателя преломления дифракция с сохранением плоскости поляризации, с тем отличием, что для световых волн, поляризованных "необыкновенным" образом, эффективная глубина модуляции фазовой дифракционной решетки оказывается в 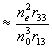 */ (величина ≈9 в LiNbO3 /10/) paз больше, чем для "обыкновенных" световых волн. */ (величина ≈9 в LiNbO3 /10/) paз больше, чем для "обыкновенных" световых волн.
2. Если оптическая ось кристалла " C" перпендикулярна плоскости падения световых пучков (рис.1в), тензор σε в пренебрежении малым электрооптическим коэффициентом r22<<r31≈r33 /10/ приобретает /10/ вид:
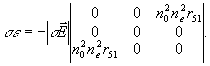 (15) (15)
Так как при рассматриваемой геометрии "необыкновенные" световые пучки поляризованы перпендикулярно, а "обыкновенные " - в плоскости падения, будет наблюдаться дифракция, сопровождающаяся поворотом плоскости поляризации света на 90°.
При произвольной ориентации оптической оси кристалла "С" относительно плоскости падения световых лучей возможны, очевидно, любые промежуточные значения угла поворота плоскости поляризация от 0 до 90°.
2. Особенности выполнения условий Брэгга в
одноосных кристаллах
Рассмотрим некоторые частные случаи выполнения брэгговских условий в одноосных кристаллах, когда а) либо считывание осуществляется светом, поляризованным ортогонально по отношения к исходным, записывающим голограмму световым пучкам, б) либо наблюдается дифракция с поворотом плоскости поляризации.
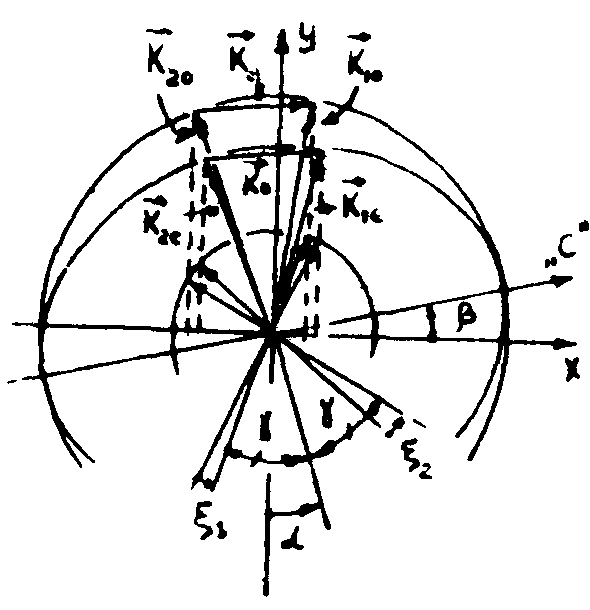
1 . Изображенная на рис.1б геометрия голографического эксперимента, когда и оптическая ось "С" кристалла и нормаль к его поверхности лежат в плоскости падения световых пучков, наиболее широко используется при записи голограмм в LiNbO3 и Sr0.75Ba0.25Nb2O6/1-3/. В предыдущем параграфе было показано, что в LiNbO3 при выбранной схеме дифракция света может происходить только без поворота плоскости поляризации, а именно: из "обыкновенного" в "обыкновенный" световой пучок или из "необыкновенного" в "необыкновенный". В силу ортогональности указанных типов световых волн запись голограмма в этом случае также может производиться только парой "обыкновенных" либо парой "необыкновенных" пучков света. При полностью симметричной системе записи (углы падения записывающих пучков одинаковы и ось "С" параллельна поверхности образца) голографические решетки  и и 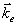 , формируемые парами световых пучков, поляризованных "обыкновенным" и "необыкновенным" образом, совпадают как по периоду, так и по ориентации (рис.16). Поэтому условия Брэгга (4) для дифракции "необыкновенного" пучка света на решетке, записанной "обыкновенными" световыми пучками (и наоборот), выполняются при той жe ориентации образца, при которой происходила запись. , формируемые парами световых пучков, поляризованных "обыкновенным" и "необыкновенным" образом, совпадают как по периоду, так и по ориентации (рис.16). Поэтому условия Брэгга (4) для дифракции "необыкновенного" пучка света на решетке, записанной "обыкновенными" световыми пучками (и наоборот), выполняются при той жe ориентации образца, при которой происходила запись.
Однако, в общем случае, когда либо углы падения записывавших пучков не равны, либо ось "С" непараллельна поверхности кристалла, голографические решетки, записываемые в "обыкновенно" и "необыкновенно" поляризованном свете уже не совпадают друг с другом ни по
шагу, ни по ориентации в пространстве (рис.2а). При этом, очевидно, уже нельзя одновременно выполнить брэгговские условия дифракции ортогонально поляризованных световых пучков на одной и той же голограмме. Поэтому для наблюдения, например, максимума дифракции "необыкновенного" светового пучка на голограмме 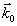 , записанной ранее в "обыкновенной" свете , записанной ранее в "обыкновенной" свете 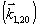 , кристалл необходимо повернуть на некоторый угол ξ (или, что то же самое, изменить на ту же величину угол падения считывающего пучка) (рис.2а). , кристалл необходимо повернуть на некоторый угол ξ (или, что то же самое, изменить на ту же величину угол падения считывающего пучка) (рис.2а).
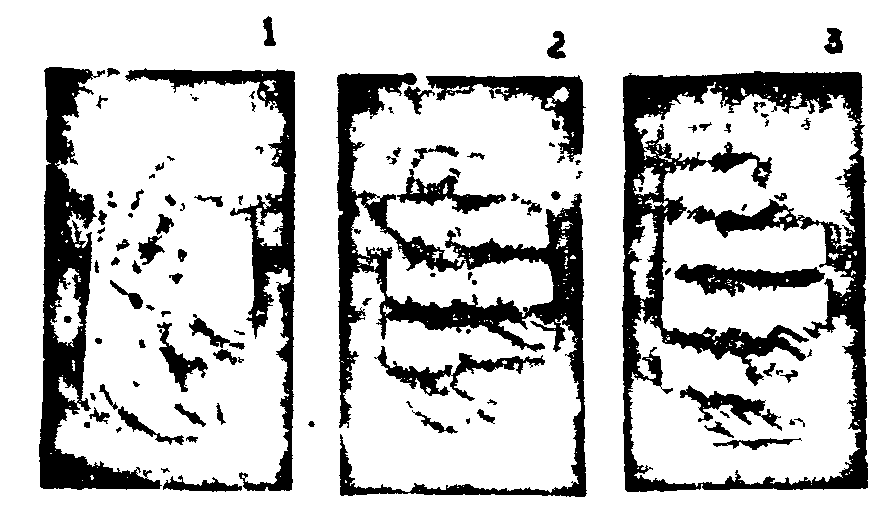
Благодаря чрезвычайно высокой угловой селективности объемных голограмм условия записи могут быть выбраны таким образом, что при неизменной ориентации образца "необыкновенная" компонента опорного светового луча при считывании изображения будет дифрагировать на голограмме, записанной одноименными компонентами опорного и предметного световых пучков и только на ней, а "обыкновенная" компонента, соответственно, только на "обыкновенной" голограмме. Указанное свойство было впервые предложено авторами в /6/ для голографической записи поляризационных характеристик изображения, что впоследствии и было экспериментально продемонстрировано на примере одноосного LiNbO3. На рис.2б представлены фотографии восстановленного изображения кварцевого клина, снятого через поляризатор, иллюстрирующие восстановление сложного распределения поляризации по сечении предметного пучка.
2. Значительно меньше исследованы и к настоящему времени практически не используются ни в практических применениях, ни в физических исследованиях процессы дифракции на объемных голограммах, при которых световые волны, связанные брэгговскими условиями, принанадлежат разным оболочкам поверхности показателя преломления кристалла, хотя явления подобного рода уже достаточно давно исследуются в рассеянии света на бегущих объемных решетках - гиперзвуковых волнах /11/. Ниже мы рассмотрим некоторые частные случаи такого типа дифракции в одноосных кристаллах, представляющие интерес с голографической точки зрения.
Как было показано в предыдущем параграфе при геометрии эксперимента, представленной на рис.1в, когда ось "С" перпендикулярна плоскости падения световых лучей, данный тип дифракции, сопровождающийся поворотом плоскости поляризации световой волны на 90°,
а)
б)
Рис.2. а) Общий случай несовпадения брэгговских углов падения при воспроизведении голографической решетки 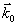 , записанной в "обыкновенном" свете ( , записанной в "обыкновенном" свете (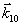 и и 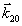 ), при ее воспроизведении световыми пучками "необыкновенной" поляризации; ), при ее воспроизведении световыми пучками "необыкновенной" поляризации;
б) фотографии восстановленного изображения кварцевого клина, снятые: 1 - без поляризатора; 2 и 3 - через поляризатор при двух взаимноперпендикулярных ориентациях последнего.
достаточно эффективен в LiNbО3. Поскольку распространение подобной пары ортогонально поляризованных световых волн в кристалле, очевидно, не может привести к записи голограммы, наибольший интерес представляет анализ условий, при которых дифракция с поворотом плоскости поляризации происходит на голограмме, записанной в кристалле двумя одинаково поляризованными ("обыкновенными" или "необыкновенными") световыми пучками.
Простое рассмотрение, проведенное для геометрии, изображенной на рис. 3а в приближении 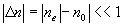 , приводит к результату: , приводит к результату:
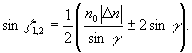 (16) (16)
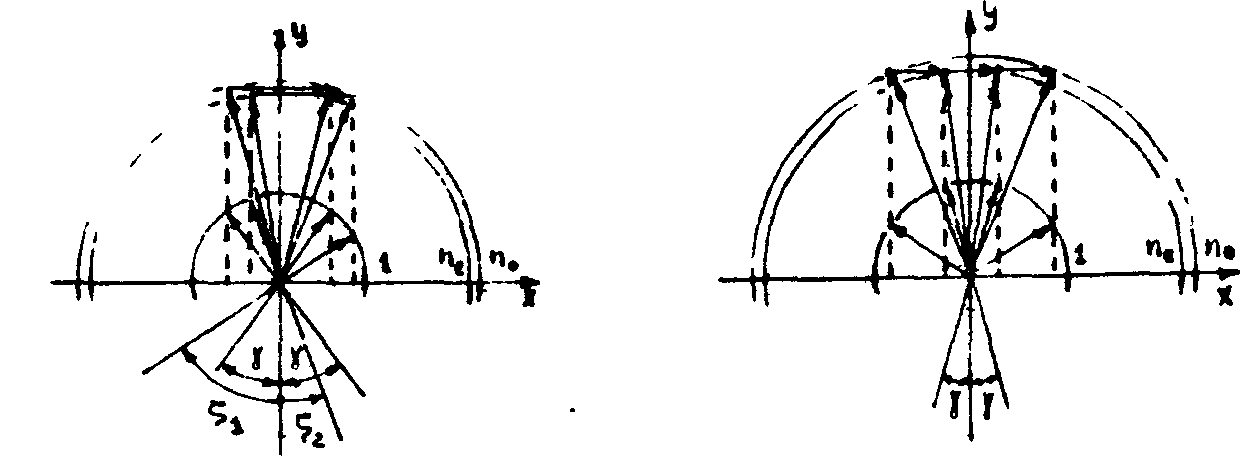
а) б)
Рис.3. Брэгговская дифракция света с поворотом плоскости поляризации в одноосном кристалле:
а) общий случай (16);
б) частный случай одновременного выполнения брэгговских условий для рассеяния обоих, записывающих дифракционную решетку, "необыкновенных" световых пучков в первый и минус первый порядки дифракции (17).
В качестве другого интересного примера можно рассмотреть случай, когда брэгговские условия для дифракции с поворотом плоскости поляризации выполняются одновременно для двух "необыкновенных" световых пучков, записывающих исходную дифракционную решетку (рас.3б).
В этом случае уже в процессе записи голограммы без дополнительного поворота кристалла должна наблюдаться дифракция обоих пучков, внешне проявляющаяся в виде дифракционных максимумов первого порядка, но противоположного по отношению к обычной брэгговской дифракции знака. Единственным условием, которое необходимо выполнять для наблюдения такого эффекта, является:
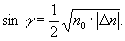 (17) (17)
3. Следует отметить, что при попытке прямого использования дифракции с поворотом плоскости поляризации для воспроизведения изображения, записанного в анизотропном кристалле световыми пучками, поляризованными одинаковым образом, возникают те же трудности, что и при воспроизведении сложного изображения, запись которого была произведена в изотропном кристалле на другой длине волны. Из-за невозможности одновременного выполнения брэгговских условий для широкого спектра пространственных гармоник голограммы сложного объекта эффективно воспроизводится только некоторая часть записанного изображения. Однако в анизотропных кристаллах при использовании для считывания изображения дифракции света, сопровождающейся поворотом плоскости поляризации с одновременным изменением длину волны источника считывающего светового сучка, в большей степени удается скомпенсировать указанное рассогласование брэгговских условий. Последнее открывает новые возможности по использованию рассмотренного типа дифракции для неразрушающего считывания информации, записанной в двупреломляющих фоторефрактивных сегнетоэлектриках типа LiNbO3.
Л и т е р а т у р а
1. Von der LindeDD., Glass A.M., Appl.Phys., 8, 85, 1975.
2. Amodei J.J., Staebler D.L. RCA Rev., 33, 71, 1972.
3. Thaxter J.B., Kestigian M., Appl.Opt., 13, 913, 1974.
4. Kogelnik H., Bell Syet.Tech.J., 48, 2909, 1969.
5. В.Б.Волошинов, В.Н.Парыгин, Л.Е.Чирков. II Всесоюзная конференция по голографии, тезисы, ч.1, Киев, стр.93, I975.
6. Степанов С.И., А.А.Камшилин, М.П.Петров. ФТТ, 19, 810, 1977.
7. С.И.Степанов, А.А.Камшилин, М.П.Петров. Письма в ЖГФ, 3, 70, 1977.
8. Huignard J.P., Micheron F. Appl.Phys.Lett., 29, 591, 1976.
9. Ю.И.Сиротин, М.П.Шаскольская. Основы кристаллофизики, М., "Наука", 1975.
10. Ю.С.Кузьминов. Ниобат и танталат лития, М., "Наука", 1975.
11. Дж.Такер, В.Рэмптон. Гиперзвук в физике твердого тела, М., "Мир", 1975.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

