|
|
 |
 |

|
| |
ПРОБЛЕМА РЕКОНСТРУКЦИИ ПАРАМЕТРОВ ТРЕХМЕРНЫХ ОБЪЕКТОВ ПО РАДИОГОЛОГРАФИЧЕСКИМ ИЗМЕРЕНИЯМ
И.С.Зиновьев
Методом физической оптики исследуется проблема реконструкции параметров гладких трехмерных идеально проводящих объектов по измерениям поля в радиодиапазоне. Показана ее связь с классической задачей электродинамики - обратной задачей дифракции. Приводится трехмерное интегральное тождество, позволяющее решить задачу для однородной и изотропной среды и квазиоптической области рассеяния. Рассмотрен общий метод решения (метод Боярского-Левиса). Проанализирован частный случай усечения информационного 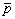 -пространства по направлению и частоте, соответствующий радиоголографическим измерениям. Поставлен вопрос о корректности обратной задачи рассеяния. Намечены основные направления дальнейшего развития теории. -пространства по направлению и частоте, соответствующий радиоголографическим измерениям. Поставлен вопрос о корректности обратной задачи рассеяния. Намечены основные направления дальнейшего развития теории.
В в е д е н и е
Последние годы, наряду с оптической голографией, широкое развитие получили методы радиоголографии. Впервые на необходимость использования строгой дифракционной теории для описания процесса формирования изображения в радиодиапазоне методом радиоголографии было обращено внимание в /1/. Там жe было показано, что задача реконструкции неизвестных параметров рассеивателя (внутренняя задача голографии) эквивалентна классической проблеме электромагнитной теории поля - обратной задаче дифракции. Для двумерных слабо рассеивающих объектов эта задача решалась в /2,3/, а для трехмерных - в работах /4,5/. Однако до настоящего времени отсутствует строгое электродинамическое обоснование проблемы реконструкции параметров гладких трехмерных, идеально проводящих объектов с помощью
метода радиоголографии. Подобное обоснование должно базироваться на строгом решении обратной задачи дифракции для объектов указанного класса. Обратная задача впервые била решена в аналитической форме методом физической оптики Боярским и Левисом /6/. Дальнейшее развитие метод Боярского-Левиса получил в /7-9/. В настоящей работе на основе частного решения задачи обратного рассеяния развит подход, позволяющий обосновать процесс восстановления геометрических параметров объекта с бесконечной проводимостью по радиоголографическим измерениям в дальней зоне.
Подход справедлив для гладких трехмерных объектов, не имеющих центров рассеяния ("блестящих" точек). Радиоголографические методы, позволяющие восстанавливать одномерное радиоизображение трехмерных объектов, обладающих центрами рассеяния были рассмотрены ранее в /10,11/.
1. Основное равенство обратного рассеяния в приближении
физической оптики
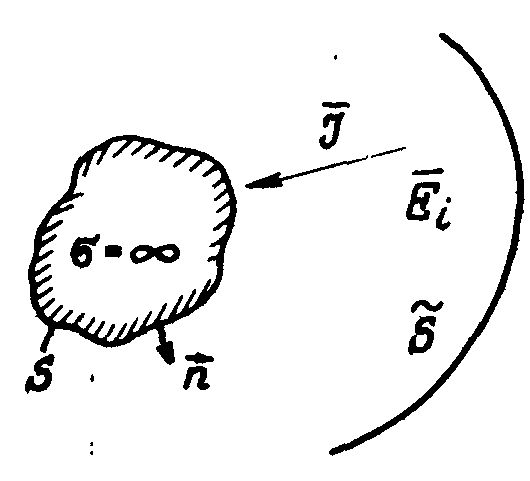
Пусть на идеально проводящем трехмерном выпуклом объекте, ограниченном гладкой поверхностью S, происходит рассеяние плоской электромагнитной волны, пришедшей с направления, заданного единичным вектором 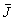 (рис.1). Предположим также, что в дальней зоне на поверхности (рис.1). Предположим также, что в дальней зоне на поверхности 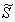 происходит регистрация рассеянного поля. Тогда задача обратной дифракции формулируется как задача определения размеров и формы тела при условии, если известно падающее и рассеянное поле, а также существует электродинамическая модель взаимодействия падающего поля с телом. происходит регистрация рассеянного поля. Тогда задача обратной дифракции формулируется как задача определения размеров и формы тела при условии, если известно падающее и рассеянное поле, а также существует электродинамическая модель взаимодействия падающего поля с телом.
К обоснованию этой модели мы и перейдем. Рассеяние будем рассматривать в приближении физической оптики. Падающую плоскую волну зададим в виде
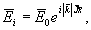 (1) (1)
где 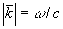 - модуль вектора - модуль вектора 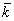 ; k - волновое число; ; k - волновое число; 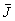 - единичный вектор в направлении падения волны; - единичный вектор в направлении падения волны; 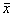 - радиус-вектор координатной системы, связанной с объектом. - радиус-вектор координатной системы, связанной с объектом.
|
|
Рис.1.
Дифракция плоской волны на трехмерном объекте. |
Отраженное от объекта поле в дальней зоне имеет вид:
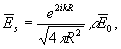 (2) (2)
где R - расстояние от объекта до точки наблюдения. Величина ρ определяется выражением
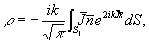 (3) (3)
где 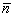 - единичный вектор, нормальный к поверхности объекта и направленный наружу; S1 - освещенная часть поверхности объекта. Из уравнений (2) и (3) видно, что - единичный вектор, нормальный к поверхности объекта и направленный наружу; S1 - освещенная часть поверхности объекта. Из уравнений (2) и (3) видно, что
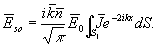 (4) (4)
Таким образом,
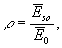 (5) (5)
где 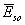 - поле в дальней зоне, нормированное на расстояние. - поле в дальней зоне, нормированное на расстояние.
Введем теперь, согласно /6/ трехмерное пространство векторов 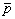 . Подобное . Подобное  - пространство будем называть информационным - пространство будем называть информационным 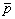 -пространством. В этом пространстве направление векторов совпадает c направлением от объекта к точке наблюдения, а модуль -пространством. В этом пространстве направление векторов совпадает c направлением от объекта к точке наблюдения, а модуль
равен
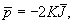 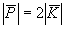 , ,  . (6) . (6)
Уравнение (3) тогда можно переписать в виде
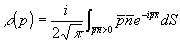 (7) (7)
Из равенства (7) следует, что
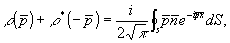 (8) (8)
где S - полная замкнутая поверхность рассеивателя.
Преобразуем поверхностный интеграл в уравнении (8) в интеграл по объему V, занимаемому объектом. С этой целью используем теорему Гаусса. В результате находим:
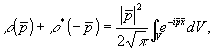 (9) (9)
Для связи измеряемой функции 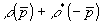 c геометрическими характеристиками объекта в работе /6/ вводится характеристическая функция объема V, занимаемого объектом, c геометрическими характеристиками объекта в работе /6/ вводится характеристическая функция объема V, занимаемого объектом,
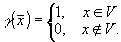 (10) (10)
Тогда
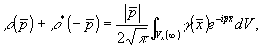 (11) (11)
где Vx(∞) означает, что интегрирование ведется по всему 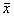 - пространству. - пространству.
Вводя функцию
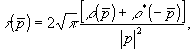 (12) (12)
получим равенство Боярского, впервые опубликованное в работе /6/:
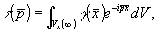 (13) (13)
или в трехмерных декартовых координатах -
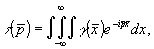 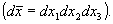 (14) (14)
Из равенств (13) и (14) видно, что их правая часть представляет собой трехмерное Фурье-преобразование характеристической функции 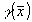 . Так как функция . Так как функция 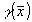 абсолютно интегрируема, то трехмерное обратное преобразование Фурье существует и является единственным; абсолютно интегрируема, то трехмерное обратное преобразование Фурье существует и является единственным;
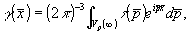  , (15) , (15)
где Vp(∞) означает, что интегрирование ведется по всему 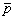 - пространству. - пространству.
Следует отметить, что пара преобразований Фурье (14) и (15) справедлива только при выполнении условия ka>>1, где а -характерный размер рассеивателя. Таким образом, равенство (15) устанавливает, что характеристическая функция области V занятой объектом (в трехмерном 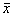 -пространстве) относится к величине -пространстве) относится к величине 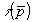 в трехмерном в трехмерном 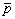 -пространстве с помощью трехмерного преобразования Фурье. -пространстве с помощью трехмерного преобразования Фурье.
Выражение (15), связывающее величину 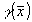 с функцией с функцией 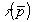 , доступной для измерений, представляет собой электродинамическую модель взаимодействия падающего поля с объектом, которая позволяет решить обратную задачу дифракции. Из (15) следует, что для нахождения функции , доступной для измерений, представляет собой электродинамическую модель взаимодействия падающего поля с объектом, которая позволяет решить обратную задачу дифракции. Из (15) следует, что для нахождения функции 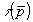 необходимо измерить значение необходимо измерить значение 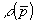 , т.е. в конечном итоге спектр поля в дальней зоне рассеяния, для всех частот и всех направлений относительно объекта. На практике такие измерения осуществить невозможно. Рассмотрим, какую инфор- , т.е. в конечном итоге спектр поля в дальней зоне рассеяния, для всех частот и всех направлений относительно объекта. На практике такие измерения осуществить невозможно. Рассмотрим, какую инфор-
мацию об объекте можно получить, если использовать для регистрации спектра поля метод радиоголографии. Как известно, этот метод позволяет зафиксировать поле в ограниченном секторе углов наблюдения на одной частоте, либо спектр поля в узкой полосе частот, которая определяется требуемым интервалом когерентности измерительной системы. Следовательно, решение проблемы обратного рассеяния сводится в этом случае к решению усеченной задачи обратного рассеяния в 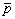 -пространстве, ограниченном по частоте и направлению. Вначале рассмотрим кратко общий метод усечения, предложенный Левисом /6/. -пространстве, ограниченном по частоте и направлению. Вначале рассмотрим кратко общий метод усечения, предложенный Левисом /6/.
2. Общий метод решения (метод Боярского-Левиса)
Метод основан на том, что необходимая часть 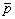 -пространства (область D), в которой возможно проведение измерений -пространства (область D), в которой возможно проведение измерений 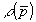 а следовательно, и а следовательно, и 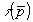 выделяется путем введения характеристической функции области D выделяется путем введения характеристической функции области D
 (16) (16)
Далее вводится пара преобразований Фурье
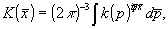 (17) (17)
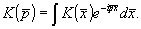 (18) (18)
Теперь целесообразно говорить уже об измерении величины 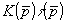 , которую можно найти за счет правильного выбора области D. Таким образом, можно построить функцию , которую можно найти за счет правильного выбора области D. Таким образом, можно построить функцию
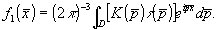 (19) (19)
С другой стороны, поскольку спектральная плотность свертки двух функций равна произведению их спектральных плотностей и так как
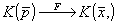 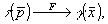
то
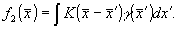 (20) (20)
Функция f1(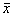 ) строится по измерениям ) строится по измерениям 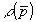 (см.далее). (см.далее).
Интегральное уравнение (20) позволяет выделить информацию о геометрических характеристиках цели. Приравнивая 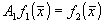 , где A1=const, можно построить уравнение, которое дает решение задачи. Наиболее трудным моментом является выбор такой функции , где A1=const, можно построить уравнение, которое дает решение задачи. Наиболее трудным моментом является выбор такой функции 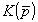 , которая выделяла бы максимум информации об объекте, исходя из величины , которая выделяла бы максимум информации об объекте, исходя из величины  . .
В качестве примера рассмотрим случай усечения 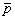 - пространства по углу наблюдения и частоте для гладких объектов в виде поверхностей вращения. - пространства по углу наблюдения и частоте для гладких объектов в виде поверхностей вращения.
3. Решение для случая усечения 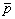 - пространства по углу наблюдения и частоте - пространства по углу наблюдения и частоте
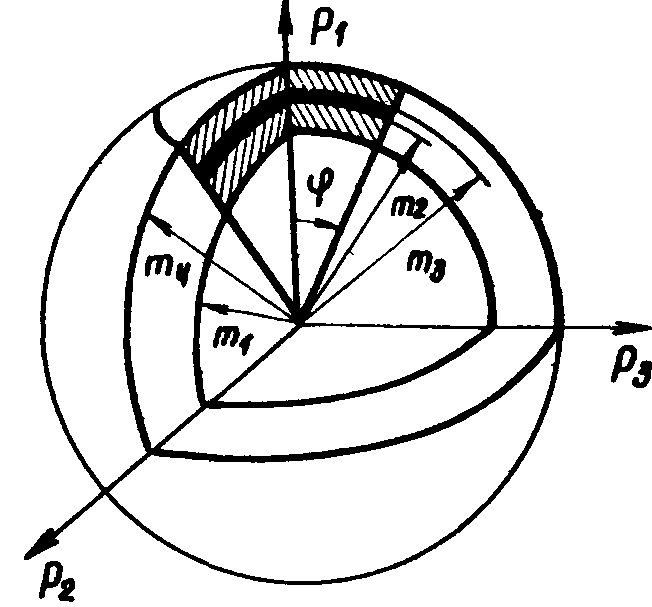
На практике измерение поля (или его спектра) в дальней зоне проводится для ограниченного подмножества данных. Рассмотрим четыре сферы с центрами, совпадающими с началом координат в 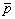 -пространстве (рис.2). Обычно верхняя частота (m4=2ω4 -пространстве (рис.2). Обычно верхняя частота (m4=2ω4/c ) ограничена возможностями измерительной аппаратуры, а нижняя частота (m4=2ω4/c ) выбирается из условия ka>>1. Вводя усечение по углу наблюдения φ, выберем в качестве D -области шаровой сегмент толщиной (m3-m4), вырезаемый внутренними сферами (рис.2). Область D, заданная подобным образом, соответствует случаю радиоголографических измерений.
Выберем теперь в качестве K(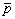 ) функцию вида ) функцию вида
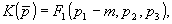 (21) (21)
где 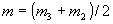 . .
|
|
Рис.2.
Схема усечения в 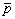 -пространстве по направлению и частоте. -пространстве по направлению и частоте.
|
Можно показать, что в этом случае
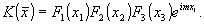 (22) (22)
При увеличении области D величины F1(x1),.......,F3(x3) стремятся к одномерным дельта-функциям. Тогда, используя выражение (20), получим
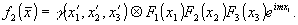 (23) (23)
Уравнение (23) содержит информацию о геометрических характеристиках объекта (вопрос об аналитическом описании поверхности объекта в данной работе не рассматривается).
Теперь необходимо определить значение функции 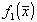 . Для решения этой задачи требуется упростить выражение (19). Провода замену переменных, можно показать, что . Для решения этой задачи требуется упростить выражение (19). Провода замену переменных, можно показать, что
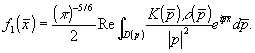 (24) (24)
Введем теперь в х -пространстве, которое связано с объектом, цилиндрическую систему координат
 , ,
а в 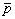 -пространстве используем сферическую систему -пространстве используем сферическую систему
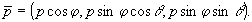
Тогда получим
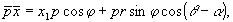 (25) (25)
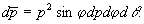 (26) (26)
Подставляя (25) и (26) в (24), найдем
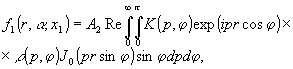 (27) (27)
где А 2=Const.
Учитывая теперь, что по параметрам р и φ проведено усечение, будем иметь
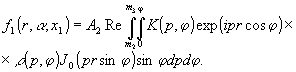 (28) (28)
Используя тот факт, что 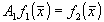 , получаем решение задачи, т.е. находим связь между геометрическими параметрами объекта и измеряемой функцией , получаем решение задачи, т.е. находим связь между геометрическими параметрами объекта и измеряемой функцией 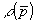 . Следует отметить, что для простых случаев усечения /6/ (например, для . Следует отметить, что для простых случаев усечения /6/ (например, для 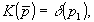 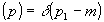 решение можно довести до конца в аналитическом виде. Изучение этих решений показывает, что усечение информационного решение можно довести до конца в аналитическом виде. Изучение этих решений показывает, что усечение информационного  -пространства приводит к частичному (неполному) описанию параметров объекта. При -пространства приводит к частичному (неполному) описанию параметров объекта. При
этом оказывается, что измерения в частотной области дают больше информации о параметрах, чем измерения поля при фиксированной частоте под разными углами наблюдения, т.е. радиоголографическим методом. Таким образом, одночастотный радиоголографический метод не является оптимальным для получения максимальной информации о геометрических характеристиках гладких трехмерных идеально проводящих объектов.
В некоторых работах /7,8,9/ было отмечено, что метод Боярского-Левиса обладает неустойчивостью. Это обусловлено тем, что задача обратной дифракции относится к классу некорректно поставленных задач. Действительно, как было показано, нахождение функции 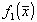 связано с решением интегрального уравнения Фредгольма I рода (20). Решения таких уравнений, как известно, неустойчивы. Причина неустойчивости в нашем случае связана с информационной недоопределенностыо некорректной задачи, вызванной усечением связано с решением интегрального уравнения Фредгольма I рода (20). Решения таких уравнений, как известно, неустойчивы. Причина неустойчивости в нашем случае связана с информационной недоопределенностыо некорректной задачи, вызванной усечением 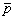 -пространства в низкочастотной области. Таким образом, оказывается /8/, что степень стабильности решения прямым образом зависит от величины m2. Чем больше низкочастотной информацией мы располагаем, тем более стабильным является метод. Следовательно, наиболее выгодным для измерений является диапазон частот, расположенный на границе с резонансной областью рассеяния. Для получения устойчивых решений необходимо использовать метод регуляризации А.Н.Тихонова. -пространства в низкочастотной области. Таким образом, оказывается /8/, что степень стабильности решения прямым образом зависит от величины m2. Чем больше низкочастотной информацией мы располагаем, тем более стабильным является метод. Следовательно, наиболее выгодным для измерений является диапазон частот, расположенный на границе с резонансной областью рассеяния. Для получения устойчивых решений необходимо использовать метод регуляризации А.Н.Тихонова.
З а к л ю ч е н и е
Результаты исследования показывают, что метод Боярского-Левиса может быть использован при решении внутренних задач радиоголографии для идеально проводящих объектов и сигналов с конечной шириной спектра. Дальнейшее развитие метода требует оценки его эффективности при использовании дискретных измерений (как по направлению, так и по частоте), оценки его устойчивости при воздействии шумов, а также совершенствования способов усечения 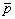 -пространства. Неустойчивость метода может быть преодолена, если доопределить задачу путем введения дополнительной априорной информации. -пространства. Неустойчивость метода может быть преодолена, если доопределить задачу путем введения дополнительной априорной информации.
Л и т е р а т у р а
1. R.Mittra and R.L.Ransom in Modern Optics, J.Fox, Ed (Polytechnic Press, Вrооkyn, 1967, J.WilleySons, Jnc.N.Y.)
2. E.Wolf, J.R.Shewell. J.Opt. Soc. Am., 58, 12, 1596, 1968.
3. E.Lalor, J.Math. Phys., 9, 2001, 1968.
4. Д.И.Мировицкий. В сб."Проблемы голографии", вып.2, стр.242-248, 1973.
5. Э.И.Крупицкий. Материалы IX Всесоюзной школы по голографии, Л., стр.21-31, 1977.
6. R.M.Lewis. JEEE Trans., AP-17, p.308, May, 1969.
7. W.Tabbara. JEEE Тrans., AP-21, p.245, Mar, 1973.
8. W.L.Perry, JEEE Trans., АР-22, p826, Nov, 1976.
9. S.Rosenbaum - Raz. J ЕЕЕ Trans., AP-24, P66, Jan, 1976.
10. С.А.Попов, Б.А.Розанов, Ю.С.Зиновьев, А.Я.Пасмуров. Материалы VIII Воесоюзной школы по голографии. Л., стр.275-297, 1976.
11. Ю.С.Зиновьев, А.Я.Пасмуров. Письма в ЖТФ, 3, вып.1, стр.28-32, 1977.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

