ИНФОРМАЦИОННЫЕ ХАРАКТЕРИСТИКИ ОБЪЕКТИВА
К.Г.Предко
Рассмотрены такие характеристики объектива как информационная емкость, размер информационных ячеек, число уровней освещенности в изображении. Показана связь между этими характеристиками и функцией передачи модуляции. Учет условий регистрации изображения сделан с помощью функции пороговой модуляции.
Предложен метод измерения функции передачи модуляции объектива с симметричной функцией размытия путем измерения светимости в центре изображения щели переменной ширины. В случае несимметричной функции размытия предложен метод определения функции передачи модуляции и фазы с помощью измерения пограничной кривой.
В в е д е н и е
Голография часто характеризуется как безлинзовая, так как позволяет получить изображение без линз. Тем не менее, любая голографическая экспериментальная установка имеет различные фокусирующие элементы, выполняющие, в основном, вспомогательную роль. В то же время голография сфокусированного изображения уже принципиально требует применения объектива, строящего изображение. Широко применяются объективы и в устройствах для оптической обработки информации. Во всех этих случаях важно знать количество информации, которое может быть воспроизведено в изображении. Такого рода информационная оценка интересна и при изучении различных изобразительных систем в фотографии, телевидении, киносъемке.
Ниже в обзорном плане рассмотрены некоторые информационные характеристики объективов и описаны методы их определения. Особое внимание уделено функциям передачи модуляции, которые не только
используются для определения информационных характеристик, но и представляют самостоятельный интерес для оценки качества воспроизведения изображения.
Количество информации в изображении
С точки зрения теории информации объектив можно представить как оптическую линию связи. Поток информации об объекте поступает на вход такой линии, частично теряется в ней и формируется в плоскости наблюдения. Полученное изображение описывается некоторым распределением световой энергии по координатам х , у, длине волны λ, направлению α поляризации, времени t. Диапазон изменения каждого аргумента x, у, λ, α, t можно разбить на некоторое число интервалов nx, ny, nλ, nα, nt. Tогда вышеуказанное распределение будет состоять из N=nxnynλnαnt элементарных объемов, элементарных информационных каналов с различной световой энергией. В каждом из элементарных объемов можно раздельно различить m ступеней, градаций энергии. В соответствии с этим, количество информации в изображении определяется числом различных комбинаций в N каналах m градаций энергии. При условии независимости информационных каналов и равной вероятности реализации любой градации количество информации по логарифмической шкале определится /1/ как
I=Nlog2(m+1). (1)
Единственное количество информации, так называемый бит, соответствует количеству информации, получаемой в результате воспроизведения в изображении черного или светлого равномерного поля при условии равной вероятности появления этих полей.
Соотношение (
1) определяет информационную емкость, т.е. максимальное количество информации, которое может содержаться в изображении. Ему соответствует такой объект, в котором реализованы все возможные отдельные информационные каналы и градации энергии. Естественно, что количество информации в изображении реального пред-мета зависит не только от свойств объекта, но и от изображаемого предмета. В дальнейшем будем рассматривать максимальное количество информации. Оно зависит от свойств предмета, и в силу этого более удобно для характеристики самого информационного канала. Ограничимся также случаем, когда распределение энергии в изображении зависит только от координат х и у, т.е. будем рассматривать пространственную информацию.
Размер элементарных информационных каналов
Количество N=nхny элементарных информационных каналов при формировании изображения объективом зависит от площади S изображения и размеров ΔS отдельного канала: N=S/ΔS. Величина ΔS определяется степенью размытости, которая характеризуется функцией передачи модуляции T(ν) объектива. Функция Т(ν) физически выражает зависимость контраста (модуляции) в изображении синусоидальной штриховой миры абсолютного контраста от пространственной частоты ν. Контраст при этом определяется по формуле:
T=(Em-En)/(Em+En),
где Е
m и Еn - максимальное и минимальное значение освещенности. Для безаберрационного объектива c круглым зрачком Т(ν) имеет простой вид /2/:
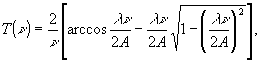 (2)
(2)
где А - числовая апертура. Значения Т для различных обобщенных пространственных частот S
=λν/2A приведены в таблице. Она позволяет найти для заданных λ и А, контраст в изображении объективом синусоидальной миры с частотой ν лин./мм.
Как следует из /2/, объектив не может сформировать изображение миры с частотой, большей S=1. Соответствующая предельная пространственная частота
νm=2A/λ определяет наименьшие размер элементарного информационного канала ΔS=1/4 νm2. Легко подсчитать, например, что на кадре размером 24´
36 мм безаберрационным объективом с относительным отверстием 1:а=1:8 при длине волны
Таблица
Функция передачи модуляции безаберрационного объектива
с круглым зрачком
|
|
|
|
|
|
|
|
|
|
0,00 |
1,0000 |
0,25 |
0,6850 |
0,50 |
0,3910 |
0,75 |
0.1443 |
|
0,05 |
0,9364 |
0,30 |
0,6238 |
0,55 |
0,3368 |
0,80 |
0,1041 |
|
0,10 |
0,8729 |
0,35 |
0,5636 |
0,60 |
0,2848 |
0.85 |
0,0681 |
|
0,15 |
0,8097 |
0,40 |
0,5046 |
0.65 |
0,2351 |
0,90 |
0,0374 |
|
0,20 |
0,7471 |
0,45 |
0,4470 |
0,70 |
0,1881 |
0,95 |
0,0133 |
632,8 нм может быть сформировано 134∙10
6 отдельных каналов размером 2,5´
2,5 мкм. Таким образом, объектив может работать в качестве элемента оптической линии связи с числом независимых каналов порядка 108. Плотность записи информации в изображении определяется величиной 4νm2 и составляет 1,6∙105 бит/мм2.
Для упрощения оценочных расчетов цифровые значения 1:а, А, ν
m и λ объединены приводимой ниже номограммой. С ее помощью, зная значения любых двух величин из трех (λ, νm,
А или 1:а), можно найти оставшуюся величину. Штриховая линия на номограмме соответствует рассмотренному числовому примеру.
Объектив воспроизводит в изображении предельные пространственные частоты только в идеальном случае, когда воспринимающее устройство может зарегистрировать предельно малые значения контраста. В реальных случаях при оценке информационных параметров объектива следует брать частоты, соответствующие заданным значениям пороговой контрастной чувствительности Тпор. Эти частоты можно найти из решения трансцендентного уравнения (2). Решая его, получим, что для Тпор=0,02 величина пороговой пространственной частоты составляет 1,872 А/λ, для 0,05-1,756 А/λ, для 0,05-1,616 А/λ
.
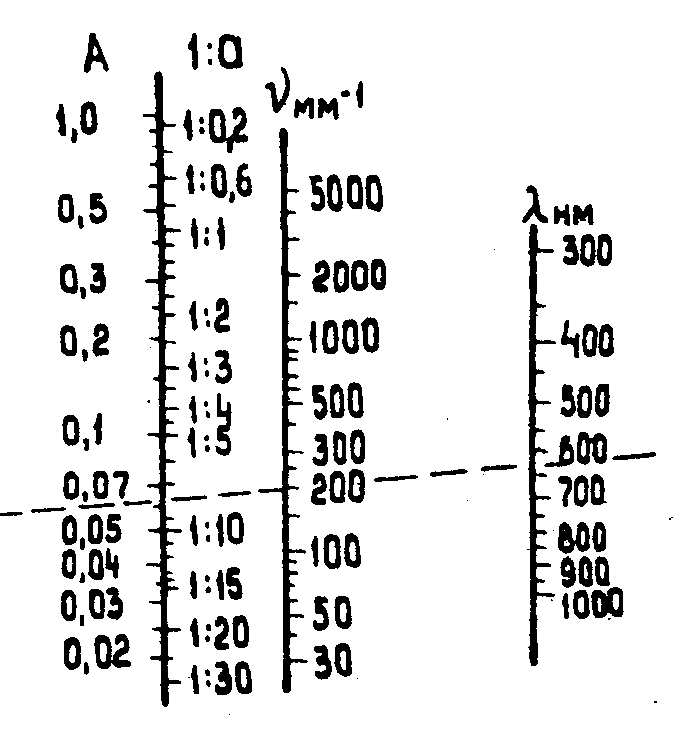
Номограмма для определения предельной пространственной частоты в изображении, создаваемом безаберрационным объективом.
Число различимых градаций в изображении
Количество информации в изображении зависит не только от размера элементарных информационных каналов и связанного о ним числа N этих каналов, но и от числа m различимых градаций освещенности. Как видно из равенства (1), m определяет количество информации log2(m+1) в изображении, отнесенное к одному информационному каналу. Характерно, что при одинаковом N количество информации с ростом m растет медленно, так как m находится под знаком логарифма.
Величина m определяется максимальным сигналом Е0 и значением минимального сигнала Е'. При равной вероятности реализации градаций их число m=Е0/Е'. Минимальный сигнал Е пропорционален среднеквадратичному отклонению колебаний освещенности Eш: Е'=kЕш. Коэффициент пропорциональности k~1÷3 õарактеризует надежность измерения, т.е. вероятность того, что измеряемая освещенность находится в заданном интервале. Таким об-
разом, величина m фактически определяется отношением сигнал/шум Ψ=Е0/Еш /1/.
Стремление повысить число информационных каналов ведет к уменьшению их геометрических размеров. При этом происходит процесс взаимного влияния соседних каналов друг на друга, что способствует уменьшению разности ΔЕ между максимальной и минимальной освещенностью. Величина ΔЕ определяет значение информативного сигнала и уменьшается с ростом пространственной частоты. Шумовой сигнал в первом приближении можно считать при этом неизменным, не зависящим от ν. Тогда
m(ν)=ΔE(ν)/kEш. Воспользовавшись данным ранее определением функции передачи модуляции, легко показать, что m(ν)=T2(ν)m0, где m0=E0/kEш - число градаций при нулевой пространственной частоте. Учитывая, что как размер элементарных информационных каналов, так и число различимых градаций связаны с пространственной частотой, можно представить и распределение предельного количества информации в изображении по пространственным частотам:
I(ν)=4ν
2S log
2[m
0T
2(ν)+1], (3)
где
S - площадь, на которой формируется изображение. На практике функция передачи модуляции и максимальное значение освещенности меняются по кадру. Для учета этой зависимости вместо формулы (3) следует использовать
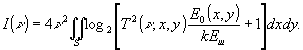 (4)
(4)
Как видно из соотношений (3) и (4), количество информации распределено по пространственным частотам неравномерно. С увеличением ν величина
I обычно быстро растет за счет увеличения числа отдельных информационных каналов. Однако при этом одновременно уменьшается число различимых градаций, снижаются значения функции передачи модуляция. Поэтому зависимость I(ν) может достигнуть максимума и затем значения I при увеличении ν будут уменьшаться. Наибольшая пространственная частота ν', на которой окан-
чивается зависимость
I(ν), определяется из равенства (3):
T2
(ν)=kEш/E0. (5)
В соответствии с этим условием на пространственной частоте
ν' будет различима одна градация освещенности. Тогда I(ν')=4ν'2S.
В качестве информационных критериев, применяемых для оценки изображения, можно использовать
/1/ плотность записи информации
I'(ν)=4ν
2 log
2[m
0T
2(ν)+1], (6)
равную числу двоичных единиц информации, которые могут бить записаны на единице площади, а также максимальную информационную емкость
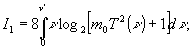 (7)
(7)
равную максимальному количеству двоичных единиц информации, которая может быть записана на единице площади во всем диапазоне пространственных частот.
Влияние условий регистрации изображения
Принципиальной особенностью процессов передачи информации является то, что информация сама по себе не представляет никакого интереса. Она имеет смысл только при наличии приемника информации, регистрирующего ее и соответствующим образом реагирующего на нее. В последнее время разработаны оптоэлектронные системы, в которых она передается, регистрируется и оценивается автоматическими устройствами. Однако даже эти системы часто предназначены для отображения информации в виде, удобном для ее восприятия человеком. Поэтому оптическое изображение, сформированное на фоточувствительном материале, проекционном или люминесцентном экране, не может считаться последней стадией процесса передачи. Оно рассматривается человеком и оценка характера и качества этой информации про-
исходит в мозгу человека. Таким образом, в подавляющем большинстве случаев для суждения о характеристиках изобразительной системы необходимо учитывать свойства зрения, имеющие сложную, до сих пор мало исследованную, психофизическую природу. Это значительно усложняет задачу объективной оценки информации, так как нахождение физически измеряемой характеристики, полностью коррелирующей с субъективной оценкой наблюдателем информации, является пока не решенной проблемой.
Критерии определения информационных характеристик изобразительной системы в большой степени зависят от точного представления о тех целях, которые поставлены перед системой. Ясно, например, что если целью является получение картины с синусоидальным распределением освещенности, то наиболее подходящим способом оценки изобразительной системы явится определение ее функции передачи модуляции. А при оценке системы, формирующей изображение объектов сложной формы, кроме функции передачи модуляции, следует знать ряд других характеристик, связанных с пространственными спектрами изображаемых объектов и условиями регистрации изображения. Многообразие изобразительных задач обуславливает существование большого числа критериев и параметров качества воспроизводящих систем /3-5/. Не останавливаясь на их рассмотрении, отметим, что все они имеют оценочный, частный характер, а обычно несопоставимы друг с другом. Наибольший интерес представляют информационные характеристики, которые могут быть едиными для всех воспроизводящих систем. Эта особенность заметна при рассмотрении сложных, многозвенных систем, включающих оптические, электронные, радиотехнические и визуальные средства передачи формирования и регистрации изображения. В этом случае функция передачи модуляции всей системы будет равна, с учетом коэффициентов увеличения, произведению таких функций для каждого звена сложной системы. Таким образом, информационные характеристики можно определять по выше приведенным соотношениям, найдя предварительно функцию передачи модуляции общей системы воспроизведения.
Несколько другой способ учета условий и свойств регистрации изображения можно осуществить на основе функций пороговой модуля-
ции /6/. Причем показана их зависимость от наименьшей пространственной частоты ν и пороговой модуляции K, которая может быть зарегистрирована в изображении. Такая функция показана кривой 2 на рисунке для случая визуальной регистрации изображения, зафиксированного на фотопленке типа Plus-X. При ν=0 значение K равно пороговой контрастной чувствительности Тпор глаза. Для некоторой пространственной частоты R минимальная различимая модуляция в изображении должна быть абсолютной, равной 100%. Естественно, что в этом случае можно говорить о реальной информации только в полосе частот от 0 до R. Следовательно, наименьший размер элементарного информационного канала будет определяться величиной 1/4R2.
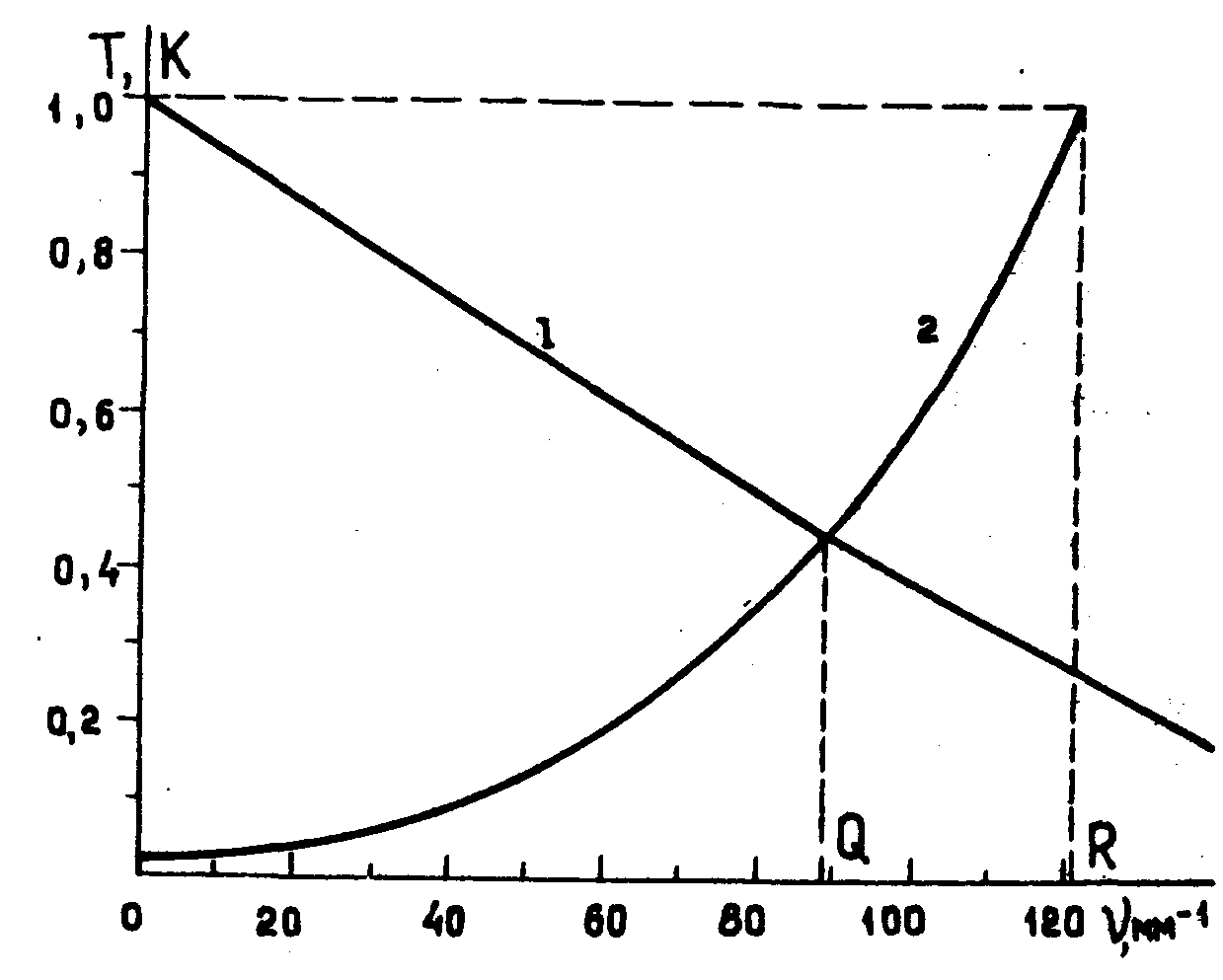
Рис. Определение пространственной разрешающей способности с учетом условий регистрации изображения.
В том случае, когда изображение формируется в плоскости регистрации с помощью, например, объектива, необходимо учитывать уменьшение контраста на разных пространственных частотах. Функция передачи модуляции, представленная на рисунке кривой 1, характеризует это уменьшение для безаберрационного объектива с относительным отверстием 1:8 при λ=632,8 нм. Видно, что уже при пространственной частоте
Q контраст формируемого изображения равен пороговому регистрируемому контрасту. Поэтому наименьший размер элементарного канала следует брать равным 1/4 Q2.
При использовании функций пороговой модуляции существенно, что они учитывают особенности регистрации и наблюдения изображения, например, эффекты проявления, зернистости регистрирующего фотоматериала, свойства зрения. Такие функции можно использовать для характеристики различных типов детекторов: фотографических материалов, микроденситометров, электрооптических приемников, глаза.
Определение функции передачи модуляции
Из предыдущего материала ясно важное значение функции передачи модуляции объектива, по которой можно определить с учетом дополнительных данных различные информационные характеристики изображения. Эти функции обычно определяются экспериментально с помощью различных методов, использующих тест-объекты с периодическим распределением светимости или такие простейшие объекты как линия, точка, граница свет-тень /7/. Вид функция передачи модуляции зависит от большого числа параметров: спектральных характеристик источника света, светофильтров и всех оптических элементов измерительной схемы, приемника излучения; расстояния от предмета до объектива; полевого и азимутального угла, относительного отверстия и других свойств объектива; положения плоскости наблюдения и т.п. Поэтому очень важно быстро и просто определить функцию передачи модуляции в реальных условиях работы объектива. Один из способов был предложен в работе /8/ в случае, когда функция размытия линии объектива симметрична. Эта ситуации реализуется для
подавляющего большинства хорошо центрированных объективов небольшой апертуры.
Указанный метод основывается на использовании в качестве тест-объекта щели переменной ширины b и измерении освещенности в центре изображения щели испытуемым объективом. Зная нормированное к 1 при b→∞ распределение освещенности С(b), легко найти
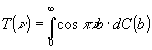 (8)
(8)
или, после интегрирования по частям,
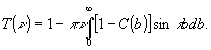 (9)
(9)
Этот метод отличается простотой тест-объекта, отсутствием каких-либо сложных узлов измерительной установки, хорошей точностью и возможной автоматизацией измерения зависимости С(
b). Методические особенности способа получения данных о С(b) и расчета функция передачи модуляции по формуле (9) приведены в работе /9/.
Функции передачи модуляции и фазы
В общем случав несимметричной функции размытия линии a(x) объектив характеризуется оптической передаточной функцией T'(ν), состоящей из функции передачи модуляции Т(ν) и функции передачи фазы φ(ν): Т'(ν)=Т(ν)eiφ(ν). причем T(ν)=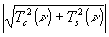 , φ(ν)=arctg
, φ(ν)=arctg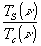 , а Тс(ν) и TS(ν) представляют нормированные косинус- и синус-преобразования Фурье функции размытия линии. Физически функция передачи фазы определяет величину смещения реального изображения синусоидального тест-объекта с пространственной частотой φ по отношению к ее идеальному изображению. Сдвиг фазы на 360° соответствует смещению изображения на расстояние I/ν Обычно используемые методы определения оптической передаточной функции описаны в работе /7/.
, а Тс(ν) и TS(ν) представляют нормированные косинус- и синус-преобразования Фурье функции размытия линии. Физически функция передачи фазы определяет величину смещения реального изображения синусоидального тест-объекта с пространственной частотой φ по отношению к ее идеальному изображению. Сдвиг фазы на 360° соответствует смещению изображения на расстояние I/ν Обычно используемые методы определения оптической передаточной функции описаны в работе /7/.
Один из методов, предложенный в работе /8/, основан на измерении нормированного распределения J(x) освещенности в изображе-
нии испытуемым объективом прямолинейной границы тень-свет. Необходимые для определения функций передачи модуляции и фазы значения Тc(ν) и TS(ν) выражаются через J(x). После интегрирования по частям равенства
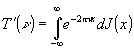 (10)
(10)
получим необходимые соотношения:
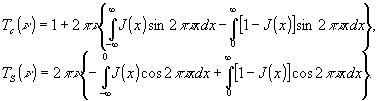 (11)
(11)
Определение оптической передаточной функции по измеренной пограничной кривой
J(х) можно производить как по формуле (10) /10/, так и по формуле (11) /8/.
Укажем на интересную особенность фазового сдвига изображения, Ф(ν), выраженного в линейной мере и связанного с угловым фазовым сдвигом φ
(ν) очевидным соотношением Ф(ν)=φ(ν)/2πν. Можно показать, что пространственный фазовый сдвиг на нулевой пространственной частоте Ф(ν=0)=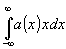 , т.е. величина этого сдвига численно равна координате центра тяжести функции размытия линии.
, т.е. величина этого сдвига численно равна координате центра тяжести функции размытия линии.
З а к л ю ч е н и е
Изложенные способы определения разнообразных информационных характеристик объектива относятся к тому случаю, когда имеет место линейность в передаче интенсивности от предмета до изображения. Практически это соответствует формированию изображения в некогерентном излучении. Применение когерентного освещения наблюдаемого предмета ведет к интерференции световых волн, идущих от разных точек объекта. В результате образуется характерная мерцающая зернистая шумоподобная структура изображения. Кроме того, получаемая картина сильно зависит от распределения амплитуды и фазы волны в плоскости предмета, его структуры. Все это затрудняет выбор удобных информационных характеристик изображения, формируемого объек-
тивом в когерентном свете /2/. Из-за нелинейности передачи интенсивности нельзя использовать функцию передачи модуляции и связанные с ней параметры качества. Тем не менее, они полезны и в этом случае как характеристики совершенства объективов, используемых в когерентно-оптических системах передачи информации.
Л и т е р а т у р а
1. С.Б.Гуревич. Эффективность и чувствительность телевизионных систем. М.-Л., Энергия, стр.344, 1964.
2. Дж.Гудмен. Введение в фурье-оптику. М., "Мир", стр.365, 1970.
3.
П.Ф.Паршин. Материалы I Всесоюзной школы по голографии. Л., стр.94, 1971.
4. П.М.Копылов, А.Н.Тачков. Телевидение и голография. М., Связь, стр.168, 1976.
5. Б.О.Карапетян, Г.Е.Смолкин. В сб. "Физическая электроника" под ред. Б.М.Степанова. М., Наука, стр.8
2, 1976.
6. Т.
J.Lauroesch, G.C.Fulmer, J.R.Edinger, G.Т.Kееnе, Т.E.Kerwick. Аррl.Opt., 9, 915, 1910.
7. О.А.Герасимова. Техника кино и телевидения, №3, 22, 1962.
8. К.Г.Предко. ДАН БССР,
13, №10, 900, 1969.
9. S.Johansson, K.Predko, Optica Acta, 23
, №7, 549, 1976.
10. J.Pospisil. Optik, 31, 613, 1970.

