К ОЦЕНКЕ ПАРАМЕТРОВ ГОЛОГРАФИЧЕСКОГО

ТОМОСИНТЕЗА

В.А.Берданосов, В.И.Горбунов, А.К.Стоянов

Рассмотрен голографический томосинтез для случая записи фурье-голограмм. Приведена оценка таких параметров томосинтеза как разрешающая способность по изображению и глубине; необходимое количество рентгенограмм, объем интеграции (глубина зоны стереовидения).

При экспериментальном осуществлении процесса голографического синтеза объемных рентгеновских изображений и томограмм по серии плоских рентгеновских ракурсов /1-2/ возникает ряд вопросов о влиянии геометрии рентгеновского просвечивания объектов и последующее записи голограмм на параметры синтезируемых изображений. Предлагаемая методика оценки дня случая кругового вращения рентгеновской трубки /1/ не дает возможность оценить разрешающую способность систем томосинтеза по глубине, кроме этого, остается неясной физическая основа получения томограмм. Для создания стереовидения следует также иметь в виду особенность формирования рентгеновских изображений: наличие зон просвечивания, для которых не всегда соблюдаются условия односторонней диспарантности /3/.

В настоящей работе предпринята попытка дать более общую методику оценки взаимосвязи параметров голографического томосинтеза. Рассмотрение ведется на основе положений, развитых в /4/, для случая прямолинейного смещения рентгеновского источника. Все расчеты даны для двумерного случая, что объясняется требованием только горизонтального параллакса для создания стереоиллюзии.

Пусть шаг смещения рентгеновского источника между последовательными экспозициями равен а; расстояние источник-рентгенограмма ровно Р<0; распределение плотности вещества исследуемого объ-

екта ρ(t,r), где z<0 - продольная координата, t - поперечная; x - координата точки на рентгенограмме. Тогда для "n"-го положения рентгеновского источника амплитудное пропускание рентгенограммы Т_n(х), согласно /4/, описывается выражением:

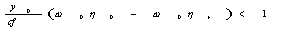(1)

где А - коэффициент пропорциональности.

Изменяя масштаб рентгенограммы в μ₀ раз, получаем для пропускания Т(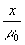). Будем использовать в томосинтезе схему линзовой фурье-голограммы (рис.1). Размеры линз считаем достаточно большими. Это предположение не оказывается на общности выводов, во проясняет физическую трактовку процесса томосинтеза. В задней фокальной плоскости распределение амплитуды света пропорционально фурье-образу пропускания рентгенограммы :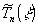

.

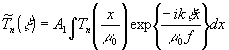В реальной схеме томосинтеза изображение "n"-ой рентгенограммы записывается на небольшой участок фотопластинки, что можно учесть введением единичной импульсной функции 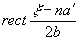, где 2b - ширина участка, а' - расстояние между центрами соседних участков. Тогда пропускание надлежащим образом обработанной фотопластинки, соответствующее "n"-ой рентгенограмме, можно записать как

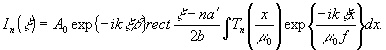(2)

При записи (2)имеется в виду компонента пропускания, соответствующая восстановлению мнимого изображения. С учетом (1) выражение (2) преобразуется к виду:

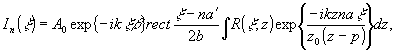  (3)

где

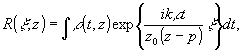(4)

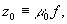
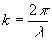
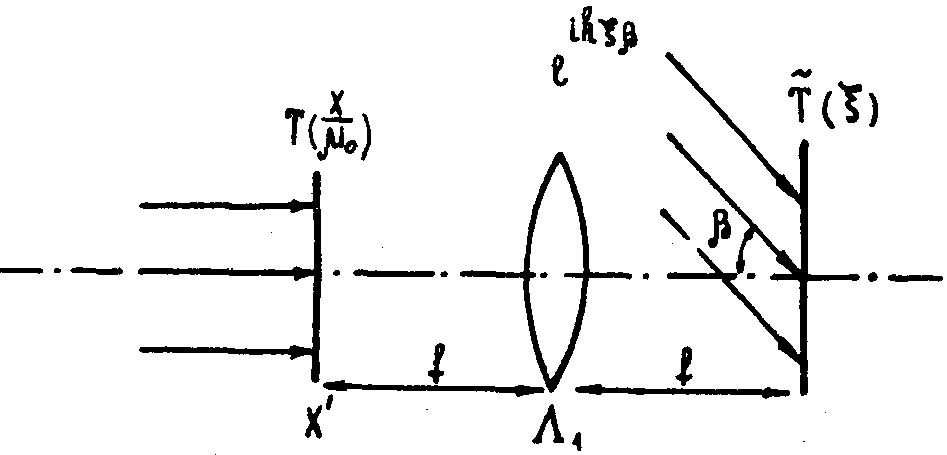
Рис.1. Схема линзовой фурье-голограммы.

Голограмма, на которой записаны все рентгенограммы, имеет пропускание 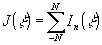, где (2n+1)-n₀, а n₀ -число рентгенограмм.

Пусть восстановление изображения ведется по схеме рис.2 и рассматривается волна в плоскости "α" на расстоянии z₂ от линзы. Амплитуда восстановленной волны Ψ(α) в данном случае равна:

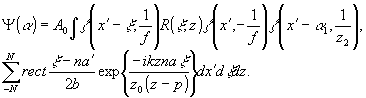(5)

Здесь ζ(х,r)=ехр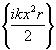 - обобщенная функция Френеля /5/. Для удобства многократные интегралы обозначаются одним знаком интеграла.

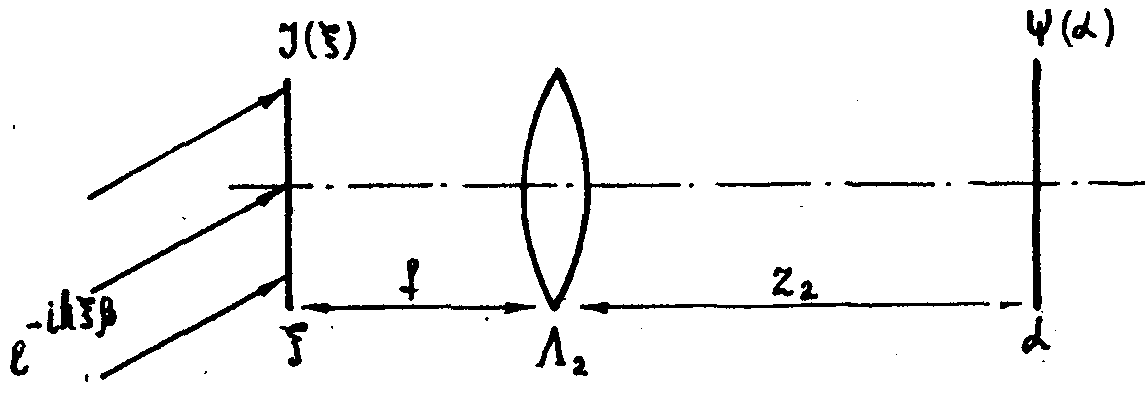
Рис.2. Схема восстановления изображения.

Рассмотрим сумму из подынтегрального выражения.

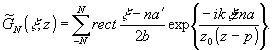(6)

Используя равенство,

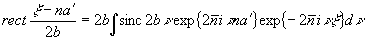(7)

и полагая а'=mа.

где m - коэффициент масштабного преобразования, для (6) получим

следующее выражение:

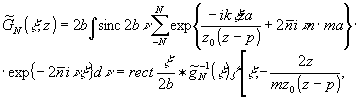(6a)

Через 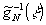обозначена функция

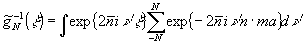, (8)

* - символ ввертки.

Если

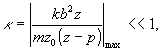(9)

то в (6а) функции Френеля можно извлечь из-под символа свертки /6/, т.е. записать равенство:

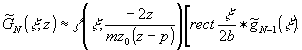(10)

Для амплитуды восстановленной волны (5) с учетом (10) получим:

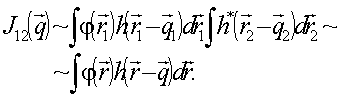(11)

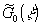означает функцию 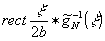. Полагая, z/p<<1, обычное для радиографии, и выбирая 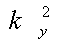, где γ - любое число, не равное нулю, (11) можно представить двумя способами:

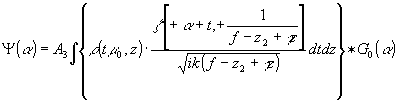(12a)

либо

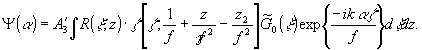(12б)

Выражение (12а) содержит сверточный член, совпадающий с параксиальным приближением для поля световой волны от распределения источников с плотностью ρ(-μ₀,z) в двумерном случае. Это означает, что наблюдатель в плоскости (α, z₂) увидит объектное рентгеновское изображение исследуемого объекта. Член g₀(α), являющийся фурье-образом функции 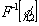, вносит дополнительное размытие и определяет разрешающую способность по синтезированному изображению. Нетрудно получить

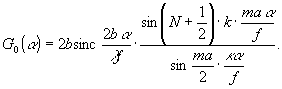(13)

Если принять разрешающую cпоcобноcть по изображению обратно пропорциональной размером пятна размытия и ограничиться главным максимумом функции 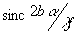, то граничная частота по изображению при соблюдении равенства 2b=-ma есть

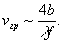(14)

Из рассмотрения (12а) ясно, что при z₂=f+γz волна 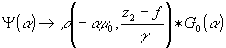, поскольку .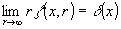

Иными словами, фотопленка, размещенная в плоскости (α,z₂), даст возможность наблюдать изображение среза объекта, т.е. томограмму. Разрешение по синтезированной томограмме дается соотношением (14).

Вернемся к неравенству (9). Оно описывает взаимосвязь геометрических параметров получения рентгенограмм и записи голограмм и определяет глубину зоны рентгеновского стереовидения (объем интеграции /1/) z_max. Из (12а) видно, что продольный масштаб синтезированного изображения равен γ. На риc.3 приведена зависимость z_max для разных μ₀m при γ=1 и κ=0,1. Очевидно, что для увеличения глубины стереовидения нужно иметь μ₀m≥1 при довольно малых b²/f². Если, например, фокусное расстояние используемых линз f = 500 мм, то лишь при ширине элемента матрицы 2b=1 мм при μ₀m=1 достигается глубина стереовидения z_max= 20 мм. Учитывая, что –2b=ma, нужно брать |m|~0,1 для большинства рентгеновских аппаратов, получаем значение μ₀~10, т.е. изображение рентгенограммы приходится уменьшать в 10 раз. Таким образом, видно, что синтез больших объемных изображений сопряжен с рядом неудобств и легче его осуществить при небольших размерах предметов. Экспериментальные результаты по томосинтезу приведены по малым объектам /1/.

Остановимся на возможности создания условий для получения

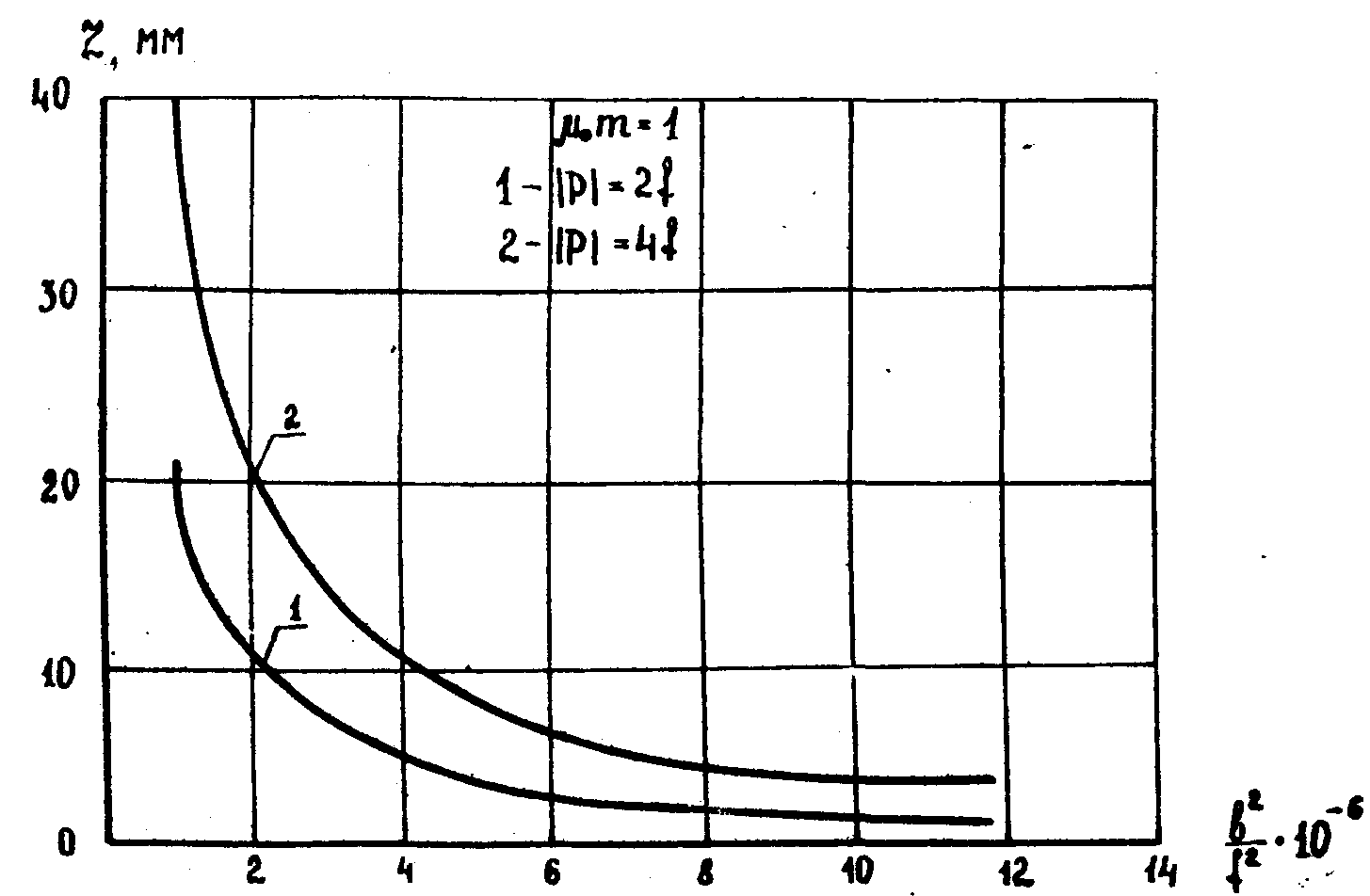
Рис.3а. Зависимость l_макс для μ₀m=1.

 

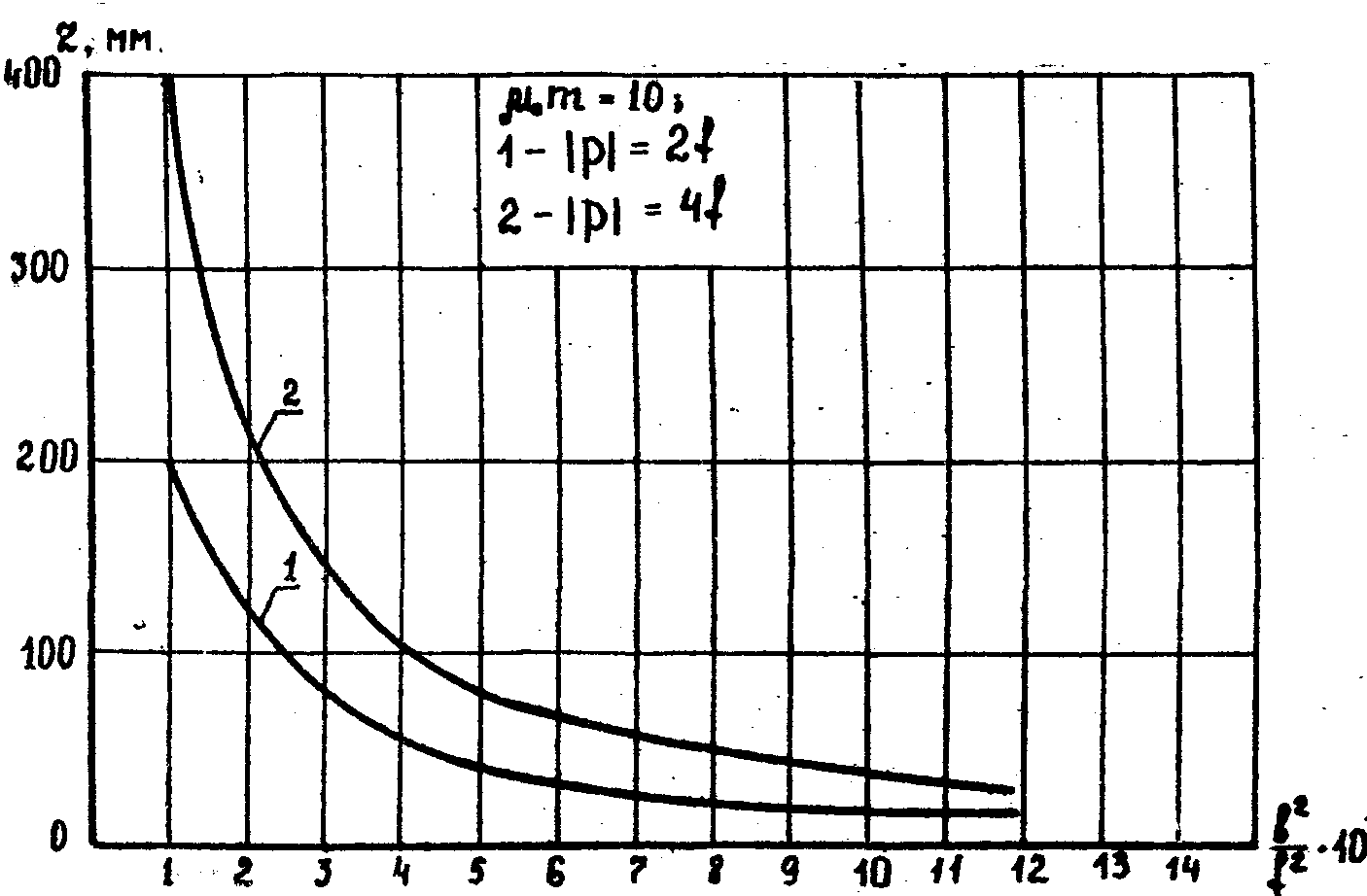
Рис.3б. Зависимость l_макс для μ₀m=10..

томограмм объектов, достаточно удаленных от плоскости рентгеновской пленки. Пусть центр объекта удален на z' от рентгенограммы, но z'/p<<1. Получив (2n+1) ракурсов, будем при записи n-го ракурса на голограмму поворачивать ее на угол, определяемый соотношением:

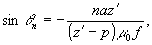
а ширину участка записи положим равной 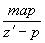. В этом случае, производя соответствующие выкладки, получим:

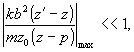
при этом (12а) и (12б) сохраняют свой вид, только в функции Френеля z следует заменить на Δz=z'-z.

Величина зоны стереовидения не изменится, но сместится на z'. Таким образом, можно исследовать большой объект, разбив его на несколько зон стереовидения.

Оценим теперь разрешающую способность голографического томосинтеза по глубине. Для такой оценке удобнее пользоваться формой записи восстановленной волны (126), положив ρ(t,z)=ρ(z)δ(t). Тогда r(ξ,z)=ρ(z). Плоскость регистрации (наблюдения) возьмем z₂=f+γr₀. Это соответствует изображению сечения 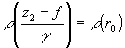. Вблизи z₀=r₀ будет существовать эффективный слой размерами |Δ|, дающий существенный вклад в результирующую интенсивность в плоскости регистрации томограммы. Считая для этого слоя z=r₀+Δ и применяя к (12б) неравенство Шварца-Коши, получим выражение для интенсивности, зарегистрированной на синтезированное томограмме:

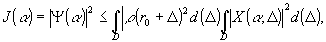(15)

где d - область задания Δ, а

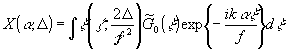. (16)

Очевидно, что разрешение по глубине зависит от функции |Х(α,Δ)|². Если

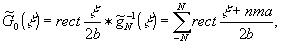
где

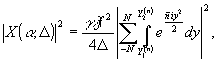(17)

Используя стандартные обозначения интегралов Френеля, (17) можно записать в следующем виде:

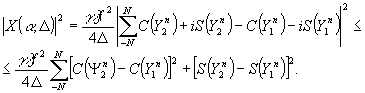(18')

Количественный вклад интенсивностей от различных слоев удобнее характеризовать отношением:

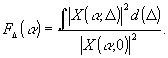(19)

Для определения величины слоя размытия и необязательно знать истинный ход зависимости f_Δ(α). Ξбращаясь к (18), можно заметить, что, поскольку

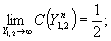
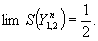
то |x(α,Δ)|²→0. следовательно, и fΔ(α)→const. Полагая в (18) индекс суммирования n'=n+n, потребуем соблюдения неравенства для n>>1;

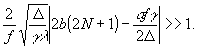(20)

Графики зависимости слоя размытия Δ от числа рентгенограмм n₀ приведены на рис.4. Кривые приведены для α=0 и |α|=λf/2b, соответствующих координатам максимума и первого нуля функции (13), описывающей разрешающую способность по изображению. Видно, что когда вклад слоя |z|=r₀ равен нулю, значительную долю в изображение дают слои, отстоящие при n₀~10 примерно на 1 мм от |z|=r₀.

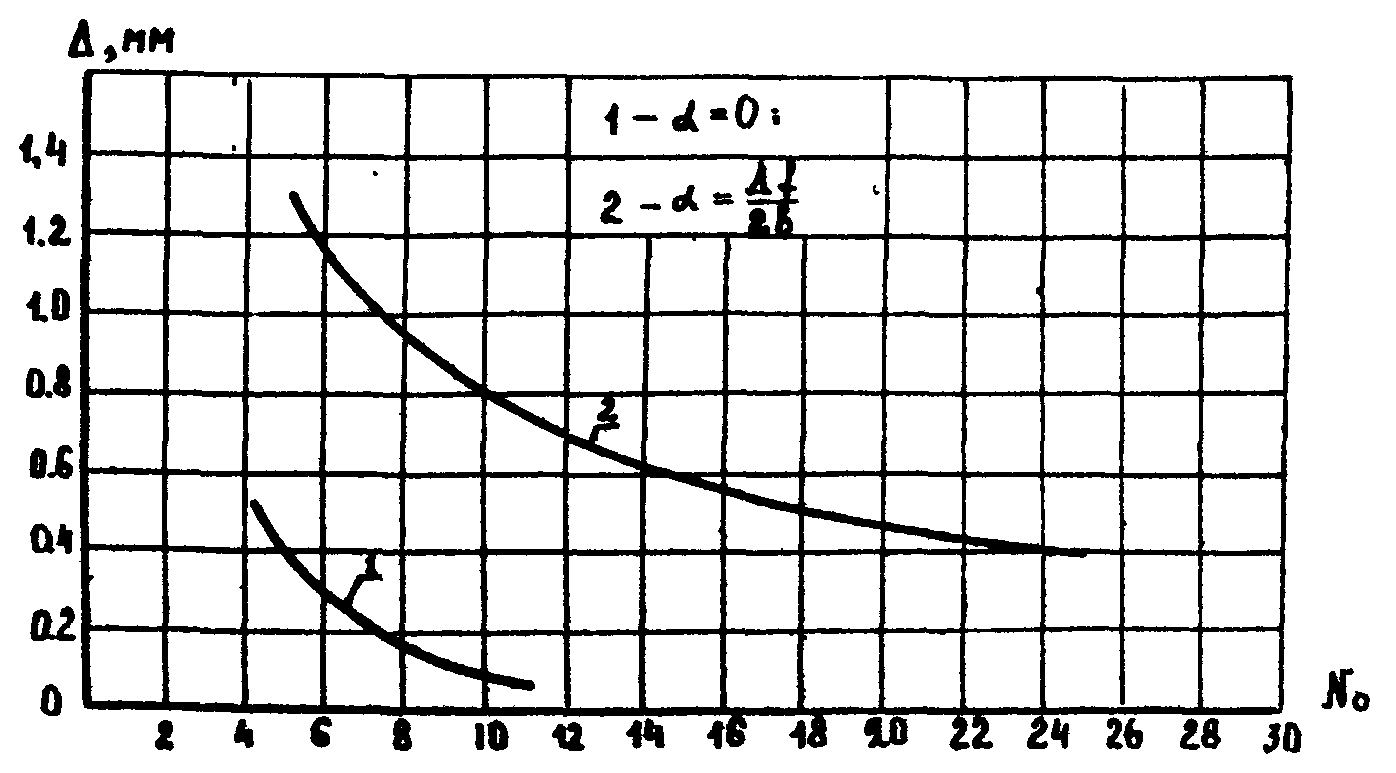
Рис.4. Зависимость размытия от числа рентгенограмм.

Таким образом, система голографического томосинтеза позволяет обеспечивать разрешение по глубине, сравнимое с обычными томографическими устройствами /7/ при числе рентгенограмм примерно равном (10÷15). Число томограмм при этом может значительно превышать число использовавшихся при синтезе рентгенограмм, и, в принципе, возможно наблюдение объемного рентгеновского изображения. Необходимые параметры систем томосинтеза даются соотношениями: (9) (14), (20), Следует однако иметь в виду, что на разрешающую способность по глубине и изображению большое влияние оказывают неточнос-

ти установки рентгенограмм, в реальной ситуации снижающие расчетные величины.

Л и т е р а т у р а

1. m.kock and n.timens, "opt.comm", 7(3), 260-265, 1973.

2. w. ellingson, a.read, w.riley, "trans.amer.nucl.soc.", v.19., n2., juppl, 10-11, 1974.

3. В.Ф.Петушенко, Д.И.Свирякин. Дефектоскопия, 3, стр.60-63, 1976.

4. В.А.Берданосов, В.И.Горбунов, А.К.Стоянов, материалы vii Всесоюзной школы по гологрвфии, 278-288, Л., 1975.

5. Л.М.Сороко. Основы голографии и когерентной оптики, "Наука", М., 1971.

6. А.Папулис. Теория систем и преобразований в оптике, "Мир", М., 1971.

7. Э.Г.Чикирдин, С.М.Стольцер, Ф.А.Астреханцев. Рентгеновские томографические аппараты, "Медицина", М., 1976.