ЦИФРОВАЯ ГОЛОГРАФИЯ. ДОСТИЖЕНИЯ И ПРОБЛЕМЫ

В.А.Сойфер

Рассмотрены методы анализа на ЭВМ голограмм плоских и трехмерных объектов. Показано, что задача цифровой реконструкции, вообще говоря, является некорректной, и предложены методы ее решения в частотной области. Рассмотрены перспективные методы получения голограмм на ЭВМ и дан их сравнительный анализ. Обсуждаются некоторые приложения цифровой голографии и перспективы ее развития.

1. В в е д е н и е

Сфера применения голографии непрерывно расширяется, однако на пути практического использования голографии в прикладных задачах возникает ряд трудностей принципиального характера. Оптическая голография дает возможность регистрации на светочувствительном материале амплитуд и фаз волнового фронта и последующего восстановления объемного изображения объекта, которому этот волновой фронт соответствует. На плоской голограмме компактно записывается колоссальный объем данных о трехмерном объекте. Как правило, в практических приложениях задача не исчерпывается необходимостью хранения и визуализации информация об объекте, а ставится значительно паре как задача исследования, т.е. количественного и качественного анализа и использования полученных данных для построения моделей, для решений и выводов. Именно здесь возникает принципиальное противоречие между колоссальным объемом данных, воспроизводимых с голограммы и малой информационной пропускной способностью исследователя, осуществляющего визуальные наблюдения восстановленного изображения. Вторая трудность заключается в том, что голограмма наиболее просто позволяет визуализировать объекты, которые можно увидеть в обычном свете. Однако наиболее заманчивым для исследователя является, как раз "увидеть невидимое" или же создать некий видимый

образ объекта по его математической модели. Обе сформулированные и многие другие трудности на пути практического применения голографии могут быть преодолены с помощью ЭВМ и методов цифровой голографии.

Цифровая голография - это получение голограмм и восстановление изображений о физических голограмм при помощи ЭВМ, оснащенных специализированными устройствами ввода-вывода и специализированным математическим обеспечением. Современные устройства ввода-вывода изображений обладают разрешающей способностью порядка 10²-10³ мм^-1 при числе уровней квантования 10²-10³. Быстродействие ЭВМ нынешнего поколения позволяет выполнять 10⁶-10⁷ арифметических операций в секунду, памяти их составляют сотни мегабайтов, в состав их математического обеспечения входят алгоритмы быстрых спектральных преобразований. Все это обеспечивает возможность практического применения методов цифровой голографии.

2. Анализ физических голограмм на ЭВМ

2.1. Измерение и дискретизация полей для ввода в ЭВМ

Голограмма несет большой объем информации об объекте. Для получения количественных данных о параметрах объекта и решения сложных задач визуализации внутренней структуры и различных видов объекта необходима автоматизация голографического эксперимента. Одним из наиболее удобных путей автоматизации является ввод голограммы в ЭВМ с последующим восстановлением (реконструкцией) в цифровом виде.

Цифровое восстановление (реконструкция) изображений основано на моделировании процесса распространения света от голограммы к объекту. В простых случаях возможно использование приближения Кирхгофа и следующих из него методов дифракции Френеля и Фраунгофера /1,2/. Для цифровой реконструкции более, сложных объектов должны быть применены методы теории рассеяния /3,4/.

Ввод голограмм в Эbm требует разрешения ряда трудностей. Аналоговый объект (физическое поле) переводится при вводе в ЭВМ в цифровую форму. При этом имеют место дискретизация и квантование, вно-

сящие методические погрешности в результаты измерений.

Для ввода оптических голограмм, в принципе, могут быть использованы методы сканирования и устройства /5/, применяемые при передаче и цифровой обработке изображений.

Физическая оптическая голограмма может формально рассматриваться как некоторое изображение. Но имеются существенные количественные отличия голограммы от обычных изображений в смысле требований к разрешение систем ввода в ЭВМ. Так, для перевода обычных изображений в цифровую форму достаточно выбрать отсчета с плотностью, не превышающей 10¹-10² мм^-1 (по каждой оси). Известно также /1/, что разрешение на внеосевой голограмме имеет порядок 10³-10⁴ линейна миллиметр, что на один-два порядка превышает возможности известных систем. Возможны усовершенствования систем ввода, несколько повышающие их разрешающую способность. Однако такая мера не является радикальной и сопряжена со значительным повышением стоимости соответствующих систем.

Другой путь состоит в применении специальных методов снижения полосы пространственных частот на голограммах /6/.

2.2. Восстановление плоских и трехмерных объектов

по голограммам Френеля

Цифровая реконструкция для широкого класса голограмм может быть основана на использовании приближения Френеля-Кирхгофа задачи о дифракции.

Строгое решение интеграла Френеля-Кирхгофа в частотной области /1/ дает следующий результат. Если плоская волна единичной амплитуды распространяется в направлении оси z и падает на помещенный в плоскости z=0 транспарант с амплитудным пропусканием t(u,v), то спектр А(ε,η) комплексной амплитуды волан в плоскости z=d имеет вид:

a(ε,η)=t(ε,η)Ф(ε,η,d), (1)

где

t(ε,η)=f{t(u,v)}, (2)

Ф(ε,η,d)=exp[-j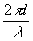(1-λ²ε²-λ²η²)^1/2]. (3)

Символами f и f^-1 здесь и далее обозначаем, соответственно, прямое и обратное преобразования Фурье. Символами f_d и f_d^-1, соответственно, прямое и обратное дискретные преобразования Фурье (ДПФ) /1/.

С использованием опорной волны комплексная функция Ф(ε,η,d) может быть зарегистрирована в виде интенсивности интерференционной картины. Предположим, что в память ЭВМ записан двумерный массив данных А(k,l), полученный путем дискретизации функции А(ε,η) по аргументам с шагом Δ, и вместо соотношения (3) используется

a(k,l)=t(k,l)Ф(k,l,d), (4)

где Т(k,l), Ф(k,l,d) - отсчеты функций t(ε,η) и Ф(ε,η,d), соответственное шагом Δ по осям ε и η.

Задача решения уравнения (1) относительно t(u,v) в области пространственных частот (ε,η) эквивалентна решению интегрального уравнения Фредгольма 1 рода в области пространственных переменных (u,v) и является некорректной в смысле устойчивости решения /7/. Малым отклонениям наблюдаемой функции А(ε,η), вообще говоря, могут соответствовать большие отклонения решения 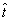(u,v). Для решения этой задачи следует использовать метод регуляризации академика А.Н.Тихонова /7/. Регуляризованное решение уравнения (1) в спектральной области имеет вид:

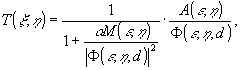(5)

где α - параметр регуляризации; М(ε,η) - четная неотрицательная функция, определяющая регуляризующий функционал.

Для самого широкого класса функций можно показать, что при использовании регуляризаторов тихоновского типа,

m(ε,η)=ε^2pη^2l, (6)

существует такая зависимость погрешности регуляризованного решения от погрешности наблюдения, при которой последовательность приближенных регуляризованных решений сходится к точному решению. Используя регуляризованное решение (5) в дискретной форме:

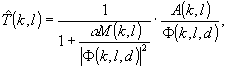(7)

и применяя к функции Т(k,l) ДПФ, получим искомое решение:

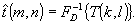(8)

Реконструкция в частной области - не единственный путь решения задачи. Если справедливо параболическое приближение /1/, функция Ф(ε,η,d) с точностью до постоянного множителя совпадает с функцией Френеля, а функции t(u,v) и а(х,у) = f^-1{А(ε,η)} связаны прямым и обратным преобразованиями Френеля. В этих условиях спектр объекта может быть вычислен через наблюдаемую функцию a(ε,η) из сooтношения:

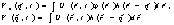(9)

или в дискретной форме:

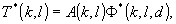(10)

где * - символ комплексно-сопряженной величины. Соответствующее решение имеет вид:

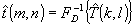(11)

и получается с использованием ДПФ. Заметим, что несмотря на внешнюю простоту записи, вычисления по формулам (10), (11) требуют значительных затрат машинного времени для вычисления фазового множителя Ф(k,l,d) в каждой точке голограммы.

До сих пор мы рассматривали восстановление плоских объектов. Восстановление трехмерного объекта t(u,v,z) не вызывает трудностей, если этот объект может быть представлен совокупностью плоских сечений, параллельных плоскости голограммы:

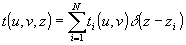. (12)

Такими объектами, в частности, являются пространственные ансамбли частиц /8/. Для реализации цифровой реконструкции объекта по сечениям можно использовать любой из методов, описанных в этом разделе, варьируя параметр d, соответствующий расстоянию от голограммы до восстановленного сечения.

2.3. Восстановление фазовых объектов

Изложенные выше методы применимы к реконструкции простых объектов в виде набора плоских транспарантов, т.е. объектов, дифракция на которых удовлетворительно описывается в приближении Кирхгофа. В прикладных задачах исследуемые объекты часто имеют иную структуру, например, турбулентный поток газа или жидкости.

Теория обратного рассеяния /3/ позволяет по голографическим измерениям полностью восстанавливать трехмерную структуру слабо рассеивающего полупрозрачного объекта.

Рассеивающий объект характеризуется потенциалом рассеяния f(x',y',z'). Для прозрачного (чисто фазового) объекта

f(x',y'z')=-k²[u²(x',y'z')-1], (13)

где k - волновое число; u(x',y',z') - показатель преломления. При освещении такого объекта волной u⁽ⁱ⁾(x',y',z') комплексное волновое поле, рассеянное объектом в плоскости голограммы, имеет вид:

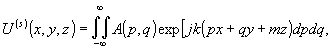(14)

где

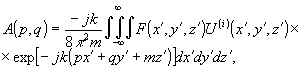(15)

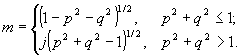(16)

На голограмме, отстоящей на расстоянии z₀ от объекта, регистрируется функция

i(x,y)=|u_s(x,yz₀)+u_r(x,y)|², (17)

содержащая полную информацию о функции u_s,

где u_r(x,y) - поле опорного, пучка.

Из уравнений (14) и (15) может быть определен потенциал рассеяния. Для этого требуется /3/ регистрация серия голограмм с освещающими плоскими волнами

u⁽ⁱ⁾(x',y',z')=exp[jk(p₀x'+q₀y'+m₀z')],

падающими по различным направлениям (р₀,q₀,m₀) на рассеивающий объект. Соответствующий эксперимент описан в /4/. Ввод голограммы в ЭВМ осуществлялся автоматическим цифровым микроденситометром, сопряженным с ЭВМ. Для снятия отсчетов в нем используется освещение лазерным лучом диаметра 1 мкм. Поскольку опорный пучок дает высокую пространственную частоту на голограмме лишь в одном направлении (ось х), применялась различная точность дискретизации по оси х и у. По оси х снималось 10 отсчетов оптической плотности, на расстоянии 1 мкм друг от друга при периоде пространственной не-

сущей 21 мкм. Отсчеты подвергались квантованию по 400 уровням от 0,01 до 4.00 единиц оптической плотности. Для снятия характеристической кривой фотоматериала с голограммой всегда оптически формировался эталонный клин. В ЭВМ отсчеты плотности перекодировывались в отсчеты интенсивности (15), с использованием данных с характеристической кривой. Затем производилось вычисление фурье-образа функции u^(s) и определение потенциала рассеяния, а следовательно, и коэффициента преломления объекта.

2.4. Имитация на ЭВМ физических голографических процессов

Метод цифрового моделирования голографических схем и процессов позволяет исследовать влияние различных шумов и искажений на качество волнового фронта, восстанавливаемого с голограммы при различных способах голографирования широкого класса объектов.

В /9/ сообщается о создании пакета прикладных программ для анализа аберраций, свойственных голограммам вследствие 1) относительного смещения опорного пучка при записи голограммы и освещающего пучка при восстановлении; 2) изменения длины волны; 3) конечности толщины регистрирующей эмульсии, а также эффектов усадки эмульсии. Отмечается, что возможен анализ аберрации голограмм методами, аналогичными анализу аберраций линз. Однако положение осложняется наличием у голограмм ряда асимметрических аберраций, не свойственных линзам. Таким образом, анализ становится довольно сложным и трудно обозримым. Значительные удобства как по скорости, так и по точности для анализа аберраций голограммы дает метод цифрового моделирования. Рассматриваются четыре типа голограмм: осевые (габоровские), внеосевые, голограммы сфокусированных изображений и безлинзовые фурье-голограммы. Основное внимание уделено установлению на базе геометрической оптики наиболее общих соотношений, являвшихся основой для моделирования на ЭВМ.

В рассмотрение включены произвольные сферические и плоские опорные пучки. Однако в качестве объекта рассмотрен лишь простейший точечный источник. Аберрации оценивались по отклонению восстановленного с голограммы волнового фронта от идеального сферического. Численные значения отклонений в зависимости от перечисленных

выше факторов, полученные в результате моделирования на ЭВМ, предоставляемые методом цифрового моделирования для изучения аберрации голограмм, подтверждены созданием специальной оптимизирующей программы, позволяющей найти вид и параметры схемы голографирования, регистрирующей эмульсии и источника освещения, обеспечивающие взаимную компенсацию различных видов аберраций.

Имитация голографического процесса на ЭВМ позволяет исследовать сложное влияние турбулентной среды на качество изображения, полученного в результате голографического эксперимента. Автором проведен анализ влияния турбулентной среды на голограммы Фурье и Френеля пространственного ансамбля частиц, позволивший предложить ряд методов улучшения качества реконструируемых изображений. Предложен гибридный метод моделирования, сочетающий достоинства физического голографического эксперимента и имитации голографического процесса на ЭВМ. Метод заключается в вводе в ЭВМ физической оптической голограммы частиц, полученных в условиях нетурбулентной среды и дальнейшей имитации на ЭВМ воздействия турбулентной среды на голограмму. Такой метод позволяет получить количественные результаты, а также сделать качественные выводы путем визуальных наблюдений изображений частиц, восстановленных с искаженных "средой" голограмм.

2.5. Анализ интерферограмм на ЭВМ

В настоящее время широко распространены интерферометрические измерения, в особенности лазерная интерферометрия. Интерференция испытываемого волнового фронта с идеальным опорным фронтом дает систему полос, отражающих различия менее, чем в полволны. Применяемая визуальная обработка интерферограммы является трудоемкой и не позволяет получить данные достаточной точности и объема. Актуальной является автоматизация обработки интерферограмм с использованием ЭВМ. Для этого координаты полос на интерферограмме подвергаются дискретизации и вводятся в ЭВМ. Далее данные интерферометрии обрабатываются с помощью специально разработанных алгоритмов. Результатом обработки может быть визуализация поля параметра, исследуемого интерферометрическими методами, а также численные дан-

ные об объекте изучения. В /5/ приведены некоторые результаты исследования возможностей анализа и автоматической обработки интерферограмм с помощью ЭВМ.

В /10/ описывается пакет fred прикладных программ для обработки интерферометрических данных. Пакет ориентирован на ЭВМ С С - 3300, хранится на магнитных дисках, имеет блочную структуру и включает около сорока программ. Программы ввода позволяют производить ввод координат интерференционных полос в различных форматах. Вычислительные программы осуществляют различимо аппроксимации идеальных поверхностей по методу наименьших квадратов с оценкой точности; интерполяцию данных об интерферограмме на регулярную сетку отсчетов, виньетирование апертуры; компенсацию неосесимметричных аберраций оптики, используемой при съеме интерферограмм; удаление статистически недостоверной информации; сглаживание данных; преобразование координат; анализ данных специальных тестов плоских зеркал; синтез объекта из нескольких интерферограмм. Программы работы с данными позволяют производить накопление, выборку, сложение, вычитание, усреднение интерполированной информации, записанной в виде файлов на дисках. Программы вывода осуществляют визуализацию линий уровня, перспективных видов, выдачу числовых параметров на печать и на перфокарты.

В /10/ описаны принципы построения некоторых вычислительных программ. В программе синтеза объекта из нескольких перекрывающихся интерферограмм основной проблемой является масштабирование отдельных интерферограмм. Для этого производится их согласование на перекрыващихся областях путем минимизации суммарного среднеквадратического различия во всех общих участках. Для сглаживания и интерполяции дискретизированных данных используются полиномы Церника, ортогонализированные методом Грамма-Шмидта.

Имеется также сообщение /11/ об автоматизации обработки данных многолучевой интерферометрии чисто фазовых асимметричных объектов.

3. Синтез голограмм на ЭВМ

3.1. Формулировка проблемы

Для полной регистрации волнового поля объекта требуется заре-

гистрировать как амплитуду, так и фазу рассеянного объектом излучения. В физической голографии полная регистрация достигается, как известно, введением опорного пучка. В цифровой голографии проблема рассматривается в более общем виде. Пусть распределение комплексной амплитуды поля в плоскости голограммы описывается комплексно-значной функцией

u(x,y)=a(x,y)e^jφ(x,y)=u₁(x,y)+ju(x,y). (18)

Любое устройство синтеза голограмм позволяет отобразить лишь функции h(x,y) из некоторого класса Н реализуемых функций. Таким образом, комплекснозначная функция u должна быть закодирована некоторой функцией hÎ h. Совокупность класса и способа кодирования назовем методом регистрации синтезированных голограмм. Следует заметить, что метод регистрации обычно применим к синтезу различных типов голограмм (Френеля, Фурье, голограмм сфокусированных изображений и т.д.). Однако связанные с методом регистрации аппроксимации различны в каждом случае и приводят в различной степени к появлению сопряженных и ложных изображении, а также различных видов шума на восстановленном изображении.

Во многих случаях класс h состоит из вещественных неотрицательных функций. Ранние способы кодирования, описанные, например, в /2/ представляли собой формальное моделирование на ЭВМ физической схемы Лейта и Упатниекса. Впоследствии были созданы более эффективные способы кодирования комплексной функции, вещественной, неотрицательной.

В случае фазовых голограмм и киноформа класс h состоит из комплекснозначных функций, равных по модулю 1 (или же имеющих постоянный модуль А(х,у)º А=const).

Одним из последних достижений в области цифровой голографии является использование многослойных носителей для регистрации голограмм. Такие среды позволяют реализовать комплекснозначную цифровую голограмму (т.е. h включает комплеконозначные функции), изображение от которой восстанавливается на оси оптической системы, что обеспечивает высокую дифракционную эффективность (теоретически до 100%).

Появляются также сообщения о первых попытках синтеза цветных голограмм, т.е. голограмм, с которых восстанавливаются многоцветные изображения.

Общей проблемой при синтезе голограмм является изучение дискретизации и квантования компонент функции пропускания (например, амплитуды и (или) фазы, вещественной и мнимой части и т.п.). Специфические проблемы возникают при попытке синтеза нестационарных голограмм. Решение этих проблей лежит на пути использования динамической регистрации.

Перейдем к систематическому рассмотрению методов регистрации синтезированных голограмм.

3.2. Имитация на ЭВМ процесса получения физических голограмм

Дня регистрации амплитуд и фаз волнового поля объекта можно так же, как это делается в физической голографии, использовать опорную волну.

Алгоритм получения голограммы на ЭВМ в этом случае выглядят следующим образом. Сначала решается задача дифракции и рассчитывается распределение световой волны объекта в плоскости голограммы

g(x,y)=a(x,y)exp[jφ(x,y)], (19)

где х, y - пространственные координаты в плоскости голограммы, а А и φ - соответственно, амплитуда и фаза поля g.

После расчета световой волны g(х,y) к ней добавляется плоская опорная волна

r(x,y)=bexp(jbx), (20)

где В и b - соответственно, амплитуда и пространственная частота плоской волны.

Далее модуль образуемой суммы волн возводится в квадрат, в результате чего образуется поле, принимавшее неотрицательные значения.

u(x,y)=|g(x,y)+bexp(jbx)|². (21)

Рассматриваемому методу получения голограмм на ЭВМ присущ принципиальный недостаток, ограничивающий его практическое применение. Действительно, для полного разделения вещественного и мнимого изображений пространственная частота плоской волны должна быть выбрана достаточно большой. В практических приложениях она составляет величину порядка 10³ мм^-1. Это означает, что регистрации синтезированной голограммы необходимо иметь устройство отображения с разрешающей способностью 10³-10⁴ мм^-1. Для разрешения мельчайших деталей объекта вполне достаточной обычно оказывается разрешающая способность 10² мм^-1, а увеличение ее значения на один или два порядка связано исключительно с необходимостью регистрации опорной волны, не несущей никакой информации о голографируемом объекте и выполняющей лишь вспомогательные функции кодирования комплексных чисел вещественными. На основании сказанного можно сделать вывод, что такой способ кодирования, очевидно, не принадлежит к числу лучших в цифровой голографии.

Гибкость ЭВМ позволяет предложить множество других способов кодирования цифровых голограмм, не допустимых для голограмм физического происхождения.

3.3. Бинарные голограммы

Простейшим типом синтезированных голограмм являются бинарные голограммы, амплитудное пропускание которых принимает лишь два значения {1,0}. Таким образом, любой способ синтеза бинарной голограммы является способом кодирования комплекснозначной функции в вещественнозначную, принимающую значения {1,0}. Предложено множество способов такого кодирования, особенно для голограмм Фурье и Френеля.

Голограммы Фурье. Амплитудное пропускание двумерного объекта t(u,v) связано с распределением света от объекта в плоскости голограммы преобразованием Фурье

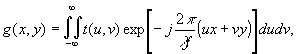(22)

где λ - длина волны света, f - фокусное расстояние линзы, используемой для Фурье-преобразования.

При машинных вычислениях объект задается матрицей t=(t_pr) размера n´ n своих равноотстоящих отсчетов, соответственно, ДПФ позволяет получить n´ n комплексных отсчетов спектра, отстоящих друг от друга на расстоянии d, и дискретная голограмма Фурье описывается выражением

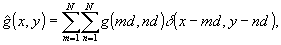(23)

где δ(х,y) - двумерная единичная импульсная функция

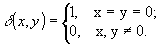(24)

Значения спектра g(md,nd) нельзя непосредственно отобразить на фотопленке, т.к. они комплексные. Для такого отображения предложен ряд методов.

Сущность метода Ломана /2/ заключается в следующем. Поле голограммы размера А´ А разбивается на элементарные ячейки размера δ´ δ, число которых составляет n´ n (cм.рис.1). Каждой (m,n)-ой ячейке соответствует комплексная величина

g(md,nd)=|g(md,nd)|exp[jφ(md,nd)]. (25)

Значение амплитуды кодируется абсолютно прозрачной щелью внутри (m,n)-ой ячейки, площадь которой пропорциональна величине |g(md,nd)|. Значение фазы кодируется сдвигом центра щели относительно центра ячейки (например по оси х) на величину p_mn∙δ (где |p_mn|≤1 - относительное смещение), пропорциональную фазовому углу φ(md,nd) (см. рис.2). В результате применения описанной процедуры получаем голограмму, каждая точка которой имеет прозрачность

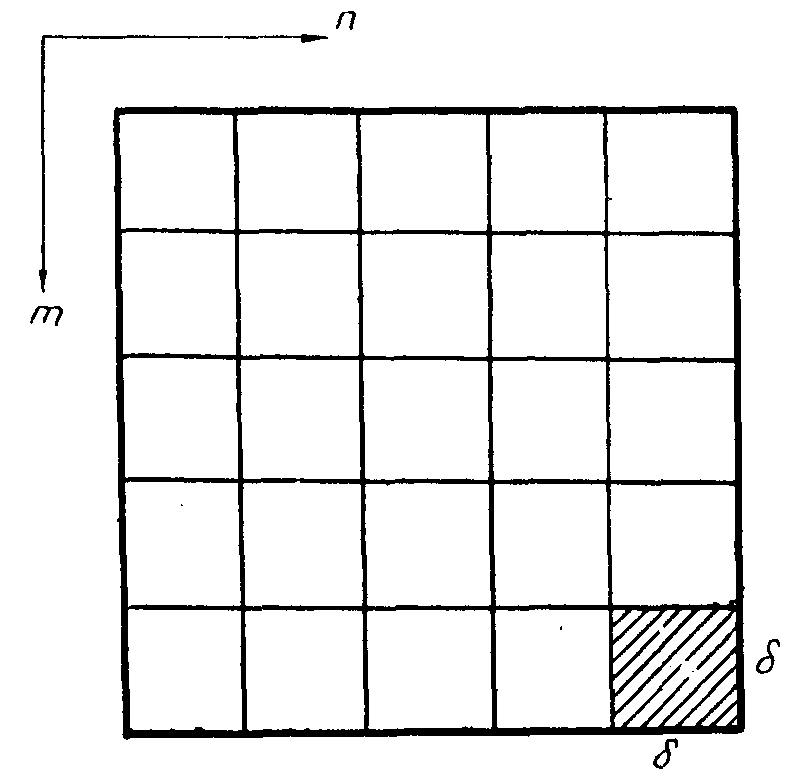
Рис.1. Поле бинарной голограммы.

 

 

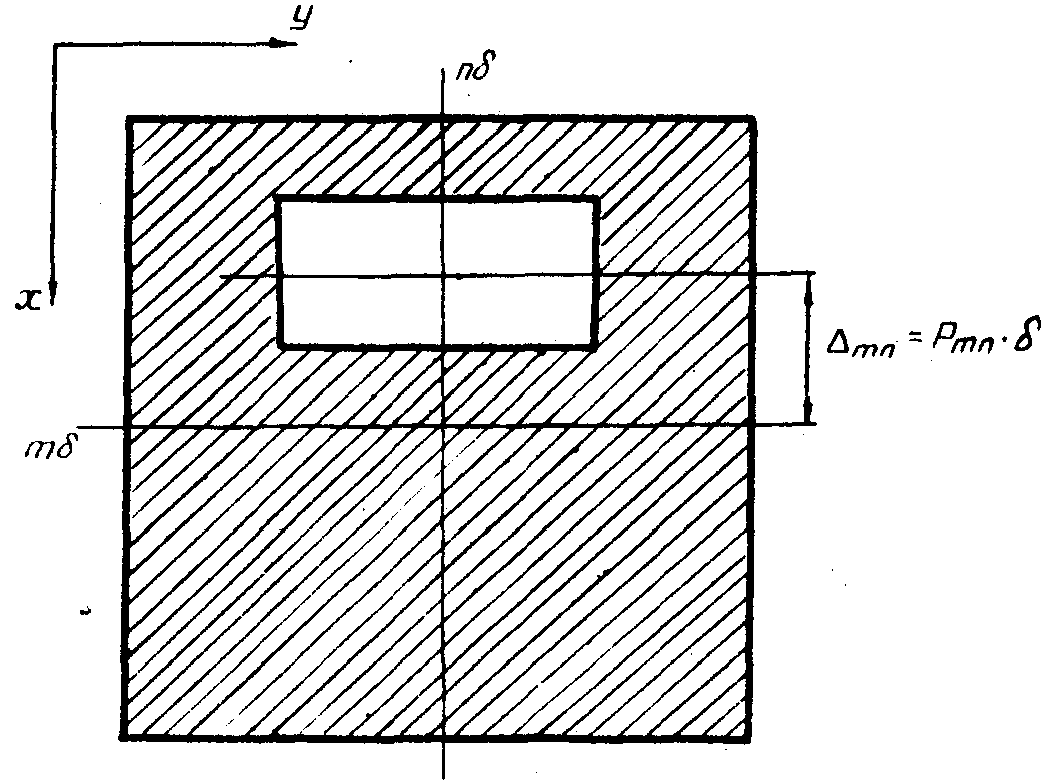
Рис.2. Структура голограммы Ломана.

либо 0, либо 1.

При оптическом восстановлении голограмма Ломана освещается плоской волной. Дифракционная картина первого порядка создает в задней фокальной плоскости линзы, выполняющей фурье-преобразование, восстановленное изображение объекта t(u,v).

При использовании метода ли комплексное значение каждого отсчета g(md,nd) отображается на голограмме четырьмя действительными неотрицательные величинами. Имеющаяся система четырех базисных векторов r⁺=(1,0), r^-=(-1,0), i⁺=(0,1), i^-=(0,-1) позволяет записать любой вектор g в виде

g=g₁r⁺+g₂i⁺+g₃r^-+g₄i^-. (26)

Неотрицательные величины g₁, g₂, g₃, и g₄ отображаются внутри элементарной ячейки голограммы в виде абсолютно прозрачных отверстий, площади которых пропорциональны значениям соответствующих величин, а центры смещения относительно друг друга на расстоянии δ/4. Процесс оптического восстановления осуществляется так же, как в случае голограммы Ломана.

Известны различные модификации методов Ломана и Ли.

Структура голограмм, предложенных Ломаном, а также Ли, приспособлена для использования механических графопостроителей. Использование электронных лучевых трубок затрудняет управление такими параметрами, как площадь ячейки (определяемая площадью луча). Использование же модуляции интенсивности луча, дающее полутоновые голограммы, предъявляет повышенные требования к линейности фотопроцессов. В связи с этим предложено /12/ использовать следующий формат ячейки на синтетической голограмме (см.рис.3). В ячейке разрешения с помощью электронного пучка формируются два пятна одинакового диаметра и интенсивности.

Фаза φ волнового фронта aexp(iφ) отображается как и в голограмме Ломана величиной p_mn∙δ смещения центра тяжести ячеек от оси симметрии ячейки, дающее "фазу обхода" (detourphose). Для управления амплитудой используется существенно другой метод, чей в голограммах Ломана и Ли. В /13/ предложено управлять амплитудой за счет изменения распределения энергии излучения по порядкам

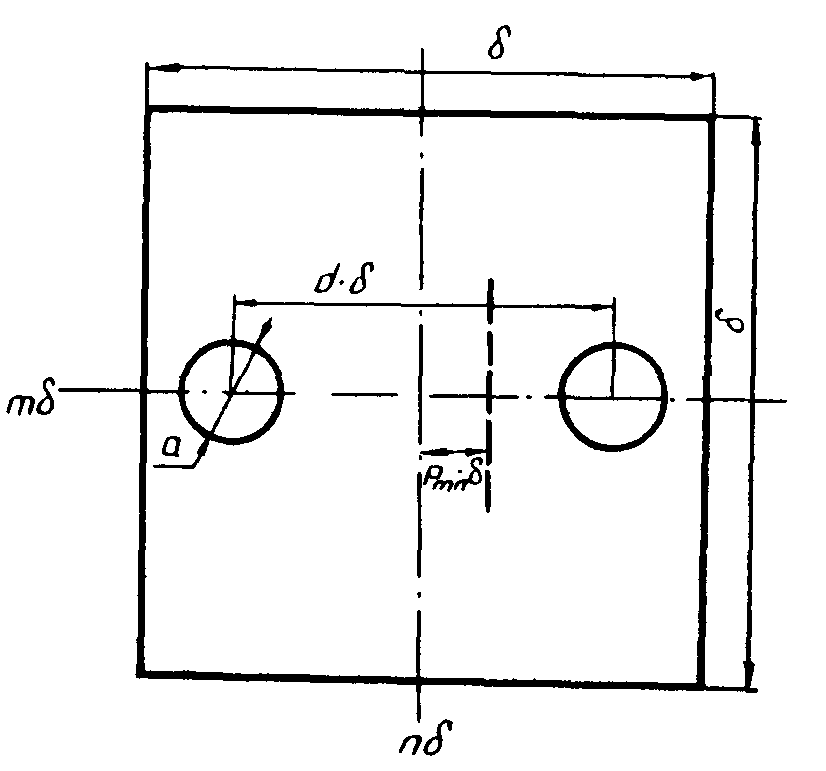
Рис.3. Структура бинарной голограммы, ориентированной на использование ЭЛТ.

дифракции. Меняя расстояние d между точками (пятнами), мы будем изменять мгновенную пространственную частоту в данной ячейке, направляя требуемую часть энергии излучения в первый (точнее в 1,0) порядок дифракции. Ли предложен /14/ и другой метод синтеза голограмм, в котором функция пропускания голограммы может быть произвольной бинарной.

Пусть требуется получить волновой фронт a(x,y)exp(jφ(x,y)) в плоскости (х,у). В оптической голографии такой фронт записывается в виде интерференционной картины. Вначале рассматривается чисто фазовый фронт exp(jφ(x,y)). Если используется плоская опорная волна, то пропускание голограммы будет меняться как

f(x,y)=cos[φ(x,y)+2πx/t], (26)

где Т - "период" интерференционной картины.

Бинарную голограмму предлагается получить, пропуская f(х,у) через идеальный ограничитель (рис.4). Поскольку отклик ограничите-

 

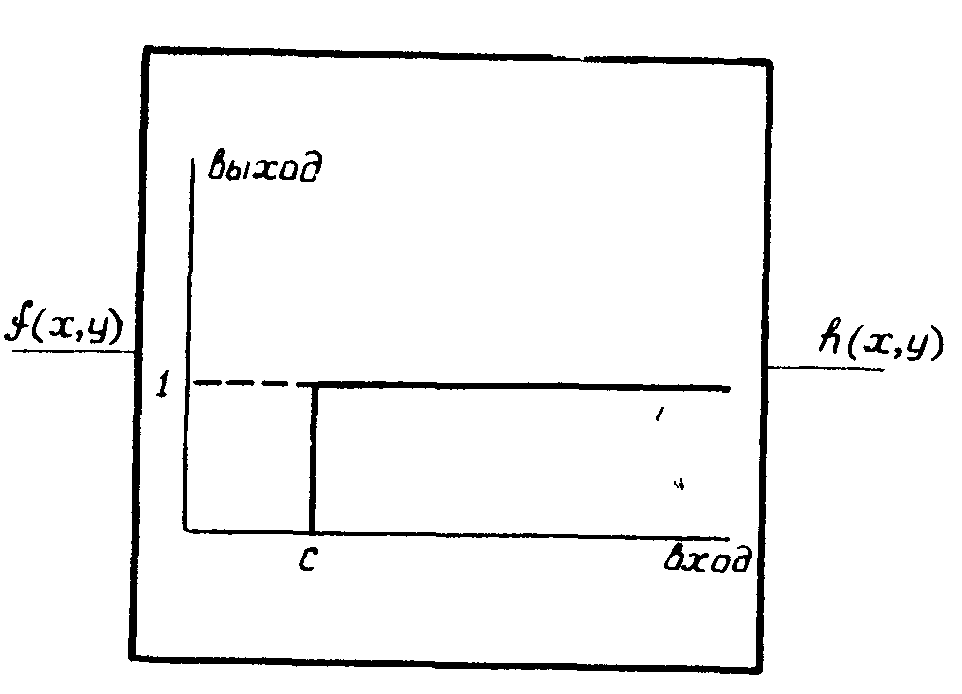
Рис.4. Идеальный ограничитель.

ля на (26) является бинарным и имеет вид:

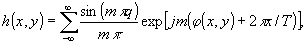(27)

то бинарная голограмма такого вида позволит получить любой фронт (при m=1). Здесь g=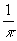arccosc. Из рис.4 видно, что бинарная функция, описывающая голограмму, отлична от 0, если

cosφ(x,y)≥cosπq,

что может быть записано в виде

-q/2≤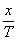++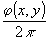n≤q/2, (28)

где n - целое число. Это неравенство дает общее выражение для синтеза бинарных голограмм. Если φ(x,y)=const, то (26) дает периодическую решетку с периодом Т. Величина Т и определяет угловое разделение дифракционных порядков при восстановлении.

Голограммы Френеля. Выражение для комплексной амплитуды поля объекта t(u,v,z) в плоскости голограммы (х,у) с точностью до постоянного множителя описывается выражением

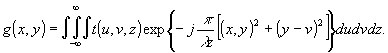(29)

Этот интеграл особенно просто вычисляется, если трехмерный объект представляет собой конечный набор точечных рассеивателей, расположенных в точках (u_k,v_k,z_k), т.е.

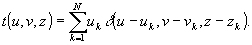(30)

В этом случае из (29) следует:

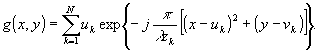(31)

В более общем случав для вычисления по формуле (29) целесообразно представить трехмерный объект в виде суммы равноотстоящих на расстоянии Δz поперечных сечений, перпендикулярных оси z.

Амплитудное пропускание двумерного объекта t(u,v), находящегося на расстоянии d от плоскости голограммы связано с распределением света g(х,y,d) от этого объекта в плоскости голограммы преобразованием Френеля.

Для вычисления на ЭВМ функции g(x,y,d) можно применять способы, описанные в разделе 2. Вычислив функцию g(x,y,d), ее можно зарегистрировать с помощью любого из методов, описанных в 3.2.

3.4. Многоградационные голограммы

Наряду с многими достоинствами бинарные голограммы обладают рядом недостатков. Наиболее существенным является значительная потеря разрешения, поскольку на каждую ячейку бинарной голограммы требуется несколько элементарньх ячеек отображавшего устройства.

С такой точки зрения наиболее предпочтительными являются устройства вывода изображений, дающие несколько (более двух) града-

ций интенсивности или непрерывные по уровням. Для построения синтетических голограмм на таких устройствах разработаны специальные методы кодирования комплекснозначных величин в виде вещественных неотрицательных. Эмпирический метод, обобщающий метод Ломана для бинарных голограмм, предложен в /15/. В этом методе голограмма состоит из набора n´ n ячеек размера δх´ δх. В каждой ячейке расположено пятно с относительным размером а и функцией рассеяния

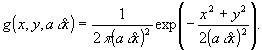(32)

Яркость i_nm пятна (n,m) соответствует амплитуде комплексной функции в данной ячейке, а сдвиг Р_nmδ пятна от центра ячейки определяется фазой. Амплитудное пропускание голограммы имеет вид:

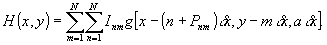(33)

Два свободных параметра i_nm и p_nm в каждой ячейке должны быть определены таким образом, чтобы в первом дифракционном порядке с голограммы восстанавливался нужный волновой фронт. Выбирая значения этих параметров, оптимальные по критерию минимума высших порядков дифракции, мы, в сущности, вводим в голограмму целенаправленные предыскажения. Детальное исследование многоградационных голограмм проведено в /5/.

3.5. К и н о ф о р м

Значительным шагом в развитии цифровой голографии явилось создание киноформа. Предположим, что поле a(x,y)exp(jφ(x,y)), созданное объектом в плоскости голограммы, имеет амплитуду А(х,у)≡1. Для изготовления киноформа фаза φ(х,у) приводится к интервалу 0≤φ(x,y)<2π. Изготавливается транспарант с амплитудным пропусканием φ(х,у). После отбеливания получается синтетическая голограмма, называемая киноформ. Заметим, что приведение фазы к интервалу [0,2π] делает невозможным использование киноформа для

динамической регистрации в нестационарной голографии. Существенным недостатком метода является наличие, вообще говоря, ограничения А(х,у)≡1. Это имеет место лишь для диффузных объектов. Теоретическое рассмотрение влияния игнорирования информации об амплитуде на качество изображения, восстановленного только по фазе волны от объекта, зарегистрированной в плоскости голограммы, приведено в /2/. Показано, что при таком восстановлении около 80% энергии поля в плоскости восстановленного изображения несут в себе полезную информацию об объекте. Остальные 20% энергии принадлежат помехам, которые портят качество восстановленного изображения.

Для уменьшения влияния этих помех предложены различные методы преобразования для приведения поля, рассеянного объектом, к чисто фазовому. Среди них отметим идею использования псевдослучайных последовательностей /16/ при синтезе киноформа. В этой статье получен критерий такого вывода фаз излучения, рассеянного объектом, состоящий из конечною числа точек, чтобы А(х,у)≈1.

Предлагались также /17-19/ специальные методы формирования спектра, позволяющие закодировать произвольный пространственный спектр А(х,у)exp(j φ(x,y)) так, чтобы он стал чисто фазовым. Кодирование приводит на стадии восстановления к появлению вспомогательных элементов изображения. Эти элементы пространственно отделены от основного изображения и потому не влияют на его качество. Они лишь перераспределяют анергию пучка, несколько уменьшая яркость восстановленного изображения.

3.6. Регистрация на многослойных носителях

Ключевой проблемой цифровой голографии является реализация транспаранта, воздействующего как на амплитуду, так и на фазу световой волны. Простейшим решением является использование сэндвичей из амплитудного и фазового отбеленного транспарантов.

В /20/ предложен оригинальный метод синтеза амплитуднофазовых транспарантов. В качестве носителя используется цветная обращаемая 35 мм фотопленка Кодакхром ii. На экране ЭЛТ отображается амплитудное пропускание фильтра, регистрируемое на пленке через красный фильтр на линейной участке характеристической кривой "красного"

эмульсионного слоя. Затем через синий фильтр аналогично регистрируется на той же пленке фазовое пропускание, приведенное к [0,2π]. После обработка пленка освещается красным 0,6328 мкм гелий-неоновым лазером. "Красная" эмульсия играет роль амплитудного фильтра, а синяя (и зеленая) воздействует на фазу. Предполагается, что фазовый сдвиг пропорционален плотности почернения. Эксперимент показывает, что экспозиция, требуемая для получения фазового сдвига от 0 до 2π, попадает на линейный участок характеристической кривой. Сдвиг фаз, вносимый красной эмульсией, компенсируется вычитанием из логарифма синей экспозиции логарифма красной экспозиции.

Имеются также а другие нескомпенсированные источники ошибок. Во-первых, красная экспозиция воздействует в некоторой степени и на синюю и на зеленую эмульсию и обратно. Далее, зеленая эмульсия влияет на амплитудное пропускание. И, наконец, рельеф изображения зависит от пространственной частоты.

Однако, даже без компенсации этих погрешностей получились удивительно хорошие результаты во описанному методу.

3.7. Цветные голограммы

Для получения цветных изображений несуществующих объектов требуются /21/ три синтезированные на ЭВМ голограммы, управляющие получением красного, зеленого и синего изображения, соответственно. Набор трех голограмм можно назвать цветной синтезированной голограммой. Для восстановления могут использоваться красный гелий-неоновый лазер с длиной волны 0,6328 мкм и два аргон-неоновых лазера с длинами волн 0,5140 мкм (зеленый) и 0,4579 мкм (синий), поскольку из таких трех цветов может быть получен любой другой цвет.

В /21/ выделяются две основные проблемы синтеза цветных голограмм, во-первых, если голограмма для одного из цветов частично пропускает два других цвета, то, кроме нужного изображения, появляются и ложные изображения. Во-вторых, масштаб изображения, восстановленного с голограммы, зависит от длины волны. При синтезе голограмм требуемое масштабирование может быть введено в цифровом виде или путем фотографического уменьшения с разной кратностью, а также изменением растра устройства вывода. Кроме того, масштабирование

можно ввести и на стадии восстановления.

Существует и другой метод синтеза цветных голограмм, автоматически устраняющий ложные изображения. Он состоит в изготовлении трех одноцветных бинарных голограмм типа Ломана в трех слоях цветной фотопленки, каждая из которых экспонируется через цветной фильтр. Поскольку в этом методе каждая голограмма пропускает лишь нужный цвет и поглощает остальные, то ложные изображения не появляются. Пространственное разделение трех голограмм может быть произведено смещением рядов ячеек разрешения, однако это требует тройного разрешения устройства вывода изображений по сравнению с синтезом одноцветных голограммы. Таким образом, желательно синтезировать голограммы, чтобы апертуры, соответствующие различным цветам, не перекрывались. Для такой цели наиболее подходит обобщение бинарных голограмм с "фазой обхода", предложенное в /22/. Каждая ячейка бинарной голограммы состоит из 5´ 5 "подъячеек", которые открываются или закрываются в зависимости от значения отсчета соответствующей функции. Такая структура ячейки оставляет достаточно места для пространственного разнесения трех цветов без наложения или потери разрешения устройства вывода изображений. Масштабирование для данного метода проводится в цифровом виде.

3.8. Применения синтезированных голограмм

Визуализация информации. Под визуализацией информации понимается синтез образов объектов или явлений, которые не существуют физически или не имеются в распоряжении исследователя, но имеют достаточно полное математическое описание в виде аналитической или цифровой модели. Задачей визуализации является отображение математической функции, описывающей объект в виде вариаций светового поля, содержащего, вообще говоря, весь видимый спектр цветов.

Схема решения такой задачи состоит в следующем. На основании выбранной модели объекта и заданной схемы голографирования рассчитывается процесс распространения света от объекта до плоскости, в которой предполагается установить голограмму. Полученный комплексный волновой фронт регистрируется методами, описанными выше. Результат регистрации называется искусственной или синтезированное

голограммой. Оптическое восстановление такой голограммы дает действительное и (или) мнимое изображение объекта. Качество изображения определяется сложностью объекта и выбором метода регистрации. Подробное рассмотрение методов визуализации содержится в /5/.

Пространственные фильтры. Под пространственной фильтрацией будем понимать выполнение над двумерными полям линейных преобразований, описываемых уравнением

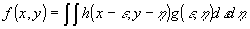(34)

Здесь g, f - поля на входе и выходе системы, соответственно, h - импульсный отклик или функция рассеяния системы. Операция (34) легко осуществляется в когерентной оптической системе, содержащей транспарант с пропусканием, определяемым функцией h. Системы оптической пространственной Фильтрации применяются при решении задач распознавания образов /23/ согласованной фильтрации /24/, улучшения качества изображений /25/, получения сверхдифракционного разрешения, выделения сигналов на фоне шумов и т.п.

Наиболее общие методы синтеза пространственных фильтров дает цифровая голография. Функция h(ε,η)=f{h(x,y)}, описывающая фильтр, является, вообще говоря, комплексной. Соответственно, для синтеза комплексных пространственных фильтров применимы методы регистрации синтезированных голограмм. Большое распространение для синтеза фильтров получил метод Ломана-кодирование комплексных величин в виде матрицы бинарных апертур. Соответствующие фильтры называются бинарными фильтрами Ломана. Развитие систем отображения информации, сопряженных с ЭВМ, позволило перейти к использованию многоградационных фильтров, в частности, синтезированных методом Ли или фильтров с несущей пространственной частотой, вводимой на этапе цифровых расчетов.

Широкое распространение в различных приложениях имеет задача вычисления коэффициентов некоторого ортогонального ряда:

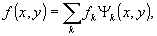(35)

где

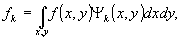(36)

а 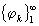- ортогональная система функций.

В частности, (35) может быть разложением Уолша или Фурье.

Наиболее перспективным для решения задач распознавания образов является разложение Карунена-Лоэва, которое приводит к некоррелированным коэффициентам разложения. В работе /26/ предложен оптимизационный подход к синтезу голограмм пространственных фильтров, вычисляющих коэффициенты ортогональных разложений по формуле (36). Предложены критерии минимума среднеквадратичной погрешности выполняемой операции и минимума корреляции между вычисляемыми коэффициентами разложения.

Оптические элементы и контроль оптических систем. Использование синтезированных на ЭВМ голограмм позволяет создать голографические оптические элементы как копирующие по своим функциям традиционные элементы, так и элементы с новыми функциональными возможностями. Последнее возможно вследствие большой гибкости методов цифровой голографии, позволяющих оказать практически произвольные воздействия на волновой фронт. В этом смысле рассмотренные пространственные фильтры являются обобщенными оптическими элементами.

Более близкими к традиционным оптический элементам является синтезированные линзы. Особенно перспективными являются киноформные линзы /27/.

Использование ЭВМ позволяет получить широкий класс диффузоров с заданными свойствами /28/. Получение таких диффузоров чисто оптическими методами затруднительно, а часто полностью невозможно.

В /29/ описан еще один нестандартный оптический элемент, синтезированный методами цифровой голографии, позволявший формировать заданное распределение мощности по сечению лазерного пучка. Синтезированная голограмма формируется на одном из зеркал резонатора лазера. Варьирование голограммы дает возможность конструировать лазеры с различной пространственной структурой луча.

Одной из основных проблем в изготовлении сложных оптических элементов высокой точности является контроль их качества. Такой

контроль наиболее эффективно производится методами лазерной интерферометрии. Наиболее распространены два метода контроля.

1. Интерферометрическое сравнение поверхности исследуемого оптического элемента с эталонным волновая фронтом или поверхностью, имеющим, по крайней мере, на порядок больщую точность.

2. Метод нулевой линзы. Последний метод сводит исследование качества асферических волновых фронтов к исследованию сферического фронта. Для этого асферический фронт трансформируется в сферический с помощью специального преобразования излучения, называемого нулевой линзой.

Изготовление эталонных оптических поверхностей и нулевых линз традиционными оптико-механическими методами является крайне сложной задачей. В то же время наиболее общие методы синтеза волновых фронтов и изготовления сложных преобразователей излучения (пространственных фильтров) дает цифровая голография. В ряде работ /30,31/ сообщается об использовании голограмм и пространственных фильтров, синтезированных на ЭВМ, в качестве генераторов эталонного волнового фронта и нулевой линзы.

4. З а к л ю ч е н и е

Цифровая голография находится на этапе перехода от изучения разрозненных явлений к формированию общей теории анализа и синтеза голограмм на ЭВМ.

С первого момента возникновения цифровой голографии результаты ее стали находить практическое применение, поскольку само возникновение было стимулировано потребностями практики и, прежде всего, потребностями физической голографии и ее приложений.

Дальнейший прогресс в области цифровой голографии связан, в первую очередь, с развитием ее теории и методов, с прогрессом в области ЭВМ, оснащенных соответствующими устройствами ввода-вывода, памятями и математическим обеспечением.

Отметим, что перспективным направлением в развитии самих ЭВМ являются гибридные оптико-цифровые процессоры и голографические памяти, создание которых, в свою очередь, базируется на достижениях цифровой голографии.

Сочетание методов физической и цифровой голографии позволит в недалеком будущем исследовать целый ряд сложных физических явлений и решить важные прикладные задачи.

Л и т е р а т у р а

1. Р.Кольер. К.Беркхарт, Л.Лин. Оптическая голография, М., "Мир", 1973.

2. Т.Хуанг. Применения голографии. М., "Мир", стр.65. 1973.

3. b.wolf. josa, 60, 1, 18, 1970.

4. w.h.carter. josa. 60, 3, 306, 1970.

5. Л.П.Ярославский, Н.С.Мерзляков. Методы цифровой голографии. М., "Наука", 1977.

6. d.casasent, r.l.herold. appl.opt., 13, 10, 2268, 1974.

7. А.Н.Тихонов, В.Я.Арсенин. Методы решения некорректных задач. М., "Наука", 1975.

8. А.И.Водзинокий, В.А.Сойфер. Автоматизация вкспериментальных исследований. Куйбышев, КуАИ, стр.41, 1976.

9. j.n.latta. appl.opt.. 10, 12, 2698, 1971.

10. М.r.rimmer, c.m.king, d.g.fox. appl.opt., 11, 12, 2790, 1972.

11. d.w.sweeney, c.m.vest. appl.opt., 12, 11, 2649, 1973.

12. j.p.hugolin, p.chavel. qpt.commun., 13, 3, 342, 1976.

13. r.e.haskell. b.С.Сulvеe. appl.opt., 11, 11, 2712, 1972.

14. w.h.lee. appl.opt., 13, 7, 1677, 1974.

15. g.ichioka, М.izumi, Т.suzuki. appl.opt., 10, 2, 403, 1971.

16. r.h.katyl. appl.opt., 11, 1, 198, 1972.

17. d.c.chu, j.w.goodman. appl.opt., 11, 8, 1716, 1972.

18. d.c.chu. josa. 63, 11, 1325, 1973.

19. d.c.chu, j.r.fienup. opt.eng., 13, 3, 189, 1974.

20. d.c.chu, j.r.fienup, j.w.goodman. appl.opt., 12, 7, 1386, 1973.

21. j.h.fienup, j.w.goodman, nouv.rev.optique, 5, 5, 269, 1974.

22. r.b.haskell. josa, 63, 4, 504, 1973.

23. t.kawatani, opt.Соmmun., 10, 3, 243, 1974.

24. w.h.lee, m.o.greer. appl.opt., 13, 4, 925, 1974.

25. g.w.stroke, m.haliona. v.srinivasan. phys.lett., А51, 7, 383, 1975.

26. М.А.Голуб, В.А.Сойфер. iv Международный симпозиум по теории информации (тезисы докладов, часть 1), М.-Л., стр.31, 1976.

27. j.j.clair. opt.conmun., 8, 2, 135, 1972.

28. p.heriharau, z.hegedus. opt.commun., 10, 3, 238, 1974.

29. d.w.sweeney, w.h.stevenson, d.k.campbell, g.shaffer. appl.opt., 15, 12, 2959, 1976.

30. j.c.wyant, p.k.o'neill., appl.opt., 13, 12, 2762, 1974.

31. t.takahashi, k.konno, m.kawai, m.isshiki. appl.opt., 15, 2, 546, 1976.