ИССЛЕДОВАНИЕ ПРОСТРАНСТВЕННЫХ АНСАМБЛЕЙ ЧАСТИЦ

С ПРИМЕНЕНИЕМ МЕТОДА ЦИФРОВОЙ ГОЛОГРАФИИ

А.И.Водзинский, В.А.Сойфер, А.Г.Храмов

Исследуется возможность цифрового восстановления объекта по голограмме, полученной при экспериментальном исследовании динамического пространственного ансамбля аэрозольных частиц. Рассматривается оптическая схема перекодировки, позволяющая сократить избыточность на голограмме перед вводом ее в ЭВМ. Предлагается алгоритм классификации микрочастиц по размерам на восстановленном изображении объекта.

В в е д е н и е

Одной из наиболее сложных и интересных задач голографии является регистрация и исследование пространственных ансамблей аэрозольных частиц /1/. Голографический метод регистрации волновых полей позволяет зависать и хранить полную информацию об исследуемом объекте, в частности, информацию о размерах и пространственном расположении аэрозольных частиц. Для регистрации голограммы быстро-движущихся частиц обычно применяется импульсный рубиновый лазер с длительностью импульса порядка 10^-8 с. Апостериорное изучение описанного динамического объекта в настоящее время производится путем визуального наблюдения восстановленного с помощью непрерывного газового лазера изображения объекта в микроскоп, обладающий малой глубиной резкости. Это дает возможность наблюдать отдельные сдои исследуемого объекта. Такой метод исследования обладает существенными недостатками, главный из которых - отсутствие какой-либо автоматизации обработки данных эксперимента. Кроме этого, на восстановленном изображении присутствуют шумы, создаваемые частицами объемного ансамбля, находящимися вне плоскости фокусировки микроскопа. Существуют также погрешности, связанные с шумами фотоэмульсии, нелинейностью записи и т.д.

Детальный анализ ансамблей частиц, компенсация погрешностей и фильтрация шумов могут быть выполнены при восстановлении изображения объекта по голограмме на ЭВМ с применением методов цифровой голографии.

В данной работе исследовались голограммы аэрозольных частиц размерами порядка 30 мкм, полученные по классической осевой схеме голографии с использованием импульсного рубинового лазера с длиной волны λ=6943 Å. Показана возможность применения устройств ввода-вывода изображений, обладающих разрешающей способностью порядка 100 мм^-1, для непосредственного ввода в память ЭВМ значений распределения интенсивности интерференционной картины на голограмме.

Кроме того, рассмотрены методы обработки на ЭВМ восстановленных оптическим способом изображений сечений пространственных ансамблей частиц, позволяющие сократить время анализа и повысить точность получаемых данных.

1. Требования к разрешающей способности устройств ввода

голограмм в ЭВМ

Получим соотношения, необходимые для определения разрешающей способности устройств ввода голограммы аэрозольных частиц в память ЭВМ. Для описания процесса распространения света от объекта к голограмме воспользуемся дифракционными соотношениями Фраунгофера, описывающими дифракцию света в дальней зоне. Дифракция Фраунгофера плоской монохроматической волны имеет место при выполнении следующего условия /2/:

z>(2a)²/λ, (1)

где 2а - диаметр круглой частицы; z - расстояние от частицы до плоскости голограммы.

Для частиц размером 5...50 мкм при z>20 мм (1) всегда удовлетворяется.

Известно /2/, что в результате дифракции Фраунгофера однородной плоской волны когерентного света на круглой частице радиуса "а " в плоскости голограммы создается распределение интенсивности:

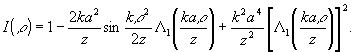(2)

Здесь k=2π/λ; ρ - радиус полярной системы координат на плоскости голограммы; Λ₁(x)=j₁(x)/x, j₁(x) - Функция Бесселя первого рода первого порядка.

Результирующее распределение интенсивности (2) содержит три члена, из которых только средний член,

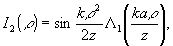(3)

является информационным при восстановлении изображения по голограмме. Он представляет собой результат интерференции между дифракционной картиной Фраунгофера частицы и когерентным опорным фоном.

Из графика функции Λ₁(х) видно, что основная энергия функции Λ₁(х) заключена на отрезке [0;2π]. Причем на конце этого отрезка в точке х = 2π значение "огибающей" функции падает до 0,04 от своего начального значения Λ₁(0)=1.

Максимальную пространственную частоту на голограмме и максимальный угол рассеяния излучения данной частицей можно определить из (3), полагая, что Λ₁(х)=0 при х>2π. Полагая аргумент функции Λ₁(х) равным 2π, найдем максимальный угол рассеяния φ_max, кoтopый определяет требуемые линейные размера голограммы:

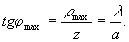(4)

Максимальная пространственная частота на голограмме определяется частотой функции "sin" из (3) в точке ρ_mах:

(5)

Таким образом, максимальная пространственная частота на голограмме Фраунгофера ν_max обратно пропорциональна диаметру микрочастицы 2а.

Известное правило Релея /3/ гласит, что любая хорошая опти-

ческая система не должна искажать фазу волнового фронта более, чем на π/2. Принимая этот критерий, получаем, что разрешающая способность устройства ввода изображений их должна удовлетворять условию:

Δx<2/4. (6)

В таблице 1 приведены требования к разрешающей способности устройств ввода и необходимые линейные размеры голограммы для регистрации микрочастиц различной величины при условии, что голограмма находится на расстоянии z=50 мм от объекта.

Таблица 1

Диаметр частицы 2а, мкм	Угол рассеяния, φmах	Минимальный размер голограммы, мм2	Разрешение устройства ввода Δх, мкм	Количество отсчетов на голограмме, n´ n
100	0,015	1,5´ 1,5	25,0	60´ 60
50	0,03	3,0´ 3,0	12,5	240´ 240
25	0,06	6,0´ 6,0	6,25	1000´ 1000
10	0,15	15,0´ 15,0	2,5	6000´ 6000

2. Цифровое восстановление трехмерного объекта до осевой

голограмме

Для цифрового моделирования процесса восстановления изображения по голограмме требуется знание основных принципов распространения волнового поля в пространстве. Цифровое восстановление основано на использовании приближения Кирхгофа задачи о дифракции. Интеграл Френеля-Кирхгофа устанавливает связь между распределениями комплексной амплитуды света в плоскости объекта (или голограммы) и в плоскости, удаленной на некоторое расстояние в направлении распространения волн.

Строгое решение интеграла Френеля-Кирхгофа в частотной области /4/ дает следующий результат.

Если плоская волна единичной амплитуды распространяется в направление оси "z " и падает на помещенный в плоскости z=0 транспарант с амплитудным пропусканием t(u,v) , то спектр a(ε,η,d) комплексной амплитуды волны в плоскости z=d имеет вид:

a(ε,η,d)=t(ε,η)∙Φ(ε,η,d), (7)

где

t(ε,η)=f{t(u,v)},

Φ(ε,η,d)=exp[-i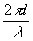(1-λ²ε²-λ²η²)^1/2],

f - оператор двумерного преобразования Фурье.

Если t(u,v) представляет собой амплитудное пропускание голограммы, зарегистрированной по классической схеме с осевым опорным пучком, то соотношение (7) моделирует процесс восстановления действительного изображения объекта. В этом случае a(ε,η,d) - спектр восстановленного сечения объекта при d=const. Комплексное распределение амплитуды света в произвольном сечении z=d восстановленного объекта определяется следующим образом:

a(u,v,d)=f^-1{Ф(ε,η,d)f{t(u,v)}}. (8)

Как видно из (8), восстановление объекта по слоям легко реализуется на ЭВМ и алгоритмически описывается следующими операциями.

1. Выполнение двумерного преобразования Фурье над массивом исходных данных.

2. Умножение результата на известный фазовый множитель.

3. Выполнение обратного двумерного преобразования Фурье. Заменим, что п.п. 2÷3 выполняются заново для каждого восстанавливаемого сечения.

Рассмотрим схему записи голограммы с осевым опорным пучком (рис.1). Объект освещается плоской волной с амплитудой i(х,у), которая дифрагирует на микрочастицах и создает в плоскости голограммы информационное поле и (х,у). Голограмма регистрирует интенсивность интерференционной картины объектного и опорного пучков:

i(x,y)=|1+u(x,y)|²=[1+|u(x,y)|²]+u(x,y)+u^*(x,y). (9)

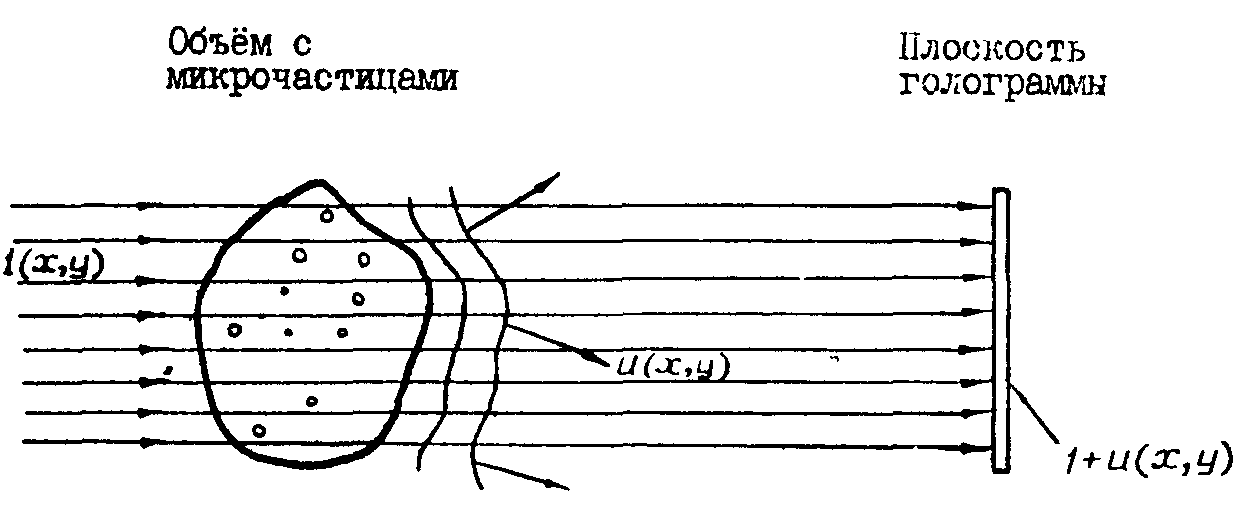
Рис.1. Осевая схема записи голограммы микрочастиц.

Последние два слагаемых в (9) несут информацию об объекте, а первые два создают шумы. Для ввода в ЭВМ требуется лишь одна из функций, u(х,у) или u^*(x,y), соответствующих действительному и мнимому изображению. Другая из них будет создавать шумовой фон при цифровом или оптическом восстановлении.

Восстановленное действительное трехмерное изображение объекта (рис.2) является результатом дифракции плоской волны i(х,у) на интерференционной структуре голограммы в описывается функцией p(x₁,y₁,d), которую можно аппроксимировать набором поперечных сечений p(x₁,y₁,d_n):

d_n=d₀+n∙Δd, n=1,2,... К, К - количество сечений.

Если размера голограмма и объекта малы по сравнению с расстоянием между ними r то справедливо параксиальное приближение Френеля, которое приводит (7) к следующему виду:

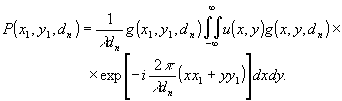(10)

Здесь

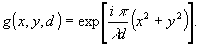
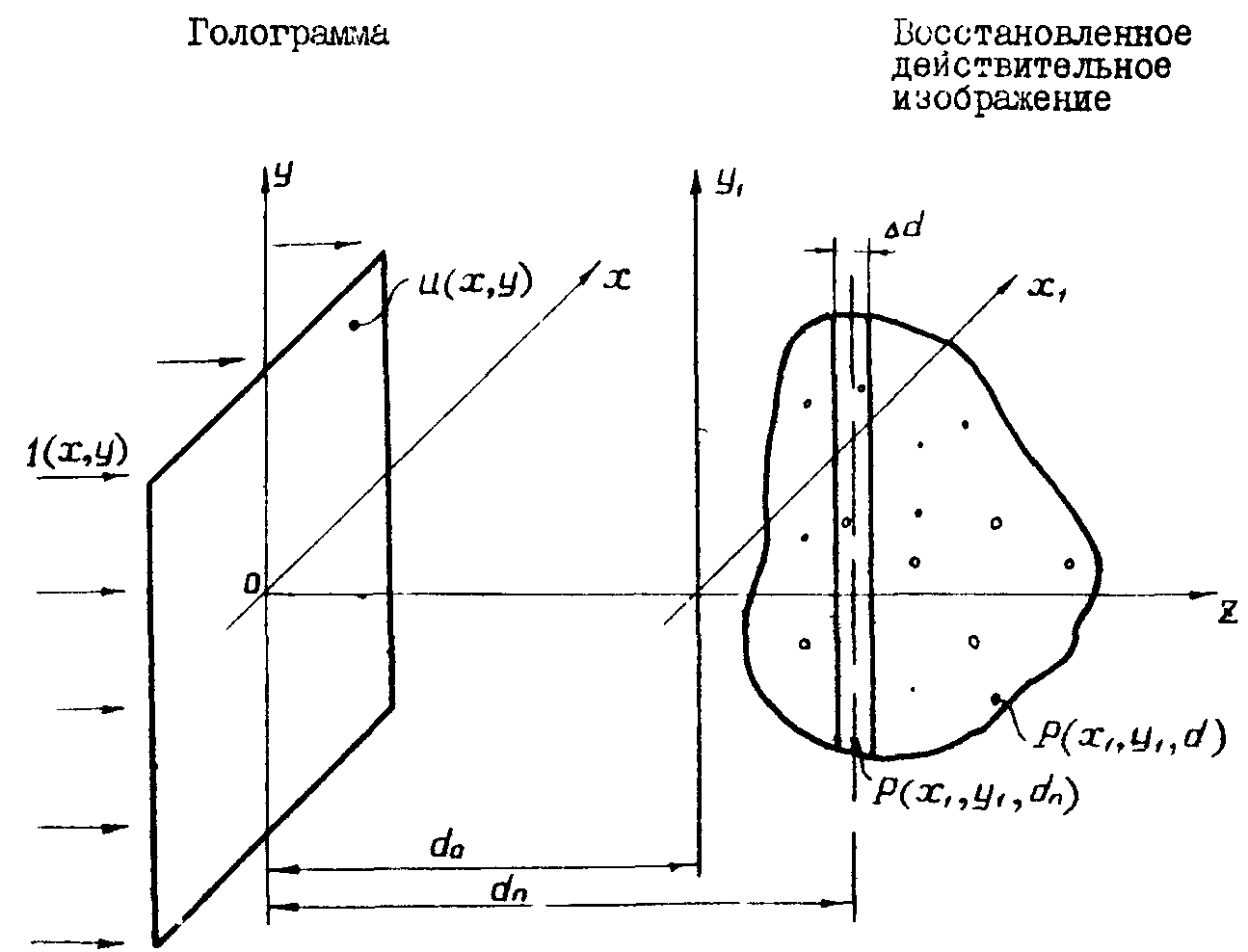
Рис.2. Схема восстановления действительного изображения ансамбля микрочастиц.

Переходя от непрерывных величин к дискретным, можно получить следующую цифровую модель:

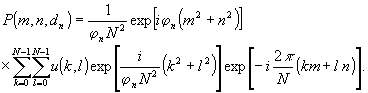(11)

Здесь

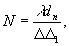
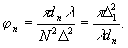
Δ θ Δ₁ - интервалы дискретизации в плоскости голограммы и плоскости восстановленного сечения объекта, соответственно.

Двойная сумма (11) легко подсчитывается на ЭВМ с использованием алгоритма быстрого преобразования Фурье.

Как показано в /5/, восстановление голограммы на ЭВМ имеет свои преимущества и недостатки. Основной недостаток цифрового восстановления заключается в том, что объект восстанавливается не сразу, а по отдельным плоским сечениям, что вызывает появление помех от соседних несфокусированных сечений. Проведенное нами моделирование показало, что эти помехи существенно уменьшаются при уменьшении периода дискретизации голограммы при вводе и, соответственно, увеличении количества отсчетов во введенной голограмме.

3. Оптическая схема для устранения голографической

избыточности

В настоящее время широко применяется двухлучевая схема записи голограммы /1/, которая имеет значительные преимущества по сравнению с однолучевой схемой. В частности, она позволяет полностью разделить действительное и мнимое изображения при оптическом восстановлении голограммы. Однако такая схема приводит к высокой плотности записи информации на голограмме. Пространственная несущая частота на голограмме, равная sinθ/λ, δостигает величины порядка 10³ мм^-1 уже при угле наклона опорного пучка θ=30°, что не позволяет ввести и обработать голограмму на ЭВМ. В то же время информационная составляющая занимает лишь 5% пространственного диапазона частот.

Возникает задача сжатия информации оптическими методами для ликвидации избыточности до ввода в ЭВМ. Это можно сделать путем устранения пространственной несущей частоты.

Голограмма с наклонным опорным пучком регистрирует интенсивность:

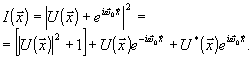(12)

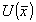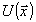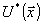Для выделения из (12) функции , требующейся для ввода в ЭВМ, предлагается использовать схему перекодировки голограммы, представленную на рис.3. Световые волны и и распространяются под углами ±θ к голограмме, освещенной плоской волной 1().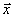

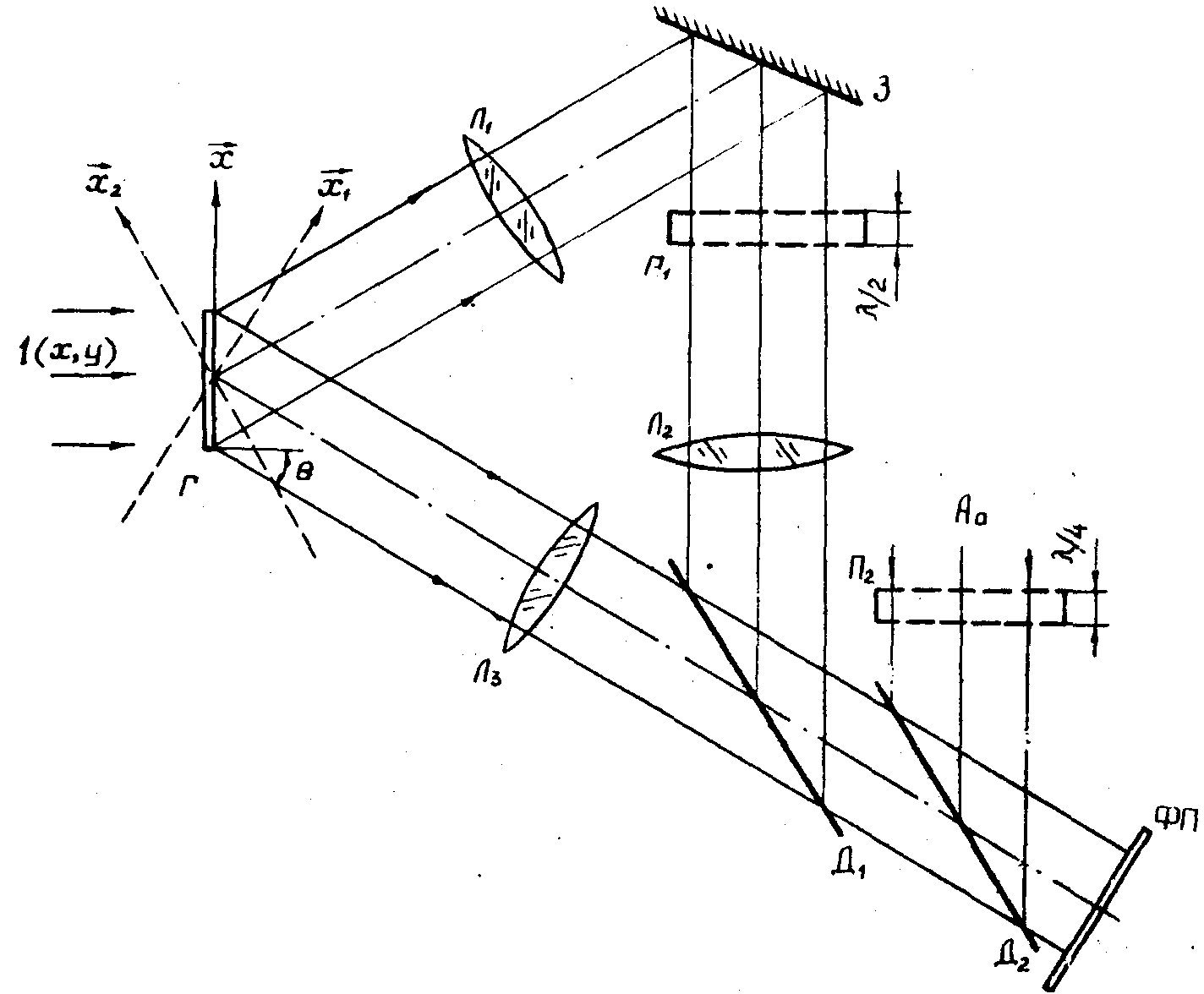
Рис.3. Схема оптической перекодировки голограммы.

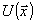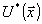Суммируя комплексные амплитуды и с помощью рассматриваемой оптической системы, можно выделить вещественную и мнимую компоненты комплексного поля u(х), которые вводятся в ЭВМ в виде матриц неотрицательных вещественных чисел. С помощью оптической системы, состоящей из линз Λ₁, Λ₂ и Λ₃, зеркала З, светодели-

телей Д₁ и Д₂ комплексные поля 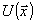и 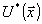переносятся из плоскости голограммы на плоскость фотопластинки ФП, которая зарегистрирует либо сумму, либо разность полей u и u^* в зависимости от наличия или отсутствия фазовых пластинок П₁ и П₂ "толщиной" λ/2 и λ/4, соответственно:

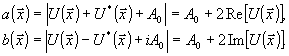(13)

Выбрав амплитуду опорной волны А₀ достаточно большой, можно провести однозначное восстановление на ЭВМ комплексной функции 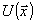по введенным величинам 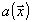и .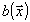

4. Классификация микрочастиц по размерам

Восстановленное на ЭВМ или оптическим способом изображение сечения ансамбля микрочастиц необходимо обработать с целью классификации аэрозольных частиц по размерам и определения их координат. Полученные данные могут в дальнейшем использоваться для расчета, например, плотностей распределения частиц в различных точках исследуемого объема.

Алгоритм классификации основан на преобразовании изображения в бинарное способом порогового квантования и выделении контуров областей высокой интенсивности. Эти области нумеруются последовательными целыми числами с одновременным подсчетом площади частицы и координат ее центра тяжести. Характерной особенностью данного алгоритма является возможность обработки изображений больших размеров, хранящихся на магнитной ленте построчно, т.к. в оперативной памяти ЭВМ одновременно находятся лишь две строки изображения.

Результатом такой предварительной обработки является массив данных {si,xi,yi,zi}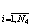, где s_i - площадь частицы, а (x_i,у_i,z_i) - декартовы координаты центра частицы. На рис.4 показан пример работы алгоритма. Рассмотренный алгоритм был использован для автоматизации обработки изображений сечений, восстановленных оптическим способом из тестовой голограммы ансамбля микрочастиц, в качестве которых использовались споры ликоподий, имею-

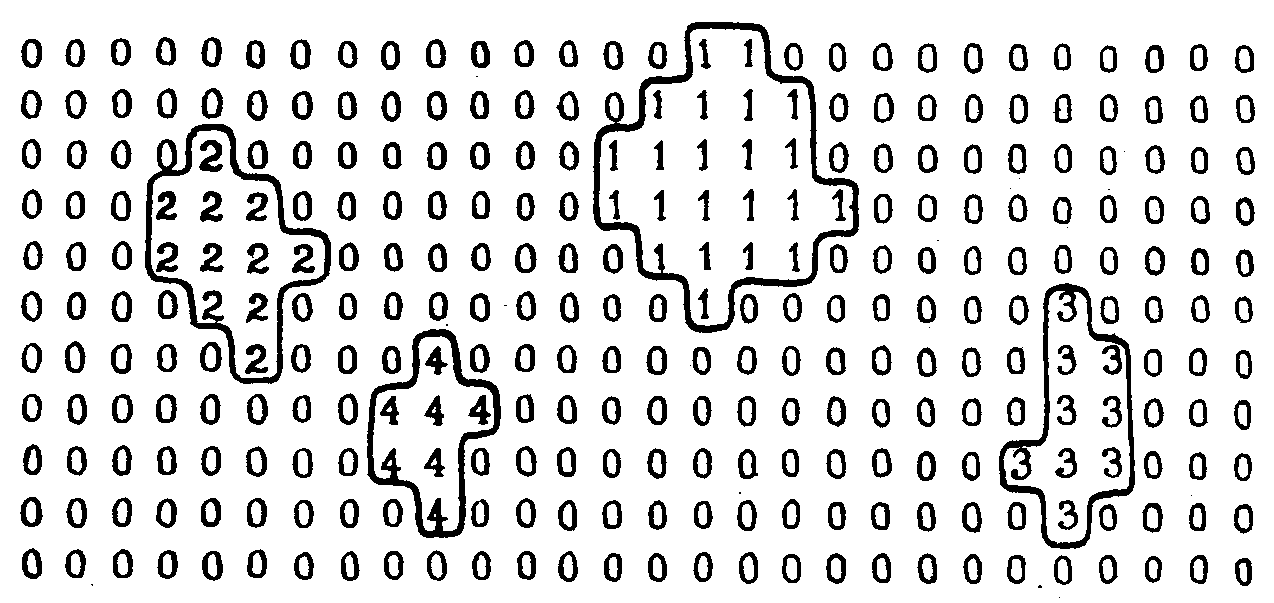
Рис.4. Результат работы построчного алгоритма классификации частиц по размерам.

щие размеры порядка 30 мкм в диаметре. В результате построены гистограммы распределения микрочастиц по размерам в каждой из рассматриваемых сечений, находящихся на расстоянии 40 мм и 50 мм от плоскости голограммы. Каждое изображение сечения, восстановленное с голограммы, увеличивалось в 100 раз с помощью микроскопа, регистрировалось на фотопленку и вводилось в ЭВМ с шагом дискретизации 25 мкм. 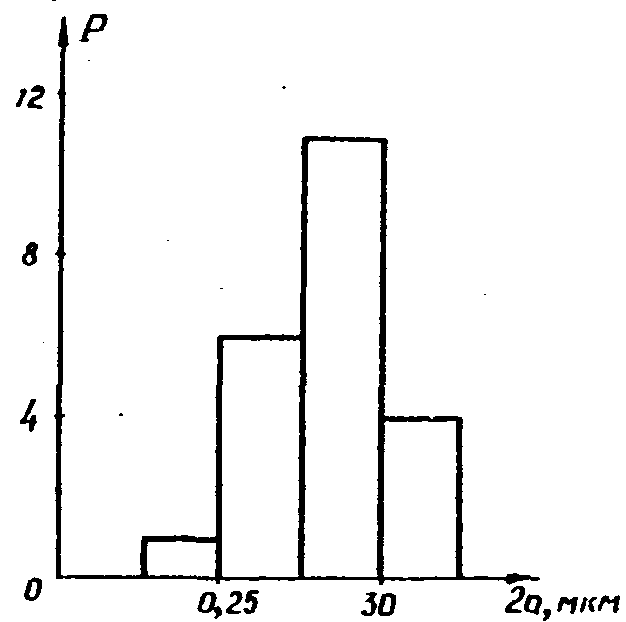Количество отсчетов - 1000´ 1000. Рассчитанные гистограммы, показанные на рис.5 и 6, совпадают с гистограммами, полученными при визуальном наблюдении.

Рис.5. Распределение частиц в сечении z=40 мм.

 

 

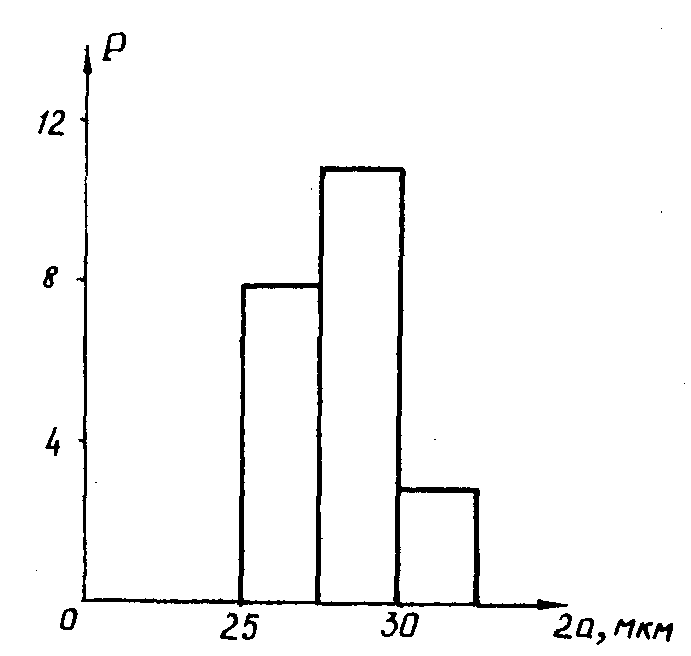
Рис.6. Распределение частиц в сечении z=50 мм.

 

Л и т е р а т у р а

1. Д.И.Стаселько. Особенности голографической регистрации быстро-протекающих процессов при использовании импульсного лазера на рубине. В сб."Оптическая голография", Л., "Наука", стр.4, 1975.

2. В.a.silverman, В.j.thompson, 3, 12, ward.

journal of applied meteorology, 3, 12, 792, 1964.

3. М.Борн, Э.Вольф. Основы оптики. М., "Наука", стр.428, 1973.

4. Р.Кольер, К.Беркхарт, Л.Лин. Оптическая голография. М., "Мир", стр.126, 1973.

5. Т.Н.demetrakopoulos, r.mittrа.

applied optics, 13, 3, 665, 1974.