Media-security

МЕТОДЫ ЦИФРОВОГО СИНТЕЗА ЭЛЕМЕНТОВ КОГЕРЕНТНЫХ ОПТИЧЕСКИХ УСТРОЙСТВ ОБРАБОТКИ СИГНАЛОВ

Н.С.Мерзляков

Обсуждаются методы цифрового синтеза оптических элементов. Анализируются условия согласования результатов расчетов с характеристиками реально существующих и используемых сред и средств регистрации. Приведены экспериментальные результаты по синтезу на ЦВМ фильтров, дифракционных решеток и линз.

В в е д е н и е

Создание гибридных оптико-электронных устройств обработки сигналов, сочетавших в себе достоинства когерентных оптических устройств и возможности цифровых электронных вычислительных машин является наиболее перспективным в развитии систем высокоэффективной обработки информации. Одна из основных задач, которую необходимо решить для того, чтобы создать такие устройства, заключается в разработке методов синтеза и регистрации оптических транспарантов, управляемых с помощью ЦВМ: фильтров, линз, дифракционных решеток, в том числе киноформного и многослойного типа.

Наиболее широко распространенными являются фоторегистрирующие устройства с вращающимся барабаном и электромеханической разверткой, режим которой управляется директивами, поступающими из ЦВМ. Модулируемым источником света служит лазерный диод, излучающий чаще всего в красной области спектра, а регистрирующей средой является фотопленка, чувствительностью порядка 180-250 ед.Госта.

Методы цифрового синтеза элементов оптических систем можно разделить на две группы: синтез элементов по заданному математическому описанию и синтез элементов (также чаще всего по заданному математическому описанию) методами цифровой голографии, позволяющими регистрировать комплекснозначные величины и создавать

многослойные оптические элементы типа "сэндвича", управляющие комплексной амплитудой проходящего через транспарант света.

Основная проблема задачи регистрации оптических элементов, синтезированных на ЦВМ, заключается в согласовании результата расчетов с возможностями реально существующих регистрирующих устройств и сред регистрации, коррекции их нелинейности.

Один из возможных способов учета нелинейности регистратора заключается в нелинейном предыскажении, обратном характеристике регистратора, которому следует подвергнуть матрицу чисел, описывающих оптический элемент перед его регистрацией на фотопленку в устройстве регистрации.

Поскольку, как правило, регистрируемая величина пропорциональна плотности почернения фотоматериала, которая, в свою очередь, нелинейно связана с коэффициентом пропускания света по интенсивности, существенным при взаимодействии светового потока с синтезированным транспарантом, перед регистрацией транспаранта на фотопленку необходимо компенсировать эту нелинейность регистрирующего устройства с учетом характеристической кривой реально используемой фотопленки при стабилизированном режиме обработки пленки.

Коррекцию нелинейности характеристической кривой используемой фотопленки можно выполнить следующим образом: для каждого усредненного значения плотности почернения, полученного при фотометрировании сенситометрического клина, синтезированного в ЦВМ и зарегистрированного на данной пленке, вычислить соответствующий коэффициент пропускания. Результаты расчетов, представленные, например, в виде таблицы, ввести в ЦВМ и использовать на этапе регистрации транспаранта, предыскажая регистрируемый сигнал в соответствии с характеристической кривой фотопленки.

1. Синтез простейших оптических фильтров

Наличие прецизионного фоторегистратора и учет нелинейности регистрирующей среды позволяют решить задачу синтеза с помощью ЦВМ простейших масок и фильтров когерентных оптических устройств обработки сигналов. Первыми простейшими фильтрами, синтезирован-

ными на ЦВМ, были фильтры, описываемые степенной зависимостью регистрируемого параметра:

В(ξ,η)=(ξ-ξ₀)ⁿ(η-η0)^m, (1)

Результаты расчетов по формуле (1) регистрировались в виде распределения плотности почернения, пропорциональной значениям b(ξ,η). Время, требуемое для расчета такого фильтра, состоящего из 200´ 200 элементов, порядка 10 минут для программ, написанных на алгоритмическом языке bаsic. На рис.1 приведен пример центральносимметричного фильтра с параболическим законом распределения плотности пропускания от центра фильтра к его краю вида

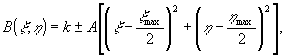(2)

где k, А - некоторые константы, которые можно изменять программным путем.

Число элементов в этих фильтрах переменно и может достигать 1024´ 1024 элементов. Время расчета фильтра типа (2) и размером 1024´ 1024 элементов составляет порядка 2 минут. Кроме того, синтезировались маски в виде регулярных прямоугольных решеток (типа дифракционных) заданной частоты, прямоугольных дифракционных решеток со сбоем, масок типа "шахматное поле" и "шахматное поле со случайным распределением элементов"

В некоторых случаях результаты расчетов приходится записывать

на дополнительный носитель, например, перфоленту, магнитную ленту и т.д., в случае, когда расчет выполняется на ЦВМ, не имеющей специального устройства фоторегистрации, или когда расчет проводится в реальном времени при измерении одного или нескольких физических параметров. В этом случае регистрация, как правило, выполняется непосредственно с того носителя, на котором результаты расчетов и измерений.

2. Синтез сложных комплексно-значных оптических элементов

методами цифровой голографии

Методы цифровой голографии позволяют сравнительно простым способом синтезировать на ЦВМ достаточно сложные комплексно-значные фильтры, являющиеся по существу голограммами, и различные оптические элементы и с помощью специализированного устройства регистрации зарегистрировать результат расчетов на фотопленке. Методы регистрации синтезированных на ЦВМ оптических элементов (фильтров, линз) можно разделить на две группы: методы бинарной (двухградационной) регистрации - в этом случае амплитуда световой волны передается величиной площади полностью прозрачного отверстия, а фаза - смещением этого отверстия относительно его регулярного положения на некоторой решетке - и методы многоградационной (полутоновой) регистрации /1/. В случае полутоновой регистрации используется либо искусственное симметрирование заданной исходной функции, описывающей, например, импульсный отклик реальной оптической системы для того, чтобы результат расчета был чисто действительным, либо вводится пространственная несущая, позволяющая зарегистрировать амплитуду и фазу световой волны и сместить восстановленный сигнал из нулевого порядка дифракции в более высокий. Методы синтеза и регистрации голограммных элементов подробно рассмотрены в /2/.Описанная в /2/ методика была использована для создания фильтра-голограммы, представляющего собой двумерный спектр Фурье исходного сигнала, заданного, например, в виде фототранспаранта. Этот фильтр можно рассматривать как фильтр, согласованный с исходным сигналом, и использовать его в когерентных оптических корреляционных устройствах для обнаружения и выделения данного сигнала.

Пример исходного сигнала, заданного в виде полутонового транспаранта и голограммы - фильтра этого сигнала, рассчитанных и зарегистрированных по методике /2/, показан на рис.2 и 3, соответственно.

Остановимся более подробно на методике синтеза амплитудно-фазового фильтра, предназначенного для устранения геометрической дефокусировки изображения, вносимого оптической системой. Импульсный отклик такой системы в параксиальном приближении представляет собой кружок рассеяния некоторого конечного радиуса r, а соответствущая передаточная функция такой системы имеет вид 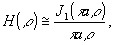/3/:

(3)

где а - некоторая константа, 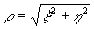- пространственная круговая частота, а j₁ - функция Бесселя 1-го порядка. Для того, чтобы устранить дефокусировку оптической системы, необходимо синтезировать фильтр (типа винеровского), передаточная характеристика которого с учетом шумов была бы обратной передаточной характеристике изображающей системы. Блок схема синтеза такого фильтра показана на рис.4. В блоке 1 осуществляется синтез импульсного отклика оптической системы; с учетом действующей апертуры оптической системы, ее фокусного расстояния и максимальной пространственной часто-

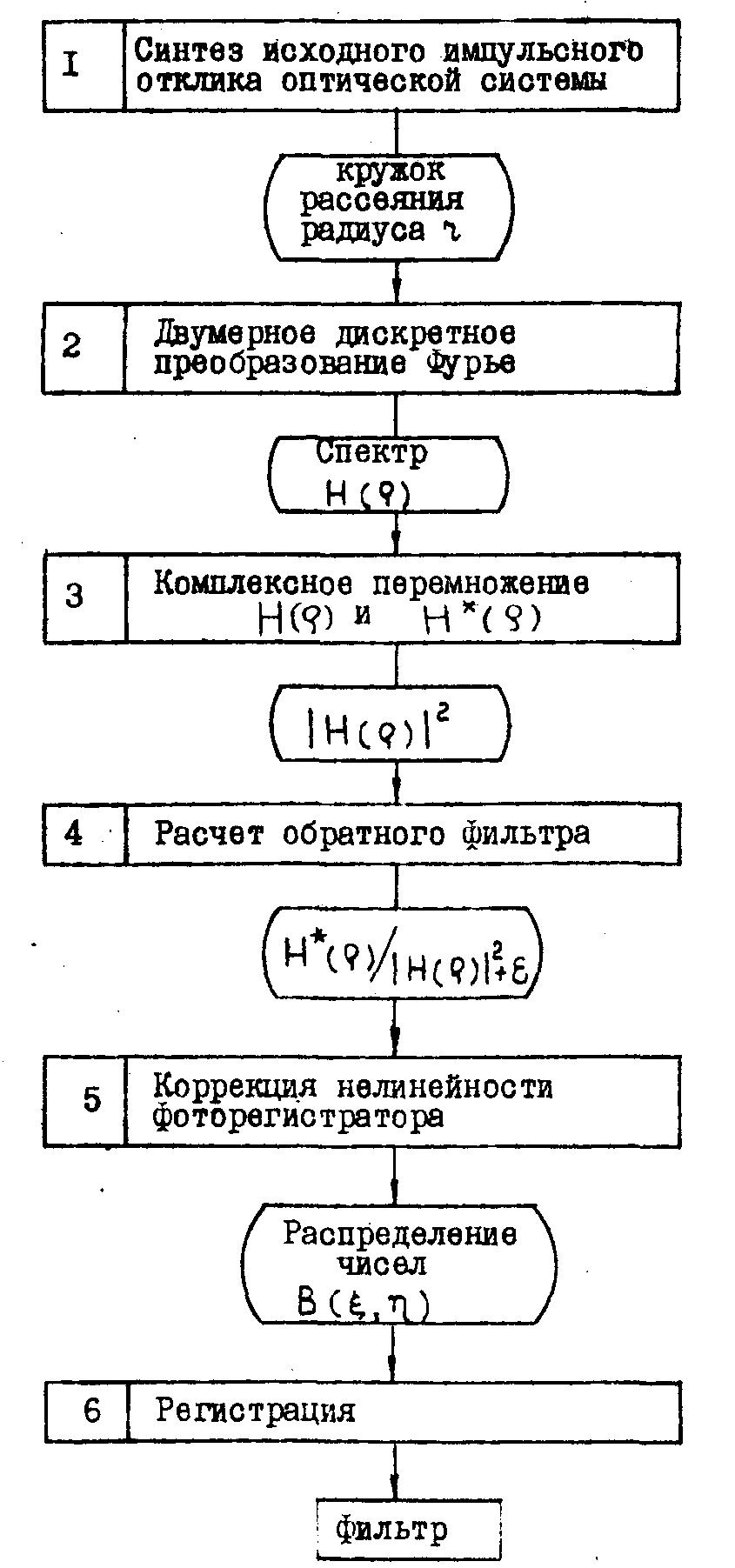
Рис.4. Блок-схема синтеза фильтра для устранения геометрической дефокусировки оптической системы.

ты ν=40 л/мм радиус кружка рассеяния r= 125 мкм и имел постоянную амплитуду. Для того, чтобы уменьшить краевые эффекты, возникающие при выполнении дискретного преобразования Фурье, кружок подвергался сглаживанию по следующему закону:

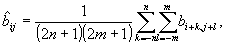(4)

где b_ij - исходный элемент кружка рассеяния, а 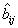- преобразованный.

После применения преобразования (4) амплитуда кружка рассеяния на краях быстро уменьшалась. В блоке 2 выполнялось двумерное дискретное преобразование Фурье. В силу центральной симметрии импульсного отклика результат фурье-преобразования был вещественным и также центральносимметричным. На рис.5 показана зависимость модуля амплитуды спектрального сигнала (в логарифмическом масштабе) от пространственной частоты в центральном сечении передаточной характеристики системы. А на рис.6 приведен в аксонометрической проекции логарифм модуля передаточной функции оптической системы с расфокусировкой. В действительности же каждая четная полуволна передаточной функции имеет отрицательный знак.

В блоке 3 выполняется перемножение спектра Н(ρ) в силу его действительности самого на себя. В блоке 4 рассчитывается фильтр с обратной передаточной характеристикой, причем значение ε, яв-

ляющееся отношением полезного сигнала к шуму, выбирается экспериментально и с учетом ограниченного числа уровней квантования регистрируемого сигнала. В блоке 5 полученный в результате расчетов массив чисел подвергается предыскажению, компенсирующему нелинейность регистратора, в этом же блоке вводится пространственная несущая.

Введение пространственной несущей продиктовано следующими соображаниями: хотя результат Фурье-преобразования веществен, тем не менее необходимо передать отрицательные значения соответствующих Фурье-коэффициентов b(ξ,η). Поэтому для передачи одного отсчета фильтра (одного Фурье-коэффициента), отводится 2 отсчета регистратора по следующему закону:

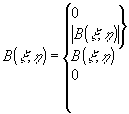
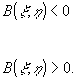(5)

Рис.7 поясняет приведенные выше соображения.

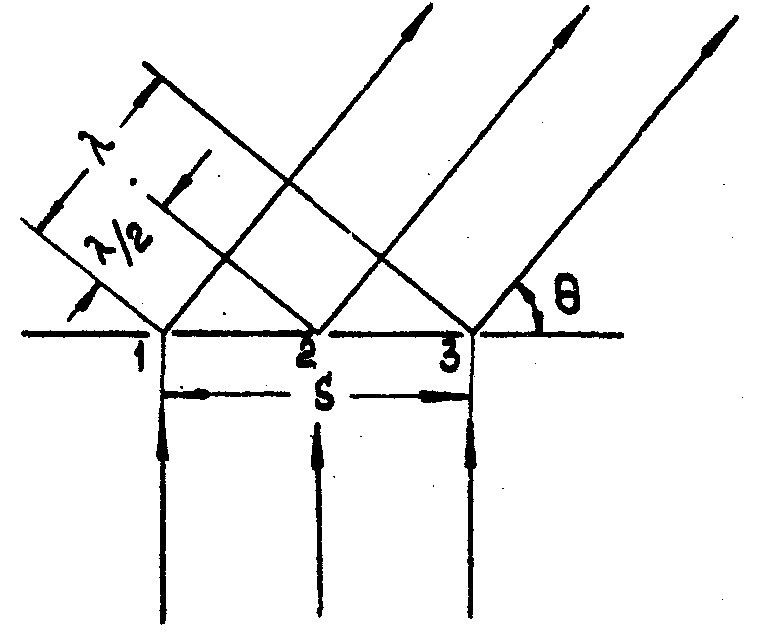
Рис.7. Сечение части фильтра.

Рассмотрим дифракционную картину первого порядка в дальнейшей зоне дифракции, наблюдаемую под углом θ=arccos (λ/s) 1/s- частота следования отсчетов фильтра γ, при освещении фильтра плоской однородной волной длины λ. Легко показать, что разность хода волн из точек 2, 3 относительно волн из точек 1, 2 равна λ/2 для каждой пары волн, а это соответствует сдвигу фазы между ними на π. Поэтому в соответствии с (6) сдвиг фаз, вносимый двумя отсчетами фильтра, будет равен π или кратен ему только тогда, когда эти отсчеты имеют разные знаки в расположены, например, в точках 1 и 2, соответственно (см.рис.7).

Таким образом, две отрицательные величины, расположенные в соседних элементах разрешения регистратора, эквивалентны одной величине, принимающей как положительные, так и отрицательные значения.

В блоке 6 осуществляется регистрация на фотопленку скорректированного массива чисел, описывающих закон изменения амплитуды и фазы с обратной передаточной характеристикой. При выводе фильтра для придания ему симметричной формы каждая его строка повторяется дважды. Фильтр содержит 512´ 512 независимых отсчетов, которые закодированы с помощью 512´ 1024 чисел. Симметрированный фильтр содержит 1024´ 1024 отсчета, имеет размер при растре 25 мк равный 25,6 мм и показан на рис.8.

На рис.9 показана зависимость амплитудного пропускания такого фильтра от координаты (по вертикальной оси отложен коэффициент пропускания, по горизонтальной - координата).

Передаточная характеристика оптической системы с расфокусировкой была использована при проведении экспериментов по моделированию дефокусировки изображения и его восстановлению на ЦВМ с использованием обратного фильтра.

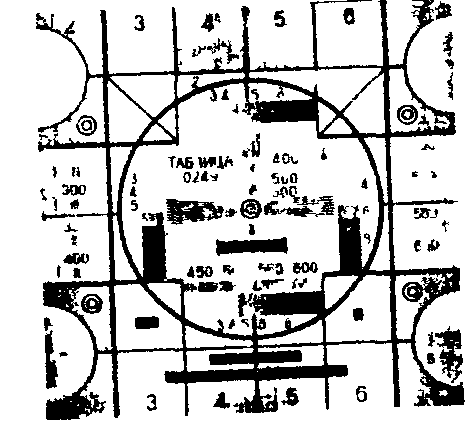
На рис.10а приведено изображение, расфокусированное в ЦВМ, а на рис.10б изображение, восстановленное в ЦВМ с помощью синтезированного фильтра, описанного ранее.

Кроме синтеза фильтров, методы цифровой голографии применимы и к синтезу различного рода оптических элементов, таких как линзы Френеля, цилиндрические линзы.

На рис.11а, б приведены изображения линзы Френеля и цилиндрической линзы, зарегистрированные с введением пространственной не-


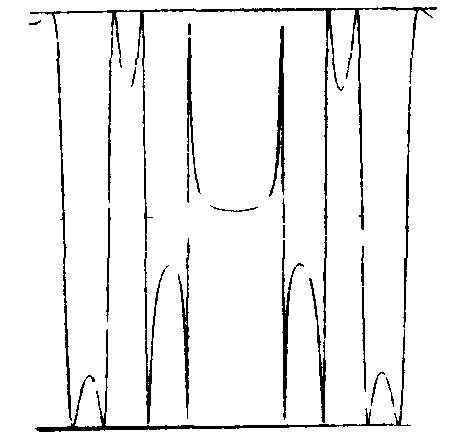
Рис.8. Фильтр для устранения геометрической дефокусировки оптической системы.	Рис.9. Зависимость амплитудного пропускания фильтра от координаты (по вертикальной оси отложен коэффициент пропускания).

а)	б)
Рис.10. Моделирование дефокусирующего действия оптической системы, формирующей изображение и устранение результата дефокусировки с помощью обратного фильтра: а -расфокусированное изображение; б - восстановленное.

сущей. По внешнему виду каждая из них очень сильно отличается от своего классического аналога, тем не менее обе они обладают фокусирующим действием. Например, линза Френеля имеет передний и задний фокусы, которые расположены по обеим сторонам от оптической оси системы в +1 и -1 порядках дифракции, соответственно. На рис. 12а,б,в приведено изображение, восстановленное в оптической систе-

а)	б)
Рис.11. а - сферическая линза; б - цилиндрическая линза.

ме с голограммы, при расчете которой на нее накладывалась положительная сферическая линза (массив чисел, описывающих голограмму, умножался на массив чисел, описывающих линзу):

а) изображение в передней фокальной плоскости линзы (+1 порядок дифракции),

б) изображение в плоскости Фурье (0 порядок дифракции),

в) изображение в задней фокальной плоскости синтезированной линзы (-1 порядок дифракции).

а) б) в)

Рис.12. Изображения, восстановленные с цифровой голограммы, содержащей сферическую линзу: а - передняя фокальная плоскость линзы; б - плоскость Фурье; в - задняя фокальная плоскость линзы.

Для сравнения на рис.13 приведено изображение, восстановленное с обычной синтезированной голограммы Фурье, содержащее как и обычно два сопряженных изображения, находящихся в одном фокусе.

Приведенные результаты позволяют надеяться, что уже в ближайшее время оптические элементы, синтезированные на ЦВМ, найдут широкое применение в когерентных оптических устройствах обработки сигналов,

Л и т е р а т у р а

1. Т.Хуанг. Цифровая голография. В сб. "Применение голографии" под ред. Дж.Гудмена, М., "Мир", стр.65-78, 1973.

2. Л.П.Ярославский, Н.С.Мерзляков. Методы цифровой голографии, М., "Наука", 1977.

3. Дж.Гудмен. Введение в фурье-оптику, М., "Мир", 1970.