ОЦЕНКА ТОЧНОСТИ МОДЕЛИРОВАНИЯ ПРОЦЕССА

ЗАПИСИ И ВОССТАНОВЛЕНИЯ ГОЛОГРАММ

А.М.Беккер

В работе оценивается точность моделирования процесса записи и восстановления голограмм. Дня оценок используется полиномиальная аппроксимация функции амплитудного пропускания эмульсии. Получено выражение для оценки вклада высоких порядков в восстановленное изображение и точности моделирования. Эти величины рассчитаны для ряда случаев и показано, что точность моделирования является вполне приемлемой для его эффективного использования.

При решении задачи выбора параметров записи голографических элементов когерентнооптических систем обработки информации приходится прибегать к моделированию процесса записи и восстановления голограмм. В нашей предыдущей работе /1/, а такие в работах ряда других авторов /2-3/ используется следующая схема моделирования: по измеренной или вычисленной зависимости дифракционной эффективности голограмм двух плоских волн с отношением амплитуд q и временем экспозиции Т (в наших обозначениях d²(q,t)) вычисляется функция комплексного-пропускания голограмм Ф(ξ) по формуле:

Ф(ξ)=d(q(ξ),t), (1)

где q(ξ) - распределение амплитуды предметной волны в плоскости записи голограммы. Преимущества такого метода состоят в том, что он позволяет избежать интегрирования быстроосциллирующих функций амплитудного пропускания голограммы для вычисления значений требуемых характеристик. Он позволяет также использовать предварительное табулирование и интерполяцию значений функции d(q,t). Это значительно сокращает объем вычислений, что особенно важно при решении задач нелинейного программирования. Пример использования

указанных преимуществ метода моделирования в задаче нахождения оптимальных параметров записи голографических фильтров содержится в работе /1/.

Целью настоящей работы является оценка точности описанного выше способа моделирования, не проводимая ни в одной из работ. Для упрощения выкладок рассмотрим одномерный случай. Кроме того, будем считать, что функция пропускания входного транспаранта при записи голограммы Фурье положительная и четная, это обеспечивает вещественность амплитуды поля в плоскости записи. Обобщение этого случая не вызывает никаких трудностей.

Введем обозначения и отметим априорные предположения относительно рассматриваемых в работе функций.

Обозначим функцию амплитудного пропускания входного транспаранта через g(x). Относительно g(х) предположим, что 0≤g(x)≤m и что g(x)=g(-x), кроме того, естественно считать, что g(x)=0 при |x|>d, Фурье-образ функции g(х) обозначим q(ξ). Через χ(Е) обозначим функцию зависимости амплитудного пропускания эмульсии от экспозиции. Будем считать, что χ(Е) дважды непрерывно дифференцируема. Через Ф_А(ξ) θ Ф(ξ) обозначим, соответственно, функции амплитудного и комплексного пропускания голограммы, а через φ₁(х) амплитуду восстановленной голограммой волны в первом порядке дифракции в фурье-плоскости.

Отметим некоторые свойства функции q(ξ):

1° q^k(ξ)Î l2(-∞,∞), где k³ 1;

2° q(ξ) → 0 при ξ→∞; это свойство вытекает из предположений, сделанных относительно функции g(x) (очевидно, что g(x)Î l₁(-∞,∞)) по теореме Римана-Лебега (см. /4/);

3° 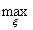q(ξ) = q(0), В самом деле

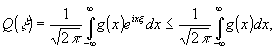(2)

а при ξ = 0 достигается равенство.

В дальнейших рассмотрениях мы будем использовать аппроксимацию функции амплитудного пропускания эмульсии χ(e) полиномом. Поэтому вначале докажем следующую, лемму.

Лемма. Пусть функция f(ξ)Î l₂ ограничена и f(ξ)→0 при ξ→∞. Тогда существует полином Р(Е) такой, что

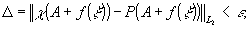(3)

где А - постоянная, а ε - произвольно малое положительное число.

Под ||g(ξ)|| мы, как обычно, понимаем

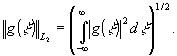(4)

Выпишем подробно значение

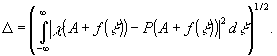(5)

Введем обозначение

δ(ξ)=χ(a+f(ξ))-p(a+f(ξ)). (6)

Разобьем область интегрирования в формуле (5) на три участка:

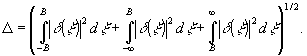(7)

Здесь В выбрано так, чтобы f(x )<<1 при |ξ|³ В и

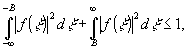(8)

это можно сделать в силу свойств функции f(ξ).

Оценим теперь три интеграла, входящие в формулу (7). Для первого из них оценка очевидна:

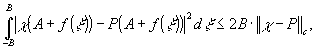(9)

где под ||g(ξ)||_с понимается 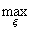|g(ξ)|.

Для того, чтобы оценить второй интеграл (а аналогично и третий), разложим подынтегральную функцию в ряд Тейлора в окрестности точки

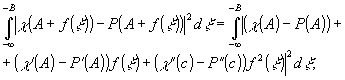(10)

где С лежит в интервале [А-m_f, А+m_f], m_f=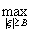f(ξ). Аргумент функции χ(Е) из-за ограниченности f(ξ) изменяется на ограниченном интервале [А-maхf; А+maхf], следовательно по теореме Вейерштрасса (см. /5/) функция χ(Е) может быть равномерно приближена полиномом. Приближающий полином может быть выбран так, чтобы χ(А)=Р(А). В самом деле, если требуемая точность приближения ε, то можно выбрать полином Р₁(Е), приближающий χ(Е) с точностью ε/2, и в качестве Р(Е) рассмотреть

p(e)=p₁(e)+χ(a)-p₁(a). (11)

Учитывая (9) и (10), а также способ выбора числа В, можно вделать cледующую оценку величины Δ²:

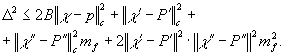(12)

Так как по теореме Бернштейна (см. /5/) всякая дважды непрерывно дифференцируемая функция может быть равномерно приближена полиномом вместе со своими производными, все слагаемые суммы в формуле (12) могут быть сделаны сколь угодно малыми. Лемма доказана. Рассмотрим теперь амплитудное пропускание голограммы:

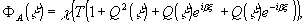(13)

где 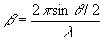; q - угол между опорной и предметной волнами. Положив Т=a и f(ξ) = q²(ξ) + q(ξ)e^iβξ + q(ξ)e^-iβξ , а такие учитывая сформулированные выше свойства функции q(ξ), мы удовлетворим всем условиям леммы. Таким образом, мы можем проводить все рассмотрения, считая χ(Е) полиномом. Погрешность при этом может быть сделана сколь угодно малой. Ее можно оценить, используя формулу (13).

Введем теперь в рассмотрение функцию двух переменных:

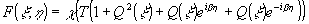(14)

Эта функция такова, что

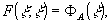(15)

а описанный нами в начале работы процесс моделирования состоит в том, что комплексная функция пропускания голограммы определяется по формуле:

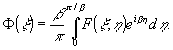(16)

Нам нужно оценить разность двух функций: модели восстановления функции φ_м(x₁), определяемой выражением

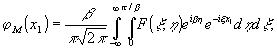(17)

и реально восстановленной амплитудой поля :

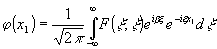(18)

(множитель е^iβξ введен для того, чтобы перенести восстановление из окрестности точки β в окрестность начала координат, что автоматически получается у φ_м(x₁)).

Воспользуемся теперь отмеченным выше следствием леммы и заменим функцию амплитудного пропускания эмульсии приближающим ее по-

линомом Р(Е):

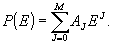(19)

Подставив (19) в (14), получим выражение для f(ξ,η):

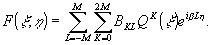(20)

Здесь b_kl могут быть определены непосредственной подстановкой выражения для распределения энергии в плоскости голограммы в формулу (19):

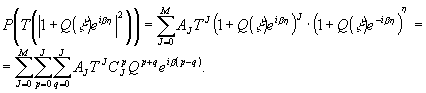(21)

Рассмотрев это выражение, можно заключить, что

а) b_kl = 0, если l>К, (22а)

б) b_kl = 0, если один из индексов четный, а другой

нечетный, (22б)

в) b_kl=b_k-l, это следует из того, что 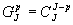, (22в)

г) b_kl= 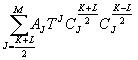при k>l≥d. (22г)

Введем обозначение

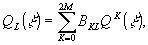(23)

в этих обозначениях

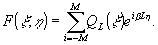(24)

Подставим теперь выражение для f(ξ,η) в формулу (17), получим

формулу для φ_m(х₁):

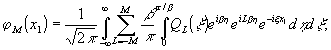(25)

в силу ортогональности системы экспонент в сумме остается только одно слагаемое, соответствующее l=1. Таким образом,

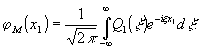(26)

Подставив (24) в (18), мы получим выражение для

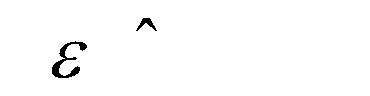(27)

здесь "штрих" означает суммирование по всем l≠1. Из выражений для φ_m(x₁) и φ(х₁) следует, что

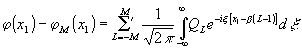(28)

Прежде чем перейти непосредственно к оценке разности 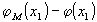, остановимся более подробно на 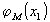. Вспомнив обозначения (23), можно записать выражение (26) в виде:

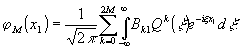(29)

Если q(0) достаточно мало и χ(Е) хорошо аппроксимируется полиномом первой степени при 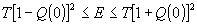, мы можем записать

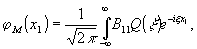
откуда следует, что 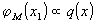. Это согласуется с обычными представлениями о восстановлении линейно записанных голограмм. Члены суммы, содержащие q^k(ξ), k≠1, соответствуют нелинейным искажениям, вносимым эмульсией. Таким образом, используя аппроксимацию функции χ(Е) полиномом, можно оценить величину нелинейных искажений восстановленного изображения. Однако, такой анализ выходит за рамки настоящей работы.

Вернемся к оценке точности моделирования, т.е. величины φ(x₁)-φ_m(х₁). Подставив в выражение (28) значения q_l(ξ) из формулы (23), получим

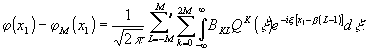(32)

Сделав преобразование Фурье и воспользовавшись теоремой о свертке, получим

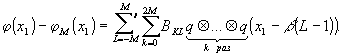(32)

Естественно предполагать, что угол между опорной и предметной волной выбран таким, что в корреляционной плоскости восстановления в различных порядках разнесены достаточно далеко. Иными словами, β>>d, пусть β=n₀∙d, n₀~0. Тогда первые n слагаемых внутренней суммы в формуле (32) равны нулю при k≤n₀. Это следует из того очевидного факта, что носитель свертки есть сумма носителей сворачиваемых функций (cм., например /6/). Для оценка оставшихся членов суммы воспользуемся центральной предельной теоремой (см. /6/). В силу сделанных предположений относительно функция q(х) среднее значение q(х) равно нулю, а дисперсия не превосходят величины d. В самом деле, выше отмечено, что

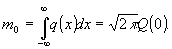(33)

Найдем теперь величину

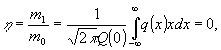(34)

так как q(x)=q(-x);

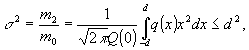(35)

причем равенство может достигаться, только еcли

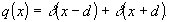(36)

Для таких функций центральная предельная теорема не справедлива и, кроме того, они не являются физически реализуемыми. То есть мы можем считать, что σ²<d². Например, для функции

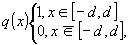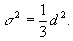, (37)

Таким образом,

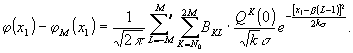(38)

Это и есть основная, формула для вычисления погрешности моделирования. Кроме того, эта формула дает возможность оценить вклады от нулевого, второго и других порядков в изображение, восстановленное в первом порядке дифракции. Отметим, что для малых q(0) тем же способом, что и при выводе формулы (30) мы можем заключить, что при линейной записи вклады высоких порядков в восстановленное изображение равны нулю, что также хорошо, согласуется с обычными представлениями.

Прежде чем перейти к результатам вычислений с использованием формулы (38), отметим, что рассмотренный случай легко обобщается на случай, когда q(x) - произвольная положительная функция. Действительно, в этом случае в формулу (20) будут входить не только

степени q(ξ), но и степени q*(ξ) ("*" означает комплексное сопряжение). Следовательно в свертке в формуле (32) будут участвовать не только g(х), но и q(-x), что однако не отразятся на окончательном результате. С легкостью можно обобщить результаты на двумерный случай, если вспомнить, что модуляция по второй координате отсутствует и интегрирование всех выражений по ней не вызывает затруднений. Отметим также, что аналогичные рассмотрения могут быть проведены в случае, когда t(ξ)≠const, что соответствует неплоскому опорному пучку.

В выражение для φ(x)-φ_m(x) входят коэффициента, значения которых зависят от конкретной кривой пропускания эмульсии, поэтому все оценю, нами делались для двух видов кривых пропускания, характерных для материалов, используемых в голографии. Первая - кривая пропускания эмульсии agfa-gevaert8e75, проявленной в проявителе d -76, вторая - та же эмульсия, проявленная в пироаммиачном проявителе. Отличие этих кривых состоит в наличии у второй кривой "участка просветления" (см. рис.1).

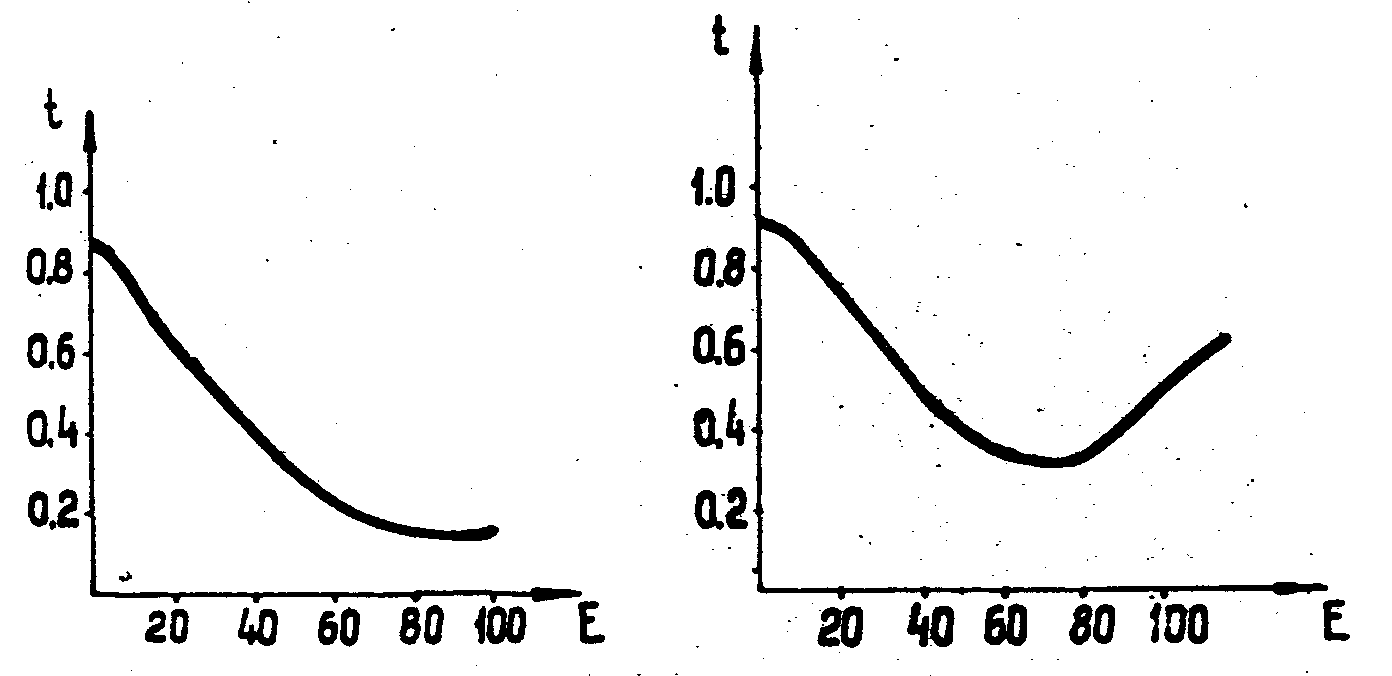
Рис.1. Кривые амплитудного пропускания эмульсии фотопластинок

Аgfa gevaert 8e75, проявленной а) в проявителе Д-76; б) в пироаммиачном проявителе.

Время экспозиции Т выбиралось равным 10, что соответствует среднему значению пропускания. Величина β считалась такой, что n₀ = 10. Были рассчитаны величины вкладов первых десяти порядков в восстановленное изображение, значения амплитуды восстановленной волны в точке 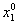, соответствующей среднему значению φ_m(x₁). Кроме того, вычислялись величины амплитуды восстановления в различных порядках для голограммы плоских волн по формуле:

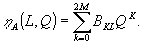(37)

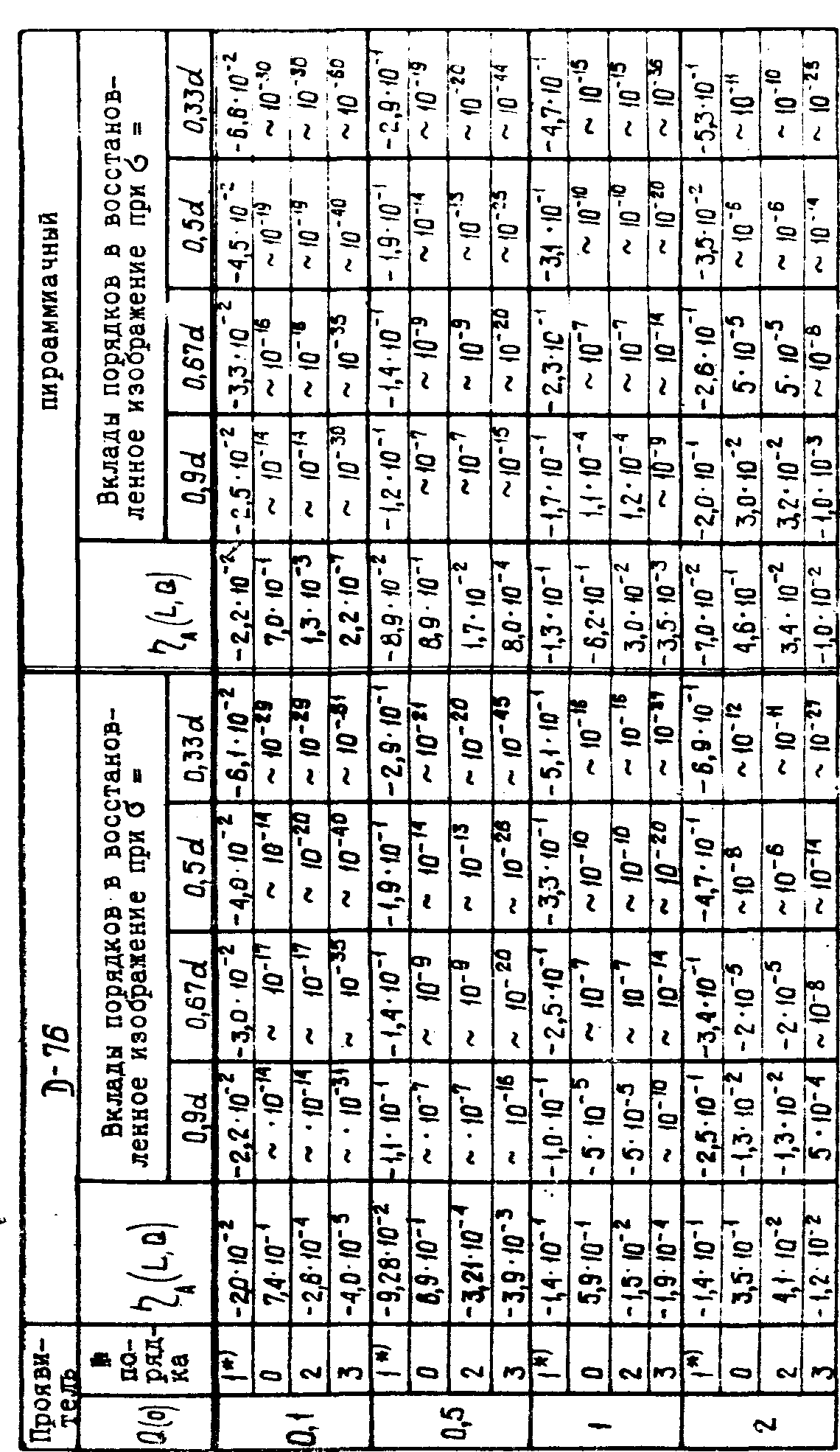
Для получения значений коэффициентов В_kl функции χ(Е) в обоих случаях приближались полиномом 33 степени. Точность аппроксимации при этом составляла величину порядка 1∙10^-4. Далее по формулам (22) вычислялись В_kl. Интервал для значений Е, на котором приближалась функция, был выбран [0,100], что соответствует интервалу значений q(0) ~ [0,2]. Результаты приведены в таблице. В таблице даются вклады лишь трех первых порядков, так как остальные исчезающе малы. Например, при q=2 и σ=0,9 вклад четвертого порядка для первой и второй кривых составляет соответственно, 1∙10^-8 и 4∙10^-9.

Как видно из таблицы, во всех рассмотренных случаях при q=2 вклад дальних порядков пренебрежимо мал. При q=2 этот вклад также не превосходит 10% амплитуда восстановленной волны в быстро убивает с уменьшением σ и возрастанием номера порядка. В частности, для бинарных объектов (σ = 1/3) даже при q=2 вклад составляет не более 10^-8%.

Исходя из этих результатов, можно заключить, что в рассматриваемых случаях (qÎ [0,2], Т~10) процесс моделирования может быть с успехом применен для оценки ожидаемые результатов эксперимента и выбора оптимальных параметров записи голограмм в соответствии со схемой, рассмотренной нами в работе /1/.

Отметим, что объем вычислений, необходимый для получения приведенных результатов, относительно невелик (~3' времени БЭСМ-6). Таким образом, оценка точности моделирования (а значит и величины вклада высоких порядков) может быть проведена предвари-

тельно при каждом конкретной значении параметров q(0),Т, β, σ.

Автор благодарит Б.Г.Турухано за полезное обсуждение.

Л и т е р а т у р а

1. А.М.Беккер, Б.Г.Турухано. Материалы vii Всесоюзной школы по голографии. Л., ЛИЯФ, стр.165, 1975.

2. Э.И.Крупицкий, И.С.Барбанель. Оптика и спектроскопия. ХХ Хiii, вып.3, стр.571, 1972.

3. И.С.Гибин, Е.Ф.Пен, А.В.Трубецкой. Автометрия, №3, стр.26, 1975.

4. Н.И.Ахиезер. Лекции по теории аппроксимации, изд. 2-е, М., стр.124, "Наука", 1965.

5. В.Л.Гончаров. Теория интерполирования и приближения функций, изд. 2-е Гос.издат.техн.-теор.лит., М., стр.98, 114, 1954.

6. А.Папулис. Теория систем и преобразований в оптике. М., "Мир", стр.33, 86, 1971.