СПОСОБ КОМПЕНСАЦИИ НЕРАВНОМЕРНОСТИ

ОПОРНОГО ПУЧКА

Д.М.Беккер, Н.И.Бухтоярова, Б.Г.Турухано

Рассмотрена возможность компенсации неравномерности опорной волны при записи голограммы с использованием нелинейных свойств регистрирующего материала. Приведены результаты экспериментальной проверки теории на примере голографического транслятора.

При записи голограмм во многих случаях опорный пучок нельзя считать плоской волной. При этом в восстановленном изображении возникают нелинейные искажения даже при так называемом линейном режиме записи, т.е. при отношении амплитуд предметной и опорной волн q<<1. Эти искажения вызваны тем, что различные участки голограммы соответствуют различным участкам кривой амплитудного пропускания эмульсии. В этом случае можно поставить две естественные задачи. Первая - изготовить голограмму так, чтобы при освещении голограммы плоской волной восстановилась без искажений первоначальная предметная волна, вторая - чтобн линейное восстановление произошло при освещении голограммы первоначальной опорной волной.

Математически эти задачи могут быть сформулированы так. Пусть f(r) -распределение амплитуды предметной, а g(r) - опорной волн в плоскости записи голограммы. Ф(r) - комплексная функция пропускания изготовленной голограммы. Следует найти такой способ изготовления голограммы, при котором в задаче i

Ф(r)µ f(r), (1)

а в задаче ii

g(r)Ф(r)µ f(r). (2)

В работе /1/ для компенсации искажений предлагается применять дополнительный амплитудный фильтр. Однако это весьма сложно осуществимо технически и влечет значительную потерю дифракционной эффективности.

В настоящей работе предлагается использовать нелинейные свойства регистрирующих сред.

Воспользуемся результатом работы /2/ и запишем выражение для функции комплексного пропускания голограммы:

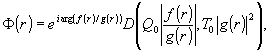(3)

где

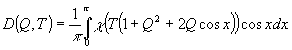(4)

Отметим, что в задаче i фаза (аргумент) функции g(r) должна быть постоянной, иначе плоская волна не может восстановить функцию f(r), так как d(q,t) вещественна. В задаче ii фазовые соотношения в восстановленной волне выполняются автоматически (с точностью до знака d(q,Т)). В самом деле,

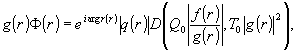(5)

a d(q,t), как уже отмечалось, вещественна.

Таким образом, нас интересует только амплитуда восстановленной волны.

Опишем приближенно идею предлагаемого метода на примере задачи i. Запишем выражение для интенсивности поля в плоскости регистрации голограммы, считая, что f(r) и g(r) вещественны.

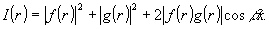(6)

Здесь 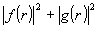определяет среднюю интенсивность, a 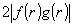- амплитуду модуляции. Если не учитывать "несинусоидальность" модуляции, можно считать, что амплитуда восстановлен-

ной волны определяется амплитудой модуляции амплитудного пропускания голограммы.

Рассмотрим два участка голограммы, на которых значения f(r) одинаковы, a g(r) различны. Задача состоит в том, чтобы найти такой режим записи, что плоская волна восстановит на обоих участках волну с одинаковой амплитудой. Обратимся к рис.1. При увеличении g(r) сдвигается вправо средняя интенсивность и увеличивается амплитуда модуляции. Следует подобрать участок кривой пропускания, на котором увеличение амплитуды модуляции компенсируется уменьшением крутизны (производной) кривой χ(e). Тогда модуляция амплитудного пропускания голограммы будет иметь одну и ту же амплитуду на обоих участках.

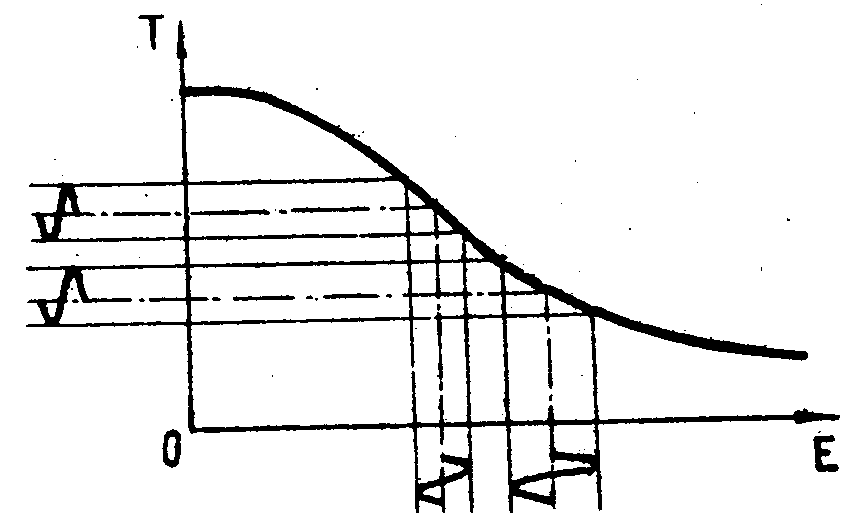
Рис.1. Иллюстрация идеи метода использования нелинейности регистрирующего материала.

Обратимся теперь к более точным расомотрениям. Будем рассматривать обе задачи параллельно, обозначая формулы и функции, относящиеся к разным задачам, где это потребуется, римскими цифрами i и ii. Итак, следуя (3), модуль функции комплексного пропускания голограммы Ф(r) выразится формулой:

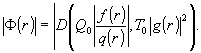(7)

Обозначим функцию, описывающую распределение амплитуды восстановленной волны, через φ(r). Тогда в задаче i

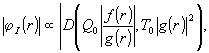(8.i)

а в задаче ii

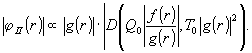(8.ii)

Ясно, что если в первом случае найти участок, на котором

d(q,t)µ q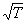, (9.i)

а во втором такой, что

d(q,t)µ q (9.ii)

и не зависит от Т, и выбрать параметры q₀ и Т₀ так, чтобы область изменения 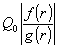и 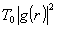лежала внутри указанных областей - это и будет решением нашей задачи (см.риc.2).

Действительно, тогда подставив (9.i; 9.ii) в (8.i; 8.ii) получим в обоих случаях

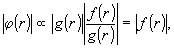(10)

а фазовые соотношения, как было отмечено выше, выполняются при любом режиме записи. Если |g(r)| меняется в достаточно больших пределах (в частности принимает на некоторых участках нулевое значение), то с нелинейным восстановлением или даже полной потерей значений f(r) при некоторых r придется примириться. Например, если записывается голограмма Фурье, то следует подбирать режим регистрации так, чтобы наиболее важные участки спектра попали в указанную выше область.

Займемся вопросом дифракционной эффективности такай голограммы. Пусть α коэффициент пропорциональности в формулах (9.i) и

 

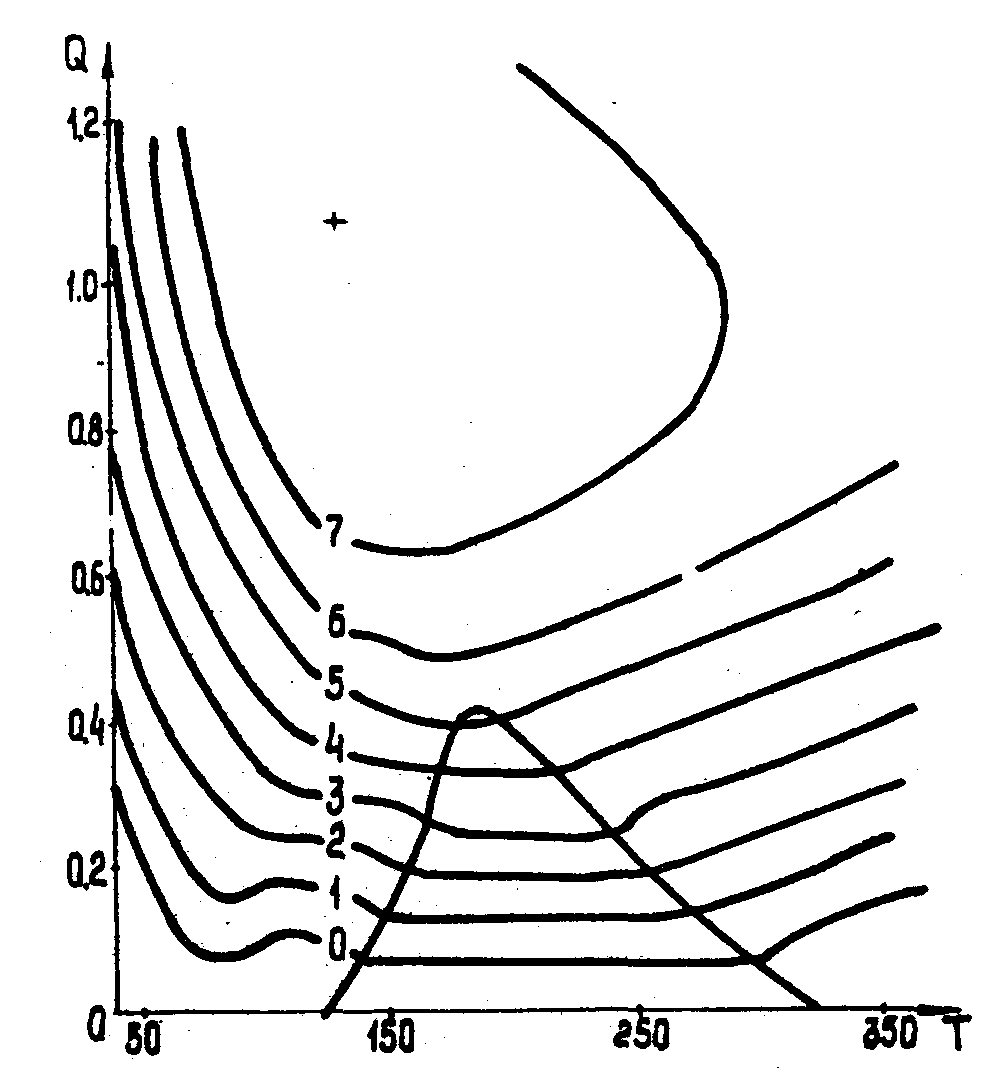
Рис.2. Проекции линий уровня d(q,t) на плоскость t,q. Отмечен участок, на котором d(q,t)µ q и не зависит от Т.

(9.ii). Тогда

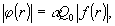(11)

и если считать интенсивность восстанавливающей волны равной 1, то дифракционная эффективность

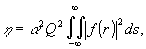(12)

то есть

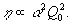(13)

Учитывая это, можно поставить задачу нахождения оптимальных параметров записи, при которых нелинейные искажения, определяемые как максимальное относительное отклонение коэффициента пропорциональности α от постоянной, не превосходило бы величины ε, a h было бы максимальным.

Пусть на участке, где требуется линейное восстановление,

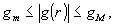
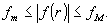(14)

Следует найти q₀, Т₀ и α такие, что h принимает максимальное значение. При этом на область изменения параметров наложены ограничения тем, что

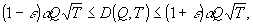(15.i)

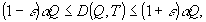(15.ii)

где 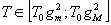, а при каждом фиксированном значении Т,q может изменяться в пределах между 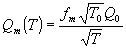и 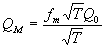. Это станет ясно, если вспомнить, что экспозиция 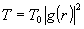, то есть .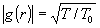

Таким образом, а стандартной форме для задач нелинейного программирования /3/ задача нахождения оптимальных параметров формулируется так: найти q₀, Т₀ и α такие, что целевая функция

h (q₀,t₀,α)=αq₀ (16)

принииает максимальные значения, при условиях

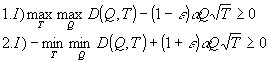(17.1)

где Т, q изменяются в пределах ,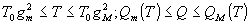

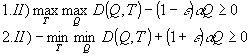(17.2)

где Т, q изменяются в пределах .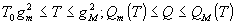

d(q,t) описывается формулой (4).

Такая задача может быть решена одним из методов решения задач нелинейного программирования (градиентным, симплексным методом и т.д.). Количество программ, реализующих эти методы, в настоящее время достаточно велико. Однако, из-за сложности вычисления значений выражений, входящих в (17), решение может потребовать весьма большого времени счета даже на мощных ЭВМ.

Ниже мы опишем простой способ приближенного решения сформулированных задач. Предположим, что во всей области изменения r, где требуется линейное восстановление голограммы, выполняется условие

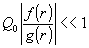. (18)

Разложим d(q,t) в ряд Тейлора по q в окрестности точки 0:

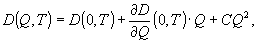(19)

d(0,t)=0, значит с точностью до членов второго порядка малости имеем

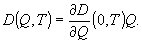(20)

Вычислим 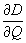(0,Т):

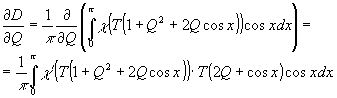(21)

Значит

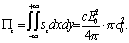. (22)

Иа равенств (9.i) и (9.ii) можно заключить, что в случае i нужно потребовать, чтобы 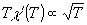, а в случае ii - 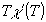=const . Или, соответственно,

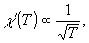(23.i)

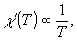(23.ii)

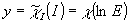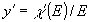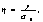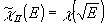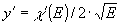Для нахождения соответствующих участков кривых пропускания воспользуемся следующим приемом. В случае i построим график зависимости , тогда и значит нужно найти линейный участок на кривой у=. В задаче ii построим график y=, тогда и значит нужно выбрать линейный участок на кривой y=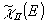. Найдя такой линейный участок, выберем t₀ так, чтобы Т₀g_m и Т₀g_m принадлежали атому участку. Величина q выбирается таким образом, чтобы погрешность с q² в формуле (19) была в пределах возможных нелинейных искажений.

Рассмотрим пример использования изложенного метода в задаче запаси голографического транслятора. Более подробно: следует записать голограмму Фурье с функцией амплитудного пропускания объекта f(ρ) и опорным объектом g(ρ), так чтобы при восстановлении голограммы опорным объектом g(ρ) восстановился объект f(ρ). Распределения амплитуд опорной и предметной волн в плоскости голограммы представляются функциями f(r) и g(r), связанными с f(ρ) и g(ρ) преобразованием Фурье. Отметим, что функция g(r) имеет нули и, следовательно, условие (18) не может быть выполнено во всей плоскости голограммы, значит спектр предмета f(r) может быть линейно восстановлен лишь частично. В нашем эксперименте в качестве объекта выбирался транспарант с прозрачным словом "monday " на непрозрачном фоне, а опорным - русский перевод - слово "понедельник", пред-

ставленное аналогично. Использовалась эмульсия agfa-gevaert8e75. проявленная в проявителе Д-76 в течение 5 мин. Кривая амплитудного пропускания эмульсии при этих условиях приведена на рис.3. Следуя изложенному выше методу, кривая построена в координатах τ, lne.

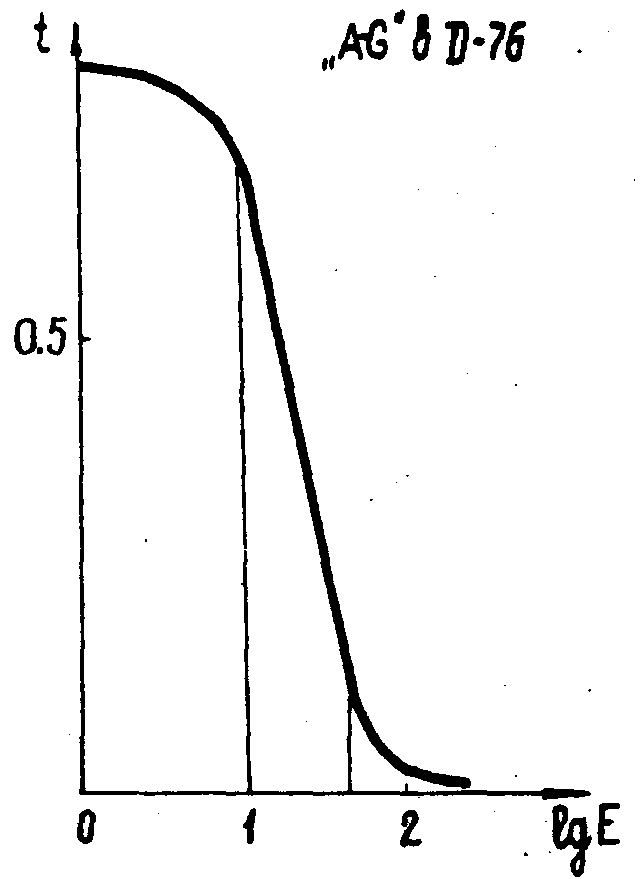
Рис.3. Кривая амплитудного пропускания эмульсии

agfa -gevaert 8e75.

На рисунке отмечен линейный участок кривой. Параметры запаси выбирались так, чтобы в нужную область (на линейиый участок кривой) попали значения интенсивности опорной волны, соответствующее значению |g(r)|² в как можно более широкой области. При этом мы исключали из рассмотрения окрестность нуля (нулевой порядок) из-за слишком большого перепада значений интенсивности спектра в этой окрестности и остальной области. Нелинейному восстановлению спектра f(ρ) в окрестности нуля соответствует оператор, близкий к дифференцированию, что экспериментально выглядит как появление провалов внутри восстановленных линий. Результаты эксперимента приведены на рисунках 4 и 5.

 

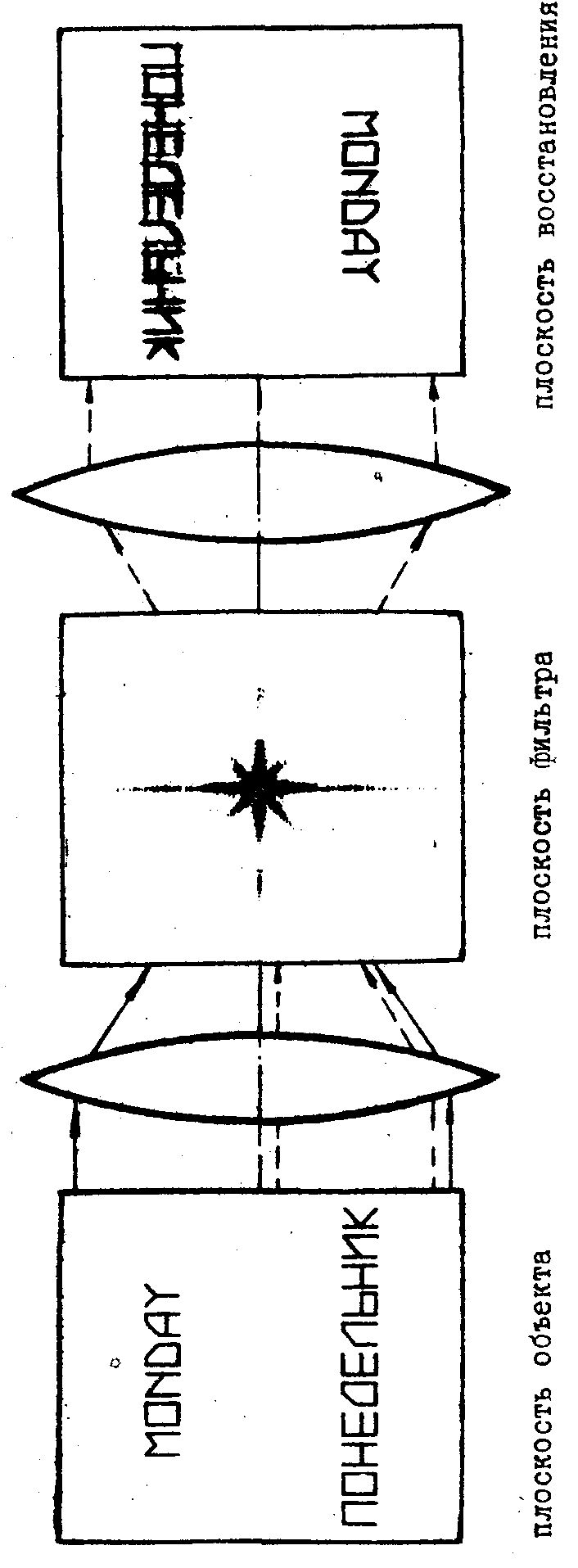
Рис.5. Восстановленное изображение.

Л и т е р а т у р а

1. Л.Ц.Сороко. Основы голографии и когерентной оптики. М., "Наука", стр.564, 1971.

2. А.М.Беккер, Б.Г.Турухано. Материалы Уii Всесоюзной школы по го-лографии. Л., ЛИЯФ, стр.165, 1975.

3. А.Фиакко, Г.Мак-Кормик. Нелинейное программирование. М., "Мир, стр.3, 1972.