СТРОГИЙ АНАЛИЗ ОБЪЕМНЫХ ГОЛОГРАФИЧЕСКИХ РЕШЕТОК

С ПРОИЗВОЛЬНЫМ НАКЛОНОМ cЛОЕb

Э.И.Крупицкий, Б.К.Чернов

Задача дифракции плоской электромагнитной волны на объемной голографической решетке с произвольным наклоном "слоев" сведена к вычислению собственных значений и собственных векторов матрицы и последующее решению системы граничных условий. Исследовано влияние угла наклона "слоев" на дифракционную эффективность отражательных и пропускающих решеток.

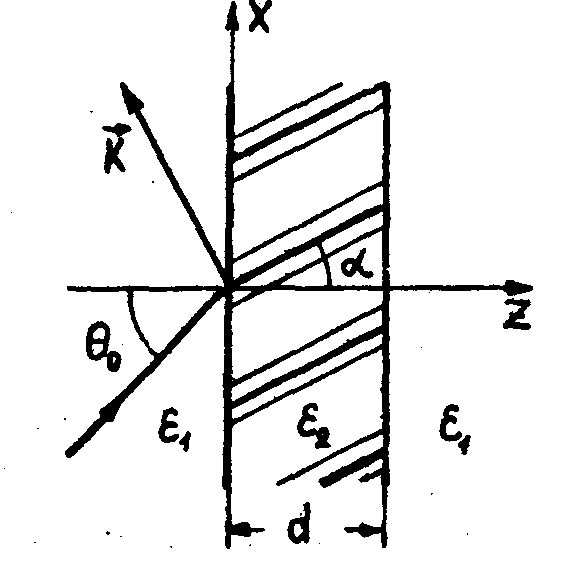
В настоящей работе в отличив от известных работ /1-4/ методом характеристических волн строится строгое решение задачи дифракции плоской электромагнитной волны на объемной голографической решетке для случая произвольной периодической модуляции комплексной диэлектрической проницаемости и произвольного направления модуляции (произвольного α, рис.1). Решение приведено к форме, которая удобна для проведения расчетов на ЭВМ. Как показано в /1/, задача сводится к решению волнового уравнения:

Δu(x,z)+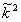(x,z)u(x,z)=0, (1)

где для Н-волн u=e_у,

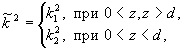(2)

для Е-волн u=h_y/k₂ внутри слоя, u=h_y/k₁ вне слоя,

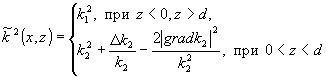(3)

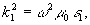
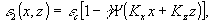
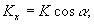
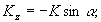(4)

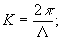
где Λ - период решетки, γ - глубина модуляции, ε_c - средняя проницаемость среды слоя, α - угол наклона "слоев" к оси z. Функция Ψ(t)-2π периодическая, непрерывно дифференцируемая, макс.|Ψ(t)|=1.

Уравнение (1) необходимо решить отдельно для областей z<0, 0<z<d, z>d и "сшить" на границах слоя с помощью условий непрерывности касательных составляющих полей. Переходя в (1) к безразмерным координатам 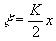, , 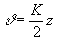получим

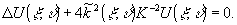(5)

Учитывая периодичность Ψ(х,z), запишем

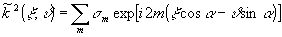. (6)

В системе координат, повернутой относительно системы 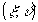на угол α, переменные в уравнении (5) разделяются в оно сводится к системе двух обыкновенных дифференциальных уравнений, одно из которых - уравнение с периодическим коэффициентом (уравнение Хил-

ла /5/).

Учитывая структуру решений этих уравнений, ищем решение (5) в виде:

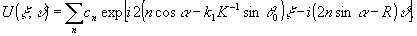(7)

где r и c_n пока неопределенные параметры.

Соотношение (7) представляет собой характеристическую волну, которая может существовать независимо от других характеристических волн (с другими r) в безграничной модулированной среде. Какие именно характеристические волны будут реально существовать в каждом конкретном случае, определяется условиями возбуждения.

Подставляя (7) в (5), с учетом (6), получаем систему алгебраических уравнений:

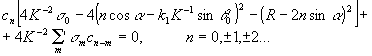(8)

Штрих у знака суммы означает, что суммирование ведется по всем m, за исключением m=0. Введем в рассмотрение коэффициенты

.

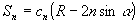Тогда система (8) может быть представлена в виде:

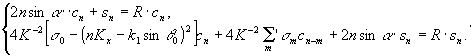(9)

Предположим, что можно ограничиться 2n+1 коэффициентом (n=0, ±1, ±2 ... ±n). Тогда усеченная система (9) может быть записана в матричной форме:

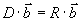, (10)

где 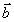- вектор-столбец с элементами

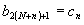
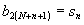, (11)

d- квадратная матрица порядка 2(2n+1)´ 2(2n+1) с элементами

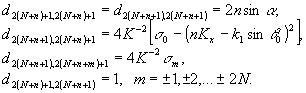(12)

Остальные элементы матрицы равны нулю. Соотношения (11), (12) несколько отличаются от приведенных в /5/ за счет перестановки отрок матрицы с целью облегчения численных расчетов. Система (10) имеет нетривиальное решение, если det(d-rj)=0 (j- единичная матрица). Задача определения значений параметра r, при которых det(d-rj)=0, является задачей определения собственных значений матрицы d. Подобные задачи в настоящее время с успехом решаются на ЭВМ. В результате получим 2(2n+1) собственных значений {r_ν}. Каждому собственному значению r_ν соответствует собственный вектор b_ν, элементами которого являются коэффициенты c_n^ν и s_n^ν. В зависимости от условий нормировки собственных векторов, один из элементов каждого собственного вектора может быть выбран произвольно. Поле внутри модулированного слоя строим в виде суперпозиции частных решений вида (7) с коэффициентами А_ν, которые определяются из граничных условий, то есть

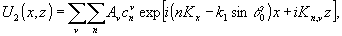(13)

где Â

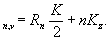
Учитывая (13), зададим поле слева от модулированного слоя:

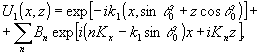(14)

где .

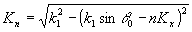Поле cправа от слоя

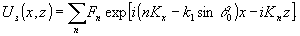(15)

Рассмотрим случай дифракции Н-волн, тогда u=e_y. Подставляя (13), (14), (15) в граничные условия и приравнивая коэффициенты при одинаковых экспонентах по x, получаем

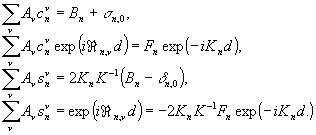(16)

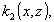
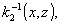
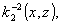
В системе (16) число неизвестных a_ν, b_n, f_n равно числу уравнений, и эта система может быть разрешена относительно любого из неизвестных. Случай дифракции Е-волн несколько усложняется за счет граничных условий. Однако, и в этом случае можно получить соотношения, аналогичные (16), если разложить в ряды Фурье функции 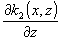и осуществить перегруппировку членов получающихся двойных сумм.

Рассмотрим два предельных случая - продольной (α=0) и поперечной (α=90°) модуляции диэлектрической проницаемости.

При продольной модуляции система (8) не изменяется при замене r на -r, поэтому если r собственное значение матрицы d, то -r также будет собственным значением, причем при определенной нормировке соответствующие им собственные векторы будут иметь одинаковые элементы c_n и противоположные по знаку элементы s_n. Тогда система (16) переходит в систему, аналогичную полученной в работе /2/ для случая α=0.

При поперечной модуляции замена в системе (9) r на r+2r (где r-целое) приводит лишь к сдвигу бесконечной системы (9), поэтому, если r₀ - собственное значение, то

r_r=r₀+2_r (17)

также будет собственным значением. Кроме того, одновременная замена в (8) r на -r и n на -n также не изменяет вида системы. Следовательно, множество собственных значений распадается на два подмножества {r'_r} и {r"_r}, элементы которых отличаются только знаками (r'_r= -r"_r, r = 0, ±1, ±2,...), а внутри каждого подмножества связаны соотношением (17). При соответствующем выборе нормировки для элементов собственных векторов выполняются соотношения:

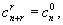
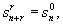
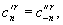
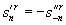. (18)

Просуммируем каждое из соотношений в (16) по n, учитывая (18), получаем

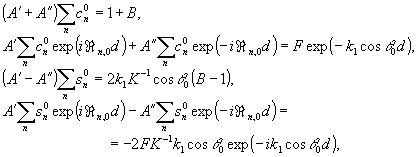(19)

где .

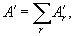
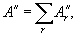
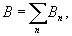
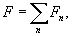
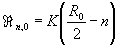Нужно иметь в виду, что строго суммирование следует проводить не для усеченной матрицы d, а по всем n,r = 0, ±1, ±2, ... В систему (19) фактически входит только одно собственное число r₀. Таким образом, в случае поперечной модуляции система (16) сводится к линейной алгебраической системе четвертого порядка. Рассматривая соотношения (13) и (18), нетрудно убедиться, что при α=90° решение внутри модулированного слоя строится в виде суперпозиции двух линейно независимых решений уравнения Хилла с коэффициентами

А' и А", это находится в полном соответствии с результатами работы /6/. Причем r₀ является характеристическим показателем уравнения Хилла. Из (14) и (15) следует, что при дифракции на поперечно модулированном слое дифракционных порядков нет, имеются только отраженная и прошедшая плоские волны, однако такой слой обладает селективными свойствами, коэффициенты отражения и прохождения зависят от его параметров.

На основе представленной выше теории была составлена программа расчета на ЭВМ дифракционной эффективности объемных решеток. Программа написана на языке "АЛГОЛ", расчеты проводились на ЭВМ БЭСМ-6 и М-222. Программа позволяет проводить вычисления дифракционной эффективности во многих (до нескольких десятков) порядках дифракции для фазовых, амплитудных и амплитудно-фазовых пропускающих и отражательных решеток. Предусмотрена возможность расчета дифракционной эффективности голографических решеток с учетом нелинейности характеристики фотоматериала, а также для решеток со сложной формой модуляции диэлектрической проницаемости (допускающей, однако, представление в виде ряда (6)), в частности, решеток, получаемых при записи на нескольких частотах одновременно. Число порядков дифракции и членов ряда (6), принимаемых во внимание при расчетах, определяется объемом памяти используемой ЭВМ.

Приведем некоторые результаты расчета дифракционной эффективности фазовой синусоидальной решетки при дифракции Н-волны. На рис.2 представлена зависимость дифракционной эффективности решетки толщиной 10 мк., помещенной в иммерсионную среду (ε₁=ε_с= 2,3225), от угла наклона "слоев" α. Глубина модуляции диэлектрической проницаемости γ=0,01, угол падения дифрагирующей волны θ_б, соответствует углу 30° в вакууме, λ = 0,6328 мк. Предполагалось, что при изменении α изменялся и период решетки так, чтобы выполнялось условие Брэгга. Сплошной линией изображены дифракционная эффективность в +1 порядке дифракции, пунктирной в -1 порядке. Под графиком для различных значений α схематически изображена дифракционная решетка, падающая волна и дифракционный порядок (+1 или -1), в который дифрагирует наибольшая часть энергии (нулевые порядки не изображены). При αÎ (α₁,α₂) решетка работает как пропускающая, вне этой области как отражательная. По мере приближения α

 

 

 

 

 

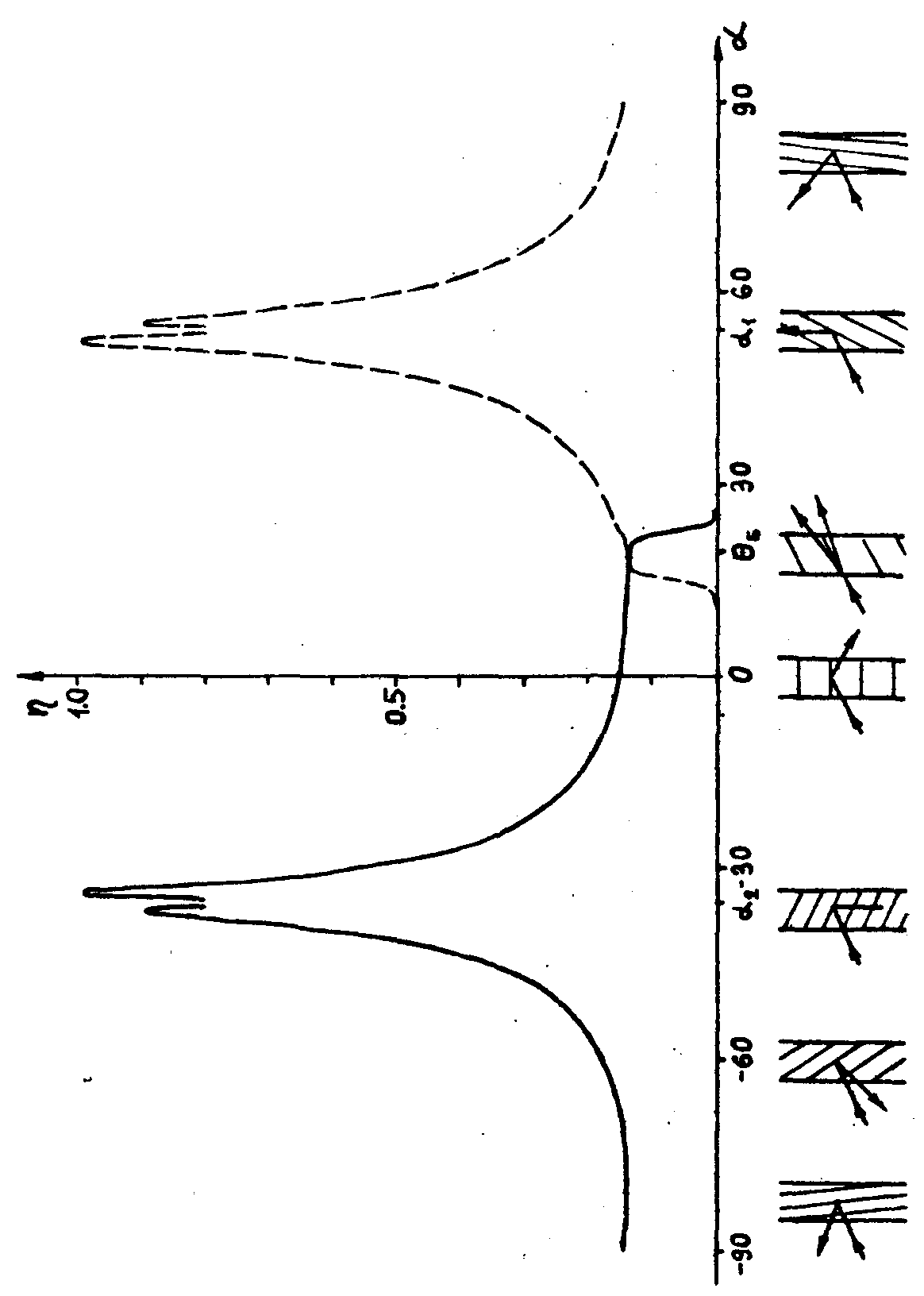
к значениям 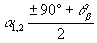дифракционная эффективность нарастает, а затем начинает быстро осциллировать (на рис.2 осцилляции не показаны). При α→θ_б период решетки, удовлетворяющей условию Брэгга, увеличивается, появляется множество распространяющихся дифракционных порядков, +1 и -1 порядки становятся близкими по модулю. Если α→90°, то также появляется много распространяющихся дифракционных порядков, но картина распределения мощности по порядкам не симметрична, при α→90°-0 преобладает -1 порядок, при α→90° +1 порядок. При α= 90° все дифракционные порядки сливаются с нулевыми порядками.

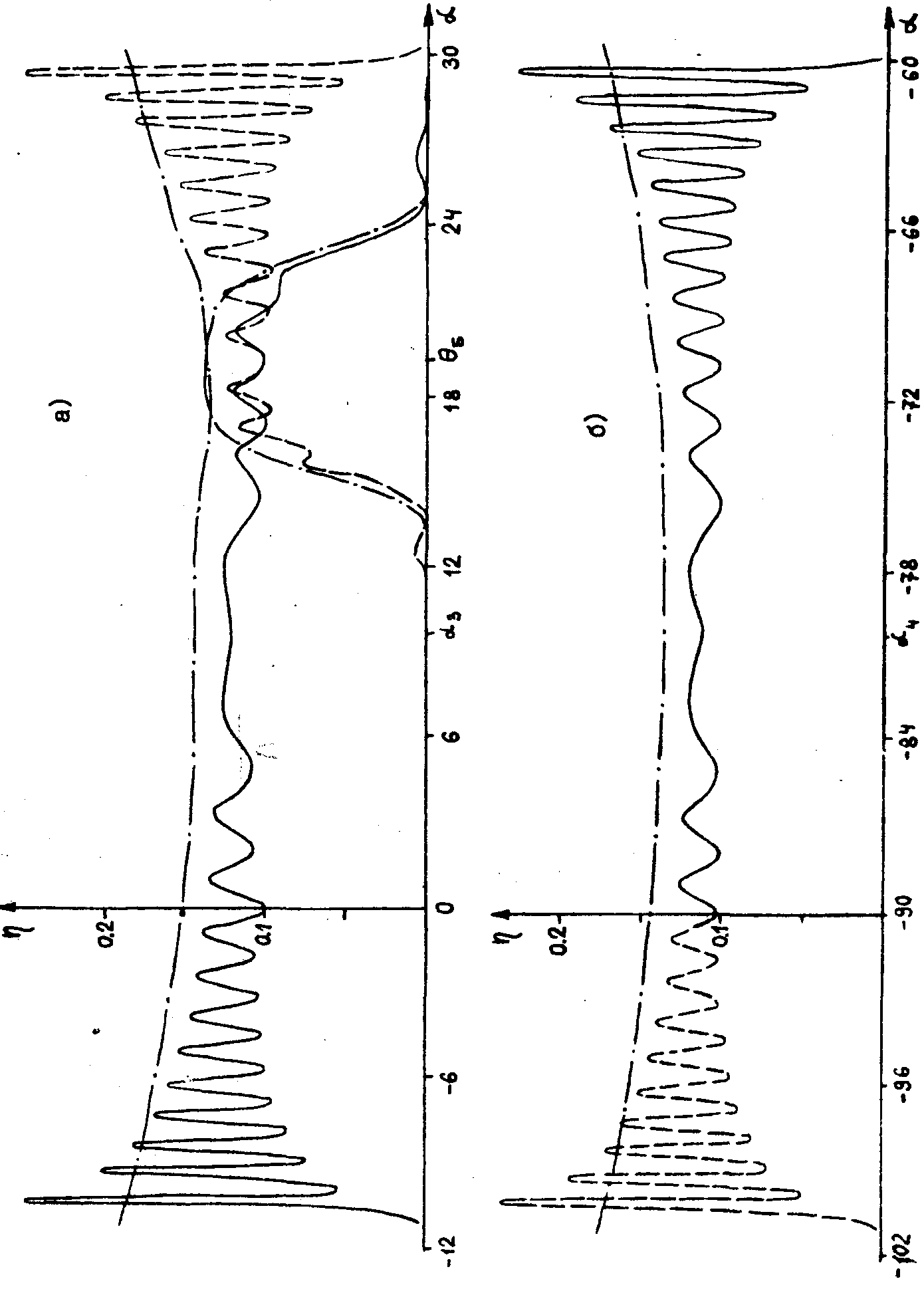
На рис.3 показана зависимость дифракционной эффективности от α при тех же параметрах задачи, но без иммерсии (ε₁=1). Риc.3а соответствует пропускающей решетке, рис.3б - отражательной. Картина дифракции при отсутствии иммерсии качественно другая. В окрестности точек α₁ и α₂ появляются довольно широкие (в данном случае около 48°) области значений α, при которых отсутствуют дифракционные порядки (за исключением нулевых). График дифракционной эффективности осциллирует при изменении α, причем частота осцилляции возрастает при увеличении толщины решетки. При фиксированной толщине наименьшая частота и величина осцилляции наблюдается в окрестности точки α₃=θ_б/2 для пропускающих решеток и α₄=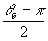 для отражательных решеток, при этом дифрагировавшая волна распространяется в направлении, близком к нормали к границам слоя. Величина осцилляции возрастает по мере приближения к границам зоны распространения дифракционных порядков. Штрих-пунктирной линией на рис.3 изображена зависимость дифракционной эффективности для решетки в иммерсии. Дифракционная эффективность решетки в иммерсионной среде несколько выше, так как отсутствует отражение от передней границы слоя и вся падающая волна взаимодействует с периодически модулированной средой.

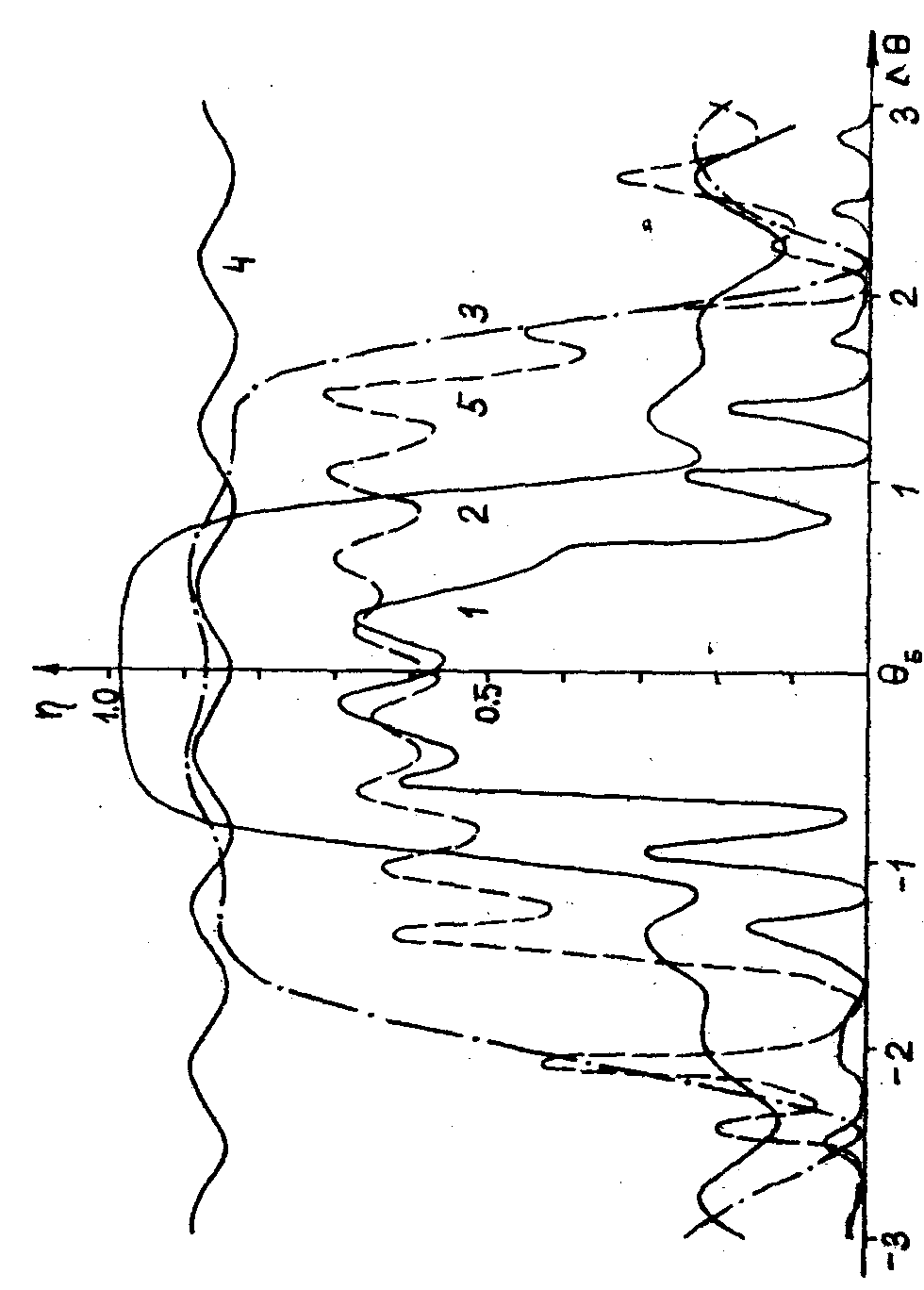
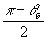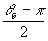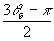На рис.4 изображены графики дифракционной эффективности отражательной решетки толщиной 70 мк. при различных значениях α в зависимости от отклонения угла падения от угла Брэгга (остальные параметры задачи те же). Кривая 1 соответствует α₅=, кривая 2-α=90°, кривая 3-α₄=, кривая 4-α₆ =θ_б-90°, кривая 5-α₇=. При приближении к границам зоны распростра-

 

 

 

 

 

 

 

 

 

 

 

 

 

 

нения ±1 порядков угловая селективность решетки возрастает и угловая зависимость носит все более изрезанный характер. Наименьшей селективностью обладает решетка при α=α₆. На рис.4 (кривая 4) изображена только часть главного максимума дифракционной эффективности, ширина этого максимума на уровне 0,5 около 15°. Увеличение угловой селективности по мере приближения к границам зоны распространения дифракционных порядков может быть объяснено тем, что при этом увеличивается "область взаимодействия" излучения с модулированной средой, так как дифрагировавшая волна распространяется почти вдоль слоя. При α=α₆ дифрагировавшая волна распространяется под тем же углом, что и падающая волна, и "область взаимодействия", а следовательно, и угловая селективность наименьшие. При α=90° проведенные по изложенной выше методике расчеты полностью согласуются с результатами, полученными авторами ранее несколько другим методом /6/.

Были проведены также расчеты дифракционной эффективности пропускающих решеток. В частности, при α=0 проведено сравнение с результатами расчетов, опубликованными в /2/, расхождение не превышало 0,5%.

Таким образом, проведенные расчеты показали возможность строгого решения методом характеристических волн задачи дифракции плоской волны на объемных голографических решетках при любых практически реализуемых параметрах системы. Это позволяет изучить качественно картину процесса дифракции, а также получить количественные данные, необходимые для оптимизации параметров решеток.

Л и т е р а т у р а

1. Э.И.Крупицкий, Б.К.Чернов. Материалы vi Всесоюзной школы по голографии, ЛИЯФ, Л., стр.46, 1974.

2. С.В.burckhardt. j.opt.soc. amer. 56, 1502, 1966.

3. f.g.kaspar. j.opt.soc. amer. 63, 37, 1973.

4. m.kogelnik. bell syst.techn. j. 48, 2909, 1969.

5. Э.И.Крупицкий, Б.К.Чернов. В сб."Проблемы голографии", М., вып.5, 51, 1975.

6. Э.И.Крупицкий, Б.К.Чернов. Оптика и спектроскопия, 39, 571, 1975.