ТЕОРЕТИКО-ГРУППОВАЯ
МОДЕЛЬ АБСТРАКТНОГО ГОЛОГРАФИЧЕСКОГО ПРОЦЕССА
В.Б.Немтинов
Рассмотрен
ряд общих аспектов групповой теории голографии. Построена
обобщенная математическая модель абстрактного голографического
процесса. Для описания регистрирующей среды введено понятие
голографического оператора. Найдено, что универсальной характеристикой
процесса записи является абстрактная голограмма, представляющая
собой абстрактную функцию (голографический оператор), заданную
на голографической группе и принимающую значения в группе
голограммных образов. Показано, что процесс реконструкции
можно рассматривать как представление абстрактной голограммы
в группу реконструирующих (голограммных) операторов. Голограммный
оператор действует в линейном пространстве реконструирующих
волн и определяет поле восстановленной волны.
Рассмотрена
реализация абстрактной голограммной группы в виде мультипликативной
группы амплитудных коэффициентов пропускания и введено понятие
усиливающей голограммы.
В
в е д е н и е
В работах
/1,2/ предложен теоретико-групповой метод анализа голографического
процесса и разработаны основы групповой теории голографии.
Показано, что голографический процесс обладает групповой
структурой, которая обуславливает внутреннюю связь отдельных
этапов голографического цикла. В основе теоретико-группового
под
хода
лежит идея инвариантности интерференционного поля, регистрируемого
на голограмме. Симметрия процесса голографической записи
находит свое наиболее полное выражение в факторизации интерференционного
поля путем введения аддитивной голографической фактор-группы
g/h. Последняя задает правильное разбиение исходной аддитивной
группы g дифракционных образов на голографические классы
эквивалентности 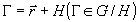 ,
где
,
где 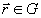 - комплексная амплитуда опорной волны; Н - собственная подгруппа
соответствующих дифракционных образов, инвариантный характер
которой обусловлен симметрией процесса записи голограммы.
- комплексная амплитуда опорной волны; Н - собственная подгруппа
соответствующих дифракционных образов, инвариантный характер
которой обусловлен симметрией процесса записи голограммы.
Построена
/1/ - теоретико-групповая модель обобщенной голограммы,
описание которой сводится к заданию некоторой операторной
функции (например, амплитудного коэффициента пропускания),
определенной на голографической фактор-группе g/h. В частности,
при описании групповой структуры голографического процесса
/2/ математическая модель плоской голограммы сводится к
заданию некоторой реализации амплитудной gА или фазовой
gФ аддитивной матричной группы. Предложенная модель позволяет
с единой теоретико-групповой точки зрения классифицировать
все имеющиеся в настоящее время разновидности голограмм,
исследовать их групповые свойства и, исходя из этого, прогнозировать
новые типы голограмм.
В настоящее
время общая теория восстановления волнового фронта из объемной
голограммы разработана недостаточно. В то же время, хотя
плоская голограмма представляет собой идеальный случай строго
двумерной голограммы, некоторые результаты, полученные при
анализе плоских голограмм, могут быть с успехом применены
и к объемным голограммам. В работе, опираясь на теоретико-групповой
анализ плоских голограмм /1,2/, дан общий подход к структурному
описанию всего голографического цикла, введено понятие абстрактной
голограммы и построена математическая модель абстрактного
голографического процесса. Рассмотрены некоторые применения
математической модели для анализа свойств плоских и объемных
голограмм.
1.
Обобщенная структурная модель голографического
процесса
В работе
/2/ дано структурное описание всего голографического процесса
в целом от стадии записи пространственного распределения
предметной волны до стадии восстановления исходного волнового
фронта. На примере тонких голограмм построена трехкаскадная
теоретико-групповая модель голографического процесса. Однако
сформулированные при этом основные идеи остаются справедливыми
и для объемных голограмм.
1. В
голографии по мере ее развития, как и в других физических
науках, проявляется тенденция ко все большей математизации.
Это происходит потому, что по мере дальнейшего продвижения
вперед, все, кто занимается голографией, начинают все более
отчетливо понимать, что представляет собой предмет голографии,
и все больше отдают себе отчет в тех методах, при помощи
которых они делают свои выводы. При этом отправные идеи
становятся все более ясными и возрастает возможность их
дальнейшего логического развития.
Однако,
в отличие от чисто математических наук, которые стремятся
к полностью дедуктивному подходу, голография, как и всякая
физическая дисциплина, только отчасти дедуктивна. Наряду
с существованием некоторых общих отправных положений (вроде
принципов дифракции и интерференции) многие голографические
термины и понятия являются весьма расплывчатыми или даже
совсем неопределяемыми, продолжая развиваться и уточняться.
Это обусловлено тем, что голография не является строго формальной
дисциплиной и в ней наряду с логическими выводами всегда
требуются наблюдения, опыт и здравый смысл.
В связи
с этим большое значение имеет построение математической
модели абстрактного голографического процесса, которая позволяет
с общих позиций посмотреть на весь голографический цикл
как нечто единое целое. В основу модели должны быть положены
некоторые физические принципы. Их разумная математизация
помогает выработать четкие отправные положения, являющиеся
обобщением конкретного физического опыта. С другой стороны,
дальнейшее чисто логическое развитие общих отправных идей
позволит получить новые результаты, ко-
торые
могут быть реализованы на практике.
Таким
образом, удачная математическая модель голографического
процесса позволяет сделать некоторые расчеты, выводы и предсказания.
Одновременно с этим изучение математической структуры модели
открывает новые стороны исследуемого физического явления.
Иначе говоря, хорошая математическая модель дает возможность
анализировать голографический процесс на языке описывавших
его математических объектов и интерпретировать сходные или
вторичные физические явления на языке построенной модели.
В итоге исследование внутренней математической структуры
модели может значительно расширить и даже изменить имеющиеся
представления о голографическом процессе в целом.
2. Достаточно
общее описание всего голографического цикла и целом дает
теоретико-групповая модель голографического процесса /2/.
Группы - очень важный объект в математике. Самым замечательным
является то, что на основе относительно простой аксиоматики
теории групп можно построить грандиозную теорию. Группы
входят в удивительно широкий круг физико-математических
исследований. С помощью теории групп можно получить самые
неожиданные, не связанные друг с другом, результаты.
Так,
можно показать, что существует 32 точечные группы симметрии
кристаллов, что уравнение пятой степени неразрешимо алгебраическими
методами, а также получить важные сведения о системе уровней
энергии в квантовой механике иди структуре молекул в химии.
Одно время даже считалось, что группы, учитывая их универсальный
характер, являются ключом к раскрытию всех тайн вселенной.
3. Задание
групповой структура голографического процесса /2/ дает возможность
выявить его наиболее характерные особенности. Для дедуктивного
описания голографического цикла с целью дальнейшего его
логического исследования можно обобщить трехкаскадную теоретико-групповую
модель голографического процесса, построенную на примере
тонких голограмм (см.рис.3 и 4 работы /2/), и ввести понятия
абстрактной голограммы и абстрактного голографического процесса.
Такое естественное обобщение приведено на рис.1.
Теоретико-групповой
метод анализа позволяет выявить следующие основные структурные
категории.
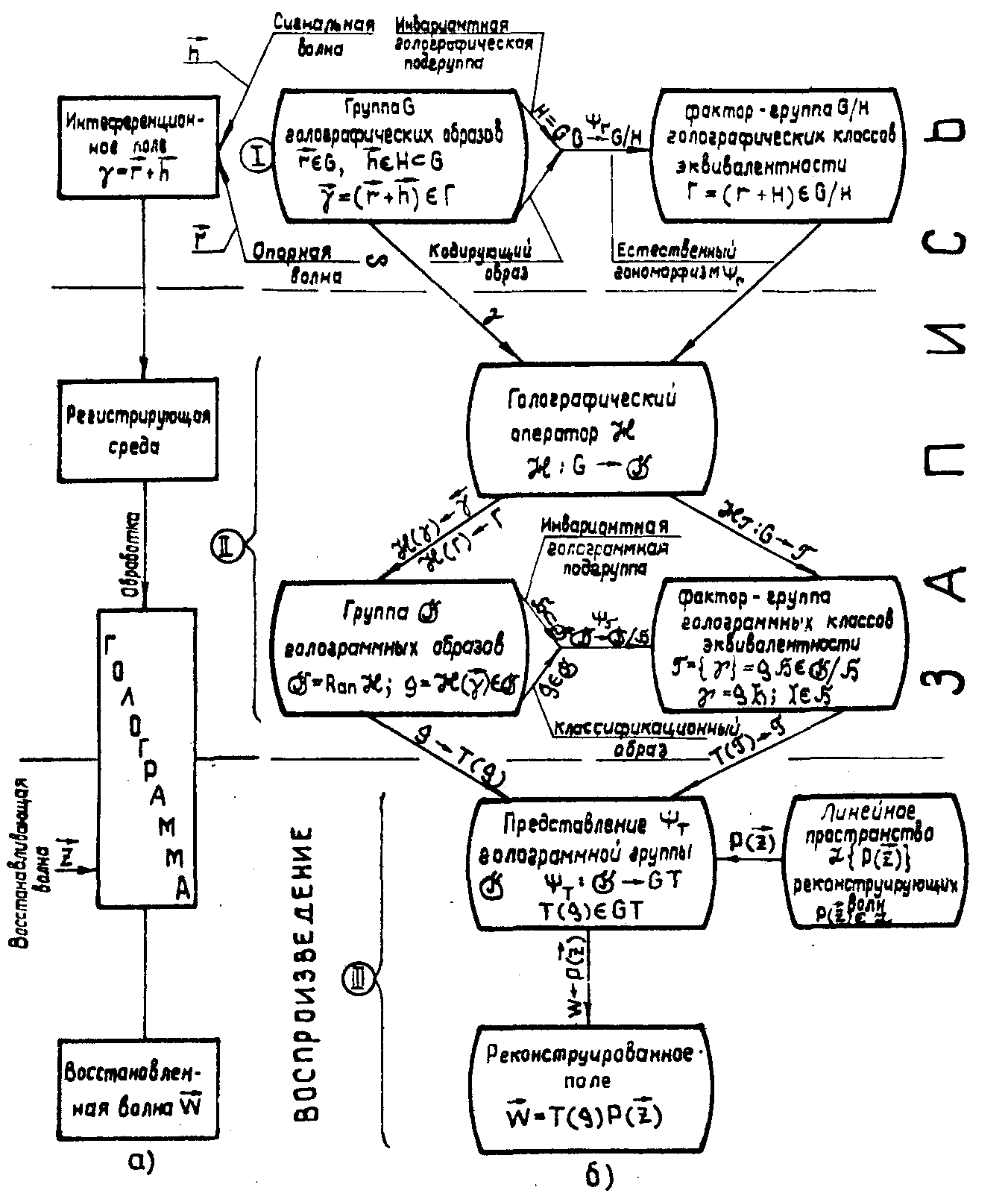
Рис.1.
Структурное модельное описание голографического
процесса:
а -
физическая модель голографического процесса;
б -
теоретико-групповая модель абстрактного голографического
процесса.
3.1.
Исходная голографическая группа g. В приближении
скалярной теории дифракции это аддитивная группа дифракционных
образов, т.е. множество решений уравнения Гельмгольца. Известно,
что при заданных граничных условиях решение уравнения Гельмгольца
единственно /3/. Однако, если в теореме единственности ставится
физическая задача выяснения тех граничных условий, при которых
существует единственное решение, то структурная концепция,
опираясь на классификационные принципы, предполагает потенциально
одновременное существование множества решений. Поэтому отправным
моментом структурного подхода в скалярной приближении является
уравнение Гельмгольца без граничных условий. Тогда в силу
линейности уравнения Гельмгольца множество его решений образует
группу g. Строго говоря, множество решений представляет
собой линейное пространство, но для построения группы достаточно
того очевидного факта, что сумма двух решений снова является
решением. Это лишний раз подчеркивает простоту исходной
групповой аксиоматики, лежащей в основе всякой теории, которая
базируется на теории групп.
Следует
заметить, что обычно решение уравнения Гельмгольца выражается
в виде интеграла Кирхгофа, соответствующего некоторым граничным
условиям. Тогда суммарное решение индуцирует суммарное граничное
условие, которой можно рассматривать с двух точек зрения.
Во-первых, так как при структурном анализе голографического
процесса интерес представляет только тот факт, что сумма
двух решений снова является решением, то суммарное граничное
условие не обязательно должно физически реализовываться.
Иначе говоря, для выделения какого-либо типа голограммы
совершенно не обязательно одновременное существование волновых
фронтов, обуславливающих этот тип голограммы. В частности,
в двухэкспозиционной голограмме при некогерентном накоплении
информации записываются волновые фронты, не перекрывающиеся
друг с другом ни в пространстве, ни во времени. Однако оба
они являются решениями уравнения Гельмгольца, а их сумма,
которая тоже является решением, индуцирует физически нереализованное
суммарное граничное условие.
Во-вторых,
если на реальной голограмме записывается когерентная сумма
двух волн, то это означает, что суммарное граничное условие
каким-то образом физически реализовано на практике.
Оно
может представлять собой либо когерентную cyммy двух граничных
условий, либо в простейшем случае сумму двух условий, заданных
на непересекающихся пространственных областях. При этом
в последнем случае область определения суммарного граничного
условия равна прямой сумме составляющих частей.
В работе
теоретико-групповой подход рассмотрен в приближении скалярной
теории дифракции. Однако исходная группа g голографических
образов может описывать также интерференцию двух векторных
сигналов произвольного спектрального состава. В общем случае
в основе построения некоторой реализации абстрактной группы
g голографических образов должна лежать некоторая групповая
операция, учитывающая специфику кодирования оптического
излучения, возмущенного взаимодействием с объектом наблюдения,
относительно заданных параметров невозмущенной части его
/4/. С квантово-механической точки зрения /4/ - группа g
может, в частности, выступать как группа функций взаимной
корреляции объектного потока света с опорным потоком света,
пространственно-временные параметры которых априорно известны,
т.е. заданы с максимальной точностью.
3.2.
Инвариантная собственная подгруппа Н(Н Ì g)
определяет характер поля, регистрируемого на голограмме.
Отыскание и анализ возможных подгрупп позволяет исследовать
различные разновидности голографической записи. В структуре
группы g можно выделить подгруппу теневых Нт,
френелевских Нф, фраунгоферовских Нf
и Фурье-образов Нf.
3.3.
Голографическая фактор-группа g/Н задает гомоморфное
представление группы g в виде правильного разбиения на голографичeские
классы эквивалентности Г (ΨГ:g→g/h)и
учитывает инвариантный характер интерференционного поля,
обусловленный симметрией процесса записи. Разложение исходной
группы и на непересекающиеся подмножества и выбор представителя
внутри класса лежат в основе классификации и прогнозирования
новых типов голограмм. Таким образом, три группы g, Н и
g/h полностью описывают групповую структуру интерференционного
поля.
3.4.
Голографический- оператор h описывает действие
регистрирующей среды. Иначе говоря, регистрирующая среда
с общих пози-
ций
рассматривается как некоторая система, осуществляющая преобразование
совокупности входных воздействий в ряд выходных функций
/3/. При этом понятие регистрирующей среды как системы отождествляется
с понятием оператора Н, свойства которого определяются
как свойствами светочувствительного материала, так и условиями
обработки. Голографический оператор Н считается заданным
на группе g голографических образов или на голографической
фактор-группе g/Н. Введение голографического оператора Н
позволяет говорить об универсальной регистрирующей среде,
которая включает в себя также процесс обработки, если последний
необходим. Задавая соответствующие свойства оператора Н,
можно тем самым строить различные модели голографических
регистрирующих сред. С другой стороны, характеристики реальных
сред позволяют глубже понять специфические особенности голографического
оператора в каждом конкретном случае.
З.5.
Группа Á ("же" - готическое) голограммных образов
Á (gÎ Á ) является областью значений
голографического оператора b представляет собой совокупность
некоторых математических объектов с определенной теоретико-групповой
аксиоматикой, которые могут быть использованы для характеристики
различных типов голограмм. Вид групповой операции зависит
от конкретной реализации голограммной группы. При этом задание
множества голограммных образов определяет структуру абстрактной
голограммы и позволяет дать обобщение математической модели
голограммы /1,2/.
Введем
в рассмотрение понятие абстрактной голограммы, под которой
будем в дальнейшем понимать голографический оператор Н,
заданный на голографической группе g (или голографической
фактор-группе g/Н) и принимавший значения в группе g голограммных
образов. В соответствии с этим формальное описание процесса
записи с помощью абстрактной голограммы задается выражением
h:g→Á
, (1)
где
множество
Á
=ranh (2)
представляет
собой область значений функции Н. Сужение голографического
оператора
Н|(g/h)
(3)
на голографическую
фактор-группу g/h позволяет выяснить структуру голограммных
образов h(Г) голографических классов эквивалентности
Г. Понятие абстрактной голограммы является универсальной
характеристикой процесса записи, включающей в себя все возможные
разновидности голограмм. При этом фиксированный голограммный
образ g(γ)Î Á задает некоторую вполне конкретную
голограмму. g этой точки зрения классификация всех возможных
типов голограмм, выявление новых разновидностей и построение
различных моделей сводится к анализу и описанию свойств
различных реализации голограммных образов. Более того, построенная
математическая конструкция является настолько общей, что
описывает все голографические направления.
Физическая
реализация абстрактной голограммы 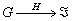 зависит от конкретной реализации голографической группы
g (или фактор-группы g/h), свойств голографического оператора
h и задания голограммной группы Á . На практике
это определяется структурой интерференционного поля, видом
и характером отклика регистрирующей среды, условиями записи
и обработки и т.п. В частности, для плоских амплитудных
и фазовых голограмм голограммная группа Á может быть
реализована, соответственно, в виде аддитивной амплитудной
ga или фазовой gФ матричной группы /2/, которые задают групповое
описание свойств квадратичной регистрирующей среды. Иначе
говоря, множество голограммных образов g реализуется либо
в виде амплитудных матриц ga=А=h(
зависит от конкретной реализации голографической группы
g (или фактор-группы g/h), свойств голографического оператора
h и задания голограммной группы Á . На практике
это определяется структурой интерференционного поля, видом
и характером отклика регистрирующей среды, условиями записи
и обработки и т.п. В частности, для плоских амплитудных
и фазовых голограмм голограммная группа Á может быть
реализована, соответственно, в виде аддитивной амплитудной
ga или фазовой gФ матричной группы /2/, которые задают групповое
описание свойств квадратичной регистрирующей среды. Иначе
говоря, множество голограммных образов g реализуется либо
в виде амплитудных матриц ga=А=h(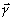 )
(aÎ ga), либо в виде фазовых матриц gф=Ф=h(
)
(aÎ ga), либо в виде фазовых матриц gф=Ф=h(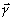 )
(ФÎ gФ). Ниже будет построена мультипликативная реализация
группы Á голограммных образов, которая позволит описать
усиливающие свойства голограмм. Кроме того, исследование
структуры и возможных реализации голограммной группы может
оказаться полезным для разработки теории объемных голограмм.
)
(ФÎ gФ). Ниже будет построена мультипликативная реализация
группы Á голограммных образов, которая позволит описать
усиливающие свойства голограмм. Кроме того, исследование
структуры и возможных реализации голограммной группы может
оказаться полезным для разработки теории объемных голограмм.
3.6.
Инвариантная собственная голограммная подгруппа 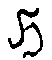 Ì
Á ("аш" - готическое) представляет собой определенную
совокупность голограммных образов
Ì
Á ("аш" - готическое) представляет собой определенную
совокупность голограммных образов 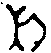 Î
Î
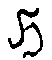 , обладающих
некоторыми характерными
, обладающих
некоторыми характерными
свойствами.
Отыскание и анализ возможных подгрупп позволяют выделять
основные типы голограмм в зависимости от групповой структуры
подобласти 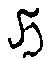 значений голографического оператора Н. Иначе говоря,
различие свойств голографического оператора на этих подгруппах
обуславливает реализацию некоторой разновидности абстрактной
субголограммы
значений голографического оператора Н. Иначе говоря,
различие свойств голографического оператора на этих подгруппах
обуславливает реализацию некоторой разновидности абстрактной
субголограммы
Н:g→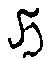 .
(4)
.
(4)
В частности,
ниже будет показано, что выделение амплитудных и фазовых
голограмм непосредственно связано с существованием голограммных
подгрупп амплитудных коэффициентов пропускания (соответственно,
амплитудной at и фазовой Фt подгруппы)
в голограммной группе Á , которая реализуется в виде
мультипликативной группы 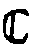 *
комплексных чисел за вычетом нуля.
*
комплексных чисел за вычетом нуля.
3.7.
Голограммная Фактор-группа Á /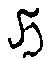 задает естественное гомоморфное представление группы Á
в виде правильного разбиения на голограммные классы эквивалентности
τ(Ψτ:Á →Á /
задает естественное гомоморфное представление группы Á
в виде правильного разбиения на голограммные классы эквивалентности
τ(Ψτ:Á →Á / 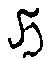 ).
Различные голограммные классы эквивалентности являются элементами
голограммной фактор-группы (τÎ Á /
).
Различные голограммные классы эквивалентности являются элементами
голограммной фактор-группы (τÎ Á /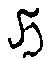 )
и строятся с помощью инвариантной собственной подгруппы
)
и строятся с помощью инвариантной собственной подгруппы
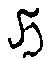 . В мультипликативной
форме записи
. В мультипликативной
форме записи
τ=g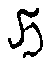 ,
(5)
,
(5)
т.е.
является некоторым подмножеством голограммных образов, представимых
в виде γ=g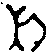 (γÎ τ), где
(γÎ τ), где 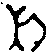 Î
Î
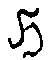 . Произвольный
фиксированный голограммный образ gÎ Á , обуславливающий
выделение определенного голограммного класса эквивалентности
τ, в дальнейшем будем называть классификационным образом.
Таким образом, факторизация голограммной группы Á с
помощью абстрактной субголограммы
. Произвольный
фиксированный голограммный образ gÎ Á , обуславливающий
выделение определенного голограммного класса эквивалентности
τ, в дальнейшем будем называть классификационным образом.
Таким образом, факторизация голограммной группы Á с
помощью абстрактной субголограммы 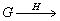
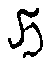 позволяет выделять различные типы голограмм (голограммные
классы эквивалентности τ) в зависимости от специфических
особенностей голографического оператора (регистрирующей
среды), так что
позволяет выделять различные типы голограмм (голограммные
классы эквивалентности τ) в зависимости от специфических
особенностей голографического оператора (регистрирующей
среды), так что
Нτ:g→τ.
(6)
Например,
построенные ниже голограммные фактор-группы 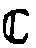 */at
и
*/at
и 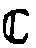 */Фt
дают возможность, соответственно, говорить либо о совокупности
амплитудных голограмм
*/Фt
дают возможность, соответственно, говорить либо о совокупности
амплитудных голограмм 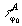 с постоянным фазовым сдвигом φ0, либо о
совокупности фазовых голограмм
с постоянным фазовым сдвигом φ0, либо о
совокупности фазовых голограмм 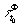 с постоянным пропусканием t0.
с постоянным пропусканием t0.
3.8.
Представление Ψт голограммной группы
Á в группу операторов gt описывает процесс восстановления
абстрактной голограммы, т.е. гомоморфное отображение /2/
ΨТ:Á
→gt. (7)
Иначе
говоря, построение математической модели процесса реконструкции
абстрактной голограммы сводится к заданию некоторого гомоморфизма
Ψт группы Á в группу gТ голограммных
или реконструирующих операторов Т. При этом группа gТ характеризует
реконструирующие свойства абстрактной голограммы, а процесс
восстановления изображения конкретной голограммой описывается
некоторым фиксированным голограммным (реконструирующим)
оператором Т(g) который порожден вполне определенным голограммным
образом gÎ Á (конкретной голограммой). Так как
реконструирующие свойства абстрактной голограммы полностью
определяются структурой голограммной группы Á , то
в дальнейшем для описания процесса воспроизведения изображения
на стадии восстановления вместо термина представление голограммной
группы будем часто использовать термин представление абстрактной
голограммы. Сужение представления
Ψт|(Á
/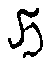 )
(8)
)
(8)
на голограммную
фактор-группу Á /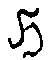 позволяет исследовать особенности восстановления различных
типов голограммы, обусловленные спецификой представления
Т(τ) голограммных классов эквивалентности τÎ
Á /
позволяет исследовать особенности восстановления различных
типов голограммы, обусловленные спецификой представления
Т(τ) голограммных классов эквивалентности τÎ
Á /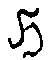 .
.
3.9.
Линейное пространство l{p(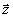 )}
реконструирующих волн, в котором действуют операторы
Т(g), называется пространством представление /2/. Обычно
оно реализуется в виде пространства многочленов p(
)}
реконструирующих волн, в котором действуют операторы
Т(g), называется пространством представление /2/. Обычно
оно реализуется в виде пространства многочленов p(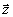 )
от одного или нескольких комплексных переменных /2/
)
от одного или нескольких комплексных переменных /2/
и описывает
тем самым множество возможных линейных комбинаций реконструирующих
волн. При анализе процесса восстановления конкретной голограммы
g голограммный оператор Т(g) преобразует заданную линейную
комбинацию реконструирующих волн Р(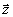 )
и восстановленную волны
)
и восстановленную волны  ,
так что реконструированное поле имеет вид:
,
так что реконструированное поле имеет вид:
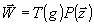 .
(9)
.
(9)
На этом
голографический цикл можно считать законченным.
4. Таким
образом, дано аксиоматическое описание абстрактного голографического
процесса и построена его математическая модель, которая
может быть использована для дальнейшего дедуктивного логического
исследования. В основе построения модели лежит теоретико-групповой
подход, позволяющий дать абстрактное математическое описание
трем основный этапам голографического процесса, начиная
от регистрации и кончая реконструкцией исходного волнового
фронта.
4.1.
Задание групповой структуры интерференционного поля сводится
к построению трех основных групп: g, Н и g/Н.
4.2.
Групповое описание свойств регистрирующей среды задается
с помощью голографического оператора h и голограммной
группы Á , что позволяет ввести понятие абстрактной
голограммы 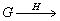 Á
. Анализ групповой структуры абстрактной голограммы приводит
к выделению инвариантной собственной подгруппы
Á
. Анализ групповой структуры абстрактной голограммы приводит
к выделению инвариантной собственной подгруппы 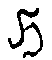 в построению абстрактной субголограммы
в построению абстрактной субголограммы 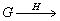
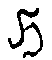 .
Факторизация голограммной группы Á обуславливает выделение
различных типов голограмм в зависимости от специфических
особенностей голографического оператора. Таким образом,
построение трех групп Á ,
.
Факторизация голограммной группы Á обуславливает выделение
различных типов голограмм в зависимости от специфических
особенностей голографического оператора. Таким образом,
построение трех групп Á , 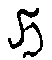 и Á /
и Á /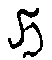 ,
характеризующих определенные структурные совокупности математических
объектов, которые применяются для описания голограмм, фактически
сводится к заданий групповой структуры голограммного поля,
задаваемого абстрактной голограммой.
,
характеризующих определенные структурные совокупности математических
объектов, которые применяются для описания голограмм, фактически
сводится к заданий групповой структуры голограммного поля,
задаваемого абстрактной голограммой.
4.3.
Наконец, процесс реконструкции можно рассматривать как представление
абстрактной голограммы, понимая под этим представление группы
Á голограммных образов в группу gТ реконструирующих
операторов. Иначе говоря, на стадии восстановления действие
кон-
кратной
голограммы на восстанавливающую волну описывается с помощью
некоторого голограммного оператора. Голограммный оператор
t(g)Î gt (gÎ Á ) действует в линейном пространстве
l{p(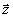 )}
реконструирующих волн и определяет реконструированное поле.
)}
реконструирующих волн и определяет реконструированное поле.
5. Эти
три основных этапа абстрактного голографического процесса
на рис.1 обозначены, соответственно, римскими цифрами i,
ii, iii и условно отделены друг от друга пунктиром.
Построенная
теоретико-групповая модель абстрактного голографического
процесса позволит решить задачи систематизации свойств и
особенностей все возрастающего множества голограмм и различных
голографических направлений, а также прогнозирования новых
разновидностей, которые без такой модели не могла быть даже
сформулирована. В теоретико-групповой трактовке эта задача
ставится как задача исследования свойств абстрактной голограммы
и описания всех возможных ее представлений. При этом в основе
такого подхода лежат общие соображения симметрии, обусловленные
инвариантным характером интерференционного поля, инвариантными
свойствами регистрирующей среды и инвариантным строением
голограммного поля, определяемого абстрактной голограммой.
С другой
стороны, логическое исследование возможных реализации голограммой
группы Á и ее представлений позволит описать некоторые
новые свойства как плоских, так и объемных голограмм. Рассмотрим
некоторые примеры, иллюстрирующие применение теоретико-групповой
модели абстрактного голографического процесса.
ii.
Групповое представление тонких голограмм
В настоящее
время теория тонких (плоских) голограмм разработана достаточно
полно и образует хорошую базу для дальнейшего развития голографии
/5/. В частности, исследование групповой структуры голографического
цикла, проведенное в /2/ на примере плоских голограмм, позволило
в данной работе построить математическую модель абстрактного
голографического процесса. При этом разработанная модель
не только описывает уже известные свойства, но и позволяет
чисто логическим путем предсказать новые.
В данном
разделе, опираясь на мультипликативные свойства ам-
плитудных
коэффициентов пропускания тонких голограмм, построена мультипликативная
реализация 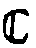 * голограммной группы Á , которая с необходимостью
приводит к понятию усиливающей голограммы. Выделение амплитудной
Аt и фазовой Фt голограммной подгруппы
(Аt,Фt Ì
* голограммной группы Á , которая с необходимостью
приводит к понятию усиливающей голограммы. Выделение амплитудной
Аt и фазовой Фt голограммной подгруппы
(Аt,Фt Ì 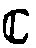 *)
обуславливает две реализации абстрактной субголограммы,
которые позволяют говорить об амплитудных голограммах с
постоянным фазовым сдвигом или о фазовых голограммах с постоянным
пропуcканием как о некоторых голограммных классах эквивалентности
*)
обуславливает две реализации абстрактной субголограммы,
которые позволяют говорить об амплитудных голограммах с
постоянным фазовым сдвигом или о фазовых голограммах с постоянным
пропуcканием как о некоторых голограммных классах эквивалентности
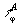 или
или
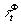 .
.
1.
Групповое представление тонких амплитудных голограмм
1.1.
Амплитудный коэффициент пропускания ta(x,у) тонкой
поглощающей голограммы задает параметризованную по координатам
(x,y) некоторую совокупность Аtп векторов 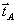 ,
лежащих на полуинтервале (0,1] вещественной прямой
,
лежащих на полуинтервале (0,1] вещественной прямой 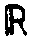 (рис.2), т.е.
(рис.2), т.е.
atП={taÎ
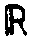 |0<ta≤1}. (10)
|0<ta≤1}. (10)
При
этом с физической точки зрения значение ta=1
соответствует отсутствию голографической записи в случае
идеальной непоглощающей регистрирующей среды, а значение
ta=0 исключается из рассмотрения, так как обусловлено
физически не реализуемой ситуацией бесконечно большой оптической
плотности.
Строго
говоря, при непрерывном обходе всех точек (х,у) конкретной
голограммы годограф вектора 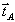 (х,у)
на рис.2 представляет собой в общем случае только некоторое
подмножество
(х,у)
на рис.2 представляет собой в общем случае только некоторое
подмножество 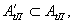 так что
так что
a'tп={taÎ
atп| ta=t(x,y)}.
(11)
Подмножество
А'tп значений амплитудного коэффициента пропускания
конкретной голограммы в зависимости от множества точек,
в которых регистрируется интерференционное поле, может быть
непрерывным (физически реализуемые голограммы) или дискретным
(машинные и составные голограммы).
В соответствии
с теоретико-групповой моделью задание конкрет-
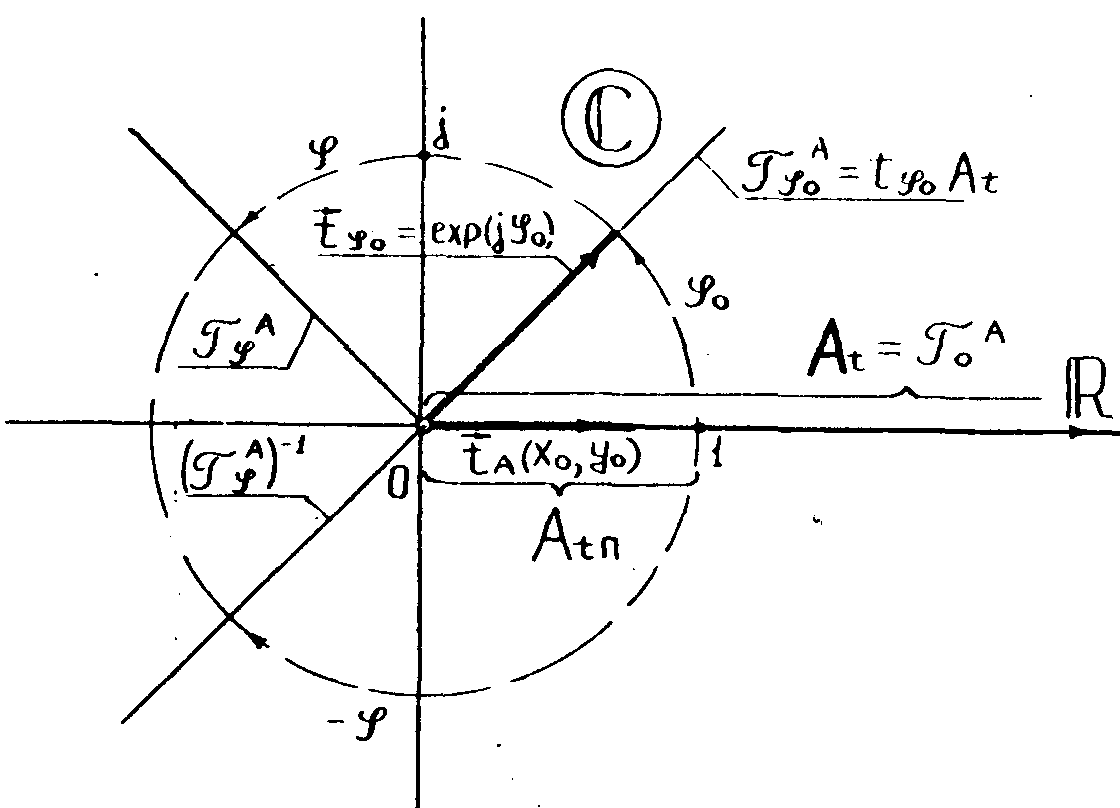
Рис.2.
Факторизация тонких амплитудных голограмм.
ной
голограммы сводится к построению некоторой операторной функции
Н, определенной на группе g голографических образов.
Реализация голограммной группы Á =ranht
в виде множества  *
амплитудных коэффициентов пропускания tc(x,y)
приводит к понятию тонкой голограммы
*
амплитудных коэффициентов пропускания tc(x,y)
приводит к понятию тонкой голограммы 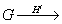
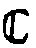 *.
Более детальная конкретизация функции ht
в виде амплитудного поглощающего оператора
*.
Более детальная конкретизация функции ht
в виде амплитудного поглощающего оператора 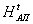 ,
принимающего вещественные значения tА(х,у), которые
удовлетворяют условию (10), выделяет класс тонких амплитудных
поглощающих голограмм.
,
принимающего вещественные значения tА(х,у), которые
удовлетворяют условию (10), выделяет класс тонких амплитудных
поглощающих голограмм.
Если
рассмотреть множество g всех голографических образов, зафиксировать
некоторую точку (х0,y0) на голограмме
и учесть все возможные режимы обработки, то на этом множестве
функция 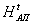 принимает вcе значения ta(x0,y0)
из atп, так что
принимает вcе значения ta(x0,y0)
из atп, так что
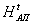 [g]={ta(x0,y0)
| taÎ atп}. (12)
[g]={ta(x0,y0)
| taÎ atп}. (12)
Иначе
говоря, множество значений ta(x0,y0)
совпадаете Аtп, т.е. с геометрической точки зрения
годограф вектора 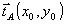 на
на
множестве
g описывает весь полуинтервал (0,1] (рис.2). Так как (х0,у0)
- произвольная точка, то все сказанное остается справедливым
для всех точек (х,у) каждой голограммы. Именно в этом смысле
будем в дальнейшее говорить о множестве atп амплитудных
коэффициентов пропускания tА(x,y) тонких поглощающих
голограмм как об области значений функции 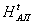 ,
так что
,
так что
Аtп=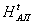 [g]=ran
[g]=ran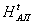 ,
(13)
,
(13)
геометрически
отождествляя Аtп с единичным полуинтервалом.
1.2.
Известно /1/, что множество всех вещественных чисел r за
вычетом нуля
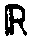 *=
*=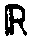 \{0}
(14)
\{0}
(14)
образует
мультипликативную абелеву группу с обычной операцией умножения
в поле вещественных чисел 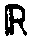 (мультипликативная группа поля
(мультипликативная группа поля 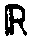 ).
Нейтральным (единичным) элементом в такой группе является
обычная единица, а противоположным элементом служит обратный
элемент.
).
Нейтральным (единичным) элементом в такой группе является
обычная единица, а противоположным элементом служит обратный
элемент.
Используя
геометрическую интерпретацию множества atп и
учитывая, что АtпÌ 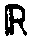 ,
рассмотрим индицируемую на этом множестве бинарную операцию
умножения. Физически эта операция реализуется путем взаимного
наложения одной голограммы на другую, так что суммарное
пропускание ta двух голограмм равно
,
рассмотрим индицируемую на этом множестве бинарную операцию
умножения. Физически эта операция реализуется путем взаимного
наложения одной голограммы на другую, так что суммарное
пропускание ta двух голограмм равно
ta=ta1∙ta2,
(15)
где
ta1,ta2Î Аtп. При
этом предполагается, что максимальный линейный размер голограмм
ограничен, т.е. амплитудный коэффициент пропускания ta(х,у)
задан в пределах некоторой ограниченной области d((x,y)Î
d). Амплитудный коэффициент пропускания голограммы меньших
размеров, определенной в области d'Ì d, на дополнении
d\d' подобласти d' до области d считается равным единице,
так что
d\d'={(x,y)Î
d|ta(x,y)|º 1}. (16)
Очевидно,
что бинарная операция умножения замкнута, но не обратима
на множестве Аtп. Следовательно, множество Аtп
амплитудных коэффициентов пропускания тонких поглощающих
голограмм, которое является образом амплитудного голографического
оператора 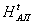 ,
не образует подгруппы в мультипликативной группе
,
не образует подгруппы в мультипликативной группе 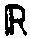 *(АtпÎ
*(АtпÎ
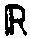 *).
Таким образом, теоретико-групповой подход, опираясь на чисто
логические соображения, требует расширения класса atп
амплитудных поглощающих голограмм. Естественным расширением
является мультипликативная подгруппа at (рис.2)
всех положительных вещественных чисел (АtÌ
*).
Таким образом, теоретико-групповой подход, опираясь на чисто
логические соображения, требует расширения класса atп
амплитудных поглощающих голограмм. Естественным расширением
является мультипликативная подгруппа at (рис.2)
всех положительных вещественных чисел (АtÌ 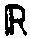 *).
В этом множестве для любого элемента ta существует
обратный элемент ta-1Î at,
такой что
*).
В этом множестве для любого элемента ta существует
обратный элемент ta-1Î at,
такой что
ta∙ta-1=1.
(17)
С физической
точки зрения такое расширение класса atп амплитудных
поглощающих голограмм, т.е. переход к подгруппе at, приводит
к понятию усиливающей голограммы. В самом деле, так как
для поглощающей голограммы ta≤1, то по
определению обратный элемент ta-1≥1.
Назовем амплитудную голограмму усиливающей (или частично
усиливающей), если амплитудный коэффициент пропускания ta(х,у)
на всей поверхности голограммы (соответственно на каких-то
ее участках) оказывается больше единицы (ta(x,у)>1).
Тогда
голографический амплитудный оператор 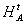 ,
заданный на голографической группе g, принимает все значения
tА(x0,y0) из at
и описывает не только поглощающие, но и усиливающие голограммы,
так что по аналогии с (12)
,
заданный на голографической группе g, принимает все значения
tА(x0,y0) из at
и описывает не только поглощающие, но и усиливающие голограммы,
так что по аналогии с (12)
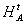 [g]={ta(x0,y0)|taÎ
at}. (18)
[g]={ta(x0,y0)|taÎ
at}. (18)
Именно
в этом смысле можно говорить о подгруппе Аt амплитудных
голограмм как об области значений функции 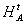 ,
т.е.
,
т.е.
at=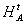 [g]=ran
[g]=ran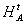 .
(19)
.
(19)
С физической
точки зрения такое расширение области значений 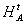 [g]
амплитудного голографического оператора
[g]
амплитудного голографического оператора 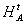 обусловлено расширением его свойств, т.е. введением усиливающих
голограмм. При этом теоретико-групповая конструкция говорит
только о самом факте су-
обусловлено расширением его свойств, т.е. введением усиливающих
голограмм. При этом теоретико-групповая конструкция говорит
только о самом факте су-
ществования
таких голограмм, ничего не говоря о возможном способе их
практической реализации.
В дальнейшем
будем называть подгруппу at для кратности амплитудной
подгруппой, геометрически отождествляя ее с положительной
полуосью, т.е. с лучом, выходящим из точки 0, которая ему
не принадлежит. При этом по определению группы для любой
поглощающей голограммы ta(x,y)≤1 существует
с учетом (17) усиливающая голограмма ta-1(x,y)=[1/ta(х,у)]≥1.
Роль единичного (нейтрального) элемента подгруппы играет
идеальная непоглощающая обработанная регистрирующая среда
без голографической записи, т.е. ta0(х,y)=1 для
соответствующих точек (x,y)Î d.
Таким
образом, построена реализация теоретико-групповой модели
тонкой амплитудной голограммы, которая представляет собой
отображение голографической группы g на амплитудную голограммную
подгруппу at. Иначе говоря, в данном случае абстрактная
субголограмма (4) задается в виде:
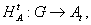 (20)
(20)
где
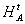 и Аt
- соответсвующие реализации голографического оператора h
и голограммной подгруппы
и Аt
- соответсвующие реализации голографического оператора h
и голограммной подгруппы 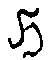 .
.
2.
Амплитудная факторизация тонких голограмм
Построенная
выше математическая модель 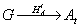 тонкой амплитудной голограммы дает теоретико-групповое описание
только амплитудных (поглощающих и усиливающих) голограмм,
действие которых основано на чисто амплитудной модуляции
реконструирующей волны. В общем случае амплитудная голограмма
наряду с амплитудной модуляцией может вносить и некоторый
постоянный фазовый сдвиг φ0. С теоретико-групповой
точки зрения этот факт приводит к факторизации тонких голограмм
на амплитудные голограммные классы эквивалентности
тонкой амплитудной голограммы дает теоретико-групповое описание
только амплитудных (поглощающих и усиливающих) голограмм,
действие которых основано на чисто амплитудной модуляции
реконструирующей волны. В общем случае амплитудная голограмма
наряду с амплитудной модуляцией может вносить и некоторый
постоянный фазовый сдвиг φ0. С теоретико-групповой
точки зрения этот факт приводит к факторизации тонких голограмм
на амплитудные голограммные классы эквивалентности 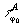 ,
структура которых обусловлена амплитудной подгруппой at.
Для описания таких голограмм необходимо расширить исходную
группу
,
структура которых обусловлена амплитудной подгруппой at.
Для описания таких голограмм необходимо расширить исходную
группу 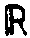 *,
являющуюся реализацией голограммной группы Á .
*,
являющуюся реализацией голограммной группы Á .
Известно
/1/, что множество всех комплексных чисел 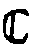 *
за вычетом нуля,
*
за вычетом нуля,
 *=
*= \{0},
(21)
\{0},
(21)
образует
мультипликативную абелеву группу с обычной операцией умножения,
заданной в поле комплексных чисел  (мультипликативная группа поля
(мультипликативная группа поля  ).
При этом, как
).
При этом, как 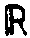 *,
так и амплитудная группа at, являются подгруппами
группы
*,
так и амплитудная группа at, являются подгруппами
группы  *(
*(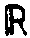 *,АtÌ
*,АtÌ
 *).
*).
Амплитудный
коэффициент пропускания голограммы, которая вносит постоянный
фазовый сдвиг φ0, можно представить в виде:
ta(x,y;φ0)=exp(jφ0)ta(x,y)=t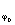 ta(x,y),
(22)
ta(x,y),
(22)
где
t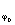 =exp(jφ0)
- составляющая амплитудного пропускания, обусловленная наличием
фазовой задержки. ecли ta принимает все значения
из at, то выражение (22) определяет некоторую
совокупность,
=exp(jφ0)
- составляющая амплитудного пропускания, обусловленная наличием
фазовой задержки. ecли ta принимает все значения
из at, то выражение (22) определяет некоторую
совокупность,
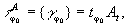 (23)
(23)
элементов
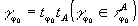 в виде
амплитудного голограммного класса эквивалентности. О геометрической
точки зрения
в виде
амплитудного голограммного класса эквивалентности. О геометрической
точки зрения 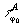 представляет собой луч (рис.2), выходящий из точки 0 под
углом φ0.
представляет собой луч (рис.2), выходящий из точки 0 под
углом φ0.
С другой
стороны, at является инвариантной подгруппой
группы  *.
Тогда голограммные классы эквивалентности τ0А
являются элементами амплитудной голограммной фактор-группы
*.
Тогда голограммные классы эквивалентности τ0А
являются элементами амплитудной голограммной фактор-группы
 */at
и получаются путем поворота луча at на угол φ
(рис.2). Таким образом, амплитудная факторизация голограммной
группы
*/at
и получаются путем поворота луча at на угол φ
(рис.2). Таким образом, амплитудная факторизация голограммной
группы  *
приводит к тому, что вся комплексная плоскость
*
приводит к тому, что вся комплексная плоскость  за вычетом нуля разбивается на совокупность непересекающихся
лучей, которые исчерпывают всю эту плоскость и физически
интерпретируются как амплитудные голограммы, вносящие постоянный
фазовый сдвиг φ.
за вычетом нуля разбивается на совокупность непересекающихся
лучей, которые исчерпывают всю эту плоскость и физически
интерпретируются как амплитудные голограммы, вносящие постоянный
фазовый сдвиг φ.
Исходная
амплитудная подгруппа at=τ0А
является нейтральным элементом амплитудной голограммной
фактор-группы  */Аt.
Обратным элементом для τφa=tφat
служит голограммный класс (τφa)-1=tφ-1at,
который объединяет амплитудные голограммы, вносящие фазовый
сдвиг (-φ), так что
*/Аt.
Обратным элементом для τφa=tφat
служит голограммный класс (τφa)-1=tφ-1at,
который объединяет амплитудные голограммы, вносящие фазовый
сдвиг (-φ), так что
tφ-1=t-φ=tφ*=exp(-jφ).
(24)
Таким
образом, дополнительное расширение области значений 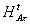 [g]
амплитудного голографического оператора
[g]
амплитудного голографического оператора 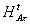 в виде
в виде
 *=
*=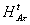 [g]=ran
[g]=ran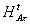 (25)
(25)
связано
с введением постоянного фазового сдвига φ, который
обусловлен фазовомодулирующими свойствами реальной регистрирующей
среды (голографического оператора 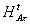 ).
Соответствующая математическая модель обобщенной тонкой
амплитудной голограммы, учитывающая усиливающие и постоянные
фазовомодулирующие свойства регистрирующей среды (голографического
оператора
).
Соответствующая математическая модель обобщенной тонкой
амплитудной голограммы, учитывающая усиливающие и постоянные
фазовомодулирующие свойства регистрирующей среды (голографического
оператора 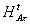 ),
имеет вид
),
имеет вид
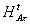 :g→
:g→ */at.
(26)
*/at.
(26)
Усиливающий
характер голограммы связан с наличием амплитудной группы
at. Факторизация голограммной группы  *
(области значений
*
(области значений 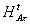 [g]
амплитудного голографического оператора
[g]
амплитудного голографического оператора 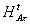 )
обусловлена введением некоторой фазовой задержки. При этом
построение амплитудной голограммной фактор-группы
)
обусловлена введением некоторой фазовой задержки. При этом
построение амплитудной голограммной фактор-группы  */Аt,
элементами которой являются амплитудные голограммные классы
эквивалентности τφa, позволяет
выделять различные типы амплитудных голограмм с одним в
тем же постоянным фазовым сдвигом φ.
*/Аt,
элементами которой являются амплитудные голограммные классы
эквивалентности τφa, позволяет
выделять различные типы амплитудных голограмм с одним в
тем же постоянным фазовым сдвигом φ.
Заметим,
что введение постоянного вещественного множителя t0Î
at не изменяет класс эквивалентности τφa=(t0tφ)at=tφat.
С физической точки зрения это означает, что изменяются только
пропускающие свойства регистрирующей среды, а фазовомодулирующие
свойства остаются неизменными.
3.
Групповое представление тонких фазовых голограмм
3.1.
Амплитудный коэффициент пропускания
tф(x,y)=exp[jφ(x,y)]
(27)
тонкой
фазовой голограммы по аналогии с амплитудной голограммой
задает параметризованную по координатам (х,у) некоторую
совокупность Ф't векторов 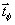 комплексной плоскости
комплексной плоскости  ,
лежащих на окружности Φt единичного радиуса
(рис.3), где
,
лежащих на окружности Φt единичного радиуса
(рис.3), где
Фt={tфÎ
 |
|tф|=1}. (28)
|
|tф|=1}. (28)
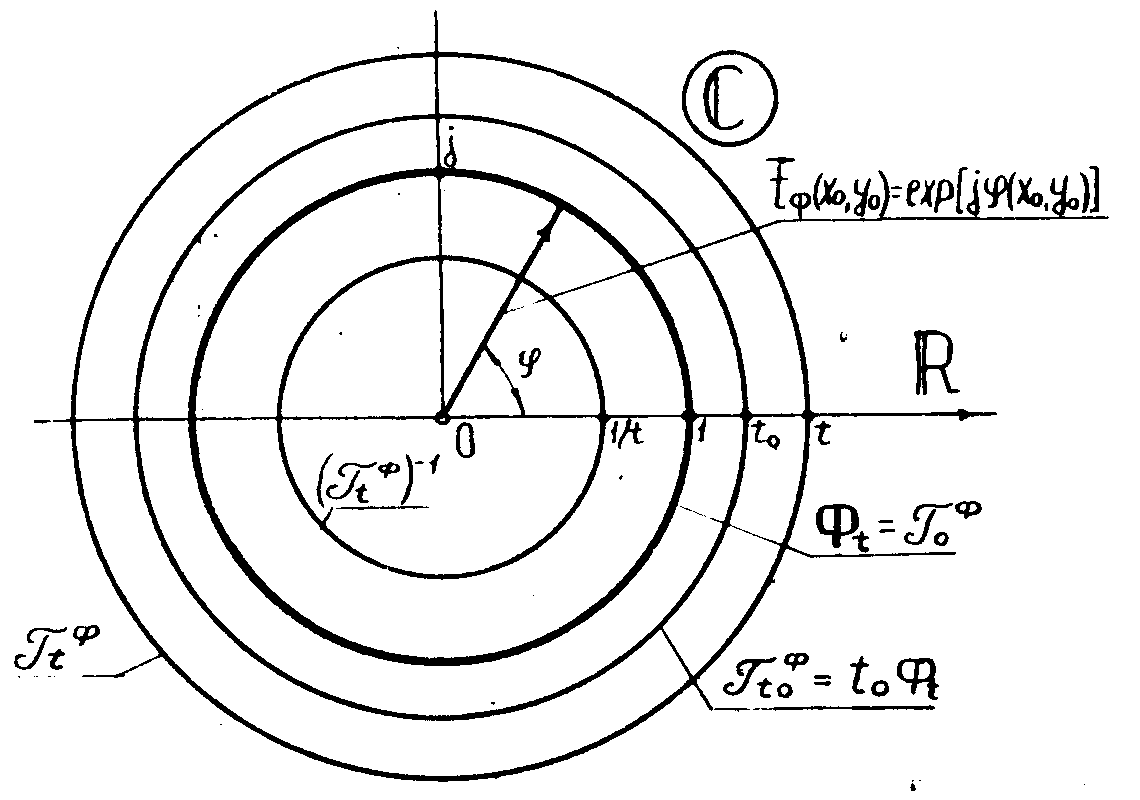
Рис.3.
Факторизация тонких фазовых голограмм.
В случав
произвольной голограммы множество Ф't=Ф, но не
обязано совпадать с Фt, так как фазовый сдвиг
φ(x,у), вносимый голограммой, может не принимать всех
значений внутри [0,2π]. Пoэтому при непрерывном обходе
всех точек (х,у) голограммы годограф вектора 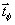 (х,у)
(рис.3) представляет собой в общем случае только часть окружности
Фt.
(х,у)
(рис.3) представляет собой в общем случае только часть окружности
Фt.
В соответствии
с теоретико-групповой моделью абстрактной голограммы реализация
области значений ranht голографического
оператора в виде множества Фt фазовых коэффициентов
пропускания приводит к понятию фазового оператора 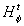 и выделению класса тонких фазовых голограмм. Иначе говоря,
функция
и выделению класса тонких фазовых голограмм. Иначе говоря,
функция 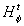 ,
заданная на множестве g голографических образов, принимает
все значения tф(x0,y0)
из Фt, так что
,
заданная на множестве g голографических образов, принимает
все значения tф(x0,y0)
из Фt, так что
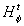 [g]={tф(x0,y0)|tфÎ
Фt}. (29)
[g]={tф(x0,y0)|tфÎ
Фt}. (29)
Фазовый
сдвиг φ(x0,y0) на этом множестве
принимает все значения от 0 до 2π, а годограф вектора
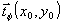 описывает
окружность Фt. Поэтому в дальнейшем будем говорить
о множестве Фt амплитудных коэффициентов пропускания
tф(x,y) тонких фазовых голограмм как об области
значений функции
описывает
окружность Фt. Поэтому в дальнейшем будем говорить
о множестве Фt амплитудных коэффициентов пропускания
tф(x,y) тонких фазовых голограмм как об области
значений функции 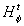 ,
так что
,
так что
Фt=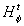 [g]=ran
[g]=ran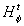 .
(30)
.
(30)
Известно
/1/, что множество Φt всех комплексных чисел,
по модулю равных 1, образует подгруппу в мультипликативной
группе  *(ФtÌ
*(ФtÌ
 *).
Будем для краткости называть подгруппу Фt фазовой
подгруппой, геометрически отождествляя ее с окружностью
единичного радиуса на комплексной плоскости
*).
Будем для краткости называть подгруппу Фt фазовой
подгруппой, геометрически отождествляя ее с окружностью
единичного радиуса на комплексной плоскости  (рис.3). Физически операция умножения в фазовой подгруппе
at осуществляется как и в амплитудной подгруппе
Аt путем взаимного наложения одной голограммы
на другую.
(рис.3). Физически операция умножения в фазовой подгруппе
at осуществляется как и в амплитудной подгруппе
Аt путем взаимного наложения одной голограммы
на другую.
Таким
образом, построена реализация теоретико-групповой модели
тонкой фазовой голограммы, которая представляет собой отображение
голографической группы g на фазовую голограммную подгруппу
Фt. При этом абстрактная субголограмма (4) имеет
вид:
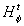 :g→Фt,
(31)
:g→Фt,
(31)
где
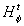 и Фt
- реализации голографического оператора h и голограммной
подгруппы
и Фt
- реализации голографического оператора h и голограммной
подгруппы 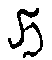 .
.
3.2.
В отличие от амплитудных голограмм фазовые голограммы обладают
определенной групповой структурой, обусловленной специфическим
характером фазовой модуляции. Эта специфика проявляется
а том, что построенная фазовая подгруппа Фt является
однопараметрической подгруппой /6/ группы  *,
так как каждому вещественному числу φ поставлен в соответствие
элемент tФ(φ)=tФ(x0,y0)=exp[jφ(x0,y0)].
При этом для любых φ1 и φ2
выполняется равенство:
*,
так как каждому вещественному числу φ поставлен в соответствие
элемент tФ(φ)=tФ(x0,y0)=exp[jφ(x0,y0)].
При этом для любых φ1 и φ2
выполняется равенство:
tФ(φ1)tФ(φ2)=exp(jφ1)exp(jφ2)=exp[j(φ1+φ2)]=tФ(φ1+φ2).
(32)
Из (32)
вытекает, что
tФ(0)=tФ(φ-φ)=tФ(φ)tФ(-φ)=exp[j(φ-φ)]=1.
(33)
С другой
стороны, так как
tФ(φ)tФ-1(φ)=1,
(34)
то с
учетом (33)
tФ-1(φ)=tФ(-φ)=exp(-jφ).
(35)
Таким
образом, фазовая подгруппа Фt изоморфна подгруппе
вращении вокруг фиксированной оси /6/ в группе всех вращении
евклидова пространства.
4.
Фазовая факторизация тонких голограмм
Построенная
выше реализация математической модели абстрактной субголограммы
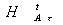 Фt,
в виде тонкой фазовой голограммы позволяет осуществить факторизацию
голограммной группы
Фt,
в виде тонкой фазовой голограммы позволяет осуществить факторизацию
голограммной группы  *
с помощью подгруппы Фt. С теоретико-групповой
точки зрения это обусловлено тем, что всякая инвариантная
субголограмма позволяет выявлять некоторые голограммные
классы эквивалентности.
*
с помощью подгруппы Фt. С теоретико-групповой
точки зрения это обусловлено тем, что всякая инвариантная
субголограмма позволяет выявлять некоторые голограммные
классы эквивалентности.
В общем
случае фазовая голограмма наряду с фазовой модуляцией может
иметь и некоторое поглощение. Амплитудный коэффициент пропускания
такой голограммы можно представить в виде:
tФ(x0,y0;t0)=t0exp[jφ(x,y)]=t0tФ(x,y),
(36)
где
величина t0=|tФ(x,y;t0)|
задает абсолютное значение пропускания. Если tфÎ
Фt, то выражение (36) определяет некоторую
совокупность
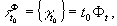 (37)
(37)
элементов
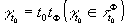 , которая
называется фазовым голограммным классом эквивалентности.
Геометрически
, которая
называется фазовым голограммным классом эквивалентности.
Геометрически 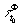 представляет собой окружность (рис.3) радиуса t0.
представляет собой окружность (рис.3) радиуса t0.
В силу
инвариантности подгруппы Фt голограммные классы
эквивалентности 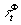 являются элементами фазовой голограммной фактор-группы
являются элементами фазовой голограммной фактор-группы 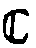 */Фt.
Геометрически они получаются путем сжатия (t<1) или растяжения
(t>1) окружности единичного радиуса Фt(t=0).
Случай t>1 соответствует усиливающим фазовым голограммным
классам эквивалентности, возникновение которых тесно связано
с введенным выше понятием усиливающей голограммы. Таким
образом, фазовая факторизация голограммной группы
*/Фt.
Геометрически они получаются путем сжатия (t<1) или растяжения
(t>1) окружности единичного радиуса Фt(t=0).
Случай t>1 соответствует усиливающим фазовым голограммным
классам эквивалентности, возникновение которых тесно связано
с введенным выше понятием усиливающей голограммы. Таким
образом, фазовая факторизация голограммной группы 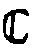 *
приводит к тому, что вся комплексная плоскость
*
приводит к тому, что вся комплексная плоскость 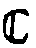 за вычетом нуля разбивается на совокупность непересекающихся
концентрических окружностей, которые исчерпывают всю эту
плоскость (рис.3). Физически эти окружности (фазовые голограммные
классы эквивалентности
за вычетом нуля разбивается на совокупность непересекающихся
концентрических окружностей, которые исчерпывают всю эту
плоскость (рис.3). Физически эти окружности (фазовые голограммные
классы эквивалентности 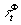 )
интерпретируются как фазовые голограммы, обладающие некоторым
поглощением (t<1) или усилением (t>l).
)
интерпретируются как фазовые голограммы, обладающие некоторым
поглощением (t<1) или усилением (t>l).
Исходная
фазовая подгруппа Фt=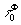 является нейтральным элементом фазовой голограммной фактор-группы
является нейтральным элементом фазовой голограммной фактор-группы
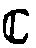 */Фt.
Обратным элементом для
*/Фt.
Обратным элементом для 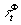 =tΦt
служит голограммный класс (
=tΦt
служит голограммный класс (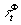 )=t-1Фt,
который объединяет фазовые голограммы с абсолютной величиной
пропускания:
)=t-1Фt,
который объединяет фазовые голограммы с абсолютной величиной
пропускания:
t-1=1/t.
(38)
Дополнительное
расширение области значений 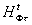 [g]
фазового голографического оператора
[g]
фазового голографического оператора 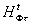 в виде
в виде
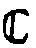 *=
*=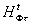 [g]=ran
[g]=ran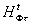 (39)
(39)
обусловлено
наличием поглощения или усиления в регистрирующей среде.
Математическая модель обобщенной тонкой фазовой голограммы,
учитывавшая фазовомодулирующие и постоянные усиливающие
свойства
голографического
оператора 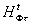 ,
имеет вид:
,
имеет вид:
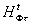 :g→
:g→ */Φt.
(40)
*/Φt.
(40)
Фазовый
характер модуляции, осуществляемой голограммой, обусловлен
наличием фазовой группы Фt. Факторизация голограммной
группы 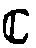 *
связана с наличием некоторого поглощения или усиления. При
этом построение фазовой голограммной фактор-группы
*
связана с наличием некоторого поглощения или усиления. При
этом построение фазовой голограммной фактор-группы 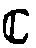 */Φt,
элементами которой являются (разовый голограммные классы
эквивалентности τtΦ, позволяет
выделять различные типы фазовых голограмм с одним и тем
же постоянным пропусканием t.
*/Φt,
элементами которой являются (разовый голограммные классы
эквивалентности τtΦ, позволяет
выделять различные типы фазовых голограмм с одним и тем
же постоянным пропусканием t.
Заметим,
что введение постоянного фазового множителя t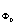 =(t
=(t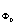 t)Φt=tΦt
изменяет класс эквивалентности τtΦ=(t
t)Φt=tΦt
изменяет класс эквивалентности τtΦ=(t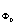 t)Φt=tΦt.
Физически это означает, что изменяются только фазовомодулирующие
свойства голограммы, а пропускание (т.е. вид окружности
на рис.3) не меняется.
t)Φt=tΦt.
Физически это означает, что изменяются только фазовомодулирующие
свойства голограммы, а пропускание (т.е. вид окружности
на рис.3) не меняется.
5.
Ортогональные свойства тонких голограмм
Реализация
голограммной группы Á в виде группы 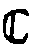 * амплитудных коэффициентов пропускания приводит к
теоретико-групповой модели тонкой голограммы:
* амплитудных коэффициентов пропускания приводит к
теоретико-групповой модели тонкой голограммы:
ht:g→
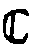 *, (41)
*, (41)
где
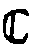 *=ranht.
При таком отображении каждому голографическому образу
*=ranht.
При таком отображении каждому голографическому образу 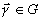 ,
т.е. некоторому распределению поля в плоскости голограммы
ставится в соответствие определенный голограммный образ
γÎ Á в виде комплексного амплитудного коэффициента
пропускания:
,
т.е. некоторому распределению поля в плоскости голограммы
ставится в соответствие определенный голограммный образ
γÎ Á в виде комплексного амплитудного коэффициента
пропускания:
tc(x,y)=ta(x,y)exp[jφ(x,y)]=ta(x,y)tФ(x,y),
(42)
где
γ=tcÎ  *.С
геометрической точки зрения группа
*.С
геометрической точки зрения группа  *
отождествляется с комплексной плоскостью
*
отождествляется с комплексной плоскостью  с выколотым нулем, а голограммные образы γ=tc
интерпретируются в виде точек (векторов) этой плоскости.
Тогда произвольная голограмма (42), параметризованная по
координатам (х,у), геометрически представляет собой неко-
с выколотым нулем, а голограммные образы γ=tc
интерпретируются в виде точек (векторов) этой плоскости.
Тогда произвольная голограмма (42), параметризованная по
координатам (х,у), геометрически представляет собой неко-
торую
область τc в плоскости  (τсÌ
(τсÌ  *).
*).
Амплитудная
at и (разовая Фt подгруппы группы
 *
соответствуют двум физическим моделям регистрирующей среды
соответственно с амплитудной (
*
соответствуют двум физическим моделям регистрирующей среды
соответственно с амплитудной (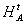 )
или фазовой (
)
или фазовой (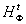 )
модуляцией и позволяют построить математическую модель тонкой
амплитудной голограммы
)
модуляцией и позволяют построить математическую модель тонкой
амплитудной голограммы 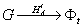 и тонкой фазовой голограммы
и тонкой фазовой голограммы 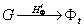 .
Инвариантный характер этих подгрупп обусловлен инвариантными
свойствами амплитудных коэффициентов пропускания тонких
голограмм, что находит свое выражение в коммутативности
голограммной группы
.
Инвариантный характер этих подгрупп обусловлен инвариантными
свойствами амплитудных коэффициентов пропускания тонких
голограмм, что находит свое выражение в коммутативности
голограммной группы  *.
Таким образом, мультипликативная симметрия подгрупп at
и Фt приводит к двум различным разбиениям группы
*.
Таким образом, мультипликативная симметрия подгрупп at
и Фt приводит к двум различным разбиениям группы
 *
на голограммные "типы эквивалентности"
*
на голограммные "типы эквивалентности" 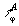 и
и 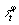 . Если
за основу берутся амплитудномодулирующие свойства регистрирующей
среды, то это приводит к математической модели обобщенной
тонкой амплитудной голограммы
. Если
за основу берутся амплитудномодулирующие свойства регистрирующей
среды, то это приводит к математической модели обобщенной
тонкой амплитудной голограммы 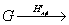
 */at,
которая учитывает наличие постоянной фазовой задержки. Анализ
фазовомодулирующих свойств регистрирующей среды позволяет
построить математическую модель обобщенной тонкой фазовой
голограммы в виде
*/at,
которая учитывает наличие постоянной фазовой задержки. Анализ
фазовомодулирующих свойств регистрирующей среды позволяет
построить математическую модель обобщенной тонкой фазовой
голограммы в виде 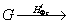
 */Фt,
характеризующем наличие некоторого постоянного пропускания.
*/Фt,
характеризующем наличие некоторого постоянного пропускания.
Реальная
регистрирующая среда (голографический оператор ht)
вносит как амплитудные, так и фазовые искажения, так что
в общем случае амплитудный коэффициент пропускания тонкой
голограммы задается выражением (42). Идеальные случаи сред
с амплитудной ta(х,у) и фазовой tф(х,у)
модуляцией соответствуют двум предельным формам выражения
(42). Существование двух таких предельных моделей регистрирующей
среды находит свое аналитическое выражение в ортогональности
амплитудной at и фазовой Фt голограммных
подгрупп в смысле ортогональности их геометрических образов:
луча, совпадающего с положительной вещественной осью, и
окружности единичного радиуса (угол между касательными в
точке пересечения равен прямому углу).
Таким
образом, используя эту геометрическую аналогию, можно говорить
об ортогональности амплитудных и фазовых тонких голограмм,
подчеркивая тем самым независимость амилитудномодулирующих
и фазовомодулирующих свойств регистрирующей среды. Факторизация
голограммной группы  *
с помощью ортогональных подгрупп at и Фt
индуцирует разбиение множества голограммных образов на две
совокупнос-
*
с помощью ортогональных подгрупп at и Фt
индуцирует разбиение множества голограммных образов на две
совокупнос-
ти
ортогональных амплитудных и фазовых голограммных классов
эквивалентности τφА, τtΦ.
Геометрически эти ортогональные голограммные классы эквивалентности
задают ортогональную сетку на комплексной плоскости  с выколотым нулем в виде системы расходящихся лучей τφa
и концентрических окружностей τtΦ
(рис.4). Так как любой луч τta
перпендикулярен каждой окружности τtΦ
, то можно говорить о двух ортогональных голограммных фактор-группах
с выколотым нулем в виде системы расходящихся лучей τφa
и концентрических окружностей τtΦ
(рис.4). Так как любой луч τta
перпендикулярен каждой окружности τtΦ
, то можно говорить о двух ортогональных голограммных фактор-группах
 */Аi
и
*/Аi
и  */Фt
как о двух ортогональных представлениях группы
*/Фt
как о двух ортогональных представлениях группы  *
амплитудных коэффициентов пропускания тонких голограмм.
*
амплитудных коэффициентов пропускания тонких голограмм.
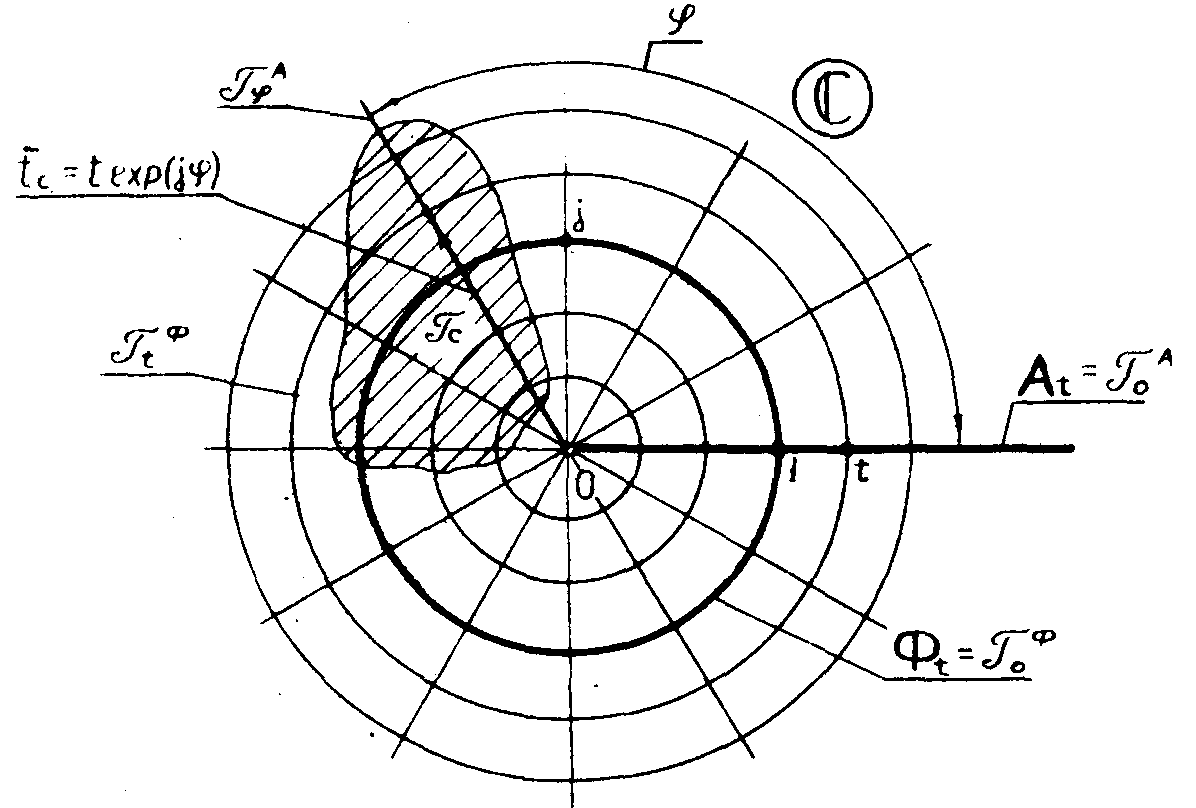
Рис.4.
Ортогональность амплитудных и фазовых голограммных классов
("типов") эквивалентности.
Ортогональная
сетка на рис.4 геометрически иллюстрирует два возможных
структурных типа тонких голограмм, обусловленных специфическими
свойствами голографического оператора ht.
Амплитудная голограммная фактор-группа  */at
позволяет говорить об амплитудных голограммах τφa,
вносящих постоянный фазовый сдвиг φ. Ортогональная
ей фазовая голограммная фактор-группа
*/at
позволяет говорить об амплитудных голограммах τφa,
вносящих постоянный фазовый сдвиг φ. Ортогональная
ей фазовая голограммная фактор-группа  */Фt
выделя-
*/Фt
выделя-
ет фазовые
голограммы τtФ, обладающие постоянным
пропусканием t. Очевидно, что произвольный голограммный
образ γ=tc, который геометрически интерпретируется
в виде некоторой области τc (рис.4), может
быть задан с помощью параметризованного по (х,у) произведения
двух любых ортогональных голограммных классов τφА
и τtφ, проходящих через
эту область. Однако с физической точки зрения такая неоднозначность
не играет существенной роли, ибо связана с внесением постоянного
поглощения t0 и постоянного фазового сдвига φ0.
С другой
стороны, значение амплитудного пропускания tc(x0,y0)=
=ta(x0,y0)tΦ(x0,y0)
в некоторой фиксированной точке (x0,y0)
произвольной голограммы задает два ортогональных голограммных
класса τφa=tΦ(x0,y0)at=exp[jφ(x0,y0)]
и τtΦ=ta(x0,y0)Φt.
В этом смысле произвольную голограмму можно рассматривать
как разложение по двум ортогональным голограммным фактор-группам
(по ортогональному групповому базису). Более общо можно
говорить о разложении в фиксированной точке (х0,у0)
голограммной группы  *
(множества всех амплитудных коэффициентов пропускания тонких
голограмм) на произведение двух ортогональных голограммных
классов τφa и τtΦ,
так что
*
(множества всех амплитудных коэффициентов пропускания тонких
голограмм) на произведение двух ортогональных голограммных
классов τφa и τtΦ,
так что
 *=τφa∙τtΦ.
(43)
*=τφa∙τtΦ.
(43)
Выражение
(43) является теоретико-групповым обобщением формулы (42).
В частности, если τφa=τ0А=at,
a τtФ∙τ0Φ=Фt,
то имеем разложение тонких голограмм на амплитудные и фазовые
голограммы
 *=at∙Фt.
(44)
*=at∙Фt.
(44)
Таким
образом, в основе групповой классификации тонких голограмм
лежат их ортогональные свойства, обусловленные ортогональностью
голограммных фактор-групп и порождающих их голограммных
подгрупп.
З
а к л ю ч е н и е
Построение
теоретико-групповой модели абстрактного голографического
процесса представляет собой доказательство обобщенной тео-
ремы
существования в голографии /1/. Абстрактная голограмма g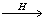 Á
описывает все возможные типы голограмм с заданными групповыми
свойствами и лежит в основе теоретико-группового классификационного
подхода. Представление абстрактной голограммы Á
Á
описывает все возможные типы голограмм с заданными групповыми
свойствами и лежит в основе теоретико-группового классификационного
подхода. Представление абстрактной голограммы Á 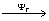 gt
характеризует свойства абстрактной голограммной группы Á
посредством группы gТ линейных преобразований и задает абстрактный
процесс реконструкции голографического изображения.
gt
характеризует свойства абстрактной голограммной группы Á
посредством группы gТ линейных преобразований и задает абстрактный
процесс реконструкции голографического изображения.
Таким
образом, дано общее описание групповой структуры абстрактного
голографического процесса, которое сводится к следующему:
1) описание
групповой структуры {g,h,g/h} интерференционного поля;
2)
введение голографического оператора h, описание групповой
структуры {Á ,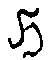 ,
Á /
,
Á /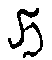 }
голограммного поля и построение на их основе абстрактной
голограммы g
}
голограммного поля и построение на их основе абстрактной
голограммы g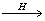 Á
;
Á
;
3) задание
представления Á 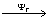 gt
абстрактной голограммы, описывающего абстрактный процесс
реконструкции голографического изображения.
gt
абстрактной голограммы, описывающего абстрактный процесс
реконструкции голографического изображения.
Такой
подход (рис.1) позволяет рассматривать голографическую систему
как некоторую систему передачи информации /7/. Выделение
отдельных математических объектов с определенными групповыми
свойствами позволит не только оценить информационную емкость
соответствующего каскада, но и найти основные причины потерь
информации в голографической системе. При этом именно структурный
анализ даст возможность выяснить оптимальные соотношения
между параметрами системы, при которых информация может
быть передана без существенных потерь.
Рассмотрено
применение теоретико-групповой модели абстрактного голографического
процесса для анализа тонких голограмм, когда голограммная
группа Á реализуется в виде мультипликативной группы
 *
комплексных амплитудных коэффициентов пропускания.
При этом требование построения замкнутой теоретико-групповой
конструкции с необходимостью приводит к понятию усиливающей
голограммы, что позволяет расширить понятие тонкой амплитудной
и фазовой голограммы. Хотя понятие усиливающей голограммы
вводится, опираясь на групповую теорию плоских голограмм,
их практическая реализация осуществляет-
*
комплексных амплитудных коэффициентов пропускания.
При этом требование построения замкнутой теоретико-групповой
конструкции с необходимостью приводит к понятию усиливающей
голограммы, что позволяет расширить понятие тонкой амплитудной
и фазовой голограммы. Хотя понятие усиливающей голограммы
вводится, опираясь на групповую теорию плоских голограмм,
их практическая реализация осуществляет-
ся
с помощью объемных голограмм /8/. Это говорит о том, что
объемные голограммы также обладают групповыми свойствами,
анализ которых требует отыскания новых реализации голографической
g и голограммной Á групп. Последние, очевидно, в каком-то
смысле должны быть связаны с группой  *.
*.
С другой
стороны, в работе /2/ показано, что для описания процесса
реконструкции удобно использовать реализацию голограммной
группы Á в виде аддитивной матричной группы gА или
gФ. Иначе говоря, мультипликативная реализация  *
позволяет говорить об усиливающих свойствах голограмм. В
то же время для анализа усиливающего процесса реконструкции
с помощью двух восстанавливающих волн используется представление
аддитивной матричной реализации в виде gА или gФ. Выбор
инвариантных классификационных подгрупп НÌ g и
*
позволяет говорить об усиливающих свойствах голограмм. В
то же время для анализа усиливающего процесса реконструкции
с помощью двух восстанавливающих волн используется представление
аддитивной матричной реализации в виде gА или gФ. Выбор
инвариантных классификационных подгрупп НÌ g и 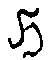 Ì
Á обуславливает выделение определенных "типов эквивалентности"
голограмм в виде голографических ГÌ g/Н и голограммных
τÎ Á /
Ì
Á обуславливает выделение определенных "типов эквивалентности"
голограмм в виде голографических ГÌ g/Н и голограммных
τÎ Á /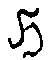 классов эквивалентности. Причем, относительная независимость
различных структурных типов голограмм обусловлена ортогональным
характером инвариантных классификационных голограммных подгрупп.
классов эквивалентности. Причем, относительная независимость
различных структурных типов голограмм обусловлена ортогональным
характером инвариантных классификационных голограммных подгрупп.
Анализ
групповой структуры дифракционного поля /1/ показывает,
что в абелевой группе g дифракционных образов существует
пять собственных инвариантных подгрупп: теневых Нт,
френелевских hФ, фраунгоферовских Нf,
фурье Нf и сфокусированных hf
образов. По любой из собственных подгрупп Н можно построить
разложение группы g на дифракционные классы эквивалентности
Гrh={γrh}
= r+h, где γrh=r+uh,
uhÎ h - дифракционный образ. Если ограничиться
анализом плоских голограмм, то в качестве области значения
голографического оператора ranh можно рассмотреть
группу gА амплитудных матриц
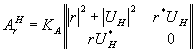 ,
,
где
Кa - коэффициент пропорциональности. Голографический
оператор Н задает реализацию абстрактной голограммы
в виде отображения Н: g→gА, так что arh=h{r+uh}.
Тогда описание всех дифракционных типов голограмм (рис.5)
сводится к анализу различных пар объектов {Гrh,
h[Гrh]} дифракционно-групповой
голографической

классификационной
категории Кr.
Таким
образом, построенная математическая модель абстрактного
голографического процесса представляет собой обобщенное
отражение накопленных знаний о структуре реального голографического
цикла. В то же вpeмя абстрактный теоретико-групповой характер
модели и ряд выводов, полученных с ее помощью, позволяют
рассматривать теоретико-групповую модель абстрактного голографического
процесса как новое опережающее отражение действительности,
позволяющее пред оказывать неизвестные аспекты голографического
цикла.
Л
и т е р а т у р а
1. В.Б.Немтинов.
Групповые свойства голограым. Материалы vii Всесоюзной школы
по голографии, Л., стр.102, 1975.
2.
В.Б.Немтинов. Групповая структура голографического процесса.
Материалы viii Всесоюзной школы по голографии, Л., стр.57,
1976.
3.
Дж.Гудмен. Введение в фурье-оптику, "Мир", М., 1965.
4. И.А.Дерюгин.
Физическая сущность голографического процесса. Материалы
viii Всесоюзной школы по голографии, Л., стр.7, 1976.
5. Р.Кольер,
К.Беркхарт, Л.Лин. Оптическая голография, "Мир", М., 1973.
6. Н.Я.Виленкин.
Специальные функции и теория представлений групп, "Наука",
М., 1965.
7. С.Б.Гуревич.
Об информационной емкости когерентных систем обработки информации.
Материалы viii Всесоюзной школы по голографии, Л., стр.46,
1976.
8.
Е.В.Ивакин, И.П.Петрович, А.С.Рубанов. Усиливающие голограммы
в просветляющих веществах. Тезисы докладов ii Всесоюзной
конференции по голографии, часть ii., К., стр.18, 1975.

