ОБОБЩЕННАЯ
ТЕОРИЯ ПОЛЯРИЗАЦИННОЙ ГОЛОГРАФИЧЕСКОЙ ЗАПИСИ
Ш.Д.Какичашвили
Рассматривается
обобщение теории поляризационной голографии в двух аспектах:
а) запись на фотоанизотропных средах со смешанным, векторно-скалярным
откликом произвольного характера; б) запись, отображающая
на голограмме, наряду с эксцентриситетом и ориентацией суммарного
светового эллипса, также информацию о направлении его вращения.
В ряде
работ по поляризационной голографической записи рассматривается
круг вопросов, связанных с теоретическим обоснованием и
поиском новых возможностей, появившихся в результате обобщения
голографического метода на область векторных полей /1-6/.
Ведутся также экспериментальные разработки метода и поиск
новых сред, пригодных для векторной записи /5-11/.
В данной
работе рассматривается поляризационная голографическая запись
на вариациях комплексного коэффициента преломления фотоанизотропной
среды с одновременным учетом как векторной, так и скалярной
ее реакции. Рассмотрение не ограничивается случаем слабого
поглощения и, в принципе, может быть использовано для сред
со значительно отличной от нуля проводимостью.
Рассматривается
танке наиболее общий случай поляризационной голографической
записи, когда наряду с геометрическими параметрами суммарного
светового эллипса поточечно отображается и состояние его
вращения. Физическим явлением, позволяющим реализовать подобную
запись, является известный эффект фотоиндуцированной оптической
активности.
1.
Голографическая запись на фотоанизотропной
среде
с произвольными параметрами
Предварительно
рассмотрим обобщение матрицы Джонса однородной линейной
фазовой пластины /12/ для комплексного коэффициента преломления.
Заменим
в линейном приближении этой матрицы вещественный коэффициент
преломления nj комплексным 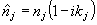 ,
где kj - коэффициент экстинкции. Имеем
,
где kj - коэффициент экстинкции. Имеем
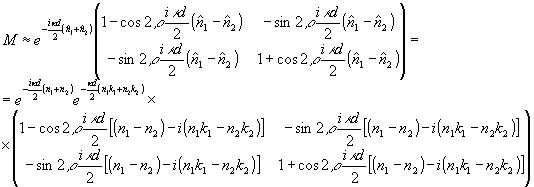 (1)
(1)
Здесь
n1 - коэффициент преломления в направлении оси
наибольшей скорости; ρ - ее азимут /13/.
Выпишем
введенный в работах /1,2/ закон векторной реакции фотоанизотропной
среды в виде:
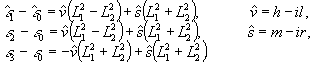 (2)
(2)
или
в эквивалентной форме:
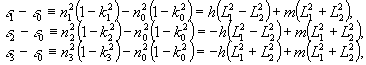
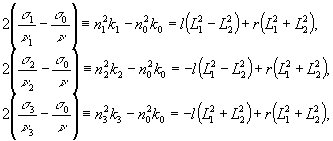 (2')
(2')
где
ε0 - исходный коэффициент диэлектрической
проницаемости среды; εj - конечный коэффициент
анизотропной диэлектрической проницаемости среды после воздействия
поляризованного света. Аналогично σ0, σj
- электрическая проводимость среды до и после воздействия
cвета; h, l - соответственно, коэффициенты векторной реакции
среды для диэлектрической проницаемости и электрической
проводимости; m и r аналогичные коэффициенты скалярной реакции
среды; 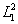 и
и 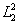 -
энергетические величины: квадраты большой и малой полуосей
воздействующего на среду светового эллипса.
-
энергетические величины: квадраты большой и малой полуосей
воздействующего на среду светового эллипса.
Нашей
ближайшей задачей будет выражение величин, входящих в (1),
n1-n2, n1k1-n2k2,
n1+n2, n1k1+n2k2,
через 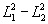 ,
,
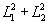 , h,
l, m, r, т.е. внесение в матрицу Джонса элементарного участка
голограммы информации о воздействующем на среду поле и характеристиках
реакции этой среды.
, h,
l, m, r, т.е. внесение в матрицу Джонса элементарного участка
голограммы информации о воздействующем на среду поле и характеристиках
реакции этой среды.
Для
упрощения дальнейших выкладов воспользуемся приближением:
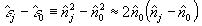 (3)
(3)
Это
приближение, сконструированное по аналогии с вещественным
эквивалентом этих величин справедливо в условиях 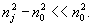
В параксиальном
приближении двумерной голограммы (2) представляется в виде
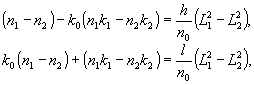 (4)
(4)
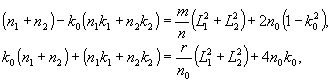
Откуда
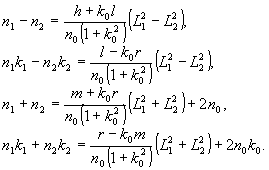 (5)
(5)
Подставляя
(5) в (1) получаем для обобщенной матрицы Джонса элементарного
участка голограммы:
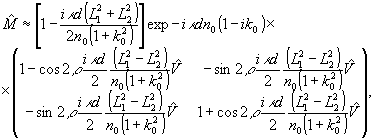 (6)
(6)
где
введены обозначения:
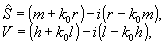
Напомним,
что суммарное (объектное + опорное) поле в плоскости голограммы,
поточечные параметры которого фигурируют в (6) в виде 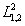 и ρ, представимо в виде /1,2/:
и ρ, представимо в виде /1,2/:
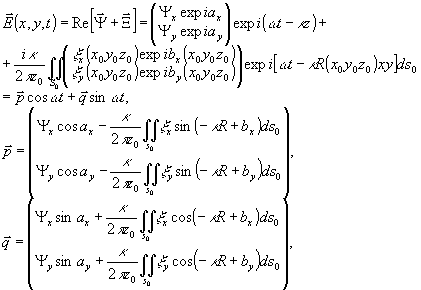 (7)
(7)
где
первое слагаемое описывает опорную волну, а второе - объектную.
Просветив
голограмму реконструирующей волной идентичной опорной, получим
три волны (сверточные компоненты формируемые в пространственном
интервале между опорной волной и полезными изображениями
здесь не рассматриваются):
недифрагированный
компонент
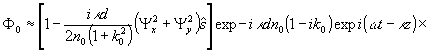 (8)
(8)
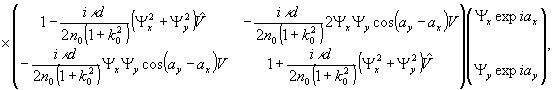
мнимое
изображение
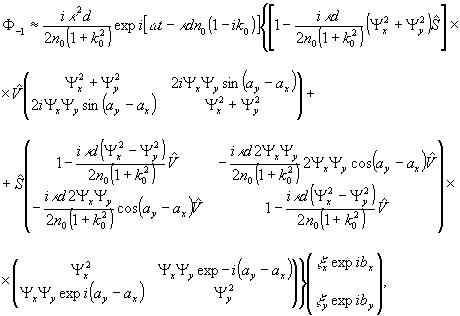 (9)
(9)
действительное
изображение
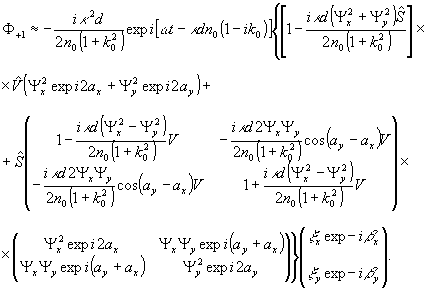 (10)
(10)
Сравнение
(9) и (10) показывает явно выраженную асимметрии в состояниях
поляризации реконструированных мнимого и действительного
изображения. Это утверждение относится к первым слагаемым
этих выражений, где фигурирует множитель, связанный с векторным
откликом среды 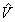 .
.
Представляется
полезным рассмотреть два частных случая состояния поляризации
опорной волны - линейной и циркулярной.
Полагая
Ψx=Ψy и ay-ax=0,
имеем линейную поляризацию под углом 45°; формируемые при
этом волны имеют вид:
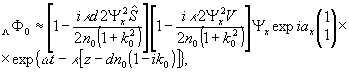 (8')
(8')
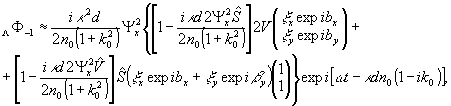 (9')
(9')
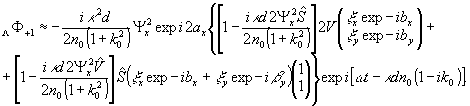
Таким
образом, при использовании линейно поляризованной опорной
волны мнимое и действительное изображения оказываются информационно
равнозначными. Здесь первый член описывает неискаженное
по состоянию поляризации реконструированное изображение
объекта. Второй член связан с остаточным скалярным откликом
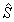 и как
бы накладывает на реконструкцию отпечаток опорной волны.
При этом в полном соответствии с логикой вещей вклад второго
члена зависит от относительной ориентации поляризации объекта
к опорной волне.
и как
бы накладывает на реконструкцию отпечаток опорной волны.
При этом в полном соответствии с логикой вещей вклад второго
члена зависит от относительной ориентации поляризации объекта
к опорной волне.
Полагая
Ψx=Ψy и аy-ax=π/2,
имеем циркулярную поляризацию опорной волны. Реконструируемые
волны представляются в виде:
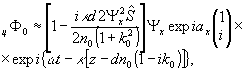 (8'')
(8'')
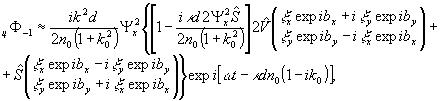 (9'')
(9'')
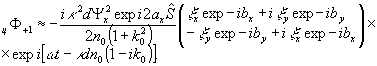 (10)
(10)
В отличие
от предыдущего случая здесь четко проявляется неравнозначность
мнимого и действительного изображений. Так, в мнимом изображении
влияние векторного отклика эквивалентно действию на поле
объекта циркулярного поляризатора с обратной опорной волной
(в данном примере левоциркулярного поляризатора). Скалярный
же отклик среды приводит к дополнительному действию, эквивалентному
действию циркулярного поляризатора с совпадающей с опорной
волной циркуляцией.
В действительном
изображении векторный отклик среды не проявляется. При этом
скалярный отклик эквивалентен действию на поле объекта нелинейного
устройства в виде совокупности линейной фазовой пластины
со сдвигом фазы на π и циркулярного поляризатора с
совпадающей с опорной волной циркуляцией.
Здесь
следует особо подчеркнуть, что полученная группа выражений
(8') - (10') и (8") - (10") чрезвычайно интересна, благодаря
появляющейся возможности получить из чисто голографического
эксперимента значения 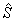 и
и 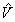 , связанные
с фундаментальными постоянными фотоанизотропной среды h,
l, m, r. Подобная возможность может оказаться весьма плодотворной
в молекулярно-оптических исследованиях различных сред.
, связанные
с фундаментальными постоянными фотоанизотропной среды h,
l, m, r. Подобная возможность может оказаться весьма плодотворной
в молекулярно-оптических исследованиях различных сред.
2.
Голографическая запись состояния вращения суммарного
поля
В предыдущем
разделе, так же как и в ранних разработках поляризационной
голографической записи /1-11/ рассматривалась регистрация
на голограмме информации об эллиптичности и ориентации суммар-
ного
светового эллипса. Использованные при этом явления позволяли
отображать на голограмме именно эти параметры светового
поля без учета направления его циркуляции. Тем не менее,
реконструированное изображение в случае опорной волны линейной
поляризации полноценно восстанавливается с сохранением всех
деталей состояния поляризации, включая направление циркуляции
для объекта произвольного характера /2/.
В данном
разделе мы рассмотрим полную регистрацию на голограмме всех
трех параметров суммарного светового эллипса, включая направление
его вращения.
Для
того, чтобы выяснить специфику, вносимую в теорию учетом
последнего параметра, предварительно рассмотрим случай,
когда на голограмме моделируется только направление циркуляции.
Можно полагать, что подобная запись информационно беднее
рассмотренной выше. Тем не менее она может представить определенный
интерес с точки зрения исследования класса преобразований
состояния поляризации, которому подвергается реконструированное
изображение.
Получим
полную матрицу Джонса оптически активного устройства -ротатора
в случае чистого кругового двулучепреломления. Для этого
представим полный вектор Джонса эллиптически поляризованного
света в виде суммы циркулярных колебаний:
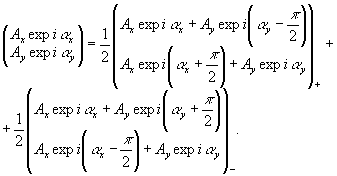 (11)
(11)
После
прохождения излучения через двулучепреломляющий круговой
ротатор оно опишется новым вектором Джонса:
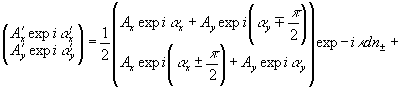
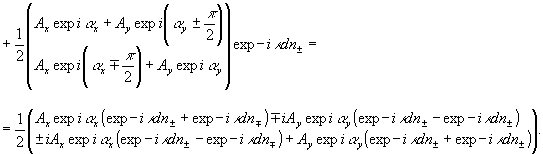 (12)
(12)
Откуда
легко получить матрицу Джонса двулучепреломляющего ротатора:
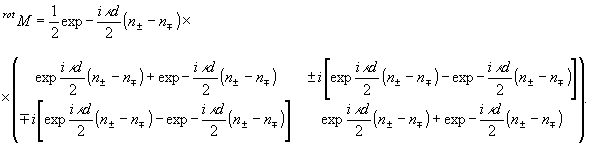 (13)
(13)
Переходя
к линейному приближению, имеем
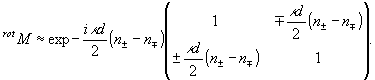 (13')
(13')
Вернемся
к выражению суммарного светового эллипса (7), представив
его в эквивалентной форме:
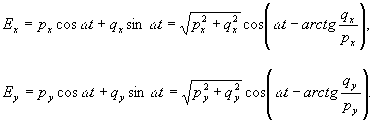 (14)
(14)
Нам
в дальнейшем потребуется четвертый параметр Стокса /12/,
который выпишем в форме
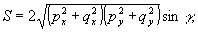 (15)
(15)
где
угол
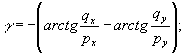
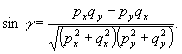 (16)
(16)
Напомним,
что s имеет размерность энергия я является наблюдаемой величиной.
При этом его знак определяет направление вращения электрического
вектора. Подставляя (16) в (15), получим
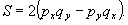 (15')
(15')
Как
показал впервые Садовский в 1899 году /14/, эллиптически
поляризованная световая волна обладает моментом количества
движения, который может быть передан взаимодействующему
со светом веществу. При этом имеет место связь с параметром
Стокса следующего характера:
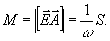 (17)
(17)
Это
соотношение играет особо важную роль в процессах взаимодействия
света с веществом, где им фактически определятся правила
квантования. Кроме того, оно позволяет применять к квантовым
явлениям закон сохранения количества движения.
При
фотохимических реакциях взаимодействие циркулярно поляризованного
света с молекулярным агрегатом может привести к переходу
в новое состояние с отличным от исходного моментом количества
движения. Это приводит к макроскопическому наведению оптической
активности соответствующего знака. Подобные явления наблюдались
в хлоридах серебра Зохером и Копером в 1930 г /15/ при воздействии
циркулярно поляризованного актиничного света. Имеются также
работы по использованию фотоиндуцированной оптической активности
для выделения из рацемической смеси молекул наперед заданной
изомерии /16/.
Приведенное
в последних абзацах иллюстрирует физическую возможность
отображения на голограмме состояния циркуляции света в виде
наведенной им же оптической активности.
Для
количественного описания фотоиндуцированной оптической активности
как функции воздействующего поля, мы сопоставим вариации
диэлектрической проницаемости соответствующего знака вращения
момент импульса светового поля в линейном виде:
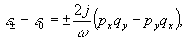 (18)
(18)
где
ω - частота, a j - коэффициент пропорциональности.
Для
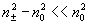 приближенно
имеем
приближенно
имеем 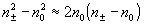 :
:
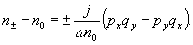 (19)
(19)
Подставив
последнее выражение в матрицу ротационного элемента и выразив
pxqy-pyqx через
исходные параметры опорного и объектного полей, получим
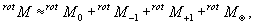 (20)
(20)
где
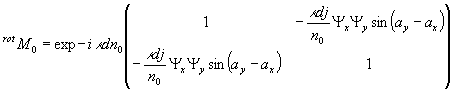 ,
,
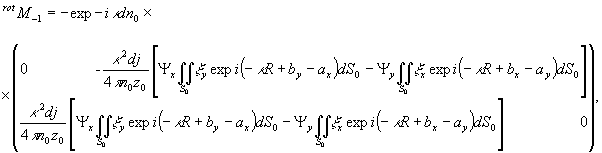
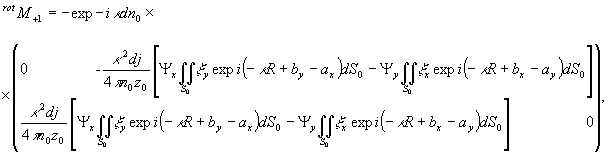
Просветив
голограмму реконструирующим опорным пучком, в асимптотическом
приближении получим для недифрагированного, мнимого и действительного
изображений :
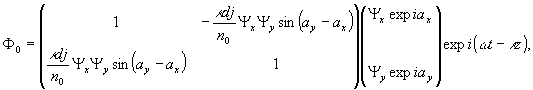 (21)
(21)
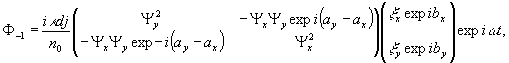 (22)
(22)
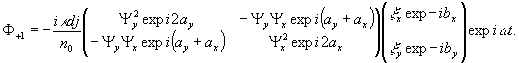 (23)
(23)
Рассмотрим
частные случаи опорной волны.
Ψx=Ψy;
ay-ax=0
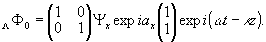 (21)
(21)
В направлении
недифрагированного пучка действие подобной голограммы равноценно
действию изотропной пластины.
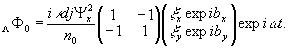 (22')
(22')
Матрица
в мнимом члене действует на реконструированное изображение
подобно линейному поляризатору с -45° ориентацией оси пропускания.
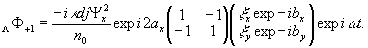 (23')
(23')
Аналогичное
положение имеет место для действительного изображения.
При
Ψx=Ψy; аy-аx=π/2
имеет место
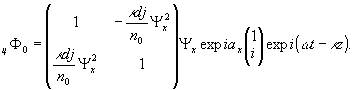 (21'')
(21'')
В недифрагированном
пучке действие голограммы сводится к действию частично анизотропной
нелинейной фазовой пластинки со сдвигом фазы на π/2.
Циркуляция обратна опорной волне.
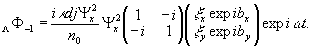 (22'')
(22'')
В мнимом
изображении матрица преобразования соответствует линейной
фазовой пластине со сдвигом фазы на π/2 с ориентацией
под -45°.
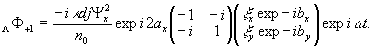 (23")
(23")
В действительном
изображении матрица преобразования соответствует совокупному
действию линейной фазовой пластины со сдвигом
на π/2
и нелинейному поляризатору с совпадающей с опорной волной
циркуляцией.
Перейдем
к совокупной записи всех трех параметров светового эллипса.
Для этого сконструируем матрицу Джонса, одновременно учитывающую
как линейное двулучепреломление, так и оптическую активность.
В линейном приближении подобную матрицу можно получить перемножением
соответствующих матриц Джонса и игнорированием членов высшего
порядка малости относительно элементарной толщины. В этом
приближении произведение этих матриц коммутативно.
Ограничиваясь
случаем чистого линейного двулучепреломления, чистое циркулярное
двулучепреломление имеем в качестве результирующей матрицы:
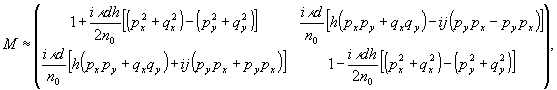 (24)
(24)
где
h - коэффициент векторной реакции среды на наведенное фотоиндуцированное
линейное двулучепреломление; j - аналогичным коэффициент
реакции той же среды на фотоиндуцированное круговое двулучепреломление
(фотоиндуцированная оптическая активность).
Просветив
подобным образом промодулированную голограмму исходной опорной
волной, получим реконструированные поля:
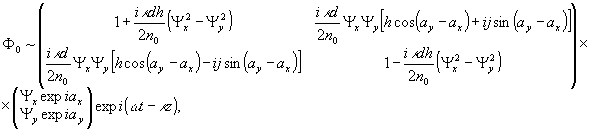 (25)
(25)
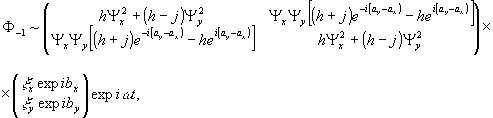 (26)
(26)
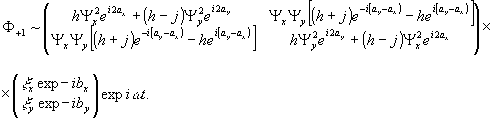 (27)
(27)
Анализ
полученных выражений показывает, что реконструированное
поле объекта по состоянию поляризации необратимо преобразовано.
Кратко
резюмируем основные результаты теории поляризационной голографической
записи.
При
использовании линейно поляризованной опорной волны с поточечной
регистрацией эллиптичности и ориентации суммарного светового
эллипса изображение реконструируется с полным восстановлением
состояния поляризации без ограничений на характер объекта.
В тех
же условиях запись с использованием циркулярной опорной
волны приводит к преобразованию изображения объекта по состоянию
поляризации.
К преобразованию
состояния поляризации приводит также наличие остаточной
скалярной реакции фотоанизотропной среды (в одной из ближайших
публикаций автор рассматривает схемное решение, при которой
влияние остаточной скалярной реакции среды исключается).
Наконец,
запись, отображающая на голограмме наряду с эллиптичностью
и ориентацией и направление циркуляции суммарного светового
эллипса, также приводит к преобразованию состояния поляризации
восстановленного изображения.
Вывод
последнего абзаца представляется несколько неожиданным.
Голографически записывая фактически более полную информации
о поле стоячих волн, мы в процессе реконструкции получаем
лишь искаженное по состоянию поляризации изображение объекта.
Подобное положение дел создает впечатление, что классическая
голографическая схема фиксации поля стоячих волн, по-видимому,
недостаточно приспособлена к векторной специфике реальных
электромагнитных полей. Не исключено существование схем
записи, эквивалентных по информационным возможностям двухлучевой,
в пределах которых не возникает подобных парадоксальных
ситуаций.
На часто
задаваемый вопрос о значимости поляризационной голографии
можно ответить следующим образом.
По-видимому,
основное значение этого подхода не только, или вернее не
столько в том, что реализуется принципиально полный опыт
в голографии - реконструкция векторной комплексной амплитуды
объектного поля, что само по себе является важным, а в том,
что разработка метода привела к общему подходу к задачам
дифракции на анизотропных прозрачностях произвольного характера
и уверенности в разрешимости этих задач в самом общем виде,
что до недавнего времени представлялось безнадежно сложным
и запутанным.
Л
и т е р а т у р а
1. Ш.Д.Какичашвили.
Материалы v Всесоюзной школы по голографии. Л., 511, 1973.
2.
Ш.Д.Какичашвили. Квантовая электроника. 1, 1435,
1974.
3. Ш.Д.Какичашвили,
Т.Н.Квинихидзе. Оптика и спектроскопия. 38, 807,
1975.
4. Ш.Д.Какичашвили,
Т.Н.Квинихидзе. Квантовая электроника. 2, 1449, 1975.
5. Ш.Д.Какичашвили.
Материалы vii Всесоюзной школы по голографии. Л., 31, 1975.
6.
Ш.Д.Какичашвили. Оптика и спектроскопия. 42, 390,
1977.
7. Ш.Д.Какичашвили.
Оптика и спектроскопия. 33, 324, 1972.
8. Ш.Д.Какичашвили,
В.Г.Шавердова. Оптика и спектроскопия. 41, 892, 1976.
9. Ш.Д.Какичашвили.
В.И.Тарасашвили. Физика и химия стекла, в печати.
10.
Ш.Д.Какичашвили, В.Г.Шавердова. ЖНИПФИК, в печати.
11.
Ш.Д.Какичашвили, И.В.Туниманова, В.А.Цехомский. ЖНИПФИК,
22, вып.2, 1977.
12.
У.Шерклифф. Поляризованный свет. "Мир", М., 1965.
13.
М.Борн, Э.Вольф. Основы оптики. "Наука", М., 1970.
14.
Д.И.Садовский. ЖРФХО, 29, 82, 1897.
15.
h.zocher, k.koper., zs.phys.chem., 132, 313, 1928.
16.
w.kuhn. zs.phys.chem., 7, 292, 1930.

