ВНУТРЕННЯЯ
3aДaЧa ГОЛОГРАФИИ
Э.И.Крупицкий
Доказываются
теоремы, касающиеся строгого решения задачи математического
восстановления неоднородных анизотропных, а также идеально
страдающих тел по данным голографических измерений поля
на окружающей поверхности.
Под
внутренней задачей голографии оправдано понимать нахождение
источников поля, рассеивающих тел, либо параметров среды,
заключенных внутри поверхности голографической регистрации
волнового поля (оптического, радио или акустического). Таким
образом, внутренние задачи голографии можно разбить на две
группы: 1) обратные задачи излучения (нахождение распределений
токов  ,
,
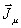 , либо
полей на излучающей поверхности
, либо
полей на излучающей поверхности 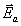 ,
,
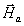 , рис.1);
2) обратные задачи рассеяния (нахождение формы полупрозрачной
рассеивающей области и распределения параметров
, рис.1);
2) обратные задачи рассеяния (нахождение формы полупрозрачной
рассеивающей области и распределения параметров 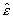 и
и 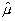 внутри
нее, либо нахождение поверхности sт идеально
отражающего тела, рис.2).
внутри
нее, либо нахождение поверхности sт идеально
отражающего тела, рис.2).
Обратная
задача излучения возникает, например, при контроле СВЧ антенн
по результатам радиоголографических измерений в ближней
зоне. К обратным задачам рассеяния относятся задачи радио
и акустического видения в оптически непрозрачных средах,
нахождение неоднородностей прозрачных и полупрозрачных сред
(газовой плазмы, стекол, кристаллов и т.п.), определение
механических деформаций металлических поверхностей и многие
другие.
Иногда
решение внутренней задачи голографии является промежуточным
этапом при решении внешней задачи, например, определение
поля в раскрыве СВЧ антенны с целью расчета полей в дальней
зоне, математическое построение поверхности рассеивающего
тела по радио, либо акустическим голограммам с целью синтеза
оптической голограммы и получения естественного оптического
изображения предмета и т.д. Заметим, что простое масштабирование
голограмм не позволяет
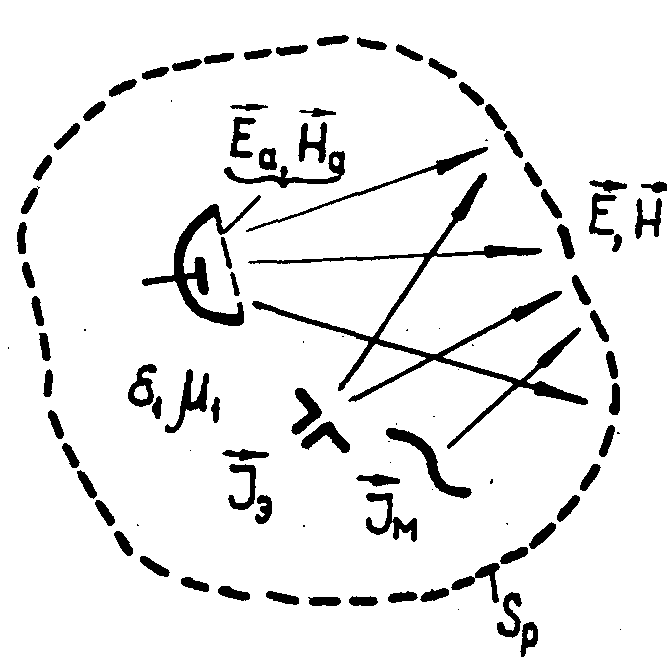
Рис.1.
Обратная задача излучения.
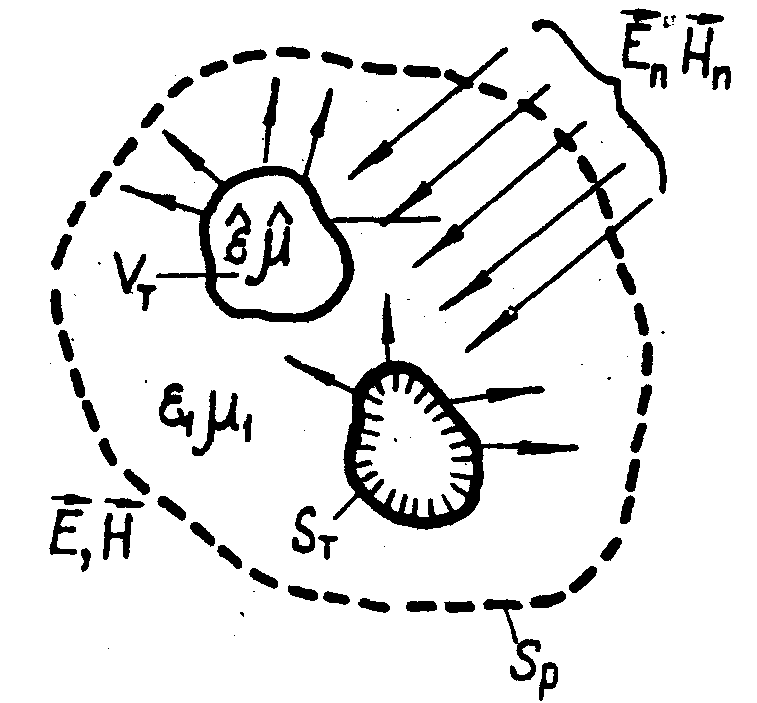
Рис.2.
Обратная задача рассеяния.
получить
естественное оптическое изображение.
Ддя
решения внутренней задачи применяются метода физического
моделирования и математического решения на ЭВМ. В первом
случае используется главным образом сопряженная волна, восстанавливаемая
с помощью оптической голограммы, которая, в частности, может
являться оптической моделью радио или акустической голограммы
(метод Бахраха-Курочкина /1/, метод матового экрана /2/
и др.).
Особый
интерес представляют математические методы решения внутренней
задачи. К ним относятся: метод геометрической оптики /3/,
метод "амплитуды рассеяния", являющийся аналогом одноименного
метода квантовой механики /4,5/, метод "вспомогательной
плоской волны", метод аналитического продолжения /6/ и метод
интегральных уравнений /7/. Два последних метода соответствуют
некорректной, постановке задачи, однако в сочетании с методами
регуляризации /8/, они представляют определенный практический
интерес. Ниже мы воспользуемся методами амплитуды рассеяния
и вспомогательной плоской волны для установления ряда общих
теорем, касающихся строгого решения обратной задачи рассеяния.
Обратные задачи излучения предполагается рассмотреть в отдельной
работе.
В дальнейшем
все волновые поля предполагаются монохроматическими.
Восстановление
неоднородных прозрачных тел по
рассеянному
полю
Пусть
на прозрачное (либо полупрозрачное) тело неопределенной
формы, имеющее конечный объем vт(рис.1), расположенное
в однородной изотропной среде с параметрами ε1,
μ1( и характеризуемое неизвестными тензор-функциями
проницаемостей 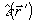 и
и 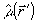 , падает
заданная плоская волна
, падает
заданная плоская волна 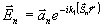 ,
,
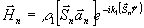 , где
, где
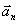 - единичный
вектор поляризации,
- единичный
вектор поляризации, 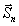 - единичный вектор направления,
- единичный вектор направления, 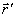 - радиус-вектор точки,
- радиус-вектор точки, 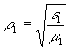 .
.
Среда
внутри объема vт может быть в общем случае анизотропной.
гиротропной, неоднородной и поглощающей, но не обладавшей
пространственной дисперсией. На тензор-функции 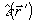 и
и 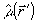 мы
мы
наложим
единственное ограничение, полагая, что они представимы в
виде 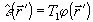 ,
,
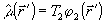 , где
Т1 и Т2 - известные постоянные тензоры
в общем случае комплексные и неэрмитовые, а
, где
Т1 и Т2 - известные постоянные тензоры
в общем случае комплексные и неэрмитовые, а 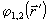 - вещественные скалярные функции точки (функции неоднородности),
подлежащие определению.
- вещественные скалярные функции точки (функции неоднородности),
подлежащие определению.
Сделанное
допущение позволяет охватить случаи неизвестного распределения
плотности среды, малых деформаций упругой среды, например,
кристаллической, и ряд других. В случае изотропной среды
тензоры t1 и Т2 переходят в скалярные
множители.
Теорема
1
Для
однозначного определения функций неоднородности 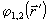 и границы рассеивающей области, достаточно зарегистрировать
на удаленной сферической поверхности (r→∞) две
пары квадратурных голограмм при k1→∞
для всех возможных направлений распространения падающей
плоской волны.
и границы рассеивающей области, достаточно зарегистрировать
на удаленной сферической поверхности (r→∞) две
пары квадратурных голограмм при k1→∞
для всех возможных направлений распространения падающей
плоской волны.
Доказательство
Представим
полное поле 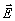 ,
,
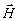 в виде
суммы падающего
в виде
суммы падающего 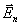 ,
,
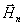 и рассеянного
(вторичного)
и рассеянного
(вторичного)  ,
,
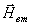 . Полное
и падающее поля удовлетворяют во всем пространстве системам
уравнений Максвелла:
. Полное
и падающее поля удовлетворяют во всем пространстве системам
уравнений Максвелла:
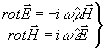 a)
a) 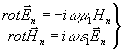 б) (1)
б) (1)
где
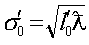
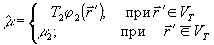
Вычитая
эти системы и учитывая, что 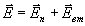 ,
,
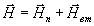 , получим:
, получим:
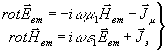 a)
a) 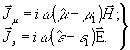 б) (2)
б) (2)
Здесь
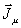 и
и 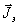 - фиктивные магнитные и электрические токи. Из (2) следует,
что в дальней зоне (r→∞) ввиду конечности vт
поле рас-
- фиктивные магнитные и электрические токи. Из (2) следует,
что в дальней зоне (r→∞) ввиду конечности vт
поле рас-
сеяния
будет чисто поперечным и может быть определено по формулам
/9/:
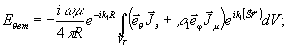 (3)
(3)
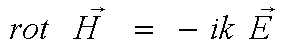 (4)
(4)
где
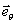 и
и 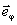 - единичные координатные векторы сферической системы, взятые
в точке наблюдения. Следуя работе /4/ введем вектор
- единичные координатные векторы сферической системы, взятые
в точке наблюдения. Следуя работе /4/ введем вектор 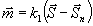 и положим k1→∞ (λ1→0).
При этом для произвольного вектора
и положим k1→∞ (λ1→0).
При этом для произвольного вектора 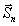 модно получить любые значения модуля
модно получить любые значения модуля 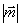 ,
изменяя вектор
,
изменяя вектор 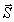 (отклоняя его от вектора
(отклоняя его от вектора 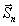 на малый угол). Полагая, что такая процедура выполняется
при определении поля
на малый угол). Полагая, что такая процедура выполняется
при определении поля 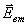 ,
получим:
,
получим:
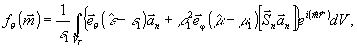 (5)
(5)
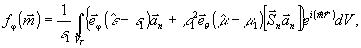 (6)
(6)
где
fθ и fφ - так называемые
"амплитуды рассеяния", определяемые выражениями:
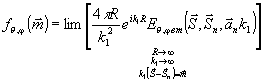 (7)
(7)
При
выводе (5), (6) мы учли, что, согласно лемме Римана-Лебега,
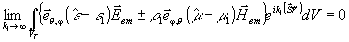 .
(8)
.
(8)
Из (5)
и (6), учитывая, что 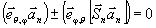 ,
находим
,
находим
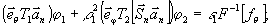 (9)
(9)
 (10)
(10)
где
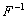 - символ
обратного преобразования Фурье.
- символ
обратного преобразования Фурье.
Решая
систему (9), (10), получим искомые функции:
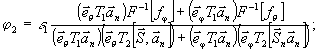 (11)
(11)
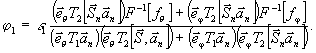 (12)
(12)
Заметим,
что формулы (11), (12) соответствуют наиболее общему случаю,
который крайне редко встречается на практике. В частных
случаях они существенно упрощаются.
Например,
при 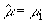 ,
,
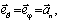 и3 (5)
и (6) находим:
и3 (5)
и (6) находим:
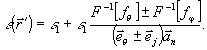 (13)
(13)
Согласно
(5) и (6), амплитуды рассеяния fθ и fφ
являются целыми функциями конечной степени. Следовательно,по
теореме Винера-Пэли-Шварца /10/ соотношения (11)-(13) однозначно
определяют как функции неоднородности, так и границу рассеивающей
области, так как при  правые части (11)-(13) будут тождественно обращаться в нули.
Так как однозначное определение eθвт и Еφβт
требует записи четырех квадратурных голограмм для всех возможных
ориентации вектора
правые части (11)-(13) будут тождественно обращаться в нули.
Так как однозначное определение eθвт и Еφβт
требует записи четырех квадратурных голограмм для всех возможных
ориентации вектора 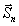 /11/, то теорема доказана.
/11/, то теорема доказана.
Сделаем
ряд примечаний.
1. Соотношения
(11)-(13) автоматически распространяются на случай двумерной
задачи.
2. Если
рассеиващая область обладает сферической, либо аксиально-цилиндрической
симметрией, то измерения достаточно сделать для одного любого
направления распространения падающей волны (одного вектора
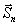 ).
).
3. Случай
скалярной задачи получаем из (13), полагая
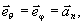
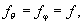
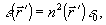
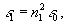
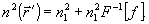 (14)
(14)
Теорема
2
Для
однозначного определения функций 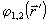 и границы рассеиващей области достаточно зарегистрировать
три пары квадратурных голограмм на произвольной замкнутой
поверхности sp, охватывающей объем vт,
при k1→∞ для всех возможных направлений
распространения падающей плоской волны.
и границы рассеиващей области достаточно зарегистрировать
три пары квадратурных голограмм на произвольной замкнутой
поверхности sp, охватывающей объем vт,
при k1→∞ для всех возможных направлений
распространения падающей плоской волны.
Доказательство
Введем
в рассмотрение, кроме падающей, вспомогательную плоскую
волну 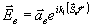 ,
,
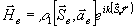 , удовлетворяющую
системе уравнений:
, удовлетворяющую
системе уравнений:
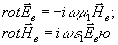 (15)
(15)
Умножая
уравнения (2а) на  и
и 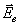 , а
уравнения (15) на hвт и Евт, вычитая
и складывая, получим лемму Лоренца:
, а
уравнения (15) на hвт и Евт, вычитая
и складывая, получим лемму Лоренца:
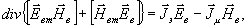 (16)
(16)
где
фиктивные токи 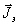 и
и 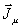 определяются
формулами (26). Интегрируя по объему vp, заключенному
внутри поверхности sp, получим:
определяются
формулами (26). Интегрируя по объему vp, заключенному
внутри поверхности sp, получим:
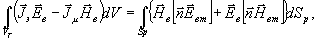 (17)
(17)
где
 - единичный
вектор нормали к поверхности sp. Введем вектор
- единичный
вектор нормали к поверхности sp. Введем вектор
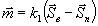 , полагая
k→∞ и учитывая, что в точках поверхности sp
, полагая
k→∞ и учитывая, что в точках поверхности sp
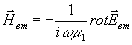 пoлучим:
пoлучим:
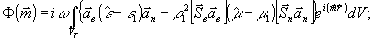 (18)
(18)
где
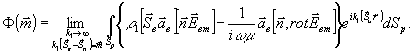 (19)
(19)
mы учли,
что в силу леммы Римана-лебега при k1→∞
обращается в нуль интеграл, подобный (8), содержащий 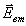 и
и 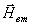 .
.
Для
нахоадения функций 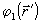 и
и 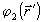 следует
задать два множества взаимноортогональных векторов
следует
задать два множества взаимноортогональных векторов 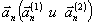 .
Им будут соответствовать функции
.
Им будут соответствовать функции 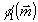 и
и 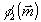 , определяемые
по данным голографических измерений. В результате получим
линейную систе;лу уравнений, подобную (9)-(10), содержащую
величины
, определяемые
по данным голографических измерений. В результате получим
линейную систе;лу уравнений, подобную (9)-(10), содержащую
величины 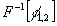 Решая систему, нетрудно определить функции φ1
и φ2. Определение функций
Решая систему, нетрудно определить функции φ1
и φ2. Определение функций 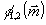 требует нахождения всех трех составляющих поля
требует нахождения всех трех составляющих поля 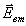 на поверхности sp, а следовательно, регистрации
трех пар квадратурных голограмм. Единственность решения
следует из соображений, аналогичных приведенным в конце
доказательства предыдущей теоремы.
на поверхности sp, а следовательно, регистрации
трех пар квадратурных голограмм. Единственность решения
следует из соображений, аналогичных приведенным в конце
доказательства предыдущей теоремы.
Теорема
3
Для
однозначного восстановления идеальноотражающей гладкой поверхности
sт рассеивающего тела достаточно зарегистрировать
две пары квадратурных голограмм на удаленной сферической
поверхности (r→∞), либо три пары на произвольной
замкнутой поверхности sp, охватывающей рассеиващее
тело, при k1→∞ для всех возможных
направлений распространения падающей плоской волны.
Доказательство
Поле,
рассеянное идеальной гладкой поверхностью в дальней зона,определяется
выражением /9/
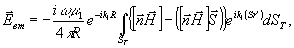 (20)
(20)
где
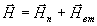 - полное
магнитное поле. Учитывая, что
- полное
магнитное поле. Учитывая, что 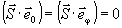 ,
имеем:
,
имеем:
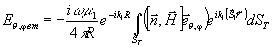 .
(21)
.
(21)
Полагая
k1→∞ и 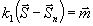 будем иметь:
будем иметь:
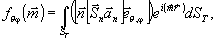 (22)
(22)
где
амплитуды рассеяния fθ,φ определяются
выражением:
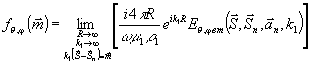 (23)
(23)
Из (22)
следует, что обратное преобразование функций fθ
и fφ позволяет определить поверхность sт.
Ддя
доказательства второй половины теоремы применим лемму Лоренца
к полному и вспомогательному полям, рассматривая точки пространства,
заклиненного между поверхностями sт и sp.
Тогда получим:
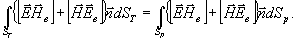 (24)
(24)
Так
как 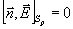 ,
ввиду идеальной проводимости поверхности, то при k1→∞
(вводя вектор
,
ввиду идеальной проводимости поверхности, то при k1→∞
(вводя вектор 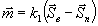 ),
получим
),
получим
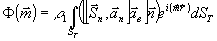 (25)
(25)
где
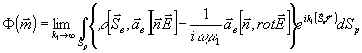 (26)
(26)
Для
задания функции 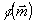 требуется регистрация трех пар квадратурных голограмм на
поверхности sp для всевозможных векторов
требуется регистрация трех пар квадратурных голограмм на
поверхности sp для всевозможных векторов 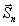 .
Поверхность st определится обратным преобразованием
Фурье от
.
Поверхность st определится обратным преобразованием
Фурье от 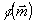 .
.
Примечания
1. Развитый
подход без труда распространяется на случай скалярной дифракции.
2. Формулы
(22)-(26) почти автоматически распространяются на двумерный
случай.
3. Если
рассеяние происходит не на одном теле, а на множестве тел
конечных размеров, находящихся на конечных расстояниях внутри
поверхности регистрации, то формулы (22)-(26) остаются справедливыми;
следует лишь под sт понимать сумму поверхностей
отдельных тел.
З
а к л ю ч е н и е
Доказанные
выше теоремы устанавливают достаточные условия строгого
решения обратных задач рассеяния по данный голографичеcких
измерений. В рамках корректной постановки задачи, обеспечивающей
устойчивость решения к малым погрешностям измерений и вычислений,
эти условия, по-видимому, и необходимы. Однако в общем случае
практическое использование полученных алгоритмов вызывает
серьезные затруднения. Это обусловлено их асимптотическим
характером (k1→∞) и необходимостью
изменения направления распространения падающей волны. Правда,
следует учитывать, что при больших значениях k1
измерения поля в дальней зоне достаточно выполнять при углах
θ, φ, весьма близких к θn, φn,
это существенно уменьшает объем измерений.
Важным
направлением дальнейших исследований является обобщение
теории на случай неизвестных тензоров Т1, t2
и сопоставление с другими методами решения обратной задачи
рассеяния.
Ли
т е р а т у р а
1. Л.Д.Бахрах,
А.П.Курочкин. ДАН СССР, т.171, в.6. 1966.
2. Э.И.Крупицкий,
А.А.Ризкин, С.В.Морозов. Сб. "Проблемы голографии", вып.2,
М., 83-87, 1973.
3. Голография.
Методы и аппаратура. Под ред.В.М.Гинзбург и Б.М.Степанова,
М., "Сов.радио", 1974.
4. Л.Д.Фаддеев.
Вестник ЛГУ, т.7, №2, 126-130, 1956.
5. Левис.
Зарубежная радиоэлектроника, №2, 100-111, 1970.
6. А.Г.Рамм.
22-ая Всесоюзная научная сессия, посвященная Дню Радио.
Секция распространения радиоволн. М., 3-6, 1966.
7. Д.И.Мировицкий.
Радиотехника и электроника, т.11, №7, 1966, 1169.
8. А.Н.Тихонов,
В.Я.Арсенин. Методы решения некорректных задач. М., "Наука",
1974.
9. Антенны
сантиметровых волн. Под ред. Я.Н.Фельда, М., "Сов. радио",
1950.
10.
Я.И.Хургин, В.П.Яковлев. Финитные функции в физике и технике.
М., "Наука", 117, 1971.
11.
Э.И.Крупицкий. Материалы vi Всесоюзной школы по голографии.
Л-д, 128-164, 1974.

