СВОЙСТВА
ОДНОМОДОВОГО ГАУССОВОГО ПУЧКА ЭЛЕКТРОМАГНИТНЫХ ВОЛН
Г.В.Скроцкий
Находится
решение волнового уравнения в диффузионном приближении,
описывающее стационарное поле монохроматического волнового
пучка. Распределение амплитуды и энергии пучка в направлении,
поперечном направлению его распространения, гауссово. Находятся
составляющие векторов напряженности электрического и магнитного
полей. Рассматривается преобразование пучка при прохождении
его через тонкую линзу. Дается простая геометрическая интерпретация
этого преобразования.
1. При
решении задач физической оптики, и в частности голографии,
световое поле обычно задают в виде плоской или сферической
волны. Однако световые пучки, формирующиеся в резонаторах
оптических квантовых генераторов, во многих случаях не могут
быть отнесены ни к одному из этих предельных типов волн.
Ниже рассматривается монохроматическое волновое поле, имеющее
характер пучка, зависящего от одного параметра σ, и
выясняются некоторые его свойства, важные для применений.
Распределение
фазы рассматриваемого поля вблизи выделенного направления
(оси (оz) ) всегда имеет характер сферической волны. Амплитуда
его в плоскости z=const определяется распределением Гаусса.
В плоскости z=0 радиус распределения равен σ0.
Будем
искать решение Ψ(x,y,z,t) скалярного волнового уравнения
в свободном пространстве в виде
Ψ(x,y,z,t)=u(x,y,z)ei(kz-ωt),
(1)
где
u(x,y,z) зависящая от координат амплитуда.
Тогда,
как легко убедиться,
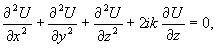 (2)
(2)
где
k=ω/с=const.
Решение
амплитудного уравнения (2) удобно представить в виде суперпозиции
плоских волн частоты
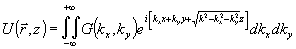 ,
(3)
,
(3)
где
учтено, что k2=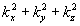 ,
a
,
a  .
.
В плоскости
z=0
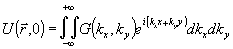
можно
рассматривать как разложение Фурье заданного в ней распределения
поля. Полагая, что оно гауссово,
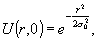 (4)
(4)
найдем
g(kx,kу), воспользовавшись обратным
преобразованием Фурье:
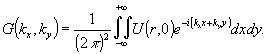
Теперь
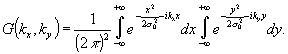
Согласно
известному равенству
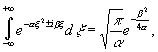 (5)
(5)
находим
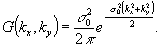 (6)
(6)
Таким
образом, решение амплитудного уравнения (2) описывает в
полупространстве z>0 такое поле, амплитуда которого в
плоскости z=0 определяется распределением (4). Согласно
(6) и (3), искомое решение имеет вид:
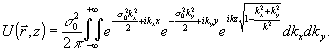 (7)
(7)
Интеграл
(7) не выражается через элементарные функции. Его, однако,
можно вычислить в хорошем приближении, раскладывая входящий
в него корень в ряд по степеням отношения
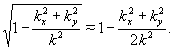 (8)
(8)
Может
показаться, что, используя такое разложение, мы пренебрегаем
поперечными составляющими волнового вектора 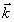 ,
которые не малы по сравнению с его величиной. Это, однако,
не так, если ширена гауссового распределения в пространстве
волновых чисел i/σ0 достаточно мала. Быстро
убывая с ростом
,
которые не малы по сравнению с его величиной. Это, однако,
не так, если ширена гауссового распределения в пространстве
волновых чисел i/σ0 достаточно мала. Быстро
убывая с ростом 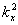 и
и 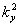 , гауссовые
множители зарезают высокие пространственные частоты, делая
их взнос в значение интеграла тем меньшим, чем больше величина
σ0. Поэтому для получения вполне хорошего
приближения оказывается вполне достаточным ограничиться
в разложении (8) только квадратичными членами. Тогда
, гауссовые
множители зарезают высокие пространственные частоты, делая
их взнос в значение интеграла тем меньшим, чем больше величина
σ0. Поэтому для получения вполне хорошего
приближения оказывается вполне достаточным ограничиться
в разложении (8) только квадратичными членами. Тогда
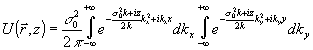
или,
согласно (5),
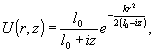 (9)
(9)
где
введено обозначение 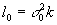 .
.
2. Это
удивительно простое выражение удовлетворяет "укороченному"
амплитудному уравнению
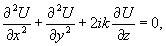 (10)
(10)
в котором
по сравнению с (2) отброшен член 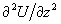 .
Записав полное уравнение (2) в безразмерных естественных
переменных
.
Записав полное уравнение (2) в безразмерных естественных
переменных
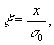
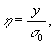
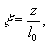
получаем
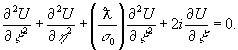
Легко
видеть, что членом, содержащим вторую производную по 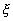 ,
модно пренебрегать, когда
,
модно пренебрегать, когда 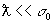 или иначе σ0<<l0. Это обозначает,
что ширина σ0 гауссового распределения пучка
в плоскости z=0 (в горле пучка) должна быть велика по сравнению
с длиной волны излучения
или иначе σ0<<l0. Это обозначает,
что ширина σ0 гауссового распределения пучка
в плоскости z=0 (в горле пучка) должна быть велика по сравнению
с длиной волны излучения 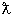 =λ/2π.
=λ/2π.
Уравнения
вида (2) или (10) напоминают по виду уравнение диффузии,
однако с комплексным коэффициентом диффузии. Оно совпадает
c уравнением Шредингера для свободной частицы. Решение (9)
описывает с этой точки зрения эволюцию волнового пакета
в пространстве.
Учтя
(1), согласно (9), после несложного преобразования находим
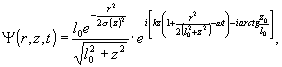 (11)
(11)
где
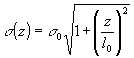 (12)
(12)
или
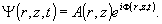 (13)
(13)
Амплитуда
волнового поля пучка
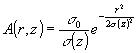 (14)
(14)
медленно
убывает в направлении распространения (oz) и быстро спадает
в поперечном ему направлении r. Распределение расплывается,
оставаясь гауссовым. Ширина его σ(z) растет в согласии
с (12). Большая часть энергии волны сосредоточена в узком
канале радиуса σ(r). Эта область пространства находится
внутри однополого гиперболоида (рис.1)
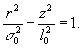 (15)
(15)
Для
достаточно больших z>l0 юбка гиперболоида
вписывается в асимптотический конус с углом раствора θ.
Легко видеть, чтo
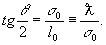 (16)
(16)
Для
малых θ
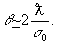
Таким
образом, угол раствора пучка простым образом выражается
через параметр пучка σ0 и длину волны излучения
в свободном пространстве.
Фаза
Ф(r,z,t) решения (13), согласно (11), равна
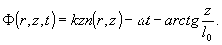 (17)
(17)
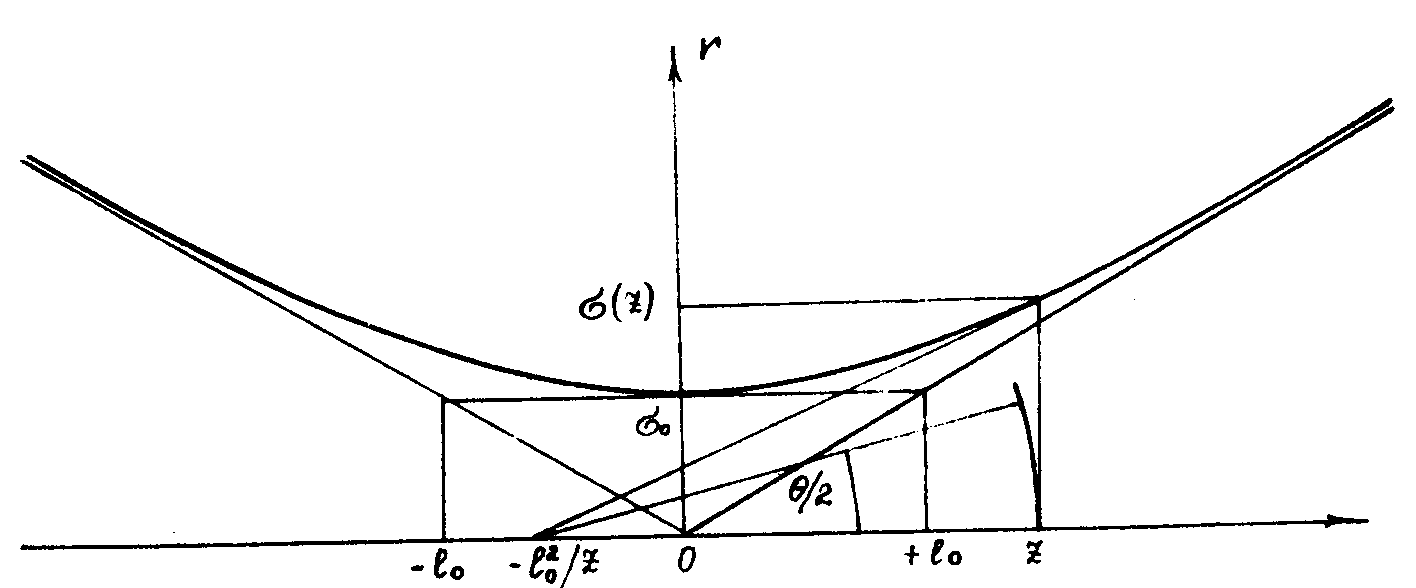
Рис.1.
Построение каустики одномодового гауссового пучка. Расстояние
между зеркалами конфокального резонатора равно 2l0.
Радиус пучка в горле равен σ0. Угол раствора
пучка θ. Касательная в точке z к каустике пересекает
ось пучка в точке -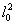 /z.
Радиус кривизны r(z) волнового фронта в точке r равен z+
/z.
Радиус кривизны r(z) волнового фронта в точке r равен z+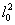 /z.
/z.
При
увеличении z от нуля до ∞ входящее в (17) слагаемое
arctgz/l0 изменяется от нуля до π/2. Это
соответствует хорошо известному в волновой оптике положению,
согласно которому при прохождении волны через фокус (горло)
ее фаза испытывает изменение фазы на π. Множитель
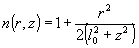 (18)
(18)
играет
роль "показателя преломления". На оси пучка он равен нулю.
По мере удаления от горла пучка он убывает, приближаясь
к единице. Он обеспечивает расширение пучка, которое носит
характер "поперечной диффузии". Можно записать содержаний
n фазовый множитель в виде
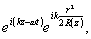
Второй
сомножитель в этом выражении exp[ikr2/2r], где
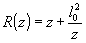 (19)
(19)
называют
"линзовым". Он определяет набег фазы, имеющей место при
прохождении плоской волны через идеальную линзу с фокусным
расстоянием r. Это обозначает, что в каждой точке z фронт
пучка можно рассматривать как сферический. Его радиус r
зависит от z . Сферическая волна в точке z имеет центром
точку -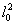 /z.
В плоскости z=0, фронт волны плоский. Наибольшую кривизну
он имеет в точке z=l0. Далее при z→∞
его радиус опять растет, в окрестности оси (oz) форма фронта
опять приближается к плоской.
/z.
В плоскости z=0, фронт волны плоский. Наибольшую кривизну
он имеет в точке z=l0. Далее при z→∞
его радиус опять растет, в окрестности оси (oz) форма фронта
опять приближается к плоской.
В точках
z=±l0 радиус кривизны равен ±2l0.
Если в этих точках поместить сферические зеркала c такой
кривизной, они образуют конфокальный лазер (фокусное расстояние
сферического зеркала равно половине его радиуса).
3.
Составляющие напряженности электрического 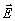 и магнитного
и магнитного 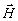 полей циркулярно поляризованного светового пучка можно вычислить,
полагая
полей циркулярно поляризованного светового пучка можно вычислить,
полагая
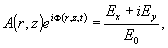 (20)
(20)
а
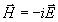 (21)
(21)
В этом
случае векторные уравнения Максвелла для амплитуд пoля
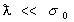 ,
,
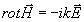
удовлетворяются
тождественно, в чем можно убедиться, умножив первое из них
на i и сложив.
Оставшаяся
пара скалярных уравнений позволяет по уже известным составляющим
Еx, Еy, Нx, Ну
найти ez и hz:
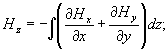
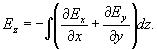
Пренебрегая
квадратичными по 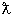 членами, находим
членами, находим
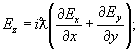
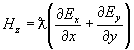
Таким
образом,
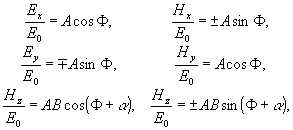 (22)
(22)
где
Ф определяется (17)
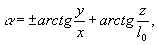 (23)
(23)
а
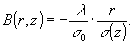 (24)
(24)
Верхний
знак в формулах (22) соответствует правополяризованной волне,
а нижний - левополяризованной. e0 - амплитуда
поля в плоскости z=0.
Эти
простые выражения описывают электромагнитное поле основной
моды лазера со сферическими зеркалами. Особенностью всякого
пучка является наличие продольной составляющей поля. Это
неудивительно, так как только плоские волны являются чисто
поперечными. Поле суперпозиции любого числа плоских электромагнитных
волн неизбежно обладает продольной составляющей. Ее величина
тем больше, чем уже пучок. В горле пучка она имеет максимальное
значение. На оcи (r=0) - равна нулю. Появление продольной
составляющей при-
водит
к тому, что скорость пучка отлична от скорости света в вакууме.
Фазовая скорость uf=dz/dt, как легко убедиться,
полагая dΦ=0, является функцией точки и всюду, кроме
оси пучка, больше скорости света.
Теперь
нетрудно вычислить плотность и поток энергии, переносимой
пучком. Средняя по времени плотность энергии
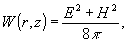
согласно
(20) равна
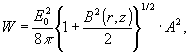 (25)
(25)
а средняя
плотность потока энергии
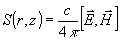
имеет
составляющие:
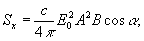

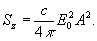
Таким
образом,
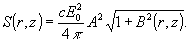
Скорость
распространения us энергии
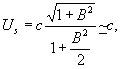
как
в должно быть, не превышает скорости света в вакууме.
Вычисляя
полную энергию u и составляющие потока энергии  для циркулярно - поляризованного пучка в слое толщиной Δz,
получим простые, легко обозримые выражения:
для циркулярно - поляризованного пучка в слое толщиной Δz,
получим простые, легко обозримые выражения:
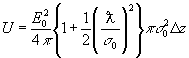 (26)
(26)
и
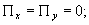
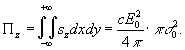 (27)
(27)
Отбрасывая
в (26) малое слагаемое, видим, что средняя энергия пучка,
заключенная в слое между плоскостями z и z+Δz, равна
плотности энергии плоской волны с амплитудой Е0,
умноженной на объем цилиндра с площадью основания π и длиной Δz. Аналогичным образом z - составляющая потока
энергии Пz равна составляющей вектора Пойнтинга
той же плоской волны, умноженной на площадь сечения пучка
в начале координат.
и длиной Δz. Аналогичным образом z - составляющая потока
энергии Пz равна составляющей вектора Пойнтинга
той же плоской волны, умноженной на площадь сечения пучка
в начале координат.
Пондеромоторное
действие пучка определяется составляющими тензора максвелловских
напряжений:
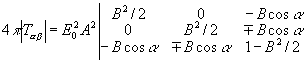 (28)
(28)
4. Мы
видели, что для полного задания всех характеристик монохроматического
светового пучка длины волны 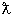 =1/k
в произвольной точке z>0 достаточно знать только один
параметр, например, половину расстояния между зеркалами
конфокального лазера l0. Поперечный размер пучка
σ(z), радиус кривизны фронта r(z), угол раствора θ
и набег фазы α, характеризующий разность фаз между
гауссовым пучком и плоской волной простым образом выражается
через
=1/k
в произвольной точке z>0 достаточно знать только один
параметр, например, половину расстояния между зеркалами
конфокального лазера l0. Поперечный размер пучка
σ(z), радиус кривизны фронта r(z), угол раствора θ
и набег фазы α, характеризующий разность фаз между
гауссовым пучком и плоской волной простым образом выражается
через
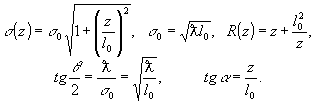 (29)
(29)
Два
числа l0 и z удобно объединить в одно комплексное:
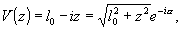 (30)
(30)
получившее
название варианса. Эта величина обладает рядом интересных
свойств. Ее применение позволяет существенно упростить решение
задач, связанных с прохождением светового пучка через оптические
системы. Легко видеть, что
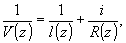 (31)
(31)
где
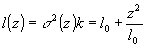 – (32)
– (32)
поперечный
фокус пучка. Сразу видно, что
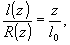 (33)
(33)
Далее
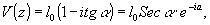
а
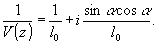
Сравнивая
с (31) находим
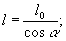
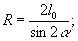
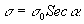
Полученные
соотношения позволяют выразить характеристики пучка через
угол α.
При
смещении вдоль оси на z', как видно из (30),
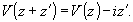 (34)
(34)
Если
пучок проходит через тонкую (положительную) линзу, помещенную
в точке z, оптическая ось которой совмещена с осью (оz),
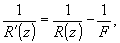 (35)
(35)
где
f - ее фокусное расстояние, a r'(z) - радиус фронта пучка,
прошедшего линзу, т.е. расстояние от линзы до горла сфокусированного
пучка. Так как поперечные фокусы пучка в точке z равны l'(z)=l(z),
то
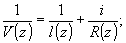
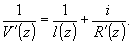 (36)
(36)
Оба
выражения (36), воспользовавшись (35), можно объединить
в одно:
 (37)
(37)
Формулы
(34) и (37) позволяют аналитически рассмотреть прохождение
пучка через любую сложную оптическую систему, заданным образом
преобразующую его параметры: размер горла, диаметр в любой
точке и кривизну фазового фронта пучка. При этом тип пучка
(моды) не изменяется. Выражения (34) и (37) вполне аналогичны
известным формулам для импеданса в многозвенной электрической
цепи. Они позволяют свести задачу о прохождении светового
пучка через сложную оптическую систему, к задаче о распределении
напряжений в эквивалентной электрической цепи, содержащей
активные и реактивные сопротивления.
Полученные
соотношения имеют простую геометрическую интерпретацию,
позволяющую при помощи циркуля и линейки построить и измерить
все параметры пучка, а также рассмотреть прохождение, его
через -оптическую систему.
Как
и раньше, будем считать известными длину l0 и
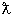 . Построим
в точке 0 оси oz, перпендикулярный к ней отрезок длины l0
в соединим его конец c точкой z (рис.2). Затем через точку
b проведем линию (aс), перпендикулярную к (bz). Она пересечет
в точке a ось (oz), а в точке с перпендикуляр к оси (oz),
восстановленный из точки z. Легко видеть, что длины катетов
прямоуголь-
. Построим
в точке 0 оси oz, перпендикулярный к ней отрезок длины l0
в соединим его конец c точкой z (рис.2). Затем через точку
b проведем линию (aс), перпендикулярную к (bz). Она пересечет
в точке a ось (oz), а в точке с перпендикуляр к оси (oz),
восстановленный из точки z. Легко видеть, что длины катетов
прямоуголь-
ного
треугольника (аzс) равны, соответственно, r(z) и l(z) ,
a угол α=arctgz/l0.
Если
поместить в точку z центр тонкой положительной линзы с фокусным
расстоянием f, то проходящий через нее пучок, горло которого
находится в точке z=0, соберется в точке e(z+r'(z), где
r'(z) определяется по формуле линзы (35) (рис.3). Соединим
точку С с точкой е, опустим из точки z перпендикуляр (zd)
на биссектрису полученного прямоугольного треугольника и,
наконец, из точки d проведем перпендикуляр к оси (оz) в
точку o'. Отрезок (do') имеет, как легко убедиться, длину
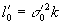 . Горло
пучка находится в точке о', его радиус в этом месте
. Горло
пучка находится в точке о', его радиус в этом месте 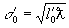 .
Если отсчет расстояний теперь вести от точки o' , то уравнение
пучка по-прежнему определяется выражением (13), а радиус
пучка в точке z определяется по формуле σ'(z)=
.
Если отсчет расстояний теперь вести от точки o' , то уравнение
пучка по-прежнему определяется выражением (13), а радиус
пучка в точке z определяется по формуле σ'(z)=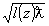 .
Угол α' характеризует набег фазы прошедшего через линзу
пучка.
.
Угол α' характеризует набег фазы прошедшего через линзу
пучка.
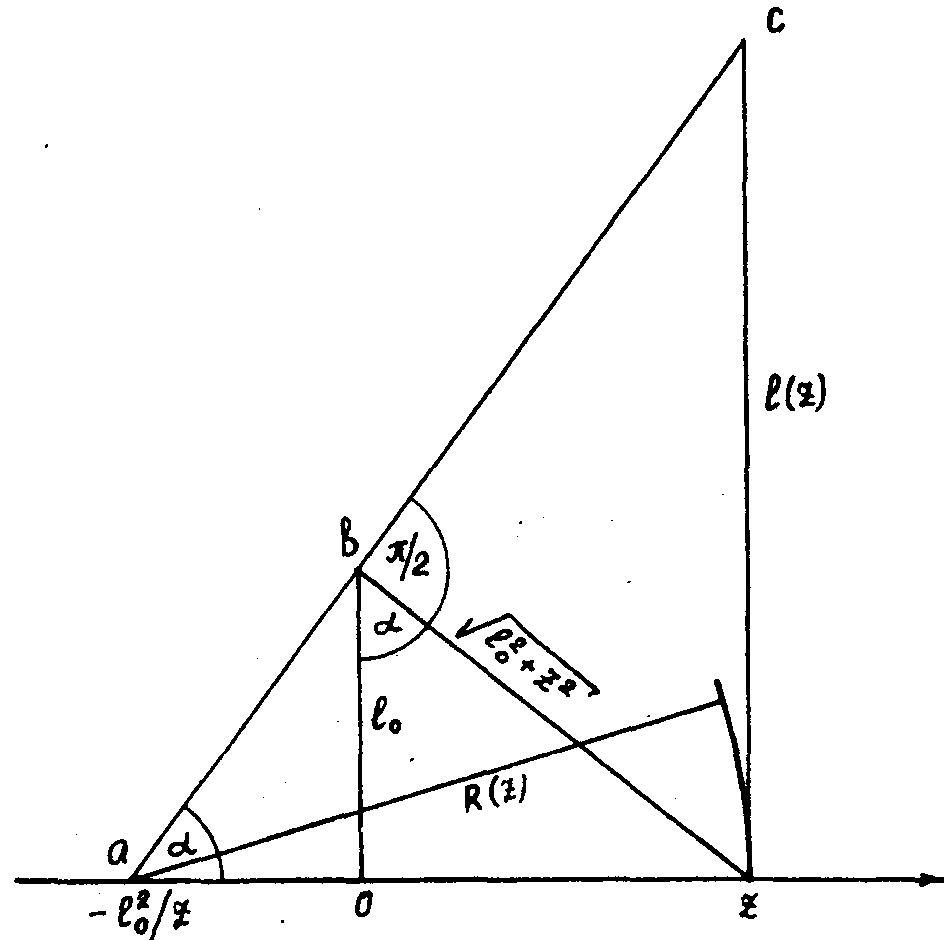
Рис.2.
Построение, позволяющее определить параметры пучка для точки
z по заданной длине l0.
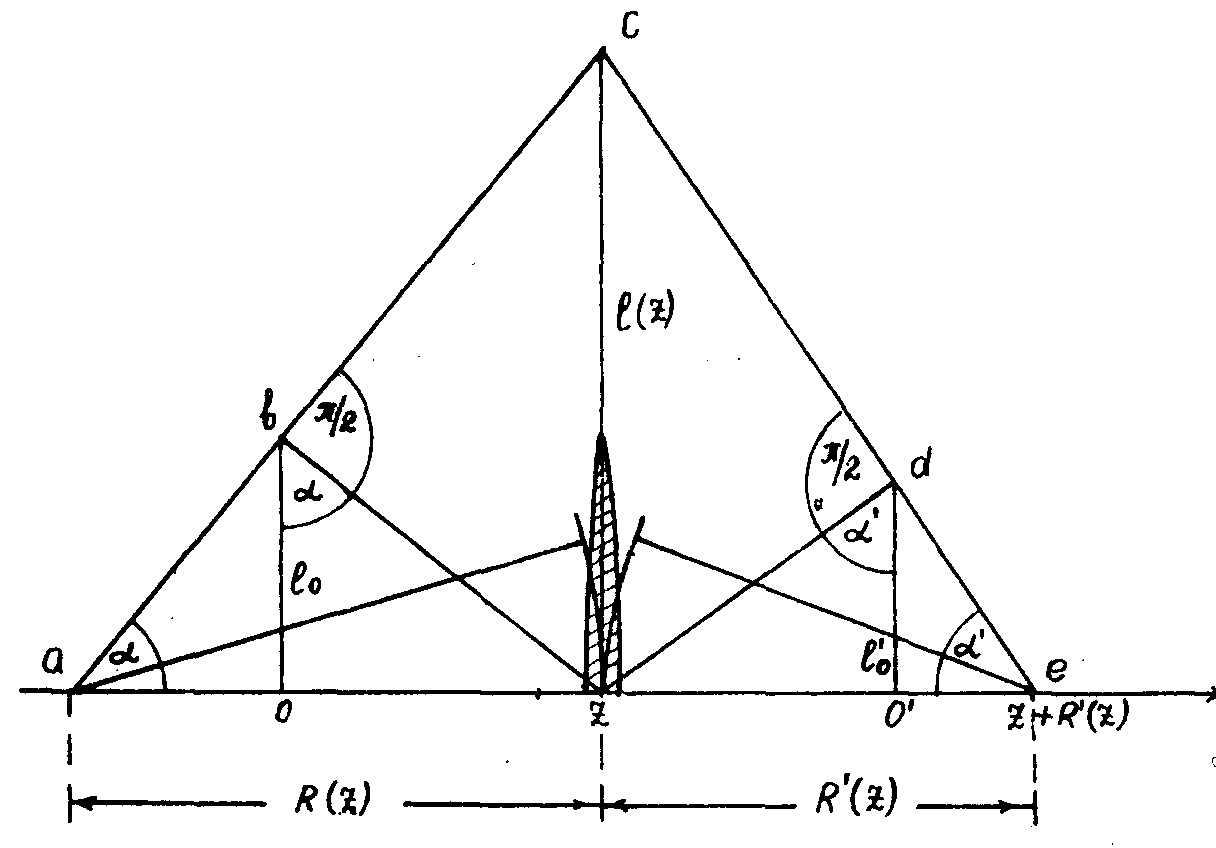
Рис.3.
Построение, позволяющее определить параметры пучка после
прохождения тонкой линзы c известным фокусным расстоянием
f. Здесь 1/r'(z) =1/r(z) - 1/f.
Теория
световых пучков была развита в работах Когельника и Ли /1/.
Физические свойства одномодового пучка рассмотрены в /2/.
Геометрическую интерпретацию пучков модно найти в /3/.
Л
и т е р а т у р а
1.Н.Коgеlniк
and Т. li, laser beams and resonators, proc ieee, 54,
№10, october 95 (1966).
2. А.Ю.Ардашев,
В.А.Капин, Г.В.Скроцкий. ЖЭТФ, 55, 869, 1968. Классическая
теория неидеальных когерентных световых пучков.
3. Ж.Дешан
и М.Маст. Преобразование пучка при распространении в системе
квадратичных линз. Квазиоптика. Сборник докладов. Мир, М.,
стр.189, 1966.

