ОСНОВНЫЕ ПРИНЦИПЫ ОБРАЩЕННОГО СИНТЕЗИРОВАНИЯ РАДИОГОЛОГРАММ
С.А.Попов, Б.А.Розанов, Ю.С.Зиновьев, А.Я.Пасмуров
Кратко рассматриваются методы получения и типы радиоголограмм. Анализируются принципы синтезирования радиоголограмм за счет собственного вращения объекта вокруг центра масс. Обсуждаются особенности комплексных радиоголограмм и возможности их цифровой и оптической обработки. Приводятся результаты цифрового моделирования и экспериментальной проверки двух методов радиоголографии Фурье.
1.
Методы получения радиоголографических апертур
Одной из существенных трудностей, с которыми сталкивается радиоголография, является сложность создания радиоголографических апертур.
В радиодиапазоне прямой метод формирования голограмм, используемый в оптическом диапазоне, находит ограниченное применение из-за отсутствия подходящего микроволнового аналога фотопластинок. Поэтому применяются косвенные методы формирования радиоголографических апертур. Один из них связан с созданием реального раскрыва, когда измерение поля производится в дискретных точках, а запись радиоголограмм осуществляется путем коммутации каналов на выходе антенной решетки /1,2/. Возможен случай, когда обработка сигналов ведется параллельно по всей каналам с помощью оптических методов /3/. Второй метод предполагает применение синтезированного раскрыва, характерного тем, что поле в различных точках апертуры радиоголограммы регистрируется последовательно во времени с помощью одной приемной антенны. В ряде работ /4-6/ показано, что синтез радиоголограмм, в принципе, возможен при любом виде относительного движения объекта, источ-
ника излучения и регистрирующего устройства - важно лишь, что при взаимном перемещении происходило изменение наблюдаемого ракурса объекта.
В настоящее время известно два основных метода синтезирования радиоголограмм - прямой и обращенный. Первый из них может быть реализован путем сканирования приемной (или передающей) антенной либо с помощью одновременного сканирования приемной и передающей антеннами относительно неподвижного объекта /7-9/. Существуют комбинированные способы регистрации поля. Например, в голографических РЛС землеобзора /2/ используется сочетание прямого синтезирования вдоль линии пути и реального раскрыва (в виде одномерной антенной решетки) в поперечном направлении. Методы синтезирования радиоголограмм, использующие поступательное движение объекта или его собственное вращение относительно неподвижной приемно-передающей системы, называются обращенными. Если методы прямого синтезирования разработаны достаточно подробно, то обращенному синтезу в литературе уделено недостаточное внимание, хотя получаемое таким образом радиоголограммы обладают рядом интересных свойств, а сами методы легко реализуются на практике.
2.
Типы радиоголограмм
В радиодиапазоне возможна запись двух типов радиоголограмм. Первый из них аналогичен оптической голограмме, второй оптического аналога не имеет. Пусть а ехр(iФ) - объектная волна, a0eхр(iФ0) - опорная волна. В первом случае фиксируется квадратичная радиоголограмма, уравнение которой
H1
(х,y) = |a ехр(iΦ) + а0e
хр(iΦ0)|
2 =
а02 + a
2 + 2
аа0 c
оs(Ф-Ф0), (1)
Такие радиоголограммы можно регистрировать с помощью квадратичного детектора как на высокой (рис.
1а), так и на промежуточной частоте (рис.16) с использованием опорной волны на высокой частоте. До втором случае формируется перемножительная радиоголограмма /10/, уравнение которой
H1
(х,y) = Re[a ехр(iΦ) + а0e
хр(iΦ0)] =
аа0 c
оs(Ф-Ф0). (2)
Перемножительная радиоголограмма также может быть получена как на высокой (рис.1в), так и на промежуточной частоте (рис.1г).
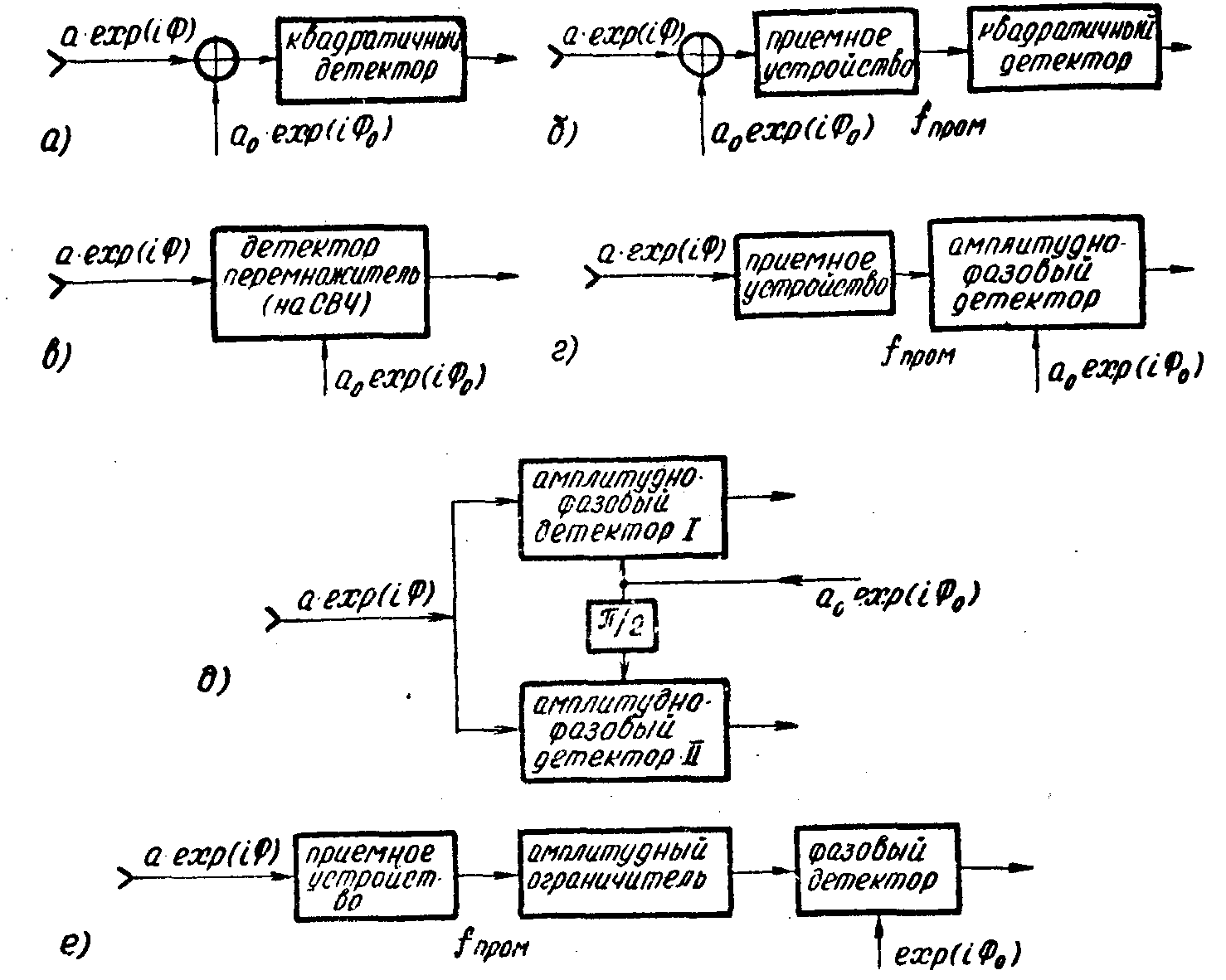
Рис.
1. Схемы формирования радиоголограмм.
Во всех случаях возможна запись квадратурных радиоголограмм:
H2
(х,y) = а02 + a
2 + 2
аа0 sin(
Ф-Ф0), (3)
H2(х,y) = аа0 sin(Ф-Ф0), (4)
Регистрация пары квадратурных радиоголограмм (
1), (3) или (2), (4) достигается с помощью идентичных опорных волн, сдвинутых по фазе на π/2 друг относительно друга (рис.1д, например).
Для фоторегистрации двухполярных функций (2) и (4) (с целью последующего оптического восстановления изображения) необходим опорный уровень
Hоп, который определяется из условия
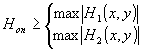 (5)
(5)
и условия линейности записи радиоголограмм. В этом случае получим уравнения:
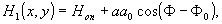 (6)
(6)
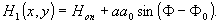 (7)
(7)
Каждая пара квадратурных радиоголограмм образует единую комплексную радиоголограмму:
H(x,y)=H1
(х,у)+iH(x,y). (8)
Величина
i в уравнении (8) вводится на этапе восстановления, а на этапе регистрации фиксируются лишь две квадратурные составляющие, например, типа (6) и (7). Однако такая форма записи уравнения комплексной радиоголограммы позволяет оперировать с ней как с единым целым, что особенно удобно при аналитическом описании процесса восстановления изображения (это будет показано далее).
С точки зрения объема зарегистрированных данных об объектной волне в радио голографии можно различать следующие случаи.
Если при формировании радиоголограммы сохраняются данные и об
амплитуде, и о фазе объектной волны, то можно говорить об амплитудно-фазовой радиогологpaммe. Если перед сложением (или умножением) объектной волны с опорной, пренебрегают амплитудным множителем а(х,у), то фиксируется чисто фазовая ("phasе-only") радиоголограмма
/11/ (рис.1е, например).
В радиодиапазоне могут быть использованы приемники, фиксирующие амплитуду и фазу объектной волны в чистом виде, т.е., регистрирующие распределение компонентов волнового поля
a ехр(iФ) на некоторой поверхности. Строго говоря, сформированная в этом случае картина на является голограммой, под которой обычно понимают запись, сохраняющую информацию о фазе за счет интерференции объектной и опорной волны. В работе /12/ в связи с этим был предложен термин "салограмма" (от греческого слова σαλξσ, ξзначающего "колебание" или "волна"). Основное различие голограммы и салограммы заключается в отсутствии у последней неоднозначности регистрации фазы объектной волны. В этом смысле комплексная радиоголограмма также образует салограмму, поскольку обе являются средством записи полного поля, излученного (или рассеянного) объектом. Далее будет показано, что на этапе реконструкции вследствие этого восстанавливается единственное изображение объекта.
3.
Обращенное синтезирование одномерных радиоголограмм
Фурье
Перейдем теперь к рассмотрению основных принципов обращенного синтезирования радиоголограмм за счет вращения объекта вокруг своего центра масс. Можно показать, что получаемая при этом одномерная радиоголограмма (будем называть ее далее просто синтезированной) эквивалентна классической безлинзовой голограмме Фурье, регистрируемой вдоль дуги сферической поверхности.
Если реальный объект (рис.2а) заменить совокупностью независимых дискретных отражателей ("блестящих" точек), размерами которых можно пренебречь, а отражающие свойства учесть с помощью соответствующих амплитудных множителей, то синтезированную радио-
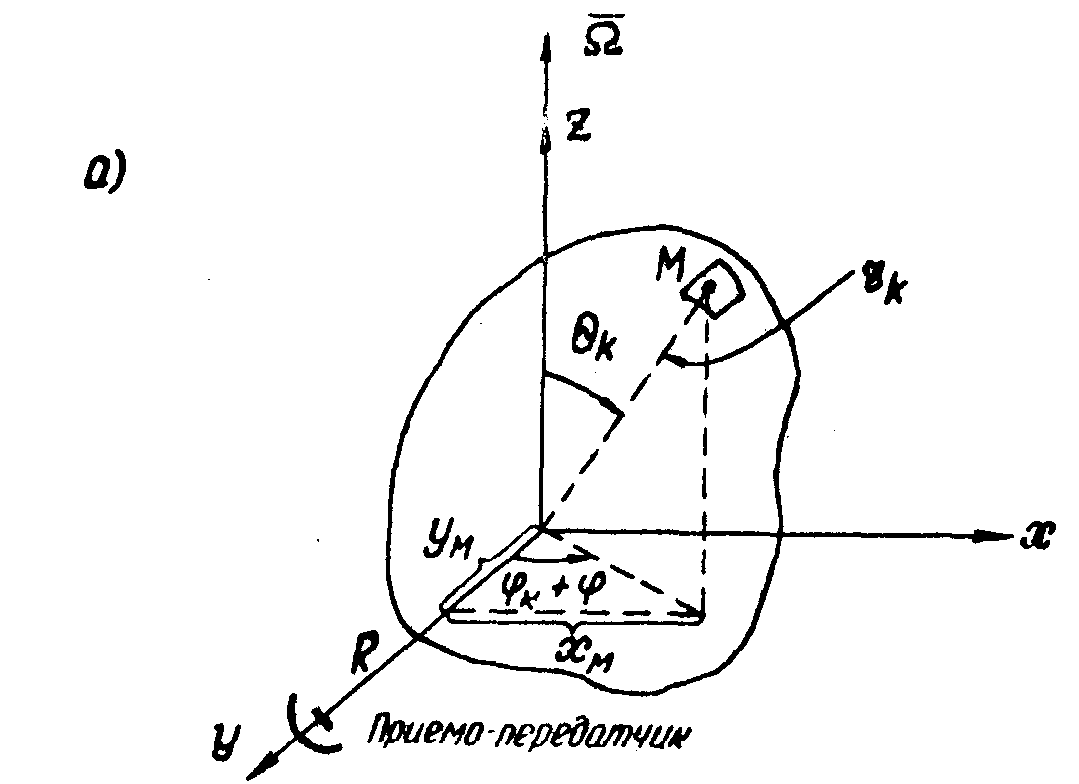
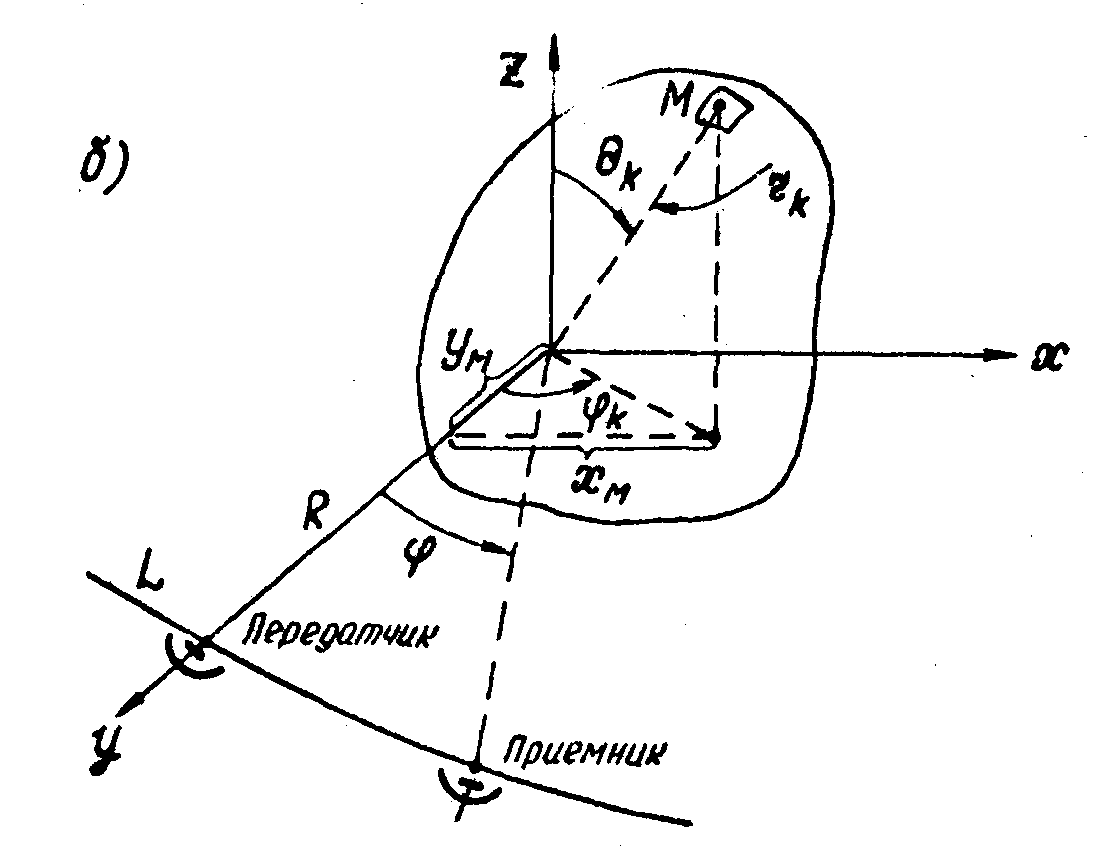
Рис.2. Схемы синтезирования одномерных радиоголосами Фурье. а) обращенное синтезирование;
б) прямое синтезирование.
голограмму перемножительного типа можно представить в виде:
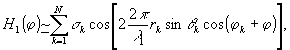 (9)
(9)
где
σk - амплитудный множитель, учитывающий отражающие свойства k - той блестящей точки; rk, θk, φk - сферические координаты k-той блестящей точки; λ1 - длина волны в радио диапазоне; φ=Ωτ, Ω - угловая скорость собственного вращения объекта вокруг центра масс.
Уревнение (9) справедливо в приближении дальней зоны. Классическая радиоголограмма Фурье этого же объекта, регистрируемая путем сканирования приемником вдоль дуги
L сферы радиуса R (рис.26), имеет вид:
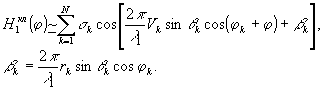 (10)
(10)
Сравнение выражений (9) и (10) показывает, что синтезированная радиоголограмма отличается от классической лишь вдвое большей способностью изменения аргумента и несущественной для восстановленного изображения начальной фазой
βk. В результате синтезированная радиоголограмма имеет вдвое лучшее разрешение, поскольку выглядит так же, как классическая, снятая в поле, у которого длина волны вдвое меньше реальной. В работе /8/ отмечено, что такой эффект достигается в итоге одновременного сканирования несколькими элементами из совокупности передатчик -объект - приемник. Легко убедиться, что радиоголограмма, полученная с помощью одновременного сканирования приемо-передатчиком вдоль дуги L (рис.2б) при неподвижном объекте, полностью соответствует радиоголограмме Н1(φ). Ξднако в случае обращенного синтезирования вращение одного лишь объекта эквивалентно перемещений двух элементов - передатчика и приемника.
Поскольку в остальном функция Н
1(φ) ρовпадает с Н1кл(φ), δля реконструкции изображений по синтезированным радиоголограммам Фурье в видимом свете могут применяться те же схемы, что и
в оптической фурье-голографии (рис.3).
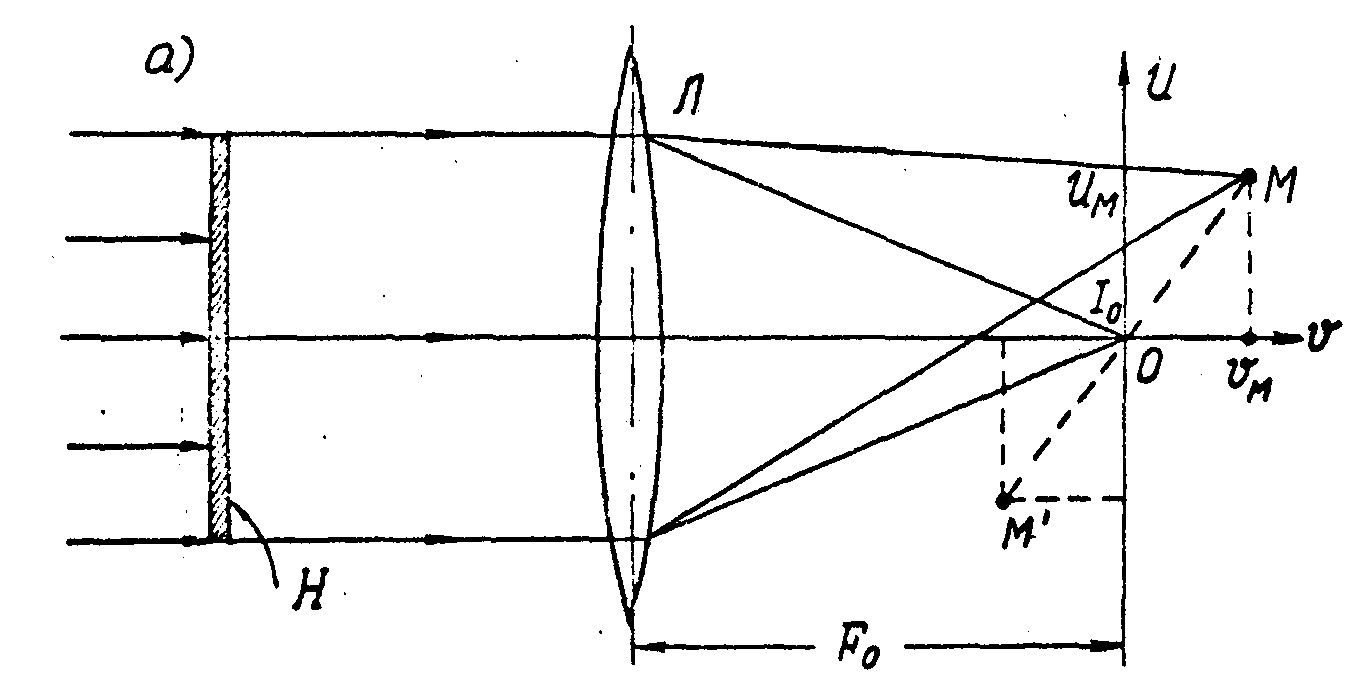
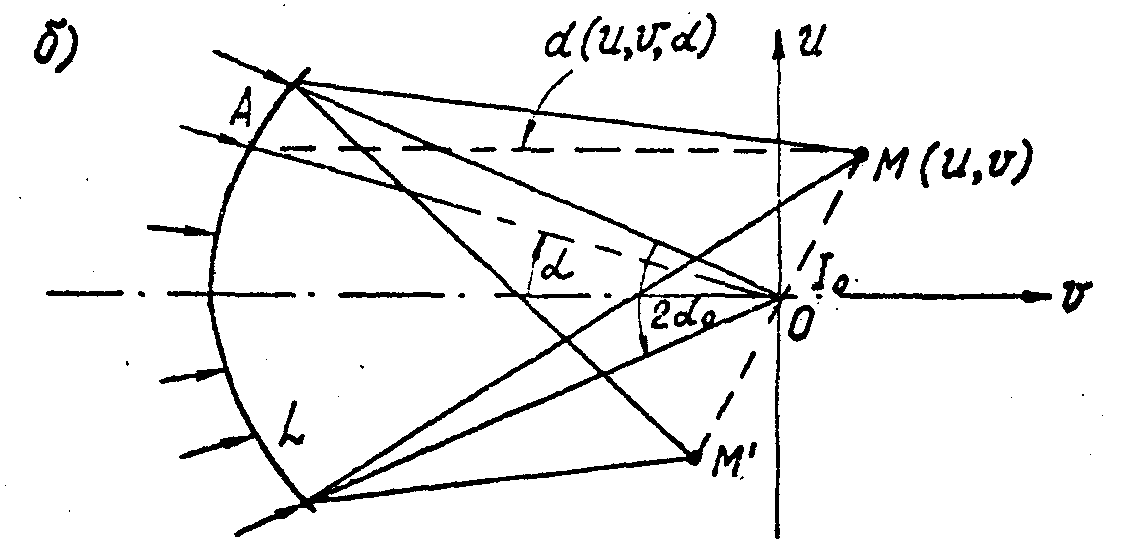
Рис. 3. Схемы оптического восстановления изображений по одномерным радиоголограммам Фурье.
В одном случае радиоголограмма, записанная на плоский транспарант, помещается в переднюю фокальную плоскость линзы Л (рис.3а). При освещении транспаранта плоской волной когерентного света вблизи задней фокальной плоскости линзы формируются две действительных сопряженных изображения объекта М и М
'. В другом варианте (рис.3б) используется сферический транспарант
радиуса
F0, освещаемый сходящимся в центр сферы О пучком когерентного света. Обе схемы идентичны в смысле выполняемых ими операций. На практике удобно использовать первую схему, а анализ вести применительно ко второй.
Если радиоголограмму записывать на равномерно движущийся со скоростью
vт оптический транспарант, то угловая координата на транспаранте
α=vтτ/F0 в пространстве реконструкции будет связана с угловой координатой α=Ωτ на радиоголограмме в пространстве регистрации соотношением
α = φv
т/ωF0 = φ/μ, μ = ωF0/v
т.
Распределение комплексных амплитуд света в пространстве изображений
u, v в окрестности точки O для радиоголограммы одноточечного объекта можно представить интегралом (для случая θk=90°):
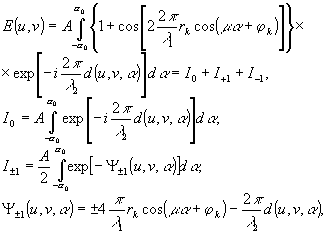 (11)
(11)
где
λ2 -
длина волны в оптическом диапазоне; A - комплексный коэффициент пропорциональности; d(u,v,α) - расстояние от произвольной точки А дуги L до точки M на изображении:
d(u,v,α) = [
 + 2F0(vcosα - usinα) + u2
+ 2F0(vcosα - usinα) + u2 + v
2]
1/2.
Интегралы
I0, I+1, I-1 описывают распределение комплексных амплитуд света в нулевом и первом (положительном и отрицательном) порядках дифракции. Если угловые размеры радиоголограммы и объекта не слишком велики, то функции cos(μα+φk)
и d(u,v,α) можно
представить первыми членами соответствующих рядов разложения и записать функцию Ψ
±1(
u,v,α) в виде
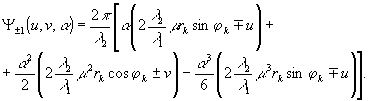 (12)
(12)
При этом были опущены постоянные члены разложения, не зависящие от аргумента
α. Координаты точек М(uм,vм) и М
'(uм',v
м'), в которых образуются два сопряженных изображения одноточечного объекта, можно определить из уравнений
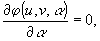
 (13)
(13)
Учитывая, что
xM=rksinφk и yM=rkcosφk, из уравнений (13) получим
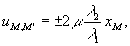
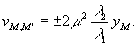 (14)
(14)
Из равенств (14) легко определить продольный и поперечный масштабы восстановленного изображения:
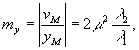
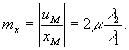 (15)
(15)
Неискаженное воспроизведение изображения объекта возможно лишь при условии равенства нулю одновременно всех производных функции
Ψ(u,v,α) по аргументу α. Нетрудно показать, что это условие выполняется в одной точке (М и М'), когда
μ=ΩF
0/v
T=1
или φ=α.
Последнее тождество определяет критерий оптимальности схемы обработки синтезированных радиоголограмм Фурье: угловые размеры апертуры радиоголограммы в пространствах регистрации и реконструкции должны быть равны. Если схема реконструкции построена оптимальным образом, то
mx=my=m и объект воспроизводится без искажений как в продольном, так и в поперечном направлениях.
Отличительной особенностью синтезированных радиоголограмм Фурье является независимость получаемого разрешения от расстояния до объекта. Действительно, примем в качестве меры разрешающей способности величину
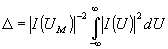 , (16)
, (16)
где
|I(U)|2 - распределение интенсивности света в изображении "блестящей" точки; UM - координата максимума интенсивности сфокусированного изображения - "блестящей" точки. Функция (16) представляет собой отклик приемной системы на точечную цель. Тогда, пренебрегая в уравнении (12) всеми членами, кроме первого, и используя масштабные соотношения (15), можно показать, что разрешающая способность на объекте
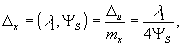 (17)
(17)
где
Ψs - угловой размер апертуры, радиоголограммы. Следовательно, в случае малых угловых размеров радиоголограммы разрешавшая способность на объекте зависит от длины волны и угловых размеров синтезированной апертуры и не зависит от расстояния до объекта и параметров схемы реконструкции.
Члены высших порядков в уравнении (12) определяют искажения изображения. Это объясняется тем, что при наблюдении изображения объекта в одной плоскости часть "блестящих" точек оказывается смещенной относительно этой плоскости, т.е. расфокусированной. Распределение поля в расфокусированном изображении точки с учетом квадратичного члена функции (12) имеет вид:
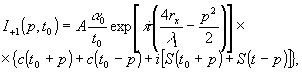 (18)
(18)
где
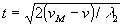 характеризуют смещение плоскости наблюдения относительно плоскости фокусировки, р=UМ/λ2
характеризуют смещение плоскости наблюдения относительно плоскости фокусировки, р=UМ/λ2t, t
0=α0t
и S(z), С (z) -интегралы Френеля.
Разрешающая способность расфокусированного изображения определяется функцией
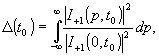 (19)
(19)
вид которой приведен на рис.4.Очевидно, наилучшее разрешение,
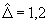 , достигается при некотором оптимальном
, достигается при некотором оптимальном 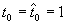 , которому соответствует оптимальный размер апертуры:
, которому соответствует оптимальный размер апертуры:
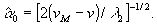 (20)
(20)
При
v=0, т.е. когда плоскость наблюдения совмещена в фокальной плоскостью линзы, c учетом (14),
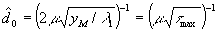 , (21)
, (21)
где
τmax=2L
max/λ1 - максимальный продольный размер объекта, выраженный в полудлинах волн.
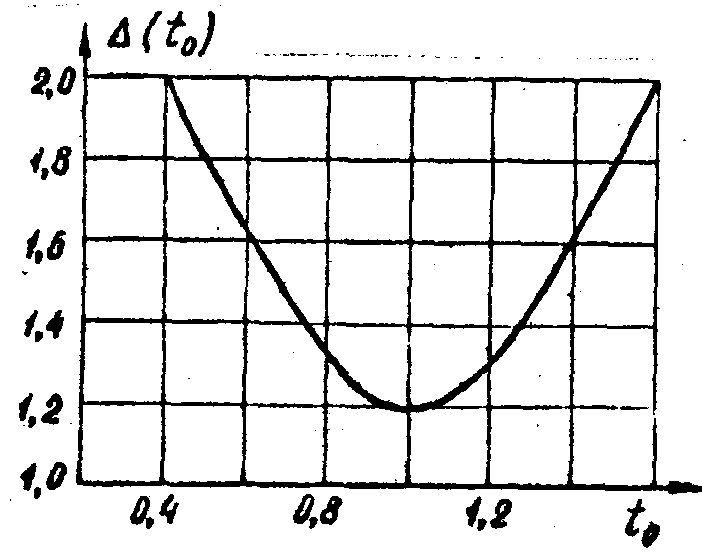
С увеличением размеров объекта или апертуры радиоголограммы влияние членов более высокого порядка в (12) становится заметным, что приводит к искажению изображения и ухудшению разрешающей способности. Эти явления ведут к ограничению предельного размера синтезированной апертуры.
Реконструкция изображений по радиоголограммам Фурье имеет
особенности, связанные со способом создания искусственной опорной волны. Если модуляция фазы опорного сигнала не производится, то фаза когерентного опорного фона вдоль радиоголограмма будет постоянной, что эквивалентно точечному источнику, размещенному в центре вращения объекта. Поэтому при реконструкции все три изображения - опорного источника и два сопряженных изображения объекта - перекрываются. Для их разделения необходимо введение пространственной несущей частоты
. Для этого достаточно изменять фазу опорного сигнала с постоянной скоростью, согласно условию
d
Ф0/
dτ>4πΩrmax/λ1,
где
rmax - радиус-вектор "блестящей" точки, максимально удаленной от центра вращения объекта.
Модуляцию фазы опорной волны можно осуществить с помощью фазовращателя либо дополнив вращательное движение объекта поступательными вдоль линии визирования. В последнем случае, необходимо, чтобы скорость поступательного движения
vл удовлетворяла неравенству
vл > Ωrmax.
4.
Особенности комплексных одномерных
радиоголограмм Фурье
Уравнение одной из квадратурных радиоголограмм Фурье совпадает с выражением (9), уравнение другой имеет вид:
 (22)
(22)
Согласно определению (8) они образуют комплексную радиоголограмму Фурье:
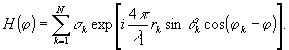 (23)
(23)
Последнее выражение можно записать в более простом виде:
H(x)=σexp(iΦ),
(24)
где σ и Ф - соответственно, амплитуда и фаза суммарного поля, рассеянного объектом, в плоскости регистрации радиоголограммы. Аргумент φ функции Н заменен на линейную координату х, поскольку запись одномерной радиоголограммы осуществляется на плоский транспарант.
Восстановление изображения плоской волной сводится в параксиальном приближении к преобразованию Фурье функции радиоголограммы (для простоты полагаем, что запись и восстановление происходят на одной и той же длине волны):
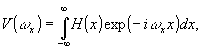 (25)
(25)
где
ωх - пространственная частота, соответствующая координате в пространстве изображения.
Подставляя в выражение (25) уравнения квадратурных радиоголограмм (9) и (22), записанных в формуле (24), получим соответственно,
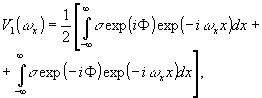 (26)
(26)
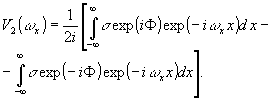 (27)
(27)
Таким образом, использование каждой квадратурной радиоголограммы дает по два сопряженных изображения, которые соответствуют отдельным слагаемым в выражениях (26) и (27).
В случае комплексной радиоголограммы первая квадратурная составляющая создает два сопряженных изображения (26), а по второй составляющей восстанавливаются изображения:
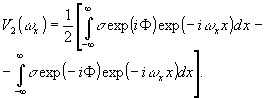 (28)
(28)
Первые слагаемые в уравнениях (26) и (28) идентичны, а вторые отличаются знаком, т.е. сдвинуты по фазе на π. В результате совместного восстановления после сложения полей (26) и (28) одна пара сопряженных изображений усилит друг друга, а другая пара взаимно уничтожится, т.е. получим
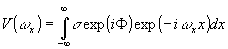 . (29)
. (29)
Комплексная функция
V(ωx)
описывает единственное изображение, восстановленное по комплексной радиоголограмме. Интенсивность изображения можно определить как
W(ω
x) = |V(ωx)|
2. (30)
Для примера рассмотрим случай, когда объект состоит из одной точки, а параметры
θ1 и φ1 принимают значение, равное π/2. Для достаточно малых значений φ (φ < 1 πад), учитывая, что φ = Ωυ/vT где vT - скорость движения регистрирующего материала (лента самописца, например), уравнение (23) сведется к
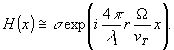 (31)
(31)
Поскольку синтез радиоголограммы происходит в конечном интервале времени
τÎ
[-T/2,T/2], из уравнения (25) получим
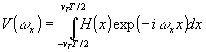 (32)
(32)
Подставляя (31) в (32) и интегрируя, имеем:
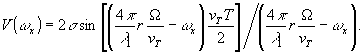 (33)
(33)
Очевидно, эта функция типа
sinz/z имеет максимум при ωx =
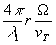 , который соответствует изображению точки.
, который соответствует изображению точки.
При цифровом восстановлении, которое сводится к вычисление интеграла (25), нулевой порядок отсутствует. Это позволяет формировать комплексную радиоголограмму без введения несущей час-
тоты, что приводит к сокращению объема обрабатываемое данных. Одна квадратурная радиоголограмма требует, по крайней мере, вдвое большего количества дискретных отсчетов из-за высокой пространственной несущей частоты.
При оптическом восстановлении кроме единственного изображения создается нулевой порядок, причиной возникновения которого является опорный уровень Ноп (см.уравнение (5)-(7)). При обработке комплексной радиоголограммы Фурье, записанной без несущей частоты, нулевой порядок налагается на изображение. Задача их пространственного разделения достаточно просто решается с помощью несущей частоты. Использование комплексной радиоголограммы при этом теряет смысл, поскольку полное устранение сопряженного изображения становится излишним. Кроме того, оптическое восстановление изображения по комплексной радиоголограмме затруднено в силу жестких требований по юстировке двухканальной схемы обработки, предложенной в работе /13/, например. Таким образом, запись комплексных радиоголограмм Фурье следует осуществлять без введения несущей частоты, а восстановление изображения проводить только цифровым способом.
5.
Цифровое моделирование
Для исследования и сопоставления различных методов радиоголографии Фурье был разработан алгоритм цифрового моделирования процессов записи квадратурных и комплексных одномерных радиоголограмм Фурье и их обработки. Алгоритм состоит из двух основных блоков, в первом из которых производится синтез радиоголограммы, согласно уравнению (23), а во втором - реконструкция изображения (вычисление интеграла (25)). Восстановление изображений по отдельным квадратурным радио голограммам производится с помощью дополнительной процедуры, позволяющей вычислить интегралы Фурье действительных функций Н1 и Н2 по результатам преобразования Фурье комплексной функции Н = Н1 + iН2.
На рис.5 приведена некоторые результаты цифрового моделирования. По оси ординат отложена интенсивность изображения в от-
носительных единицах, по оси абсцисс - приведенные размеры изображения. При цифровом восстановлении изображение представляет собой последовательность дискретных отсчетов, расстояние между которыми
–λ1/2Ψs.
Объект состоял из двух точек, расположенных в виде гантели длиной 10∙λ1, и вращался с постоянной угловой скоростью вокруг центра масс. Величина θk (рис.2а) была принята равной π/2 . Изображение на рис.5а восстановлено по одной квадратурной радиоголограмме Фурье. Максимумы 1 и 2 соответствуют одному сопряженному изображению двух точек, максимумы 3 и 4 - другому. Разделение изображений происходит с помощью несущей частоты, введение которой моделировалось за счет

Рис.5. Результаты цифрового
моделирования
радиального перемещения центра вращения объекта относительно приемника с постоянной скоростью
vл. При обработке комплексной радио голограммы одно из сопряженных изображений исчезает (рис.5б), и несущая частота становится излишней, что подтверждает рис.5в, где показано изображение, восстановленное по комплексной радиоголограмме Фурье, записанной без несущей.
На рис. 5г,д,е показана зависимость вида восстановленного изображения от угловых размеров радиоголограммы. Сравнение этих результатов подтверждает вывод, полученный выше, о существовании оптимального размера синтезированной апертуры. При увеличении угла Ψs разрешающая способность растет до определенных пределов, после чего возникают искажения в структуре изображения. Оценка предельной разрешающей способности метода по результатам цифрового моделирования составила величину ~λ1.
6. Результаты эксперимента
В настоящее время предложено дав метода радиоголографии Фурье /14/. Первый из них основан на записи одной квадратурной амплитудно-фазовой радиоголограммы типа (9), применении пространственной несущей частоты и оптическом восстановлении изображения, а второй - на записи комплексной чисто фазовой радиоголограммы типа (23) без введения несущей и цифровом восстановлении изображения.
На рис.6а показаны результаты оптического восстановления изображения (по схеме, приведенной на рис.3а) объекта, состоящего из трех тонких стержней (в центре виден нулевой порядок, а по краям - сопряжение изображения). На рис.6б приведена серия одного из сопряженных изображений двух шаров, полученная для измерения разрешающей способности в поперечном направлении (под каждым изображением показан вид объекта в плане). Диаметр шаров - 4∙λ1, расстояние между их центрами - 8∙λ1. Изображения соответствуют изменению ракурса объекта через 18° в интервала 0-90°, величина Ψs составляла 9°. Расчетное разрешение Δ@
3λ1 достигнуто экспериментально (для кадров №2 и №3 поперечные расстояния между центрами составляют, соответственно, 2,5∙λ1 и 4,4∙λ1).
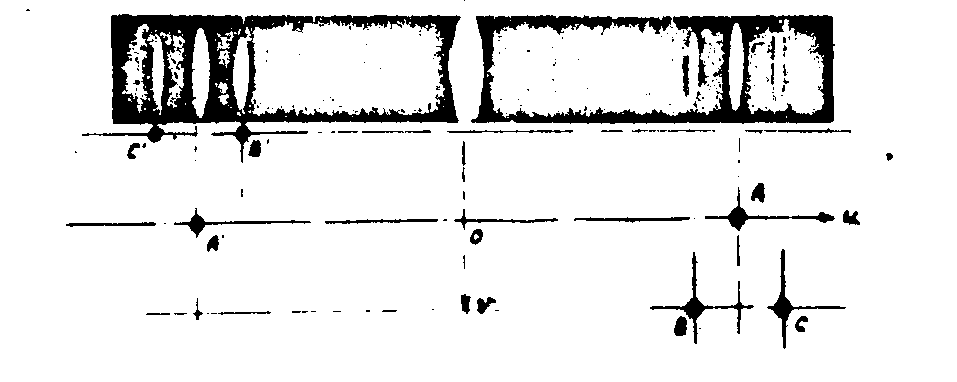
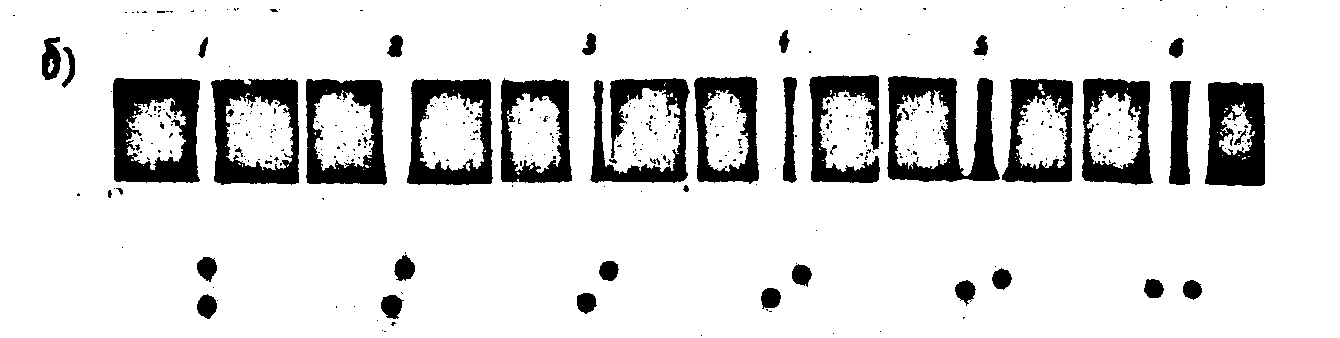
Рис.6. Результаты оптического восстановления изображений по отдельным квадратурным радиоголограммам Фурье;
а) восстановленное изображение трех тонких стержней;
б) серия одного из восстановленных сопряженных изображений двух шаров для различных ракурсов.
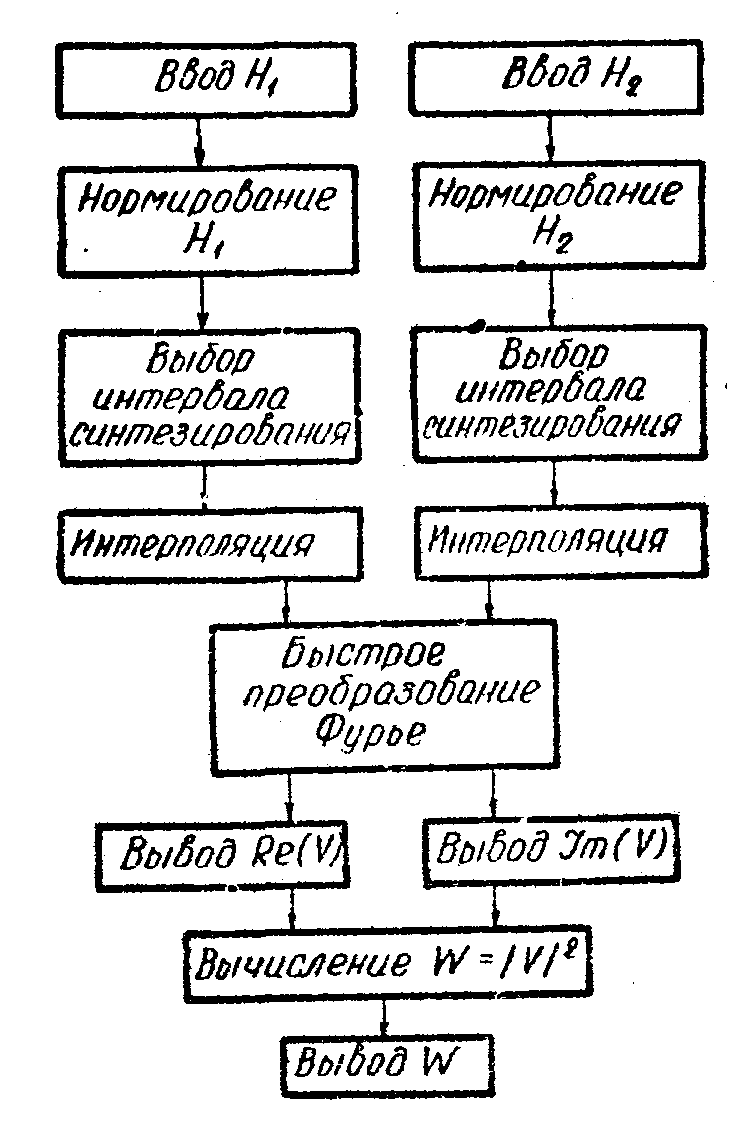
На рис.7 показан алгоритм цифрового восстановления изображений, который функционирует следующим образом. После ввода дискретных данных производится их нормирование (приведение к интервалу изменения /-1, 1/). Запись радиоголограмм производится обычно для полного поворота объекта на 2π рад, поэтому для последующей обработки выбирается последовательность отсчетом, количество которых соответствует оптимальной апертуре, а положение в общем массиве - необходимому ракурсу объекта. Блок интерполяции формирует из них двоично-рациональную выборку. Непосредственно восстановление происходят в блоке преобразования Фурье, который реализован с помощью алгоритма БПФ для комплексной функции Н(х). На выходе блока БПФ формируются массивы
чисел
Re(V) и Im(V) , определяющие изображение, интенсивность которого подсчитывается как W = Re2(V) + Im2(V),
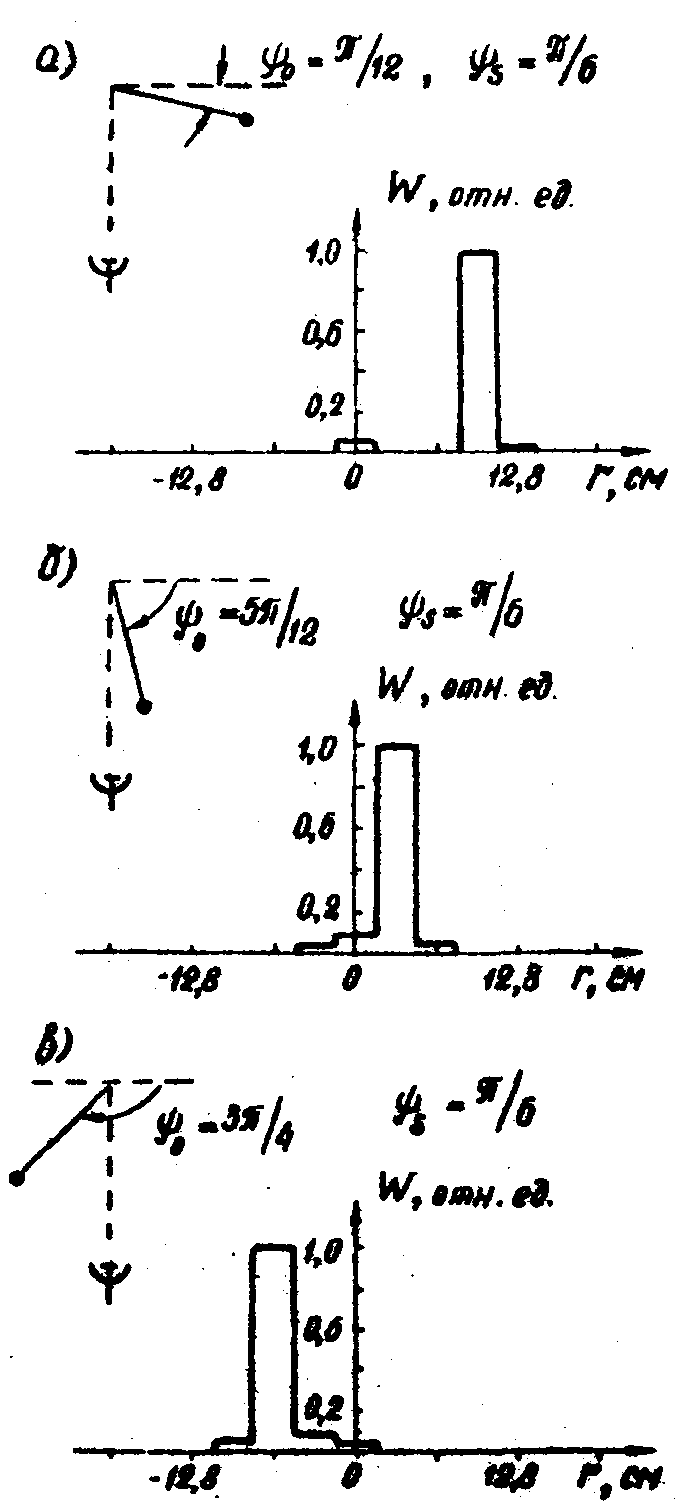
На рис.8 приведены результаты цифровой обработки одномерных комплексных радиоголограмм Фурье, полученных экспериментально в безэховой камере
/15/. По оси ординат отложена интенсивность изображения в относительных единицах, по оси абсцисс - его линейный размер. Объект - металлический шар радиусом 0,3λ1, вращавшийся по окружности радиусом 3λ1. Положение изображения точки на рис.8а,б,в различно в зависимости от ракурса объекта Ψ0, который схематически показан на каждом рисунке.
Рассмотренные методы имеют свои преимущества и недостатки. Система записи отдельных квадратурных радиоголограмм, является
одноканальной, но требует введения несущей частоты каким-либо способом. Система записи комплексных радиоголограмм не требует введения несущей, но она сложнее из-за обеспечения строгой квадратурности каналов, идентичности их основных параметров,
Синхронизации измерений и т.п. Однако погрешности записи, вы-
званные этими особенностями двухканальной схемы регистрации, достаточно просто устраняются на этапе цифровой обработки (как отмечалось ранее, обработку комплексных радиоголограмм Фурье следует проводить только цифровым способом). Восстановление изображений по квадратурным радиоголограммам возможно как цифровым, так и оптическим способом. Запись радиоголограмм в виде, пригодном для цифровой обработки, повышает динамический диапазон системы регистрации и не требует сложных узлов (например, ЭЛТ с высоким разрешением и прецизионной фокусирующе-отклоняющей системы для нее). Размер апертуры при оптической обработке, как правило, ограничен параметрами схемы восстановления и не достигает оптимального значения. С другой стороны, оптическая схема обработки позволяет легко перефокусировать плоскость наблюдения, т.е. обеспечивает двумерное (в продольном и поперечном направлениях) изображение.
7.
Заключение
Результаты исследования методов радиоголографии Фурье подтвердили возможность их применения для получения изображений объектов, которые можно представить совокупностью "блестящих" точек, и для измерения амплитуд отдельных "блестящих" точек. Эти методы представляют существенный интерес для изучения явлений дифракции на телах в безэховых камерах, в частности, для экспериментального определения пределов применимости физической теории дифракции П.Я.Уфимцева в геометрической теории дифракции Келлера.
Л и т е р а т у р а
1. R.W.Larson, J.S.Zelenka, E.L.Johansen,
Рrос.JЕЕЕ, 57, 12, 2162, 1969.
2. R.W.Larson, J.S.Zelenka, E.L.Johansen. JEEE Trans, AES-6, 2, 208, 1972.
3. K.F.Ross
, Патент США, №3, 284, 799, 1966.
4. W.M.Brown, JEEE Trans., AES-3, 3, 217, 1967.
5. J.E.A.Ormsby, N.M.Tomlianovich, H.S.Ostrowsky., M.R.Weiss, JEEE Trans., AES-6, 3, 295, 1970.
6.
С.А.Попов, Б.А.Розанов. В сб. "Труды юбилейной научно-технической конференции факультета "Приборостроение" МВТУ им.Н.Э.Баумава, М., 1969.
7. B.Hildebrand, B.Brenden. On introduction to acoustical holography, N.Y., 1972.
8. Голография. Методы и аппаратура. Под.ред. В.М.Гинзбург и Б.М.Степанова, изд."Сов.радио", М., 1974.
9. А.П.Реутов, Б.А.Михайлов, Г.С.Кондратенков, Б.В.Бойко. Радиолокационные станции бокового обзора, изд."Сов.радио", М., 1970.
10. G.Deschamps. Proc. JEEE, 55, 4, 570, 1967.
11. Дж.Пауэрс, Дж.Ландри, Г.Уэйд. В кн."Акустическая голография", пер. с англ. изд. "Судостроение", стр.
131-146, Л., 1975.
12. О
nое Mario, in "Ultzasonic Jmaging and Holography in Med., Sonar and Opt. Appl.", 455-502, 194.
13. Э.И.Крупицкий, И.С.Барбанель. "Оптика и спектроскопия", т.25, вып.1, 125, 1973.
14. С.А.Попов, С.С.Зиновьев, А.Я.Пасмуров. В сб. "Проблемы голографии", МИРЭА, М., 1976 (в печати).
15. Л.Т.Тучков, В.М.Вяткина, Ю.C.Зиновьев. А.П.Пономаренко, Р.Т.Уланов. В сб. "Проблемы голографии", МИРЭА, М., вып.1., стр. 112-116, 1973.

