|
|
 |
 |

|
| |
ПРЕДЕЛЬНАЯ ПРОСТРАНСТВЕННАЯ КОГЕРЕНТНОСТЬ
ПУЧКОВ ГАЗОВЫХ ЛАЗЕРОВ *)
А.С.Чиркин
В ряде приложений важной характеристикой лазерных пучков является пространственная когерентность. Рассказывается об экспериментах по измерению предельной пространственной когерентности пучков гелий-неоновых лазеров и предельного значения коэффициента поперечной диффузии их фазы, которые определяются спонтанным излучением лазера. Рассмотрен вопрос об ошибках измерения указанных параметров пучка. Кратко рассказано о некоторых преимуществах использования высококогерентных пучков в экспериментах по рассеянию света.
1. Изменения пространственной когерентности (ПК) излучения лазеров /1-2/ были выполнены почти сразу же после запуска первых рубиновых и гелий-неоновых лазеров и относятся к 1960-61 г.г. В настоящее время насчитывается несколько десятков публикаций (см.обзор /3/), посвященных ПК лазерного излучения. Измерены ПК излучения различных типов лазеров; помимо твердотельных и газовых лазеров исследовалась когерентность лазеров на органических красителях /4/ и полупроводниковых лазерах. О пространственных когерентных свойствах последних рассказывалось на этой вводе в лекции Ларкина /5/.
По ряду причин наилучшей ПК обладают пока газовые лазера, тем не менее полученные здесь данные можно разделить на две группы. В одной группе работ пространственная корреляционная функция излучения заметно спадала к краю пучка. Этот эффект авторы объясняют возбуждением либо высших поперечных мод, либо нескольких продольных мод. Однако специальные измерения Дерюгина, Курашова и
Мирзаева /6/ показали, что в газовых лазерах продольные моды не влияют на ПК излучения. В другой серии работ степень ПК в пределах ширины пучка была около 0,9 или отличалась от единицы на несколько сотых, причины же отличия частичной ПК от полной, однако, не изучались.
В настоящей лекции речь пойдет об исследованиях /7-9/ у ПК излучения Не- Ne лазеров, выполненных в течение последних двух лет в лаборатории профессора Ахманова. Целью исследований было определение предельной ПК излучения газовых лазеров и выяснение причин, ее обуславливающих. По аналогии с временными флуктуациями лазерного излучения следовало ожидать, что предельная когерентность лазерных пучков связана со спонтанным излучением в лазере. Будет такие рассказано об экспериментах по рассеянию света с использованием лазерных пучков с предельной ПК, дающих определенные преимущества в подобного рода экспериментах.
Однако, прежде чем перейти к непосредственному предмету лекции, отметим, что измерения ПК лазеров характеризуются многообразием применяемых интерферометров. Наиболее часто применялся интерферометр Юнгa и Маха-Цендера. Ряд исследователей, в частности Стаселько и Денисюк /10/, для измерения ПК использовали голографические способы.
2. Измерения предельной ПК лазерных пучков были выполнены с помощью поляризационного интерферометра /11/. Схема установки изображена на рис.1. Исследуемый пучок, пройдя через поляризатор 1, попадает на систему из двух идентичных плоскопараллельных пластин 3 и 5, вырезанных из двулучепреломляющего кристалла вдоль оптической оси, и полуволновой пластинки 4, помещенной между ними. Пластины 3 и 5 могут поворачиваться вокруг своих оптических осей, ориентированных параллельно друг другу, перпендикулярно плоскости чертежа и падающему пучку и образующих угол 45° с его поляризацией. Пройдя через первую пластину 3, пучок делится на два пучка с взаимно перпендикулярными поляризациями, смещениях друг относительно друга в плоскости чертежа на величину S, зависящую от толщины l пластины и угла φ падения пучка на пластину: S = f1(α,φ) /11/. При этом пучки приобретают некоторую временную задержку r = f2(α,φ).
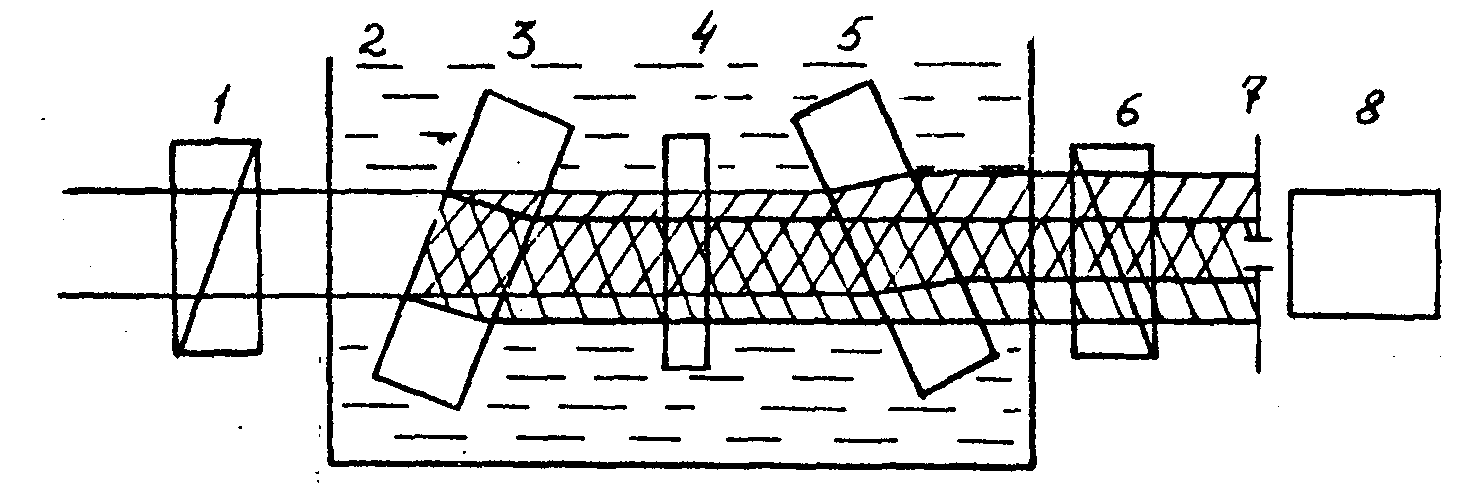
Ри c.1. Схема поляризационного интерферометра.
При прохождении через пластину 4 векторы поляризации пучков поворачиваются на 90°. Вследствие этого в пластине 5, повернутой на угол (-φ ), временная задержка пучков полностью компенсируется; пространственные смещения при этом складываются.
Пластины 3-5 помещаются в кювету 2 с иммерсионной жидкостью, показатель преломления которой равен показателю преломления обыкновенной или необыкновенной волн в двулучепреломляющем кристалле, это делается для того, чтобы избежать нежелательного абсолютного смещения пучков.
Анализатор 6 сводит поляризации пучков в одну плоскость; в области перекрытия пучки интерферируют. Диафрагма 7 вырезает часть интерференционной картины, регистрируемой устройством 8.
В выполненных экспериментах пластины 3 и 5 толщиной l = 25 мм были из кальцита, инверсионной жидкостью служило касторовое масло. При повороте пластины 3 пластина 5 не поворачивалась, поэтому один пучок проходил через всю систему, не испытывая смещения. Поворотом анализатора 6 варьировались интенсивности интерферирующих лучей.
3. Степень пространственной (поперечной) когерентности между интерферирующими лучами |γ(S)|=|Γ(S)|/Г(О),
Г( S)=<E(r+s;z,t)E*(r;z,t)>,
где E(r;z,t) - электрическое поле; z - координата вдоль направления распространения пучка, определялась по видности интерференционной картины:
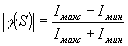 . (1) . (1)
При измерении корреляционной функции высококогерентных лазерных пучков максимум Iмакс и минимум Iмин в интерференционной картине резко различаются и существенное влияние на измеренное значение γ(s) оказывает динамический диапазон регистрирующей системы. Наилучшим с этой точки зрения является методика счета фотонов; она и использовалась в описываемых экспериментах, динамический диапазон регистрирующей системы без введения дополнительных ослабителей 106÷10 7. Собственные шумы ФЭУ были 2∙102 имп/сек и вычитались при измерениях. Порог чувствительности системы регистрации 2∙10-16 Вт при времени измерения Тизм = 1 сек.
Для контроля поперечной структуры лазерного излучения измерялся профиль интенсивности лазерного пучка, который по диаграмме спрямления сравнивался с гауссовым распределением основной моды ТЕМ 00. Отклонение измеренного распределения интенсивности I(S) и гауссова не превышало 5% по всему сечению пучка вплоть до значений I(S)/I(О)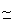 1∙10-3. 1∙10-3.
4. Исследовалась ПК излучения гелий-неоновых лазеров (длина волны 0,633 мкм), обычного и с неоновой поглощающей ячейкой в резонаторе. Выделение основной моды осуществлялось введенной в резонатор ирисовой диаграммой.
На рис.2 представлены пространственные корреляционные функции |γ (S)| лазера ЛГ-36 (выходная мощность 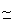 1 мкВт). Длина лазерного резонатора L = 1,2 м, внутренний диаметр трубки 6 мм. Выходное зеркало было плоским, а сферическое зеркало имело радиус кривизны R=10 м, коэффициенты отражения зеркал соответственно равнялись 99,3% и 99,8%. Вблизи центра (S 1 мкВт). Длина лазерного резонатора L = 1,2 м, внутренний диаметр трубки 6 мм. Выходное зеркало было плоским, а сферическое зеркало имело радиус кривизны R=10 м, коэффициенты отражения зеркал соответственно равнялись 99,3% и 99,8%. Вблизи центра (S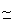 0) пучка 0) пучка
|γ(0)|= 0,99997±1÷10-5. При удалении от центра (увеличении S) ПК пучка уменьшается, оставаясь, однако, достаточно высокой: |γ(S)|=0,9991±1÷10-4 и |γ(S)|=0,998±1÷10-3, соответственно, для точек, в которых интенсивность составляет 0,1 и 0,001 от максимальной.
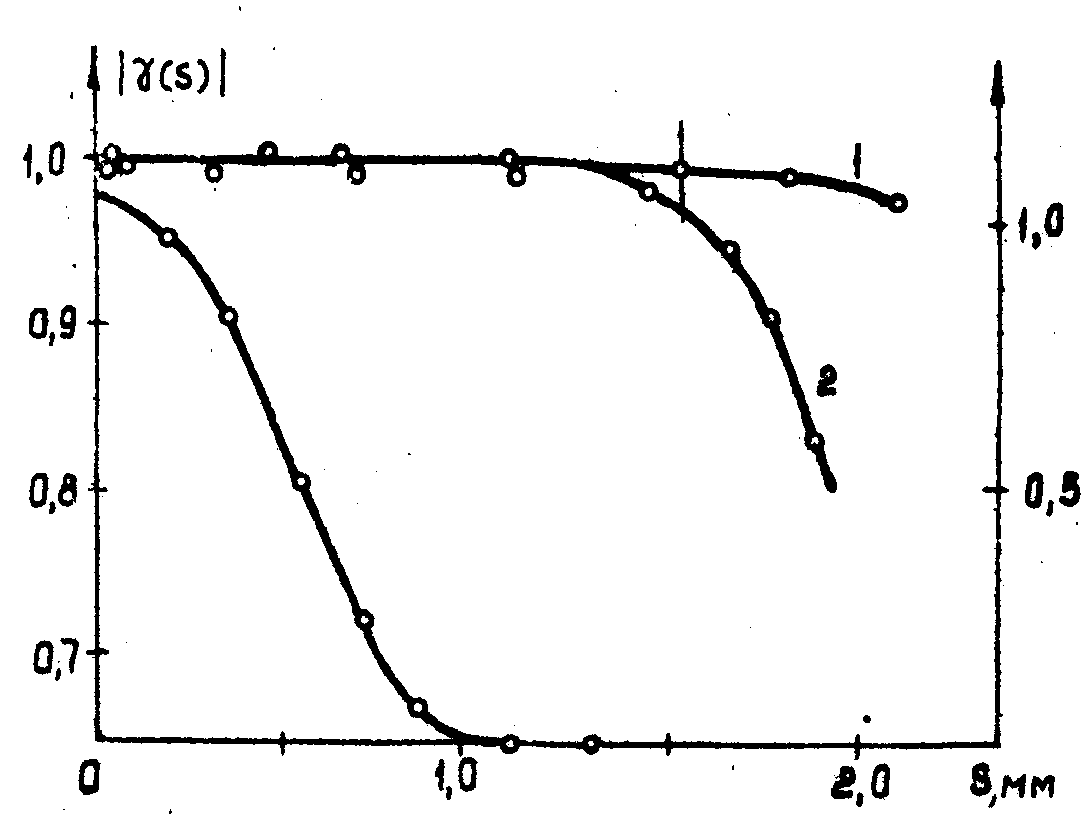
Рис.2. Пространственные корреляционные функции |γ(S)| (кривые 1 и 2) обычного гелий-неонового лазера для двух режимов работы; профиль пучка - кривая 3. Вертикальной чертой отмечены значения при I(S)/I(J)=1∙10-3.
В качестве лазера с нелинейной поглощающей ячейкой использовался лазер JIT-159 (выходная мощность 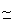 0,1 мВт). Резонатор лазера имел длину 0,1 мВт). Резонатор лазера имел длину 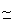 1,7 м, длина лазерной трубки 1,0 м; внутренний диаметр трубки - 3 мм, ячейки - 2,5 мм. Сферическое зеркало с радиусом кривизны R = 2 м имело коэффициент отражения 99,6%, а 1,7 м, длина лазерной трубки 1,0 м; внутренний диаметр трубки - 3 мм, ячейки - 2,5 мм. Сферическое зеркало с радиусом кривизны R = 2 м имело коэффициент отражения 99,6%, а
выходное плоское зеркало - 98,5%. На рис.3 представлена пространственная корреляционная функция излучения этого лазера для области смещений S, где интенсивность от максимальной изменяется меньше чем на порядок. Вблизи центра пучка ПК была такова, что I - |γ(О)|= (2±1)∙10-7.
5. В связи со столь близким значением пространственной когерентности лазерных пучков с полной и высокой точностью, с которой она измеряется, остановимся специально на вопросе об ошибках измерения |γ |.
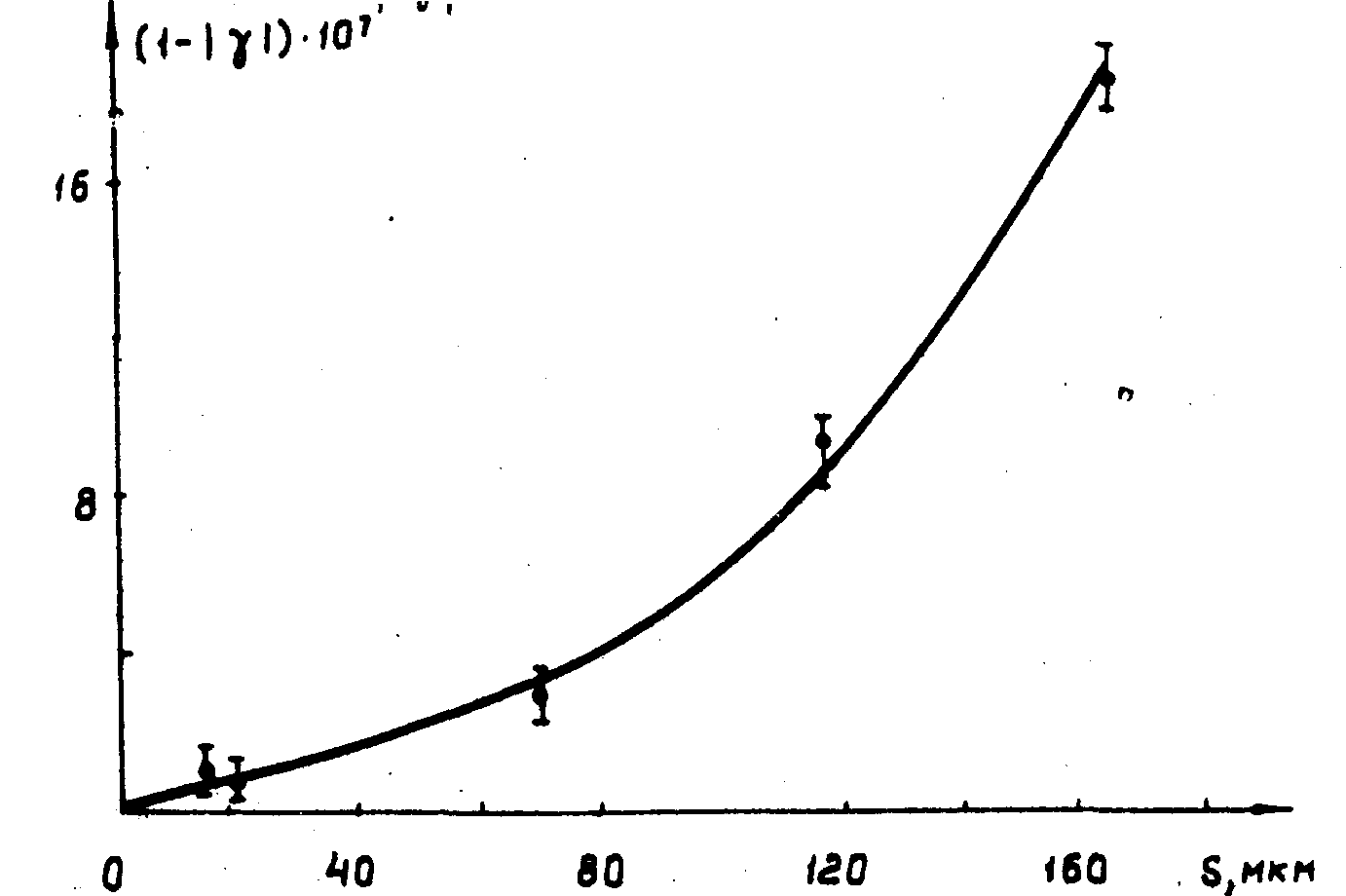
Рис.3. Степень отличия пространственной когерентности от полной для гелий-неонового лазера с поглощавшей ячейкой в зависимости от смещения S.
Статистические ошибка измерения |γ| обусловлены ограниченностью времени измерения Т изм и неточностью определения значений Iмакс и Iмин в интерференционной картине из-за нестабильности работы лазера и регистрирующей системы и других случайных причин. В силу того, что Iмакс >> Iмин, основная ошибка
измерения |γ| = 1-2 (Iмин/Iмакс) возникает из-за неточности ΔIмин определения Iмин и равна
Δγ = (1-|γ|)(Δ Iмин/Iмин). (2)
Что касается ограничения, связанного с Тизм, то оно приводит к ошибке /12/ ΔγФ 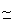 τk/Тизм, где τk - время когерентности излучения. Ошибка ΔγФ τk/Тизм, где τk - время когерентности излучения. Ошибка ΔγФ для исследованных лазеров была несущественна: для обычного лазера Δ γФ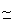 1∙10-9, а для лазера с поглощающей ячейкой и ΔγФ<1∙10-7. 1∙10-9, а для лазера с поглощающей ячейкой и ΔγФ<1∙10-7.
Систематические ошибки измерения |γ| связаны с конкретной геометрией эксперимента. Они обусловлены: 1) частичной временной когерентностью излучения; 2) ограниченным радиусом кривизны фазового фронта пучка и конечным размером диафрагмы 7 перед ФЭУ; 3) отражением от поверхностей пластин 3 и 5, которые представляют собой, по существу, интерферометре низкой добротностью; 4) несовершенством элементов поляризационного интерферометра (неточным подбором иммерсионной жидкости, непараллельностью граней пластины друг другу и оптической оси; 5) рассеянием света в иммерсионной жидкости и на элементах оптики. Перечисленные источники в условиях наших экспериментов давали систематическую ошибку, гораздо меньшую статистической; подробно они проанализированы в работе /13/. Здесь мы рассмотрим эффект кривизны фазового фронта. На рис.4 показаны фазовые фронты пучков, центры которых смещены на величину S; R - радиус кривизны фронта; точка О - центр диафрагмы 7. На расстоянии Х в плоскости диафрагмы появляется разность фаз Δφ = 2πSX/(λR), где S, Х << R, дополнительная к разности фаз φ0 между волнами, имеющей место в точке О. При φ0=π β точке Х интенсивность I(х)= 4I(S)Sin2(πSX/λR). Отсюда следует, что для диафрагмы диаметром d даже в случае полностью когерентного излучения степень когерентности оказывается меньше I:
δγ = (1-|γ изм(S)|) = (1/6)(πSd/λR)2. (3)
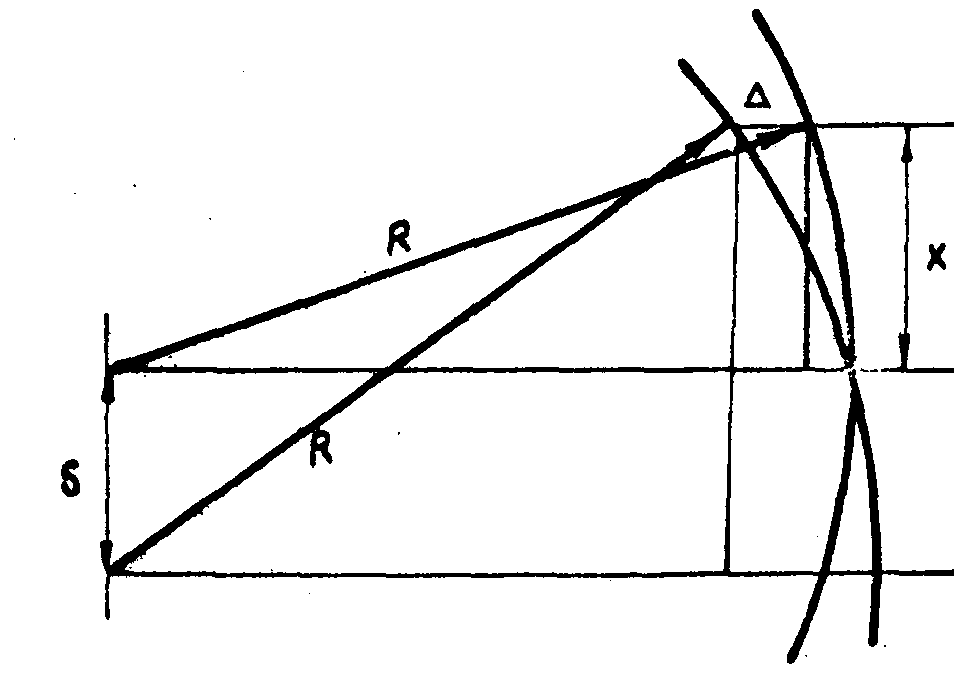
Рис.4. К расчету разности фаз интерферирующих пучков со сферическим фазовым фронтом.
Для наших экспериментов при R = 10 м, d = 20 мкм и S = 2мм δγ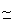 7∙10-5. В то же время для обычных условий в экспериментах со схемой Юнга R 7∙10-5. В то же время для обычных условий в экспериментах со схемой Юнга R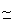 3 м, d = 0,2 мкм и δγ 3 м, d = 0,2 мкм и δγ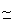 1∙10-1 при S = 2 мм. Следовательно, интерферометр Юнга дает большую систематическую ошибку при измерении γ; в этом одна из причин невысоких значений ПК в ранее выполненных экспериментах. 1∙10-1 при S = 2 мм. Следовательно, интерферометр Юнга дает большую систематическую ошибку при измерении γ; в этом одна из причин невысоких значений ПК в ранее выполненных экспериментах.
Указанные ошибки измерения |γ (S)|, приведенные: на рис.2 и 3, связаны со статистическим разбросом при многократных измерениях и соответствуют 10% точности определения Iмин.
6. Полученные отличия значений |γ (S)| от единицы отражают таким образом реальные свойства самого лазерного излучения. Излучение с частичной когерентностью всегда можно представить в виде суперпозиции полностью когерентного и некогерентного излучений /14/. Выясним природу пространственно некогерентного излучения в лазере. По аналогии с временными флуктуациями в лазере, рассмотрим модель лазерного излучения с пространственными флуктуациями в виде:
E(r;z,t)=A(r)[1+m(r)]cos[ωt-kx+φ(r;z)], (4)
где m(n) - случайный коэффициент амплитудной модуляции; φ(r) - флуктуирующая фаза, причем средние значения 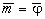 = 0.Амплитуда А(r) определяет регулярный профиль лазерного пучка: = 0.Амплитуда А(r) определяет регулярный профиль лазерного пучка:
I(r)=(cn/8π)A 2(r)=I 0exp{-(r/r 0) 2}.
Согласно (4), степень когерентности излучения между центром пучка и точкой, отстоящей от него на расстоянии S,
 . (5) . (5)
Здесь D - коэффициент диффузии фазы в поперечном сечении пучка, 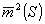 =Iнеког/I(S), Iнеког =Iнеког/I(S), Iнеког - интенсивность некогерентного излучения. Обработка результатов, приведенных в разделе 4, дает следующие значения: для обычного гелий-неонового лазера 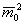 (S (S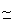 0)= 3∙10-5, Iнеког,0 = 4∙10-15 Вт/см2, некогерентная мощность излучения в пучке Рнеког,0 0)= 3∙10-5, Iнеког,0 = 4∙10-15 Вт/см2, некогерентная мощность излучения в пучке Рнеког,0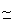 3∙10-11 Вт; для лазера с нелинейной поглощающей ячейкой 3∙10-11 Вт; для лазера с нелинейной поглощающей ячейкой 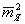 (S (S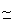 0) 0) 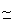 8∙10-8; Рнеког,я = 3∙10-12 Вт и Dя = 5∙10-5 см-1 8∙10-8; Рнеког,я = 3∙10-12 Вт и Dя = 5∙10-5 см-1.
Сравним подученные значения мощности пространственного некогерентного излучения в лазерах с мощностями некогерентного излучения в опытах по измерению временных флуктуации. Такое сравнение возможно провести для обычного гелий-неонового лазера, который относится к наиболее исследованным лазерам. В работе /15/ по отклонению фотостатистики лазерного излучения от пуассоновской, соответствующей излучению со стабилизированной амплитудой, было найдено 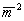 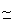 5∙10-5. Из опытов Зайцева /16/, в которых спонтанный шум лазера выделялся методом спектроскопии квадратичного детектирования, для условий нашего эксперимента 5∙10-5. Из опытов Зайцева /16/, в которых спонтанный шум лазера выделялся методом спектроскопии квадратичного детектирования, для условий нашего эксперимента 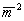 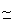 1∙10-5. Видно, что среднеквадратичные коэффициенты амплитудной модуляции лазерного излучения как во времени, так и по пространству близки. Отсюда можно сделать вывод, что природа этих флуктуации одинако- 1∙10-5. Видно, что среднеквадратичные коэффициенты амплитудной модуляции лазерного излучения как во времени, так и по пространству близки. Отсюда можно сделать вывод, что природа этих флуктуации одинако-
ва. Помимо относительного сравнения можно выполнить оценку абсолютной мощности спонтанного излучения. Для этого воспользуемся формулой (37) работы Гордона /17/. Тогда для наших условий мощность спонтанного шума в случае генерации одной продольной моды Рспонт = 4∙10-13Вт. Из эксперимента с учетом неполяризованного характера спонтанного излучения и наличия интерференционного фильтра с полосой Δλ = 20 Å перед ФЗУ получаем Рнеког,0 = 8∙10-13 Вт, следовательно, и по абсолютным величинам мощностей согласие вполне удовлетворительное.
Обратимся теперь к коэффициенту диффузии D, который ответствен за флуктуационное уширение углового спектра; приведем упрощенный вывод формулы для D. Дисперсионное уравнение (ω/v)2 = k z2 + (Δk^
)2/2kz для параксиальных пучков можно записать в квазиволновом приближения ω/v = kz + (Δk^
)2/2kz. Отсюда находим связь между угловым Δk^
и частотным Δω ρпектром (Δk^
/kz)2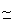 2Δω/ω, отличающуюся от строгого вывода наличием справа дополнительного коэффициента 2. Воспользуемся для Δω формулой Шавлова-Таунса, тогда 2Δω/ω, отличающуюся от строгого вывода наличием справа дополнительного коэффициента 2. Воспользуемся для Δω формулой Шавлова-Таунса, тогда
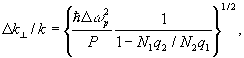 (6) (6)
где Δ ωр - частотная ширина пассивного резонатора, Р - мощность излучения лазера, N1 и N2 - населенности нижнего и верхнего рабочих уровней, qn - кратности их вырождения. Оценка углового уширения (Δk^
/kz) по формуле (6) дает 1∙10-8 и 2∙10-9, соответственно, для лазера без поглощающей ячейки и с ячейкой. В то же время из экспериментов (D0/k)=8∙10-8 и (Dя/k)=0,5∙10-9, которые по порядку величины согласуются c теоретическими оценками. Наибольшее различие экспериментальных и теоретических значений D в случае обычного лазера обусловлено, по-видимому, генерацией нескольких продольных мод. Заметим, что уширения углового спектра из-за дифракционной расходимости лазерных пучков Ω = (Δk^
/kz) = 2λ/πr0 следующее: Ω0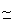 8∙10 -4 и Ωя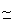 2∙10-4. 2∙10-4.
Таким образом, спонтанное изучение лазера является причиной неполной пространственной когерентности пучка н конечного значения коэффициента поперечной диффузии его фазы. Спонтанное излучение, как и в случае временных характеристик, определяет принципиально предельные (естественные) значения указанных статистических характеристик.
7. В заключении настоящей лекции кратко рассмотрим некоторые преимущества использования лазерных пучков с предельной ПК в экспериментах: по рассеянию света. Такие пучки в совокупности с поляризационным интерферометром позволяют, в частности, обойти трудности измерения коллинеарного рассеяния света.
На выходе рассеивающей среды ПК лазерного излучения равна:
|γ(S)| = [|γ p(S)| I p + I(S)]/[I(S) + I p + I неког], (7)
где Iр и γp(S) - интенсивность и корреляционная функция рассеянного излучения. Для условий эксперимента, когда Iр, Iнеког << I(S) и в интерференционной картине Iмин<<Iмакс
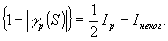 (8) (8)
Если выход рассеивающей среды спроектировать на вход регистрирующего устройства, то непосредственно измеряется значение Iр на выходе:
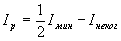 . (9) . (9)
В общем случае γ(S)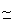 0 для смещений S≥Sпр = 0,6 λL/rn 0 для смещений S≥Sпр = 0,6 λL/rn /14/, где L - расстояние от объема рассеяния, и тогда опять измеряется прямо значение Ip. Интенсивность спонтанного излучения лазера Iнеког определяет минимально обнаружимое значение рассеянной интенсивности I р.
Были выполнены эксперименты по рассеянию лазерного излучения в нитробензоле. Под нулевым углом к падающему пучку коэффициент
рассеяния равнялся R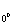 = (3,5±1,5)∙10-5 см-1; измерение интенсивности рассеяния под углом 90° дало R90° =(4±1)∙10-5 см-1 = (3,5±1,5)∙10-5 см-1; измерение интенсивности рассеяния под углом 90° дало R90° =(4±1)∙10-5 см-1.
Наконец, в экспериментах по рассеянию света нами использовалось другое преимущество, связанное в значительной мере с высококогерентными пучками, - возможность регистрации малых отличий ПК. Это обстоятельство позволяет исследовать параметры динамических систем. Кривые рис.5 показывают изменение ПК (для заданного смещения S) лазерного пучка, прошедшего через жидкий кристалл МББА, в зависимости от времени измерения, цифры у кривых указыва-

Рис.5. Зависимость ( I-|γ(S)|) для лазерного пучка, прошедшего через нематический жидкий кристалл, от времени измерения максимума и минимума в интерференционной картине; величина смещения S постоянна.
ют значение электростатического поля V в вольтах, приложенного к жидкому кристаллу. В режиме электродинамического рассеяния (при V > 9B) перегиб на кривых рис.5 соответствует среднему времени перемешивания в объеме рассеяния.
Л и т е р а т у р а
1. R.J.Collins, D.F.Nelson, A.L.Schawlow, W.Bond, C.G.Garrett, W.Kalser. Phys.Rev.Lett., 5, 707, 1960.
2. D.R.Herriot. J.Opt.Soc.Amer., 52, 31, 1962.
3. В.Г.Тункин, А.С.Чиркин. Дополнение к книге Я.Перина "Когерентность света". Мир, 1974.
4. Т.И.Смольская, Ф.Пинтер, Л.Визе, Л.Гати.
Acta physica et сhеmiса, 20, 1974 (на русском языке).
5. А.И.Ларкин, В.А.Елхов, Ю.А.Быковский. Материалы VII Всесоюзной школы по голографии, Л.,стр.260, 1975.
6. И.А.Дерюгин, В.Н.Курашов, А.Т.Мирзаев. Укр.физ.ж., 17, 944, 1972.
7. С.М.Аракелян, С.А.Ахманов, В.Г.Тункин, А.С.Чиркин. Письма в ЖЭТФ, 19, 571, 1974.
8. С.М.Аракелян, А.Г.Арутюнян, С.А.Ахманов, В.Г.Тункин, А.С.Чиркин. Квантовая электроника, 1, 215, 1974.
9. С.М.Аракелян, А.С.Чиркин, В.Б.Пахалов. Доклад на III Всесоюзн. конф. по жидким кристаллам и их применению, Иваново, 1974.
10. Д.И.Стаселько, Ю.Н.Денисик. Оптика и спектроскопия, 28, 323, 1970.
11. А.Г.Арутюнян, В.Г.Тункин, А.С.Чиркин. Квантовая электроника. №1, 111, 1973; Авторское свидетельство №421880. Официальный бюллетень, №12, стр.115, 1974.
12. В.И.Татарский. Распространение волн в турбулентной атмосфере, Наука, 1967.
13. С.М.Аракелян. Автореф.канд.дис., М., МГУ, 1975.
14. М.Борн, Э.Вольф. Основы оптики, Наука, М., 1973.
15. P.S.Magill, R.P.Soni. Phys.Rev.Letters, 16, 911, 1966.
16. Ю.И.Зайцев. ЖЭТФ, 50, 525, 1966; канд. дис., НИРФИ, Горький, 1971.
17. E.I.Gordon. Bell System Tech. J., 43, 507, 1964.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

