|
|
 |
 |

|
| |
ГОЛОГРАФИЯ В МНОГОМОДОВОМ ИЗЛУЧЕНИИ ЛАЗЕРА И.С.Клименко
Рассмотрены возможные методы голографической регистрации в многомодовом излучении лазеров. Показано, что восстановление изображений, свободных от пространственных искажений, возможно только в случае получения голограмм сфокусированных изображений при диффузном рассеянии опорного и объектного пучков. Рассмотрены теоретически процессы регистрации таких голограмм и восстановления изображений. Приводятся экспериментальные данные по уменьшению дифракционной эффективности голограмм с ростом количества генерируемых мод и сопровождающим его падением степени когерентности излучения. Объясняется приводимый характер зависимости дифракционной эффективности от модового состава излучения.
Одним из важнейших условий успешного осуществления голографического эксперимента и разработки технических устройств голографического типа является высокая степень когерентности используемых источников излучения. Хорошо известна ситуация в начале пятидесятых годов, когда из-за низкой степени когерентности существовавших тогда источников излучения надолго затормозились исследования по голографии. Своим бурным развитием в середине шестидесятых годов голография обязана появлению лазеров, которые по характеристикам когерентности значительно превосходят другие источники излучения. Сегодня лазеры являются основными источниками излучения в голографических устройствах, причем некоторые типы лазеров разрабатываются специально для целей голографии. Это обусловлено тем обстоятельством, что голография предъявляет к степени когерентности лазеров более серьезные требования, чем другие области их применения.
Суть этих требований заключается в необходимости обеспечения полной пространственной когерентности в зоне регистрация голограммы
и значительной (~1 м) длины когерентности *).
Указанные требования в значительной степени выполняются при использовании лазеров, генерирующих одну поперечную моду (обычно моду наиболее низкого порядка – ТЕМ 00). В этом случае пространственную когерентность можно считать полной, а степень временной когерентности, определяемая спектром продольных (аксиальных) мод, обеспечивает достаточную длину когерентности. Правда, в случав использования импульсных лазеров, длина когерентности не всегда бывает достаточной для осуществления голографического эксперимента, и возникает необходимость перехода к одночастотному режиму генерации (т.е. с одной поперечной и одной продольной модой). Однако осуществление одномодового, а тем более одночастотного режимов генерации связано с существенным ограничением мощности (энергии) излучения. Так, по сравнению с многомодовым режимом генерации, мощность излучения непрерывных лазеров в одномодовом режиме уменьшается в среднем в 3÷5 раз, а энергия импульсных лазеров - в 10÷50 раз. Тем не менее, голографическая регистрация в многомодовом лазерном излучении производится крайне редко, поскольку в этом случае использование обычных схем голографирования приводит к появлению в восстановленных изображениях значительных искажений (шумов). Эти искажения обусловлены тем обстоятельством, что излучение различных поперечных мод лазерного пучка практически некоррелировано, следствием чего является исключительно низкий контраст интерференционной картины в зоне наложения различных мод. В этой связи представляет определенный интерес разработка методов голографической регистрации в многомодовом излучении, обеспечивающих восстановление изображений, свободных от искажений. Кроме того, голография в многомодовом излучении в связи с обеспечением полной записи оказывается полезной при изучении характеристик когерентности реальных лазеров. В частности, новые возможности измерения характеристик временной и пространственной когерентности импульсных лазеров, изучение, модового состава излучения были продемонстрированы в работах /1-4/.
Следует отметить, что в отдельных случаях удается обеспечить
высокий контраст интерференционной картины при использовании многомодового излучения, если имеется возможность полного пространственного совмещения одноименных мод опорного и предметного пучков *). При голографировании фазовых объектов или прозрачных транспарантов без диффузного рассеяния объектного пучка совмещение модовой структуры достигается наиболее просто. При голографической регистрации в проходящем излучении с использованием диффузора в предметном пучке такое совмещение было достигнуто /5/ путем проекции диффузора на голограмму. Наконец, в случае диффузно отражающих объектов задача решается путем регистрации голограммы сфокусированного изображения, когда модовая структура на объекте воспроизводится в плоскости голограммы.
Однако во всех этих случаях в силу, неравномерного освещения объекта существенно неоднородным многомодовым пучком восстановленное изображение оказывается пространственно промодулированым в соответствии с модовой структурой пучка. При этом между модовым промежуткам соответствуют практически темные участки изображения. Очевидно, что однородное освещение объекта при использовании многомодового излучения можно обеспечить путем диффузного рассеяния предметного пучка (самим предметом или с помощью дополнительного диффузора). При этом нерассеянный многомодовым опорный пучок в зоне суперпозиции сложный образом взаимодействует с полем предметной волны - каждая пространственная составляющая этого пучка "выбирает" из однородного поля излучение, соответствующее именно этой поперечной моде, образуя стабильную интерференционную картину. Суперпозиция с излучением, соответствующим другим поперечным модам, приводит к возникновению бегущей интерференционной картины, которая усредняется за время экспозиции, давая однородный фон. В этом случае междумодовые промежутки также проявляются в восстановленном изображении в виде искажений.
Для того, чтобы обеспечить однородное распределение излучения по произвольному сечению опорного пучка, необходимо в него также ввести диффузный рассеиватель, что эквивалентно использованию про-
тяженного опорного источника. В этом случае, как известно /6/, при получении френелевских голограмм требуется с большой точностью воспроизводить исходную конфигурацию на этапе восстановления, что создает значительные неудобства.
Совершенно очевидно, что здесь целесообразно воспользоваться схемой голографии сфокусированных изображений, не требующей воспроизведения исходной геометрии в случае, когда опорный источник протяженный /7-8/. При диффузном рассеянии и опорного и объектного пучков обеспечиваются условия корреляции излучения во всей зоне суперпозиции этих пучков, что эквивалентно существованию интерференционной картине без каких-либо разрывов. Следует, правда, отметить, что контраст этой картины, как будет показано ниже, оказывается не очень высоким.
Рассмотрим процесс голографической регистрации плоского (для простоты) объекта в случае его диффузной подсветки и диффузного рассеяния плоского опорного пучка (рис.1). Запишем амплитудно-фазовое распределение в некотором сечении пучка многомодового лазерного излучения, согласно /4/ в виде
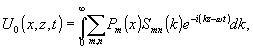 (1) (1)
где Р m(х) - амплитудно-фазовое распределение в m-ой поперечной моде; Smn(k) - амплитудно-фазовое распределение по спектру; k = 2π/λ = ω/с - волновое число.
Распределение света в пучке, прошедшем через диффузный рассеиватель и играющем роль опорного пучка, запишем в приближении малых углов, пользуясь Фурье-преобразованием, в виде
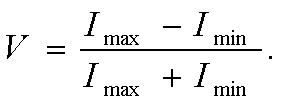 (2) (2)
Здесь ξ - координата в плоскости диффузного рассеивателя; х - координата в плоскости голограммы; z0 - расстояние между этими плоскостями; Δ(ξ)- ρлучайное изменение фаз, вносимое в пучок диффуз-
ным рассеивателем.
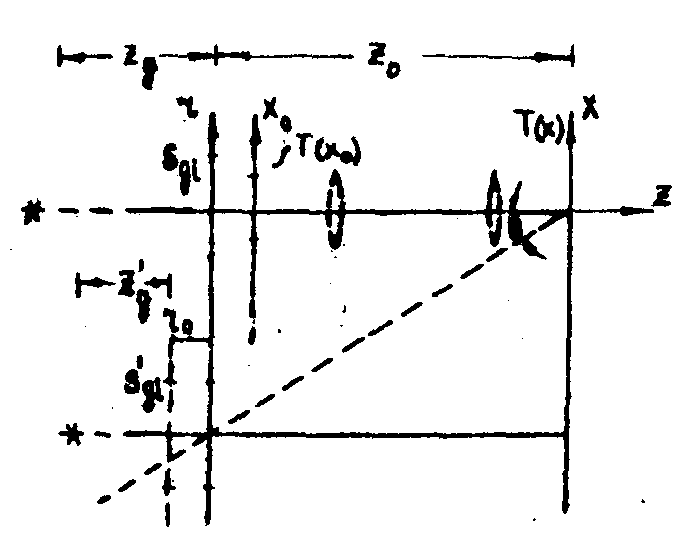
Рис.1. Схема регистрации сфокусированной голограммы с диффузной подсветкой объекта в диффузным рассеянием опорного пучка.
Объектный пучок, т.е. пучок, прошедший через диффузный рассеиватель, и объект, характеризуемый функцией амплитудного пропускания Т (x0), в плоскости голограммы формируют сфокусированное изображение, описываемое выражением
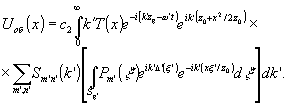 (3) (3)
Запишем интенсивность, регистрируемую сфокусированной голограммой, в обычном виде:
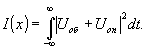 (4) (4)
Будем рассматривать только тот член амплитудной передаточной функции зарегистрированной голограммы (совпадавшей с I(х) с точно-
стью до постоянного множителя), который соответствует мнимому изображению:
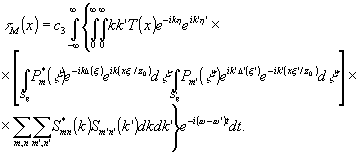 (5) (5)
Здесь η=z0+(x 2/2z 0)-z g и η'=z0+(x2/2z0)-z'g -длины оптических путей интерферирующих пучков.
Упростим (5), пользуясь выражением для дельта-функции,
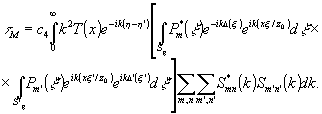 (6) (6)
Если принять во внимание, что для большинства лазеров спектры различных мод не перекрываются и, кроме того, k0 – k ≤ k0 (где k0 - среднее значение волнового числа излучения, используемого при голографировании), а вносимые диффузным рассеивателем изменения фазы малы, т.е. 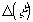 <λ θ <λ θ 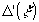 <λ, ςо (6) можно свести к виду: <λ, ςо (6) можно свести к виду:
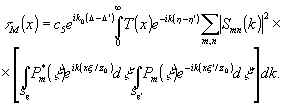 (7) (7)
Здесь множители k2≈k02 и еikΔ≈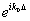 вынесены за знак интеграла по k. вынесены за знак интеграла по k.
Как известно /9/, функция 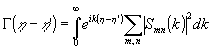
пропорциональна функции временной когерентности источника и не зависит от х. Поэтому, заменяя интегрирование по площади диффузных ра ccеивателей интегрированием по бесконечным пределам, представим (7) в виде
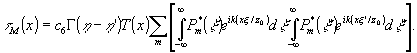 (8) (8)
Выражение в квадратных скобках представляет собой произведение двух фурье-образов. Воспользуемся символической записью Фурье-преобразования и перепишем (8) в виде
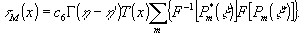 (9) (9)
Нетрудно показать, что
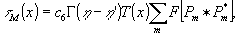 (10) (10)
где 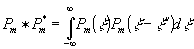 - функция автокорреляции. В соответствии со смыслом операции автокорреляции фурье-образ функции автокорреляции представляет собой постоянную функцию координаты, т.е. - функция автокорреляции. В соответствии со смыслом операции автокорреляции фурье-образ функции автокорреляции представляет собой постоянную функцию координаты, т.е.
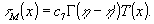 (11) (11)
Наконец, примем во внимание, что функция временной когерентности Г(η -η') не зависит от х, а значит, не оказывается пространственной модуляции светового поля, тогда
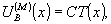 (12) (12)
т.е. восстановленное изображение характеризуется распределением амплитуд, пропорциональным амплитудному пропусканию объекта.
Таким образом, диффузное рассеяние опорного пучка, обеспечивающее квазиоднородное распределение излучения всех поперечных мод в плоскости голограммы, позволяет зарегистрировать интерференцион-
ную картину во всему полю, вследствие чего восстановленное изображение оказывается свободным от характерных для случая голографирования в многомодовом излучения помех.
Эксперименты по регистрации в многомодовом излучении голограмм сфокусированных изображений с диффузным рассеянием опорного и объектного пучков /8/ полностью подтвердили выводы теории. Для восстановленных изобретений характерным оказалось полное отсутствие помех, в то время как голограммы, зарегистрированные в тех же условиях без .диффузного рассеяния формировали существенно искаженные изображения.
Интересно, что в случае регистрации без диффузного рассеивателя квазиосевых голограмм интенсивностей /8/ их качество (в силу отсутствия опорного пучка) практически не зависит от подового состава излучения. Диффузная подсветка объекта в этом случае приводит лишь к увеличению яркости восстановления, что обусловлено их физической природой /10/. С увеличением числа поперечных мод в излучения лазера на этапе регистрации голограммы в силу изменения степени когерентности имеет место уменьшение дифракционной эффективности внеосевого изображения при восстановлении как в монохроматическом, так в в белом свете. Характер зависимости дифракционной эффективности от модового состава излучения иллюстрируется рис.2 /8/. В эксперименте изменение модового состава осуществлялось путем варьирования размера диафрагмы лазерного резонатора. В случае получения голограмм диффузно отражающего объекта дифракционная эффективность уменьшается с 4,5% (что соответствует генерации одной поперечной моды) до 0,6% при полном открытии диафрагмы резонатора.
Такой ход экспериментальной кривой хорошо согласуется с данными об уменьшении когерентности лазерного излучения с ростом количества генерируемых мод. Как известно, дифракционная эффективность голограммы линейно связана с контрастом зарегистрированной ею интерференционной картины или с видностью наблюдаемых интерференционных полос, которая определяется простой формулой:
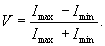 (13) (13)
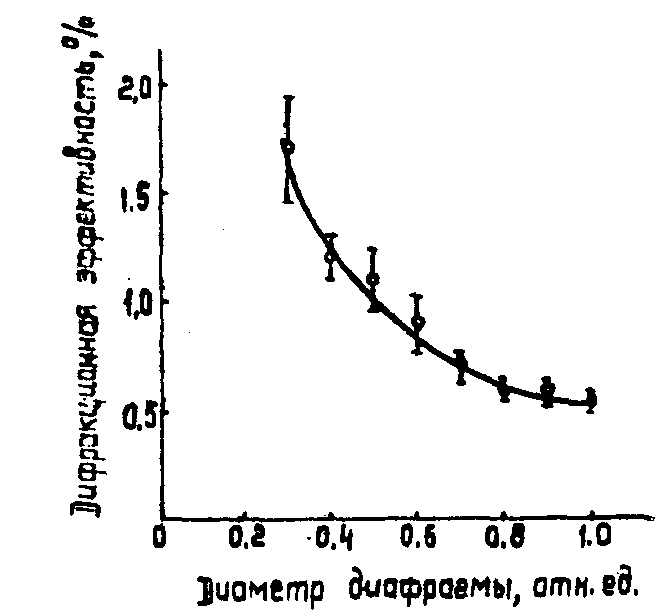
Рис.2. График зависимости дифракционной эффективности от размера диафрагмы, регулирующей модовый состав излучения.
Интенсивность интерференционной картины обычно определяется как
I=I1+I2+2Re[<V1V2>], (14)
где V1, V2 - комплексные векторы амплитуда интерферирующих волн, а скобки < > означают усреднение по времени. Усредненное по времени значение интерференционного члена (третье слагаемое (14)) выражается через комплексную степень когерентности, которая определяется как нормированная корреляция между V1 и V2.
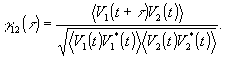 (15) (15)
Тогда
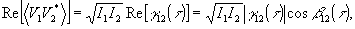 (16) (16)
где β12(τ) - τаза величины γ12(τ).
Отсюда нетрудно показать, что
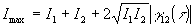
при cosβ12 = 1 и
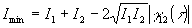
при cosβ12 = -1.
Подставим значения Imax и Imin в (13), тогда
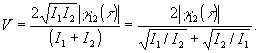 (17) (17)
Следовательно, при I1=I2
V=|γ 12(τ)|.
Кроме того, видность полос, как известно, зависит от угла между направлениями поляризации интерферирующих пучков.
В эксперименте, о котором шла речь выше, излучение, соответствующее различным поперечным модам, равномерно распределено по пространству и о помощью телескопической оптической системы из него выделялся достаточно узкий пучок. Эта ситуация эквивалентна наличию одной поперечной моды с большим количеством продольных мод, поэтому условие пространственной когерентности интерферирующих пучков оказывается обеспеченный, и стабильная интерференционная картина существует во всей зоне суперпозиции опорного и объектного пучков. Следовательно, вместо степени когерентности |γ12(τ)| следует рассматривать только степень временной когерентности |μТ(τ)|.
Воспользуемся известной формулой, связывающее видность со степенью временной когерентности /11/.
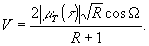 (18) (18)
Для голографии сфокусированных изображений оптимальным является соотношение интенсивностей интерферирующих пучков R=1, это значение R и вздергивалось в эксперименте. Для лазерного излучения обеспечивается также значение cosΩ=1.
Таким образом, в нашем случае видность интерференционной кар-
тины, а с нею дифракционная эффективность голограммы однозначно определяются степенью временной когерентности:
V=|μ T(τ)|.
Как известно / 11/, степень временной когерентности лазера, генерирующего N продольных мод, описывается выражением
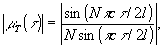 (19) (19)
где l - длина лазерного резонатора.
Легко видеть, что функция |μT(τ)| является периодической, причем имеет ряд главных максимумов, равных единице. Интересно построить зависимость функции временной когерентности от количества генерируемых продольных мод, когда параметром является оптическая разность хода ΔL=cτ (с - скорость света).
График такой зависимости /12/ приведен на рис.3*). Функция |μT(τ)| при ΔL=const также является периодической, но с единственным главным максимумом, равным единице, который соответствует генерации одной продольной моды (одночастотный режим).
Для реального лазера степень временной когерентности с ростом количества мод уменьшается монотонно, т.е. функция |μT(τ)| может быть представлена с помощью огибающей построенной периодической функции. Это объясняется тем, что разности хода различных пар интерферирующих лучей при получении голограммы неодинаковы, а малые отклонения величины ΔL от значения, взятого в качестве параметра, приводят к сдвигам максимумов в построенной кривой, т.е. к осреднению их в виде огибающей.
С этой огибающей (сплошная кривая) с высокой точностью совпадают экспериментальные точки графика зависимости нормированной к единице дифракционной эффективности относительного размера диафрагмы лазерного резонатора, определяющей количество генерируемых мод. За единицу принято максимальное значение дифракционной эффек-
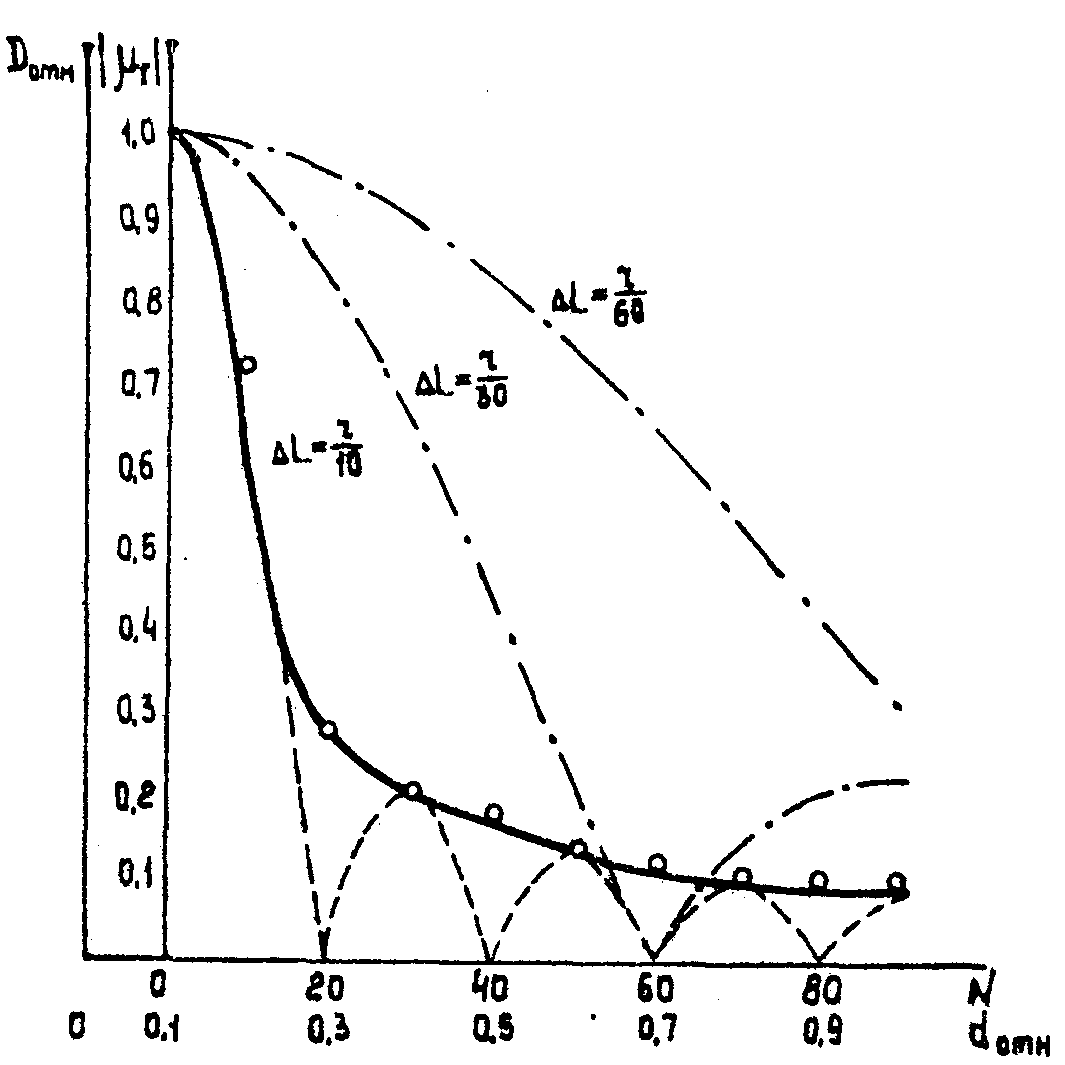
Рис.3. Совмещенные графики зависимости степени временной когерентности от количества генерируемых мод (теория) и относительной дифракционной эффективности от размеров диафрагмы лазерного резонатора (экспериментальные точки).
тивности, достигаемое в случае плоской голограммы в равное, как известно, 6,25%. Масштабы двух совмещенных графиков легко подобрать на основе данных относительно предельного количества мод, генерируемых гелий-неоновыми лазерами.
Таким образом, наблюдаемая закономерность изменения дифракционной эффективности голограмм, регистрируемых при диффузном рассеянии обоих интерферирующих пучков, от кодового состава излучения хорошо согласуется с данными об уменьшении видности (контраста) интерференционных полос вследствие уменьшения степени временной когерентности излучения.
На основе измерения дифракционной эффективности голограмм, как нетрудно видеть, модно получить информацию о значении функции временной когерентности, а также о количестве продольных и поперечных мод в излучении лазеров.
Л и т е р а т у р а
1. M.Lurie J. Opt.Soc, Am., 58, 614, 1968.
2. С .С. Aleksoff. J.Opt.Soc. Am., 61, 1426, 1971.
3. Д.И.Стаселько, Ю.Н.Денисюк, А.Г.Смирнов. Оптика и спектр, 26, 413, 1969.
4. Д.И.Стаселько, Ю.Н.Денисюк. Оптика и спектр, 28, 323, 1970.
5. R.E.Brooks, L.Heflinger, I.O.Wuerker, IEEE. J.Quant. Electr. 2, 275, 1966.
6. А.Л.Макаэлян, В.И.Бобринев, Э.Х.Гуланян, Г.Н.Акимова. Сб. "Квантовая электроника", вып.1, 143, 1971.
7. И.С.Клименко, Е.Г.Матинян. Оптика и спектр, 31, 471, 1971.
8. И.С.Клименко, Е.Г.Матинян, Г.В.Скроцкий. Оптика и спектр, 33, 1139, 1972.
9. М.Борн, Э.Вольф. Принципы оптики. Изд. "Наука", М., 1970.
10. И.С.Клименко, Е.Г.Матинян, Г.В.Скроцкий. ДАН СССР, 211, 571, 1973.
11. Р.Кольер, К.Беркхарт, Л.Лин. Оптическая голография. Изд. "Мир", М., 1973.
12. И.С.Клименко, Е.Г.Матинян, Г.В.Скроцкий. Квантовая электроника, 3, 1976.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

