ИССЛЕДОВАНИЕ КОНЦЕНТРАЦИИ НАПРЯЖЕНИЙ В КОМПОЗИЦИОННЫХ МАТЕРИАЛАХ МЕТОДОМ СПЕКЛ-ИНТЕРФЕРОМЕТРИИ
Е.Е.Гайдачук, А.А.Капустин, А.А.Россоха
Сопоставляются выражения для интенсивности "безопорной" голографии сфокусированных изображений и голографии с наклонным опорным пучком. Подтвержден вывод о том, что при формировании низкочастотной пространственной структуры в голографии сфокусированных изображений роль протяженной опорной волны для каждого элементарного изображения играет совокупность всех остальных изображений.
Анализируются результаты исследования полей деформаций, полученных различными методами голографической интерферометрии. Делается вывод о целесообразности применения спекл-интерферометрии при исследовании полей деформаций в тонких пластинах и оболочках из композиционных материалов.
В качестве примера приводятся результаты спекл-интерферометрических исследований распределения деформаций в плоском образце из стеклопластика, которые сравниваются с теоретическим решением.
В настоящее время все более широкое применение в несущих элементах конструкций находят композиционные материалы типа стекло-, угле-, боро- и органопластикой.
Из-за существенной разницы в механических свойствах составляющих композит материалов актуальными являются вопросы механического взаимодействия матрицы и арматуры. Существующие теоретические зависимости, описывающие деформации в волокнах и связующей элементе, например /1/, не проверены экспериментально, причем тради-
ционными методами (с помощью тензометрии, поляризационно-оптическим, Муара, сеток и другими) проверить их, не моделируя структуру материала, невозможно ввиду малых расстояний между армирующими элементами и большими базами измерения деформаций.
Анизотропность композиционных материалов вызывает особые трудности при теоретическом описании полей деформаций вблизи концентраторов. Достаточно сказать, что в настоящее время неизвестно теоретическое определение поля деформаций вблизи круглого отверстия в растягиваемом анизотропном плоском образце, когда его ширина соизмерима с диаметром отверстия. Экспериментально установить концентрацию напряжений в элементах конструкций из композиционных материалов с достаточной точностью вблизи сложных вырезов или ослаблении традиционными методами измерения деформаций также не представляется возможным в силу указанных выше причин.
Теории, учитывающие ряд других особенностей композитов, также часто остаются экспериментально не проверенными в силу большей базы и контактности традиционных методов измерения деформаций.
Таким образом, голографическая интерферометрия и особенно те ее способы, с помощью которых можно измерять деформации достаточно точно, просто и не малых длинах, позволяют решить ряд насущных проблем механики композиционных материалов.
С помощью классической схемы голографической интерферометрии методом двойной экспозиции нами получена интерференционная картина, характеризующая пространственные смещения точек образца из стеклопластика при одноосном растяжении (рис.1). Ввиду малой жесткости образца из плоскости, небольшой эксцентриситет в приложении нагрузки, неизбежно на практике, приводит к смещениям точек поверхности образца из плоскости. Однако эти смещения, сравнимые со смещениями, вызванными деформациями в плоскости, практически не приводят к возникновению напряжений. Поэтому при исследовании деформаций тонких пластин и оболочек, из которых в основном состоят конструкции летательного аппарата, смещения точек поверхности из плоскости при определении деформаций
и напряжений необходимо исключать как ненужные из величин смещений в пространстве. Поэтому для исследования полей деформаций в тонких элементах конструкций целесообразно использовать спекл-интерферометрию, в которой смещения из плоскости автоматически исключаются, так как опорный и объектный пучки проходят один и тот же оптический путь.
Рис.1. Полосы равных смещений в пространстве на образце из стеклопластика.
1.
К теории образования спекл-структуры
В самом деле, в работах /2-4/, посвященных "безопорной" голографии сфокусированных изображений, для интенсивности в плоскости регистрирующей апертуры получено выражение:
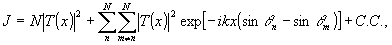(1)
где N - число плоских волн. формирующих изображение; T(х
n) -
функция амплитудного пропускания (отражения) объекта; k=2π/λ - волновое число; θn - угол между направлением падения n-oй плоской волны в нормалью к плоскости записывающей апер-
туры.
Первое слагаемое (1) описывает регистрируемое негативное изображение, а второе - низкочастотную пространственную структуру (спекл-структуру), возникающую в результате интерференции пространственных составляющих диффузно рассеянной волны.
На основе анализа выражения (1) в работах /2-4/ делается вывод о том, что для каждого элементарного изображения роль протяженной опорной волны играет совокупность всех остальных изображений.
Для подтверждения этого вывода, а также для анализа и сопоставления процессов формирования голографической структуры в голографии с опорным пучком и в голографии сфокусированных изображений (в том числе и "безопорной"), целесообразно получить выражение интенсивности для более общего случая голографического эксперимента.
Пусть волновой фронт, отраженный при облучении плоской когерентной волной оптически неровного объекта "О", необходимо записать голографическим методом на регистрирующую пластинку р, помещенную в плоскости (х,у) на расстоянии
R от плоскости расположения исследуемого объекта (х',у') (рис.2). Согласно принципу Гюйгенса-Френеля, полное поле, распространившееся на
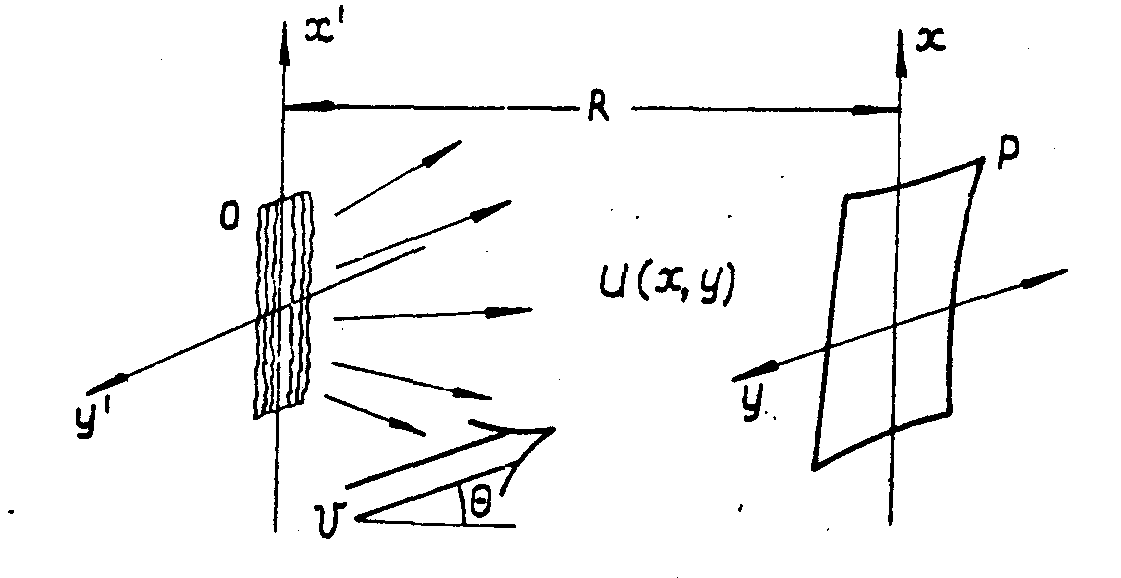
Рис.2. Схема голографии с опорным пучком.
регистрирующую пластинку от объекта, может быть записано как
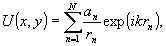(2)
где а
n - некоторая постоянная, зависящая от n; rn - расстояние между точечным излучателем n и записывающей апертурой; k=2π/λ - волновое число; N - число излучателей; величина an/rn - функция амплитудного отражения (пропускания) объекта, учитывающая структуру поверхности.
Опорный пучок, направленный на апертуру записи, можно представить. в виде
V(x,y) = bexp(ikx sinθ),
(3)
где
b - постоянная. Тогда суммарная амплитуда в плоскости фотопластинки будет равна:
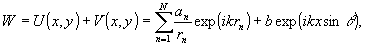(4)
а интенсивность после ряда преобразований запишется в виде
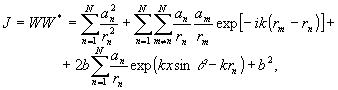(5)
Сопоставляя зависимости (1) и (5) можно заметить подобие между первым и вторым членом формулы (1) и первым и вторым слагаемым, соответственно, выражения (5). Действительно, первый член последнего выражения также описывает регистрируемое негативное изображение, а второй - низкочастотную пространственную структуру (спекл-структуру). Третий член выражения (5) описывает голографическую интерференционную структуру, причем в отсутствии опорной волны (
b=0) третий и четвертый (равный интенсивности опорного пучка) компоненты становятся равными нулю.
Выражение (5) не учитывает высокие порядки
пространственных частот, ввиду представления объектного пучка (2) набором плоских волн, при малых
rn. rn для всех n не может быть одновременно равен нулю из-за шероховатости диффузно отражающих объектов, так как случай малых rn соответствует регистрации изображения в сфокусированной области. Неучет дифракции высших порядков на диффузно отражающем объекте при малых rn соответствует ограниченной апертуре фокусирующей системы в голографии сфокусированных изображений.
Если
b = 0, а rn достаточно малы, то выражение (5) описывает формирование голографической структуры в "безопорной" голографии сфокусированных изображений. Для более общей схемы с опорным пучком (рис.2) выражение (5) справедливо только при достаточно больших rn, так как в противном случае на фотопластину фиксируются не только низшие пространственные частоты, как принято при выводе зависимости (5).
Таким образом, из анализа выражения (5) следует, что спекл-структура, описываемая вторым членом этого выражения, присутствует на всех видах голограмм более или менее ярко выраженной, причем, во всех случаях, для каждого элементарного изображения (или точечного излучателя на диффузно отражающем объекте) роль опорной протяженной волны играет совокупность всех остальных изображений (излучателей).
Вид спекл-структуры, сфотографированной с помощью микроскопа при увеличении в 600 раз, приведен на рис.3.
Рис. 3. Спекл-структура восстановленного голографического изображения.
2.
Спекл-интерферометрическое исследование распределения
деформаций в образцах из композиционных
материалов
Ни рис. 4 показана схема эксперимента, реализованная в созданной нами на базе комплекта СИН установке. Расшифровка голограмм, полученных по схеме рис.4 методом двойного экспонирования, производилась путем определения дифракционного угла по интерференционной картине на специальном экране при сканировании луча по негативному изображению образца на "безопорной" голограмме сфокусированных изображений.
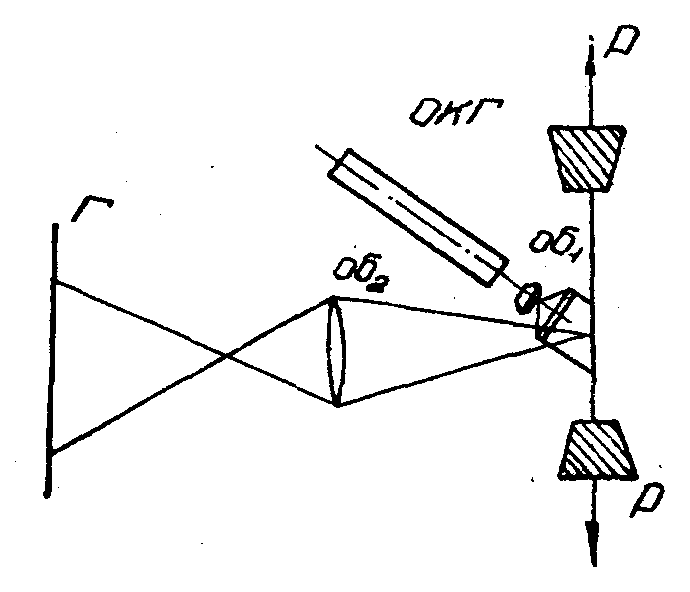
Рис. 4. Схема спекл-интерферометрического эксперимента.
Исследованы поля деформаций в образцах из нескольких конструкционных композитов с различными концентраторами (отверстия, сложные вырезы, надрезы и т.д.) при освещении объекта как сферическим, так и плоским фронтом волн. Наличие в схеме рис.4 линзы, коллимирующей освещающий объект пучок, оказалось не обязательным, так как в обоих случаях (при освещении сферическим и плоским фронтом волн) качество спекл-картины было одним и тем же, а соответствующие величины смещений совпадали.
В качестве примера здесь представлены результаты исследования поля деформаций в образцах толщиной 5 мм шириной 20 мм из материала КАСТ-В с двухсторонними надрезами (каждый глубиной 6 мм) с радиусом закругления в вершине
b/2 = 0,5 мм при одноосном растяжении вдоль основы материала. Для теоретического описания поля деформаций в таком образце используется аппарат Колосова-Мусхелишвили. Распределение продольных деформаций εх в образце между вершинами надрезов, например, найдено в виде
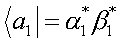(6)
Здесь
k - определяется из условия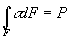 
, где р - площадь в рассматриваемом сечении, Р - действующая на образец продольная сила; r - расстояние от вершины ближайшего надреза до рассматриваемой точки c напряжением σ; Еx - модуль упругости материала вдоль растяжения.
На рис.5 приведено распределение деформации
εx между надрезами, установленное экспериментально - кривая 1 и соответствующее формуле (6) - кривая 2.
Значения смещении и определялись по формуле:
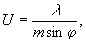(7)
где
m - коэффициент увеличения объекта 2 на схеме рисунка 4; λ - длина волны используемого излучения, φ - угловое расхождение интерференционных полос на экране. Компоненты смещения- Ux и Uy определялись по формулам:
Ux
= Ucosα, Uy = Usinα, (8)
где
α - угол между осью х негативного изображения образца на голограмме и направлением полного смещения рассматриваемой точки образца, совпадающим с нормалью к интерференционным полосам на экране. Здесь уместно отметить, что, поскольку α с экрана можно определять с точностью до слагаемого кратного π,
то направление смещения и деформации определяются с точностью до знака. Истинный знак деформации возможно установить, если на "безопорной" голограмме сфокусированных изображений отображена точка, направление смещения или знак линейной деформации в которой
известны заранее.
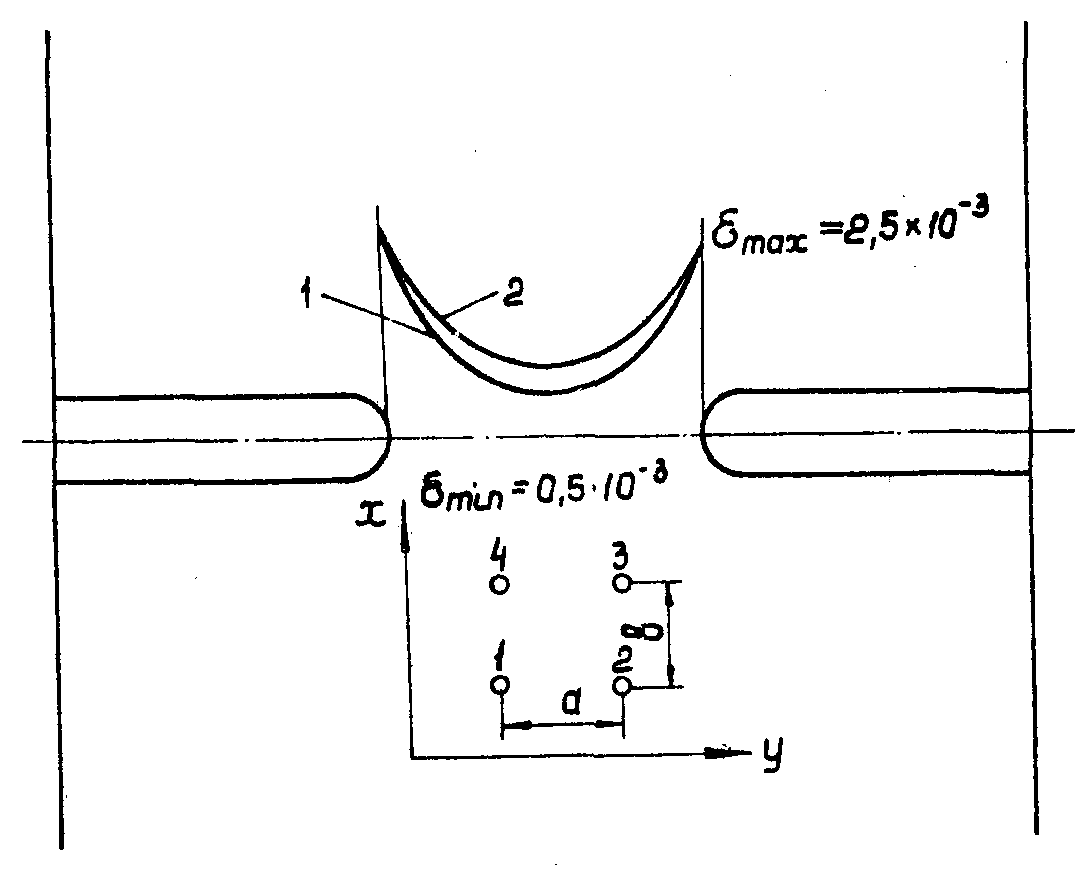
Рис.5. Распределения продольной деформации между
надрезами в растягиваемом
стеклопластиковом образце.
Теоретическая кривая - 2 и экспериментальная кривая - 1.
Линейные деформации между точками образца 1-4 (рис.5) εх и 1-2 - εу определялись по формулам:
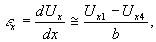
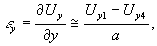(9)
а сдвиговые деформации - γху в плоскости х-у на площадке между точками-1-2-3-4 по формулам:
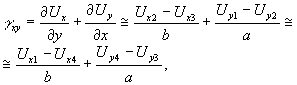(10)
или с большей статистической достоверностью:
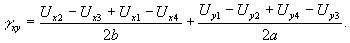(11)
В приводимом здесь примере величины
εу и γ
ху оказались значительно меньше, чем величина ε
х.
Значения деформаций вдали от концентраторов, полученные спекл-интерферометрическим методом, удовлетворительно совпадал с деформациями, полученными с помощью тензометрирования. При этом применялись датчики типа ПКБ (ПКБ-10, ПКБ-20) с базами 10 и 20 мм.
Деформации вблизи концентратора измерялись на базах 0,5÷1 мм, что достигалось при
m≥3 на стадии записи и диаметре сканирующего луча 1 мм при расшифровке. Средняя погрешность измерения деформации εх на базе 1 мм составляла 15% и была прямо пропорциональна величине базы в широком интервале изменения последней, так, например, базе 5 мм соответствовала средняя погрешность - 3%.
При больших градиентах деформаций картина интерференционных полос на экране при расшифровке размывается. Замечено, что этот эффект, снижавший точность измерений, ослабевает, если применять большие оптические увеличения на стадии записи и лазерный луч малого диаметра при расшифровке.
Смещения исследуемого объекта из плоскости в процессе записи не влияли в проведенных экспериментах на точность измерения деформаций, если не приводили к существенному нарушению фокусировки объекта. Частичная прозрачность некоторых композитов в свойство зеркально отражать падающие лучи приводят к падению
точности измерения смещений и деформаций образцов из таких композиционных материалов по сравнению с аналогичными образцами из металлов и сплавов, если не применять специальные меры, повышающие диффузность освещения объекта или увеличивающие диффузность самой поверхности.
Замена расшифровки спекл-голограмм по интерференционным полосам на экране на расшифровку методом оптической фильтрация (с получением полос равных смещений) приводило к значительному падению точности измерения деформаций, невозможность простыня способами определить сдвиговые деформации и не давало возможности значительно уменьшать базы измерения деформаций.
В заключение следует отметить, что такие свойства, как простота, надежность, точность, небольшая трудоемкость (при автоматизированной расшифровке), нечувствительность к смещениям из плоскости и вибрациям объекта, а также к перемещениям лазера, практически неограниченные (сколь угодно малые) базы измерения деформаций и большой объем информации о поле деформаций на малом материальном носителе, что присуще методу спекл-интерферометрии, делают особо перспективным его применение для исследования полей деформаций в композитах, в местах сильной концентрации напряжений и в тонких элементах конструкций.
Л и т е р а т у р а
1. Г.А. Ван Фо Фы. Конструкции из армированных пластмасс. Киев, "Техника", стр. 220, 1971.
2. И.С.Клименко, Е.Г.Матинян, Г.В.Скроцкий, ДАН СССР, 211, 571, 1973.
3. И.С.Клименко, Г.В.Скроцкий , УФН, 109. вып.2, 269, 1973.
4. И.С.Клименко, Г.В.Скроцкий, Материалы
VI Всесоюзной школы по голографии, Л., стр.355, 1974.
