Media-security

НЕКОТОРЫЕ ВОПРОСЫ ГОЛОГРАФИЧЕСКОЙ ИНТЕРФЕРОМЕТРИИ Н.Г.Власов, А.Е.Штанько

Лекция является продолжением сделанного на предыдущей школе обзора по современному состоянию и задачам голографической интерферометрии. Рассмотрены следующие вопросы голографической интерферометрии диффузно-отражающих объектов: интерференционные измерения по изменению микроструктуры голограммы; расчет интерферограмм при неизвестных порядках интерференционных полос; предельно достижимая точность измерения и снижение требований к когерентности источников освещающего излучения.

1. Интерференционные измерения по изменению

микроструктуры голограммы

Голограмма сфокусированного изображения для прозрачного фазового объекта практически идентична обычной интерферограмме этого же объекта, полученной при настройке интерферометра на полосы конечной ширины. Единственное (и не принципиальное) отличие заключается в том, что период интерференционных полос на голограмме примерно на порядок больше. Таким образом, для рассматриваемого случая можно считать, что классическая интерферограмма составляет микроструктуру голограммы. Существенно, что пространственная структура интерферограммы носит регулярный характер, что позволяет исследовать указанные объекты методами как классической, так и голографической интерферометрии.

При переходе к диффузно-когерентному излучению (когерентному лазерному излучению, рассеянному диффузно отражающим объектом), его интерферограмма, а следовательно, и микроструктура голограммы существенно изменяется, принимая случайный по пространственным координатам характер /1,2/. Именно это обстоятельство послужило, по-видимому, причиной хорошо известного утверждения о том, что

методы классической интерферометрии неприменимы к диффузно-отражающим объектам и они могут быть исследованы только методами голографической интерферометрии.

Покажем, что в некоторых частных случаях упомянутое ограничение недействительно. Рассмотрим отдельный элемент случайной зернистой структуры, характерной для диффузно-когерентного излучения. Простой эксперимент с наложением опорного волнового поля показывает, что внутри каждого такого элемента фаза остается практически постоянной, резко изменяясь на границе между элементами. Результат этого эксперимента можно объяснить следующим образом. Как отмечалось в нашей лекции на предыдущей Школе, функция взаимной когерентности для диффузно-когерентного излучения, введенная усреднением по пространству, совпадает с функцией взаимной когерентности для теплового излучения, введенной усреднением по времени. Последняя, как известно, в плоскости изображения совпадает с трехмерным распределением комплексной амплитуды вблизи фокуса /3/, причем ее фазовая часть является именно такой, какой она и наблюдается в описанном эксперименте, так как средний размер отдельных элементов зернистой структуры и определяет область когерентности диффузно-когерентного излучения. Таким образом, внутри каждого отдельного элемента случайной зернистой структуры фаза постоянна, и можно пользоваться методами классической интерферометрии, т.е. исследовать объект в реальном масштабе времени, не записывая предварительно голограмму.

Оптические схемы, реализующие изложенный метод, в принципе, аналогичны схемам интерферометров. Отличие состоит в том, что для настройки на полосы конечной ширины необходимо, чтобы период интерференционных полос при настройке был меньше средних размеров отдельных элементов случайной зернистой структуры. Названное условие выполняется, если угол между объектным и опорным волновыми полями больше или апертуры оптической системы, переотображающей объект (в варианте голографии сфокусированных изображений), или угловых размеров объекта (в варианте голографии Френеля).

Оценим теперь область применения метода. Кроме определения величины смещения объекта, как единого целого, его целесообразно применять тогда, когда требуется проследить за смещением только

нескольких точек на поверхности объекта. Такие задачи возникают, например, при отбраковке изделий по максимальной величине смещения в отдельных заданных точках поверхности.

Рассмотрим, по аналогии, описанный метод на различные варианты интерференционных измерений, основанные на пространственной корреляции интенсивности в диффузно-когерентном излучении.

В работах /4-6/ было предложено получать интерферограммы, дважды фотографируя исследуемый объект, до и после приложения деформирующей нагрузки, причем, согласно /4/, объект освещался по двум различным направлениям, а в другом варианте /5,6/ фотографировался фактически по двум направлениям за счет использования диафрагмы, содержащей два отверстия, расположенных на некотором расстоянии друг от друга. Оба варианта применяются для определения проекций вектора перемещения, перпендикулярных оптической оси фотографирующей системы. Анализ литературных данных показывает, что методы, аналогичные предложенным в /4-6/, но использующие для измерений изменение микроструктуры голограммы (в данном случае голограммы интенсивности), уже существуют. Они рассмотрены в работе /7/ в приложении к исследованию вибраций диффузно-отражающих объектов.

В работе /8/ предложен метод интерференционных измерений, объединяющий достоинства обоих вариантов метода /4-6/ - чувствительность и точность. Исследуемый объект и освещался и фотографировался по двум направлениям, а за счет использования поляризованного света и оптических элементов типа поляризатор - анализатор из четырех волновых полей (два освещающих и два отраженных) выделялись два, между которыми были максимальные углы, что и обеспечивало максимальную чувствительность. Вариант этого метода, основанный на непосредственной регистрации изменений микроструктуры голограммы интенсивности, был применен нами при определении модуля упругости некоторых материалов, полученная чувствительность составляла 0,2 мкм на интерференционную полосу.

Следующим методом интерференционных измерений в диффузно-когерентном излучении является сдвиговая интерферометрия диффузно-отраженных объектов /9,10/. Соответствующий "микровариант" описан в /11/ где он применен, однако только для определения смещения

объекта как единого целого в направлении, перпендикулярном его поверхности. В общем же случае сдвиговая интерферометрия применяется для определения деформации поверхности исследуемого объекта.

Наконец, последний вариант интерференционных измерений в диффузно-когерентном излучении - это сравнение различных диффузно-отражающих объектов по размерам и форме /12,13/, предложенный для контроля всей поверхности изделия за счет сравнения с образцовым изделием. Его "микровариант", позволяющий поточечно сравнивать отличие в размерах и форме или отличие в деформациях, может найти применение только в некоторых специальных случаях.

2. Расчет голографических интерферограмм при неизвестных

порядках интерференционных полос

Метода, с помощью которых в настоящее время осуществляется расшифровка голографических интерферограмм, можно разделить на две основные группы.

1. Методы, основанные на идентификации порядковых номеров интерференционных полос, наблюдаемых на восстановленном изображении объекта по нескольким различным направлениям и решении системы из трех линейных уравнений относительно неизвестных проекций вектора смещения /14,15/.

2. Методы, основанные на подсчете числа интерференционных полос, пересекающих исследуемую точку на восстановленном изображении объекта при изменениях направления наблюдения и решении соответствующей системы линейных уравнений /16/.

Достоинством первых является возможность интерференционных измерений со сравнительной невысокой погрешностью по нескольким низкоапертурным голограммам. Однако, для идентификации порядковых номеров интерференционных полос необходимо иметь на восстановленном изображении полосу с известным порядковым номером, что ограничивает возможности метода. Указанная трудность обходится в методах второй группы, оперирующих с разностями порядковых номеров интерференционных полос, однако необходимость непрерывного наблюдения восстановленного изображения при переходе от одного направления к другому, а также большая погрешность измерений при малых

углах между этими направлениями /17/ требуют записи высокоапертурных голограмм. Кроме того, процесс измерений является трудоемким и трудноавтоматизируемым. Опишем метод расшифровки, объединяющий достоинства указанных методов и состоящий в следующем.

Для каждой пары точек i и j объекта, в которых рассчитываются проекции векторов перемещения 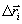, , 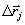составляется уравнение вида

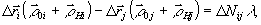(1)

где 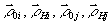- единичные векторы по направлениям освещения и наблюдения для точек i и j, ΔN_ij - число интерференционных полос, укладывающихся между точками i и j при наблюдении восстановленного изображения с какого-либо определенного участка голограммы. Пусть число исследуемых точек на объекте равно n, тогда число линейно не зависимых уравнений вида (1) равно n-1, общее число неизвестных – 3n (по три проекции вектора перемещения в каждой точке). Поскольку для измерения величин ΔN_ij не требуется высокоапертурной голограммы, можно записать m отдельных низкоапертурных голограмм. Система уравнений вида (1) имеет решение для m и n≥4. Представляет интерес вариант, когда n>4. Тогда указанная система становится избыточной, что дает возможность повышения точности измерений. Таким образом, оперируя лишь с разностями порядков интерференционных полос по данным, полученным с четырех низкоапертурных голограмм, можно осуществить расчет на ЭВМ смещений исследуемых точек объекта. Оценка возможностей предложенного метода расшифровки была проведена нами с помощью ЭВМ на модельных математических экспериментах. В результате было установлено, что точность измерения смещений растет с увеличением угловых размеров объекта α по отношению к точкам наблюдения угла β между средними направлениями наблюдения объекта и, как и ожидалось, с увеличением числа исследуемых точек на объекте. Для примера приведем следующие данные: при α~35°, β~70÷90°, n=20 и погрешности в определении чисел ΔN_ij равной 0,15, погрешность определения искомых проекций вектора смещения имеет величину ~ 0,1 мкм, причем последняя падает приблизительно как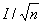

с ростом n. Таким образом, предложенный метод позволяет осуществлять расчет голографичеcких интерферограмм со сравнительно высокой точностью.

3. К оценке предельно достижимой точности в

голографической интерферометрии отражающих объектов

В нашей лекции на предыдущей Школе была проведена оценка погрешности голографических интерференционных измерений диффузно-отражающих объектов. Перечисленные там источники погрешностей, носящие аппаратурный характер, имеют место и в методах, изложенных в первом разделе настоящей лекции.

Однако, в отличие от классической интерферометрии, в интерферометрии диффузно-отражающих (рассеивавших) объектов возникает погрешность, обусловленная случайным по пространственным координатам характером распределения амплитуда и фазы диффузно-когерентного волнового поля, которая является неустранимой даже при исключении аппаратурных погрешностей и накладывает принципиальные ограничения на предельно достижимую точность интерференционных измерений в диффузно-когерентных волновых полях.

Действительно, при взаимном смещении двух даже полностью идентичных волновых полей со случайно распределенной по пространственным координатам начальной фазой, возникающая между ними разность фаз складывается из двух составляющих. Одна из них - регулярная, однозначно связана с величиной сдвига волновых полей, другая - случайная, обусловлена различием случайных начальных фаз каждого из полей в точках пространства, отстоящих на величину сдвига. Наличие случайной составляющей разности фаз интерферирующих волновых полей и приводит к погрешности измерения регулярной разности фаз. В дальнейшем для крайности эту погрешность будем называть статистической. Она может быть вызвана такая наличием процессов, приводящих к декорреляции сравниваемых волновых полей, т.к. распределение начальной фазы волнового поля при его декорреляции претерпевает случайные изменения.

Пользуясь соотношениями, известными из теории случайных процессов, оценим статистическую погрешность измерений. В работе /18/

установлено, что пространственное распределение комплексной амплитуды диффузно-когерентного волнового поля представляет собой нормальный случайный процесс с независимыми действительной и мнимой частями. Для оценки погрешности необходимо установить статистические свойства случайной начальной фазы. Согласно /19/, двумерная плотность вероятности фазы стационарного нормального процесса выражается формулой:

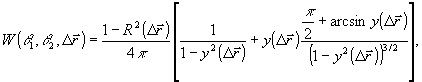(2)

где в нашем случае 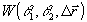- плотность вероятности того, что в двух точках, отстоящих друг от друга на расстоянии 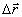, начальные фазы волнового поля принимают значения θ₁ и θ₂;

R(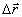) - функция когерентности комплексной амплитуды диффузно-когерентного волнового поля, введенная усреднением по пространственным координатам,

y = R_ccos(θ₂-θ₁)+R_ssin(θ₂-θ₁),

где R_c и R_s, соответственно, функции когерентности действительной и мнимой частей комплексной амплитуды.

Учитывая статистическую независимость действительной и мнимой частей комплексной амплитуды и тождественность их статистических свойств имеем:

y=RCos(θ₂-θ₁-π/2).

Интересующая нас погрешность определяется разностью случайных начальных фаз интерферирующих волновых полей. Из (2) легко получить плотность вероятности разности фаз, положив θ₁-θ₂=φ=Const.

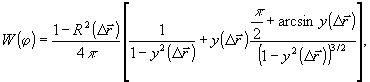(3)

где у=RCos(φ-π/4),

Оценкой статистической погрешности может служить дисперсия

σ² разности фаз интерферирующих волновых полей

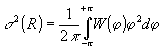. (4)

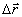
Из (3) и (4) следует, что σ² растет с уменьшением функции когерентности R. Вид этой зависимости представлен на рис.1а. Исходя из полученной зависимости σ²(R) можно получить зависимость σ²() ( 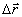- величина взаимного смещения интерферирующих волновых полей), поскольку зависимость R(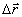) известна (см., например /20/). На рис.16 для примера представлена зависимость σ²(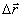) для случая смещения объекта нормально к оси оптической системы, с помощью которой ведется наблюдение объекта. Как видно из рисунка, высокоточные интерференционные измерения могут осуществляться только при сравнительно малых величинах смещений объекта. В связи с этим, к сообщениям о повышении точности интерференционных изменений путем фиксации малых дробных долей интерференционных полос /21/ следует отнестись с осторожностью, поскольку статистическая погрешность авторами не учитывалась.

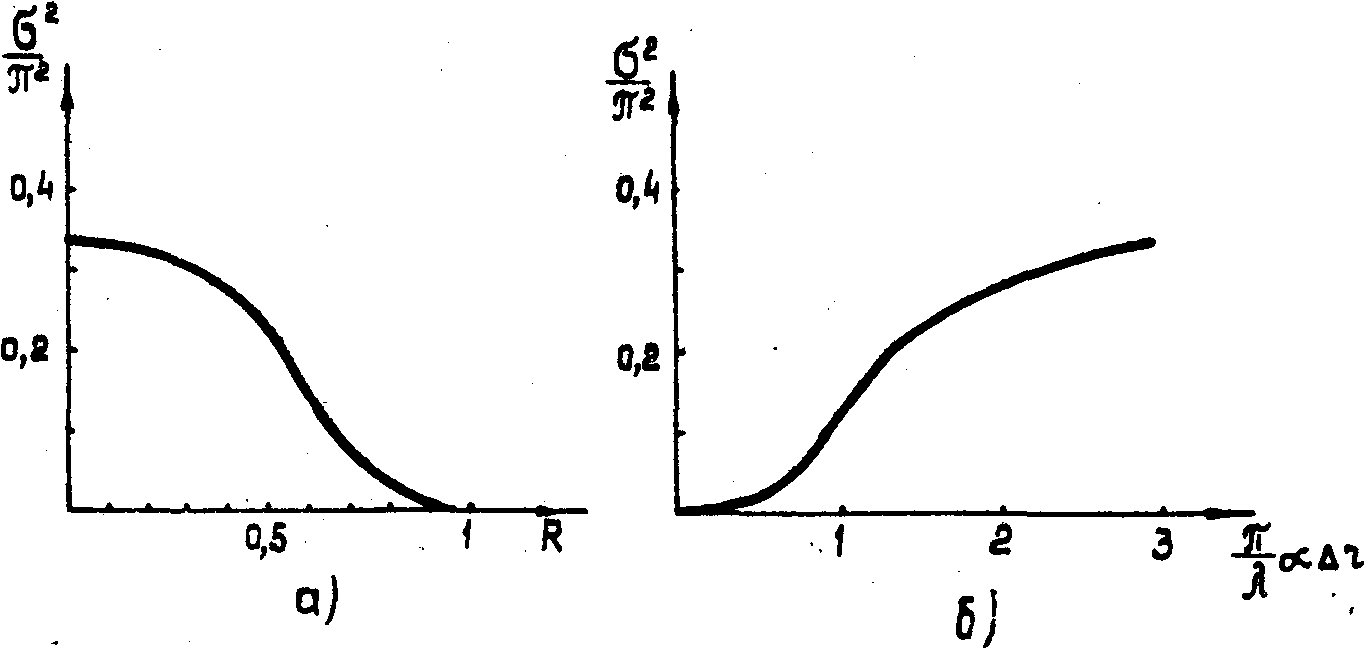
Рис.1. Зависимость дисперсии разности фаз от значения функции когерентности (а) и от поперечного смещения объекта (б); α - апертура оптической системы.

Приведенная оценка статистической погрешности имеет место для случая, когда разность фаз интерферирующих волновых полей измеряется по изменению интенсивности или непосредственно, например, как в /21/, с помощью детектора, размеры которого значительно меньше области когерентности комплексных амплитуд интерферирующих волновых полей. Если размеры детектора превышают область когерентности, то вследствие процесса усреднения дисперсия разности фаз интерферирующих волновых полей будет уменьшаться. Можно показать /22/, что результирующее значение дисперсии σ²_уср приближенно выражается как

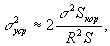
где S_кор и S - площади области когерентности и детектора, соответственно.

Следует однако отметить, что на практике величина S всегда ограничена требованием отсутствия усреднения по периоду интерференционных полос на восстановленном изображении, поэтому статистическая погрешность не может быть сколь угодно малой.

4. Снижение требований к когерентности источников

освещающего излучения в голографической

интерферометрии

В наших лекциях на предыдущих Школах и в работе /9/ мы отмечали, что при переходе от голографической интерферометрии в ее обычном варианте к голографической интерферометрии, основанной на пространственной корреляции интенсивности, существенно снижаются требования к источникам освещающего излучения и становится возможным использовать лазеры, работающие в многомодовом режиме. Покажем теперь, что в некоторых методах упомянутого направления в интерференционных измерениях возможно использование источников теплового излучения, в частности, обычных ламп накаливания.

Рассмотрим вначале условия, при которых в плоскости изображения диффузно-отражающего объекта наблюдается зернистый эффект, свидетельствующий о наличии пространственной корреляции интенсивнос-

ти. В когерентном лазерном излучении для этого достаточно, чтобы вариации оптического пути на поверхностной микроструктуре равнялись или превосходили длину волны /23/, а сама микроструктура не разрешалась оптической системой.

При переходе к полихроматическому излучению необходимо наложить некоторые ограничения на пространственную и временную когерентность освещающего волнового поля. В /24/ отмечено, что освещающее волновое поле должно иметь достаточно узкий угловой спектр. Такое определение нуждается в некотором уточнении, которое можно сделать, исходя из простых физических соображений.

В оптической системе, переотображающей объект, происходит усреднение отраженного волнового поля по элементу разрешения оптической системы в первом приближении по диску Эйри. Для того, чтобы такое усреднение происходило когерентно, область когерентности освещающего источника на поверхности объекта должна разрешаться оптической системой. Другими словами, угловые размеры источника освещения должны быть меньше угловой апертуры оптической системы, тогда когерентные свойства волнового поля, освещающего объект, передаются оптической системой без искажения. Может быть проведена некоторая аналогия рассматриваемого случая с другим, хорошо известным в классической оптике, когда изображение, созданное одним объективом, наблюдается с помощью другого объектива. Когерентность в плоскости вторичного изображения зависит тогда от соотношения угловых апертур обоих объективов /3,25/. Требования к временной когерентности также могут быть найдены из условия когерентного усреднения волновых полей по диску Эйри. Разность оптических путей усредняемых волновых полей должна быть меньше длины когерентности. Математическое выражение этого условия можно найти в /24/. Очевидно, что при фотографической регистрации длина когерентности определяется не только полихроматическим волновым полем, но и спектральной селективностью приемника излучения. Оба рассмотренных условия нетрудно выполнить, например, для матового стекла при освещении последнего белым светом обычной лампы накаливания. Случайная зернистая структура в плоскости изображения оптической системы легко наблюдается в микроскоп. Возможно и визуальное наблюдение зернистой структуры на матовом стекле, если угловые размеры

источника освещения достаточно малы.

Как известно, негатив, полученный в диффузно-когерентном излучении, способен восстанавливать позитивное изображение. Такими же свойствами обладали и негативы полутоновых транспарантов, полученные нами экспериментально при выполнении обсужденных выше условий. Объект - полутоновой транспарант освещался через матовое стекло обычной лампой накаливания и фотографировался через круговую апертуру и через апертуру, диафрагмированную экраном с двумя круговыми или щелевыми отверстиями. В последнем случае, как и в когерентном лазерном излучении, возникала несущая пространственная частота /5,6/, обеспечивающая восстановление ярких позитивных изображений в узком диапазоне направлений, определяемом углами дифракции восстанавливающего излучения. По сравнению с записью в когерентном излучении, качество восстановленного изображения было выше благодаря отсутствию щупа, обусловленного дифракцией на пылинках и других дефектах оптической системы.

Существенно, что интерференционные методы, развитые в диффузно-когерентном излучении на основе пространственной корреляции интенсивности, могут быть осуществлены в полихроматическом излучении тепловых источников. Такая возможность была подтверждена прямыми экспериментами. Интерферограммы диффузно-отражающих объектов были получены методом двухкратной экспозиции с приложением к объекту между экспозициями деформирующей нагрузки, причем фотографирование производилось как с круговой, так и с частично заполненной апертурой. Размеры зарегистрированной сцены составляли 60´ 60´ 10 см, источником излучения служила лампа накаливания.

Отметим, что выполнение условия передачи оптической системой когерентных свойств волнового поля, освещающего объект, позволяет, в принципе, записать голограмму, наложив в плоскость изображения волновое поле, когерентное по отношению к полю, освещающему объект. Таким образом, открывается возможность не только развития интерференционных методов, но и записи голограмм в полихроматических волновых полях, что позволят, в частности, проводить исследования в широком спектральном диапазоне, включая инфракрасную и ультрафиолетовые области.

Л и т е р а т у р а

1. Tanner L.H., J.Sci.Instrum., 43, 81(1966).

2. Э.Лейт, Ю.Упатниекс, УФН, 87, 52, 1965.

3. М.Борн, Э.Вольф. Основы оптики, М., Наука, 1975.

4. Leendertz J.A. J.Sci, Instrum., 3, 214 (1966).

5. Н.Г.Власов, Ю.П.Пресняков, С.Н.Смирнова. ЖТФ, 10, 2021, 1974.

6. Duffy D.E., Appl, Opt., 11, 1178 (1972).

7. Jouyeux D., Lowenthal S., Opt.Comuns., 4, 108 (1971).

8. Н.Г.Власов, А.Б.Штанько, В.Б.Ровенский, Е.Александров. В сб. "Проблемы голографии", вып.7, 1976.

9. Н.Г.Власов, Ю.П.Пресняков. Квантовая электроника, №2 (14), 80, 1973.

10. Hung YY., Taylor C.E., Exp. Mech, July, 281 (1975).

11. В.М.Кубатов, Г.Н.Павлыгин. В сб. "Современные проблемы прикладной голографии", М., МДНТП, 98, 1974.

12. Н.Г.Власов, Ю.П.Пресняков, Э.Г.Семенов. Оптика и спектрометрия, 37, 369, 1975.

13. Jones R., Butters J.N., J.Sci.Instrum., 8, 231. (1975).

14. Ennos A.E., J.Sci.Instrum., 1, 731, (1968).

15. Sollid J.E., Apl.Opt., 1987 (1963).

16. Е.Б.Александров, А.М.Бонч-Бруевич. ЖТФ, 37, 360, 1967.

17. А.С.Богомолов, А.Е.Штанько. В сб. "Проблемы голографии", вып.3, 24, 1973.

18. Dainty J.G., Opt.Acta, 17, 761 (1970).

19. В.Р.Левин. Теоретические основы статистической радиотехники, ч.1, изд."Советское радио", М., 1974.

20. Welles S., Arkiv for fysik., 40, №26, 299 (1970).

21. Dandliker R., Ineichen B., Mottier F.M., Opt Communs 9, №4, 412 (1973).

22. Г.Я.Мирский. Аппаратурное определение характеристик случайных процессов, изд."Энергия", М., 1972.

23. Fujii Н., Asakura T., Opt. Communs., 11, 35 (1974).

24. George N., Jain A., Appl. Phys., 4, 201 (1974).

25. М.Франсон, С.Сланский. Когерентность в оптике, изд."Наука", М., 1967.