НЕКОТОРЫЕ ПРОБЛЕМЫ ГОЛОГРАФИЧЕСКОЙ ОПТИКИ
(СОЗДАНИЕ И ПРИМЕНЕНИЕ)
М.М.Бутусов
Проводится обзор основных направлений, в которых применение голографической оптики представляется перспективным. Анализируются основные трудности на пути создания элементов с оптимальными характеристиками. Подробно рассматривается использование периодических структур сложного профиля для мультипликации изображений.
§ 1.
Основные направления использования
Основные направления, где в настоящем или ближайшем времени предполагается использовать оптические элементы голографического типа (ОЭГТ), - это оптическое приборостроение и экспериментальная техника.
Очевидно, что перспективы развития ОЭГТ нужно оценивать, исходя прежде всего из возможностей, которыми располагают конкурирующие методы, основанные на традиционных принципах.
1.1.
Метрические системы и устройства
В этой области перспективы ОЭГТ довольно обширны, прежде всего в спектральных приборах, где применение голографических дифракционных решеток в работах фирмы "
Jobin-yvan" /1/ позволило резко улучшить характеристики ряда приборов, а также начать изготовление решеток с пространственными частотами до Vmax ≈ 6000 мм-1 для дальнего ультрафиолета. Кроме более высоких пространственных частот, голографические принципы записи позволяют избежать появление "духов", реализовать несложную схему формирования решеток на сферических подложках различной кривизны, достичь небывалых размеров рабочих апертур (40´
40 см2). Хотя технология изготовления решеток остается привилегией фирмы, нет сомнения в том, что скоро решетки сходных типов появятся в странах, заинтересованных в соз-
дании мощных, но малогабаритных спектральных приборов космического применения.
Методы голографической фурье-спектроскопии, предложенные Строуком /2/, и развитые в работах Н.Турухано /3/, основываются на анализе характеристик голограммы, получаемой при интерференции двух пучков, в каждом из которых содержится несколько взаимно некогерентных спектральных линий. Разрешающая способность этих методов недостаточна,
но это восполняется рядом достоинств, например, возможностью получать информацию о когерентных свойствах источников. Новые интересные практические применения голография некогерентных источников нашла в работах группы французских ученых /4/.
Весьма перспективно использование ОЭГТ в оптических системах для измерения параметров механических перемещений (дальномеры, кольцевые лазеры, датчики перемещений с использованием муарового эффекта). Так, ОЭГТ, располагающиеся в зоне интерференции двух лазерных пучков
, могут служить безынерционными и чувствительными датчиками следующих величин:
а) механических перемещений, если ОЭГТ, слегка рассогласованный с интерференционным полем по углу или пространственной частоте, жестко скреплен с перемещающимся объектом /3/.
б) фазы или разностной частоты двух лазерных пучков, если ОЭГТ неподвижен и согласован с полем по углу и пространственной частоте, но временные частоты двух пучков несколько различны. В таком варианте использование ОЭГТ перспективно в кольцевых ОКГ для вывода сигнала
/6/.
1.2.
Проекционные системы
Основные надежды на применение ОЭГГ в светопроекционной технике связывают с трудностями, существующими пока в проекционной фотолитографии при производстве интегральных схем. Переход от контактных методов к проекционным в этой области - дело практически решенное, но как осуществись точную юстировку и абсолютную виброустойчивость современных фотолитографических столов, использующих принцип последовательных перемещений. Некоторые исследователи видят альтернативное решение в создании голографических мультипликаторов изображений различного типа /7-10/. Эта область явля-
ется одной из самых интересных в голографической оптике, но и весьма трудной для реализации.
В отличие от мультипликаторов, будущее голографических линз в этой области представляется проблематичным, особенно если принять во внимание характеристики лучших уникальных объективов, используемых в фотолитографии. Однако в проекционных системах, где на первый план выдвигается не достижение рекордных разрешений по максимальному полю, а иные требования, возможности ОЭГТ должны активно использоваться. Сюда относятся размерная обработка материалов о помощью мощных лазеров /11/ устройства для проекции визуально наблюдаемых изображений /12/ и т.д.
1.3.
Интерферометры
ОЭГТ используются в интерферометрах (классических и голографических) в качестве эталонных, компенсирующих, светоделительных элементов, а такие вместо матовых рассеивателей. При контроле качества асферических поверхностей искусственные голограммы, синтезированные в соответствии с формой изготовляемой детали, позволяют контролировать в интерферометре качество волнового фронта, отраженного от этой детали /13/. При этом небольшое значение дифракционной эффективности такой голограммы можно считать полезным фактором: используются как прямая, так и дифрагированная волны.
На этом же принципе основано успешное использование ОЭГТ в качестве регулируемых светоделителей /14,15/ а также при исследовании фазовых объектов методами голографии, где ОЭГТ удачно заменяют традиционные матовые рассеиватели /16/. По сути дела, в этой области используются свойства ОЭГТ как мультипликаторов, в данном случае создающих на выходе набор плоских световых волн, пронизывающих фазовый объект в различных направлениях.
1.4.
Системы обработки информации
Оптические свойства элементов когерентно-оптических процессоров в большой степени определяют предельные характеристики этих устройств. Поэтому неслучаен интерес к изучению характеристик регистрирующих сред (см., например, /17,18/) применительно к использованию их в устройствах оптической памяти. Если же под ОЭГТ понимать элементы с выраженной периодической микроструктурой, то в таком
варианте предполагается использование их в качестве мультипликаторов для многоканальной обработки, дефлекторов дифракционного типа /19/ и т.п. Наконец, голографическая техника создания периодических структур начинает активно использоваться в интегральной оптике /20,21/. В связи с этим направлением и необходимостью получения сверхвысоких пространственных частот ( V0≈6000 мм-1) особое внимание должно быть уделено результатам работ по интерференции запирающих волн /22,23/.
§ 2.
Методы синтеза ОЭГТ
2.1.
Механические и фотолитографические способы
При использовании этих способов уравнение голограммы рассчитывается, исходя из того преобразования, которое синтезируемая голограмма должна совершать над реконструирующим волновым фронтом. Затем в соответствии с этим уравнением программируются нарезающее или фотонаборное устройства.
Искусственные ОЭГГ обладают рядом неоспоримых достоинств - они выполняются на оптически совершенных подложках, паразитное светорассеяние практически отсутствует, а дифракционная эффективность может быть сделана достаточно высокой. Однако существует ряд практически трудно преодолимых факторов, которые мешают более широкому распространению искусственных ОЭГТ, но, с другой стороны, стимулируют развитие чисто голографических методов синтеза ОЭГТ.
Во-первых, технология создания искусственных ОЭГТ трудна, во-вторых, тенденции развития искусственных и голографических дифракционных решеток приводят к выводу о целесообразности голографического синтеза решеток с V>1000 мм-1, наконец искусственными способами нельзя реализовать ОЭГТ с брэгговским механизмом дифракции (см.,например,/12/).
2.2.
Голографический способ
Преимущества этого способа достаточно весомы, но какие же трудности мешает его широкому использованию?
По-видимому, основным фактором здесь является недостаточно
полное представление обо всем комплексе физических и физико-химических процессов, определяющих когерентную передаточную функцию ОЭГГ, недостаточное уменье управлять этими процессами для достижения требуемых характеристик.
Естественно, для различных регистрирующих сред эта проблема имеет свою специфику. Обращаясь к галоидосеребряным эмульсиям, заметим, что для синтеза ОЭГТ недостаточно иметь равномерный слой эмульсии на оптически совершенной подложке, знать сенситометрическую и частотно-контрастную характеристики. Укажем на два процесса, точное знание которых тоже необходимо.
Во-первых, при химической обработке и последующей сушке на голограмме образуется поверхностный рельеф, высота которого определяется конкуренцией сил поверхностного натяжения и усадки эмульсии /24/. Усадка различна в местах с разной экспозицией, что связано минимум с двумя причинами: с вышиванием неэкспонированного металлического серебра при фиксировании и с дублением желатины в процессе проявления.
Во-вторых, при отбеливании голограмм, помимо хорошо известного обесцвечивания эмульсии и образования участков с различными коэффициентами преломления, происходит ряд других процессов, также связанных с дублением желатины /24/, под действием отбеливателя. В результате поверхностный рельеф нарастает, а в толще желатины образуются вредные центры рассеяния.
Полный анализ процессов дифракции на ОЭГТ должен учитывать одновременное влияние трех факторов:
а) изменение коэффициента амплитудного пропускания τ;
б) изменение геометрического рельефа поверхности, т.е. толщины
слоя Δd;
в) изменений объемного распределения коэффициента преломления
n.
К сожалению, такого анализа с учетом реальных зависимостей
всех "трех факторов от экспозиции и пространственной частоты проведено на было. Между тем, существует достаточный объем экспериментальных данных для проведения такого анализа, а важность ожидаемых результатов трудно переоценить.
§ 3.
вопросы реализации ОЭГТ для мультипликации
изображений
Основная часть этого параграфа посвящена анализу методов создания мультипликаторов изображений и дополняет результаты хорошо известных работ /9,10/, в которых исследования мультипликаторов шли по линии голографических аналогов системы типа "мушиный глаз" - /25/ или фурье-голографических мультипликаторов /7,8/, для реализации которых использовались голограммы матрицы точечных источников.
На мой взгляд, у нас недостаточно развит вопрос создания решеток сложного профиля, предназначенных для формирования
n порядков дифракции равной интенсивности. Такие решетки в сочетании с исправленными объективами позволяют весьма эффективно решить проблему мультипликации изображений, а также ряд других проблем, рассмотренных в § 1.
3.1.
Мультипликаторы с решеткой
На рис.1а приведена схема простейшего мультипликатора с использованием ОЭГТ в качестве основного элемента. Схема рис.16 отличается от предыдущей расположением мультипликатора, а в схеме рис.1в ОЭГТ работает на отражение. В этих схемах источник монохроматического излучения 1 через коллиматор 2 освещает прозрачный объект 3 (транспарант). Положение изображающего объектива 4 подбирается, исходя из требуемого увеличения в плоскости изображений 6, а положение мультипликатора 5 до или после объектива 4 определяется размерами поля ОЭГТ.
Многокаскадный мультипликатор, показанный на рис.2, позволяет использовать решетки, дающие небольшое количество n порядков, используя тот факт, что число изображений по каждой координате после m-ого каскада равно /26/
N=nm.
На рис.2 показан двухкаскадный мультипликатор. Поскольку каждая решетка дает на выхода не только
n равных по интенсивности порядков, но и высшие порядки для их фильтрации в плоскостях Р1 и
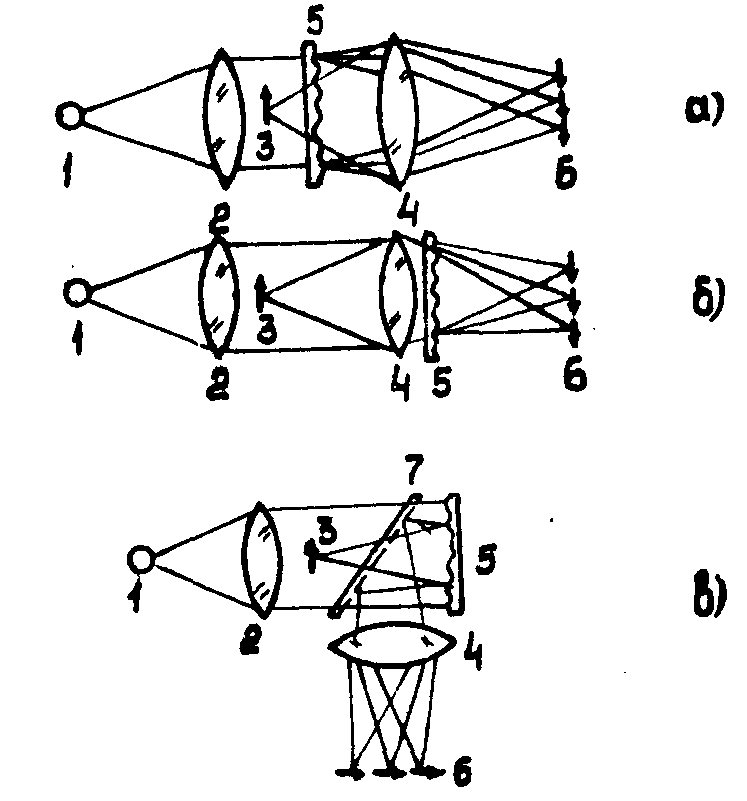
Рис.1. Различные схемы мультипликаторов
c использованием решеток:
1
- источник; 2,4 - линзы; 3 - объект;
5 - решетка; 6 - мультиплицированные изображения;
7 - светоделитель.
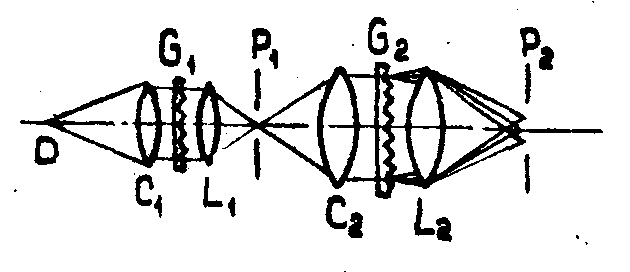
Рис.2. Двухступенчатый мультипликатор:
D
- источник; С1,С2 - коллимационные объективы;
L1,L2
- фокуcирующие объективы; G1,G2- решетки;
Р
1,
Р2 - фильтрующие диафрагмы.
Р
2 расположены диафрагмы.
3.2.
Расчет и изготовление решеток простого профиля
Очевидно, что наращивание каскадов в cхеме риc.2 нецелесообразно из-за большого количества необходимых объективов, нарастающего влияния шумов, снижения энергетической эффективности из-за фильтрации высших порядков. Однако этот путь весьма привлекателен, если оптимизирована фотолитографическая технология изготовления ОЭГТ. Какой профиль структуры является оптимальным? Здесь и впоследствии речь будет идти только о фазорельефных структурах, дающих фазовую модуляцию типа /26/
Ф(
x,у)=Ф(х) +Ф(у). (1)
Амплитуда дифрагированной волны вычисляется в соответствии
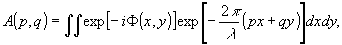 (2)
(2)
где р=
Sinθ, q=Sinβ, a интегрирование ведется по всей работающей апертуре ОЭГТ. Интенсивность I(u,v) в плоскости Р1 равна /28/
I(u,v)=E(u,v)IF(u,v)=E1(u)E1(v)I1(u)I1(v), (3)
где
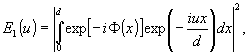 (4)
(4)
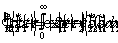 (5)
(5)
d
- период решетки; 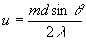 ; N - число штрихов решетки на ее освещенном участке.
; N - число штрихов решетки на ее освещенном участке.
Зависимости
E1(v), I1(v) выглядят аналогично.
Из (3)-(5) можно сделать два важных вывода: во-первых, при независимом задании функций Ф(х) и Ф(у) переменные разделяются,
и в дальнейшем можно рассматривать только однокоординатные функции; во-вторых, интенсивность в фурье-плоскости есть произведение двух членов - интерференционного
I1(u), зависящего только от общего числа элементов решетки (риc.3) и уже при N>20, представляющего собой гребенку δ-функций, центрированных вблизи значений u=mπ/2 (m=0,1,..), и дифракционного члена Е1(u), являющегося модулирующим.
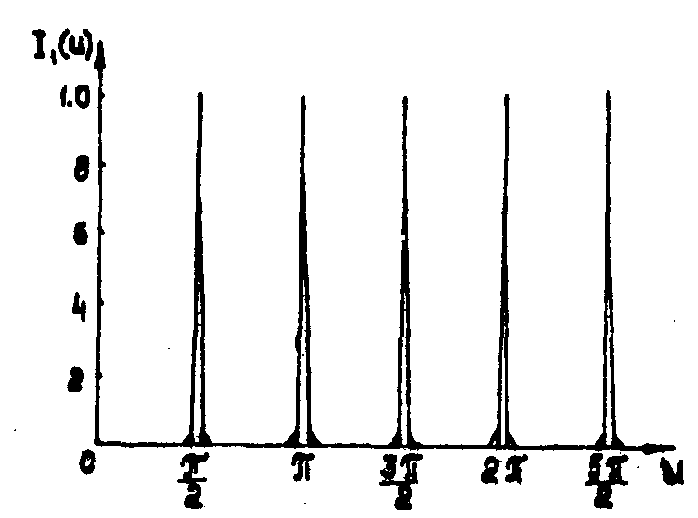
Рис.3. Нормализованный интерференционный сомножитель I(u) для дифракции на решетке, содержащей 20 штрихов.
Форма дифракционного члена Е
1(u) зависит от высоты и формы штриха, согласно (4). Рассмотрим три простых формы:
а) прямоугольную (
Rect) типа меандра
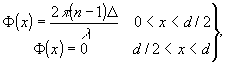 (6)
(6)
б) синусоидальную
(Sin)
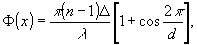 (7)
(7)
в) треугольную (Т
ri)
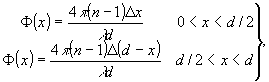 (8)
(8)
где
n - показатель преломления среды ОЭГТ; Δ - высота рельефа.
С помощью численного интегрирования на ЭВМ можно получить форму кривых Е(
u) для различных значений Δ, n, а проще - параметра α
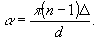 (9)
(9)
Нас, естественно, будут интересовать такие значения
α, которые позволяют реализовать мультипликацию, т.е. E(u)=Const при u=mπ/2 (m=0, ±1, ±2,...). Расчет показывает, однако, что mmax = 1, т.е. c помощью простой решетки нельзя получить более трех порядков равной интенсивности.
Формы кривых Е(
u) для оптимальных значений α соответствующих каждому профилю, приведены на рис.4. Видно, что минимальная высота рельефа, необходимая для мультипликации, соответствует прямоугольному профилю. Кривые рис.4 позволяют определить энергетическую эффективность решетки К, т.е. отношение суммарной интенсивности в полезных порядках ко всей энергии светового поля за решеткой. Важно также знать чувствительность каждого профиля к точности изготовления, т.е.
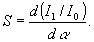
Значения
α, К и S для трех профилей приведены в таблице.
Таблица 1
|
Rec |
Sin |
Tri |
|
α |
1004 |
1435 |
1822 |
|
К |
75% |
81% |
72% |
|
S |
4.4 |
2.6 |
2.0 |
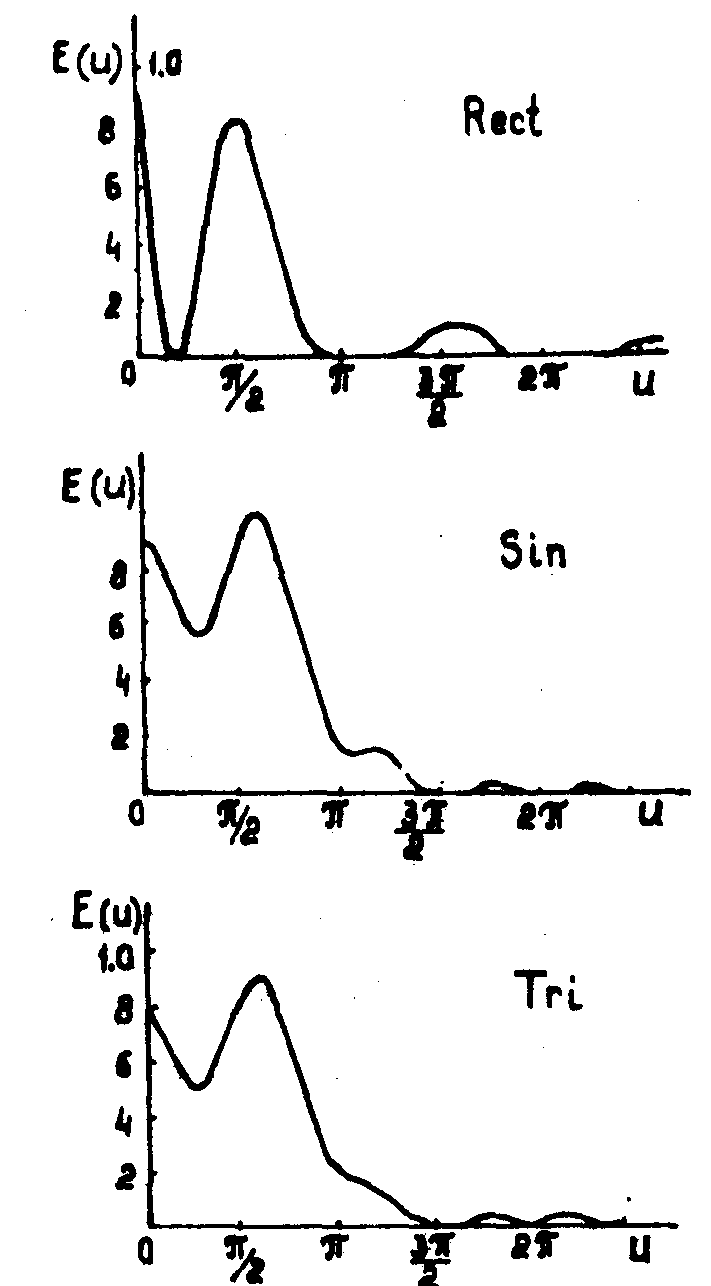
Рис.4. Дифракционный сомножитель Е(
u) для прямоугольного, синусоидального и треугольного профилей решетки.
Интересно, чем при меньших значениях
α, достигается равенство порядков, тем более точным должно быть изготовление ОЭГТ. Используя такой анализ, автор /26/ реализовал с помощью решетки с V= 40 мм-1 и прямоугольной апертурой 2,5´
2,5 см2 матрицу из 9 равноотстоящих изображений с разрешением 5 мкм на поле 0,5´
0,5 см2.
3.3. Решетки сложного профиля, изготовляемые
искусственно
Используя тот же математический аппарат, который привел к выражениям для Е (u) (рис.4), только в обратной последовательности, мы можем по заданной форме дифракционного члена найти соответствующую высоту и профиль штриха. Для различного количества равных порядков в /29/ были получены профили фазорельефных ОЭГТ (рис.5). Видно, что высота рельефа даже для 13 равных порядков практически достижима, т.к. не превышает 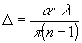 ≈1 мкм. Однако форма профиля весьма сложна, и в соответствии с § 3.2 можно заключить, что небольшие (~3%) отклонения от этого профиля приведут к резкому нарушению баланса порядков. Поэтому в /29/ предложено аппроксимировать профили рис.5 бинарными сложными профилями, заполняя каждый период решетки симметричными относительно середины периода выступами, имеющими постоянную фазовую высоту α=1. Практическое осуществление такого мультипликатора с применением фотолитографической технологии осуществлено в /30/.
≈1 мкм. Однако форма профиля весьма сложна, и в соответствии с § 3.2 можно заключить, что небольшие (~3%) отклонения от этого профиля приведут к резкому нарушению баланса порядков. Поэтому в /29/ предложено аппроксимировать профили рис.5 бинарными сложными профилями, заполняя каждый период решетки симметричными относительно середины периода выступами, имеющими постоянную фазовую высоту α=1. Практическое осуществление такого мультипликатора с применением фотолитографической технологии осуществлено в /30/.
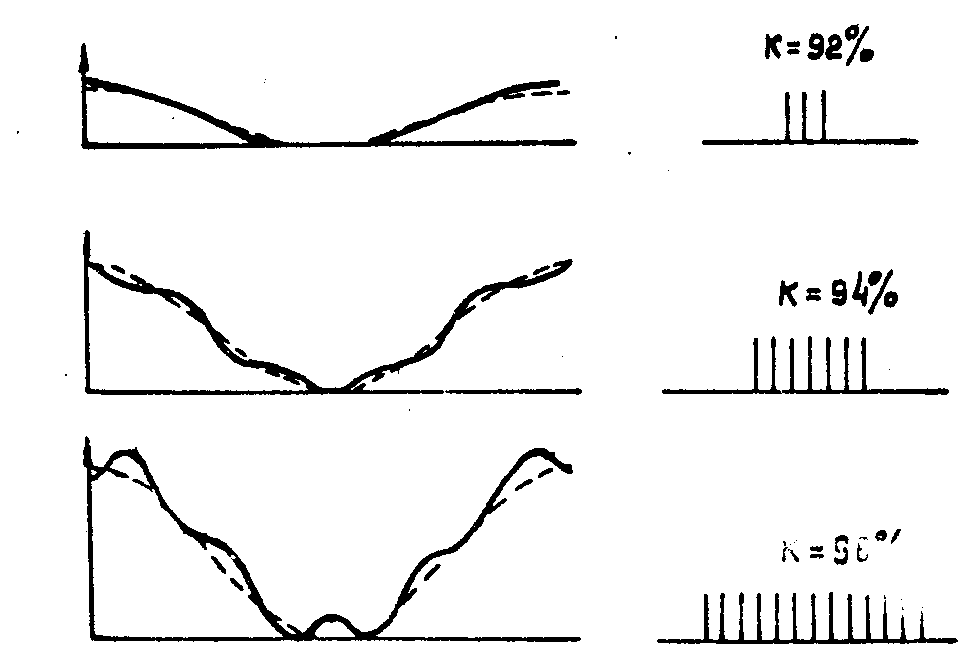
Рис.5. Некоторые профили штрихов и соответствующие им распределения интенсивности по порядкам дифракции. Штрихами нанесен синусоидальный профиль.
3.4.
Решетки сложного профиля, получаемые голографически
Представим себе голограмму G, расположенную в фурье-плоскости оптической системы (рис.6), во входной плоскости которой задано распределение F взаимно когерентных точечных источников:
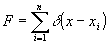
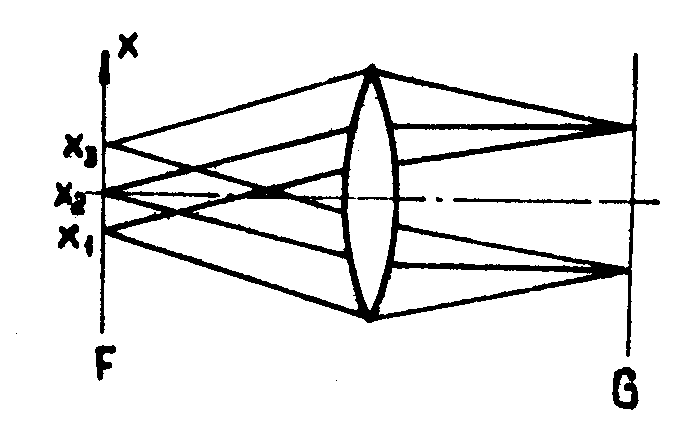
Рис.6. Схема получения мультипликатора по
/31/.
Амплитуда поля в плоскости голограммы G равна
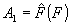 ,
,
где
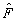 - символ Фурье-преобразования.
- символ Фурье-преобразования.
Если использовать фотоматериал с линейным (по интенсивности) откликом, то интенсивность в плоскости G, равная
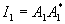 , преобразуется в соответствующее распределение пропускания τ. Поместив обработанную голограмму в плоскость F, в плоскости G получим распределение амплитуд
, преобразуется в соответствующее распределение пропускания τ. Поместив обработанную голограмму в плоскость F, в плоскости G получим распределение амплитуд
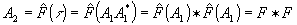 , (10)
, (10)
где
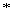 - символ автокорреляции.
- символ автокорреляции.
Если входное распределение
F представить в виде двух групп точек R и S, состоящих из r и S точек каждая (r+s=n ), т.е.
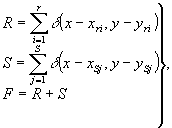 (11)
(11)
то
A2= F*F=R*R+S*S+R*S+S*R. (12)
Из (12) видно, что распределение на выходе вторичной голограммы состоит из центрального блока автокорреляционных максимумов и двух симметричных боковых блоков
/31/.
Полученные результаты предполагали линейность отклика фотоматериала голограммы. Схема реализации /31/ представляла собой интерферометр Майкельсона, в котором концевые зеркала заменены набором стеклянных плоских пластин, рассогласуя плоскости и меняя число которых можно было получить делаемое количество и расположение точечных источников.
Недостатки метода
/31/ заключаются в трудности настройки интерферометра, а главное в том, что реальные фотоматериалы обладают нелинейным откликом, и это весьма трудно учесть при расчете характеристик мультипликатора.
3.5.
Накопление нелинейностей
Можно, однако, использовать неизбежную нелинейность отклика материала голограммы, избавиться от очень большой критичности всех рассмотренных методов к условиям обработка.
Предлагаемый нами метод "накопления нелинейностей" легче всего проиллюстрировать на примере материала с теми же характеристиками, что и в 3.4, однако расчеты на ЭВМ показывают, что аналогичный результат получается при различных полиномных представлениях нелинейности.
Проэкспонируем голограмму в схеме рис.6 при наличии в плоскос-
ти (х,у) двух источников
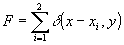 .
.
В плоскости
G распределение поля имеет вид:
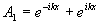 , (13)
, (13)
а пропускание обработанной голограммы τ
1 меняется по закону
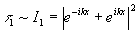 . (14)
. (14)
Теперь эту голограмму помещаем в плоскость фурье преобразующей системы, выходная плоскость которой совпадает с плоскостью
F на рис.6. Теперь в плоскости G имеем (с точностью до постоянной) распределение амплитуды
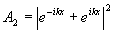 , (15)
, (15)
и пропускание обработанной вторичной голограммы меняется как
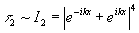 . (16)
. (16)
После
m циклов такой последовательной перепечатки получаем голограмму, поле за которой описывается формулой
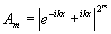 . (17)
. (17)
Если m
>>1, то в соответствии с определением распределения Пуассона находим, что коэффициенты при нулевом и примыкающих к нему порядках быстро выравниваются. Огибающая, описывающая распределение по порядкам, становится гауссовой кривой (рис.7). Конечный результат мало зависит от точного вида нелинейности, а следовательно, от тщательности соблюдения условий обработки, а эквидистантность дифракционных максимумов выдерживается автоматически. В сочетании с изучаемым у нас методом УФ задубливания желатины, позволяю-
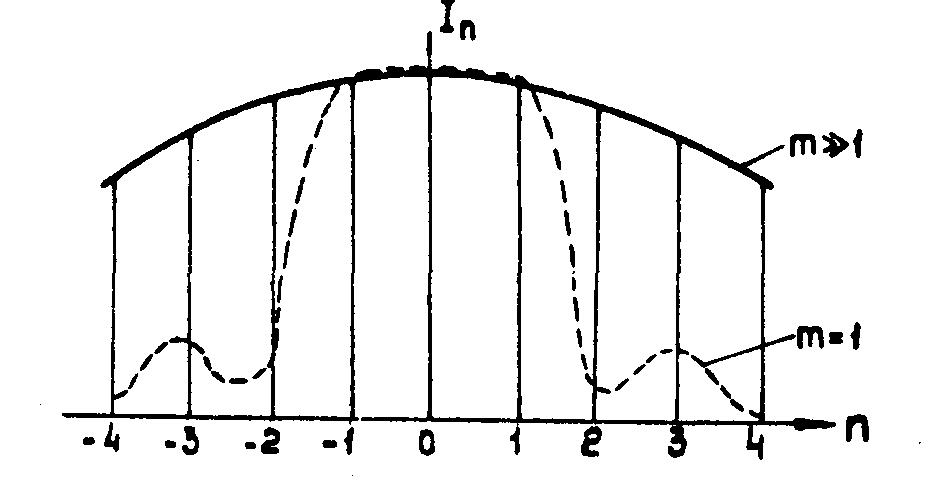
Рис.7. Распределение по порядкам дифракции после первого (
m=1) и m-го (m>>1) этапов перепечатки голограммы.
щим резко уменьшить шумы фазовых голограмм, этот способ создания мультипликаторов представляется перспективным. Первые опыты позволили получить блок из 7´
7 = 49 каналов мультипликации с разбросом интенсивностей в пределах 20%,
Л и т е р а т у р а
1. Handbook of Jobin-Yvon Optical Systems, 7, 1974;
L
аsеr grating Handbook of Jobin-Yvon Optical Systems, 23, 1975.
2. G.W.Stroke, A.Funkhouser.
Phys.Letters, 16, 272, 1965.
3. B.G.Turukhano, N.Turukhano. Opt.Commun., 6, 2, 177, 1972.
4. Cl.Froehly, A.Lacourt, J.Ch.Vienot.Nouv.Rev.Opt., 4, 183, 1973.
5. J.Ch.Yienot, A.Lacourt, J.P.Goedgebuer. Proc. of International Optical Computing Conference, Washington, 133, 1975.
6. Д.П.Лукьянов, М.М.Бутусов. В сб. "Оптическая голография" , изд.ЛДНТП, Л., стр.3, 1972.
7. S.Lowenthal, A.Werte, Rembault M. C.R.Acad.Sc., Paris, Serie
В., 267, 120, 1968.
8. G.Goh, C.H.P.Velzel. Optik, 30, 257, 1969.
9. Г.Н.Буйков, К.С.Мустафин. Оптика и спектр.,
34, 936, 1973.
10. В.В.Власов, В.Н.Славинская, Б.В.Телешов. Квантовая электроника, №11, 2360, 1974.
11. J.M.Moran Appl.Opt., 10, 412, 1971.
12. J.W.C.Gates. Proceedings of the Electrooptical Systems Design Conference, Brighton, England, 19, 1972.
13. Г.Н.Буйков, Н.П.Ларионов, А.В.Лукин, К.С.Мустафин. ОМП, №4, 6, 1971.
14. М.М.Бутуоов, Ю.Г.Туркевич. ПТЭ, №6, 179, 1970.
15. М.М.Бутусов. Автометрия, №5, 62, 1973.
16. C.M.Vest, D.M.Sveney. Appl.Opt., 9, 2321, 1970.
17. В.А.Барачев
cкий, В.М.Кожиков. В сб."Регистрирующие среды для голографии", Наука, Л., стр.26, 1975.
18. В.А.Вакин, Л.Н.Вагин, В.А.Королев. В сб. "Регистрирующие среды для голографии", Наука. Л., стр.69, 1975.
19. N.Nishida, M.Sakaguchi, F.Saito. Appl.Opt., 12, 1663, 1973.
20. S.E.Miller. IEEE J. of Quant. Electr., QE-8, 199, 1972.
21. P.K.Tien. Appl. Opt., 10, 2396, 1971.
22. H.Nassenstein. Optik, 29, 597, 1969.
23. Л.М.Сороко. В сб."Материалы
V Всесоюзной школы по голографии", изд.ЛИЯФ, Л., 100-138, 1973.
24. М.М.Бутусов, А.И.Иоффе. Квантовая электроника, №5, 374, 1976.
25. R.G.Olsson, Proceedings of the Conf. on the use of Optica in Microelectronics. Las Vegas, USA, 23, 1971.
26. L.P.Boivin. Appl.Opt., 11, 1782, 1972.
27. Дж.Гудмен. Введение в фурье-оптику. Мир, M., 1967.
28. А.Папулис. Теория систем и преобразований в оптике, Мир, М.,
1971.
29. H.Damman, K.Gortler. Optics Conmun., 3, 312, 1971.
30. С.Т.Бобров, Б.Н.Котлецов, Ю.Г.Туркевич. Микроэлектроника,
4, 375, 1975.
31. N.Aebischer, A.B.Agbani. Nouv.Rev.Optique, 6, 37, 1975.

