ГОЛОГРАММЫ С ШИРОКИМ СПЕКТРАЛЬНЫМ СОСТАВОМ ВОССТАНОВЛЕННОГО ИЗОБРАЖЕНИЯ
Д.А.Цырульников
Рассмотрены свойства голограмм с широким спектральным составом восстановленного изображения. Показано, что такие голограммы формируют изображение в основном по законам геометрической оптики. Сделанные вывода находятся в согласии с имеющимися опытными данными.
В в е д е н и е
На протяжении последнего десятилетия метод голографии, изобретенный Деннисом Габором, претерпел значительные изменения как в отношении теоретических представлений, так и в практическом приложении. Особый практический интерес в настоящее время представляют голограммы, позволяющие восстанавливать изображение во всем спектре видимого диапазона, в том числе и в белом свете - объемные голограммы. Но, как привило, спектр изображения, восстановленного по таким голограммам, узкий за счет фильтрующих свойств голограммы. Этот факт ограничивает возможности применения трехмерных голограмм в качестве таких оптических элементов, от которых требуется передача широкого спектра формируемого изображения. Поэтому задача расширения спектрального состава восстановленного изображения является несомненно актуальной. Голограммы с широким спектральным составом формируемого изображения могут найти применение в трехмерной фотографии, поскольку при восстановлении в белом свете они позволяют получать объемное черно-белое изображение объекта, в качестве голографических оптических элементов, работающих во всем видимом диапазоне, для целей визуализации звуко- , радио- и ИК-диапазона, поскольку такие голограммы формируют изображения без всяких масштабных искажений /1-3/ и т.п.
1.
Оптические свойства объемных длинноволновых голограмм. восстанавливаемых в видимой части спектра
Рассмотрим оптические свойства объемных голограмм, записанных в ИК и более длинноволновом диапазоне и восстанавливаемых в видимой области спектра, а также различные области применения таких голограмм.
Прежде, чем перейти к подробным исследованиям этих свойств, целесообразно вначале сравнить их оптические свойства с оптическими свойствами объемных голограмм, записанных в видимом диапазоне.
Известно, что по трехмерным голограммам, записанным в видимой области спектра, можно восстанавливать изображение в широком спектральном диапазоне, в том числе и в белом свете /4-7/.
Чтобы при восстановлении получить не искаженное изображение, надо осветить голограмму реконструирующей волной, являющейся копией опорной волны /4-7/. Тогда в результате отражения реконструирующей волны от зарегистрированных на голограмме изомодуляционных слоев формируется неискаженный волновой фронт исходного объекта.
Следует особо отметить, что для данной геометрии восстановление изображения будет формироваться в узком спектральном диапазоне волн.
Обычно в литературе теоретически исследуется процесс восстановления таких голограмм без учета когерентных свойств реконструирующего излучения и в том же диапазоне, в котором проводилась запись объемных голограмм. Например, если запись проводится в видимом диапазоне, то исследуется процесс восстановления в том же диапазоне. Однако, если объемную голограмму записать в ИК и более длинноволновом диапазоне и восстанавливать ее в некогерентном немонохроматическом свете (в общем случае в белом свете), то возникают, как будет показано ниже, качественно новые свойства, а именно: в процессе восстановления по таким длинноволновым голограммам будет формироваться объемное изображение с широким спектром (в общем случае черно-белое) без масштабных искажений, возникающих, как известно, у двумерных голограмм, зарегистрированных по схеме Лейта в длинноволновом диапазоне и восстанавливаемых в оптическом диапазоне /1-3/. Иными словами, подобные голограммы при реконструк-
ции в некогерентном свете практически не изменяют состава реконструирующего излучения.
С целью исследования свойств длинноволновых трехмерных голограмм рассмотрим их интерференционную структуру.
Известно, что интерференционную структуру объемной отражающей голограммы точечного объекта можно рассматривать как совокупность софокусных поверхностей второго порядка с одинаковой модуляцией оптических характеристик (изомодуляционные поверхности (слои), расположенных - друг за другом на расстоянии Λ = λ/2n, где λ - длина волны записывающего излучения, n - коэффициент преломления регистрирующей среды /4-7,8/:
Если регистрацию объемных отражательных голограмм точечного объекта проводить в видимом диапазоне, а реконструкцию изображения производить в белом свете, то от поверхности первых изомодуляционных отражающих слоев отразится небольшое количество света; большая же часть его проникнет дальше, отразится частично от вторых, третьих слоев и т.д. Если длина когерентности реконструирующего излучения превосходит расстояние между слоями (подобное условие всегда соблюдается при записи и восстановлении в видимом диапазоне), то волны, отраженные от этих слоев, интерферируют между собой и формируют изображение объекта, голограмма которого зарегистрирована в толще эмульсии. Из условий Брегга /4-7/ следует, что главным образом складываются по амплитуде волны с длиной волны, равной той, на которой производилась запись голограмм. Т.е. в процессе восстановления изображения записанная таким образом голограмма будет работать как достаточно узкополосный интерференционный фильтр. Явление, лежащее в основе физики формирования восстановленного изображения, называется Брэгговским волновым отражением.
Предположим теперь, что экспонирование объемной голограммы ведется в длинноволновой (допустим в миллиметровой) области спектра, а восстановление - в видимом диапазоне. В случае длинноволновой объемной отражающей голограммы точечного объекта изомодуляционные слои будут представлять собой софокусные поверхности второго порядка, расположенные друг за другом на расстоянии Λ = λ/2n, значительно превышающем длину когерентности белого света. Если такую длинноволновую голограмму осветить реконструирующим оптическим излуче-
нием, длина когерентности которого во много раз меньше удвоенного расстояния между изомодуляционными слоями (например, белым светом), то отраженные от изомодуляционных поверхностей этой голограммы волны не будут интерферировать между собой, точнее говоря, корреляционная функция этих волн имеет вид δ -функции, и такая голограмма не будет избирательно отражать узкую спектральную составляющую, как это происходит в отражательной голограмме, записанной в оптическом диапазоне /1,2/. Иными словами, Брэгговские отражения от этих слоев будут отсутствовать, а следовательно, будут отсутствовать фильтрующие свойства подобной голограммы. Поэтому все спектральные компоненты реконструирующего излучения отразятся одинаковым образом от них, как от систем независимых зеркальных фокусирующих элементов и, складываясь по интенсивности, соберутся (в случае сохранения геометрии записи) в той же точке, где был объект. Такая голограмма в отличие от голограммы, записанной в оптическом диапазоне, будет работать как геометрический элемент, а не как волновой.
Поскольку любой сложный объект в пренебрежении перекрестной интерференцией можно представить как совокупность светящихся точечных объектов, то можно сделать вывод, что длинноволновая отражательная голограмма сложного объекта формирует масштабно неискаженное изображение с широким спектром по законам геометрической оптики.
С целью сокращения размеров длинноволновых объемных голограмм представляет практический интерес рассмотреть объемную отражательную длинноволновую голограмму, эффективная толщина которой соизмерима с половиной длины волны регистрирующего излучения.
Рассмотрим такую голограмму на примере голограммы точки (см. рис.1). Интерференционная структура в атом случае состоит из изомодуляционных слоев (1,2,3). Поскольку разности хода лучей, отраженных от изомодуляционных слоев, и размеры этих слоев значительно превосходят длину волны реконструирующего излучения, то изомодуляционные слои формируют изображение подобно зеркальным фокусирующим элементам, т.е. по законам геометрической оптики, причем спектр отражения такой однослойной длинноволновой голограммы будет широким.
Как будет показано ниже, подобные длинноволновые голограммы
имеют аналоги, которые можно получить, записывая соответствующие голограммы в видимом оптическом диапазоне.
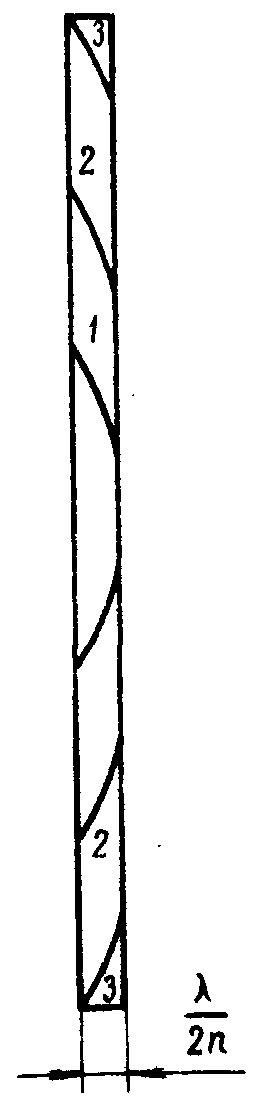
Наравне с длинноволновыми отражательными голограммами, рассмотренными выше, можно регистрировать длинноволновые объемные пропускающие голограммы при углах θ между предметной и опорной волной, существенно меньших 18
0°.
Так, например, в случае плоских предметной и опорной волны плоские изомодуляционные поверхности будут располагаться по биссектрисе угла между нормалями волновых фронтов, причем расстояние между изомодуляционными поверхностями
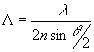 гораздо больше длины когерентности реконструирующего белого излучения. При восстановлении такой голограммы некогерентным оптическим излучением спектр
гораздо больше длины когерентности реконструирующего белого излучения. При восстановлении такой голограммы некогерентным оптическим излучением спектр
"пропускания" будет лежать во воем видимом диапазоне, поскольку длина когерентности реконструирующего излучения значительно меньше разности хода между лучами, отраженными от изомодуляционных слоев в формирующими предметную волну (см.рис.2). Таким образом длинноволновые трехмерные отражающие и пропускающие голограммы формируют масштабно-неискаженные объемные изображения объектов по законам геометрической оптики, причем спектральный состав восстановленного изображения близок к спектральному составу реконструирующего излучения и при освещении белым светом подобные голограммы формируют черно-белое неискаженное объемное изображение.
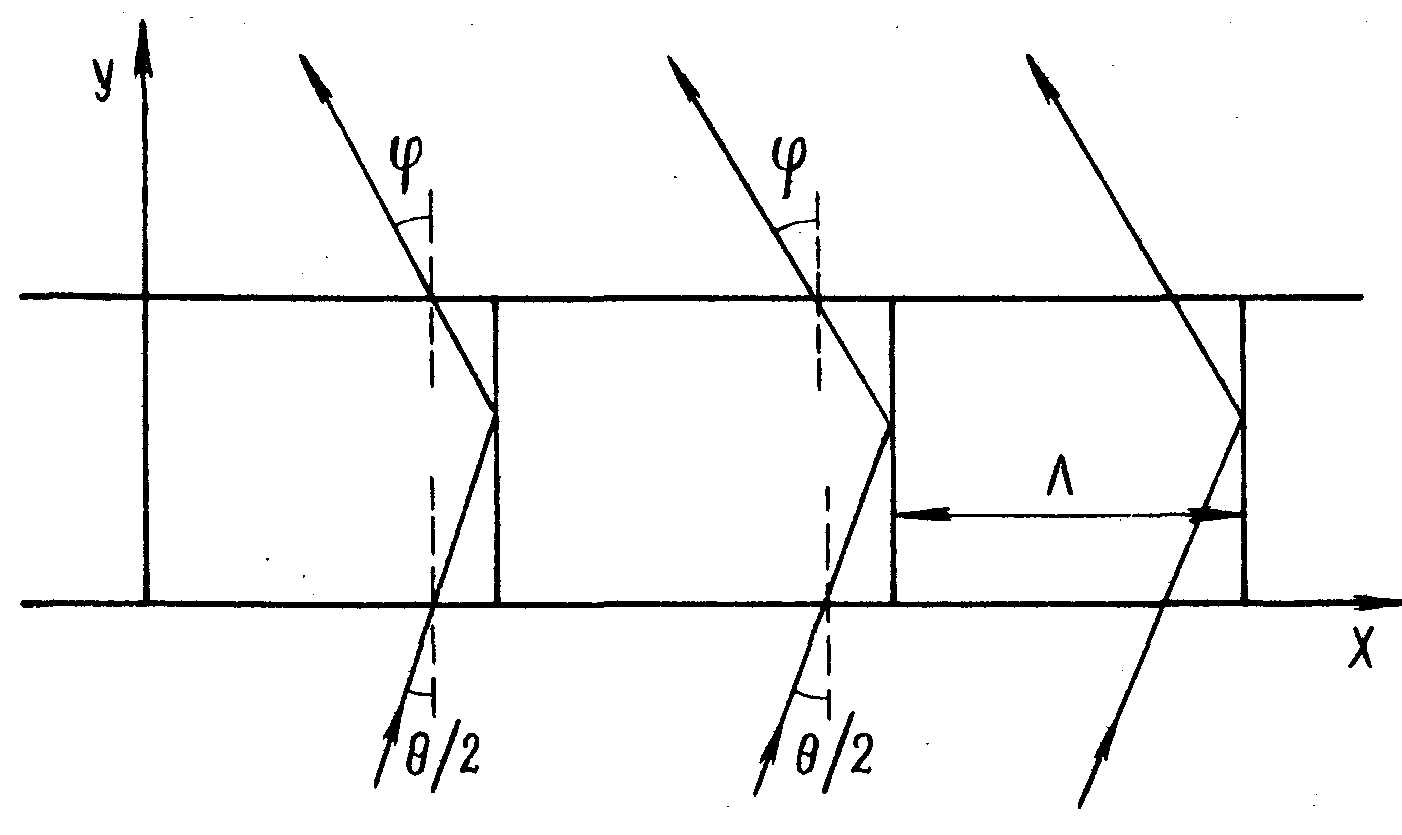
Рис.2. Длинноволновая объемная пропускающая голограмма плоских волн.
Яркость изображения, формируемого объемными длинноволновыми голограммами, может достигать большой величины, поскольку практически все спектральные составляющие реконструирующего излучения участвуют в формировании изображения.
Следует заметить, что угловая разрешающая способность таких голограмм зависит от длины волны реконструирующего излучения.
Длинноволновые голограммы могут найти применение в качестве голографических оптических, в том числе экранных, элементов, работающих во всем видимом диапазоне, а также при визуализации масштабно неискаженных объемных изображений в СВЧ и акустической голографии /1-3/
.
Перейдем теперь к обоснованию выводов, изложенных выше, и покажем, что объемные голограммы, зарегистрированные в ИК и более длинноволновом диапазоне, при восстановлении в видимом диапазоне формируют масштабно неискаженное изображение по законам геометрической оптики.
Здесь мы остановимся на анализе длинноволновых объемных голограмм, образованных двумя плоскими волнами (предметной и опорной), поскольку произвольную функций пространственных координат, в том числе и голограмму любого сложного объекта, можно разложить в ряд Фурье, т.е. представить в виде суммы синусоидальных решеток.
Предположим теперь, что объемная фазовая голограмма, образованная двумя плоскими волнами длинноволнового диапазона, угол между которыми равен θ, освещается плоской монохроматической волной видимого диапазона о угловой частотой
ω и длиной волны λ, причем нормаль к волне лежит в плоскости ху и составляет угол θ/2 с осью у (см.рис.2). Будем считать, что углы θ/2, φ θ т.д. измеряются по часовой стрелке от положительного направления оси у к направлению, по которому распространяется свет. Предполагается также, что 0≤θ/2<π/2, σглы θ/2, близкие к π/2, соответствуют случаю объемных отражающих голограмм, углы θ/2, существенно отличающиеся от π/2, соответствуют случаю объемных пропускающих голограмм.
Запишем уравнения Максвелла, котором удовлетворяют комплексные амплитуды векторов электромагнитных волн в любой точке (кроме границ раздела сред) для немагнитной непроводящей среды с диэлектрической проницаемостью ε, зависящей от пространственных координат и времени:
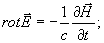
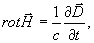
(1а)
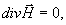
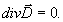
(1б)
Очевидно, что диэлектрическая проницаемость фазовой голограммы является функцией пространственных координат. В рассматриваемом случае эту функцию можно представить в виде:
ε = ε
0 + ε1coskx, (2)
где
k =2π/Λ величина волнового вектора длинноволновой пространственной решетки (голограммы), Λ - расстояние между изомодуляционными плоскими слоями.
Исключая
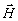 из (1а) и используя соотношения
из (1а) и используя соотношения 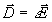 ,
, 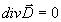 и тождество
и тождество 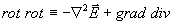 , найдем, что
, найдем, что
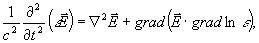 (3)
(3)
С учетом (2) можно найти, что второй член в правой части (3) приблизительно в
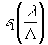 раз больше первого. Поскольку в рассматриваемом случае Λ>>λ, ςо выражение (3) можно переписать:
раз больше первого. Поскольку в рассматриваемом случае Λ>>λ, ςо выражение (3) можно переписать:
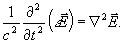 (4)
(4)
Предположим теперь, что реконструирующая монохроматическая плоская электромагнитная волна линейно поляризована и ее электрический вектор перпендикулярен плоскости падения (Е - поляризация), т.е. направлен вдоль оси
z . В этом случае компоненты Ех и Еу вектора 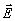 будут малыми величинами ~
будут малыми величинами ~ 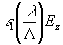 и поэтому ими можно пренебречь /9/. С учетом (2) выражение (4) можно переписать:
и поэтому ими можно пренебречь /9/. С учетом (2) выражение (4) можно переписать:
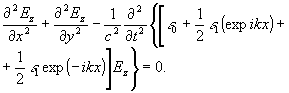 (5)
(5)
Решение уравнения (5) представимо в виде множества плоских
волн с разными направлениями распространения /9/:
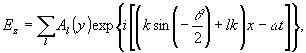 (6)
(6)
где суммирование ведется по всем целым значениям
l ( l = 0; ±1; ±2 и т.д.).
Такая форма возможного решения следует из существования многократных отражений и преломлений в слоистом веществе с плоскими параллельными поверхностями.
Подставив (6) в (5) и приравняв коэффициенты при экспонентах нулю, получим следующие рекуррентные соотношения для амплитуд спектров различных порядков (
Al(у)):
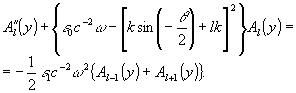 (7)
(7)
Решение уравнения (7) позволяет определить приближенные выражения для интенсивностей спектров различных порядков.
Не решая
(7), можно видеть, что (6) представляет cобой суперпозицию плоских волн c частотой ω, причем х - компонента волнового вектора этих волн - равна kSin(-θ/2)+lk. Следовательно, синус угла φ, который нормаль к волне с частотой ω образует с осью у вне рассеивающей среды, равняется
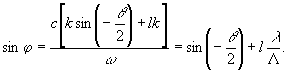 (8)
(8)
Как следует из (8), при Λ
>>λ βторым членом в правой части (8) можно пренебречь и считать, что волны распространяются в одном направлении, а следовательно, надобность в решении уравнения (7) отпадает и выражение (8) можно переписать:
φ=-θ/2. (9)
Легко видеть, что выражение
(9) справедливо в случае освещения
рассматриваемой длинноволновой голограммы белым некогерентным светом, поскольку каждая спектральная составляющая будет распространяться в направлении, описываемом этим выражением. Однако в этом случае вследствие того, что длина когерентности белого реконструирующего излучения значительно меньше разности хода между волнами, отраженными от изомодуляционных слоев (
ρ<<2Λsinθ/2) корреляционная функция этих волн описывается δ-функцией /1,2/. Как известно из теории дифракции частично когерентного света, это приводит к тому, что волны, отраженные от изомодуляционных слоев, будут складываться по интенсивности /9/:
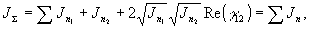 (10)
(10)
где
n - количество изомодуляционных слоев, γ12 - комплексная степень когерентности.
Следовательно, в случае реконструкции в белом свете предметная волна восстанавливается по законам геометрической оптики.
Легко показать, что полученный вывод справедлив и для амплитудных длинноволновых голограмм.
У амплитудных голограмм диэлектрическая проницаемость ε=с
onst, а проводимость σ является функцией пространственных координат:
σ = σ
0 + σ1сoskx. (11)
В случае реконструирующей монохроматичной волны уравнения для проводящей среды формально идентичны уравнениям для непроводящей среды, если в эти уравнения ввести комплексную диэлектрическую проницаемость
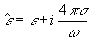 вместо вещественной диэлектрической проницаемости ε /9/. Аналогия с непроводящими средами станет еще ближе, если, кроме комплексной диэлектрической проницаемости
вместо вещественной диэлектрической проницаемости ε /9/. Аналогия с непроводящими средами станет еще ближе, если, кроме комплексной диэлектрической проницаемости 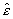 ввести также комплексное волновое число
ввести также комплексное волновое число 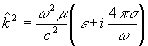 , комплексную фазовую скорость
, комплексную фазовую скорость 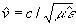 , комплексный показатель преломления
, комплексный показатель преломления 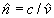 . Легко видеть, что в этом случае так же, как и в случае фазовой голограммы, рассматриваемая задача сводится к
. Легко видеть, что в этом случае так же, как и в случае фазовой голограммы, рассматриваемая задача сводится к
решению уравнения
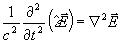 . (12)
. (12)
Решением уравнения (12) так же, как и уравнения (4), в случае Е - поляризации является совокупность плоских волн. В случае
Λ>>λ угол, который нормаль к плоской волне частотой ω образует с осью у вне рассеивающей среды, определяется выражением , аналогичным выражению (9), и в случае реконструкции в белом свете восстановленная предметная волна формируется по законам геометрической оптики.
Рассмотренными выше свойствами обладают также длинноволновые объемные динамические голограммы, у которых расстояния между изомодуляционными слоями в любой момент значительно больше длины волны реконструирующего излучения. Действительно, в случае, когда диэлектрическая проницаемость является функцией пространственных координат и времени и описывается выражением ε
= ε0 + ε1Cos(kx - Ωt) где частота колебаний диэлектрической проницаемости и значительно меньше частоты световых колебаний (Ω<<ω), решение уравнения (5) перепишется следующим образом:
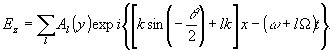 (13)
(13)
Как следует из (13), угол
φ, который нормаль к волне с частотой φ+ lΩ образует с осью у вне рассеивающей среды с учетом того, что Λ>>λ θ Ω<<ω, равняется
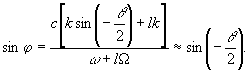 (14)
(14)
Выражение (14) совпадает с (9) и можно сделать вывод, что также динамические голограммы формируют изображения с широким спектральным составом по законам геометрической оптики при реконструкции в белом свете.
Для экспериментального подтверждения сделанных выше выводов были напылены диэлектрические зеркала с различными значениями оптической разности хода между волнами, отраженными от соседних
диэлектрических покрытий. Следует заметить, что диэлектрические зеркала можно рассматривать как искусственные голограммы, ибо в основе формирования ими изображения лежат те же законы, что и при реконструкции объемных голограмм. Как видно из рис.3, на котором приведены графики спектрального коэффициента отражения
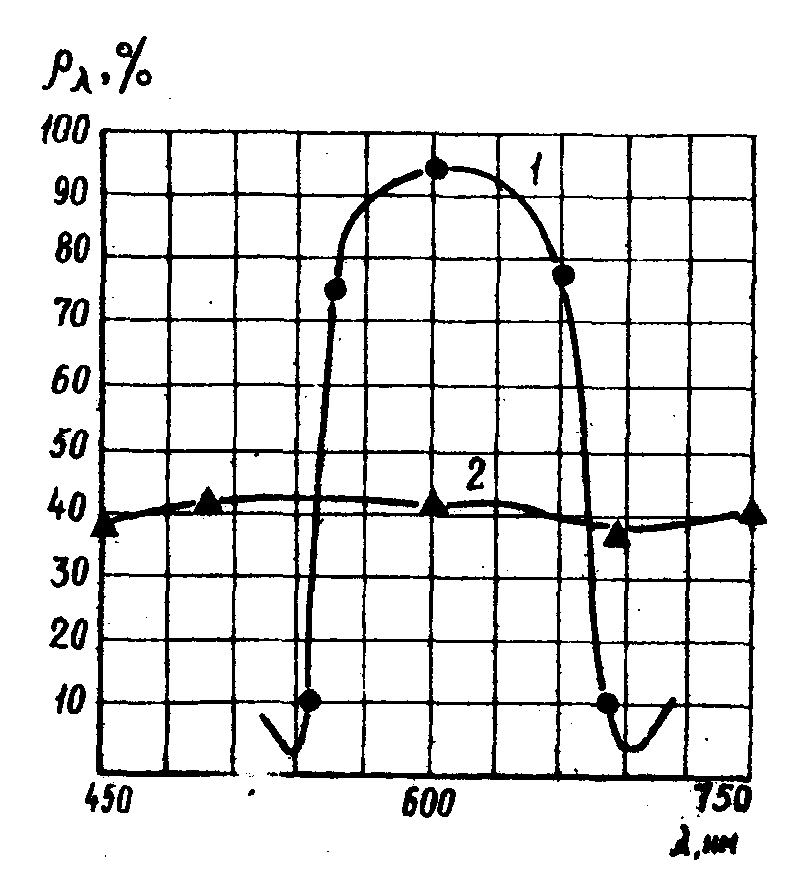
Рис.3. Кривая 1 - спектральная кривая диэлектрического зеркала с оптической разностью хода
d=0,6 мкм. Кривая 2 - спектральная диэлектрического зеркала с оптической разностью хода d=12 мкм.
и пропускания таких зеркал в зависимости от длины волны при освещении белым некогерентным светом, в случае, когда разность хода
d между волнами, отраженными от соседних изомодуляционных слоев, значительно больше длины когерентности реконструирующего излучения ρ (d=12 мкм>>ρ), ρпектр отражения расширяется.
Вообще говоря, спектр изображения, восстановленного с объемных длинноволновых голограмм, не будет сплошным, поскольку оптическая разность хода между соседними изомодуляционными слоями кратна целому числу длин волн для одних участков спектра (эти волны будут усиливаться) и кратна нечетному числу полуволн для других участков спектра (эти волны будут ослабляться).
Рассмотрим восстановление длинноволновой объемной голограммы в реконструирующих волнах λ и λ
' = λ-Δλ, δля которых разность хода между соседними изомодуляционными слоями, соответственно, равна kλ θ (к+1)λ, где k - любое целое число.
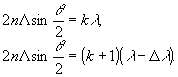
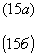
Из выражений (15а) и (15б) легко определить величину спектрального интервала между соседними участками спектра, для которых разность хода кратна целому числу длин волн:
Δλ=λ/
k. (15в)
Из 15в) следует, что с увеличением расстояния Λ спектральный интервал между соседними участками спектра, для которых разность хода кратна целому числу длин волн, уменьшается, что приводит к расширению спектрального состава восстановленного изображения, и при достаточно больших расстояниях Λ
>>ρ практически все спектральные составляющие участвуют в реконструкции изображения.
В заключение кратко остановимся на возможном способе получения длинноволновых объемных голограмм в акустическом диапазоне, а именно, на методе взвеси, который основан на открытом Релеем явлении ориентации плоских частиц в ультразвуковом поле (частица ориентируется по нормали к направлению распространения ультразвуковой волны). Последовательность получения длинноволновых голограмм данным методом состоит в следующем. На объемную кювету с суспензией (взвесь частиц, например, частиц алюминия в воде) с противоположных сторон падают когерентная предметная акустическая волна (волна, рассеянная
предметом) и опорная волна. При этом частицы алюминия, взвешенные в воде, под действием ультразвукового поля концентрируются в областях максимумов интерференционной картины. Интерференционная картина в кювете о суспензией будет представлять собой изомодуляционные слои частиц алюминия с расстоянием
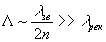 , т.е. фактически такая интерференционная картина является длинноволновой объемной отражающей голограммой. Поэтому при реконструкции белым некогерентным светом в данном случае сформируется масштабно неискаженное объемное изображение объекта.
, т.е. фактически такая интерференционная картина является длинноволновой объемной отражающей голограммой. Поэтому при реконструкции белым некогерентным светом в данном случае сформируется масштабно неискаженное объемное изображение объекта.
2.
Оптические объемные голограммы с широким спектральным
составом восстановленного изображения
Выше было показано, что длинноволновые объемные голограммы способны формировать изображение с широким спектральным составом по законам геометрической оптики.
Возникает вопрос: можно ли в оптическом диапазоне реализовать голограммы, имеющие такой же широкий спектральный состав восстановленного изображения. Оказывается, можно выделить определенный тип таких оптических голограмм. К числу таких голограмм относятся оптические отражающие голограммы с малой эффективной толщиной эмульсии порядка половины длины волны регистрирующего излучения (точнее порядка Λ~λ/2n). Рассмотрим подробно свойства подобных голограмм.
В работах /4-7/ рассмотрены спектральные свойства оптических отражающих голограмм при достаточно большой эффективной толщине эмульсии (объемных толстослойных голограмм). Как отмечалось выше, в основе физики формирования восстановленного изображения такой голограммы лежит Брэгговское отражение от расположенных достаточно близко друг за другом изомодуляционных слоев. Поэтому спектр отражения ее узкий и монохроматичный.
Если голограмма записана по схеме Денисюка, т.е. является отражающей голограммой, то интерференционная структура, соответствующая точечному объекту, представляет собой набор отражающих изомодуляционных слоев, которые описываются уравнениями второго порядка.
При малой эффективной толщине эмульсии, т.е. при малом числе
отражающих слоев, расположенных друг за другом, вклад в процесс восстановления изображения Брэгговских отражений от слоев становится пренебрежимо малым по сравнению с вкладом, вносимым зеркальными. отражениями от этих слоев реконструирующих лучей. Тем самым фильтрующие свойства отражающей голограммы с малой эффективной толщиной ослабевают. Это приводит к тому, что спектральный состав восстановленного изображения становится близким к спектральному составу реконструирующего излучения, т.е. спектр отражения такой голограммы расширяется /1,10,11/.
Для более детального исследования свойств подобных голограмм рассмотрим подробнее структуру интерференционной картины, которая образуется при эффективной толщине эмульсии голограммы порядка половины длины волны записывающего излучения. Для простоты положим, что предметная и опорная волна - сферические и что они падают на эмульсию с противоположных сторон под углом 180° друг к другу.
В этом случае изомодуляционные слои имеют гиперболическую форму и при малой эффективной толщине эмульсии, соизмеримой с половиной длины волны записывающего излучения, отрезки изомодуляционных слоев расположены таким образом, что сигнал от протяженного реконструирующего источника квазимонохроматического излучения в общем случае белого света подходит к ним с различных направлений (см.рис.4).
Полоним, что линейные размеры реконструирующего источника в расстояния между изомодуляционными слоями малы по сравнению с расстоянием R реконструирующего источника до голограммы и что реконструирующий источник представляет собой однородный источник в виде круга радиусом ρ.
В этом случае комплексная степень когерентности, которая описывает корреляцию колебаний в любой фиксированной точке Р(
y1,z1) центрального изомодуляционного слоя 1 и в переменной точки Р2(y
2,z
2), которая может располагаться на любом изомодуляционном слое рассматриваемой интерференционной структуры определяется выражением /9/:
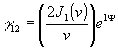 , (16)
, (16)
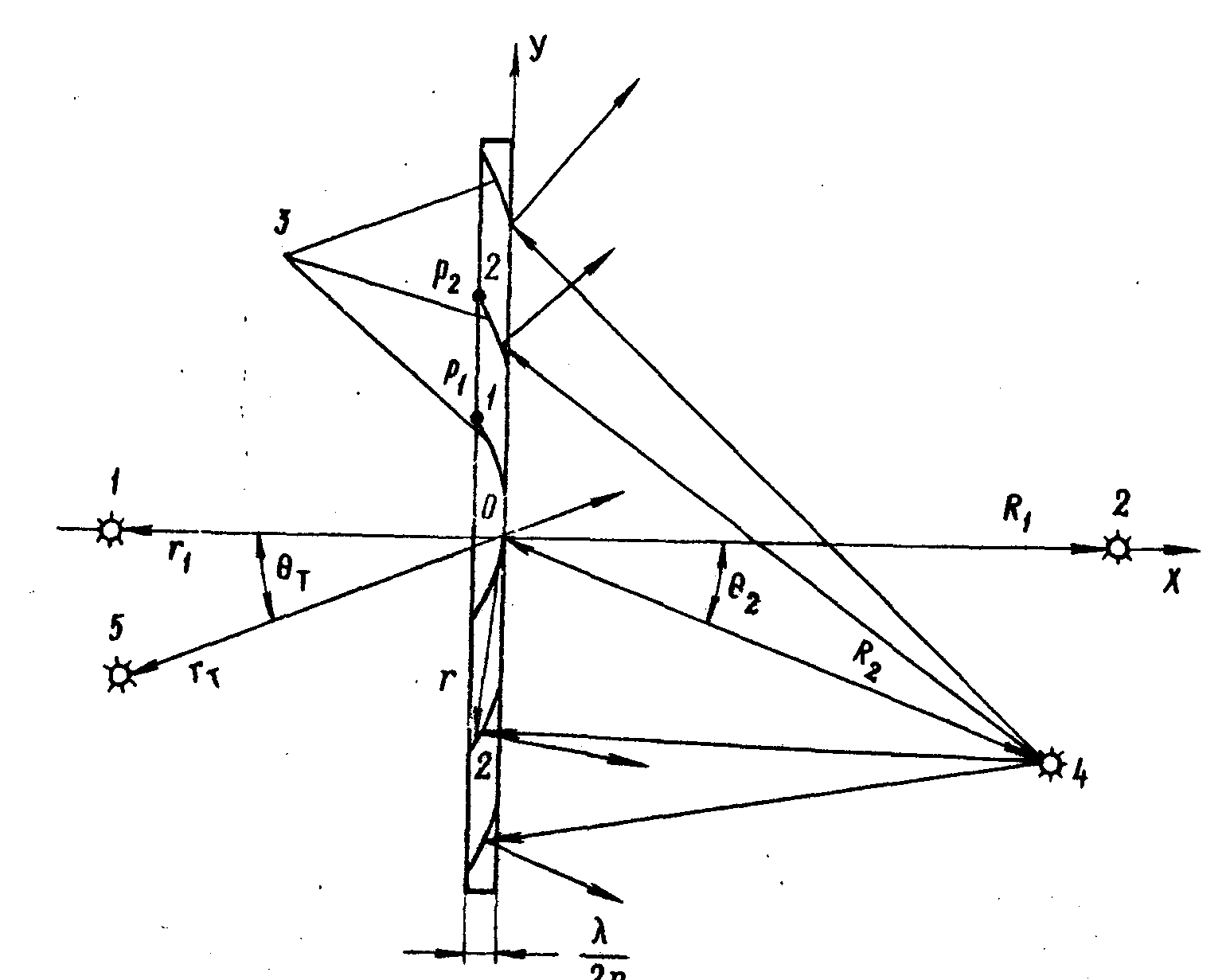
Рис.4. Геометрия запиcи и восстановления голограммы точечного объекта
c малой эффективной толщиной эмульсии:
1
- точечный объект; 2 - источник опорной волны;
3 - изомодуляционные слои; 4 - источник реконструирующей волны;
5 - мнимое изображение точечного объекта.
где
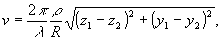
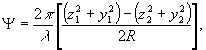
J1-
функция Бесселя первого рода первого порядка.
Из (16) видно, что степень когерентности монотонно уменьшается от значения, равного единице при v = 0,
до нулевого значения при v = 3,83, т.е. степень когерентности монотонно уменьшается, когда точки Р1 и Р2 удаляются друг от друга. При удалении Р1 и Р2 на расстояние P1Р2 =
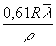 достигается полная некогерентность. При дальнейшем увеличении v вновь возникает небольшая когерентность, но степень ее остается меньше 0,14 и т.д.
достигается полная некогерентность. При дальнейшем увеличении v вновь возникает небольшая когерентность, но степень ее остается меньше 0,14 и т.д.
Таким образом, если отрезки изомодуляционных слоев располагаются на расстоянии Р
1Р2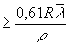 , то можно считать, что амплитуды реконструирующего сигнала на этих слоях не коррелированы между собой.
, то можно считать, что амплитуды реконструирующего сигнала на этих слоях не коррелированы между собой.
В рассматриваемом случае голограммы точечного объекта расстояние Р
1Р2 определяется выражением /12/
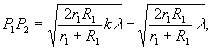 (17)
(17)
где
r1 - величина расстояния точечного объекта до голограммы; R1 - величина расстояния опорного источника до голограммы; k - номер изомодуляционного слоя.
С учетом (17) условие отсутствия фильтрации в голограмме с малой эффективной толщиной эмульсии перепишется :
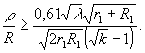 (18)
(18)
Как следует из (18), при
R1≤ 1000 см и 1 см ≤ r1 ≤ 100 cм, что справедливо для большинства практических схем голографии, амплитуды реконструирующего сигнала не коррелированы даже на первых двух соседних изомодуляционных слоях при угловых размерах реконструирующего источника 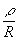 ≥ 0,24∙10-2 рад. Поскольку на практике угловые размеры реконструирующего источника белого света сравнимы c этой величиной, то амплитуды реконструирующего сигнала на различных слоях не коррелированы между собой и, следовательно, будет отсутствовать интерференция волн, отраженных от слоев, т.е. вклады каждого из слоев будут суммироваться. Поэтому в рассматриваемом
≥ 0,24∙10-2 рад. Поскольку на практике угловые размеры реконструирующего источника белого света сравнимы c этой величиной, то амплитуды реконструирующего сигнала на различных слоях не коррелированы между собой и, следовательно, будет отсутствовать интерференция волн, отраженных от слоев, т.е. вклады каждого из слоев будут суммироваться. Поэтому в рассматриваемом
случае вклад брэгговских отражений в формирование изображения мал, и в формировании изображения в основном участвуют зеркальные отражения реконструирующих лучей от каждого из этих слоев.
Таким образом, если интерференционная структура имеет достаточно малую глубину, то оптическая отражающая голограмма точечного объекта работает подобно зеркальному фокусирующему элементу, для которого соблюдаются законы геометрической оптики и, следовательно, при слабой зависимости коэффициента отражения слоев от длины волны она не меняет спектрального состава реконструирующего излучения /1,10,11/. Действительно, как следует из вышеизложенного, отрезки изомодуляционных слоев формируют изображение независимо друг от друга, причем легко показать, что каждый гиперболический изомодуляционный слой восстанавливает предметную волну в широком спектральном интервале.
Полученный результат в пренебрежении перекрестной интерференцией можно обобщить на случай голограммы с малой эффективной толщиной сложных объектов.
Перейдем к обоснованию выводов, изложенных выше, на основе теории, основные элементы которой рассмотрены в работе /10/.
Для этой цели исследуем структуру голограммы точечного объекта с малой эффективной толщиной эмульсии в кинематическом приближении теории возмущения
/13/ на примере простейших отражающих голограмм точечного объекта в системе координат с осью х, проходящей через этот объект и опорный источник.
Чтобы перейти к этому приближению, запишем скалярное волновое уравнение, учитывающее пространственную структуру голограммы /12/, ориентированной для удобства рассмотрения перпендикулярно оси х:
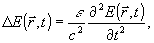 (19)
(19)
где
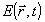 - реконструирующее излучение с учетом возмущения, вносимого голограммой, которое удобно представить его спектральным составом в виде:
- реконструирующее излучение с учетом возмущения, вносимого голограммой, которое удобно представить его спектральным составом в виде:
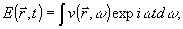 (20)
(20)
где
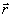 - радиус-вектор в толще голограммы; ε = ε0 + ε1 - диэлектрическая проницаемость голограммы; ε1 - изменение -диэлектрической проницаемости, вызванное экспонированием голограммы.
- радиус-вектор в толще голограммы; ε = ε0 + ε1 - диэлектрическая проницаемость голограммы; ε1 - изменение -диэлектрической проницаемости, вызванное экспонированием голограммы.
Учитывая (19) и (20), можно записать уравнение Гельмгольца для монохроматической составляющей
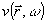 :
:
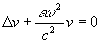 .
.
где С - скорость света в вакууме.
Предположим, что
ε1<<ε0 и что в толще голограммы вторичные переотражения достаточно малы. Тогда в кинематическом приближении
v = v0 + v1,
где v
0 удовлетворяет уравнению
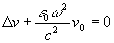 (21)
(21)
и является невозмущенной частью реконструирующего излучения, иначе говоря, нулевым приближением теории возмущения,
a v1 является возмущенной или, точнее говоря, отраженной частью реконструирующего излучения и представляет собой первое приближение теории возмущения. Оно удовлетворяет следующему уравнению:
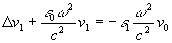 . (22)
. (22)
Для случая точечного объекта решение уравнения (21) имеет следующий вид:
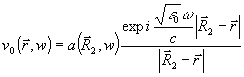 , (23)
, (23)
где
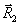 - радиус-вектор реконструирующего источника, а
- радиус-вектор реконструирующего источника, а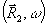 - амплитуда невозмущенной реконструирующей волны.
- амплитуда невозмущенной реконструирующей волны.
Однако это уравнение не учитывает распространение невозмущенной реконструирующей волны в толще голограммы. Этот факт можно феноменологически учесть, считая, что а зависит еще и от радиуса-вектора
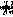 . С учетом этого
. С учетом этого
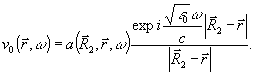
(23а)
Решение уравнения (22) представимо в виде:
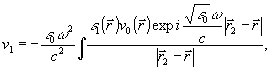 (24)
(24)
где
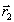 - радиус-вектор точки наблюдения.
- радиус-вектор точки наблюдения.
Учитывая соотношения (23а) и (24), а также тот факт, что
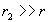 , можно приближенно представить интенсивность отраженной волны следующим выражением /11/:
, можно приближенно представить интенсивность отраженной волны следующим выражением /11/:
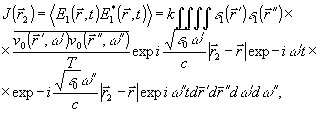 (25)
(25)
где
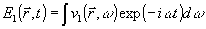 ,
,
здесь —— означает усреднение по ансамблю функций; Т - интервал времени регистрации сигнала
; k - постоянный множитель.
В силу эргодичности процесса интенсивность рассматривается как результат усреднения по ансамблю функций комплексных амплитуд.
Полученное соотношение связывает интенсивность восстановленного с отраженной голограммы изображения со спектральным составом реконструирующего излучения.
Рассмотрим полученный результат на примере отражавшей голограммы точечного объекта. В этом случае
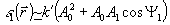 ,
,
где А
0 - амплитуда опорного излучения; А1 - амплитуда точечного объекта; k'- постоянный множитель.
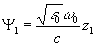 ;
; 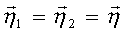 ;
;
с- скорость света в вакууме.
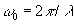 ,
,
λ- δ
лина волны записывающего излучения; 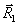 - радиус-вектор опорного излучения;
- радиус-вектор опорного излучения; 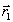 - радиус-вектор объекта.
- радиус-вектор объекта.
Выражение (25) удобно рассматривать в эллиптических координатах:
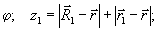
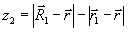 ,
,
где φ - угол вращения вокруг радиуса-вектора
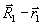 .
.
В этих координатах после интегрирования в (25) по
ω
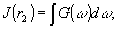
(25а)
где
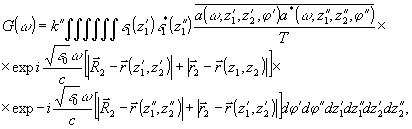
G(ω)
- спектральная плотность сигнала, формирующего восстановленное изображение; k"- постоянный множитель.
Выражение (25a) связывает интенсивность восстановленного с отражающей голограммы изображения со спектральным составом реконструирующего излучения. Как было указано выше, в случае реконструкции голограмм с малой эффективной толщиной эмульсии в белом свете, амплитуды реконструирующего сигнала на различных слоях не коррелированы между собой, т.е.
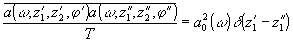 , (26)
, (26)
где
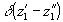 - дельта-функция.
- дельта-функция.
Рассмотрим
G(ω) с учетом соотношения (26). Тогда после интегрирования по φ' и φ"
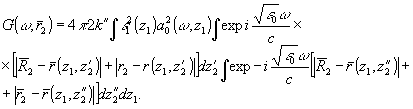 (27)
(27)
Во френелевском приближении:
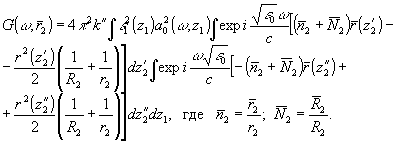
Рассмотрим в этом же приближении поверхности равной модуляции, структура которых зарегистрирована на голограмме в виде
ε1(z
1):
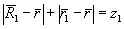 . (28)
. (28)
Разложим выражение (28) в ряд по
r:
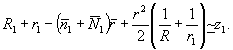
(28а)
С учетом ориентации голограммы относительно точечного объекта и опорного источника
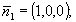
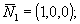
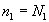 .
.
Равенство (28) легко переписать:
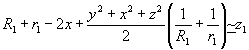 .
.
Предположим, что х
<<у,z (толщина во много раз меньше размеров голограммы), тогда
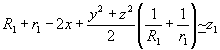 . (29)
. (29)
Таким образом, поверхности равной модуляции представимы с учетом того, что размеры голограммы значительно превосходят ее толщину, как
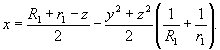
(29а)
Это уравнение описывает совокупность софокусных параболоидов вращения.
С учетом того же приближения, а также выражения
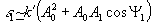 ,
,
можно представить
G в виде суммы двух слагаемых:
G=G0 + G+.
Из этих двух слагаемых интерес представляет
G+, поскольку оно формирует изображение точечного объекта:
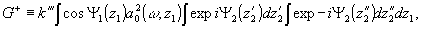
где
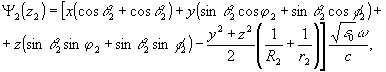 (30)
(30)
где
r2, θ2,φ2 - сферические координаты точка наблюдения;
R2
, θ2,
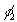 - сферические координаты реконструирующего источника;
- сферические координаты реконструирующего источника;
k'" - постоянный множитель.
Последнее выражение достигает своего максимума при условии, что отрезки изомодуляционных слоев значительно превосходят длину волны записывающего излучения и что фаза Ψ
2 стационарна, т.е. практически не меняется при переходе от центра О голограммы к ее периферии.
Фазу Ψ
2 перепишем с учетом соотношения (29а) в виде:
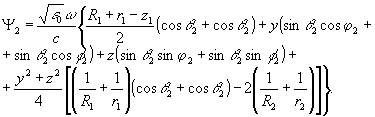 (31)
(31)
Пренебрегая аберрационными эффектами, в параксиальной области можно вывести следующие выражения для точки стационарной фазы (хт
, θт, φт):
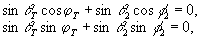
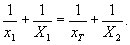
Решая эти уравнения определяем координаты восстановленного точечного изображения:
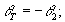
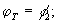
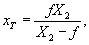
где 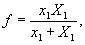 (32)
(32)
f
- эквивалентное фокусное расстояние.
Эти формулы аналогичны формулам зеркальных фокусирующих элементов.
Отсюда следует, что рассмотренные голограммы в отличие от всех
известных типов голограмм формируют объемное черно-белое изображение объектов при освещении белым светом.
Для подтверждения рассмотренных выше соображений была проведена запись голограмм по схеме Денисюка-Липпмана (см.рис.5). Излучение лазера
JIT-36A (1), расширенное коллиматором (2), освещало сквозь фотографическую эмульсию (3), на которой регистрировалась голограмма, объект (4). В толще эмульсии (3) регистрировался в виде стоячих волн результат интерференции излучения, рассеянного объектом, с излучением, идущим от лазера. Эффективная толщина эмульсии, соизмеримая с половиной длины волны записывающего излучения, достигалась образованием вблизи поверхности эмульсии хорошо отражающих и поглощающих слоев, глубина которых была сравнима с Λ ~ λ/2n, и которые не пропускали свет к глубинным слоям. С этой целью обработка проводилась с использованием пирогаллолового проявителя для пластинок ВРХ-НИИКРА и проявителя ГП-2 для пластинок ВРМ. Время проявления достигало 20 мин. При восстановлении в белом некогерентном свете формировалось объемное черно-белое изображение голографируемого объекта (в данном случае статуэтки). График распределения энергии по спектру в восстановленном изображении представлен на рис.6.
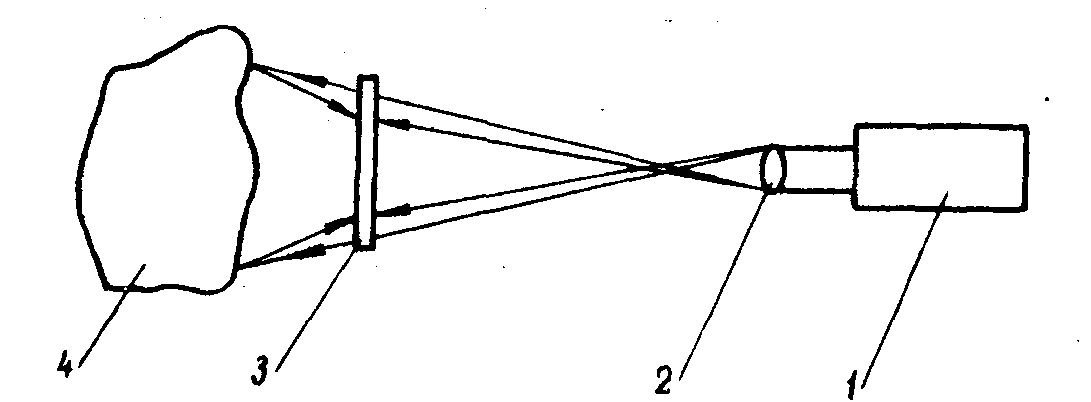
Рис.5. Схема записи голограмм с малой эффективной толщиной эмульсии:
1 - лазер; 2 - микрообъектив; 3 - фоточувствительная эмульсия; 4 - голографируемый объект.
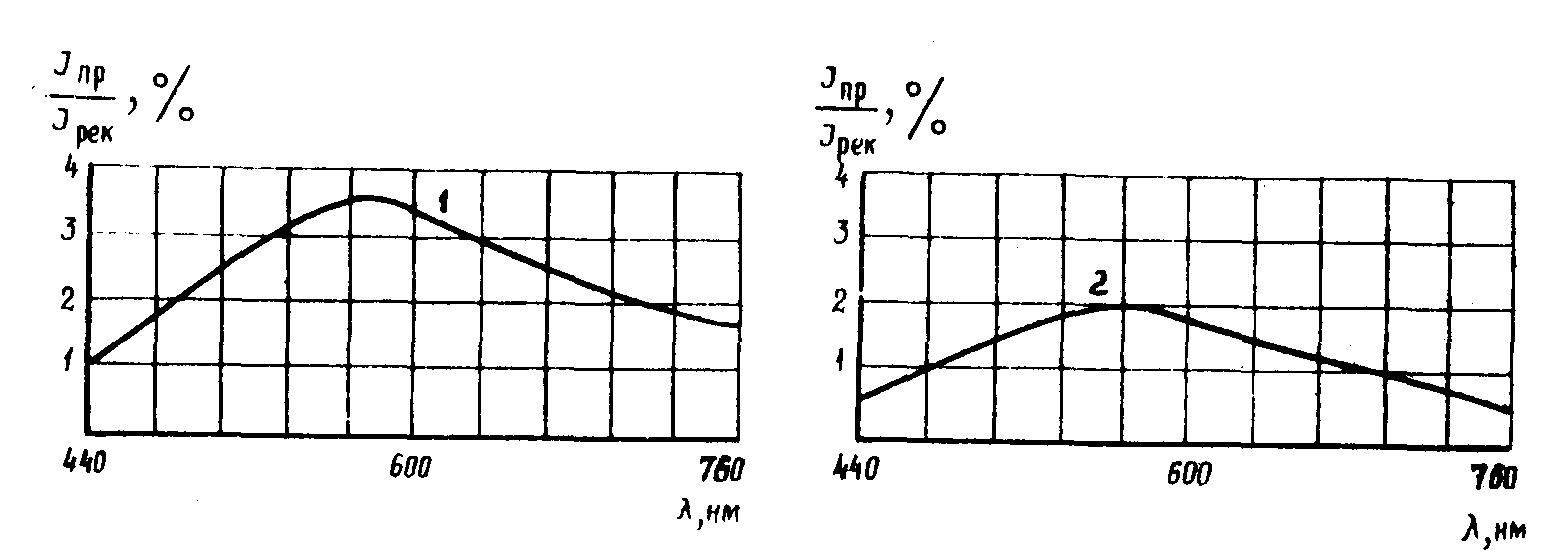
Рис.6.
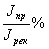 - отношение интенсивности восстановленной предметной волны к интенсивности реконструирующей волны; λ - длина волны реконструирующего излучения:
- отношение интенсивности восстановленной предметной волны к интенсивности реконструирующей волны; λ - длина волны реконструирующего излучения:
1 -
график распределения энергии по спектру в восстановленном изображении (пластинки ВРХ-НИИКРА);
2 - график распределения энергии по спектру в восстановленном изображении (пластинки ВРМ).
Была также экспериментально исследована динамика изменения спектрального состава формируемого голограммами изображения в зависимости от количества изомодуляционных слоев. С этой целью изготавливались диэлектрические зеркала (покрытия
ZnS, MgF2) с различным числом слоев. Поскольку диэлектрические зеркала можно рассматривать как искусственные голограммы, обладающие, как и отражающие голограммы, фильтрующими свойствами, то графики, показывающие изменение спектрального состава отраженными диэлектрическими зеркалами излучения в зависимости от количества диэлектрических покрытий (см.рис.7), качественно описывают динамику изменения спектрального состава восстановленного по отражающим голограммам изображения в зависимости от количества изомодуляционных слоев.
Экспериментально была получена отражающая голограмма выпуклого зеркала с малой эффективной толщиной эмульсии. Такая голограмма фактически представляла собой голографический оптический элемент, работавший во всем видимом диапазоне.
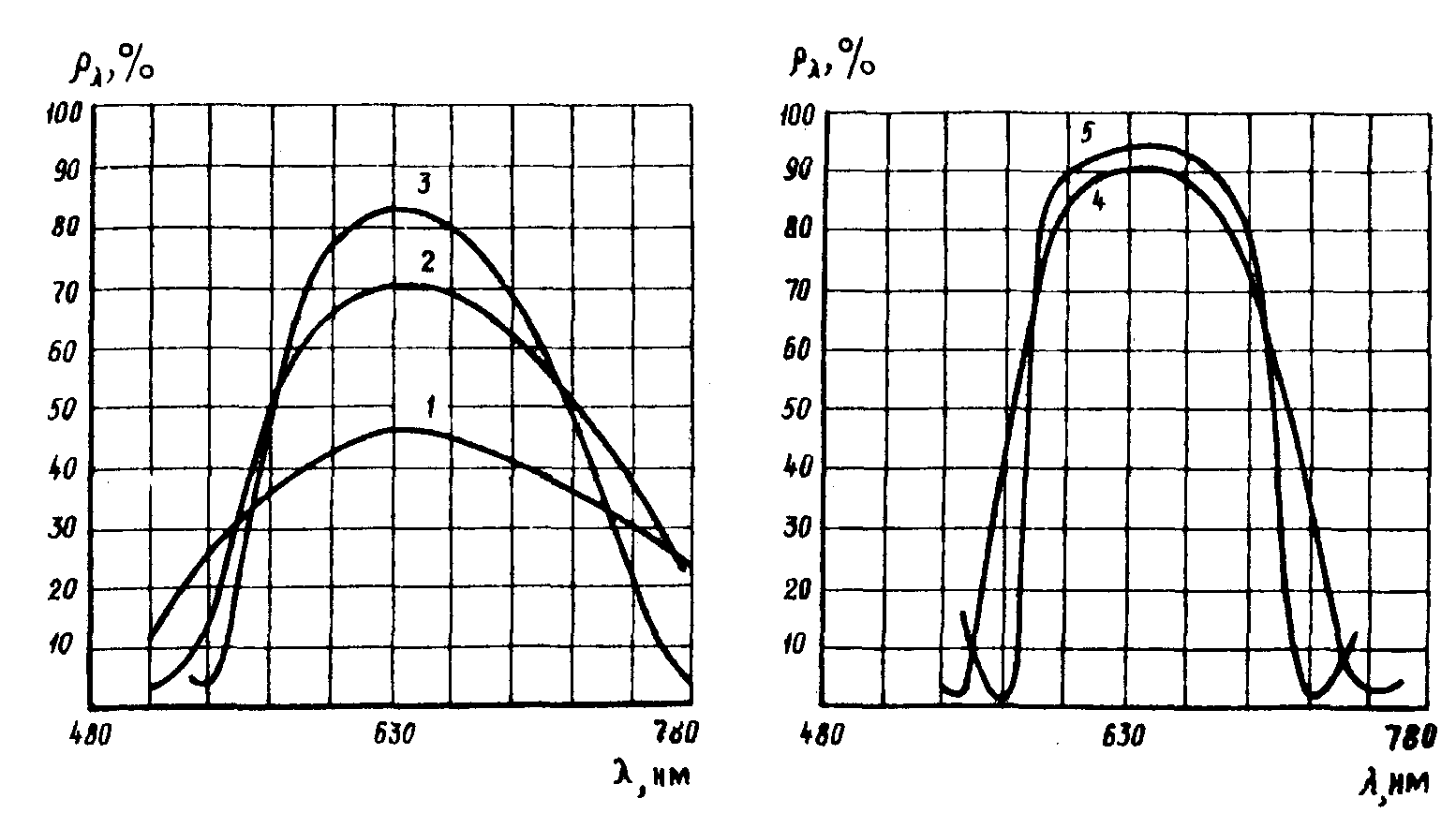
Рис.7.
1 - спектральная кривая 3-х слойного диэлектрического зеркала;
2 - спектральная кривая 5-ти слойного диэлектрического зеркала;
3 - спектральная кривая 7-ми слойного диэлектрического зеркала;
4 - спектральная кривая 9-ти слойного диэлектрического зеркала;
5 - спектральная кривая 11-ти слойного диэлектрического зеркала.
По схеме, описанной в работе /14/ был получен фрагмент голографического стереоэкрана с малой эффективной толщиной эмульсии, представляющий собой одну зону видения. Спектр отражения фрагмента широкий, что позволяет проецировать на такой фрагмент цветные изображения.
Однако следует отметить, что у всех полученных голограмм с малой эффективной толщиной эмульсии отношение интенсивности отраженной волны к интенсивности реконструирующей волны было незначительным (~3,5%).
Спектр восстановленного по оптическим объемным отражающим голограммам изображения можно расширить, увеличивая расстояние Λ между соседними изомодуляционными слоями
/1,11/. Действительно, как следует из (15в), в случае широкого спектрального диапазона реконструирующего излучения при восстановлении объемных отражающих голограмм с расстоянием Λ>>λрек фильтруется не одна, а несколько узких спектральных линий реконструирующего излучения, что и приводит к расширению спектра восстановленного изображения. Расстояние Λ можно увеличивать с помощью процессов, обратных процессу усадки эмульсии /1/. С этой целью толщину эмульсии готовой объемной отражающей голограммы, зарегистрированной по схеме Денисюка-Липпмана, увеличивали набуханием в воде и стабилизировали пропиткой в глицерине, что приводило, согласно работе /15/ к увеличению толщины эмульсии, а следовательно, и расстояния Λ, приблизительно в 10 раз. Спектр восстановленного по такой голограмме изображения расширялся, однако его яркость существенно падала, что можно объяснить уменьшением градиента комплексной диэлектрической проницаемости.
Следует отметить, что объемные отражающие голограммы при реконструкции наряду с изображением, формирующимся в отраженном излучении, в общем случае формируют еще два объемных изображения в прошедшем через голограмму излучении.
Действительно, как следует из теории объемных отражающих голограмм, распределение комплексной диэлектрической проницаемости в толще голограммы описывается выражением /4-7/:
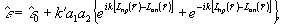
где
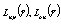 -эйконалы.
-эйконалы.
Такая голограмма, с одной стороны, будет отражать падающее на нее реконструирующее излучение за счет изменения комплексной диэлектрической проницаемости, в результате чего формируется объемное изображение в отраженном излучении. С другой стороны, изменение действительной части комплексной диэлектрической проницаемости в толще голограммы приведет к изменению фазы прошедшего через голограмму излучения.
Для простоты рассмотрим случай плоских опорных и реконструирующих волн. Если плоская реконструирующая волна является копией опорной, реконструирующее излучение, прошедшее через голограмму, описывается выражением:
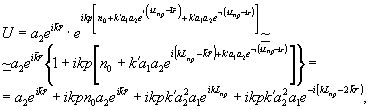 (33)
(33)
где р - толщина эмульсии голограммы.
Отсюда следует, что в данном случае объемная отражающая голограмма формирует еще два изображения в прошедшем через голограмму реконструирующем излучении.
Очевидно, к тому же выводу можно прийти при рассмотрении амплитудных отражающих голограмм с небольшим поглощением.
Легко видеть, что в случае плоских опорных и реконструирующих волн, изображения, формирующиеся в прошедшем через голограмму реконструирующем излучении с длиной волны λ
', отличаются от изображений, восстановленных на пропускание реконструирующим излучением с длиной волны λ, только добавочным фазовым сдвигом 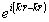 . Поэтому в прошедшем через голограмму параллельном пучке белого света сформируются два изображения с широким спектральным составом. Можно показать, что в случае сферических опорных и реконструирующих волн изображения, восстановленные на пропускание в разных длинах волн, отличаются масштабом, что в конечном итоге приводит к образованию двух хроматичных изображений при прохождении сферического пучка белого света через объемную голограмму.
. Поэтому в прошедшем через голограмму параллельном пучке белого света сформируются два изображения с широким спектральным составом. Можно показать, что в случае сферических опорных и реконструирующих волн изображения, восстановленные на пропускание в разных длинах волн, отличаются масштабом, что в конечном итоге приводит к образованию двух хроматичных изображений при прохождении сферического пучка белого света через объемную голограмму.
Как показали экспериментальные исследования при реконструкции фазовых объемных отражающих голограмм, помимо восстановленного объемного изображения в отраженном излучении с узким спектральным составом формировались два объемных изображения в прошедшем через голограмму реконструирующем излучении с широким спектром и незначительной хроматической окраской. В эксперименте использовались фотопластинки типа ПЭ-1 и ВРМ. Обработка проводилась с последующим
после проявления отбеливанием. В заключение укажем, что к оптическим голограммам с широким спектральным составом восстановленного изображения относятся объемные пропускающие голограммы, у которых расстояние между соседними изомодуляционными поверхностями Λ, формируемыми любой точкой объекта, и эффективная толщина эмульсии значительно превышают длину волны реконструирующего излучения. Подобные объемные пропускающие голограммы регистрируются в трехмерных средах при малых углах θ между предметной и опорной волной. Теоретическое и экспериментальное исследование процесса реконструкции таких голограмм проведено в работе /1/.
3.
Голограммы сфокусированных изображений с увеличенной
глубиной восстановления в белом свете
Выше были разобраны свойства оптических объемных голограмм с широким спектральным составом восстановленного изображения. Рассмотрим теперь свойства голограмм сфокусированных изображений с увеличенной глубиной восстановления в белом свете.
Как известно /12-16/, в методе голографии сфокусированных изображений регистрация стационарного интерференционного поля, возникающего в результате суперпозиции когерентных предметной и опорной волн, производится в плоскости резкого (сфокусированного) изображения предмета или вблизи нее. Основные особенности голограмм сфокусированных изображений обусловлены тем, что информация на них регистрируется в локальной форме - каждой точке предмета соответствует точка (малая область) на голограмме, благодаря чему реконструкция изображения, несомого восстанавливаемой волной, происходит в плоскости голограммы, либо вблизи нее.
При значительной глубине голографируемых объектов (сцен) восстановленные изображения локализуются на значительном расстоянии от фотопластинки, что приводит к сильному размытию изображения при восстановлении в белом свете. Кроме того, при восстановлении по таким голограммам формируется объемное изображение с искаженной на стадии регистрации через линзу перспективой, за исключением случая, когда линейное увеличение линзы, применяемой при регистрации, равно единице (β=1).
Можно показать, что при получении голограмм сфокусированных изображений и использовании как на стадии регистрации, так и на стадии восстановления либо одних и тех же, либо идентичных оптических систем (линз) с линейный увеличением на стадии регистрации, существенно меньшем единицы (βрег
<<1), можно восстанавливать в белом свете изображения объектов (сцен) без искажения перспективы, обладающих значительной глубиной /1/. Действительно, поскольку любая оптическая система вносит перспективные искажения, и сопряженные отрезки вдоль оптической оси как в пространстве предметов S1-S2, так и в пространства изображений S'1-S'2 связаны соотношением S'1-S'2=(S1-S2)β1β2, где β1, β2 -
поперечные увеличения в плоскостях, проходящих через края cопряженных отрезков /17/, то голографируемая объемная сцена глубиной S1-S2=H при восстановлении будет локализована от плоскости голограммы на максимальном расстоянии S' ~ Нβ1β2 и в случае β1β2<<0,
1 расстояние S будет незначительным даже при больших величинах H. Например, легко рассчитать, что при фокусном расстоянии f' = 100 мм и β1β2<<0,1,
что соответствует расположению объекта от линзы на расстоянии S≥110 cм, можно добиться того, что голографируемая объемная сцена практически любой глубины при восстановлении будет локализована от плоскости голограммы на расстоянии S'~1 см. Это приводит к качественной реконструкции в белом свете изображения голографируемой сцены большой глубины, причем восстановленное изображение для устранения перспективных искажений должно наблюдаться через идентичную оптическую систему, расположенную на таком же расстоянии от голограммы, что и при регистрации.
Исследуем более подробно влияние значения увеличения оптической системы, применяемой при записи голограмм сфокусированных изображений на глубину восстановления в белом свете. Размытие Δх производной точки восстановленного изображения, находящейся на некотором расстоянии S' от плоскости голограммы сфокусированного изображения, определяется очевидным соотношением /16,18/:
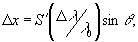 (34)
(34)
где Δ
λ - θнтервал длин волн, излучаемых источником.
С учетом того, что S'=Нβ
1β2, где Н - глубина регистрируемого объекта либо сцены, а также вследствие того, что восстанавливается изображение через ту же оптическую систему, что и на стадии регистрации, размытие Δх. определяется выражением
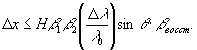 (35)
(35)
Выражение (35) можно переписать с учетом того, что βвосст
~1/βрез:
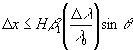 . (36)
. (36)
Из выражения (36) следует, что в случае
β1β2<<0,
1 глубина восстановления в белом свете может достигать значительно большей величины по сравнению со случаем β1β2≥0,
1. Так, например, голограмма, полученная в излучении с длиной волны λ0 = 6000Å и
угле падения опорного пучка θ = 30° при освещении источником со спектральной шириной Δλ = 60Å, в случае β1β2≥0,
1 формирует изображение объекта глубиной Н≤1 см, размытое на Δх~50 мкм. Голограмма, полученная при тех же условиях, но с увеличением β1β2<<0,
1, формирует такое же размытие при глубине объекта Н≥10 см. При одних и тех же значениях размытия Δх и глубины регистрируемого объекта Н можно в 1/β1 раз понизить требования к спектральной ширине реконструирующего источника и тем самым расширить спектральный состав восстанавливаемого изображения.
Исследуем теперь влияние увеличения оптической системы
β на требования к протяженности опорных источников в голографии.
Рассмотрение проведем на основании известных соотношений Майера для положения изображения в зависимости от геометрических параметров записи и восстановления /19/. В соответствии с этими соотношениями координаты внеосевой восстановленной точки изображения определяются выражениями:
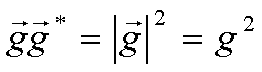 (37)
(37)
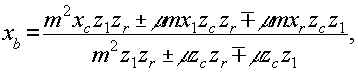 (38)
(38)
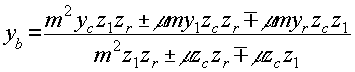 . (39)
. (39)
где
z1, у1, x
1 - координаты регистрируемого объекта; zr, yr, xr - координаты опорного источника; zс,у
с, хс - координаты реконструирующего источника; zb, уb, хb - координаты изображения; m - увеличение, реализуемое при переходе от регистрации к восстановлению; μ - отношение длин волн излучения, используемого при восстановлении и регистрации.
В рассматриваемом случае ось
Z направлена перпендикулярно плоскости голограммы, поэтому координаты zc, z1, zr и zb, характеризуют соответствующие расстояния от плоскости голограммы /19/.
Размытие точки изображения, обусловленное протяженностью восстанавливающего источника, определяется дифференцированием выражений (37-39)
:
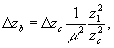 (40)
(40)
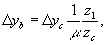 (41)
(41)
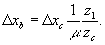 (42)
(42)
В случае голограмм сфокусированных изображений восстановленное изображение локализуется на расстоянии
z0=Hβ1β2,
от плоскости голограммы. Поэтому выражения (40-42) можно переписать с учетом того, что z0=Hβ1β2,
и того, что на стадии восстановления используется та же оптическая система, что и на стадии регистрации:
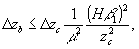 (43)
(43)
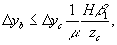 (44)
(44)
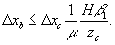 (45)
(45)
Из выражений (43-45) следует, что в случае
β1,
β2<<1
глубина регистрируемого объекта может достигать значительно большей величины по сравнению со случаем β1,
β2≥1.
При одних и тех же значениях размытия и глубины регистрируемого объекта Н в случае β1,
β2<<1
можно понизить требования к протяженности реконструирующего источника.
Следует отметить, что изменение
βрег можно добиться, варьируя положением линзы между объектом и плоскостью регистрации, а также фокусным расстоянием линзы.
Таким образом, использование при регистрации и восстановлении голограмм сфокусированных изображений одних и тех же оптических систем с увеличением на стадии регистрации, значительно меньшем единицы, приводит к увеличению глубины восстановления в белом свете и к снижению требований к протяженности и ширине спектра реконструирующего источника по сравнению со значением увеличения βрег≥1, а это, в свою очередь, приводит к расширению спектрального состава восстановленного изображения.
Поскольку изображение голографируемых объектов формируется линзой в непосредственной близости от эмульсии, то в случае регистрации голограмм сфокусированных изображений в трехмерной среде (βрег<<1) реконструкцию голограмм можно осуществлять в рассеянном излучении /20/.
Л и т е р а т у р а
1. Д.А.Цырульников. ЦИАМ. Труды №717, 1976.
2. Д.А.Цырульников. ЖНиПФиК, 20, 461, 1975.
3. Д.А.Цырульников. Сб. Метрология и измерительная техника, вып.5, 23, 1975.
4. Ю.Н.Денисюк, ДАН СССР,
144, 1275, 1962.
5. Ю.Н.Денисюк. Опт. и спектр.,
15, 522, 1963.
6. Ю.Н.Денисюк. Опт. и спектр.,
18, 275, 1965.
7. H.Kogelnik, Bell Syst.Tech.J., 48, 2909, 1969.
8. Н.Г.Власов, Ю.С.Мосякин, Г.В.Скроцкий. Квантовая электроника, вып.6, 116, 1971.
9. М.Борн, Э.Волъф. Основы оптики, "Наука", М., 1970.
10. В.И.Андросов, Д.А.Цирульников. ЖНиПФиК,
19, 447, 1974.
11. Д.А.Цирульников. ЖНиПФиК,
21, 103, 1976.
12. Р.Кольер, К.Беркхарт, Л.Лин. Оптическая голография. "Мир", М., 1973.
13. В.В.Аристов, В.Ш.Шехтман. УФН,
104, 51, 1971.
14. В.Г.Комар, В.И.Мандросов, Г.А.Соболев, Д.А.Цырульников. Некоторые свойства голографического экрана. Доклад на Международном конгрессе Интеркамера-73, г.Прага, 1973.
15. Ragnarsson Sven - Ingmar. Opt. Communs, 14, 39, 1975.
16. И.С.Клименко, Г.В.Скроцкий. УФН,
109, 269, 1973.
17. А.И.Тудоровский. Теория оптических приборов. Изд.АН СССР, М-Л, 1948.
18. G.B.Brandt, Appl.Opt, 8, 1421, 1969.
19. A.W.Meier. JOSA. 55, 987, 1965.
20. Ю.Н.Денисюк, В.И.Суханов. Опт. и спектр.,
25, 308, 1968.

