|
|
 |
 |

|
| |
ФАЗОВЫЕ ИЗМЕРЕНИЯ В КВАНТОВОЙ ОПТИКЕ
И ГОЛОГРАФИИ
В.Н.Курашов
Рассматривается проблема "полного" оптического эксперимента в квантовом пределе. Обсуждаются вопросы измеримости амплитудных и фазовых переменных для простой квантовомеханической модели интерференции двух волн; находятся состояния, минимизирующие их совместную неопределенность. Получены условия квантования коэффициента контрастности, доказана дискретность спектра собственных значений интерференционного оператора. Обсуждается связь голографических экспериментов с проблемой построения хорошо определенных фазовых операторов и их измерением.
1. В в е д е н и е
Голографическая методика регистрации волнового фронта с точки зрения общей теории измерений представляет собой реализацию "полного" оптического эксперимента, то есть определения амплитудно-фазовых характеристик электромагнитного излучения. Как известно, специфика оптических измерений не позволяет проводить прямое наблюдение полевых переменных неэнергетического типа, в том числе и фазовых. Введение референтной волны с известной фазой делает возможным косвенное измерение разности фаз (или ее функции) через регистрацию распределения интенсивности в интерференционной картине. Аналогичный принцип измерения применим, очевидно, и в квантовом пределе, однако здесь возникает целый ряд трудностей, связанных как с самой природой процесса регистрации в квантовой механике, так и со спецификой оптического детектирования, ограничивающего наблюдаемые величины лишь операторами определенной структуры /1/. Целью
настоящей работы является анализ особенностей квантовомеханических измерений фазовых переменных методом опорной волны. Рассмотрены два возможных подхода к этой задаче: первый, в идейном смысле близкий к традиционному голографическому, основан на измерении среднего значения интерференционного оператора; при втором используется представление о "хороших" фазовых операторах, наблюдаемых в квантовомеханическом смысле. Хотя оба подхода выявляют определенные общие черты процесса (разовых измерений, структура измерительного устройства для них оказывается существенно различной. В частности, строгая теория фазовых измерений основана на определении корреляционных функций высших порядков, в противоположность "интерференционному" методу, где регистрируются лишь корреляции второго порядка.
2. Квантовые эффекты в оптических измерениях
Прежде чем перейти непосредственно к обсуждению квантовомеханического измерения фазы оптического излучения, полезно коротко остановиться на обосновании необходимости такого подхода. Хотя современная теория голографии строится на чисто классическом описании, можно указать несколько причин, обуславливающих полезность более глубокого рассмотрения, учитывающего квантовые эффекты. Чаще всего достаточность классического волнового описания обосновывают большими значениями интенсивности излучения в голографии, при которых корпускулярный характер его становится несущественным. Однако, такое обоснование нельзя считать убедительным хотя бы потому, что в некоторых недавних экспериментах уровни сигнала приближались к квантовому пределу (подробное обсуждение см в /2/). Если же включить в рассмотрение многочисленные эксперименты по интерференции отдельных фотонов (описанные, например в /3,4/), становится очевидной необходимость общего формализма, объединяющего описание всех измерений подобного хода. Наконец, если рассматривать голографическую систему как систему информационную, предназначенную для передачи, хранения и преобразования оптической информации, представляют интерес ее предельные возможности, связанные с ограничениями фундаментального характера, естественным об-
разом вытекающими из квантовой природа взаимодействия электромагнитного излучения к регистрирующим приборам /5/.
Что же принципиально новое вносит квантовая теория в изучение когерентных оптических явлений? Прежде всего, квантовая механика есть теория статистическая, любое микросостояние объекта характеризуется неопределенностью измерений его физических параметров. Ввиду этого термин "измерение" может пониматься в двух различных смыслах. Чаще всего предполагается просто определение ожидаемого значения соответствующей случайной переменной. При более строгом подходе необходимо определить все статистические свойства измеряемой величины, то есть распределение вероятностей ее возможных значений в ансамбле измерений. Характерным проявлением квантовой теории в этом последнем случае оказывается собственно эффект квантования, то есть дискретизация отсчетов наблюдаемой. Как мы увидим далее, это явление возникает и для величин, представляющих непосредственный интерес в оптических когерентных системах. Наконец, существенно квантовая особенность измерительного процесса - соотношение неопределенностей - накладывает ограничения на совместное измерение двух или более переменных одновременно, ставя под сомнение возможность самого понятия "полного" эксперимента в том смысле, как он понимается в классической оптике. Пусть, например, требуется провести измерение наблюдаемых, описываемых эрмитовыми операторами 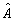 и и 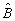 , для которых выполняется коммутационное правило , для которых выполняется коммутационное правило
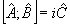 . (1) . (1)
Согласно принципу Гейзенберга, совместная неопределенность измерения этих величин удовлетворяет неравенству:
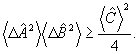 (2) (2)
Заметим, что, строго говоря, соотношение (2) не нарушается и в классическом пределе, поскольку константа t явно в него не входит. Таким образом, принципиальная возможность одновременного наблюдения двух или более физических величин определяется лишь алгеброй соответствующих операторов. Другими словами, квантовоме-
ханическое понятие полного эксперимента, основанное на определении полного набора коммутирующих операторов, образующих квантовомеханическое представление, существенно отлично от того, которое используется в классической оптике. Более того, нетрудно убедиться, что набор операторов чисел фотонов { 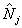 } в каждом нормальном типе колебаний возбужденного электромагнитного поля является полным, так что определение соответствующих интенсивностей {nj} представляет собой реализацию "полного" оптического эксперимента. (Аналогичное утверждение можно сделать и для набора фазовых операторов, однако, при этом необходимо использовать корректное определение последних /6/). Какой смысл в таком случае можно вкладывать в представление о голографическом эксперименте, как о совместном определении амплитудно-фазовых характеристик поля? Если мы хотим сохранить традиционный подход к этой задаче, очевидным обобщением является представление о состояниях, минимизирующих совместную неопределенность (2), как аналогах классических волн с фиксированной амплитудой и фазой, то есть "полный" оптический эксперимент оказывается лишь минимально неопределенным, для него выполняется знак равенства в (2). Метод определения таких состояний |Ψ>, основанный на вариационном принципе /7/, приводит к следующему уравнению: } в каждом нормальном типе колебаний возбужденного электромагнитного поля является полным, так что определение соответствующих интенсивностей {nj} представляет собой реализацию "полного" оптического эксперимента. (Аналогичное утверждение можно сделать и для набора фазовых операторов, однако, при этом необходимо использовать корректное определение последних /6/). Какой смысл в таком случае можно вкладывать в представление о голографическом эксперименте, как о совместном определении амплитудно-фазовых характеристик поля? Если мы хотим сохранить традиционный подход к этой задаче, очевидным обобщением является представление о состояниях, минимизирующих совместную неопределенность (2), как аналогах классических волн с фиксированной амплитудой и фазой, то есть "полный" оптический эксперимент оказывается лишь минимально неопределенным, для него выполняется знак равенства в (2). Метод определения таких состояний |Ψ>, основанный на вариационном принципе /7/, приводит к следующему уравнению:
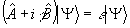 , (3) , (3)
где 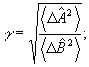 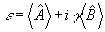 . Ввиду неэрмитовости оператора . Ввиду неэрмитовости оператора 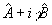 , в общем случае нельзя говорить о полноте и ортонормированности набора состояний |Ψ>, а следовательно, отождествлять скалярное произведение , в общем случае нельзя говорить о полноте и ортонормированности набора состояний |Ψ>, а следовательно, отождествлять скалярное произведение 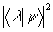 с плотностью вероятности совместного распределения с плотностью вероятности совместного распределения 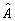 и и 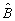 в состоянии в состоянии 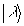 . Однако, в классическом пределе состояния с различными ε оказываются приближенно ортогональными, так что такое утверждение имеет место. В качестве примера можно привести когерентные состояния . Однако, в классическом пределе состояния с различными ε оказываются приближенно ортогональными, так что такое утверждение имеет место. В качестве примера можно привести когерентные состояния 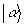 /8/, являющиеся пакетами, минимизирующими совместную неопределенность обобщенной координаты и импульса полевого осциллятора, которые в квазиклассическом смысле понимаются как состояния с заданными значениями этих величин. Аналогичные соображения можно, /8/, являющиеся пакетами, минимизирующими совместную неопределенность обобщенной координаты и импульса полевого осциллятора, которые в квазиклассическом смысле понимаются как состояния с заданными значениями этих величин. Аналогичные соображения можно,
очевидно, использовать и в амплитудно-фазовых оптических системах, определяя соответствующие наблюдаемые, эквивалентные измеряемым в эксперименте классическим величинам.
3. Квантовая модель интерференции
Для описания голографического эксперимента в квантовой оптике, рассмотрим простойную его модель, соответствующую регистрации картины интерференции двух нормальных волн в классической теории. Будем считать, что в объеме V возбуждены два типа колебаний, характеризуемые модовыми функциями Uj(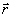 ), j = 1,2 и имеющие одинаковую частоту ω (см.рис.1). ), j = 1,2 и имеющие одинаковую частоту ω (см.рис.1).
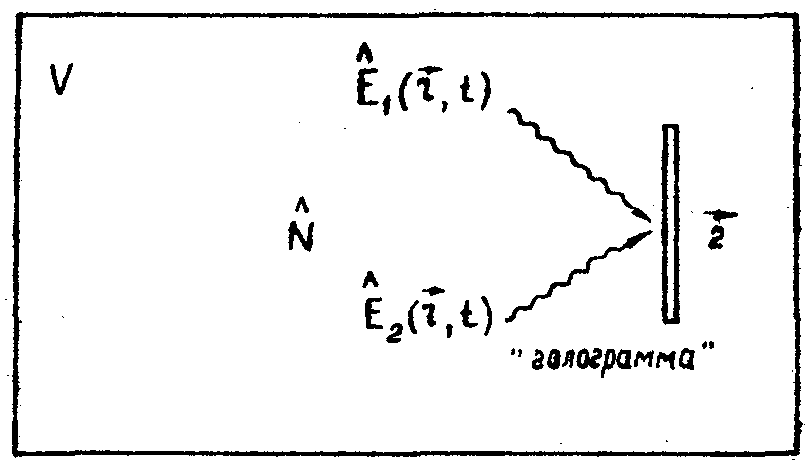
Рис.1. Регистрация интерференции двух нормальных волн в классической теории.
Идеальное регистрирующее устройство реагирует на среднюю интенсивность поля в некоторой области пространства, пренебрежимо мало возмущая его состояние. В соответствии с изложенным выше, интересующие нас эффекты можно определить следующим образом:
а) какие квантовомеханические величины подлежат измерению в эксперименте, аналогичном классической голографии?; б) имеют ли соответствующие операторы дискретный спектр, то есть являются ли такие наблюдаемые квантованными?; в) измеримы ли они совместно?; если нет, то для каких состояний произведение неопределенностей достигает минимума?
Для ответа на сформулированные вопросы учтем, что оптическое
регистрирующее устройство реагирует на величины энергетического типа. Определим поэтому оператор мгновенной интенсивности поля в точке 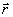 : :
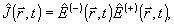 (4) (4)
где 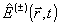 - положительно- и отрицательно-частотные части оператора напряженности электрического поля: - положительно- и отрицательно-частотные части оператора напряженности электрического поля:
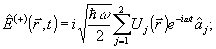 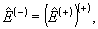 (5) (5)
и будем считать, что в простейшем эксперименте фиксируется среднее значение оператора 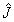 . Модовые функции . Модовые функции 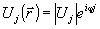 , нормированные обычным образом, , нормированные обычным образом,
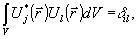 (6) (6)
определяют при этом пространственное распределение интерференционной картины, операторы рождения и уничтожения фотонов 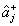 и и 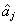 -ее контраст на заданном состоянии поля -ее контраст на заданном состоянии поля 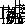 в некоторой точке в некоторой точке 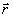 . Используя (5), представим оператор . Используя (5), представим оператор 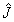 в виде в виде
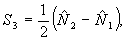 (7) (7)
где
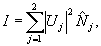 (8) (8)
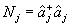
- оператор числа фотонов в j -том типе колебаний. Ясно, что слагаемое 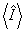 определяет среднюю интенсивность интерференционной картины при некогерентном сложении полей, а <g> - локальное значение ее контраста в некоторой точке определяет среднюю интенсивность интерференционной картины при некогерентном сложении полей, а <g> - локальное значение ее контраста в некоторой точке 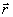 . Определим коэффициент контрастности κ( . Определим коэффициент контрастности κ(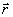 ) обычным образом, тогда: ) обычным образом, тогда:
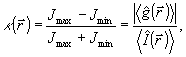 (10) (10)
где Jmax a Jmin - локальный максимум и минимум 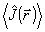 в окрестности точки в окрестности точки 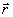 . Заметим, что поскольку оператор . Заметим, что поскольку оператор 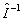 не определен ( о является точкой спектра не определен ( о является точкой спектра 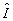 ), нельзя ввести оператор ), нельзя ввести оператор 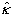 , эквивалентный коэффициенту контрастности в классическом случае. Однако, как следует из (10), измерение κ( , эквивалентный коэффициенту контрастности в классическом случае. Однако, как следует из (10), измерение κ(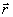 ) фактически связано с одновременным определением двух величин: ) фактически связано с одновременным определением двух величин: 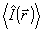 и и 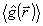 , причем эта процедура соответствует действительным измерениям в классическом пределе. Будем понимать поэтому под интерференционным измерением относительного амплитудно-фазового распределения поля , причем эта процедура соответствует действительным измерениям в классическом пределе. Будем понимать поэтому под интерференционным измерением относительного амплитудно-фазового распределения поля 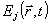 совместное определение наблюдаемых совместное определение наблюдаемых 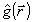 и и 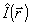 в каждой точке пространства. Таким образом, нам необходимо выяснить прежде всего, выполнимы ли такие измерения. Легко убедиться, что в общем случае они невозможны как для совпадающих, так и для различных точек пространства. Ограничиваясь в дальнейшем измерениями в одной точке в каждой точке пространства. Таким образом, нам необходимо выяснить прежде всего, выполнимы ли такие измерения. Легко убедиться, что в общем случае они невозможны как для совпадающих, так и для различных точек пространства. Ограничиваясь в дальнейшем измерениями в одной точке 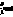 , найдем: , найдем:
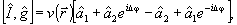 (11) (11)
где 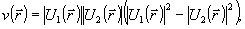 ; ; 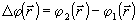 . При . При 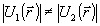 , , 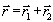 и, следовательно, и, следовательно, 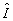 и и 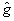 -не коммутируют. Однако, для мод определенного типа, например, плоских волн, условие коммутативности выполняется, в таком случае можно говорить о точном измерении коэффициента контрастности -не коммутируют. Однако, для мод определенного типа, например, плоских волн, условие коммутативности выполняется, в таком случае можно говорить о точном измерении коэффициента контрастности 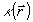 . Состояния, для которых это измерение даст определенные результаты, являются, очевидно, общими собственными функциями операторов . Состояния, для которых это измерение даст определенные результаты, являются, очевидно, общими собственными функциями операторов 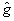 и и 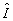 , а соответствующие измеряемые величины , а соответствующие измеряемые величины 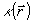 - отношением их собственных значений. Ввиду этого рассмотрим спектр операторов - отношением их собственных значений. Ввиду этого рассмотрим спектр операторов 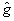 и и 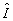 при при 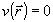 . Полагая для этого случая без ограничения общности . Полагая для этого случая без ограничения общности 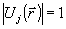 , получим , получим 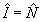 , так что собственные значения оператора , так что собственные значения оператора 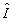 есть целые неотрицательные числа n = 0, 1,..., ∞, определяющие суммарное число фотонов в возбужденных модах. Для нахождения спектра есть целые неотрицательные числа n = 0, 1,..., ∞, определяющие суммарное число фотонов в возбужденных модах. Для нахождения спектра 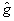 удобно перейти от полевых операторов удобно перейти от полевых операторов 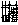 к операторам к операторам
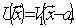 (12) (12)
обычным образом нормированным операторам уничтожения фотона, причем 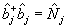 . Следуя Швингеру /9/, введем далее тройку операторов, . Следуя Швингеру /9/, введем далее тройку операторов,
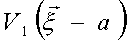 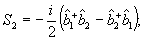 (13) (13)
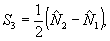
удовлетворяющих правилам коммутации проекций углового момента:
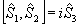 (14) (14)
и аналогично циклическим перестановкам. В этих операторах 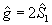 , так что собственное состояние |n,m> операторов , так что собственное состояние |n,m> операторов 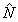 и и 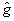 удовлетворяет уравнениям: удовлетворяет уравнениям:
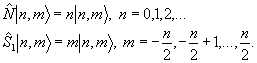 (15) (15)
Второе из равенств (15) непосредственно следует из коммутационных соотношений (14), если учесть, что оператор 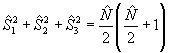 является аналогом квадрата момента количества движения с собственным значением является аналогом квадрата момента количества движения с собственным значением 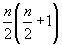 . Таким образом, точное измерение . Таким образом, точное измерение 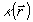 приводит к квантованным величинам коэффициента контрастности: приводит к квантованным величинам коэффициента контрастности:
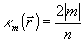 (16) (16)
для каждой пространственной точки 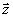 , изменяющейся от максимального значения , изменяющейся от максимального значения 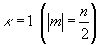 до минимального κ=0 (или до минимального κ=0 (или 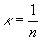 при n - нечетном). при n - нечетном).
Установим связь собственных функций | n,m> c пакетами, максимизирующими 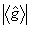 при фиксированной энергии возбуждения. Для этого рассмотрим экстремум функционала при фиксированной энергии возбуждения. Для этого рассмотрим экстремум функционала
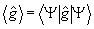 (17) (17)
при условиях
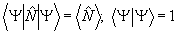 . (18) . (18)
Варьируя (17) по 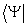 , найдем, учитывая (18), , найдем, учитывая (18),
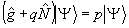 , (19) , (19)
где р, q - неопределенные множители Лагранжа. Как видно из (19), условный экстремум 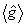 при фиксированном при фиксированном 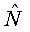 , а следовательно, и локальный экстремум κ, достигаются на собственных состояниях оператора , а следовательно, и локальный экстремум κ, достигаются на собственных состояниях оператора 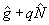 , коммутирующего как с , коммутирующего как с 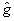 , так и с , так и с 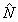 , т.е. являвшихся линейными комбинациями |n,m>: , т.е. являвшихся линейными комбинациями |n,m>:
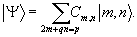 (20) (20)
Заметим, что р и q определяются через средние значения и дисперсии наблюдаемых величин. Действительно, усредняя (19) по состоянию |Ψ>, получим 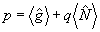 , a умножая (19) на , a умножая (19) на 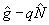 и учитывая коммутативность и учитывая коммутативность  и и 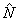 , найдем аналогично , найдем аналогично 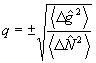 . В частности, среди состояний (20) имеются такие, для которых . В частности, среди состояний (20) имеются такие, для которых 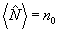 - целое и - целое и 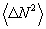 →0, так что они совпадают с функциями |n0,m0>. Нетрудно убедиться, что в этом случае q=1, р - целое число 0≤p≤2n0 /10/. Интересно отметить, что относительный экстремум видности интерференционной картины наблюдается как и в классическом случае, при равенстве интенсивностей возбужденных мод, поскольку в собственном состоянии оператора →0, так что они совпадают с функциями |n0,m0>. Нетрудно убедиться, что в этом случае q=1, р - целое число 0≤p≤2n0 /10/. Интересно отметить, что относительный экстремум видности интерференционной картины наблюдается как и в классическом случае, при равенстве интенсивностей возбужденных мод, поскольку в собственном состоянии оператора 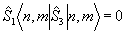 , а значит, , а значит, 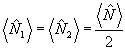 . Абсолютный максимум κ=1 достигается, однако, лишь при . Абсолютный максимум κ=1 достигается, однако, лишь при 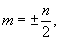 что является прямым следствием статистической природы квантовых измерений. что является прямым следствием статистической природы квантовых измерений.
4. Минимально-неопределенные пакеты
Рассмотрим теперь случай, когда для возбужденных типов колебаний 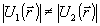 и, следовательно и, следовательно 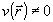 . Как было отмечено выше, точное измерение . Как было отмечено выше, точное измерение 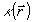 заменяется минимально неопределенным, для которого соотношение неопределенности превращается в равенство: заменяется минимально неопределенным, для которого соотношение неопределенности превращается в равенство:
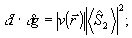 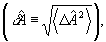 (21) (21)
так что относительная погрешность
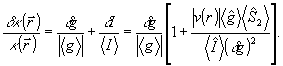 (22) (22)
Найдем состояния, на которых выполняется (22). Полагая в (3) 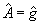 , , 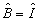 , будем искать собственную функцию оператора , будем искать собственную функцию оператора 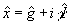 для для 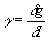 . Поскольку операторы . Поскольку операторы  и и 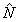 коммутируют, они имеют общую систему собственных функций |n,х>, для которых коммутируют, они имеют общую систему собственных функций |n,х>, для которых 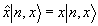 . Очевидно, что общее решение уравнения . Очевидно, что общее решение уравнения
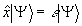 (23) (23)
для каждого собственного значения ε можно представить в виде
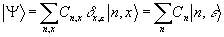 . (24) . (24)
Для определения функций | n,x> заметим далее, что они удовлетворяют уравнению
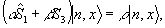 (25) (25)
где
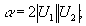 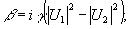 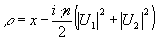 . (26) . (26)
Решение (25) удобно искать в представлении канонических полевых
операторов d, d+, определяемых равенствами:
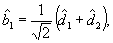 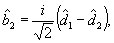 (27) (27)
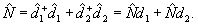 (28) (28)
Вводя собственные функции 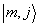 операторов операторов 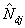 , запишем: , запишем:
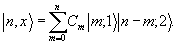 (29) (29)
Чтобы определить коэффициенты Cm, выполним замену 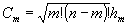 и найдем рекуррентное соотношение для hm: и найдем рекуррентное соотношение для hm:
z1(n-m+1)hm-1 + z2(m+1)hm+1 =2ρhm (30)
при граничных условиях h-1 = hn+1 = 0, в котором коэффициенты z1 и z2 определяются равенствами z1=α-iβ, z2=α+iβ. Для решения нелинейного уравнения (30) воспользуемся методом производящей функции. Положим
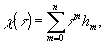 (31) (31)
так что 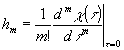 . Умножая (30) на τm и суммируя, получим уравнение для χ(τ): . Умножая (30) на τm и суммируя, получим уравнение для χ(τ):
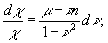 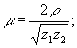 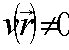 (32) (32)
интегрируя которое при начальном условии χ(0)=1, найдем
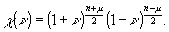 (33) (33)
Поскольку χ (ν) δолжно быть полиномом степени не выше n (иначе hn+1≠ 0), из (33) находим допустимые значения μ=2l-n, l=0,1,2,..., так что окончательно:
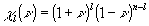 . (34) . (34)
Разлагая теперь χl(ν) по степеням ν,
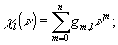 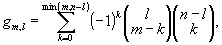 (35) (35)
найдем коэффициенты
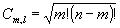 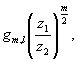 (36) (36)
определяющие функцию 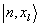 , отвечающую собственному значению , отвечающую собственному значению
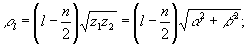 l=0,1,…n. (37) l=0,1,…n. (37)
Таким образом, решение (24) существует для собственных значений
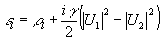
, то есть вновь, как и в предыдущем случае, оптимальные состояния, в которых измерения контраста интерференционной картины наиболее близки к классическим, образуют дискретное множество. Поскольку, далее параметр γ чисто действительный, из равенства
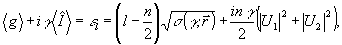 (38) (38)
где 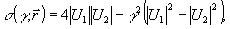 следует, что либо а) следует, что либо а) 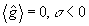 , либо б) , либо б) 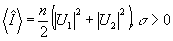 . Очевидно, что в первом случае критическое состояние описывает интерференционную картину нулевого контраста и не имеет поэтому физического интереса. В случае б), учитывая определение оператора . Очевидно, что в первом случае критическое состояние описывает интерференционную картину нулевого контраста и не имеет поэтому физического интереса. В случае б), учитывая определение оператора 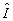 , снова получаем , снова получаем 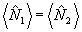 , однако здесь это равенство уже нельзя интерпретировать как классическое равенство интенсивностей, поскольку , однако здесь это равенство уже нельзя интерпретировать как классическое равенство интенсивностей, поскольку 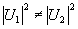 . Как и для точных совместных измерений . Как и для точных совместных измерений 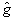 и и 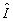 , минимально не определенные значения , минимально не определенные значения 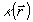 оказываются квантованными с шагом 1/n для каждого заданного значения γ: оказываются квантованными с шагом 1/n для каждого заданного значения γ:
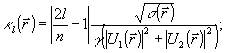 l=0,1,…,n. (39) l=0,1,…,n. (39)
Таким образом, квантовая природа измерительного процесса приводит к дискретизации локальной видности интерференционной карти-
ны. Говоря классическим языком, это явление можно было бы отождествить с эффектом квантования разности фаз Δφ двух типов колебаний. Действительно, значение контраста 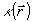 в некоторой точке в некоторой точке 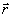 определяется величиной определяется величиной 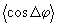 , ввиду чего дискретность , ввиду чего дискретность 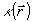 эквивалентна квантованию эквивалентна квантованию 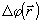 . Однако, такая прямая аналогия является лишь приближенной, поскольку не определена динамическая переменная . Однако, такая прямая аналогия является лишь приближенной, поскольку не определена динамическая переменная 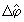 . Известные трудности, возникающие при этом, в последнее время были преодолены с помощью введения операторов, эквивалентных тригонометрическим функциям фазового угла /6,11/. В заключительном разделе установим связь такого подхода с интерференционным и дадим отрогов определение процедуры фазовых измерений в квантовой оптике. . Известные трудности, возникающие при этом, в последнее время были преодолены с помощью введения операторов, эквивалентных тригонометрическим функциям фазового угла /6,11/. В заключительном разделе установим связь такого подхода с интерференционным и дадим отрогов определение процедуры фазовых измерений в квантовой оптике.
5. Базовые операторы и их измерение
Рассмотренные выше интерференционные эксперименты можно интерпретировать как измерения фазы приближенно. Действительно, используя в квазиклассическом пределе представления Дирака 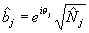 и считая, что операторы и считая, что операторы 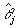 и и 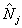 приближенно коммутируют для сильно возбужденных мод, найдем: приближенно коммутируют для сильно возбужденных мод, найдем:
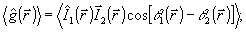 (40) (40)
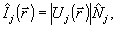
что соответствует обычно используемой процедуре фазовых измерений, основанной на определении усредненного значения косинуса разности фаз двух волн. Однако, уже из (40) видна неэквивалентность таких подходов, поскольку 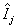 и и 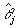 нельзя рассматривать как независимые случайные величины. Усреднение в (40) приводится по единой волновой функции, так что фазовые и амплитудные флуктуации не могут быть разделены. Более того, поскольку представление Дирака некорректно /12,6/, возникают дополнительные трудности при попытке использовать нельзя рассматривать как независимые случайные величины. Усреднение в (40) приводится по единой волновой функции, так что фазовые и амплитудные флуктуации не могут быть разделены. Более того, поскольку представление Дирака некорректно /12,6/, возникают дополнительные трудности при попытке использовать 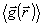 для определения самого понятия фазовых намерений. Наиболее строгий подход к этой задаче должен использовать, очевидно, прямую аналогию с классическим измерением величины <cosΔθ>, т.е. основываться на хорошо определенном опера- для определения самого понятия фазовых намерений. Наиболее строгий подход к этой задаче должен использовать, очевидно, прямую аналогию с классическим измерением величины <cosΔθ>, т.е. основываться на хорошо определенном опера-
торе 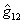 разности фаз двух полевых осцилляторов. Построение этого оператора может быть проведено известным образом /6/. Именно, определяя из принципа соответствия квантовый эквивалент величины eiθj: разности фаз двух полевых осцилляторов. Построение этого оператора может быть проведено известным образом /6/. Именно, определяя из принципа соответствия квантовый эквивалент величины eiθj:
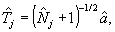 (41) (41)
положим, аналогично обычным тригонометрическим тождествам:
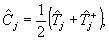 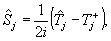 (42) (42)
так что
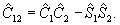 (43) (43)
Задача фазовых измерений сводится, таким образом, к определений  . Рассмотрим прежде всего некоторые общие свойства фазового оператора . Рассмотрим прежде всего некоторые общие свойства фазового оператора 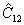 . Нетрудно показать, используя (41-43), что коммутирует с . Нетрудно показать, используя (41-43), что коммутирует с 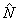 , т.е. пара операторов , т.е. пара операторов 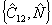 образуют квантовомеханическое представление, как и пара образуют квантовомеханическое представление, как и пара 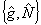 . Собственные значения . Собственные значения 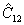 дискретны и определяются равенством: дискретны и определяются равенством:
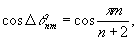 (44) (44)
а совместные собственные функции 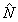 и и 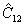
 (45) (45)
Как в для интерференционного оператора, допустимые значения косинуса разности фаз оказываются квантованными. В обычном понимания эта ситуация соответствует квантованным значениям угла между векторами состояния полевых осцилляторов на фазовой плоскости. Надо помнить, однако, что физический смысл имеет лишь величина cosΔθnm, а не угол Δθnm. Подобное рассмотрение можно выполнить и для оператора 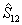 , причем представление , причем представление 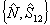 приводит к другим собственным функциям, поскольку приводит к другим собственным функциям, поскольку 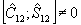 . Однако использование представления . Однако использование представления 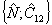 более удобно ввиду более удобно ввиду
отмеченной выше аналогии с классическим интерференционным экспериментом.
Пусть теперь требуется провести измерение 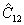 для поля двух возбужденных мод, находящихся в состоянии |Ψ>. Прямой метод вычисления для поля двух возбужденных мод, находящихся в состоянии |Ψ>. Прямой метод вычисления 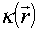 , основанный на разложении |Ψ> по функциям |n, cosθnm>, ничего не дает для построения процедуры таких измерений, поскольку не существует прибор, регистрирующий непосредственно cosθnm , основанный на разложении |Ψ> по функциям |n, cosθnm>, ничего не дает для построения процедуры таких измерений, поскольку не существует прибор, регистрирующий непосредственно cosθnm. Поэтому был предложен другой подход /13/, в котором использовалось нормальное разложение оператора 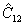 , связывающее измерение последнего с корреляционными функциями поля. Можно показать /11/, что , связывающее измерение последнего с корреляционными функциями поля. Можно показать /11/, что
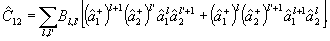 (46) (46)
где Bll' - численные коэффициенты. С точностью до детерминированного пространственного фазового сдвига 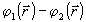 , связанного с модовыми функциями, нижайший член в (46) l=l'=0 совпадает с интерференционным оператором , связанного с модовыми функциями, нижайший член в (46) l=l'=0 совпадает с интерференционным оператором 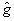 , так что измерение последнего есть, по существу, ограничение ряда (46) первым членом. Анализ показывает, что относительная величина поправки, обусловленной остаточным рядом, быстро убывает при увеличении средней интенсивности возбуждения, так что в классическом пределе измерения , так что измерение последнего есть, по существу, ограничение ряда (46) первым членом. Анализ показывает, что относительная величина поправки, обусловленной остаточным рядом, быстро убывает при увеличении средней интенсивности возбуждения, так что в классическом пределе измерения 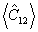 и и 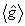 практически эквивалентны. Однако, если практически эквивалентны. Однако, если 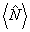 ~1, остаточные члены ряда l,l' >0 уже нельзя отбросить, а следовательно, строгая процедура измерений требует определения величин типа ~1, остаточные члены ряда l,l' >0 уже нельзя отбросить, а следовательно, строгая процедура измерений требует определения величин типа 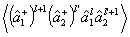 . Очевидно, что такие средние величины связаны с корреляционными функциями высших порядков, точно так же, как . Очевидно, что такие средние величины связаны с корреляционными функциями высших порядков, точно так же, как 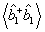 связано с функцией связано с функцией 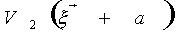 . Определим в общем случае . Определим в общем случае
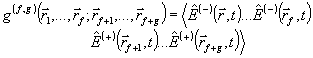 (47) (47)
и попытаемся выразить 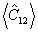 через через 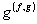 . Для этого воспользуемся соотношением ортогональности (6) и рассмотрим так называемые спектральные корреляционные функции, представляющие собой обобщенное преобразование Фурье-функций . Для этого воспользуемся соотношением ортогональности (6) и рассмотрим так называемые спектральные корреляционные функции, представляющие собой обобщенное преобразование Фурье-функций 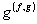 : :
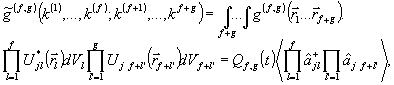 (48) (48)
где Qf,g(t) - численный множитель, содержащий е-iω(f-g)t, а каждый из индексов j может принимать значения 1 и 2. В частности , интересующее нас произведение
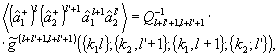 (49) (49)
где 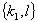 обозначает группу из l переменных k1. Таким образом, для измерения обозначает группу из l переменных k1. Таким образом, для измерения 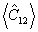 должны быть определены спектральные корреляционные функции с равными значениями индексов f = g, но различной комбинацией медовых функций. Заметим, что Qf,f не зависит от t, т.е. измерение должны быть определены спектральные корреляционные функции с равными значениями индексов f = g, но различной комбинацией медовых функций. Заметим, что Qf,f не зависит от t, т.е. измерение 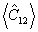 , как и в классическом случае, остается стационарным и может быть выполнено прибором с большой постоянной времени, что типично для голографического процесса. Окончательно находим: , как и в классическом случае, остается стационарным и может быть выполнено прибором с большой постоянной времени, что типично для голографического процесса. Окончательно находим:
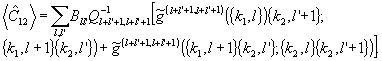 (50) (50)
Практически применимость выражения (50), конечно, ограничена нижайшими членами. С точностью до l,l≥1 соответствующие измерения требуют, кроме обычных интерференционных экспериментов, измерения корреляций интенсивности /13/. Однако полезность общего ре-
зультата (50) обусловлена установлением принципиальной связи фазовых измерений в квантовой оптике с корреляционными функциями высших порядков, а также возможностью оценить скорость сходимости квантовой процедуры измерения к классической при увеличении интенсивности излучения.
Кроме того, поскольку (50) связывает структуру идеального фазового детектора с выбором представления фазовых операторов (коэффициентов В ll'), имеется возможность избегать трудностей неоднозначности фазовых операторов /6/, устанавливая определенным образом процесс их измерения.
Л и т е р а т у р а
1. Р.Глаубер. Когерентные состояния в квантовой теории. Сб.под ред. В.И.Маноко, М., "Мир", стр.26, 1972.
2. Б.А.Гришанин, Материалы VII Всесоюзной школы по голографии. Л., cтр.118, 1975.
3. R.Pflegor, L.Mandel. Phyы.Rev., 159, 1084, 1967.
4. G.Raynolds. Adv.Electron and Electron Phys., 286, 939, 1969.
5. И.А.Дерюгин, В.Н.Курашов. Квантовая электроника, вып.2, Киев, стр.229, 1967.
6. П.Каррузерс, М.Ньето. Когерентные состояния в квантовой теории, сб. под ред, В.Маноко, М., "Мир", стр.71, 1972.
7. R.Jackiw. J.Math .Рhуs., 9, 339, 1968.
8. Р.Глаубер. Квантовая оптика и квантовая радиофизика. Сб.под ред. О.В.Богданкевича и О.Н.Крохина, М.,"Мир", стр.90, 1966.
9. J.Schwinger. Quantum Theory of angular Momentum. Ed.L.Biedenharn and H.Van Dam, N.Y., p.229, 1963.
10. A.Shalom. J.Zak.Phys.Lett., 43 А, 13, 1973.
11. И.А.Дерюгин, А.А.Вишенский, В.Н.Курашов. Изв.ВУЗ "Физика", №12, стр.44, 1972.
12. L.Susskind, J.Glogower. Phyeics, 1, 49, 1964.
13. И.А.Дерюгин, А.А.Вишенский, В.Н.Курашов. Оптика и спектроскопия, т.38, №4, стр.751, 1975.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

