ПРЕДЕЛЬНО ДОСТИЖИМОЕ КАЧЕСТВО ГОЛОГРАФИЧЕСКОГО ИЗОБРАЖЕНИЯ
О.В.Рожков
На базе ранее описанной
/1/ методики исследовано качество (дифракционная эффективность, нелинейные искажения, динамический диапазон) восстановления изображения произвольного объекта с учетом типа голограммы, формы экспозиционной кривой /2/ и частотной характеристики регистрирующего материала. Основное внимание уделено тонким фазовым голограммам, пригодным для массового тиражирования путем тиснения /3/.
В в е д е н и е
В большинстве практических применений качество макроструктуры голографического изображения может быть оценено интегрально с помощью трех основных характеристик: дифракционной эффективности h
, определяющей максимальную яркость, коэффициента нелинейности kн, определявшего правильность воспроизведения градаций яркости, и отношения сигнал/шум (S/N) Σ, ξοределяющего усредненную зашумленность изображения /1/. Дифференциальные оценки предполагают исследование микроструктуры голографического изображения и позволяют выявить пятнистость, разрешающую способность, статистические свойства шума, спектральную селективность и т.п.; перечисленные характеристики (изображения) обычно являются вторичные и в значительной степени определяются схемой голографирования /4/ и видом объекта, т.е. могут быть изменены лишь дискретно, но не непрерывно.
С другой стороны, основные (макро) характеристики (в частности, дифракционная эффективность) голографического изображения зависят от параметров голографического процесса (например, экспозиции опорного пучка Нг, соотношения интенсивностей опорного и
сигнального пучков R, экспозиционной кривой регистрирующего материала и т.п.), которые могут быть непрерывно и достаточно просто изменены в процессе эксперимента. "Потребителя" же голографического изображения в большинстве случаев не интересуют непосредственно параметры голографического процесса, для него важен конечный результат - характеристики восстановленного изображения. Используя (определенную экспериментально или аналитически) зависимость каждой из характеристик изображения от параметров голографического процесса, можно построить, параметрическую кривую /1,5/, наглядно отображающую ту взаимосвязь между основными характеристиками изображения, которая индуцируется в силу внутренней специфики голографического цикла "запись-восстановление".
При этом весьма наглядным становится, например, такой хорошо известный как аналитически /1,5,6/, так и экспериментально /1,4,7,8/ факт, что по мере уменьшения дифракционной эффективности падает зашумленность восстановленного изображения и снижаются нелинейные искажения в воспроизведении градаций яркости. В то же время в качестве исследуемых (макро) характеристик изображения могут быть приняты какие-либо другие комбинации, например, "дифракционная эффективность - искажение цветовоспроизведения - цветовой констраст" для случая многоцветной, голограммы /9/.
Существенно, что и на данном этапе развития земной цивилизации не представляется возможным наглядное изображение параметрической кривой для случая, имеющего больше трех характеристик. При этом такая пространственная параметрическая кривая (см., например, рис.4 /1/) наиболее удобна для качественного анализа (сравнение качества изображения разных типов голограмм, при разных регистрирующих средах и т.п.). В то же время для количественного анализа наиболее удобны плоские параметрические кривые, наглядно отображающие взаимосвязь двух каких-либо характеристик из неограниченного набора. При этом обычно удобно выделить основную характеристику, например, дифракционную эффективность (являющуюся, кстати говоря, первичной, ибо при нулевой дифракционной эффективности голографическое изображение отсутствует и бессмысленно говорить о его качестве).
Прежде чем перейти непосредственно к (аналитическому) иссле-
дованию основных (макро) характеристик качества голографического изображения, рассмотрим возможные варианты описания регистрирующей среды, тем более, что в отличие от описания типов голограмм (см., например, гл.8 и 9 /10/), этот вопрос недостаточно обобщен и систематизирован.
§ 1.
Возможные варианты свойств регистрирующей среды
Основной характеристикой регистрирующей среды является экспозиционная кривая /2,10,11/. При этом в зависимости от способа регистрации изображения (фотография, амплитудная голограмма, фазовая голограмма) различают следующие виды экспозиционных кривых:
а) характеристическая кривая, описывающая зависимость (оптической) плотности D (т.е. десятичного логарифма коэффициента пропускания по интенсивности Т) от логарифма экспозиции Н;
б) "tа – H" кривая, описывающая зависимость амплитудного коэффициента пропускания tа (точнее, корня квадратного из коэффициента пропускания по интенсивности Т) от экспозиции Н;
в) фазоэкспозиционная кривая /2/, описывающая зависимость вносимых (про экспонированной и обработанной) регистрирующей средой фазовых искажений δ от экспозиции Н, в частном случае тонких фазомодулирующих сред, образующих поверхностный рельеф (фоторезисты, термопластики, слой полупроводник-металл и т.п.), называемая рельефоэкспозиционной кривой Δ(Ν) /2,8/.
Экспозиционная кривая часто снимается на нулевой (или очень низкой) пространственной частоте. В то же время для голографии существенно наличие пространственной несущей (частоты). С тем, чтобы обойти это несоответствие, обычно априори полагают, что не происходит изменения формы, снятой на нулевой пространственной частоте экспозиционной кривой, а по мере роста несущей частоты в большей или меньшей степени изменяется (в большинстве случаев - уменьшается) чувствительность, определяемая коэффициентом пропорциональности между (малым по сравнению с линейной областью экспозиционной кривой) размахом синусоидального распределения экспозиция и размахом синусоидального распределения, вносимых обработанной регистрирующей средой амплитудных или фазовых искажений.
Такое изменение чувствительности к записи синусоидального распределения экспозиции характеризуется частотной характеристикой регистрирующей среды. Некогерентному случаю (например, фотографии) соответствует частотно-контрастная характеристика (ЧКХ), а. когерентному (голографии) - модуляционная передаточная функция (МПФ) М(ν) /11/. Существенно, что по определению передаточной функции она применима только к линейному участку экспозиционной кривой. Однако в связи с тем, что обычно в голографии используются малые (относительно общего среднего уровня) коэффициенты модуляции распределения экспозиции (определяемые в первом приближении величиной 2
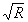 ), понятие МПФ может быть применено и к случаю регистрирующих сред с небольшой нелинейностью в пределах рабочего участка экспозиций Нмин÷Íмакс.
), понятие МПФ может быть применено и к случаю регистрирующих сред с небольшой нелинейностью в пределах рабочего участка экспозиций Нмин÷Íмакс.
В общем случае регистрирующая среда (на линейном участке экспозиционной кривой) должна описываться комплексной передаточной функцией
/11/:
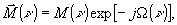
где Ω
(ν) ξοределяет сдвиг фаз между максимумами (или минимумами) распределения экспозиции и максимумами (или минимумами) амплитудных или фазовых искажений, вносимых обработанным регистрирующим материалом. Однако, поскольку на практике обычно Ω(ν) πΰвно 0 или π в зависимости от вида процесса регистрации (например, в фотографии - позитив или негатив), то учет фазовой составляющей комплексной передаточной функции необходим главным образом при анализе голограмм смешанного типа (например, тонкая амплитудная голограмма с рельефом /13/). Для большинства же применений достаточно одной МПФ (и экспозиционной кривой).
Возможные комбинации двух основных характеристик регистрирующей среды - экспозиционной кривой и МПФ - приведены в таблице 1. При этом каждая из основных кривых представлена дважды - в идеальном варианте (линейная экспозиционная характеристика в пределах рабочего участка экспозиций Нмин
÷Íмакс и горизонтальная МПФ в пределах пространственных частот 0÷
νмакс) и в общем виде. При этом негоризонтальная МПФ имеет отличную от нуля квазирезонансную частоту ν
кр, что соответствует, например, такой весьма перспективной регистрирующей среде как термопластик /14/. Однако в боль-
|
Примеры |
Прозрачные монодисперсные материалы |
Немонодисперсные фотоматериалы; фототермопластик на начальном участке экспозиц. кривой |
Фоторезист; прозрачные монодисперсные голографические фотоэмульсии |
Фототермопластик; немонодисперсные голографические фотоэмульсии |
|
Модуляционная передаточная функция |
|
|
|
|
|
Экспозиционная кривая |
|
|
|
Регистрирующая среда |
- Суперлинейная т.е. с линейнойэкспозиционной хаоактеристикой и горизонтальной МПФ
|
С линейным откликом, т.е. с линейной экспозиционной характеристикой и МПФ произвольной формы |
С нелинейной экспозиционой кривой, но горизонтальной МПФ |
Нелинейная
|
шинстве случаев, как уке упоминалось,
νкр= 0.
Легко понять, что если хотя бы одна из двух кривых (экспозиционная или МПФ), описывающих основные характеристики регистрирующей среды, имеет идеальную форму, то для описания голографической записи достаточно использовать одну интегральную характеристику - максимальное значение МПФ
[M(ν)]макс при горизонтальной МПФ, или чувствительность (определяемую произведением
[M(ν)]макс = М(ν
кр) на производную экспозиционной кривой) при линейной экспозиционной кривой, и одну дифференциальную - нелинейную экспозиционную кривую или негоризонтальную МПФ, соответственно. Это, естественно, заметно упрощает аналитические выкладки в отличие от четвертого случая, когда обе основные кривые, описывающие регистрирующую среду, не обладают идеальной формой, но нелинейность экспозиционной кривой невелика, ибо в противном случае понятие МПФ теряет смысл.
Для приведенного выше способа аналитического описания регистрирующей среды весьма существен вопрос о "линейности поведения" /2/, т.е. о справедливости использования на практике полученных в стандартных условиях слабой синусоидальной модуляции распределения экспозиции при снятии МПФ и фиксированной (обычно - нулевой) пространственной частоты при снятии экспозиционной кривой. Действительно, при реальном голографировании распределение экспозиции по плоскости голограммы носит весьма сложный характер (см., например. (7) и (8) /2/), что в силу целого ряда внутренних нелинейностей регистрирующей среды (например, из-за химического проявления) может привести к некорректным результатам. Для проверки "линейности поведения" рекомендуется /2/ сравнение семейств теоретических в экспериментальных кривых зависимости дифракционной эффективности элементарной голограммы (двух или трех плоских волн) от экспозиции при разных соотношениях R интенсивностей опорного пучка к сигнальному.
Соответствующая проверка для простейшего случая голограммы двух плоских волн была проведена для тонких амплитудных голограмм /12/ зарегистрированных на пластинках Агфа-Геверт 10E75 при пространственных частотах 11,5 и 60 л/мм /12/, и для рельефно-фазовых голограмм /2/, зарегистрированных в позитивном фоторезисте Шипли АZ-1350 /8/. В первом случае в "линейности" поведения регистри-
рующей среды можно быть более или менее уверенным для диапазона частот от 0 до ν< 60 л/мм, тогда как во втором - от 0 до ν ≈ 103 л/мм.
Зная (дифференциальное) описание свойств регистрирующей среды (экспозиционную кривую и МПФ) и будучи в большей или меньшей степени уверенным в "линейности" ее поведения, можно аналитически последовать параметры, определяющие качество голографического процесса. Приводимое ниже исследование до некоторой степени ограничено случаем тонких фазовых голограмм, что обусловлено, в частности, следующими четырьмя причинами:
1) их (предельная) дифракционная эффективность η≈0,3 весьма высока, что позволяет использовать маломощные источника для получения достаточно яркого изображения;
2) умеренная пространственная частота позволяет использовать не очень высокоразрешающие, а значит более чувствительные регистрирующие среды;
3) теория тонких голограмм достаточно строга и вместе с тем проста, чего нельзя сказать в случае толстослойных фазовых голограмм;
4) копии рельефно-фазовых голограмм при тиражировании способом тиснения имеют ничтожно малую стоимость /3/.
Тем не менее, будут частично затронуты вопросы контраста изображения, восстановленного с толстослойных фазовых голограмм, а также нелинейных искажений при воспроизведении градаций яркости голограммами всех четырех типов.
Использование в качестве основных (макро) характеристик контраста восстановленного изображения, связанного с интермодуляционным шумом (S/N)Σ /1,2,7/, и коэффициента нелинейности kн определяется их первостепенной практической значимостью, а также принципиальной неустранимостью этих искажений, по крайней мере, в случае фазовых голограмм.
§ 2.
Интермодуляционный шум фазовых голограмм
В соответствии с общими положениями теории преобразования сигналов в системах, любая нелинейность тракта (в случае голографического процесса - нелинейность экспозиционной кривой регистри-
рующего материала, нелинейность его поведения и нелинейность процесса восстановления) приводит к появлению интермодуляционных искажений. Последние в случае голографии проявляются в виде ложных изображений ("духов"), наложенных на основное изображение, восстанавливаемое в +1 порядке. В связи со сложностью расчета структуры этих "духов" рассмотрение практически всегда сводят к двум частным случаям.
В простейшем частном случае нескольких элементарных (сферических или плоских) сигнальных волн вычисляют интенсивность восстановленных изображений и интеркомбинационных тонов, дающих ложное изображение вблизи основного. Такое рассмотрение, проведенное, в частности в /6/, для двух сигнальных волн, носит скорее характер иллюстрации механизма возникновения интермодуляционных искажений в случае тонких фазовых голограмм (зарегистрированных в суперлинейной среде, т.е. в случае линейной фазоэкспозиционной кривой и горизонтальной МПФ).
В большинстве применений голографии имеют дело со случаем сложного объекта, когда расчет интеркомбинационных тонов практически невозможен, за исключением, пожалуй, случая голографических ЗУ, когда ввиду дискретной и регулярной структуры записываемого транспаранта возможно получить конечное решение /15/.
В то же время в случае сложного объекта микроструктура ложного интермодуляционного изображения ("духов") настолько сложна, что обычно не имеет смысла ее анализ как таковой, а достаточно ограничиться ее усредненной интенсивностью, определяющей в первом приближении контраст восстановленного изображения (черно-белого тест-объекта), а точнее - динамический диапазон цикла "запись-восстановление". Естественно, что такое рассмотрение может быть проведено только для (сложного) объекта с известной статистикой, в качестве которой обычно принимают релеевское распределение плотности вероятности сигнальной волны в плоскости голограммы и равновероятное распределение фазы /1,2,7/.
Положение о значительной "гладкости" микроструктуры интермодуляционного изображения легко проиллюстрировать качественно. Действительно, на стадии голографической регистрации сложного объекта, (cм.pиc.2 /2/) происходит запись гораздо более сложного (по сравнению с основным) интермодуляционного поля, распределение экспозиции
которого в плоскости голограммы (см.(7) /2/)
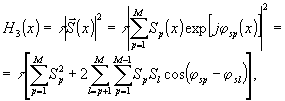
где τ - время экспозиции, а S и φ - амплитуда и фаза сигнальной волны обычно существенно сложнее собственной структуры объекта. В случае нелинейной экспозиционной кривой эта структура дополнительно (хотя и незначительно, ибо
SpSl <<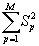 ) усложняется. На стадии восстановления шумовая субголограмма с амплитудным коэффициентом пропускания tш=exp[j F(Hs)] в случае тонкой фазовой голограммы создает сложнозашумленную восстанавливающую волну (см. рис.3 /1/ для случая суперлинейной среды, когда F=β/\∙ε, где ε - единичный оператор, a β/\ - чувствительный фазомодулирующей среды; для среды с нелинейной фазоэкспозиционной кривой соответствующая модель представлена на рис.3 /2/), микроструктура которой еще более усложнится при взаимодействии с основной (информационной) субголограммой. В результате в большинстве случаев ложное интермодуляционное изображение может в первом приближении рассматриваться как практически равномерный шум, приводящий лишь к уменьшению динамического диапазона восстановленного изображения. Однако наличие остаточной микроструктуры не позволяет полностью ликвидировать отрицательное воздействие интермодуляционного изображения на основное, используя, например, телевизионную систему с регулируемым уровнем "черного" /3,8/ с другой стороны, нет однозначных сведений о том, что шумовая микроструктура фона в системе "Holotape" /3/ - является результатом только интермодуляционных искажений набора рельефно-фазовых голограмм.
) усложняется. На стадии восстановления шумовая субголограмма с амплитудным коэффициентом пропускания tш=exp[j F(Hs)] в случае тонкой фазовой голограммы создает сложнозашумленную восстанавливающую волну (см. рис.3 /1/ для случая суперлинейной среды, когда F=β/\∙ε, где ε - единичный оператор, a β/\ - чувствительный фазомодулирующей среды; для среды с нелинейной фазоэкспозиционной кривой соответствующая модель представлена на рис.3 /2/), микроструктура которой еще более усложнится при взаимодействии с основной (информационной) субголограммой. В результате в большинстве случаев ложное интермодуляционное изображение может в первом приближении рассматриваться как практически равномерный шум, приводящий лишь к уменьшению динамического диапазона восстановленного изображения. Однако наличие остаточной микроструктуры не позволяет полностью ликвидировать отрицательное воздействие интермодуляционного изображения на основное, используя, например, телевизионную систему с регулируемым уровнем "черного" /3,8/ с другой стороны, нет однозначных сведений о том, что шумовая микроструктура фона в системе "Holotape" /3/ - является результатом только интермодуляционных искажений набора рельефно-фазовых голограмм.
А. Способы уменьшения интермодуляционных искажений
Известен ряд способов уменьшения интермодуляционного шума. С одной стороны, сюда относятся способы, устраняющие его в корне,- использование амплитудных голограмм, зарегистрированных на линейном участке "
tа - Н" - кривой. В этом случае интермодуляционное изобра-
жение возникает лишь вблизи нулевого порядка и при правильном выборе несущей частоты (см. /3,11/ также (20) в §2 п.Г) полностью отдельно от основного изображения.
В случае фазовых голограмм ввиду нелинейности фазовой модуляции как таковой /16/ в пределах основного изображения всегда возникает и интермодуляционное. Поэтому в данном случае возможно только его более или менее полное подавление, используя специфику интермодуляционного поля на стадии записи. В силу ограниченного углового размера объекта интермодуляционное поле имеет низкие пространственные частоты (включая нулевую). В результате можно попытаться либо уменьшать чувствительность регистрирующей среды к низким пространственным частотам (количественный анализ см. в §2 п.Г), что характерно, например, для фототермопластиков /14/, либо за счет специальных процессов добиться компенсации записанной на низких пространственных частотах шумовой субголограммы. Последнее достигается, например, использованием иммерсии на стадии восстановления, что компенсирует шумовую рельефно-фазовую субголограмму (при ηимм = ηрельефа). Ясно, что этот способ применим лишь в том случае, когда основная голограмма является либо амплитудной, либо толстослойной фазовой. В противном случае иммерсия приведет к ослаблению не только интермодуляционного шума, но и основного изображения.
В случае галогенидосеребряных эмульсий МПФ рельефно-фазовой составляющей часто имеет квазирезонансный характер с νкр ≈ 102 мм, что типично для интермодуляционного шума, тогда как основная МПФ плавно спадает от нуля до частот νмакс ≈ (1÷10)∙103 мм-1. В этом случае возможно использование иммерсии даже при записи основной информации в тонкой фазовой голограмме. Существенно, что в этом случае возможна "перекомпенсация", т.е. подавление даже той интермодуляционной информации, которая записана в виде тонкой фазовой шумовой субголограммы в толще эмульсии, а не на ее поверхности. Для этого обычно следует подобрать ηимм>ηрел, что обеспечит нулевые фазовые искажения для парциальных шумовых дифракционных решеток с пространственной частотой вблизи νкр за счет взаимной компенсаций фазовых искажений рельефно-фазовой шумовой субголограммы и тонкой фазовой шумовой субголограммы, записанной в толще эмульсии. При этом знак неравенства (ηимм > ηрельефа) опреде-
ляется соотношением фазовых частей Ω(ν) κξмплексной передаточной функции регистрирующего материала (см.§1) для рельефно-фазовой зaписи и для тонкой фазовой записи.
Аналогичного результата по частичной компенсации двух шумовых субголограмм (рельефной и записанной в толще эмульсии) можно достигнуть, управляя фазовой частью комплексной передаточной функции. С этой целью авторы /17/ использовали "реверсивное" отбеливание, что изменяет на 180° Ω(ν), т.е. вместо впадин рельефа образуются бугорки и наоборот.
В случае толстых фазовых голограмм можно надеяться на частичное подавление интермодуляционного шума за счет эффекта Брегга /7/. Действительно, эффективное восстановление любого изображения с толстослойной голограммы происходит только при освещении ее восстанавливающей волной под углом Брегга. Если восстанавливающая волна зашумлена, но эффект Брегга достаточно силен, то эффективно участвовать в процессе восстановления будет, в основном, только нерассеянная на (тонкой фазовой) шумовой субголограмме часть восстанавливающей волны. С другой стороны, обычно селективность реальных толстослойных фазовых голограмм по углу Брегга соизмерима с угловым размером объекта, что но позволяет полностью реализовать этот способ на практике.
Перейдем теперь к количественному анализу интермодуляционного шума, создаваемого тонкой фазовой голограммой сложного объекта.
Б. Интермодуляционный шум при линейной фазоэкспозиционной характеристике
Как показано в /1/, линейная (в пределах рабочего интервала экспозиций Нмин<Н<Нмакс) экспозиционная характеристика описывается единственным параметром - чувствительностью
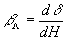 . В зависимости от формы МПФ различают суперлинейную среду (горизонтальная МПФ при 0≤ν≤νмакс
. В зависимости от формы МПФ различают суперлинейную среду (горизонтальная МПФ при 0≤ν≤νмакс) и регистрирующую среду с линейным откликом (но негоризонтальной МПФ).
Интермодуляционный шум диффузного объекта (с релеевским распределением плотности вероятности амплитуды сигнальной волны в плоскости голограммы), зарегистрированный в тонкой суперлинейной
фазомодулирующей среде, рассмотрен в /1,7/. При этом в /7/ основная (информационная) субголограмма считается толстослойной, зарегистрированной либо в суперлинейной фазомодулирующей среде, либо в толстой фазомодулирующей среде с квазирезонансной МПФ (νкр=νнес, М(νкр)=1) и линейной экспозиционной характеристикой. Последний случай является весьма проблематичным при практической реализации. В случае же суперлинейной фазомодулирующей среды из результатов /7/ следует уравнение параметрической кривой /1,5/ "отношение сигнал/шум - дифракционная эффективность":
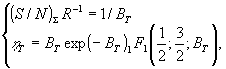
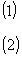
где Вт
=β/\∙Нr - параметр записи, а 1F
1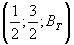
=
Ф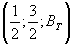 - вырожденная интергеометрическая функция.
- вырожденная интергеометрическая функция.
Удачный выбор нормировки первого уравнения позволяет обойтись единственной параметрической кривой (показанной точками на рис. ), справедливой, правда, как это следует из детального анализа /7/, только для высококонтрастного изображения (когда (
S/N)Σ >> 10). Исследование параметрической кривой, задаваемой (1)÷(2), ïоказывает, что дифракционная эффективность этой голограммы в случае диффузного, объекта не может превышать 64% /7/, что качественно объясняется неоптимальностью экспозиции при записи неравномерного по плоскости голограммы поля сигнальной волны. В результате этого одни участки оказываются недоэкспонированными, а другие переэкспонированными, что в обоих случаях дает местную дифракционную эффективность η(х,у)<100%. С другой стороны, при η<20% параметрическая кривая практически вырождается в прямую, в результате чего отношение сигнал/шум (S/N)Σ численно равно частному от деления R на η, что совпадает c результатом, полученным в /1/ -для тонкой фазовой информационной голограммы, зарегистрированной в суперлинейной среде.
Уравнение и семейство параметрических кривых "отношение сигнал/шум - дифракционная эффективность" для случая диффузного объекта, зарегистрированного в тонкой суперлинейной фазомодулирующей
среде, рассмотрено в /1/, где, однако, учтено снижение дифракционной эффективности из-за ухода части энергии восстанавливающей волны в интермодуляционное изображение (шум). Именно этот факт приводит (даже при удачном выборе нормировки) к образованию семейства параметрических кривых, что однако более или менее существенно лишь при
R<10.
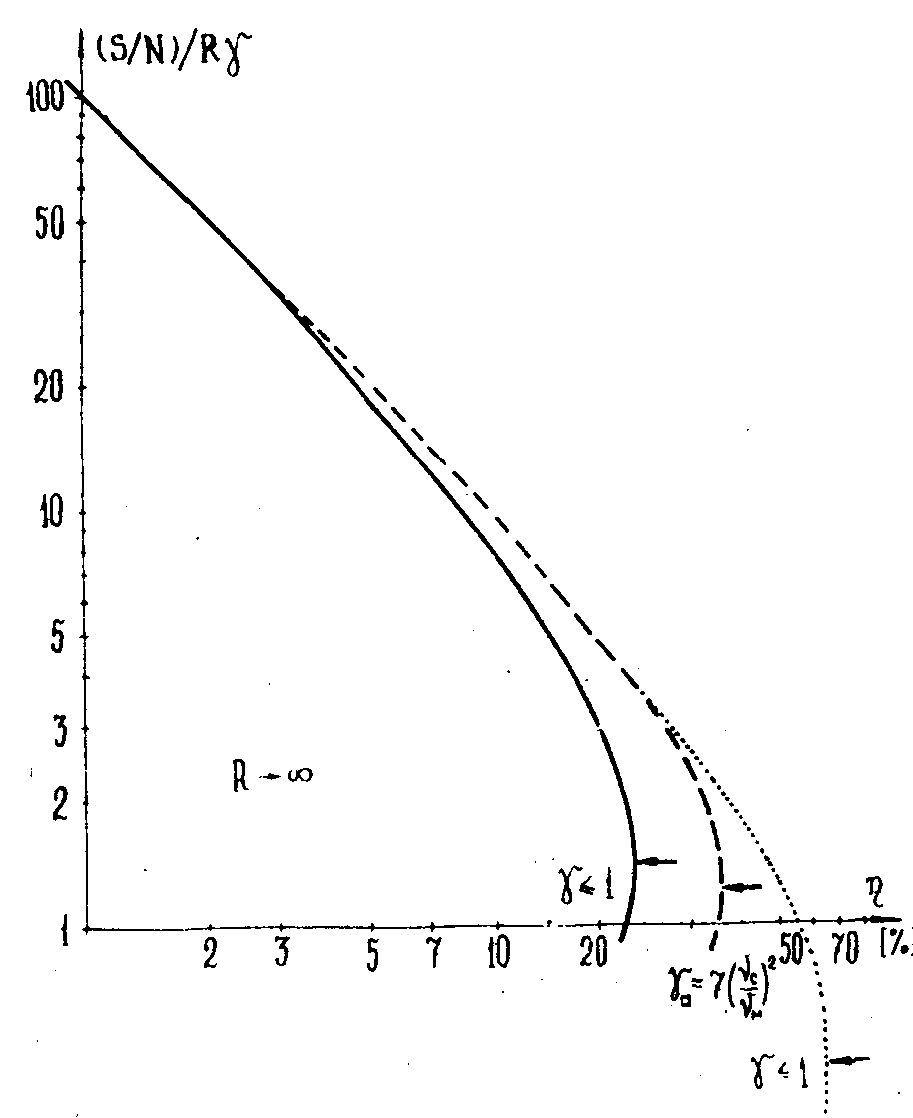
Рис. Параметрические кривые, соответствующие
уравнениям (1) - (2) – точками и (24)-(25) - пунктиром; сплошная кривая /1/ соответствует диффузному объекту, зарегистрированному в тонкой суперлинейной, фазомодулирующей среде.
В /18/
рассмотрен случай тонкой фазомодулирующей среды с линейной экспозиционной характеристикой, горизонтальной МПФ в области низких пространственных частот, характерных для интермодуляционного шума, и квазирезонансной МПФ в области пространственной несущей голограммы (β/\(νкр)=β/\(0)).
Уравнения параметрической кривой (приведенные также в /1/) и ее форма во многом схожа с предыдущим случаем, за исключением предельно достижимом дифракционной эффективности (34% против 22%).
Оба семейства параметрических кривых "отношение сигнал/шум - дифракционная эффективность" в двух рассмотренных случаях тонкой фазомодулирующей среды вырождаются в одну прямую при η<10%. Последняя совпадает с таковой для смешанного случая /7/, когда шумовая субголограмма является тонкой, а информационная - толстой (но тоже фазовой). Ту же прямую дает довольно элементарный полуколичественный анализ, проведенный в подстраничной сноске в /2/ без учета вида статистики распределения плотности вероятности амплитуды сигнальной волны в плоскости голограммы. Такое совпадение параметрических кривых вплоть до дифракционных эффективностей, не превышающих теперь максимально достижимого в каждом отдельном случае предельного значения, наводит на мысль, что само по ceбe конкретное выражение, описывающее плотность распределения вероятности сигнальной волны в плоскости голограммы (например, релеевское распределение) не влияет существенно на форму параметрической кривой. Покажем, что это действительно так на примере тонкой фазовой голограммы сложного объекта (с произвольной плотностью распределения вероятности амплитуды сигнальной волны Р
(s) в плоскости голограммы), зарегистрированной в тонкой суперлинейной фазомодулирущей среде.
В соответствии с (14) /2/ нерассеянная (на щумовой субголограмме) часть восстанавливающей волны в случае тонкой суперлинейной фазомодулирующей среды с чувствительностью β
/\=β10 дается выражением:
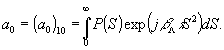 (3)
(3)
При малых фазовых искажениях β
/\τS2<<1, возникающих в регистрирующей среде,
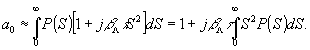 (4)
(4)
По аналогии с (28) /1/ представим (4) в виде
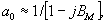 (5)
(5)
где
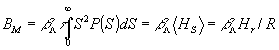 - малый параметр. Тогда отношение сигнал/шум
- малый параметр. Тогда отношение сигнал/шум
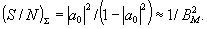 (6)
(6)
С другой стороны, в соответствий с (30) /1/ местная (для небольшой окрестности возле точки с координатами х, у ) дифракционная эффективность тинной фазовой голограммы, зарегистрированной в среде
c линейной экспозиционной характеристикой, может быть представлена так:
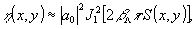 (7)
(7)
что при малости аргумента
J1 упрощается до вида 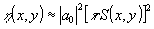 . Усреднение последнего выражения по площади голограммы для случая объекта с известной статистикой можно заменить усреднением по ансамблю /1,7/ в результате дифракционная эффективность в рассматриваемом случае
. Усреднение последнего выражения по площади голограммы для случая объекта с известной статистикой можно заменить усреднением по ансамблю /1,7/ в результате дифракционная эффективность в рассматриваемом случае
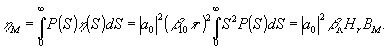 (8)
(8)
учитывая, что по определению
BM=β/\H
Г/R, из (6) и (8) получим уравнение параметрической кривой "отношение сигнал/шум - дифракционная эффективность" для голограммы сложного объекта с произвольной статистикой (распределения плотности вероятности сигнальной волны в плоскости голограммы), зарегистрированной в суперлинейной среде:
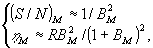 (9)
(9)
где знаки ≈ указывают на то, что применимость данной кривой ограничена условием (β
/\H
r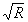 )<<1, когда дифракционная эффективность не превышает нескольких процентов.
)<<1, когда дифракционная эффективность не превышает нескольких процентов.
Существенно, что, как следует из анализа структуры (5) /2/, при линейной экспозиционной кривой плотность распределения вероятности фазы сигнальной волны вообще не играет никакой роли. В то же время плотность распределения вероятности амплитуды сигнальной волны хотя и входит (под интегралом) в величину параметра Вм, но не влияет на форму параметрической кривой "отношение сигнал/шум - дифракционная эффективность" для случая сложного объекта, зарегистрированного голографически в тонкой суперлинейной фазомодулирущей среде при дифракционной эффективности, не превышающей трети предельно достижимого значения (~ 22%).
Проведенные выше рассуждения позволяют надеяться на применимость полученных в §2 соотношений не только для френелевских голограмм, но и для других типов, в частности, голограмм Фурье (при условии, что регистрация ведется не точно в частотной плоскости, в результате чего распределение экспозиции сигнального пучка более или менее равномерно по плоскости голограммы).
В. Возрастание интермодуляционного шума из-за нелинейности фазоэкспозиционной кривой
Из проведенного в /2/ анализа интермодуляционного шума тонкой фазовой голограммы сложного объекта с произвольным распределением плотности вероятности амплитуды и фазы сигнальной волны (в плоскости голограммы) следует, что динамический диапазон в этом случае
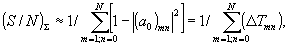 (10)
(10)
где
(ΔTmn)
-1 = [1-|(a
0)
mn|
2]
-1 -
динамический диапазон соответствующей "mn" - ной парциальной шумовой субголограммы, m,n - индексы, определяющие количество N парциальных шумовых субголограмм в зависимости от количества и членов в разложении экспозиционной кривой в степенной ряд (N=[(q+1)(q+2) - 4]/2), а также микроструктуру интермодуляционного поля соответствующем парциальной шумовой субголограммы, т.к. ее амплитудный коэффициент пропускания
tmn
(x)=exp[jμmnH
sm(x)H
rsn(x)/H
0m+n],
где
μmn и Н0 - константы, определяющие чувствительность при записи "mn"-ной шумовой субголограммы.
Как следует из (10), ввиду положительности малой величины
ΔTmn,
любая нелинейность фазоэкспозиционной кривой тонкого регистрирующего материала всегда ухудшает динамический диапазон восстановленного изображения. Существенно, что в соответствии с (15) и (17) /2/ величина динамического диапазона (S/N)Σ может быть вычислена на ЭВМ.
Г. Частичное подавление интермодуляционного шума
за счет квазирезонансного характера МПФ
Как указано в А, одним из способов уменьшения интермодуляционного шума является его неэффективная регистрация на стадии записи за счет использования существенного различия пространственных несущих шумовой и основной (информционной) субголограмм. Наиболее просто такой способ реализуется при использовании регистрирующих сред с квазирезонансным характером МПФ. Самой отработанной средой является фототермопластики (см., например, /14/). В этом случае квазирезонансный характер МПФ является принципиально неустранимый, но имеется возможность
/14/ путем изменения условий записи (потенциал заряда поверхности) и проявления (скорость разогрева) несколько менять форму МПФ. При этом увеличение потенциала поверхности и скорости проявления меняет форму МПФ в нужную (для эффективного подавления интермодуляционного шума) сторону. Кроме того, увеличение потенциала поверхности увеличивает чувствительность, линейный участок (рельеф) экспозиционной кривой, квазирезонансную частоту νкр и ши-
рину полосы пропускания, а увеличение скорости разогрева позволяет уменьшить время проявления, что не позволяет развиваться спонтанным ("морозным") деформациям, уменьшая тем самым собственный шум фототермопластика /14/.
Для количественного анализа эффекта подавления интермодуляционного шума (тонкой фазовой голограммы) за счет квазирезонансного характера МПФ рассмотрим ее простейшую аппроксимацию в виде линейно нарастающей из точки (0;0) прямой, достигающей при νкр значения βмакс. В результате чувствительность при регистрации интермодуляционного поля βш
=βмакс νш/νкр (при несущей частоте голограммы
νс < νкр) меньше чувствительности при регистрации основной голограммы
βc, т.е. βш < βc.
При нарушении условия νс < νкр, в случае выбора несущей
νс > νкр произойдет не частичное подавление, а подчеркивание некоторых пространственных частот интермодуляционного поля, т.е. динамический диапазон восстановленного изображения может
ухудшиться. Ввиду сложности описания участка, МПФ при ν
> νкр и практической невыгодности использования
νс > νкр ограничимся случаем, когда
νс < νкр и β
ш ≈ βмакс νш/νкр.
Для модели сложного объекта, состоящего из М отдельных точек (см. рис.2 /2/), несущая пространственная частота парциальной интермодуляционной решетки, образуемой точками Р и
l в окрестности Х(x,y) голограммы,
ν
pl(x)=[sinαp(x) - sinαl(x)]/λз≈[αp(x) - αl(x)]/λз, (11)
где
αp и αl - углы падения излучения от соответствующих точек; λз - длина волны при записи.
В результате чувствительность при регистрации парциальной шумовой решетки
βpl ≈
βмакс(αp - αl)/λзνкр и распределение шумовых фазовых искажений по голограмме в соответствии с (20) /1/
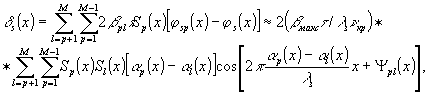 (12)
(12)
где
Sр, Sl - амплитуда парциальной сигнальной волны в плоскости
голограммы,
τ - время экспозиции, Ψpl(х) - начальная фаза, медленно меняющаяся в плоскости голограммы.
Амплитудный коэффициент пропускания шумовой субголограммы
ts(x)=exp[j δs(х)], состоящей из (М2 - М)/2 парциальных косинусоидальных шумовых решеток, можно записать как 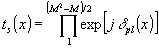 , где
, где 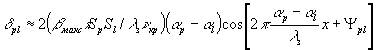 . Каждая из этих парциальных шумовых решеток пропустит без рассеяния лишь часть энергии восстанавливающей волны,
. Каждая из этих парциальных шумовых решеток пропустит без рассеяния лишь часть энергии восстанавливающей волны,
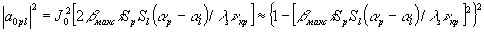 ,
,
которая практически не зависит от координаты X(х,y) голограммы, т.к. разница
[αp(x) – αl(x)
] слабо меняется вдоль х (для исключения функции Бесселя J0 она заменяется двумя членами соответствующего степенного ряда).
В результате на восстановление информационной субголограммы поступает лишь часть энергии восстанавливающей волны, определяемая
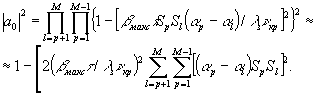 (13)
(13)
Для сложного объекта, состоящего из М примерно равноярких точек.
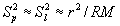 и может быть вынесена за знак суммирования. Для получения конечного результата положим, что точки объекта расположены вблизи узлов двумерной прямоугольной сетки, состоящей из V*U периодов (V*U = М). Тогда номер р точки соответствует координате (v, u), a номер l - (m, n). В результате
и может быть вынесена за знак суммирования. Для получения конечного результата положим, что точки объекта расположены вблизи узлов двумерной прямоугольной сетки, состоящей из V*U периодов (V*U = М). Тогда номер р точки соответствует координате (v, u), a номер l - (m, n). В результате
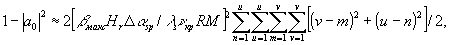 (14)
(14)
где
Δαsp - угловой шаг прямоугольной сетки. После выполнения суммирования получим
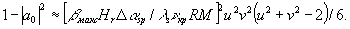
(15)
В простейшем случае квадратного (а не прямоугольного) объекта
U=V=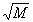 и результат несколько упрощается до вида
и результат несколько упрощается до вида
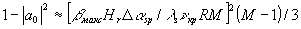 , (16)
, (16)
причем теперь
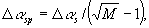 , где Δαs - угловой размер объекта.
, где Δαs - угловой размер объекта.
Легко убедиться в том, что (16) не содержит (по крайней мере грубых) ошибок: при М=1
1-|a0|2 = 0, т.е. интермодуляционный шум (точнее - интеркомбинационные тона) отсутствуют.
Динамический диапазон в рассматриваемом случае в соответствии с определением /1,6/
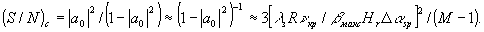 (17)
(17)
При большом числе точек М динамический диапазон восстановленного изображения не зависит от их числа, т.к. теперь
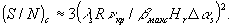 (18)
(18)
Представим (18) по аналогии с (29) /1/, тогда
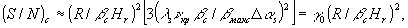 (19)
(19)
где γ
0 учитывает подавление интермодуляционного шума (сложного объекта квадратной формы) за счет квазирезонансного характера МПФ по сравнению со случаем тонкой суперлинейной фазомодулирущей среды.
Для разделения защумленного интермодуляционным изображением нулевого порядка и основного изображения пространственная несущая голограммы νс должна превышать значение
/11/ νмин ≈ 3Δαs/2λз, т.е. обычно
ν
с > 3Δαs/2λз. (20)
Тогда улучшение динамического диапазона из за неэффективной регистрации интермодуляционного поля на стадии записи за счет квазирезонансного характера МПФ может быть определено так:
γ
0 = (27/4)(νкрβс/νсβмакс)2(νс/νмин)2 ≈ 7(νс/νмин)2, (21)
где приближенное выражение соответствует наиболее оптимальному случаю записи при νс
= νкр, что обеспечивает наименьшие искажения частотного спектра объекта из-за формы МПФ при
ν ≈ νс. Существенно, что (21) справедливо толъко при условии νс < νкр, о чем уже упоминалось.
Если на нарастающем из нуля участке МПФ - знак второй производной положителен, то улучшение динамического диапазона γ
0 больше, чем 7(νс/νмин)2, если отрицателен - то меньше. Таким образом, квазирезонансный характер МПФ позволяет примерно на порядок улучшить динамический диапазон восстановленного с (тонкой) фазовой голограммы изображения по сравнений со случаем горизонтальной МПФ. Поскольку на практике обычно регистрирующие среды имеют более или менее спадающую МПФ, что ухудшает рассмотренные в Б, В параметрические кривые "отношение сигнал/шум" - дифракционная эффективность", то выигрыш в динамическом диапазоне при применении малошумящего фототермопластика будет еще больше.
Существенно, что в случае квазирезонансного характера МПФ на голограмме записывается статистически эквивалентная решетка /1,7,18/
т.е. ужа на стадии записи производятся усреднение сигнального (интерференционного) поля. Такое усреднение, как следует из анализа механизма деформаций в фототермопластике, наиболее эффективно происходит в пределах двух соседних (слева и справа от рассматриваемого) периодов образующейся решетки. Этого в большинстве случаев обычно достаточно, поскольку структура интерференционного поля более (см.фиг.1.8 /10/ и обложку /19/) или менее (фиг.12.6 /10/) близка к периодической. В результате и образуется статистически эквивалентная (или близкая к ней) фазовая решетка с амплитудным коэффициентом пропускания:
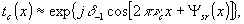 (22)
(22)
где δ
-1 = βсτr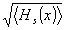 = 2βc
= 2βcH
r/
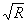
,
а информация содержится в основном в фазе этой решетки Ψsr(x)
, а не в амплитуде δ-1. Таким образом, вcе участки голограммы могут иметь оптимальные (1,84 рад) фазовые искажения δ-1.
В соответствии с (22) на стадии восстановления дифракционная эффективность такой голограммы
η
с ≈ |a0|2 J1(δ-1) = |a
0|
2 J
1(2βc H
r/
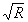
) (23)
а может достигать предельного значения 34% (при любой статистике) вместо 22% при горизонтальной МПФ (см.
II /1/ и Б) и релеевском распределении плотности вероятности сигнальной волны в плоскости голограммы.
Таким образом, в рассматриваемом случае параметрическая кривая "отношение сигнал/шум - дифракционная эффективность" задается уравнениями (19) и (23) и может быть при большом
R представлена в виде
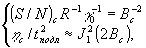
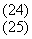
где Вс
= βc Нr /
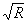 - параметр записи.
- параметр записи.
§ 3.
Нелинейные искажения при воспроизведении градаций
яркости в голографическом изображении
Наиболее подробно данный вопрос рассмотрен в /1/, где приведены (плоские) параметрические кривые "коэффициент нелинейности - дифракционная эффективность голограммы" двух плоских волн, зарегистрированных в (тонкой амплитудной) голограмме на фотопластинках Агфа-Геверт 10E70 и Кодак 649F, в тонкой фазовой голограмме с линейным, квадратичными экспоненциальным (δ(Н) =δмакс[1-exp(H/H0)]) откликом, в рельефно-фазовой голограмме на фототермопластике, в толстослойной фазовой, голограмме (бихромированная желатина, отбе-
ленные фотопластинки, Кодак 649F).
Наиболее важным для практического применения является следующее:
1) удовлетворительные нелинейные искажения тонких амплитудных голограмм могут быть достигнуты только при точном (~10%) соблюдении экспозиции опорного пучка (и режима обработки);
2) для толстослойных голограмм эти требования на порядок мягче, но завал яркостей белого может быть при предельной дифракционной эффективности заметен (>50%);
3) для тонких амплитудных голограмм, зарегистрированных в среде с линейным (и квадратичным) откликом требования к точности экспозиции вообще отсутствуют, а при экспоненциальной экспозиционной кривой допустим перепад экспозиций опорного пучка на порядок;
4) параметрическая кривая тонкой фазовой голограмм с линейном откликом хуже, чем в случае толстослойной голограммы, хотя при максимальной дифракционной эффективности завал уровня белого имеет тот же порядок (~ 50%);
5) экспоненциальный отклик дополнительно ухудшает параметрическую кривую по сравнению со случаем линейного отклика;
6) путем введения предыскажений на стадии записи можно (по крайней мере частично) компенсировать нелинейность процесса восстановления и уменьшить нелинейные искажения, что характерно, напримep, для фототермопластика;
7) специфический вид параметрической кривой тонкой фазовой голограммы, зарегистрированной в среде с квадратичным откликом, свидетельствует о существенном завале яркостей серых участков изображения;
8) форма параметрической кривой слабо меняется при переходе от плоской сигнальной волны и сложному объекту (см.рис.4 /1/), что позволяет существенно расширить сферу применения выше перечисленных рекомендаций.
Как следует из IV /2/ и В, в случае, если за счет использования регистрирующей среды с малой нелинейностью фазоэкспозиционной кривой удалось получить высококонтрастное изображение сложного объекта, нелинейные искажения в воспроизведении градаций его яркости будут практически совпадать с таковыми для случая линейного отклика
(см.параметрические кривые "коэффициент нелинейности - дифракционная эффективность" в нижней части рис.4 /1/).
З а к л ю ч е н и е
Таким образом, для получения высокоэффективных (η>0,1) голограмм с большим динамическим диапазоном и удовлетворительным завалом уровня белого следует использовать регистрирующие среды с линейной фазоэкспозиционной характеристикой, обладающие по возможности низким уровнем собственного шума. При этом величина динамического диапазона не может превышать отношения R/η в случае горизонтальной МПФ. Спад МПФ приводит к ухудшению, а подъем (в области от нуля до несущей частоты) - к увеличению динамического диапазона.
Л и т е р а т у р а
1. В.Б.Немтинов, О.В.Рожков. Метод оценки качества голографического процесса. Материалы VI Всесоюзной школы по голографии. Л., 191-211, 1974.
2. О.В.Рожков. Влияние нелинейности фазоэкспозиционной характеристики регистрирующего материала на качество голографического процесса. Материалы
VII Всесоюзной школы по голографии. Л., 244-259, 1975.
3. У.Дж.Хэннэн. Голографические кинофильмы, получаемые тиснением. Техника кино и телевидения, №8, 43-51, 1973.
4. В.Б.Немтинов. Групповые свойства голограмм. Материалы
VII Всесоюзной школы по голографии. Л., 102-117, 1975.
5. В.Б.Немтинов, О.В.Рожков. Оценка качества голографического процесса с помощью пространственной параметрической кривой КН-ДЭ-ОСШ. Тезисы докладов
II Всесоюзной конференции по голографии, ч.II, 99-101, Киев, 1975.
6. J.A.Jenny. Nonlinearities of photopolimer holographic recording materials. Appl.Opt., 11, 6, 1371, 1972.
7. J.Upatnieks, C.Leonard. Efficiency and images/Image contract of Dielectric holograms. J.Opt.Soc.Amer., 60, 3, 257, 1970.
8. R.A.Bartolini. Characteristics of Relief Phase Holograms, recorded in Photoresists. Appl.Opt., 13, 1, 129, 1974.
9. Б.Г.Турухано, В.Г.Толчин. Цветная голография. Материалы
V Всесоюзной школы по голографии. Л., 345-356, 1973.
10. Р.Кольер, К.Беркхарт, Л.Лин. Оптическая голография, "Мир", М
., 1973.
11. Дж.Гудмен. Введение в фурье-оптику, "Мир", М., 1970.
12. J.Upatnieks,
С.D.Leonard. Linear Wavefront Reconstruction from Nonlinearly Recorded Holograms. Appl.Opt., 10, 10, 2365, 1971.
13. М.М.Бутусов, С.Н.Гуляев.
O.В.Судариков. Голографическая эффективность и механизм дифракции света на голограмме. Квантовая эл., т.2, №1, 13-17, 1975.
14. Н.Г.Кувшинский и др. Голографическая регистрация на термопластических средах. Материалы
VII Всесоюзной школы по голографии, Л., 354-381, 1975.
15. В.
Hill. Point efficiency and Signal-to-Background Ratio in Exponential Holograms for Optical Memories, Appl.Opt., 11, 12, 2937, 1972.
16. Б.П.Латхи. Системы передачи информации, "Связь", М., стр.170, 1971.
17. R.L.Lamberts, C.N.Kurtz. Reversal Bleaching for Low Flare Light in Hologram. Appl.Opt., 10, 6, 1342, 1971.
18. В.Б.Немтинов и др. Интермодуляционный шум рельефно-фазовых голограмм. В сб. "Способы записи информации на бессеребряных носителях", вып.7, "Вища школа", Киев, 1976.
19. Ю.И.Островский. Голография. "Наука", Л., 1970.

