УСЛОВИЯ
ПЕРЕДАЧИ ГОЛОГРАММОЙ ИНФОРМАЦИИ ОБ ОБЪЕКТАХ, ИХ КОРРЕЛЯЦИОННЫХ
СВОЙСТВАХ И О КОГЕРЕНТНОСТИ ВОЛНОВЫХ ПОЛЕЙ
Н.Г.Власов
С целью
систематизированного описания различных голографических
методов записи и восстановления изображения, а также методов
корреляционного анализа и исследования когерентности выведено
уравнение, описывающее восстановленное изображение и учитывающее
когерентные свойства волновых полей и корреляционные свойства
объектов, участвовавших в процессах записи и восстановления.
После этого различные голографические методы представлены
как реализация решений полученного уравнения.
В
в е д е н и е
Основными
физическими факторами, действующими во время записи голограмм
и восстановления изображения, являются когерентные свойства
волновых полей и корреляционные свойства объектов, участвующих
в этих процессах. Влияние каждого из перечисленных факторов
в отдельности, например, когерентности /1-4/, на качество
восстановленного изображения было, в основном, исследовано
к 1971г. и к настоящему времени описано не только в оригинальных
работах, но, частично, и в монографиях. Тем не менее, представляется
полезным рассмотреть одновременное действие всех указанных
выше факторов. Целью такого подхода является систематизированное
описание различных голографических методов записи и восстановления
изображения, а также методов корреляционного анализа и исследования
когерентности. Для этого сначала будет получено общее уравнение,
описывающее восстановленное изображение, после чего различные
голографические методы будут представлены, как реализация
решений полученного уравнения. Для решения поставленной
задача, рассмат-
риваемой
в рамках скалярной теории дифракции, достаточно учесть влияние
только пространственной когерентности волновых полей, что
упрощает математическое описание голографического процесса.
Из тех же соображений поставленную задачу целесообразно
рассмотреть на примере голографии Фурье, однако те свойства
преобразования Фурье, которые будут использованы в дальнейшем,
например, свойство восстанавливать первоначальную функцию
после применения к ней прямого и обратного преобразования,
справедливы и для преобразования Френеля. Это обстоятельство
позволяет распространить полученные ниже результаты и на
голографию Френеля.
1.
Вывод основного уравнения
Выведем
вначале уравнение, описывающее амплитудное пропускание голограммы
Фурье, следуя работе /2/. Волновое поле, характеризующееся
функцией взаимной когерентности Г12(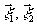 ),
освещает плоскость предметов
),
освещает плоскость предметов 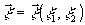 , в которой симметрично оптической оси, расположены два
объекта 1 и 2, описывающиеся функциями амплитудного пропускания
, в которой симметрично оптической оси, расположены два
объекта 1 и 2, описывающиеся функциями амплитудного пропускания
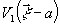 и
и 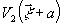 ,
соответственно. Суммарное амплитудное пропускание
,
соответственно. Суммарное амплитудное пропускание
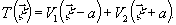 (1)
(1)
В плоскости
голограммы, являющейся также плоскостью пространственных
частот 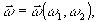
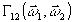 можно
найти /5-6/, зная Г12(
можно
найти /5-6/, зная Г12(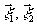 )
и функцию распространения
)
и функцию распространения 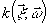 :
:
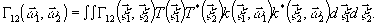 (2)
(2)
Как
известно, для преобразования Фурье
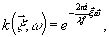 (3)
(3)
где
f - фокальная длина линзы, осуществляющей прямое преобразование
Фурье. Для перехода к интенсивности 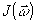 в плоскости
в плоскости 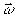 подcтавим уравнения (1) и (3) в (2), заменяя Г12(
подcтавим уравнения (1) и (3) в (2), заменяя Г12(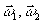 )
на
)
на
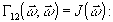
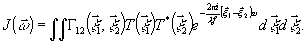 (4)
(4)
Считаем,
как обычно, амплитудное пропускание Тг(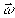 )
полученной голограммы пропорциональным зарегистрированной
интенсивности. Кроме того, из четырех членов, образующихся
в результате перемножения
)
полученной голограммы пропорциональным зарегистрированной
интенсивности. Кроме того, из четырех членов, образующихся
в результате перемножения 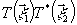 ,
оставим для дальнейшего анализа только один, содержащий
,
оставим для дальнейшего анализа только один, содержащий
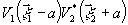 и описывающий
в уравнений голограммы первоначальное (мнимое) изображение
при восстановлении волновым полем, совпадающим по направлений
распространения с полем
и описывающий
в уравнений голограммы первоначальное (мнимое) изображение
при восстановлении волновым полем, совпадающим по направлений
распространения с полем 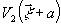 ,
имевшим место при записи голограммы. Тогда амплитудное пропускание
голограммы
,
имевшим место при записи голограммы. Тогда амплитудное пропускание
голограммы
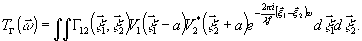 (5)
(5)
Рассмотрим
теперь процесс восстановления. Чтобы сохранить общность
считаем, что при восстановлении в плоскости предметов 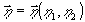 также находится объект с амплитудным пропусканием
также находится объект с амплитудным пропусканием 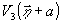 ,
расположенный, в данном случае, на месте объекта 2. Тогда
в плоскости
,
расположенный, в данном случае, на месте объекта 2. Тогда
в плоскости 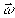 ,
непосредственно перед голограммой,
,
непосредственно перед голограммой,
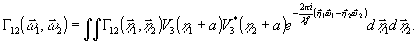 (6)
(6)
Учитывая,
что для обратного преобразования Фурье функция распространения
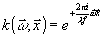 , определим
функцию взаимной когерентности Г12(Х1,
Х2) в плоскости восстановленного изображения
и переходя от нее к интенсивности J(
, определим
функцию взаимной когерентности Г12(Х1,
Х2) в плоскости восстановленного изображения
и переходя от нее к интенсивности J(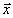 ),
найдем, что
),
найдем, что
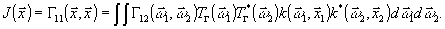 (7)
(7)
Подставляя
в (7) значение Г12(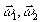 )
из (6) и значения
)
из (6) и значения 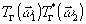 из (5), получим полное выражение, описывающее интенсивность
восстановленного волнового поля в плоскости изображения:
из (5), получим полное выражение, описывающее интенсивность
восстановленного волнового поля в плоскости изображения:
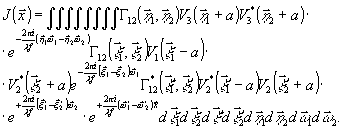 (8)
(8)
Упростим
несколько выражение (8), для чего выделим члены в экспоненциальных
множителях, содержащих 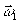 и
и 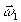 , и
проинтегрируем по этим переменным, в результате чего кратность
интеграла сократится на два, а в подынтегральном выражении
появятся дельта-функции
, и
проинтегрируем по этим переменным, в результате чего кратность
интеграла сократится на два, а в подынтегральном выражении
появятся дельта-функции 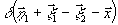 и
и 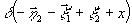 .
Проинтегрируем далее по
.
Проинтегрируем далее по 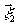 и
и 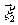 :
:
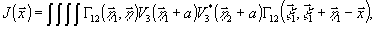
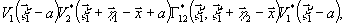 (9)
(9)
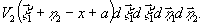
Предполагая
стационарность функций Г12, т.е. их зависимость
только от разностей пространственных аргументов и вводя
функции корреляции:
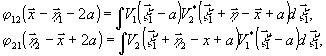 (10)
(10)
запишем
уравнение (9) в виде:
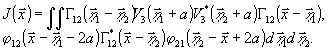 (11)
(11)
Выведенное
выражение в самом общем виде описывает интенсивность восстановленного
волнового поля в плоскости изображения. Для перекрестного
члена в уравнении голограммы, сопряженного по отношению
к рассмотренному и описывающего амплитудное пропускание
голограммы в +1-ом порядке дифракции, аналогичное рассмотрение
приводит к значению:
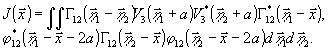 (12)
(12)
Сделаем
сначала самый общий вывод, полезный для дальнейшего анализа.
Из (8, 11, 12) видно, что интенсивность восстановленного
волнового поля содержит информацию о когерентности излучения
и об объектах (и их корреляционных функциях), имевших место
как в процессе записи, так и в процессе восстановления.
Такое переналожение различной информации приводит к ее избыточности,
которая во многих случаях может оказаться излишней и вредной.
Отметим, что предметом исследования может быть как реальный
объект, так и функция когерентности. При исследовании лишь
одного объекта информация о других объектах и когерентности
излучения является чаще всего избыточной и мешающей. Соответственно,
при исследовании когерентности на одной стадии голографического
процесса избыточной оказывается информация о когерентности
на другой стадии процесса, а также, в большинстве случаев,
и информация об объектах.
Уточним
теперь постановку задачи. Требуется найти, во-первых, условия,
обеспечивающие неискаженную передачу корреляционных свойств
волновых полей и изображений объектов. Вторая часть зада-
чи заключается
в определении условий, при которых распределение интенсивности
в плоскости изображения зависит только от функции кросс-корреляции
двух объектов. Математическое описание первой части задачи
заключается в нахождении решений уравнений (8, 11), при
которых J(х) зависит только от одной из функций, входящих
в правую часть этих уравнений. Как будет показано ниже,
каждому из упомянутых решений соответствует один из голографических
методов исследования когерентности или построения изображений
объектов. Каждому из решений второй части задачи соответствует
один из голографических корреляционных методов.
2.
Условия неискаженной передачи когерентных
свойств
волновых полей и изображений объектов
Из методических
соображений удобно рассмотреть прежде всего условия передача
без искажений когерентных свойств восстанавливающего волнового
поля, т.е. найти решения уравнений (8, 11), при которых
J(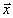 ) в
этих уравнениях зависит только от Г12(
) в
этих уравнениях зависит только от Г12(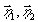 ).
Отметим сначала, что функция взаимной когерентности описывает,
как известно, корреляцию между волновыми полями, сдвинутыми
по пространственно-временным координатам, поэтому традиционным
методом исследования когерентности является сдвиговая интерферометрия.
Голографический сдвиговый интерферометр /7/ относится к
типу голограмм, получивших название голографические оптические
элементы. Голограмма - сдвиговый интерферометр - записывается
двойной экспозицией в полностью когерентном излучении с
точечными объектным и опорным источниками, причем между
экспозициями объектный источник смещается на
).
Отметим сначала, что функция взаимной когерентности описывает,
как известно, корреляцию между волновыми полями, сдвинутыми
по пространственно-временным координатам, поэтому традиционным
методом исследования когерентности является сдвиговая интерферометрия.
Голографический сдвиговый интерферометр /7/ относится к
типу голограмм, получивших название голографические оптические
элементы. Голограмма - сдвиговый интерферометр - записывается
двойной экспозицией в полностью когерентном излучении с
точечными объектным и опорным источниками, причем между
экспозициями объектный источник смещается на 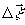 .
Математическое описание процесса записи выглядят следующим
образом:
.
Математическое описание процесса записи выглядят следующим
образом:
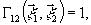
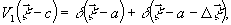 (13)
(13)
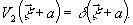
При
исследовании когерентности восстанавливающего источника
/8/ объекты отсутствуют, т.е.
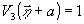 .
(14)
.
(14)
Подстановка
условий (13, 14) в (11) приводит к тому, что
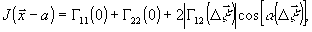 (15)
(15)
где
α(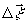 )
- аргумент функции взаимной когерентности, а
)
- аргумент функции взаимной когерентности, а 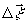 обозначает теперь сдвиг между волновыми полями в процессе
восстановления. Выражение (15) описывает интерференционную
картину, по измерению видности которой можно определить
|Г12(
обозначает теперь сдвиг между волновыми полями в процессе
восстановления. Выражение (15) описывает интерференционную
картину, по измерению видности которой можно определить
|Г12(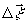 )|
. Таким образом, (13, 14) действительно являются решением
уравнения (8) или (11).
)|
. Таким образом, (13, 14) действительно являются решением
уравнения (8) или (11).
Если
когерентные свойства восстанавливающего волнового поля не
являются предметом специального исследования, то информация
о них является излишней и мешающей, поэтому процесс восстановления
целесообразно производить в полностью когерентном излучения
(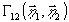 =1).
Условие
=1).
Условие 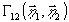 =1
позволяет несколько упростить выражения (8-12). Подставив
=1
позволяет несколько упростить выражения (8-12). Подставив
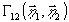 =1,
=1, 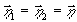 в (11) и имея в виду, что
в (11) и имея в виду, что 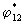 (
(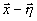 -2а),
получим
-2а),
получим
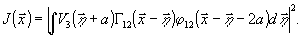 (16)
(16)
Другой
вариант исследования когерентности основан на использовании
процесса записи /2/. Условия неискаженного восстановления
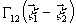 (в варианте
голографии Фурье) заключатся в том, что опорный и восстанавливающий
источники являются точечными:
(в варианте
голографии Фурье) заключатся в том, что опорный и восстанавливающий
источники являются точечными:
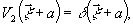
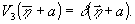 (17)
(17)
После
подстановки (17) в (16) и выполнения несложных преобразований
(16) упрощается до
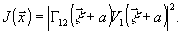 (18)
(18)
Записываемый
на голограмму объект имеет плоскую поверхность, что обеспечивает
его равномерную освещенность при наблюдении по направлениям,
стягиваемым при записи апертурой голограммы; другими словами,
функция, описывающая макроструктуру объекта, равна Const.
Таким образом, интенсивность восстановленного изображения
оказывается промодулированной только квадратом модуля функции
взаимной когерентности. Процесс записи можно использовать
и для исследования временной когерентности Г12(τ).
Ρυема получения голограмм, особенно удобная для
этого, предложена в работе /1/. В /1/ вся необходимая информация,
т.е. значения Г12(τ) οπи различных
τ записываются за одну экспозицию, что является принципиальным
преимуществом при исследовании импульсных источников. Перейдем
к восстановлению изображений объектов, начав с "некогерентной
голографии". В этом методе фазовая информация теряется и
восстановленное изображение несет информацию только о распределении
интенсивности по объекту, ввиду чего удобно сохранить применявшееся
до сих пор в нашей лекции описание восстановленного волнового
поля по его интенсивности. В некогерентной голографии делением
по амплитуде получают сначала два изображения одного и того
же объекта, в которых несмотря на некогерентное освещение,
взаимно-когерентны одноименные точки, что и позволяет осуществить
процесс записи. Рассмотрим кратко, как пример некогерентной
голографии, вариант, предложенный Дж.Строуком в 1965 г.
(см.монографии /9,10/). В методе Строука два изображения
предмета - прямое и перевернутое, располагаются в плоскости
предметов и используются для записи безлинзовой голограммы
Фурье. Запись голограммы возможна благодаря тому, что частота
интерференционных полос в ее плоскости, образованная каждой
парой одноименных точек, зависит от расстояния между ними
и, следовательно, характеризует их положения. Таким образом,
неискаженное восстановление распределения интенсивности
по объекту 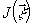 обеспечивается выполнением следующих условий:
обеспечивается выполнением следующих условий:
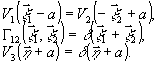 (19)
(19)
Действительно,
подстановка (19) в (16) приводит к значению
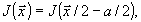 (20)
(20)
что
с точностью до масштаба совпадает с 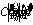 .
Когерентность излучения в процессе записи играет в данном
случае вредную роль, в чем можно убедиться, введя в (19)
вместо Г12(
.
Когерентность излучения в процессе записи играет в данном
случае вредную роль, в чем можно убедиться, введя в (19)
вместо Г12(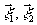 )=
)=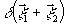 ,
,
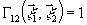 и поставив
полученные условия в (16). Такая подстановка показывает,
что вместо изображения объекта восстанавливается его автосвертка.
В принципе, возможен и промежуточный случай, когда
и поставив
полученные условия в (16). Такая подстановка показывает,
что вместо изображения объекта восстанавливается его автосвертка.
В принципе, возможен и промежуточный случай, когда 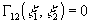 при разности
при разности 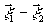 много меньшей, чем размеры объекта. Тогда значение
много меньшей, чем размеры объекта. Тогда значение 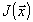 в каждой точке плоскости изображения заменяется на значение
автосвертки в интервале
в каждой точке плоскости изображения заменяется на значение
автосвертки в интервале 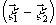 ,
причем свертка вычисляется с весовым множителем, роль которого
играет Г12
,
причем свертка вычисляется с весовым множителем, роль которого
играет Г12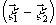 .
Возможно, что отмеченный случай найдет впоследствии применение
в системах оптической фильтрации, например как способ выполнения
некоторой сглаживающей операции. Отметим, что во всех остальных
известных случаях восстановления изображения информация
о когерентности излучения как в процессе записи, так и в
процессе восстановления является избыточной и мешающей.
.
Возможно, что отмеченный случай найдет впоследствии применение
в системах оптической фильтрации, например как способ выполнения
некоторой сглаживающей операции. Отметим, что во всех остальных
известных случаях восстановления изображения информация
о когерентности излучения как в процессе записи, так и в
процессе восстановления является избыточной и мешающей.
Основную
группу голографических методов можно охарактеризовать тем,
что и запись и восстановление происходят в полностью когерентном
излучении:
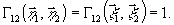 (21)
(21)
При
выполнении условия (21) оптическая система, включающая в
себя голограмму, становится линейной по амплитуде на обоих
стадиях голографического процесса и восстановленное волновое
поле теперь целесообразно характеризовать его комплексной
амплитудой. Подставляя 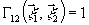 в уравнение (16) (условие
в уравнение (16) (условие 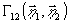 =1
уже учтено в нем), найдем, что
=1
уже учтено в нем), найдем, что
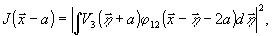 (22)
(22)
откуда
с точностью до постоянного фазового множителя комплексная
амплитуда U(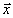 )
восстановленного волнового поля равна:
)
восстановленного волнового поля равна:
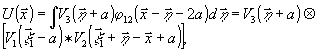 (23)
(23)
где
значки 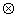 и
и 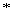 обозначают
операции свертки и корреляции, соответственно. Если записать
(23) в явном виде и изменить порядок интегрирования (сначала
по
обозначают
операции свертки и корреляции, соответственно. Если записать
(23) в явном виде и изменить порядок интегрирования (сначала
по 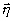 ,
а затем по
,
а затем по 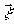 ),
то
),
то
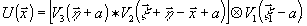 (24)
(24)
Таким
образом, комплексную амплитуду восстановленного волнового
поля можно описывать как свертку амплитуды восстанавливающего
поля с функцией корреляции объектного и опорного волновых
полей или как свертку амплитуды объектного волнового поля
о функцией корреляции восстанавливающего и опорного волновых
полей. В дальнейшем будут использованы оба определения.
Продолжим
решение поставленной задачи, заключающейся теперь в определении
условий, при выполнении которых амплитуда восстановленного
изображения, определяемая уравнением (23) или (24) зависит
только от одной из функций, входящих в эти уравнения. Начнем
с метода, положившего начало современной голографии и применяемого
сейчас наиболее широко: голограмма записывается в полностью
когерентном излучении о боковым опорным источником, и ни
опорный, ни восстанавливающий источники не модулируются
амплитудным пропусканием какого-либо объекта. В варианте
голографии Фурье этому соответствуют точечные опорный и
восстанавливающий источники:
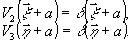 (25)
(25)
Действительно,
при подстановке (25) в (23) или в (24) получаем:
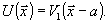 (26)
(26)
Следущее
решение, справедливость которого становится очевид-
ной
при подстановке его в (24), реализуется одновременно в методах
кодирования, ассоциативной памяти и при восстановлении фантомного
изображения:
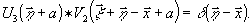 (27)
(27)
В методах
ассоциативной памяти и кодирования опорный (впоследствии
восстанавливающий) источник промодулирован одним и тем же
объектом с таким амплитудным пропусканием, что его функция
автокорреляции имеет узкий пик и может быть аппроксимирована
дельта функцией. В случае фантомного изображения опорный
объект отсутствует и его роль играет наиболее яркая часть
объекта, записываемая на голограмму. При восстановлении
одна часть объекта реально существует и восстанавливает
его другую часть. Перечисленные методы подробно описаны
в монографиях /9,10/. (По кодированию см. также лекцию /11/).
Отметим только, что для выполнения условия (27) входящие
в его левую часть функции должны быть или чисто фазовыми,
или иметь широкий спектр пространственных частот. Еще одна
возможность передачи неискаженного изображения объекта осуществляется
голограммами, являющимися оптическими элементами, действие
которых основано на явлении дифракции (см.наш обзор на III
Школе). Соответствующее решение уравнения (23) имеет вид:
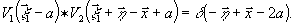 (28)
(28)
В простейшем
случае (28) справедливо при
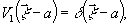
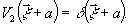 (29)
(29)
Более
сложный вариант, в котором чисто фазовые функции 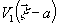 и
и 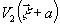 описывают
протяженные источники, рассмотрен в /12/.
описывают
протяженные источники, рассмотрен в /12/.
На примере
первого из рассмотренных вариантов записи и восстановления
изображения в полностью когерентном излучении определим,
как изменится восстановленное изображение, если излучение
станет частично когерентным (по пространственным координатам).
Так как объект, модулирующий излучение восстанавливающего
источника,
отсутствует,
для упрощения расчета начнем его с функции взаимной когерентности
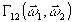 , определенной
непосредственно в плоскости голограммы. Подставляя в (8)
, определенной
непосредственно в плоскости голограммы. Подставляя в (8)
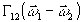 вместо
всех (функций, зависящих от
вместо
всех (функций, зависящих от 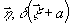 ,
,
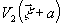 заменяя
переменные
заменяя
переменные 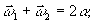
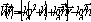 и выполняя
интегрирование в следующем порядке - по
и выполняя
интегрирование в следующем порядке - по 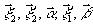 ,
получим:
,
получим:
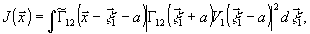 (30)
(30)
где
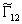 обозначает
обратное преобразование Фурье от
обозначает
обратное преобразование Фурье от 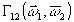 .
Таким образом, интенсивность восстановленного изображения
описывается сверткой преобразования Фурье от функциям взаимной
когерентности восстанавливающего волнового поля с квадратом
модуля произведения функции взаимной когерентности освещающего
волнового поля на функцию амплитудного пропускания объекта.
Этот результат получен в работе /2/. Влияние временной когерентности
на качество восстановленного изображения могло найти в /3/.
.
Таким образом, интенсивность восстановленного изображения
описывается сверткой преобразования Фурье от функциям взаимной
когерентности восстанавливающего волнового поля с квадратом
модуля произведения функции взаимной когерентности освещающего
волнового поля на функцию амплитудного пропускания объекта.
Этот результат получен в работе /2/. Влияние временной когерентности
на качество восстановленного изображения могло найти в /3/.
Подводя
итоги разделу, описывавшему методу восстановления неискаженного
изображения, отметим, что почти во всех методах требуется
полная взаимная когерентность между опорным источником а
всеми точками объектного волнового поля (взаимная когерентность
между отдельными точками объектного волнового поля не обязательна
/13/). Исключение составляет некогерентная голография, однако
в настоящее время она представляет, в основном, теоретический
интерес. Причина этого, подробно разобранная, например,
в монографиях /9,10/, заключается в том, что интерференционные
полосы, соответствующие каждой паре одноименных точек от
двух изображений объекта, складывается при записи голограммы
некогерентно, что существенно ограничивает число самих точек,
которые можно записать на одно и то же место голограммы.
3.
Условия получения неискаженной
кросс-корреляционной
функции
Из уравнений
(24, 25) очевидно, что выполнить операцию кросс-корреляции
в когерентном оптическом излучении можно двумя метода-
ми /9,10/.
На первом из них, предложенном Вандер Люгтом в 1964 г.,
основано большинство современных корреляторов. В корреляторе
Вандер Люгта один из объектов записывается на голограмму
с точечным опорным источником, а восстановление происходит
при помощи другого объекта. При этом распределение интенсивности
в плоскости восстановленного изображения описывается функцией
кросс-корреляции упомянутых объектов. Действительно, подставляя
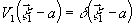 в (24),
получаем:
в (24),
получаем:
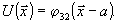 (31)
(31)
Для
того, чтобы учесть влияние когерентности излучения, подставим
значение 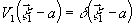 в (8) или (11). Тогда
в (8) или (11). Тогда
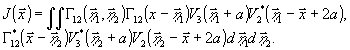 (32)
(32)
Этот
результат получен в работах /4,14/, где показано, что с
уменьшением когерентности (как 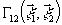 ,
так и
,
так и 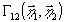 )
селективность голографического согласованного фильтра также
уменьшается.
)
селективность голографического согласованного фильтра также
уменьшается.
Анализируя
описанный метод, надо отметить, что точечный опорный источник
в процессе записи не несет дополнительной информации в предназначен
только для сохранения информации об одном из объектов (то
есть для записи голограммы - согласованного фильтра). Однако
в данном случае конечная цель - не запись голограммы, а
выполнение операции кросс-корреляции. Ее основная часть
- перемножение фурье-образа одного из объектов на сопряженный
фурье-образ другого может быть выполнена непосредственно
в процессе записи /15,16/. Следовательно возможен другой
тип голографического коррелятора, в котором амплитуда восстановленного
волнового поля описывается выражением (23) при условии,
что 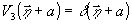 :
:
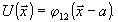 (33)
(33)
Данному
математическому описанию соответствует запись голограммы
с участием обоих объектов и восстановление точечным опорным
источником. Вероятно, в связи с развитием регистрирующих
сред многократного действия, не требующих фотопроцесса,
например, термопластиков, этот метод начнет применяться
более широко, так как в нем отсутствует проблема точного
возвращения согласованного фильтра на прежнее место или
его фотообработки на месте экспонирования. Отметим, что
голограмма, полученная описанным методом, представляет собою
интерференционную картину, а каждое из образовавших ее волновых
полей промодулировано амплитудным пропусканием одного из
двух объектов. В принципе, в такой интерферограмме содержится
вся необходимая информация и процесс восстановления является
просто средством преобразования уже имеющейся информации.
Поэтому оптическое преобразование может быть заменено электронным
/17,18/ или электронно-механическим /19/.
После
оптического преобразования (обратного преобразования Фурье)
распределение интенсивности в плоскости восстановленного
изображения описывается функцией кросс-корреляции сравниваемых
объектов, а критерием при корреляционном распознавании образов
в большинстве случаев является максимум корреляционной функции,
соответствующий, как известно, нулевому значению ее аргумента.
Корреляционные функции, имеющие резкий пик и остальные значения,
близкие к нулевому, встречаются редко - только у объектов,
обладающих широким спектром пространственных частот, т.е.
у объектов, имеющих шумоподобную структуру типа диффузного
рассеивателя или освещенных через диффузный рассеиватель.
У большинства же объектов, подлежащих корреляционному распознаванию,
функция корреляции существенно отличается от нуля не только
при нулевом, но и при других значениях аргумента, что неудобно
с точки зрения дальнейшей обработки по двум причинам. Во-первых,
для определения максимума приходится прибегать к сканированию.
Во-вторых, в случае многоканального коррелятора необходимо
дополнительно разносить каналы по пространственным частотам,
чтобы избежать перекрытия корреляционных функций, соответствующих
соседним каналам. Отмеченная избыточность затрудняет обработку
информации и тогда, когда она ведется непосредственно в
плоскости пространственных частот. Выделению
максимума
кросс-корреляционной функции здесь соответствует выделение
нулевых пространственных частот взаимного энергетического
спектра. Это означает, что в интерференционной картине,
составляющей структуру голограммы, требуется выделить составляющую,
имеющую вид параллельных эквидистантных полос, находящихся
на расстоянии λf/a друг от друга. Поставим задачу:
устранить избыточность информации в самом начале оптической
обработки - на этапе получения интерференционной картины,
составляющей структуру голограммы. Это означает, что необходимо
найти условия, при выполнении которых
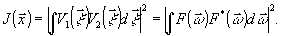 (34)
(34)
Для
определения подхода к решению поставленной задачи вернемся
еще раз к уравнению (4), введя переменные интегрирования:
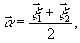
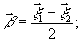
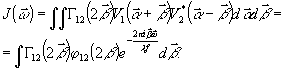 (35)
(35)
Уравнение
(34) показывает, что распределение интенсивности в частотной
плоскости зависит как от функции кросс-корреляции сравниваемых
объектов, так и от функции взаимной когерентности освещающего
излучения. Сравнение (34) и (35) позволяет найти условия,
при выполнении которых (35) переходит в (34), т.е. найти
решение поставленной задачи:
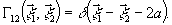 (36)
(36)
Волновое
поле о когерентными свойствами, характеризующимися (36).
можно подучить следующим образом. Пусть дифракционная решетка,
освещенная протяженным некогерентным источником, переотображается
оптической системой, осуществляющей двойное преобразование
Фурье плоскости предметов (такое переотображение возможно,
если угловые размеры источника меньше, чем углы дифракции
±1 порядков данной решетки /20/). Функция взаимной когерентности,
описывающая корре-
ляцию
между волновыми полями в ±1 порядках дифракции в частотной
плоскости, будет описываться уравнением (36), где 2а теперь
расстояние между центрами упомянутых дифракционных порядков.
Если теперь в плоскость пространственных частот поместить
два объекта с амплитудным пропусканием 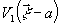 и
и 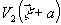 так,
чтобы они освещались излучением, дифрагировавшим в ±1 порядки,
а остальные порядки дифракции экранировать, то распределение
интенсивности в плоскости изображения дифракционной решетке,
являющейся одновременно плоскостью пространственных частот
для сравниваемых объектов, будет описываться уравнением
(34). Корреляционные свойства сравниваемых объектов оказывают
влияние только на контраст, с которым передаются линии дифракционной
решетки. Зарегистрированное изображение решетки можно рассматривать
как голограмму, соответствующую второму (по порядку рассмотрения)
типу корреляторов, в которой отсутствует избыточность. При
восстановлении такой голограммы, как голограммы Фурье, в
плоскости восстановленного изображения будет наблюдаться
только светящаяся точка, соответствующая (по амплитуде)
максимуму кросс-корреляционной функции. Корреляционное сравнение
можно производить и непосредственно в плоскости голограммы
без ее записи и последующего восстановления. Измеряемой
величиной в этом случае будет контраст интерференционных
полос. Характерной чертой описанного коррелятора является
неинвариантность к положению объекта в плоскости предметов.
Этот недостаток в некоторых случаях может быть несуществен,
а иногда даже полезен - тогда, когда на объекте (транспаранте)
есть метка, используемая как начало отсчета. Примером таких
объектов являются оптические спектры на выходе спектроанализатора.
так,
чтобы они освещались излучением, дифрагировавшим в ±1 порядки,
а остальные порядки дифракции экранировать, то распределение
интенсивности в плоскости изображения дифракционной решетке,
являющейся одновременно плоскостью пространственных частот
для сравниваемых объектов, будет описываться уравнением
(34). Корреляционные свойства сравниваемых объектов оказывают
влияние только на контраст, с которым передаются линии дифракционной
решетки. Зарегистрированное изображение решетки можно рассматривать
как голограмму, соответствующую второму (по порядку рассмотрения)
типу корреляторов, в которой отсутствует избыточность. При
восстановлении такой голограммы, как голограммы Фурье, в
плоскости восстановленного изображения будет наблюдаться
только светящаяся точка, соответствующая (по амплитуде)
максимуму кросс-корреляционной функции. Корреляционное сравнение
можно производить и непосредственно в плоскости голограммы
без ее записи и последующего восстановления. Измеряемой
величиной в этом случае будет контраст интерференционных
полос. Характерной чертой описанного коррелятора является
неинвариантность к положению объекта в плоскости предметов.
Этот недостаток в некоторых случаях может быть несуществен,
а иногда даже полезен - тогда, когда на объекте (транспаранте)
есть метка, используемая как начало отсчета. Примером таких
объектов являются оптические спектры на выходе спектроанализатора.
З
а к л ю ч е н и е
В данной
лекции мы не придерживались исторической последовательности
в развитии различных голографических методов, представив
их как реализация различных решений одного и того же уравнения,
учитывающего когерентные свойства волновых полей и корреляционные
свойства объектов (отметим, что корреляционные свойства
объектов находят свое отражение в когерентных свойствах
волновых полей, как
видно
из уравнений (2, 4, 35). Такой подход позволил показать,
что выбор некоторых сочетаний когерентных свойств волновых
полей и корреляционных свойств объектов оказывается полезным
для записи и восстановления голографического изображения
и для корреляционной обработки информации. Обобщая изложенный
подход, можно утверждать, что управление когерентными свойствами
волновых полей (и находящих в них свое отражение корреляционными
свойствами объектов) может оказаться полезным не только
в голографических, но и в других системах передачи и обработки
информации.
Л
и т е р а т у р а
1. Д.Стаселько,
Ю.Н.Денисик, А.Смирнов. Оптика и спектроскопия. 26, №3,
413-420, 1969.
2. Murata
K., Asakura T., Fujiwara H., Opt.Acta, 17, №1,5-8, 1970.
3. Murata
K., Asakura T., Fujiwara H., Opt.Acta, 17, №11, 823-838,
1970.
4.
Fujiwara H., Murata К., Annalen der Physik, 7 folge, 26,
№4, 274-282,1971.
5. М.Борн,
Э.Вольф. Основы оптики. М., "Наука", 1973.
6. Bеrаn
M.J., Parrent С.В., Theory of Partial Соherеnсе, Prentice
Hall International Series In Phusics, 1-194, 1964.
7.
Vlasov N.G., Soloviev E.G., Appl. du l'Holographie, Соmр.
Rend du Simposi.um International, Besanson, 3, 10, 1970.
8. Н.Г.Власов,
Г.В.Скроцкий, Е.Г.Соловьев. Труды I Всесоюзной конференции
по голографии. Сб "Проблемы голографии", т.1, 85-88, 1973.
9. Л.М.Сороко.
Основы голографии и когерентной оптики. M., "Наука", 1971.
10.
Р.Кольер, К.Беркхарт, Д.Лин. Оптическая голография. М.,
Мир, 1973.
11.
Х.Ленк. Материалы III Всесоюзной Школы по голографии. Л.,
ЛИЯФ, стр.133-149, 1972.
12.
Grah G., Wiess H., Optics Communications, 4, №1, 63-65,
1971.
13.
Lurie M., J.Opt.Soc.of Am., 56, №10, 1369-1372, 1966.
14.
Watrasiewics B., Opt. Асtа, 16, №3, 321-326, 1969.
15.
Rau J.E., J.Opt. Soc. of Am., 56, 1490, 1966.
16.
Weawer C.S., Goodman J.W., Appl.Opt., 5, №7, 1248-1249,
1966.
17.
Rau J.Е., J.Opt.Soc. of Am., 57, №6, 798-802, 1967.
18.
Tsuruta T., Yashinobu J., Shirasu S., Appl.Opt., 13, №5,
1089-1092, 1974.
19.
Г.Е.Корбуков, Е.Р.Цветков. Тезисы II Всесоюзной конференции
по голографии, 1, 18-20, 1975.
20.
Lohmann A., Opt.Acta, 9, №1, 1-12, 1962.

