ГРУППОВАЯ
СТРУКТУРА ГОЛОГРАФИЧЕСКОГО ПРОЦЕССА В.Б.Немтинов
Рассмотрены основы
групповой теории голографии. Построена трехкаскадная теоретико-групповая
модель всего голографического процесса в целом. Исследован
инвариантный характер групповой структуры интерференционного
поля, описываемой с помощью голографической фактор-группы.
Показано, что процесс регистрации голограммы приводит к
понятию матричной группы, элементы которой обусловлены как
строением фактор-группы, так и свойствами реальной регистрирующей
среды. Найдено, что процесс реконструкции голографического
изображения можно рассматривать как представление матричной
группы в некотором функциональном пространстве.
В
в е д е н и е
В работе
/1/ показано, что голографический процесс записи информации
обладает ярко выраженной групповой природой. В рамках скалярной
теории дифракции построена теоретико-групповая модель обобщенной
голограммы, в основе которой лежит идея инвариантности интерференционного
поля, регистрируемого на голограмме. Описание математической
модели обобщенной голограммы сводится к заданию некоторой
функции, определенной на фактор-группе G/H, которая построена
по подгруппе Н соответствующих дифракционных образцов (НcG).
Предложенная модель позволяет c единой теоретико-групповой
точки зрения классифицировать все имеющиеся в настоящее
время разновидности голограмм и прогнозировать новые типы
голограмм.
Однако процесс записи
голографической информации представляет собой только часть
полного голографического процесса, устанавливающего связь
между полем исходной предметной волны и полем восстановленной
волны. В работе на примере плоских (тонких) голограмм /2/
проведено исследование структурных закономерностей всего
голографического процесса в целом, которые обусловлены групповой
природой процесса записи и восстановления голографической
информации, и дан теоретико-групповой анализ отдельных этапов.
При этом анализ групповой структуры интерференционного поля
носит общий характер и справедлив как для плоской, так и
объемной голограммы. В то же время групповой характер процесса
регистрации интерференционной картины и восстановления исходного
волнового фронта исследован для случая плоских голограмм.
Применение теоретико-группового
подхода позволяет, с одной стороны, найти внутреннюю связь
отдельных этапов голографического процесса, обусловленную
его групповой структурой. С другой стороны, теоретико-групповой
формализм дает единое общее описание всего процесса в целом,
причем восстановление голографического изображения можно
рассматривать, используя аппарат теории представлений групп
/3/.
1.
Структурный анализ голографического процесса
Известно, что в отличие
от обычного процесса формирования изображения с помощью
оптической системы (в частности, в отличие от обычной фотографии)
голографический процесс регистрации и воспроизведения информации
носит двухступенчатый характер /2,4/, что обусловлено спецификой
голографической запаса. При этом вначале образуется голограмма,
которая в дальнейшем может быть использована как для непосредственного
формирования изображения объекта, так и в различных системах
оптической обработки информации.
1. Однако в общем
случае при анализе групповой структуры голографического
процесса от стадии записи пространственного распределения
предметной волны до стадии восстановления исход-
ного
волнового фронта необходимо различать три основных момента.
Во-первых, при наложении предметной, и опорной волны в области
регистрации голограммы формируется суммарное интерференционное
поле, имеющее групповую природу /1/. Во-вторых, в результате
взаимодействия со светочувствительной средой осуществляется
регистрация пространственного распределения интерференционного
поля (в частности, в случае квадратичной регистрирующей
среды фиксируется распределение интенсивности в интерференционной
картине). Третьим моментом является этап восстановления
волнового фронта, когда голограмма освещается восстанавливающей
волевой, обычно совпадающей с опорной.
Такое
поэтапное разделение голографического процесса схематически
показано на рис.1. Каждая из трех рассмотренных структурных
ситуаций связана с конкретным физическим этапом в процессе
проведения голографического эксперимента. На первом этапе
(I) наблюдается интерференционное взаимодействие предметной
и опорной волн, используемых для формирования голограммы.
Получаемая интерференционная картина содержит в себе в закодированной
форме еще до регистрации всю информацию (амплитудную и фазовую)
о поле предметной волны.

Рис.1.
Трехступенчатая структурная блок-схема
голографического
процесса
Регистрация
интерференционной картины приводит к изменении оптических
свойств регистрирующей среды (II), используемой для записи
голограммы. Причем, процесс записи голографической информации
в общем случае включает в себя также физико-химическую обработку
экспонированного светочувствительного материала. На третьем
этапе (III) реконструированный волновой фронт в качестве
одной из составляющих содержит первоначальную волну, распростра-
нявшуюся от объекта.
2. Выделение трех
основных этапов записи и восстановления голографической
информации, показанных на рис.1, обусловлено теоретико-групповой
природой голографического процесса, математическая модель
кoтopoго приведена на рис.2. Групповая структура интерференционного
поля описывается с помощью голографической фактор-группы
(1 каскад), построенной по подгруппе соответствующих дифракционных
образцов /1/. Процесс регистрации
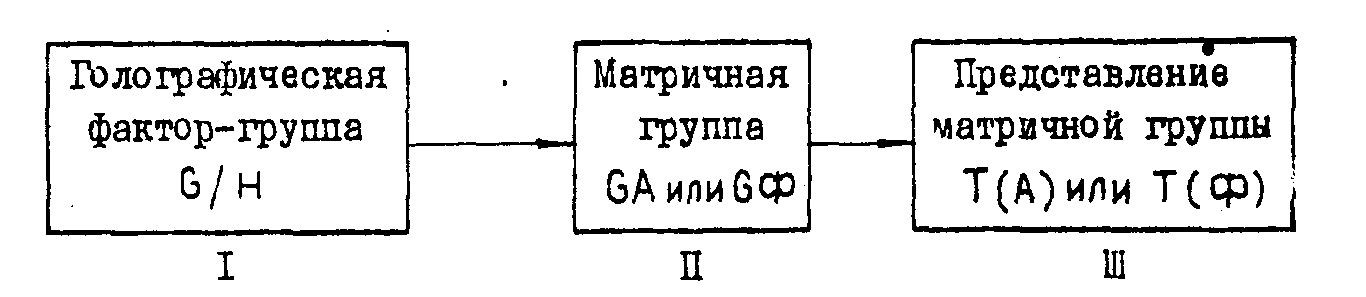
Рис.2.
Трехкаскадная теоретико-групповая модель голографического
процесса.
голограммы
приводит к понятию матричной группы (III каскад), элементы
которой обусловлены как строением голографических классов
(элементов фактор-группы), так и свойствами реальной регистрирующей
среда. Наконец, восстановление голограммы можно рассматривать
как представление этой группы матриц (III каскад) в некотором
функциональном пространстве. При этом процесс реконструкции
амплитудной или фазовой голограммы обуславливает определенную
реализацию представления.
Такой подход, позволяет,
с одной стороны, выявить групповую природу каждого этапа
голографического процесса. С другой стороны, единое теоретико-групповое
описание дает возможность установить общую групповую концепцию
процесса записи и восстановления голографической информации,
начиная от регистрации и кончая реконструкцией предметного
волнового фронта.
Ниже на примере плоских
голограмм проведен теоретико-групповой анализ каждого из
трех каскадов (рис.2) предложенной математической модели,
соответствующих трем выделенным на рис.1 структурным этапам
голографического процесса.
II.
Инвариантный характер групповой структуры
интерференционного
поля.
Математическая
структура интерференционного поля, регистрируемого на произвольной
голограмме, рассмотрена в работе /1/. Показано, что в приближении
скалярной теории дифракции множество дифракционных образов
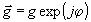 представляет
собой аддитивную абелеву группу G(
представляет
собой аддитивную абелеву группу G(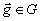 ).
Найдено, что введение факторгруппы G/Н, где Н-инвариантная
собственная подгруппа соответствующих дифракционных (например,
френелевских) образов, задает правильное разбиение группы
G дифракционных образов на непересекающиеся подмножества
).
Найдено, что введение факторгруппы G/Н, где Н-инвариантная
собственная подгруппа соответствующих дифракционных (например,
френелевских) образов, задает правильное разбиение группы
G дифракционных образов на непересекающиеся подмножества
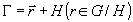 . Произвольный
смежный класс
. Произвольный
смежный класс 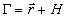 образуется из множества элементов
образуется из множества элементов 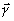 ,
представляемых в виде суммы
,
представляемых в виде суммы 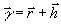 ,
где
,
где 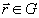 ,
,
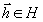 , соответственно,
комплексная амплитуда опорной и предметной волны.
, соответственно,
комплексная амплитуда опорной и предметной волны.
1.
Фактор-группа G/Н описывает групповую структуру интерференционного
поля, регистрируемого на голограмме (1 ступень на рис.1),
а ее элементы характеризуют суммарную амплитуду поля. Поэтому
группу G/H в дальнейшем будем называть голографической фактор-группой
(1 каскад на рис.2). В свою очередь, голографический структурный
смежный класс Г=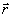 +Н
естественно называть классом голографических образов, где
под голографическим образом, вообще говоря, понимается суммарный
дифракционный образ
+Н
естественно называть классом голографических образов, где
под голографическим образом, вообще говоря, понимается суммарный
дифракционный образ 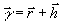 ,
записываемый на голограмме.
,
записываемый на голограмме.
Анализ
групповой структуры интерференционного поля /1/ носит общий
характер и справедлив для плоской и объемной голограммы.
В его основе лежит фундаментальная алгебраическая идея "факторизации"
(разделения) исходного множества (группа G дифракционных
образов) /5,6/. Построение голографической факторгруппы
G/Н индуцирует на группа G разбиение на голографические
классы эквивалентности Г. При этом выделение различных "типов
эквивалентности" группы G задает классификацию голограмм,
определяемую структурой интерференционного поля. Такой подход
к выделению различных типов голограмм, обусловленных строением
голографического класса, основан на отсеивании несущественных
деталей при выделении класса голографических образов и представ-
ляет
собой гомоморфное преобразование исходной группы G.
Представление
интерференционного поля в виде голографической фактор-группы
позволяет наиболее полным образом описать тот факт, что
в суммарной волне скрыта вся информация об амплитуде и фазе
предметной волны. В самом деле, физически в основе построения
голографического класса Г=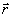 +Н
лежит принцип кодирования информации об амплитуде и фазе
предметной волны
+Н
лежит принцип кодирования информации об амплитуде и фазе
предметной волны 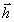 с помощью опорной волны
с помощью опорной волны 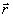 .
Иначе говоря, физический смысл класса голо графических образов
Г состоит в том, что он представляет собой совокупность
определенным образом одинаково кодируемых предметных волн
.
Иначе говоря, физический смысл класса голо графических образов
Г состоит в том, что он представляет собой совокупность
определенным образом одинаково кодируемых предметных волн
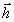 Î
Н. Таким образом, факторизация интерференционного поля позволяет
выяснить специфические особенности такого кодирования в
каждом конкретном случае.
Î
Н. Таким образом, факторизация интерференционного поля позволяет
выяснить специфические особенности такого кодирования в
каждом конкретном случае.
В частности,
инвариантность собственной подгруппы Н(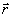 +Н=Н+
+Н=Н+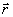 )
обуславливает инвариантный характер групповой структуры
интерференционного поля, так что
)
обуславливает инвариантный характер групповой структуры
интерференционного поля, так что
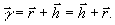 (1)
(1)
Иначе
говоря, голографический образ у инвариантен относительно
предметной 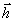 и опорной
и опорной 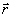 волны. Физически это означает, что на первом этапе голографического
процесса (образовании интерференционного поля) предметная
и опорная волна полностью симметричны. Однако задание голографического
класса в виде Г=
волны. Физически это означает, что на первом этапе голографического
процесса (образовании интерференционного поля) предметная
и опорная волна полностью симметричны. Однако задание голографического
класса в виде Г=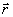 +Н
подчеркивает тот факт, что такое терминологическое разделение
все же не является совсем условным. При этом опорная волна
+Н
подчеркивает тот факт, что такое терминологическое разделение
все же не является совсем условным. При этом опорная волна
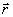 представляет
собой произвольный дифракционный образ, а предметная волна
представляет
собой произвольный дифракционный образ, а предметная волна
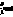 обычно
принадлежит некоторой собственной подгруппе /1/.
обычно
принадлежит некоторой собственной подгруппе /1/.
2. Для исследования
специфики инвариантного кодирования в процессе факторизации
проведем структурный анализ голографических классов.
По определению
/1/ под суммой двух голографических классов Г1=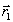 +Н
и Г2=
+Н
и Г2=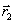 +Н
понимается голографический класс Г, такой что
+Н
понимается голографический класс Г, такой что
Г =
Г1 + Г2 = (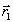 + Н) + (
+ Н) + (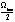 + Н), (2)
+ Н), (2)
где
r = (r1+r2)Î G. Из теории групп
/5,6/ известно, что эта операция не зависит от выбора представителей
в суммируемых голографических классах. Иначе говоря, для
любых двух голографических образов 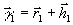 и
и 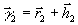 их
сумма
их
сумма 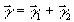 попадает в класс Г, который полностью определяется любым
своим представителем:
попадает в класс Г, который полностью определяется любым
своим представителем:
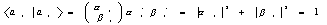 (3)
(3)
где
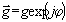 - произвольный
дифракционный образ (произвольная опорная волна),
- произвольный
дифракционный образ (произвольная опорная волна), 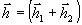 Î
Н - суммарная предметная волна.
Î
Н - суммарная предметная волна.
Из
выражения (3) следует, что в общем случае суммарный голографический
образ 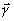 ,
хотя и изменяется, но остается инвариантен относительно
суммарной предметной
,
хотя и изменяется, но остается инвариантен относительно
суммарной предметной 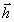 и опорной
и опорной 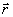 волны. Иначе говоря, суммарная предметная и опорная волна
по-прежнему полностью симметричны.
волны. Иначе говоря, суммарная предметная и опорная волна
по-прежнему полностью симметричны.
Физически
операцию сложения в голографической факторгруппе в общем
случае следует рассматривать как когерентное наложение двух
интерференционных полей (картин). Она может быть реализована
как когерентная запись двух или нескольких голограмм на
одном и том же светочувствительном материале. При этом структура
восстановленного волнового фронта полностью определяется
строением классов голографических образов, которые используются
при записи голограммы.
Для анализа структуры
суммарного голографического класса Г, определяющего специфику
кодирования голографической информации при когерентном сложении
интерференционных полей, рассмотрим ряд частных случаев.
2.1.
Пусть 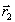 = 0, так что Г2=Г0=Н. Тогда с точки
зрения сложения двух классов при суммировании добавляется
нулевой (нейтральный) класс голографических образов Г0,
роль которого играет инвариантная подгруппа H, так что с
учетом (2)
= 0, так что Г2=Г0=Н. Тогда с точки
зрения сложения двух классов при суммировании добавляется
нулевой (нейтральный) класс голографических образов Г0,
роль которого играет инвариантная подгруппа H, так что с
учетом (2)
Г =
Г1 + Г0 = (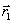 + Н) + Н = (
+ Н) + Н = (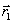 + Н) + (
+ Н) + (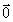 + Н) =
+ Н) = 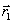 + Н = Г1. (4)
+ Н = Г1. (4)
При
этом суммарный голографический класс совпадает с исходным
голографическим классом Г1. В свою очередь, суммарный
голографический образ
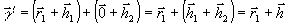 .
(5)
.
(5)
Физически
это означает, что регистрируется некоторая совокупность
голограмм с одной и той же опорной волной 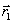 и составной предметной волной
и составной предметной волной 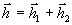 .
Иначе говоря, когерентная запись на голограмме нескольких
предметных волн
.
Иначе говоря, когерентная запись на голограмме нескольких
предметных волн 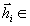 H
(т.е. обладающих одними и теми же дифракционными свойствами)
с точки зрения групповой теории голографического процесса
выражается в инвариантности (неизменности) класса голографических
образов. Переход от одной голограммы к другой обусловлен
только изменением суммарной предметной волны. При этом естественно
считать, что такое изменение не приводит к изменению угла
между предметной и опорной волной (не меняется пространственная
несущая в случае плоской голограммы), т.е. объект не меняет
своего местоположения. Без ограничения общности все изменения
этого угла можно связать с изменением опорного волнового
фронта
H
(т.е. обладающих одними и теми же дифракционными свойствами)
с точки зрения групповой теории голографического процесса
выражается в инвариантности (неизменности) класса голографических
образов. Переход от одной голограммы к другой обусловлен
только изменением суммарной предметной волны. При этом естественно
считать, что такое изменение не приводит к изменению угла
между предметной и опорной волной (не меняется пространственная
несущая в случае плоской голограммы), т.е. объект не меняет
своего местоположения. Без ограничения общности все изменения
этого угла можно связать с изменением опорного волнового
фронта 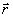 .
.
Таким
образом, регистрация на голограмме интерференционного поля,
соответствующего определенному голографическому классу Г,
обуславливает получение серии голограмм с неизменной дифракционной
структурой суммарного поля 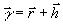 (голограммы Френеля, Фурье, Фраунгофера, сфокусированного
изображения и т.п.). При этом вид опорной волны
(голограммы Френеля, Фурье, Фраунгофера, сфокусированного
изображения и т.п.). При этом вид опорной волны 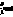 определяет тип голограммы в зависимости от схемы записи,
т.е. от величины угла между предметным и опорным пучком
(осевая голограмма, голограмма с наклонным опорным пучком,
голограмма во встречных пучках).
определяет тип голограммы в зависимости от схемы записи,
т.е. от величины угла между предметным и опорным пучком
(осевая голограмма, голограмма с наклонным опорным пучком,
голограмма во встречных пучках).
2.2.
Если теперь 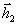 = 0, то это означает, что хотя класс Г2=
= 0, то это означает, что хотя класс Г2=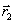 +Н
в формуле (2) не меняется, но в качестве его представителя
рассматривается частный случай голографического обра-
+Н
в формуле (2) не меняется, но в качестве его представителя
рассматривается частный случай голографического обра-
за
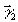 , совпадающего
с опорной волной
, совпадающего
с опорной волной 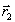 .
Это приводит к тому, что суммарный голографический образ
.
Это приводит к тому, что суммарный голографический образ
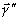 , задающий
суммарный голографический класс Г, с учетом (3) принимает
вид:
, задающий
суммарный голографический класс Г, с учетом (3) принимает
вид:
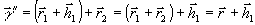 .
(6)
.
(6)
В силу
инвариантности суммарного голографического образа выражение
(6) симметрично формуле (5). Однако с точки зрения факторизации
интерференционного поля, определяемой выбором собственной
подгруппы Н, формулы (5) и (6) выражают две различные физические
ситуации. Это обусловлено тем, что голографические образы
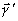 и
и 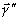 принадлежат разным голографическим классам (
принадлежат разным голографическим классам (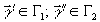 ),
а именно, в данном случае регистрируется голограмма с одной
и той же предметной волной
),
а именно, в данном случае регистрируется голограмма с одной
и той же предметной волной 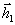 и составной опорной волной
и составной опорной волной 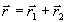 .
.
2.3.
Рассмотрим, еще один интересный частный случай. Если 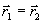 =0,
то Г1=Г2=Г0=Н, так что
суммарный класс Г тоже равен Н. Физически это означает,
что на голограмме записывается одна (голография без опорного
пучка) или несколько предметны волн (роль опорной волны
играет другая предметная волна).
=0,
то Г1=Г2=Г0=Н, так что
суммарный класс Г тоже равен Н. Физически это означает,
что на голограмме записывается одна (голография без опорного
пучка) или несколько предметны волн (роль опорной волны
играет другая предметная волна).
3.
Проведенный анализ 1 каскада теоретико-групповой модели
голографического процесса (рис.2) показывает, что интерференционное
поле, образующееся на первом этапе, носит симметричный (инвариантный)
характер и описывается с помощью голографической фактор-группы
G/Н. При этом групповая структура поля учитывает специфику
инвариантного кодирования предметной волны с помощью опорного
волнового фронта.
В то же время известно
/2/, что для реконструкции неискаженной предметной волны
используется восстанавливающая волна, пропорциональная опорной.
Последняя, в свою очередь, должна иметь относительно простой
вид. Такое нарушение рассмотренной выше симметрии предметной
и опорной волны обусловлено как характером взаимодействия
интерференционного поля с регистрирующей средой, так и спецификой
процесса восстановления. Поэтому для дальнейшего исследования
групповой структуры голографического процесса необходимо
дать групповое описание свойств регистрирующей
среды, используемой
для записи голографической информации.
III.
Групповое представление поля интенсивности
Экспонирование
и обработка (если она необходима) приводят к изменению оптических
свойств регистрирующей среды. На практике обычно изменяется
один из трех параметров светочувствительного материала:
амплитудный коэффициент поглощения κ; показатель преломления
n0 или толщина (высота) Δ записи /2/. При
этом выделяют материалы с амплитудной модуляцией (поглощающие
регистрирующие среды), у которых в процессе экспонирования
изменяется величина κ, и материалы с фазовой модуляцией
(практически не обладающие поглощением), экспонирование
которых приводит к изменению вносимой ими величины фазового
сдвига φ за счет изменения n0 или Δ.
Плоская голограмма
представляет собой идеальный случай строго двумерной голограммы.
При анализе процесса восстановления таких голограмм пренебрегают
толщиной регистрирующей среды и считают, что произвольная
амплитудно-фазовая тонкая голограмма характеризуется комплексным
амплитудным коэффициентом пропускания:
t =
tAtφ = tAexp(jφ),
(7)
где
tА - модуль амплитудного пропускания, зависящий
как от амплитудного поглощения κ, так и от толщины
слоя Δ; tφ = exp(jφ) - член, учитывающий
фазовую модуляцию.
1.
В общем случае характер взаимодействия поля с регистрирующей
средой (II ступень на рис.1) как с амплитудной, так и с
фазовой модуляцией зависит от типа светочувствительного
материала. Это обуславливает специфический вид зависимости
амплитудного пропускания tА плоской амплитудной
голограммы или фазового сдвига φ в случав фазовой голограммы
от характеристик поля. На практике в настоящее время для
записи голограмм наиболее широко используются так называемые
квадратичные регистрирующие среды (фотоэмульсия, фототермопластик
и т.п.), которые следует рассматривать как квадратичный
детектор интерференционного поля. В данном разделе показано,
что в случае квадратичной регистри-
рующей
среды взаимодействие интерференционного поля с фоточувствительным
материалом при записи плоской голограммы удобно описывать
с помощью амплитудной или фазовой группы матриц интенсивности
(II каскад на рис.2), связанной с полем интенсивности. При
этом учет влияния как частотных, так и нелинейных свойств
среды приводит к трансформации матричных элементов одной
из реализации этой группы.
Получение
плоской голограммы с помощью квадратичной детектирующей
среды, по сути говоря, является регистрацией поля интенсивности
J в интерференционной картине /2/ при взаимодействии световых
волн с фоточувствительным материалом, например, зернами
галоидного серебра. По определению интенсивность в голографии
сводится к квадрату модуля комплексной амплитуды 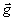 (дифракционного образа), так что
(дифракционного образа), так что
J=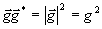 .
(8)
.
(8)
В общем
случае, когда на голограмме регистрируется некоторый голографический
образ 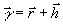 ,
величина
,
величина
J=|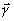 |2=
|2=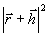 =r2+h2+
=r2+h2+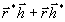 .
(9)
.
(9)
Выражение (9) можно
представить в виде следующей эрмитовой матрицы:
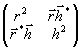 .
(10)
.
(10)
Так как определитель
этой матрицы равен нулю, то такая матрица оказывается вырожденной.
2. Известно,
что при восстановлении плоской амплитудной голограммы различают
нулевой порядок, главное и сопряженное изображения. С учетом
этого факта матрицу (10) при использовании светочувствительного
материала с амплитудной модуляцией более удобно представить
в виде треугольной матрицы:
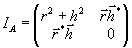 (11)
(11)
Нетрудно
видеть, что множество эрмитовых матриц U второго порядка
с эламентами α, β, γ, δ из поля комплексных
чисел образуют аддитивную абелеву группу GU с обычной
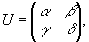 (12)
(12)
операцией
сложения матриц /1/ так что
U=U1+U2=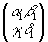 +
+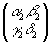 =
=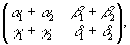 (13)
(13)
где
U1, U2,UÎ GU . Матрица U называется
эрмитовой, если транспонированная матрица U' совпадает с
комплексно-сопряженной матрицей U*. Роль нулевого
(нейтрального) элемента U0 в группе GU выполняет
нулевая матрица:
U0=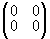 ,
(14)
,
(14)
а противоположным
(обратным) элементом U для матрицы U служит матрица
U-1=-U=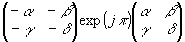 ,
(15)
,
(15)
у которой
все элементы отличаются фазовым сдвигом π. При этом
множество треугольных эрмитовых матриц UΔ.
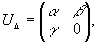 (16)
(16)
является
подгруппой GUΔ группы GU(GUΔÎ
GU).
В свою
очередь, подмножество треугольных эрмитовых матриц интенсивности
IAm, представляемых в виде
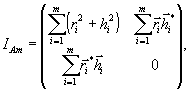 (17)
(17)
образует
подгруппу GIA группы GUΔ(GIΔÎ
GUΔ), ибо это подмножество замкнуто
и обратимо /1/ относительно заданной групповой операции
сложения матриц IA. В частности,(11) получается
из (17) при m=1. Нулевым элементом I0, в группе
GIA является матрица
I0=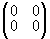 ,
(18)
,
(18)
а противоположным
элементом 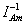 для матрицы IAm служит матрица
для матрицы IAm служит матрица
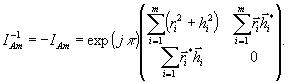 (19)
(19)
Таким
образом, каждому голографическому образу 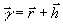 ставился в соответствие по формуле (11) некоторая эрмитовая
треугольная матрица IA из группы GIA,
которую будем, в дальнейшем называть амплитудной группой
матриц интенсивности (или для краткости просто амплитудной
матричной группой). Иначе говоря, групповая структура интерференционного
поля обуславливает групповое строение поля интенсивностей,
так что каждому гологра-
ставился в соответствие по формуле (11) некоторая эрмитовая
треугольная матрица IA из группы GIA,
которую будем, в дальнейшем называть амплитудной группой
матриц интенсивности (или для краткости просто амплитудной
матричной группой). Иначе говоря, групповая структура интерференционного
поля обуславливает групповое строение поля интенсивностей,
так что каждому гологра-
фическому
классу соответствует некоторая совокупность матриц. При
этом основная особенность теоретико-группового анализа процесса
записи плоских голограмм состоит в том, что матрица интенсивности
IA, как и голографический образ 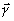 при анализе групповой структуры интерференционного поля,
считается заданной на некоторой плоскости.
при анализе групповой структуры интерференционного поля,
считается заданной на некоторой плоскости.
Формулы
(10) и (11) показывают, что построенная амплитудная матричная
группа GIA не является единственно возможной.
Например, можно рассмотреть подмножество диагональных эрмитовых
матриц
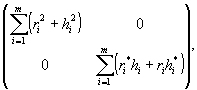 (20)
(20)
которые также образуют
аддитивную абелеву группу.
Ниже
будет показано, что выбор матрицы интенсивности IA
для среды с амплитудной модуляцией обусловлен спецификой
представления процесса реконструкции плоской амплитудной
голограммы.
3. В свою очередь,
при реконструкции тонкой фазовой голограммы изображение
восстанавливается на фоне интермодуляционного шума интенсивность
которого сложным образом связана с амплитудно-фазовым распределением
в объективной волне. Поэтому в случае сред с фазовой модуляцией
с учетом этого факта матрицу интенсивности удобно ввести
в виде:
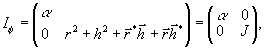 (21)
(21)
где α - некоторая
постоянная.
Легко проверить,
что множество таких диагональных эрмитовых матриц, представляемых
в виде:
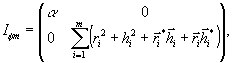 (22)
(22)
также
образует аддитивную абелеву группу, которая является подгруппой
группы GUd диагональных эрмитовых матриц
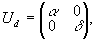 (23)
(23)
так
что GIφÎ GUd. При этом выражение
(21) получается из (22) при m = 1. Нулевым элементом по-прежнему
является матрица I0, а противоположным элементом
служит диагональная матрица
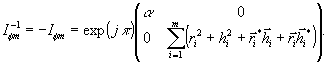 (24)
(24)
По аналогии
с группой GIA группа GIφ называется
фазовой группой матриц интенсивности или фазовой матричной
группой.
Заметим, что как
и для сред с амплитудной модуляцией здесь также можно говорить
об аддитивной абелевой группе треугольных матриц:
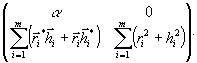 (25)
(25)
При
атом задание матрицы интенсивности Iφ для
среды с фазовой модуляцией в виде диагональной матрицы (21)
оказывается удобным при анализе процесса восстановления
тонкой фазовой голограммы.
4. В основе построения
амплитудной или фазовой матричной группы лежит операция
сложения двух матриц, которая сводится к сложению их матричных
элементов. В свою очередь, сложение матричных элементов
с учетом (9) эквивалентно сложению интенсивностей в интерференционных
картинах. Иначе говоря, операция сложения в матричной группе
имеет глубокий физический смысл, ибо она эквивалентна некогерентному
наложению интерференционных полей. Фактически такая операция
осуществляется на практике при мнотократ-
ном
экспонировании в случае регистрирующей среды с линейным
откликом. При этом группа GI матриц интенсивности индуцирует
соответствующую группу GЕ матриц экспозиции.
IV.
Групповое описание свойств регистрирующей
среды
Одной из основных
характеристик квадратичной регистрирующее среды является
экспозиционная кривая /7/, описывающая зависимость отклика
светочувствительного материала от величины экспозиции:
Ε=Jτ,
(26)
где
τ - время экспонирования. В обычной фотографии для
характеристики фотоэмульсии используется кривая почернения
(характеристическая кривая), т.е. зависимость фотографической
плотности почернения D от ε. В голографии свойства
среды с амплитудной модуляцией задаются с помощью зависимости
амплитудного коэффициента пропускания tA от экспозиции
(tA-ε кривой). Для фазомодулирующей среды
речь должна идти о фазоэкспозиционной кривой, т.е. о зависимости
величины фазового, сдвига от экспозиции (φ - ε
κривая).
1.
В случае квадратичной регистрирующей среды (II ступень на
рис.1) отклик светочувствительного материала зависит от
величины экспозиции. Тогда на основании выражения (26) с
учетом формул (11) и (21) естественно ввести в рассмотрение
экспозиционные матрицы,
EA=τIA
α IA, (27)
Eφ=τIφ
α Iφ,
(28)
b соответствующие
аддитивные абелевы группы треугольных GEA и диагональных
GЕφ
эрмитовых матриц экспозиции. Очевидно, что группы GEA
и GIA, а также GEφ и GIφ
изоморфны друг другу, т.е. GEA @ GIA
и GEφ@ GIφ. Иначе
говоря, их можно считать различными реализациями, соответственно,
амплитудной или фазовой матричной группы (II каскад на рис.2).
Реализация в виде
экспозиционной матричной группы позволяет описать с теоретико-групповой
точки зрения процесс некогерентного накопления голографической
информации. При этом процесс многократного экспонирования
в случав линейной регистрирующей среды интерпретируется
как операция сложения в группе GЕ матриц экспозиции.
Используя построенные
экспозиционные матричные группы можно непосредственно перейти
к групповому описанию свойств регистрирующей среды.
2. Амплитудный коэффициент
пропускания плоской амплитудной голограммы, записанной в
квадратичной регистрирующей среде, в линейном приближении
пропорционален экспозиции (или интенсивности). В частности,
в случае фотографической регистрирующей среды зависимость
амплитудного пропускания от экспозиции /2/ имеет вид:
tA
= t0 - k1Aε = t0 -
k1A τJ = t0 - kA J,
(29)
где
t0 - пропускание неэкспонированной фотоэмульсии;
k1A и kA - коэффициенты пропорциональности.
Такая
запись позволяет ввести еще одну очень важную реализацию
амплитудной группы в виде аддитивной абелевой группы GA
треугольных эрмитовых матриц A амплитудных коэффициентов
пропускания:
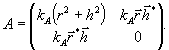 (30)
(30)
Произвольный
элемент Am этой группы (Аm Î
GA) с учетом (17) имеет вид:
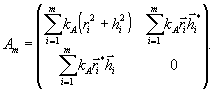 (31)
(31)
При этом в линейном
приближении матричные элементы фактически определяют амплитуды
волн, восстанавливаемых в нулевом и ±1 порядках без учета
частотных свойств регистрирующей среды. МПФ эмульсии предполагается
постоянной в рабочем диапазоне пространственных частот.
3. В
общем случае поведение фотографической эмульсии существенно
нелинейно, хотя обычно частотные свойства среды могут быть
отделены от нелинейных свойств /8/. Тогда, если f(x,y)-импульсный
отклик регистрирующей среды, то амплитудная матрица EAэф
эффективной экспозиции представляется в виде свертки функции
fc матрицей ЕA, так что
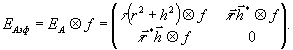 (32)
(32)
В результате
получаем еще одну изоморфную реализацию GЕАэф
аддитивной амплитудной группы (ЕАэфÎ GЕАэф),
описывающую частотные свойства регистрирующей среды. Одновременно
можно говорить о группе GAэф матриц Aэф
эффективных амплитудных коэффициентов пропускания, где
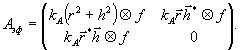 (33)
(33)
Если
импульсный отклик регистрирующей среды совпадает с δ
-функцией, то матрица ЕАэф превращается в ЕА,
а Aэф в А. Иначе говоря, группы GЕА
и GА описывают групповые свойства фоточувствительного материала
без учета влияния частотных
искажений,
вносимых средой, и являются соответствующими подгруппами
в группах GЕАэф и GАэф (GЕАÌ
GЕАэф, GAÌ GAэф).
Наконец,
учитывая эффекты нелинейности регистрирующей среды, например,
с помощью метода преобразования /8/, можно построить нелинейную
реализацию амплитудной матричной группы. В этом случае матричные
элементы должны определяться на основании выбранной модели
нелинейности. Например, используя для анализа нелинейных
искажений плоской амплитудной голограммы аппроксимацию зависимости
tA-ε кривой полиномом третьей степени /2/,
нелинейную матрицу можно представить в виде тензорного произведения
линейных матриц.
4. Величина фазового
сдвига φ при записи тонкой фазовой голограммы в квадратичной
регистрирующей среде с фазовой модуляцией в линейном приближении
пропорциональна экспозиции (или интенсивности), так что
φ=k1φε=kφJ,
(34)
где
k1φ и kφ=k1φτ
- коэффициенты пропорциональности. Выражение (34) с учетом
(28) позволяет ввести в рассмотрение основную реализацию
фазовой группы в виде группы GФ диагональных эрмитовых матриц
фазового сдвига:
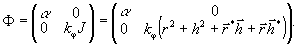 (35)
(35)
Произвольный
элемент Фm аддитивной абелевой группы GФ матриц
фазового сдвига (ФmÌ GФ) представим в виде:
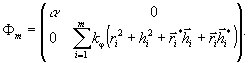 (36)
(36)
По аналогии
с (32) влияние частотных свойств фазовое регистрирующей
среды с импульсным откликом f(х,y) можно учесть, вводя в
рассмотрение фазовую группу GЕφэф матриц
Еφэф эффектив-
ной экспозиции, так
что
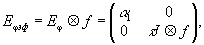 (37)
(37)
где
α1=τ α Ä f. В свою очередь,
матрица Фэф эффективного фазового сдвига φэф,
являющаяся элементом изоморфной группы GФэф,
имеет вид
 (38)
(38)
где
αэф = kφ1α1.
Нелинейность
фазоэкспозиционной φ-ε κривой приводит к
нелинейной трансформации матричных элементов.
5.
Таким образом, результат взаимодействия интерференционного
поля с регистрирующей средой при записи плоской голограммы
с учетом влияния свойств среды может быть описан с помощью
соответствующей матричной группы GA или GФ (II каскад на
рис.3). Структура матричной группы определяется интерференционным
полем, а ее реализация и строение матричных элементов зависит
от свойств светочувствительного материала. Различные реализации
амплитудной GА и фазовой GФ матричной группы характеризуют
определенные аспекты взаимодействия поля с регистрирующей
средой. При этом операция суммирования в матричной группе
физически интерпретируется как процесс некогерентного накопления
голографической информации.
В случае
плоской голограммы описание математической модели обобщенной
голограммы /1/ приобретает вполне конкретное, содержание.
Оно сводится к заданию некоторой реализации матричной группы
GА или GФ, определенной на голографической факторгруппе
G/H , которая обусловлена факторизацией интерференционного
поля.
V.
Представление процесса реконструкции
Завершающим
этапом всего голо графического цикла является процесс формирования
поля реконструированной волны (III ступень на рис.1) с целью
получения восстановленного изображения исходного объекта.
При этом анализ групповой структуры голографического процесса
показывает, что с теоретико-групповой точки зрения операцию
декодирования голографической записи следует рассматривать
как представление матричной группы, задающей групповое описание
свойств регистрирующей среды, в некотором функциональном
пространстве (III каскад на рис.2), Выбор пространства представления
обусловлен строением исходной матричной группы.
Приведем основные
математические сведения, которые лежат в основе теоретико-групповой
трактовки процесса реконструкции.
1. Между двумя произвольными
группами G и G' могут иметь место различные отношения. Одним
из основных отношений является гомоморфизм /5,9/.
Без
ограничения общности в этом пункте будем называть групповую
операцию в G и G' умножением. Тогда отображение Ψ:
G→G' элементов группы G' на элементы группы G' называется
гомоморфизмом, если из Ψ: g1→g1'
и g2→g2' следует, что в мультипликативной
форме записи
g'=Ψ(g)=Ψ(g1g2)=Ψ(g1)Ψ(g2)=g1'g2'.
(39)
Иначе
говоря, задано отображение Ψ группы G в группу G',
при котором, вообще говоря, нескольким элементам из G соответствует
один элемент из G', и при этом образ произведения из группы
G равен произведению образов в группе G'.
В широком
смысле представлением группы G называется любой гомоморфизм
Ψ группы G в некоторую группу G' /9/. Ocoбую ценность
имеют представления в такие группы G', в которых удобно
производить вычисления.
На
практике наибольший интерес представляет реализация группы
G в виде преобразований некоторого пространства L. Тогда
в узком смысле под представлением (реализацией) группы G
понимают
гомоморфизм Т этой группы в некоторую группу преобразований
(операторов Т(g) функционального пространства L/3,10/. Представление
Т называется линейным, если T -линейное пространство, а
преобразования Т(g)- линейные операторы.
Понятие
представления группы является далеко идущим обобщением понятия
показательной функции /3/. Известно, что показательную функцию
ехр(аx) можно определить как непрерывное решение функционального
уравнения
f(x+y)=f(x)f(y),
(40)
удовлетворяющее
начальному условию f'(0)=а. Обобщая это уравнение на любую
группу G, приходим к рассмотрению операторных функций Т(g)
на группе G, удовлетворяющих с учетом (39) уравнению
T(g1g2)
= T(g1)T(g2), (41)
где
g1, g2 Î G.
Итак,
в дальнейшем под представлением группы G будем понимать
непрерывную функцию Т(g) на этой группе, принимающую значения
в группе непрерывных линейных преобразований линейного пространства
L и удовлетворяющую функциональному уравнению (41). В случае
мультипликативной формы записи рассматриваются только невырожденные
линейные преобразования.
Линейное
пространство L, в котором действуют операторы Т(g), называют
пространством, представления Т(g), Если это пространство
конечномерно, то и представление Т(g) называют конечномерным.
2.
Рассмотрим линейное пространство L однородных многочленов
первой степени от двух комплексных переменных z1
и z2.
P(z1,z2)
= az1 + bz2,
(42)
где
а и b некоторые постоянные комплексные коэффициенты. Фи-
зически
выражение (42) можно трактовать как линейную комбинацию
двух восстанавливающих волн z1(х,у) и z2(х,у).
Каждой
эрмитовой комплексной матрице второго порядка UÌ GU
соответствует линейное преобразование,
ω1
= αz1 + γz2
ω2
= βz1 + δz2
(43)
двумерного
линейного комплексного пространства С2 /3/. Этому
преобразованию отвечает оператор,
T(U)P(z1,z2)=P(αz1+γz2,
βz1+δz2)=
=a(αz1+γz2)+b(βz1+δz2)=
(44)
=(aα+bβ)z1+(aγ+bδ)z2,
в пространстве
L функций от двух комплексных переменных. Легко проверить,
что оператор Т(U) является линейным оператором.
Известно,
что множество линейных операторов с обычной операцией сложения
образует аддитивную абелеву группу операторов Т, где под
суммой двух операторов Т1+T2 понимается
оператор Т, такой что
T(P)
= (T1 + T2)(P) = T1(P)
+ T2(P). (45)
Обратным
(противоположным) элементом Т-1 в группе операторов
является оператор -Т:
T-1(P)
= -T(P), (46)
а нулевым
элементом Т0 служит оператор, отображающий вектор
в тождественный нуль:
T0(P)=0.
(47)
Тогда
отображение (44) задает представление группы GU, т.е. является
гомоморфизмом. Для этого надо доказать выполнение соотношения
(41), которое в аддитивной форме записи для группы GU имеет
вид:
T(U1+U2)=T(U1)+T(U2).
(48)
В самом деле, с одной
стороны из (44) с учетом (13) имеем
T(U1+U2)P(z1,z2)=a[(α1+α2)z1+(γ1+γ2)z2]+
+b[(β1+β2)z1+(ε1+ε2)z2]=[a(α1+α2)+b(β1+β2)]z1+
(49)
+[a(γ1+γ2)+b(ε1+ε2)]z2.
С другой стороны,
[T(U1)+T(U2)]P(z1,z2)=T(U1)P(z1,z2)+T(U2)P(z1,z2)=
=a(α1z1+γ1z1)+b(β1z1+δ1z2)+a(α2z1+γ1z2)+
(50)
+b(β2z1+δ2z2)=[a(α1+α2)+b(β1+β2)]z1+
+[a(γ1+γ2)+b(δ1+δ2)]z2.
Из сравнения (49)
и (50) следует выполнение равенства (48).
3. Для
описания процесса реконструкции плоской амплитудной голограммы
сузим построенное представление на подгруппу треугольных
амплитудных матриц GA. Тогда из (44) с учетом (30) получим
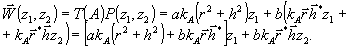 (51)
(51)
В частности, если
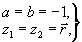 ,
(52)
,
(52)
то (51) принимает
вид:
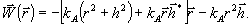 (53)
(53)
Выражение
(53) с точностью до величины 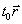 ,
пропорциональной опорной волне
,
пропорциональной опорной волне 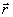 ,
задает распределение комплексной амплитуды поля в плоскости
голограммы при обычном описании процесса восстановления
(см., например, формулу (8.3) §1 гл. /2/) в случае регистрирующей
среды с линейным откликом. Последнее слагаемое, которое
содержит амплитуду предметной волны h, определяет главное
(мнимое) изображение. Более того, если взять матрицу At0Î
GU, такую что
,
задает распределение комплексной амплитуды поля в плоскости
голограммы при обычном описании процесса восстановления
(см., например, формулу (8.3) §1 гл. /2/) в случае регистрирующей
среды с линейным откликом. Последнее слагаемое, которое
содержит амплитуду предметной волны h, определяет главное
(мнимое) изображение. Более того, если взять матрицу At0Î
GU, такую что
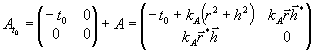 ,
(54)
,
(54)
то по аналогии с
(51) при условии (52) имеем полный аналог (8.3) из /2/:
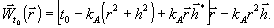 (55)
(55)
Наконец,
если в (52) положить z1=z2=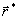 ,
то из (51) получим выражение, аналогичное (53) и соответствующее
восстановлению неискаженного сопряженного (действительного)
изображения. В общем случае форму записи, симметричную (51)
относительно сопряженной предметной волны
,
то из (51) получим выражение, аналогичное (53) и соответствующее
восстановлению неискаженного сопряженного (действительного)
изображения. В общем случае форму записи, симметричную (51)
относительно сопряженной предметной волны 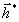 ,
можно найти, если взять транспонированную матрицу А'.
,
можно найти, если взять транспонированную матрицу А'.
Таким
образом, выражение (51) (или его более общий аналог (44)
) позволяет говорить о реконструкции плоской амплитудной
голограммы как о представлении амплитудной матричной группы
GA. При этом выделение в обобщенном реконструированном волновом
фронте  (z1,z2)
последнего слагаемого, пропорционального исходной предметной
волне h, обусловлено треугольным видом матрицы А. Хотя такое
разделение носит несколько искусственный характер (в случае
физически реализуемого процесса восстановления z1=z2),
но именно оно показывает, что в реконструированном поле
отсутствует симметрия (инвариантность) между предметной
(z1,z2)
последнего слагаемого, пропорционального исходной предметной
волне h, обусловлено треугольным видом матрицы А. Хотя такое
разделение носит несколько искусственный характер (в случае
физически реализуемого процесса восстановления z1=z2),
но именно оно показывает, что в реконструированном поле
отсутствует симметрия (инвариантность) между предметной
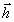 и опорной
и опорной
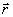 волной.
Последнее связано со структурой матричных элементов, которая
определяется свойствами квадратичной регистрирующей среды.
волной.
Последнее связано со структурой матричных элементов, которая
определяется свойствами квадратичной регистрирующей среды.
Для
учета частотных или нелинейных свойств фоточувствительного
материала необходимо рассматривать представление матричной
группы GAэф эффективных амплитудных коэффициентов
пропускания или соответствующей группы нелинейных матриц.
4.
В случав тонких фазовых голограмм в качестве линейного пространства
L рассмотрим пространство многочленов Р(z) первой степени
от одного комплексного переменного z:
P(z)
=az +b. (56)
Пo аналогии
(44) представление группы GU задается формулой:
T(U)P(z)=T(U)P(z,1)=P(αz+γ,βz+δ)=
(57)
=a(αz+γ)+b(βz+δ)=(aα+bβ)z+aγ+bδ.
Фазовый характер
модуляции восстанавливающей волны, который свойствен тонкой
фазовой голограмме, индуцирует представление
exp[jT(U)P(z)].
(58)
Сужая
это представление на группу диагональных фазовых матриц
GФ из (58) с учетом (35) и (57), получим выражение для обобщенного
волнового фронта, реконструируемого фазовой голограммой:
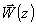 =exp[jT(Ф)P(z)]=exp{j[aαz+bkф(r2+h2+
=exp[jT(Ф)P(z)]=exp{j[aαz+bkф(r2+h2+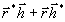 )]}=
(59)
)]}=
(59)
=exp(jaαz)exp[jbkф(r2+h2+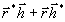 )].
)].
В частности, если
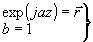 ,
(60)
,
(60)
то (59) описывает
распределение комплексной амплитуды поля, соответствующее
физически реализуемому процессу реконструкции тонкой фазовой
голограммы, так что
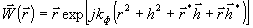 (61)
(61)
Таким
образом, можно говорить о восстановлении фазовых голограмм
в широком смысле как о представлении фазовой матричной группы
GФ, обусловленной как структурой интерференционного поля,
так и свойствами регистрирующей среды.
З
а к л ю ч е н и е
Учитывая специфику
всего голографического цикла в целой, блок-схему на рис.1
можно представить в более общем виде.
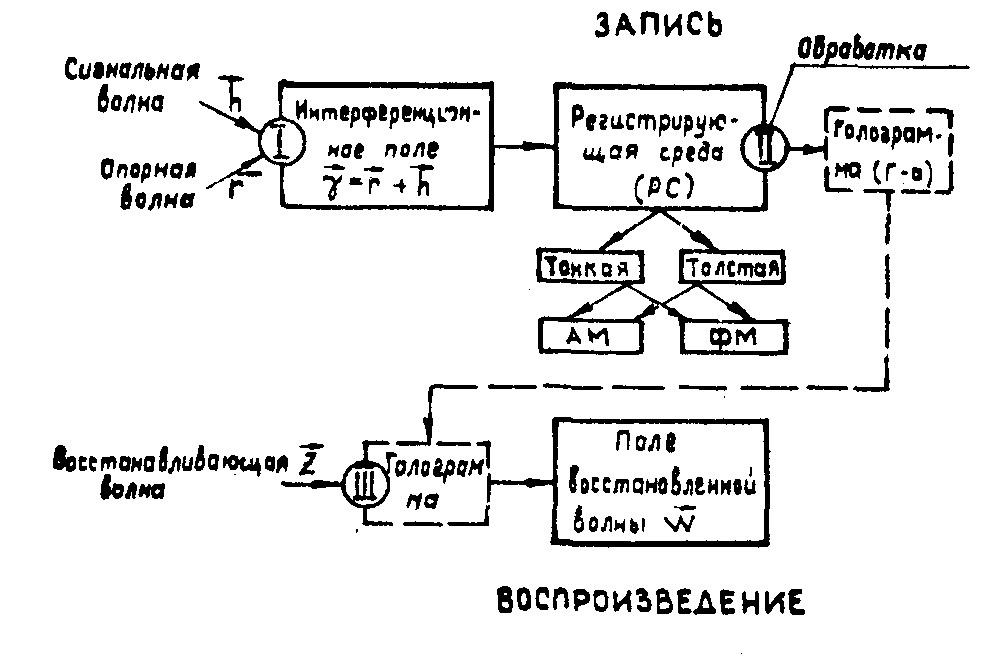
Рис.3.
Расширенная структурная блок-схема голографического процесса.
Соответствующая математическая
модель приведена на. рис.4.
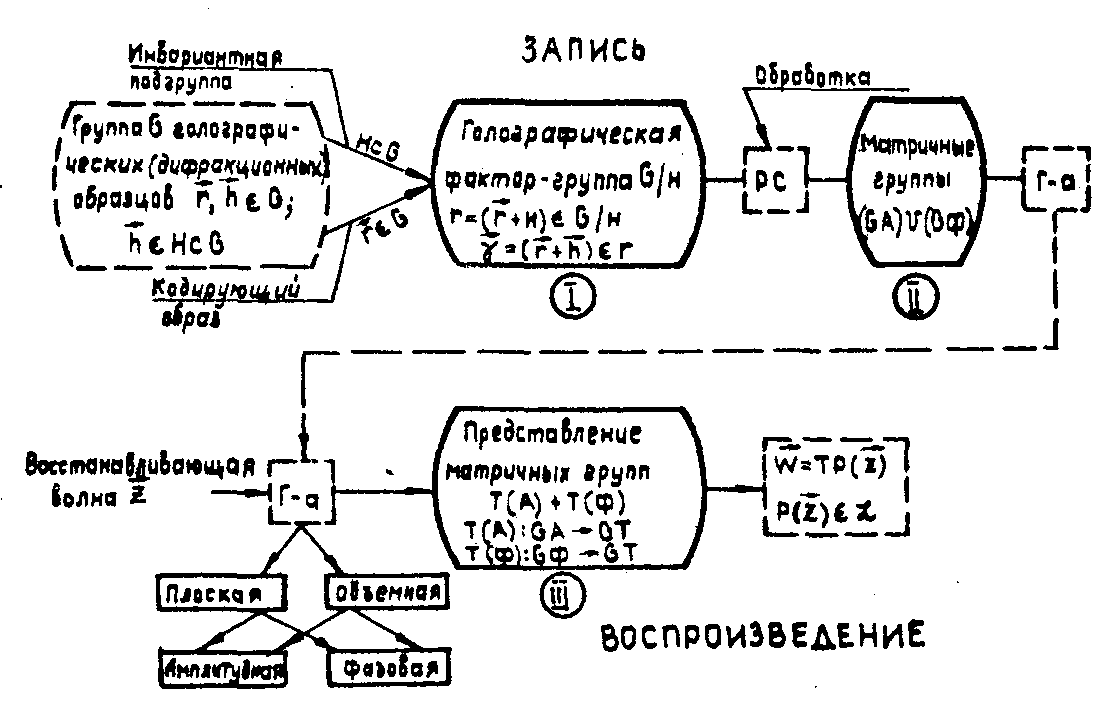
Рис.4.
Обобщенная трехкаскадная теоретико-групповая модель голографического
процесса.
В соответствии с
математической моделью, показанной на рис.4, дано общее
теоретико-групповое описание всего голографического про-
цесса в целом. Теоретико-групповой
подход позволяет выяснить структурные особенности каждого
этапа голографического цикла. При этом операция, заданная
в каждой группе, имеет вполне определенный физический смысл
и соответствует когерентному или некогерентному наложению
волновых полей.
Предложенное
модельное представление голографического процесса не только
показывает, что голографический процесс обладает ярко выраженной
групповой структурой, но и позволяет установить связь между
отдельными этапами голографического цикла. В частности,
по-видимому, можно говорить о введении предыскажений на
стадии записи голограммы для устранения нелинейных искажений,
обусловленных свойствами регистрирующей среды.
Задание групповой
структуры голографического процесса сводится к следующему:
а) построение
голографической фактор-группы G/H, обусловленной групповой
природой интерференционного поля;
б)
введение матричной группы GA или GФ, учитывающей влияние
свойств регистрирующей среды;
в)
задание представления Т(А) или Т(Ф) матричной группы, описывающего
процесс реконструкции голографического изображения.
Таким образом теоретико-групповой
анализ голографического процесса позволяет, опираясь на
групповую структуру голографического цикла:
1) классифицировать
и систематизировать все имеющиеся в настоящее время разновидности
голограмм;
2) прогнозировать
и выявлять новые типы голограмм;
3) выработать
более общий и более универсальный подход к оценке качества
голографического процесса /11/.
Л
и т е р а т у р а
1. В.Р.Немтинов.
Групповые свойства голограмм. Материалы VII Всесоюзной школы
по голографии, Л., стр.102, 1975.
2.
Р.Кольер, К.Беркхарт, Л.Лин. Оптическая голография. "Мир",
М., 1973.
3. Н.Я.Виленкин.
Специальные функции и теория представлений групп. "Наука",
М., 1965.
4. Л.М.Сороко. Основы
голографии и когерентной оптики. "Наука", М., стр.341, 1971.
5. А.Г.Курош. Теорая
групп. "Наука", М., 1967.
6. Б.А.Гостев. Гомоморфизмы
и модели. "Наука", М., стр.56, 1975.
7. О.В.Рожков.
Влияние нелинейности фазоэкспозиционной характеристики регистрирующего
материала на качество голографического процесса. Материалы
VII Всесойвной школы по голографии, Л., стр. 244, 1975.
8. Дж.Гудмен. Введение
в фурье-оптику. "Мир", стр.304, М., 1970.
9. М.Холл. Теория
групп. Изд.ИЛ, 1962.
10. А.А.Кириллов.
Элементы теории представлений групп. "Наука", М., 1972.
11.
В.Б.Немтинов, О.В.Рожков. Метод оценки качества голографического
процесса. Материалы VI Всесоюзной школы по голография. Л.,
стр.192, 1974.

