ОБ
ИНФОРМАЦИОННОЙ ЕМКОСТИ КОГЕРЕНТНЫХ СИСТЕМ ОБРАБОТКИ ИНФОРМАЦИИ
С.Г.Гуревич
Рассматриваются
изменения плотности информации в различных плоскостях схемы
оптической фильтрации изображений. Отмечаются потери информации,
вносимые различными звеньями системы оптической обработки.
Оценивается соотношение параметров системы, при которых
информация может быть передана без существенных потерь.
1. Рассмотрим
систему оптической фильтрации изображений, представляющую
собой один из вариантов когерентной системы оптической обработки
информации. Согласно рис.1, когерентный свет точечного источника
коллимируется линзой Lk, создавая на входе системы
в плоскости P1 плоский фронт волны. Предназначенное
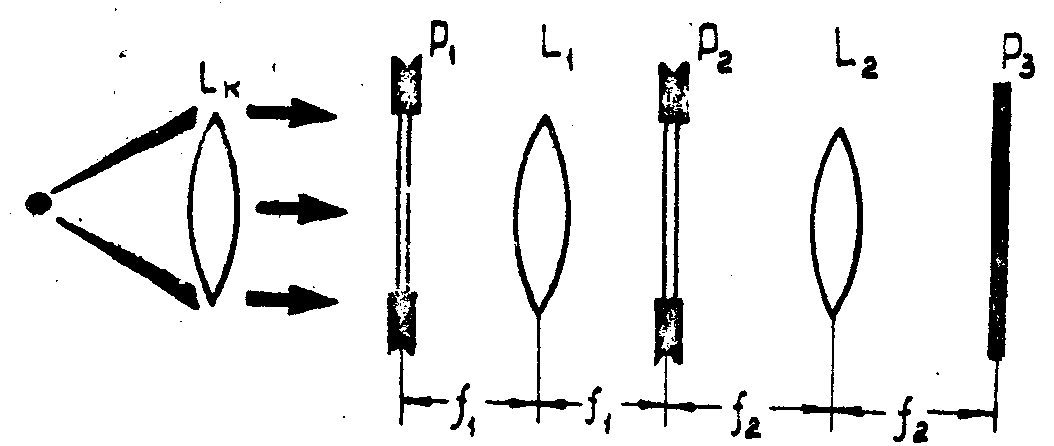
Рис.1.
Схема установки оптической фильтрации изображения.
для
фильтрации изображение помещается в эту плоскость, от которой
на фокусном расстоянии А находится линза L1,
выполняющая
фурье-преобразование.
В плоскости Р2, которую можно назвать частотной
плоскостью с точностью до постоянного множителя распределен
пространственный спектр изображения, который может быть
отфильтрован стоящим в этой же плоскости фильтром. Линза
L2 осуществляет второе фурье-преобразование отфильтрованного
спектра, создавая в выходной плоскости Р3 обработанное
изображение.
Наша
задача - определить информационную емкость такой системы
и оценить влияние различных источников потерь информации.
Показать,
что когерентные системы оптической обработки информации
обладают целым рядом общих черт с когерентными линзовыми
системами формирования изображения и голографическими системами.
В таблице
1 производится качественное сравнение по следующим свойствам
этих трех систем: 1 - характеру источника освещения; 2 -
характеру преобразования, осуществляемому системой; 3 -
необходимости наличия линз; 4 - необходимости промежуточной
записи до регистрации изображения; 5 - по времени передачи
изображения объекта; 6 - по содержанию информации в модулируемом
световом пучке; 7 - характеру модуляции пучка. Отмеченные
в различных столбцах таблицы свойства систем в известной
степени условны. Важно отметить, что наличие в когерентной
системе обработки информации элементов как линзовой, так
и голографической системы приводит к одновременному действию
источников потерь информации, присущих обеим системам, а,
следовательно, и к большим потерям информации. Если бы,
однако, этот недостаток не компенсировался другими достоинствами
(в частности, возможностью увеличения объема передаваемой
полезной информации за счет устранения ненужной, уменьшением
избыточности и т. п.), то система оптической обработки не
получила бы того признания, которое она имеет.
Рассмотрим
информационные характеристики линзовых систем /1/.
Если
возможная серия объектов не может отражать (пропускать,
испускать) в каждом из своих элементов световой поток, больший
некоторой величины, то, зная ряд характеристик объектива,
можно
подсчитать его информационную пропускную способность, т.е.
максимальное количество информации, пропускаемое объективом
в единицу времени. Если время пропускания информации ограничено
длительностью нахождения объекта в неизменном состоянии,
временем, выдержки, с которой работает затвор, временем
кадра передающей телевизионной трубки или другим временем,
то можно подсчитать информационную емкость объектива в данной
системе. Эта величина будет указывать максимальное количество
информации, которое, способен в заданное время передать
объектив на вход следующего звена системы при ограниченной
световой энергии, попадающей в зрачок объектива.
Потери
информации, вызываемые введением в систему линзы, отражаются
на двух составляющих информации. Апертура линзы пропускает
через систему лишь ограниченный световой поток, сокращая
объем градационной составляющей информации; в этом же направлении
действуют отражение и рассеяние в линзах. С другой стороны,
ограничение апертуры и эффект виньетирования приводят к
потерям пространственной информации, обусловленным сокращением
диапазона передаваемых пространственных частот, увеличивающимся
от центра к периферии поля изображения. Потери пространственной
информации и неравномерность ее передачи усиливаются в результата
существования различного рода аберраций в объективе. В случае,
когда влияние факторов, приводящих к неравномерности частотных
характеристик по полю, пренебрежимо мало. Информационная
емкость объектива определяется соотношением
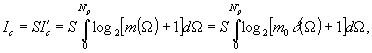
Здесь
S - площадь поля изображения объектива, Ic -
информационная емкость, приходящаяся на единицу площади,
N'p - предельное число элементов, на которое
может быть разложена единица площади поля изображения, m(Ω)-
зависимость числа различимых градаций от двумерной пространственной
частоты Ω изображения объекта, δ(Ω)=m(Ω)/m(0)
градационно-частотная характеристика. Ее ход зависит от
контрастно-частотной характеристики и от измерения отношения
сигнал/щум с частотой.
Пространственные
потери информации Нaps определяются соотношением:
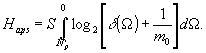
Рис.2
иллюстрирует потери информации, связанные с характером зависимости
δ(Ω).
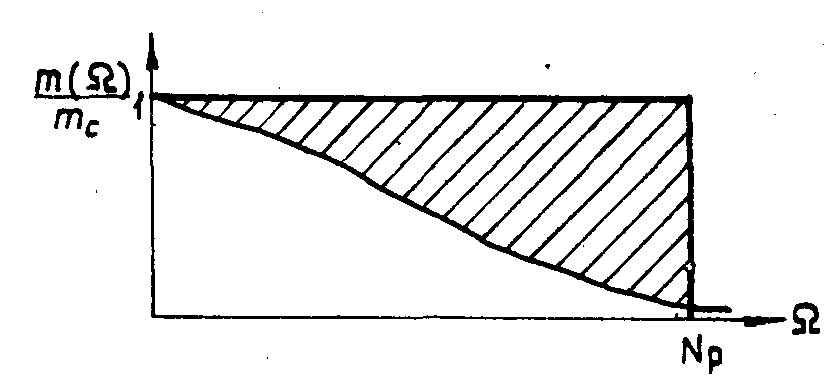
Рис.2.
Потери информации, связанные с ходом частотно-контрастной
характеристики.
В реальном
случае, когда интенсивность и частотно-контрастные характеристики
изменяются в зависимости от расстояния до центра поля изображения,
величина m оказывается зависимой не только от пространственной
частоты Ω, но и от расстояния до центра поля. В этом
случае информационная емкость объектива определяется по
формуле:
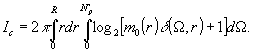
Характеристики
m0(r) и δ(Ω,r) могут быть вычислены
или получены экспериментально, в связи с чем может быть
оценена и информационная емкость объектива, формирующего
изображение.
В спектральной
плоскости Р2 схемы, представленной на рис.1,
модулированный свет проходит через фильтр, который может
являться голограммой. Поэтому представляет интерес рассмотреть,
как проходит информация через голографическую систему /2,3/.
На голограмме
записаны распределение амплитуды и фазы, и после прохождения
ее восстанавливающей волной в плоскости выходного изображения
создается распределение интенсивностей, меняющееся в зависимости
от координаты этой плоскости и от направления, в котором
проходит точку плоскости волна данной интенсивности.
Если
установить, что значение интенсивности для каждого из направлений
и элементов относится к одному из m равновероятных интервалов,
то информационная емкость Iс голографической
системы может быть определена из выражения
Ic=NeNα
log2(m+1) @ NeNα log
m,
где
Ne - число пространственных элементов (по оси
х и у), Nα - число угловых направлений от
одного элемента, в которых интенсивности могут быть различны.
Информация,
содержащаяся в выходном изображении, качественно богаче,
чем информация, содержащаяся в фотографическом изображении,
т.к. наряду с пространственной по плоскости и с градационной
информацией она содержит пространственную по направлению
информацию. Это не значит, конечно, что по сравнению с плоским
фотографическим изображением голограмма, записанная на том
же фотографическом материале в число амплитудной записи,
содержит больше информации. Предельная информационная емкость
амплитудно записывающего материала не зависит от способа
записи (голографического или линзового), а зависит лишь
от вида частотно-контрастной характеристики, отношения сигнал/шум
и динамического диапазона материала. Записывающий материал,
так же как и линза, может ограничивать объем информации,
передаваемый системой, если пространственно-частотные характеристики
недостаточно хорошие. Следует однако отметить, что в настоящее
время создаются записывающие материалы со все возрастающей
информационной емкостью. Так, показано, что разрешение пленок
ХСП (халькогенидных стеклообразных полупроводников) составляет
10000 лин/мм, что при бинарной записи (m=1) соответствует
Iс большей, чем 1010 дв.ед/см2,
а при полутоновой записи еще почти на порядок
больше.
В принципе, разрешение может быть и еще больше, но использовать
его не удается, т.к. световой поток, переносящий информацию,
имеет меньшую емкость. Можно показать, что без учета градационной
информации световой поток способен переносить информацию,
не превышающую существенно величину 109 бит/см2.
В голографии эта величина окажется еще меньшей, так как
часть информации окажется потерянной в связи с наличием
многих порядков для дифрагированных пучков. Если перейти
к световому полю в частотной плоскости схемы рис.1, то можно
заметить, что только часть этого поля содержит информацию
хотя бы об отдельных участках объекта и еще меньшая часть
содержит информацию обо всем объекте. Особенностью светового
поля в частотной плоскости является его осевая симметрия,
из чего следует, что только половина поля, переносящего
сигнал, содержит информацию (см. рис.3). Это не означает,
что другую половину поля можно отбросить при восстановлении
изображения, но в случае ее перекрытия имеется возможность
восстановить переносимый ею сигнал по сигналу неперекрытой
половины поля.
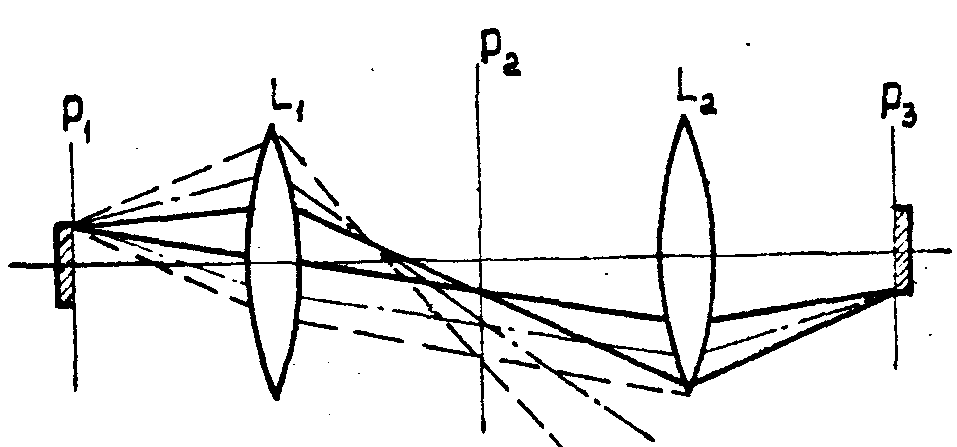
Рис.3.
Прохождение различных пространственных частот через оптическую
систему.
На объем
информации, содержащейся в световом поле в частотной плоскости,
влияет линза L1. Полную информацию может передать
только бесконечная идеальная линза. Рассмотренные выше причины
ограничения передачи информации при формировании линзой
изображения естественно окажут влияние в на передачу
информации
в частотной плоскости.
Ограничение
размеров (апертуры) линзы приводит к установлению предельных
размеров поля объекта, при которых передаются все частоты,
имеющиеся в объекте (рис.4).
а) б)
Рис.4.
Соответствие характеристик поля и пространственного фильтра;
случай анизотропного поля объекта.
Действительно,
предположим, что размер объекта в одном из направлений (например,
в х-вом) равен lx. Число разрешимых элементов
(размером Δx) в этом направлении Nx = N'x∙lx,
где Nx - число элементов, укладывающихся в единицу
длины объекта, которое равно удвоенной предельной частоте
в этом направлении N'x = 2νxlim.
Предельный угол, в который входят эти частоты, определяется
из соотношения Sin dlim = λνlim.
Если объект центрирован относительно оси линзы, размер апертур
последней равен D и объект расположен в передней фокальной
плоскости линзы, то 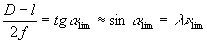 ,
следовательно,
,
следовательно,
D-l≈2fλνlim.
Идеальная
линза (без аберраций), передающая все частоты, содержащиеся
в объекте, должна обладать апертурой на величину 2fλνlim,
большую размера объекта. Так, например, при необходимости
передавать νlim = 250 мин/oм, при f = 30
см, λ = 6,3∙10-5 см,
D-l≈1
cм.
Ограничение
размера объекта до l приводит к тому, что различимое Δν
не может быть меньше, чем 1/2l, т.к. Nx = 2νхlimlx.
Поэтому при заданных Nx и νxlx
не может быть меньше, чем 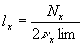 .
Таким образом, при принятых значениях и Nx =
1000 элементов в строке
.
Таким образом, при принятых значениях и Nx =
1000 элементов в строке 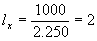 см,
а необходимый размер линзы D = 3 см.
см,
а необходимый размер линзы D = 3 см.
Заданный
объем информации от объекта, который необходимо передать,
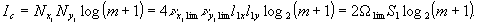
Здесь
принимается равномерность передачи градаций по всему полю
m(х,y)=сonst, а так же νxlimνylim=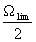 и lxly = S.
и lxly = S.
В частотной
плоскости при отсутствии потерь будет иметь место тот же
объем пропускаемой информации:
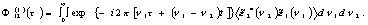
Первая
пара множителей 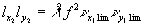 .
Вторая пара множителей выражается, следующим образом:
.
Вторая пара множителей выражается, следующим образом: 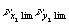 =
=
=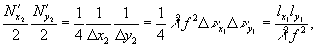 т.к.
т.к. 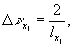 а
а 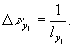
Таким
образом,
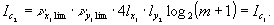
Информационная
емкость при этом остается та же, но происходит обмен составляющих:
размер поля объекта определяет полосу частот части Фурье-образа
в частотной плоскости, а спектр объекта определяет размер
поля в этой плоскости. И хотя объем передаваемой информации
остается неизменным, плотность информации в частотной плоскости
существенно отличается от плотности информации в плоскости
объекта: при 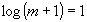 в последнем случае плотность информации
в последнем случае плотность информации 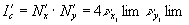 ,
тогда как в первом случае
,
тогда как в первом случае 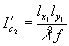 .
Таким образом плотность информации изменяется в
.
Таким образом плотность информации изменяется в
зависимости
от соотношения полосы частот и размера объекта, а также
от выбранного масштаба (коэффициент λf).
Ограничения
объема передаваемой информации вносятся помимо линз также
и пространственным фильтром, расположенным в частотной плоскости.
Информационная емкость фильтра устанавливает ограничения
и для всей системы. Но следует помнить, что дополнительные
потери информации могут быть внесены несогласованием составляющих
информации и, в частности множителей, определяющих геометрические
размеры поля и полосы частот. Материал фильтра обладает
определенной частотно-градационной характеристикой и ограниченными
размерами, которые должны быть согласованы с соответствующими
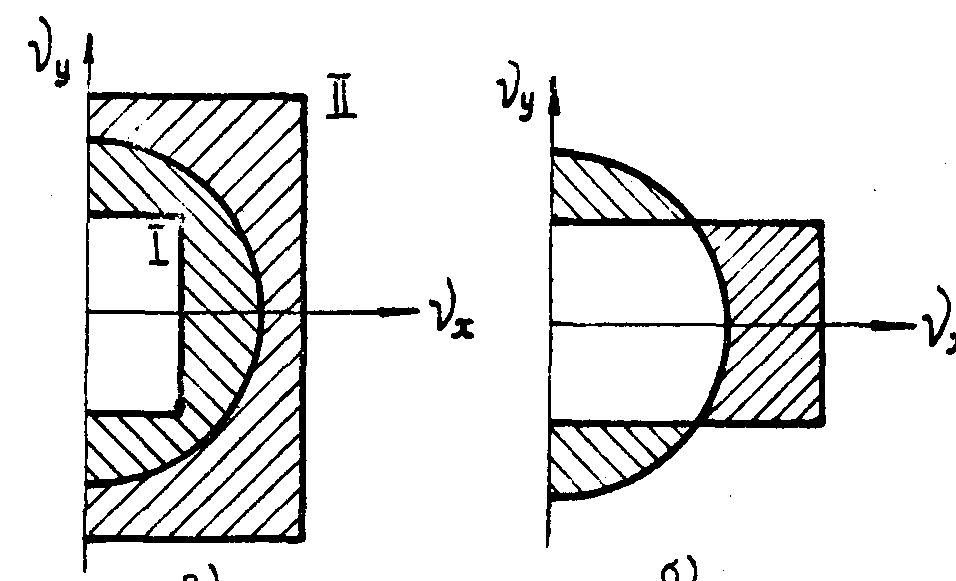
параметрами поля. На рис.4а показаны случаи: 1-плотность
бинарной информации поля по обеим составляющим (х и у) меньше
плотности бинарной информации, которую можно записать на
фильтре; в этом случае фильтр обладает некоторой избыточностью,
его емкость в данной системе полностью не загружается; 2
- плотность бинарной информации поля больше плотности бинарной
информации, которую возможно записать на фильтре. При этом
'фильтр пропускает только часть более низкочастотной информации,
имеющейся в световом поле, остальная теряется. На рис.4б
показан случай, когда при общей одинаковой плотности информации
в поле и материале фильтра ее х-вые и у-вые составляющие
имеют разную плотность: х-вая составляющая плотности в поле
больше, чем в фильтре, а у-вая - меньше. При этом часть
информации у-вой составляющей) теряется, в то время как
часть емкости фильтра (у-вой составляющей) остается неиспользованной.
Это может иметь место в случае различных размеров поля в
направлении х и у, которое создает различную плотность информации
в поле в направлении х и у, в то время как плотность записываемой
информации в материале фильтра, как правило, анизотропна.
Ограничение
информационной емкости может быть вызвано и ограничениями
размера фильтра, хотя такие ограничения, как правило, удается
снять легче, чем частотные ограничения.
Помимо
частотных и полевых ограничений информационной емкости системы,
связанных с характеристиками линз и фильтра в рассматриваемой
системе, существенные ограничения могут вносить шу-
мы и
прежде всего шумы фильтра.
Однако
из особенностей формирования шумов а данной системе является
освещение шумящего материала когерентным светом. Как известно,
в случае когерентного освещения сложение сигнала и шума
происходит по амплитуде, а не по интенсивности. В результате
этого средняя интенсивность в плоскости изображения явится
суммой средних значений сигнала и рассеянного фона:
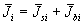 .
.
Для
случая, когда флуктуациями Jsi по сравнению с
флуктуациями Jbi можно пренебречь, ранее (см.
/4/) было получено выражение для отношения Ψ сигнал/шум:
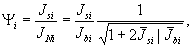
которое
дает два предельных значения 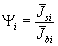 при
при 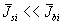 и
и 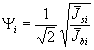 при
при
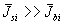 .
.
Величина
может быть найдена как расчетным путем, так и экспериментально.
Если ввести функцию Ф - винеровский спектр (зернистости),
то величину 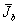 можно определить следующим образом:
можно определить следующим образом:
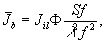
где
Jil - входная интенсивность (интенсивность поля
на частотной плоскости, в которой расположен также фильтр),
Sf - площадь фильтра. С другой стороны,
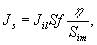
где
η - дифракционная эффективность фильтра, Sim
- площадь полученного изображения, откуда
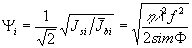 ,
,
При
значениях Ф = 10-8 мм2, η = 10-2,
λ = 6,3∙10-4, f = 150,
Sim
30´ 30 ~ 103 мм2 получим Ψ
~ 2. Нетрудно видеть, что если мы используем более шумящий
материал c меньшей дифракционной эффективностью или возьмем
большее число элементов в выходном, а, следовательно, в
входном изображении, то отношение сигнал/щум окажется настолько
низким, что различить отдельные детали заданного размера
не удается. В этом случае будут иметь место потери как пространственно-частотной,
так и градационной информации, но потери градационной информации
хотя и в меньшей степени остаются большими единицы.
Заметим,
что здесь не учтено еще влияние нелинейности материала и
воздействие фазовой неоднородности используемых фильтров.
Приведенные
примеры показывают, какое большое значение имеет согласование
информационных характеристик фильтра с требованиями решаемой
задачи и параметрами используемой системы оптической фильтрации.
Подобная же оценка может быть проведена и для других систем
оптической обработки информации.
Л
и т е р а т у р а
1. С.Б.Гуревич.
Эффективность и чувствительность телевизионных систем. "Энергия",
М-Л, 1964.
2. Gabor
D. Рrоgress in Optics, 1, p.109, 1961.
3. С.Б.Гуревич,
В.К.Соколов. О предельной информационной емкости голографических
систем, ЖТФ, т.43, стр.675, 1973.
4. Goodman
J.W., Film-Crain Noisse in Wavefront - Reconstruction Imaging,
JOSA, 57, p493-502, 1961.

