Media-security

ФИЗИЧЕСКАЯ СУЩНОСТЬ ГОЛОГРАФИЧЕСКОГО ПРОЦЕССА

И.А.Дерюгин

Дано описание голографического процесса, основанное на современных представлениях квантовой оптики о когерентности фотонных полей. Разработанные Габором, Глаубером, Вольфом в др. представления о свойствах функции корреляции фотонных полей как комплексно-аналитического сигнала, ее распространении и наблюдаемости используются для истолкования физической сущности голографического процесса. Свойства распространения функции взаимной корреляции как информационного инварианта и квантовая природа запоминания ее фоточувствительной средой являются решающими для законченного построения теории голографического процесса.

В в е д е н и е

Голография является одним из важнейших достижений современной науки и техники. Создатель ее - лауреат Нобелевской премии Деннис Габор -исходил из идеи о возможности кодирования оптического излучения, возмущенного взаимодействием с объектом наблюдения, относительно заданных параметров невозмущенной части его. Дальнейшее развитие голографии связано с работами Лейта и Упатниекса, основанных на радиофизических представлениях.

Традиционное описание голографии страдает двумя недостатками. Оно базируется на интуитивных или эмпирических данных о почернении фотослоя при взаимодействии его с интерферирующими оптическими волнами и использовании ненаблюдаемых динамических величин, так как из квантовой сущности процессов фоторегистрации следует невозможность запоминания оптической волны.

Для физически обоснованного истолкования голографического процесса весьма важным является знание свойств функций взаимной корреляции как информационного инварианта, ее распространения и наблюдаемости. Разработка их дана Вольфом и Манделем, Габором, Глаубе-

ром, Клаудером и Сударшаном.

Весьма важной для законченного истолкования голографического процесса является работа Глаубера, в которой на основании квантовой теории взаимодействия света с многоатомной фоторегистрирующей средой показано, что функция взаимной корреляции запоминается в ней.

Целью настоящей лекции является описание голографического процесса, основанное на современных представлениях о свойствах фотонного поля, распространения и наблюдаемости функций взаимной корреляции и квантовой теории явлений запоминания ее фоточувствительной средой. В результате этих обобщений можно дать следующее определение физической сущности голографического процесса.

Голографический процесс (голография) представляет собой способ передачи информации о пространственно-временных параметрах объекта наблюдения посредством функций взаимной корреляции рассеянного им объектного потока света с опорным потоком света, пространственно-временные параметры которых априорно известны, т.е. заданы с максимальной точностью.

Голография, как всякий информационный процесс, является многоступенчатой.

На первой ступени этого процесса поток света с заданными параметрами кодируется информацией о пространственно-временных свойствах объекта наблюдения, так что она становится известной относительно классически заданных параметров опорного потока. Таким образом, в голографическом процессе существенную роль играет опорный поток света, параметры которого (фазы, амплитуды, плоскости поляризации, волновые векторы) являются классически заданными, вследствие чего они могут быть избранной системой координат при кодировании. Последнее может удовлетворяться только в некотором объеме, называемом объемом когерентности, внутри которого должна находится вся сцена.

Назначением первой ступени голографического процесса является формирование функции взаимной корреляции потоков света, рассеянного объектом наблюдения и опорного. Вторая ступень связана со свойствами распространения функции взаимной корреляции, обуславливающими перенос информации о параметрах объекта наблюдения до фоторегистрирующей среды.

На третьей ступени производится запоминание функции взаимной корреляции объектного и опорного потоков света, т.е. получение голограмм.

И наконец, на четвертой ступени осуществляется создание потока света, идентичного рассеянному объектом наблюдения. (Не восстановление рассеянного потока света, а только создание идентичного исходному).

Если обе последних ступени совершаются в разное время, то для запоминания функции взаимной корреляции применяют фоточувствительные среды с большим временем памяти в аналоговом режиме. При этом, как заметил Гудмен Д., такая среда выполняет три различные функции: регистрацию, хранение информации и пространственную модуляцию света в процессе восстановления.

Когда формирование функции взаимной когерентности, ее запоминание и создание потока света, идентичного рассеянному объектом, осуществляются в известной степени одновременно, тогда голографический процесс идет в "реальном" масштабе времени.

§ 1.0 системах отсчета и наблюдаемых величинах в квантовой теории.

Наши представления о какой-либо физической переменной являются известными только по отношению к какому-то заданному уровню, их абсолютные значения не имеют физического смысла, ибо нам не дано знать абсолютные значения динамических переменных. Так, например, не имеет физического смысла абсолютная энергия, а лишь разность энергий. Точно также нет абсолютных пространственных и временных координат объектов, а существуют только их значения относительно избранной системы отсчета и т.д. Дня того, чтобы результат наблюдения имел смысл, необходимо в обобщенном пространстве задать избранную систему координат, относительно которой ведется отсчет.

Обратим внимание также на то, что введение информации в канал ее передачи осуществляется манипуляцией одного из параметров ее носителя, например, амплитуды, плоскости поляризация или фазы волны и т.п. При этой такая процедура будет успешной лишь в случае высокой стабильности начальных значений перечисленных параметров волн. Осуществляя стабилизацию этих параметров, мы задаем начало

отсчета, делая начальные параметры известными, в этом сущность классического аспекта физической интерпретации явлений передачи информации.

Таким образом, возможность реализации ситуаций, в которых параметры носителя информации становятся известными, является необходимым условием для осуществления любых наблюдений и измерений. Более того, известность, заданность параметров является принципиальным условием реализуемости различного рода информационных систем, в том числе и квантовых.

Квантовая механика является теорией наблюдаемых динамических величин, и творцы ее сразу же условились отказаться от использования неподдающихся наблюдениям динамических переменных, и хотя в квантовой теории применяются приемы идеализации, используются они только как промежуточные, их никогда не возводят в ранг наблюдаемых. Так, например, монохроматическая плоская волна, которой в реальном мире ничего не соответствует, является только некоторой математической абстракцией.

В квантовой теории имеют дело с объектами, для которых определенные динамические величины могут принимать только дискретные значения, т.е. состояния вещества и поля излучения квантуются.

Типичной абстракцией, также не имеющей ничего общего с реальной действительностью, является допущение существования отдельной, изолированной от всего мира квантовой системы.

Наличие взаимной коллективной обусловленности поведения квантовых систем является причиной статистического поведения их ансамблей.

В квантовой теории существенное значение имеет сам процесс наблюдения, результат которого в сильной степени зависит от способа реализации эксперимента. Квантовая механика налагает ограничения на возможность одновременного знания всех физических параметров носителя информации. Последнее связано с тем, что для получения информации о состоянии объекта надо привести во взаимодействие с ним измерительный прибор. Это взаимодействие всегда возмущает состояние измеряемого объекта и, по сути дела, приводит его в другое квантовое состояние, в котором измеряемая физическая характеристика имеет другое значение. Предсказать, какое из этих значений

будет получено в результате эксперимента, можно только статистически. В связи с тем, что измерительный прибор также не является изолированной системой, вызываемое им возмущение измеряемого объекта предсказуемо только статистически. В силу указанных обстоятельств в квантовой механике имеют дело со средними значениями наблюдаемой величины.

Наблюдаемой динамической переменной в квантовой механике является только та, для которой может быть записан оператор, а среднее значение ее должно быть действительной величиной. С каждой динамической переменной наблюдаемой системы связывается определенный линейный оператор, например, эрмитов, все собственные значения которого действительны. Поэтому все наблюдаемые величины в экспериментальной физике должны описываться эрмитовосопряженными операторами, в силу чего в результате измерения динамической переменной получается вещественное число.

Эрмитовость - свойство операторов, заключающееся в том, что вид матрицы эрмитового оператора не изменяется при замене всех его элементов на комплексно-сопряженные с одновременным обменом местами строк и столбцов (эта операция называется транспонированием матрицы).

В матричной форме это выглядит так:

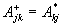Пусть имеем состояние 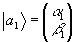, эрмитовосопряженная матрица которого будет ,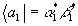

откуда

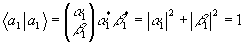Фаза оптической волны, для которой в квантовой теории нет оператора, не является наблюдаемой. В силу этого, в квантовой теории нельзя говорить об оптической волне как наблюдаемой величине, и поэтому лишены всякого физического смысла рассуждения о возможности "записи" оптической волны и "восстановления" ее любыми мыслимыми способами.

Из соотношения неопределенностей следует полная неопределен-

ность положения луча в ху - плоскости идеальной плоской волны, распространяющейся в z -направлении, а также то, что плоская монохроматическая волна, как имеющая нулевой спектр, не имеет преобразования Фурье.

В заключение обратим внимание на то, что ненаблюдаемость идеальных плоских монохроматических волн не означает отрицания волновой природа света. Реально мы наблюдаем волновой процесс с конечным спектром.

§ 2. Свойства фотонных ансамблей

Некоторая совокупность фотонов образует ансамбль, который может быть охарактеризован различными признаками: их количеством - n, фазой - φ, плоскостью поляризации, частотой - ω, длиной волны - λ, волновым вектором - k, расходимостью - θ. Все эти свойства потока фотонов могут быть сгруппированы в узком спектре, или же иметь весьма значительный их разброс. Тогда в первом случае имеется упорядоченное, а во втором - разупорядоченное хаотическое фотонное поле.

В оптических информационных системах материальным носителем информации является фотонное поле и информация о состоянии объекта может быть закодирована в нем изменением одного или некоторой совокупности перечисленных параметров. Для того, чтобы эта информация была доставлена наблюдателю, необходимо добиться, чтобы все параметры светового потока были известны во всем объеме информационного эксперимента. Таким образом, фотонный ансамбль должен представлять собой консервативную систему по совокупности своих параметров внутри объема наблюдения, а время нахождения поля в упорядоченном состоянии должно быть больше времени осуществления информационного эксперимента. Свойства фотонных полей можно описывать на основании различных физических аспектов. Для этого можно использовать представления статистической физики и термодинамики, вводя для фотонного поля понятия энтропии, степени вырождения, температуры и т.д.

Широкое применение имеет другой аспект, в рамках которого вводят понятие когерентности полей, и явления упорядоченности фотонов в них описывают посредством корреляционных функций. Этот

аспект базируется на явлениях корреляции осцилляторов вещества, имеющих место в процессах приготовления фотонных полей.

Оба аспекта теории базируются на статистической природе поля излучения и первый - термодинамичеcки-энтропией описывает меру беспорядка, а второй - когерентностью-меру упорядоченности его.

Когерентность света - объективно существующее свойство фотонного поля, заключающееся в упорядоченности его параметров, а ее альтернативой является энтропия, как мера разупорядоченности. Упорядоченность фотонного поля не может быть полной даже по некоторой части параметров, не говоря уже обо всей их совокупности.

Вселенная, в которой мы живем, представляет совокупность ансамблей частиц (атомов, молекул, электронов, протонов и т.д.) и квазичастиц (фотонов, магнонов, фононов, плазмонов и др.), отличающихся той или иной степенью взаимодействия между собой. Особенностью нашей Вселенной является систематическое возрастание беспорядка в ней. Вселенная ведет себя так, что для данного времени ее существования непреложно установленным фактом является возрастание ее энтропии. Как сказал Фейнман: "Из елки можно сделать палку, а из палки не сделаешь елки, в связи с чем наш мир постоянно меняет свой характер с елочного на палочный".

Наличие коллективной статистической обусловленности поведения квантовых систем является причиной статистической природы фотонных полей, их неупорядоченности и принципиальной невозможности получения полностью упорядоченных фотонных полей. В силу этого любые существующие в природе фотонные поля всегда имеют конечные (отличные от нуля) флуктуации его параметров - количества квантов, направления их импульсов, поляризации, фазы, частоты (длины волны). Кроме того, квантовая теорий налагает принципиальные ограничения на измеримость параметров фотонных полей.

Фотонное поле можно рассматривать как динамическую систему с бесконечным числом степеней свободы, большинство параметров состояний которого является случайными переменными величинами. Звание состояний такой системы никогда не бывает полным, так как не представляется возможным контролировать параметры системы. Поэтому теория фотонной когерентности связана со статистическим описанием флуктуации осцилляторов фотонного поля, а когерентность про-

является в корреляции их поведения.

Вследствие того, что сами фотоны в вакууме не взаимодействуют друг с другом, когерентность, как упорядоченность фотонных полей, возникает в процессе приготовления их ансамблями осцилляторов вещества, поэтому корреляции фотонных полей надо рассматривать в смысле их предыстории. Поток света состоит из большого количества фотонов, излучаемых ансамблями квантовых осцилляторов вещества, которые в процессе излучения взаимодействуют друг с другом, и электромагнитные волны несут информацию о степени корреляции их колебаний. Наличие корреляции колебаний квантованных осцилляторов вещества обуславливает когерентность электромагнитных волн, проявляющуюся в согласованности их поведения. Таким образом, корреляция колебаний квантовых осцилляторов излучающего света вещества наследуется фотонами и определяет когерентность электромагнитных волн, признаком которой является наличие определенной функциональной зависимости фазы, частоты и плоскости поляризации отдельных колебаний, а также других параметров фотонных полей. На больших расстояниях от генератора фотонное поле будет свободным и корреляционные явления в нем можно наблюдать в процессе взаимодействия поля и вещества (в частности, детектора). Сделанные выше замечания о статистической природе фотонных полей и более общих закономерностях протекания явлений во Вселенной говорят о том, что возникающая упорядоченность фотонных ансамблей может существовать только в некотором пространственно-временном объеме. Потому как фотон является ультрарелятивистской частицей, его нельзя описать в трехмерном эвклидовом пространстве. Это означает, что когерентность фотонных ансамблей необходимо рассматривать как явление в четырехмерном пространстве времени x = xyzt, в связи с чем когерентность можно определить как инвариантность фотонного скалярного поля к трансляции в четырехмерном пространстве. В общем случае поле излучения является векторным и полная когерентность наряду c инвариантностью к трансляциям в четырехмерном пространстве предполагает еще в инвариантность к повороту системы координат.

Обратим вникание на то, что условие инвариантности к трансляциям в четырехмерном пространстве полностью удовлетворяется в двух предельных случаях: в совершенно когерентных и полностью некоге-

рентных полях.

Упорядоченный фотонный поток отличается той особенностью, что остается подобным самому себе. В силу указанных выше причин это постоянство параметров фотонных ансамблей сохраняется только внутри некоторого объема. Прохождение высокоупорядоченного света через некоторый трехмерный объем, меньший объема когерентности, в силу его релятивистской природы можно рассматривать как распространение потока когерентности, в случае же хаотического поля как распространение потока энтропии.

Когерентность определяет реализуемость различных лазерных информационных систем - голографии, телевидения, кино, локации и связи.

§ 3. Квантовая теория когерентности

В квантовом аспекте теории показывают, что когерентность света обусловлена наличием корреляций в пространственно-временном распределении физических наблюдаемых, проявляющихся в существовании определенных соотношений между парциальными амплитудами вероятностей квантовых состояний и дающих вклад в конечное состояние физической системы. Поэтому когерентность представляет собой типично квантовое явление и ее описание может быть логически законченным только в квантовой механике.

Термин "когерентность" в смысле физической оптики использовался для обозначения тенденции в корреляции двух полей на разделенных в четырехмерном пространстве точках. В классической теории корреляции вводят единичную корреляционную функцию, представляющую собой усредненное по бесконечному времени произведение двух полей, разделенных конечным интервалом. Усреднение по времени может быть применено только к стационарным во времени статистическим полям. Это ограниченное определение когерентности, широко применяющееся в физической оптике, соответствует так называемой когерентности первого порядка, условием существования которой является отличие от нуля абсолютного значения нормированной функции корреляции первого порядка. Такого определения когерентности было вполне достаточно для экспериментов по интерференции излучения твидовых, ис-

точников, флуктуации в которых носят гауссов характер.

Понятия корреляции и когерентности необходимо распространить на поля с произвольной временной зависимостью и, в частности, на нестационарные поля. В связи с развитием квантовой радиофизики и ее прикладных аспектов возникла необходимость более точного определения понятия корреляции и когерентности. Приготовляемые лазерами фотонные поля принципиально отличаются от самого "когерентного" оптического излучения тепловых источников и по своим свойствам приближаются к радиоизлучений. Последнее, как известно, отличается от теплового оптического излучения весьма высокой степенью корреляции по всей совокупности параметров. Обратим внимание на то, что наиболее когерентные в представлениях классической теории когерентности поля имеют самую узкую полосу, поэтому такие представления о когерентности не могут быть применимы к нестационарным полям. Это означает, что классическая теория когерентности не может применяться к модулированным полям. Квантовая же теория когерентности, как более общая, применима к полям о любой временной зависимостью и, в частности, к нестационарным. Она не предполагает узость спектра, а условия квантовой когерентности налагают ограничения на хаотичность полей. Это обусловлено тем, что когерентные поля существуют в соответствии с собственными значениями функции корреляции при произвольном спектре. Когерентный в квантовом смысле свет может иметь широкий спектр с тем существенным отличием, что этот спектр имеет нехаотическую природу, т.е. поле может быть когерентным, имея произвольный спектр.

Упорядоченность фотонных полей описывают функцией корреляции, которая в самом общем виде может быть записана в тензорной форме через операторные бивекторы электромагнитного поля 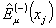, 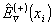и оператор матрицы плотности . Здесь x_ij = (xyzt)_ji - точка в четырехмерном пространстве, а индексы μ, ν относятся к различным компонентам декартовой системы координат к определяют поляризацию полей.

Фотонное поле высокой упорядоченности описывается тензовыми корреляционными функциями высших порядков:

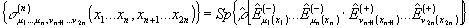В отличие от классического описания квантовая теория поля позволяет знать только средние значения по ансамблю реализации, даже в случае, когда состояние поля точно известно. Поэтому для начального состояния поля 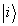вводится оператор плотности 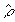как среднее по всем случайным переменным этого состояния:

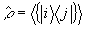Это позволяет оказать, что оператор плотности представляет собой среднее из операторов проекций на начальные состояния поля.

Функция корреляции, введенная Глаубером в первом порядке, имеет вид:

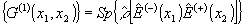Учитывая сказанное относительно оператора плотности, видим, что функция корреляции осуществляет двойное усреднение. То обстоятельство, что в квантовой теории требуется проводить усреднение измерений, сделанных даже для чистых состояний поля, является особенностью квантовой трактовки и не имеет аналога в классической аналогии. Для стационарных полей квантовая механика требует, чтобы оператор плотности 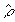коммутировал с гамильтонианом Н, это означает, что оператор 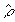не зависит от времени, а гамильтониан можно рассматривать как оператор сдвига во времени. Откуда следует, что функции корреляции высших порядков инвариантны к трансляциям во времени на интервал τ_i, называемый временем когерентности. Если оператор плотности коммутирует с компонентами импульса поля, то корреляционные функции инвариантны относительно смещения пространственных координат в соответствующих направлениях, т.е. в этом случае гамильтониан можно рассматривать как оператор сдвига в пространстве r = хуz на величину Δr=ΔxΔyΔz. Это означает, что корреляционные функции порядка выше первого инвариантны к трансляции в трехмерном пространстве внутри трехмерного объема v_c =ΔxΔyΔz, называемого трехмерным объемом когерентности. В общем случае для четырехмерного объема функция корреляции удовлетворяет следующему условию сдвига:

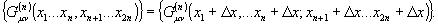
В силу чего функция корреляции инвариантна к трансляции в четырехмерном пространстве внутри некоторого четырехмерного объема, т.е. она тождественна функции корреляции, сдвинутой на элемент четырехмерного объема.

Объемом когерентности называют четырехмерный объем Δх, внутри которого выполняются условия инвариантности функции корреляции к трансляциям. Он является важной количественной мерой упорядоченности фотонных ансамблей и играет существенную роль, определяющую возможность реализации целого ряда информационных экспериментов в лазерном излучении. Многие эксперименты для своей реализации требуют, чтобы вся "сцена" была внутри объема когерентности.

Нормируя тензорные функции корреляции высших порядков, можно найти степень корреляции в n - ом порядке :

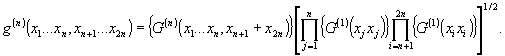
В силу того, что функция G⁽ⁿ⁾ - положительно определенная при полной когерентности любых компонент поляризации поля μ₁…μ_n, ν_n+1…ν_2n, то степень когерентности для любого n - удовлетворяет бесконечному ряду условий:

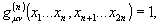
который во всех точках пространства-времени удовлетворяет классическая волна ε(х)=ехр[(k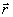 - ωt)]. Полная когерентность векторных полей означает, что ряд корреляционных функций выражается через произведение компонент векторного поля, т.е. когерентность рассматривается как свойство факторизации тензорных корреляционных функций в векторном пространстве:

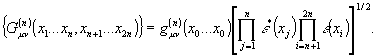
Поэтому наряду с факторизацией для когерентности в n-ом порядке

обязательным является выполнение условия

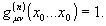
Это является фундаментальным свойством и не все поля удовлетворяют данному условию.

Обратим внимание на то, что корреляционные функции, измеряющие порядок выше первого, имеют соответствующий порядок по полю. Так функция первого порядка имеет размеренность интенсивности, т.е. второй порядок по полю, а функции корреляции второго порядка имеют размерность квадрата интенсивности, т.е. четвертый порядок по полю и т.д.

Надо иметь в виду, что функция взаимной корреляции первого порядка, хотя и имеет размерность интенсивности, но это не означает, что она является интенсивностью. Это обусловлено свойствами функции корреляции, которая описывает согласованность поведения полей в двух точках четырехмерного пространства x_j и x_i. Только в случае x_jºx_i в первом порядке когерентности функция корреляции будет просто интенсивностью, а в высших порядках соответствующей степени интенсивности и носит название функции взаимной интенсивности или автокорреляции.

Поляризация электромагнитных волн является еще одним признаком упорядоченности векторных полей, возникающей в результате корреляций квантованных осцилляторов вещества в процессе генерации фотонов. Можно показать, что в векторных полях условие когерентности означает инвариантность к процедуре поворота осей координат, в соответствии с оператором U.

Используя свойство унитарности операторов поворота U⁺=U^-1 а также то, что матрица плотност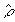и коммутирует с ним, можно показать инвариантность тензорных корреляционных функций к процедуре поворота системы координат. Таким образом, векторное поле является когерентным, если оно наряду с инвариантностью и трансляциями в четырехмерном пространстве удовлетворяет условию инвариантности к повороту системы координат. В случае полной когерентности поворот осей координат преобразует корреляционный тензор, как тензор второго ранга; если же когерентности нет, то он преобразуется как угодно. Физически это означает, что при повороте системы координат меняются проекции векторов поля (их величины и фазы), но при

полной когерентности соотношения между ними не меняются, корреляции остаются прежними, т.е. при полной когерентности векторных полей корреляционный тензор сохраняет свое значение независимо от углов его измерения.

Наиболее важными результатами квантовой теории когерентности является то, что в ней (в отличие от классической теории) в принципе допускается распространение понятий когерентности на нестационарные явления. Поэтому существенно изменяется и представление о связи монохроматичности о когерентностью.

Когерентность статистического ансамбля в квантовой трактовке представляет собой согласованность по совокупности наблюдаемых каждого его члена. Отсюда следует, что различные ансамбли будут иметь различные признаки когерентности (например, по спину). В то же время, один и тот же ансамбль может иметь различные наборы групп наблюдаемых, по которым различают когерентность. Так, например, фотонное поле может быть согласованным по всей совокупности параметров (частотам, фазам, плоскостям поляризаций и т.д.) или только по некоторой части их. Поэтому частная относительная когерентность характеризует согласованность (корреляции) только по какой-то подгруппе параметров этого ансамбля. Чем больше совокупность наблюдаемых, по которым коррелирован ансамбль, тем более когерентный является ансамбль. Общей когерентностью обладают ансамбли, все члены которого скоррелированы по всей совокупности наблюдаемых. Чем больше число признаков, по которым фотонный ансамбль ведет себя согласованно, тем выше когерентность и тем меньше различия между членами ансамбля.

§ 4. Свойства функций корреляции

функция взаимной когерентности как комплексно-

-аналитический сигнал

Покажем, что функция взаимной когерентности является комплексно-аналитическим сигналом. Запишем интегральное фурье-представление вещественной части обрезанной функции:

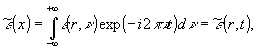
обратное фурье-преобразование которой будет

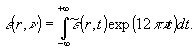
Используя это, запишем скалярную функцию взаимной корреляции первого порядка в следующем виде:

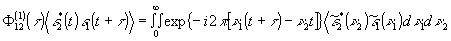
или

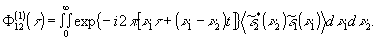
Допуская, что фотонное поле является стационарным стохастическим случайным процессом, что означает отсутствие зависимости статистики от времени, можно записать, что

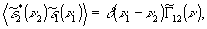
где 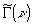- взаимная спектральная плотность, которая при r₁=r₂=r будет просто спектральной плотностью, a δ(ν₁-ν₂) - дельта функции Дирака. Учитывая это, функцию взаимной когерентности запишем:

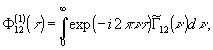
откуда видно, что она является комплексно-аналитическим сигналом.

Для нестационарных полей функция взаимной когерентности также является комплексно-аналитическим сигналом, если средние по ансамблю не зависят от времени.

Спектральное распределение 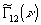связано c фурье-образом комплексной степени когерентности и в силу того, что она представляет собой нормированную функцию взаимной когерентности, также является комплексно-аналитическим сигналом :

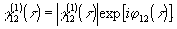
Спектр интенсивности стационарного оптического поля определяется

Фурье-преобразованием корреляционной функции первого порядка, на основании чего имеем

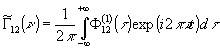(τ=t₁-t₂).

и нормированная спектральная плотность

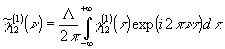
Поток лазерного излучения можно рассматривать как излучение с известными параметрами, чем лазерное излучение и отличается от фотонных полей, приготовляемых другими источниками. Ранее было обращено внимание на то, что любой информационный процесс приобретает физический смысл только тогда, когда имеется избранная обобщенная система координат. Для реализации ее необходимо располагать носителем, параметры которого заданы (известны) с достаточной точноcтью. Это обуславливает наше стремление к реализации информационного эксперимента в классической области. Таким образом, для оптических информационных систем важным является приготовление излучения с известными (классическими) параметрами. В лазерах эта процедура осуществляется более оптимально, чем в других источниках. Приготовляемое в нем векторное фотонное поле несет информацию о фазе, плоскости поляризации, импульсе (направлении распространения) и их флуктуациях в четырехмерном пространстве.

Связь между временем в производными по координатам от векторных величин дается уравнениями Максвелла:

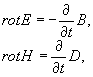
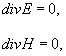
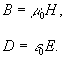
Для того, чтобы найти значение полей Е и Н в любой пространственно-временной точке x_i, надо решить эти уравнения, задав граничные условия на некоторой поверхности.

Решением уравнений Максвелла для свободного пространства источников является волновое уравнение для векторного поля :

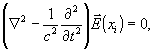где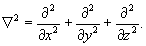

Оптические поля на могут быть описаны только гармоническими сигналами. Даже для монохроматических волн фаза их является сложной функцией, характеризуемой не свойствами в данных точках, а различными средними значениями, поэтому реальный поток света описывается функциями корреляции, являющимися комплексно-аналитическими сигналами. Поэтому важно знать, удовлетворяет ли функция корреляции волновому уравнению.

Вольф показал, что функция корреляции n-го порядка является также решением волнового уравнения и удовлетворяет 2n -волновым уравнениям:

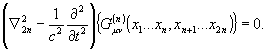
Отсюда следует исключительной важности вывод о том, что функция взаимной корреляции, не будучи волной, ведет себя как волна и является комплексно-аналитическим сигналом. Наряду с этим функция взаимной когерентности ведет себя подобно интенсивности, т.е.является наблюдаемой величиной квантовой теории.

Изложенное позволяет сделать заключение о следующих, важных для построения лазерных информационных систем свойствах корреляционных функций.

Поведение функции корреляции в различных пространственно-временных точках x_n, можно определить, располагая сведениями о ее параметрах в избранной точке x₀, в этом смысл распространения функции корреляции.

Функция корреляции любого порядка ведет себя как сложный комплексно-аналитический сигнал, переносящий информацию о предыстории поли излучения, т.е. о процессах взаимодействия его с веществом-в месте приготовления поля. Это является следствием наложенного выше ограничения на свойства статистического ансамбля, а именно, его стационарности, функция корреляции в любом порядке является наблюдаемой, поэтому уравнения Вольфа переносят все события из об-

ласти представлений в область наблюдаемых.

В процессе распространения в вакууме свет не взаимодействует со светом, поэтому информация, закодированная в виде состояний поля, переносится функцией корреляции без изменений. Из-за того, что функция корреляции инвариантна к трансляциям в четырехмерном пространстве, Габор назвал ее информационным инвариантом. В силу оказанного, функция корреляции помнит информации о состоянии фотонного поля во всем объеме когерентности и переносит ее до нового акта взаимодействия поля с веществом. Для реализации многих информационных систем вообще и лазерных локационных систем в частности существенным является величина объема когерентности. Некоторые системы, например голографические, могут быть реализованы только внутри него. Это означает, что тепловое излучение с малым объемом когерентности не может быть использовано для построения таких систем.

Взаимодействие лазерного излучения с объектом наблюдения не приводит к нарушению когерентности, если в процессе взаимодействия нет производства энтропии, т.е. взаимодействие света не носит необратимого характера. Это имеет место тогда, когда взаимодействие является линейным и в процессе взаимодействия нет случайных движений наблюдаемого объекта. В противном случае термодинамическая необратимость, вызванная случайными микроскопическими или макроскопическими движениями тел или частиц, приводит к возрастанию энтропии и обуславливает потерю когерентности.

Если же за время наблюдения свойства объекта не изменяются, то расстояние света объектом не нарушает когерентности, а вводимая в каждую парциальную волну добавка к фазе является известной. Поэтому данный процесс будет детерминированным, а рассеянный объектом наблюдения свет представляет собой совокупность сигналов, фаза каждого из которых известна относительно заданной и являющейся началом отсчета фазы. Так именно и поступают, когда между лазером и объектом помещают рассеивающее стекло.

Анализ свойств функции корреляции показывает, что она несет информацию в процессах взаимодействия света с объектом. Весьма важным является принцип Гюйгенса-Френеля, согласно которому отраженный от объекта поток света в дальнейшей распространяется автономно в соответствии с законами дифракции и полностью не зависит от объек-

та. Это фундаментальное свойство электромагнитных полей запоминать информацию о процессах взаимодействия является основой построения информационных оптических систем.

Функция корреляции n-го порядка содержит в себе большой объем информации, однако наблюдаемая ее часть зависит от организации эксперимента и искусства экспериментатора. Любой информационный эксперимент позволяет выделить столько информации, сколько допускают условия эксперимента, измерительная схема и эрудиция экспериментатора.

В силу того что в общем виде функция корреляции переносит информацию о свойствах объекта наблюдения ко всему пространственно-временному ансамблю, т.е. об изменениях в объеме и о временных изменениях объекта, основываясь на свойствах корреляционных функций, все информационные системы можно разделить на следующие.

1. Временные, переносящие информацию о временных детерминированных изменениях параметров поля. Этот тип систем передачи информации основан на изменениях временной части корреляционной функции, пространственная же информация утрачивается и информационная емкость фотонного поля используется только частично.

2. Пространственные двухмерные информационные системы, дающие принципиально плоское изображение.

3. Пространственные трехмерные требуют для своей реализации задания системы отсчета фаз посредством введения опорного сигнала с известной фазой для того, чтобы задать начало отсчета фаз всех точек корреляционных функций внутри объема корреляции. Для реализации этой схемы нет надобности в линзах, так как пространственная неопределенность снимается зависимостью φ(r)=[φ₀(r₀)-φ_i(r_i)]. Увеличение количества точек в фоточувствительном объема приводит к удивительному эффекту - почти полному соответствию восстановленного изображения и объекта голографирования.

В принципе, если бы в "фоточувствительном" объеме содержались всевозможные атомы, которые в процессе восстановления объемной голограммы могли комбинироваться а молекулы, а функция корреляции содержала всю объемную информацию о состоянии объекта, можно было бы

восстановить весь объект и заложить в него программу, определяющую его дальнейшее поведение. Во всяком случае в настоящее время можно "транслировать" рельефное изображение объекта на расстояние посредством функции корреляции.

§ 5. Фоторегистрация как процесс макроскопического

наблюдения

Квантовая теория наблюдений требует, чтобы измерительный прибор являлся макроскопической системой. Характерной особенностью квантовой трактовки процессов наблюдения является то, что энтропия динамической системы, остающаяся постоянной при временном ее развитии, увеличивается в процессе измерения. Любое макроскопическое измерение состояния квантовой динамической системы, всякое знание одной системы о состоянии другой оплачивается возрастанием энтропии.

Отличительной чертой имеющихся в нашем распоряжении способов наблюдения оптических полей является их энергочувствительный характер. Взаимодействие поля излучения с фоточувствительным веществом сопровождается обменом энергией. Индуцируемые полем переходы частиц фоторегистрирующей среды пропорциональны матричному элементу перехода, в выражение для которого поле входит в виде комплексно-сопряженных величин - в классической, или числа фотонов в операторной трактовках. Надо различать два типа наблюдений состояния поля - прямой и косвенный, поэтому ненаблюдаемость волны не означает отсутствия ее или отрицание волновой природы света. Результат наблюдения зависит от конкретной реализации информационного эксперимента.

Процесс наблюдения поля излучения описывается матрицей плотности:

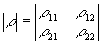в которой информация о фазовых переменных содержится в недиагональных ее элементах. В силу энергочувствительности процесса фотореги-

страции при непосредственном наблюдении поля происходит диагонализация матрицы плотности и игнорирование недиагональными членами, что обуславливает утрату содержащейся в них фазовой информации.

Голографический процесс является косвенным способом выделения фазовой информации, содержащейся в недиагональных элементах матрицы плотности поля. Надо понимать, что к этот способ также является энергочувствительным и, как будет показано ниже, основывается на зависимости степени энергообмена поля излучения и фоторегистрирующей среды от разности фаз опорного и рассеянного объектом потоков света, но не посредством какой-то, даже гипотетически неосуществимой, фазочувствительной среды.

Утрата фазовой информации при прямом энергочувствительном измерении вызвана тем обстоятельством, что процесс измерения имеет смысл для коммутирующих операторов, т.е. диагональных элементов матрицы плотности. Поэтому для понимания природы голографического процесса, гомодинного и гетеродинного приема, фотонных корреляций важно знание сущности процесса наблюдения и современных представлений о когерентности поля излучения.

В связи со сказанным необходимо обратить внимание на фундаментальные работы фон-Неймана, который ввел понятие матрицы плотности ρ, недиагональный характер матрицы, описывающий процесс измерения, а также квантовое выражение для энтропии S=Sp ρ lnρ.

Фоторегистрацию можно рассматривать как некоторый физический процесс, главным признаком которого является термодинамическая необратимость. В этом процессе энергия поля излучения лазера с малой энтропией превращается в другие, менее упорядоченные виды энергий - ток хаотических электронов, химическую, тепловую и т. д. Следовательно, в процессе фоторегистрации за время экспозиции происходит непрерывное производство энтропии, ибо сама по себе память возможна только как следствие термодинамической необратимости.

Следуя Глауберу, допустим, что представитель фоторегистрирующей среды ансамбля может находиться в одном из двух состояний |φ > и <j|. В результате элементарного акта поглощения в поле излучения согласно квантовым представлениям погибает фотон, что означает перевод поля из состояния |n> в состояние |n-1>, а представитель ансамбля вещества переводится из состояния <f| в состояние

|j> c изменением энергии.

Возбужденный атом должен прийти в равновесие с термостатом посредством какого-либо механизма, возбудив внутренний или внешний фотоэффект, или же посредством фотохимического преобразования среды. Начальные состояния не всегда известны точно, благодаря чему необходимо проводить усреднение по ансамблю начальных состояний. Значения верхнего энергетического состояния в силу связи с термостатом и другими степенями свободы составляют также некоторую группу верхних состояний.

Фотослой можно представить как пространственное распределение n - атомных фотодетекторов. Взаимодействие поля излучения с такой фоторегистрирующей средой рассмотрел Глаубер в модели из n-идентичных динамически независимых атомов, расположенных в точках поля x_j; x_i. Для правильного описания этого взаимодействия необходимо найти вероятность перехода каждого из n-атомов из нижнего состояния в верхнее с поглощением фотона за время экспозиции – τ₃. Выражение для вероятности поглощения найдено Глаубером в результате решения уравнения Шредингера в представлении взаимодействия в n-м порядке теории возмущений:

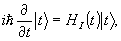
где H_I(t) - гамильтониан взаимодействия n-го атома c полем излучения.

Введем унитарный оператор изменения во времени U(t₁ t₀) преобразующий состояния |t> и |t₀> согласно соотношению |t>=U(t₁ t₀)|t₀> для решения этого оператора в виде

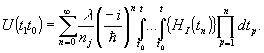
Гамильтониан взаимодействия n -атомов с полем излучения представляет собой сумму одноатомных гамильтонианов:

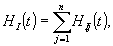
в которую входят гамильтонианы взаимодействия всех атомов фоторе-

гистрирующей среды от j = 1 до j = n;

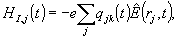
где е - заряд электрона; q_jk - оператор положения n -го электрона относительно ядер; 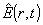- оператор, описыващий временную зависимость свободного, не возмущенного атомами поля излучения, а r - радиус-вектор ядра атома. Необратимый характер процесса фоторегистрации исключает возможность испускания атомами фотонов, в силу чего в гамильтониане должны учитываться только положительно частотные части поля.

Допуская динамическую независимость атомов, получаем возможность разделения гамильтонианов нулевого порядка и их коммутативность друг с другом, а также, предполагая, что атом участвует в процессе поглощения только один раз, можем в выражении для вероятности перехода учитывать члены, в которых одноатомный гамильтониан входит также один раз. Легко видеть, что таких членов будет - n! , поэтому для случая, когда вероятность перехода каждого атома выражается одной и той же функцией, получим

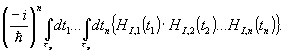
Этим показано, что оператор перехода в n -атомной фоторегистрирующей среде равен произведению операторов одноатомного перехода. Пусть начальное состояние атома |{g}>, а группа конечных состояний |{a_j}>, тогда матричный элемент перехода всей системы из состояния |f₁{a_j}> конечное состояние |e₁{g}> можно записать так:

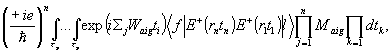
где M_ajg - матричный элемент атома.

После проведения в этом выражении операция возведения в квадрат, суммирования по конечным cостояниям и усреднения по начальным состояниям поля, можно найти формулу для вероятности перехода каждого атома в определенное конечное состояние. Делая предположение, что вероятность перехода представляет собой одну и ту же функцию

для любого атома фотодетектора, Глаубер получил выражение для вероятности фоторегистрации:

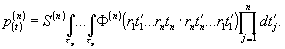
Отсюда следует важный вывод о том, что ансамбль частиц фоторегистрирующей среды запоминает функцию взаимной корреляции оптического излучения, усредненную за время экспозиции, а не оптическую волну.

Таким образом, имеющаяся в функции взаимной корреляции фазовая информация запоминается в виде необратимых изменений электрических свойств фоторегистрирующей среды. Описанный процесс носит название фазового контраста в том смысле, что непосредственно ненаблюдаемая фазовая информация перекодируется в интенсивности необратимых изменений фоторегистрирующей среды.

Так вероятность перехода атома из нижнего состояния |а_j> в верхнее |b_i> зависит от матричного элемента дипольного момента, такой переход возможен только тогда, когда имеется отличная от нуля его компонента. В силу того, что матричный элемент дипольного момента чувствителен к поляризации света, изменения свойств фоторегистрирующей среды также будут зависеть от поляризационных свойств поля излучения. В данном случав поляризационные свойства поля излучения, кодированные в функции корреляции, превращаются в изменение интенсивности и это может интерпретироваться как поляризационный контраст. Интенсивность необратимых изменений свойств фоторегистрирующей среды в данной ее точке определяется вероятностью перехода атомов в верхнее состояние, которая полностью определяется функцией взаимной корреляции:

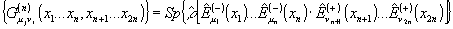В заключение обратим внимание на то, что в связи с энергочувствительным характером процесса фоторегистрации и необратимостью обусловленной связями атомов фоторегистратора со степенями свободы термостата, в фотослое невозможно записать оптическую волну. Сама память фоторегистрирующего слоя обязана своим происхождением

необратимости, которая в силу соотношения неопределенности обуславливает неполную точность записи даже параметров функции корреляции, поэтому не может быть речи о записи волны и тем более восстановлении ее. Максимум, что можно сделать, это восстановить поток света с функцией корреляции, аналогичной исходной.

Когда составляющие поля относятся к одной и той же пространственно-временной точке x_j = х_i = х = r₁t, тогда функция взаимной корреляции превращается в автокорреляционную функцию:

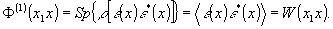
Фоторегистрирующий одой запоминает функцию автокорреляции, как некоторую усредненную за время экспозиции интенсивность, при полной утрате информации о фазах полей с вероятностью

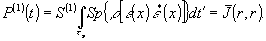
В связи с тем, что временные вариации ε(r,t) за время экопозиции усредняются, в фотослое будет запоминаться некоторая усредненная интенсивность, являющаяся функцией ху. При этом происходит запоминание распределения интенсивности в плоскости ху, что и является основой обычного фотографического процесса.

§ 6. Обобщенный голографический процесс

Как указывает Кольер, "в голографическом методе информация об амплитуде и фазе, идущей от объекта несфокусированной волны, еще до регистрации кодируется с помощью опорной волны". Для записи полной информации о параметрах фотонного поля и ее восстановления необходима соответствующая организация эксперимента. Выше было показано, что процессы, основанные на запоминании автокорреляционной функции, не позволяет восстановить всю информацию о фотонном поле. Своеобразие ситуации здесь таково, что информация об отдельных волнах не может быть записана, а поэтому и не может быть восстановлена, так как волна (амплитуда, фаза, плоскость поляризация частоты) не является наблюдаемой. В отличие от волны, функция взаимной

корреляции являются наблюдаемыми, и максимальную информацию о поле излучения можно запомнить, проведя соответствующим образом эксперимент. Для успешной реализации этого полного информационного процесса необходимо исключить из эксперимента недетерминированные вариации параметров фотонного поля во всем объеме наблюдения функции взаимной корреляции. Сущность такого процесса сводится к тому, чтобы функция взаимной корреляции несла информацию о параметрах поля излучения посредством сравнения их с известными, заданными параметрами опорного потока света. При этом безразлично, какая часть корреляционной функции является опорной, важно, чтобы свет обладал стабильными параметрами, тогда вариации одной части пучка будут заданы относительно другой.

Как было показано выше, функция взаимной корреляции является комплексной:

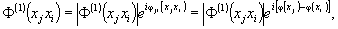
и вся фазовая информация в ней закодирована с составляющей exp[iφ(x_jx_i)] и будет известна наблюдателю, если за время осуществления эксперимента соотношения между φ(x_j) и φ(x_i) не изменялись. Это относится к модулю корреляционной функции, который должен быть достаточно медленной функцией во времени, чтобы за время наблюдения вариации его практически отсутствовали. Отсюда следует, что процесс регистрации функции взаимной корреляции в сильной степени зависит от свойств поля излучения и будет эффективен, если осуществляется внутри четырехмерного объема когерентности. Так, например, если поле излучения создается узкополосным тепловым источником или же многомодовым лазером, оно подчиняется гауссовому статистическому распределению:

где <n_k> - среднее число квантов в каждой моде, |α_k|²=n - число фотонов моды, α_k -амплитуда каждой моды.

В поле излучения с гауссовой статистикой функции корреляции высших порядков отсутствуют и все они выражаются через функции

корреляции первого порядка:

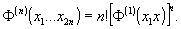
Степень корреляции для гауссовых полей будет

Поэтому такие поля называются дельта коррелированными.

Учитывая комплексный характер функции корреляции, запишем выражение для вероятности переходов атомов фоторегистрирующей среды:

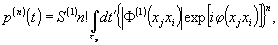
откуда следует, что вероятность обмена энергией между полем излучения и фоторегистрируюцей средой зависит от относительных фаз ехр[iφ(x_jx_i)], в этом сущность запоминания фазовой информации.

Если зависимости φ_ji - времени нет или она весьма слаба, тогда функция корреляции будет зависеть только от пространственных координат:

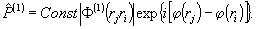
Вероятность перехода атомов фотодетектора при взаимодействии сo светом пропорционально этой пространственной функции взаимной корреляции, если время экспозиции меньше времени когерентности поля.

Объект имеет целый континуум точек, так что индексы проходят все значения j=1…m, i=m+1…2m. В этом сущность заполнения фазовой информации фоторегистрирующей среды и получения объемного изображения. Таким образом, в фоторегистрирующей среде, расположенной в области суперпозиции двух потоков света, вероятность обмена энергией между полем излучения и атомами среды зависит от относительных фаз суперпонирующих полей. Суперпонирующие поля ε(x_j) и ε(x_i) создают четыре корреляционных функции Ф⁽¹⁾(x_jx_i); Ф⁽¹⁾(х_ix_i); Ф⁽¹⁾(x_jх_i). Первые, так называемые автокорреляционные функций, определяют среднюю по поверхности интенсивность изменений свойств среды. Две последние, называемые функциям взаимной корреляции, обус-

лавливают изменения фоторегистрирущей среды, распределение которой зависит от относительных фаз exp[±iφ(x_jx_i)]:

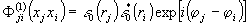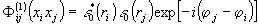В фоторегистрирующем слое запоминается некоторое пространственное распределение необратимых изменений свойств, вероятность которого зависит от относительных фаз,

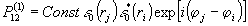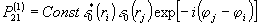по всем точкам от j=1…n и j=m+1…2n.

Записанная в виде необратимых изменений фоточувствительной среды информация о пространственном распределении интенсивностей и относительных фаз объекта называется голограммой.

Осветив голограмму восстанавливающим потоком света:

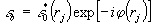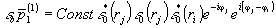получим

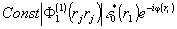При нормировке относительно Const |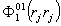| получается поток овета c параметрами, аналогичными потоку, ранее рассеянному объектом.

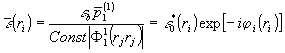Учитывая погрешность при записи информации и неадекватность восстанавливающего и записывающего потоков света, в данном случае также нельзя говорить о восстановлении потока воли. С точностью до указанных погрешностей голографический вариант может восстанавливать поток света со свойствами, более или менее близкими к исходному. Освещая голограмму сопряженным потоком света 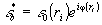, восстановим второе - сопряженное изображение.

§ 7. Обобщенный голографический эксперимент

Для реализации голографического эксперимента необходимы высоко-когерентное излучение, фоторегистрирующая среда и объект голографирования. Как отмечалось выше, успешная реализация голографического процесса возможна только внутри объема когерентности, это означает, что все параметры носителя информации должны быть известными от лазера до объекта голографирования и фоточувствительного слоя. Необходимо также, чтобы объект голографирования за время экспозиции не совершал движений в пространстве. Выполняя это условие, можно записать голограмму динамических процессов при покадровой регистрации, как в случае обычного кино.

Сущность голографического эксперимента сводится к следующему. Когерентный свет от лазера, распространяясь в направлении объектов O_j и O_i, взаимодействует с ними и после рассеяния на них в области суперпозиции создает поток с функцией взаимной корреляции:

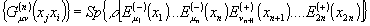Функция взаимной корреляции, распространяясь, далее попадает в фоторегистрирующую среду, где в соответствии с вероятностью поглощения,

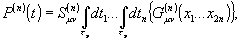
запоминается в виде пространственного распределения необратимых изменений фоторегистрирующей среды и образующей фазовоинтенсивностный контраст.

Если голографирование идет в векторных полях, тогда процесс будет записывать и информацию о плоскости поляризации, что обуславливает возникновение поляризационного контраста. Таким образом, на голограмме после усреднения по времени будет записано некоторое пространственное распределение изменения оптических свойств фотопластинки с учетом фазовой и поляризационной информации в виде соответствующих контрастов интенсивности. Для простоты рассмотрим случай полей, когерентных в первом порядке функции корреляции. После отражения от объектов O_j и O_i, в области суперпозиции общее поле будет состоять из когерентной суммы этих полей, функция взаимной корреляции которых будет

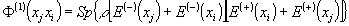Так как поле с полем не взаимодействует, то наблюдаемым будет результат взаимодействия суперпонирующих полей с атомами фоторегистрирующей среды. Вероятность поглощения света определяется и зависит от относительных фаз суперпонирующих полей, т.е. будет определяться функцией взаимной корреляций:

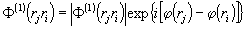Усредненная за время экспозиции интенсивность необратимых изменений свойств фоторегистрирующей среды будет содержать информацию о пространственных вариациях объекта :

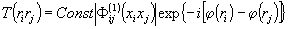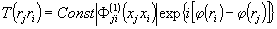В обычном фотографическом процессе φ(r_i) и φ(r_j) некоррелированы, являясь случайными функциями x_ji они беспорядочно быстро флуктуируют. В силу того, что фоторегистрирующая среда обладает интегрирующими свойствами, эти флуктуации его усредняются, что приводит к утрате фазовой информации в первом порядке функции корреляции. В

голографическом эксперименте лазерное излучение отличается тем, что параметры его классически заданы - известны. Это позволяет его фазу записать как φ_ji = Const с точностью до некоторой аддитивной постоянной m2π, где m - любое число. Если это условие выполняется на протяжении времени когерентности τ_c, то для времен τ_э<τ_с φ можно рассматривать как уровень отсчета для фазовых траекторий, поэтому по вcем частным оптическим путям детерминированные вариации фазы приведут к детерминированному кодирований потока света, рассеянного объектом.

Взаимодействие с рассеивающим объектом "О_j" или "O_i" не приводит к нарушению когерентности, так как здесь нет возрастания энтропии с точностью до тепловых движений атомов вещества объекта. В данном случае свойства рассеивателя не меняются со временем, в силу чего процесс будет детерминированным и в нем в каждую парциальную волну вводится "известная" добавка к фазе φ₀. Поэтому поток света, рассеянного объектом "O_j", является совокупностью сигналов, фаза каждого из которых известна относительно фазы опорного потока.

Обратим внимание на то, что другой объект "O_i" эквивалентен объекту "O_j" и поэтому поток света, рассеянный любым из объектов O_j и O_i может быть опорным. Однако чаще всего в качестве объекта, формирующего опорный сигнал, используют более простой, например, зеркало.

Как было показано выше, освещая голограмму потоком света, идентичным одному из двух, формировавших функцию взаимной корреляции можно восстановить другой поток. Для этого излучение лазера направляется на один из объектов, например, "О_j". В силу того, что объект не совершает движений и находится в том же положении, что и при записи голограммы, он реализует поток света по своим параметрам, весьма близким потоку света, участвовавшему в формировании функции их взаимной корреляции. При взаимодействии этого потока света с голограммой формируется поток света, идентичный потоку от объекта.

Так как оба объекта "О_j" и "O_i" не имеют преимуществ друг перед другом, то, освещая лазерным излучением один из них, восстанавливаем поток другого и наоборот. При рассмотрении глазом дифраги-

рованного голограммой потока света можно наблюдать мнимое изображение одного из объектов. Легко видеть, что в другом варианте восстанавливающим сигналом может быть поток, отраженный от объекта "О". Однако чаще всего опорный поток формируется более простым объектом, например, зеркалом.

Освещение голограмм комплексно-сопряженным потоком восстановит действительное изображение, наблюдающееся по пути распространения дифрагированного потока, отличительными свойствами которого является возможность его фотографирования без объектива. Комплексно-сопряженный сигнал является антипараллельным сопрягаемому, если голограмму повернуть на 180° относительно вертикальной оси. Действительное изображение можно сфотографировать, оно псевдоконично, т.е. объемно, вывернуто и обладает меньшим параллаксом. Мнимое изображение обладает большим параллаксом, что создает больший эффект присутствия и оно нормально объемное.

Обратим внимание на то, что, сблизив "O_j" и "O_i", мы реализуем "единый" объект, который формирует функцию взаимной корреляции этого составного объекта. С этим связан любопытный эффект - возможность восстановления всего объекта по предъявлении его части, при этом голограмма сформируется как бы "без опорного потока". Заметив, что в первоначальном голографическом процессе Габора при получении голограмм прозрачных объектов роль опорного потока выполняет нерассеянное объектом лазерное излучение.

§ 8. Особенности голограмм и голографического

изображения

Истолкование голографического процесса на основе свойств функций взаимной корреляции позволяет дать объяснение многим необычным свойствам голограмм и предсказать новые эффекты.

1. Объемность восстановленного изображения. Особенностью голографического процесса является возможность посредством фазового а поляризационного контраста в нечувствительной к фазе в поляризации света среде запоминать информацию об объемных поляризационных свойствах объекта наблюдения. Поэтому восстановленное голографическое изображение сцены отличается удивительно высокой тождествен-

ностью с наблюдавшейся сценой. Это и позволяет голографический процесс трактовать как полный эксперимент в оптике. Полнота этого эксперимента обуславливает эффект присутствия зрителя в восстановленной сцене и позволяет осуществлять наблюдение объектов, находящихся в створе, изменяя свое место наблюдения. Информация об объемных свойствах объекта наблюдения запоминается фотосредой в виде функции взаимной интенсивности. Последняя содержит в себе информацию о разности фаз волн, рассеянных точками объекта x_j и x_i относительно опорной фазы φ₀ = Const, которая определяется относительными расстояниями рассеивающих точек x_j и x_i объекта наблюдения, как [φ(x_j)-φ(x_i)]. Так как матричный элемент перехода атома фотослоя из основного состояния в возбуждаемое зависит от разности фаз и поляризации излучения, то интенсивность почернения фотослоя будет нести информацию об объемных и поляризационных свойствах объекта наблюдения.

В принципе, используя когерентное многоволновое излучение (излучение с весьма широким, но детерминированным спектром), можно осуществить еще более полный голографический процесс. В этом процессе будет получена информация не только о поверхностно-объемных, но и о внутриобъемных свойствах объекта наблюдения. Полнота информации ограничивается только эффективным поперечником сечения рассеяния излучения частицами, из которых состоит объект, и соотношениями неопределенности. Каждому участку спектра когерентного излучения можно сопоставить свой частный голографический процесс. В силу этого в полихроматическом когерентном излучении можно осуществить голографический процесс с еще большей информационной емкостью. Заметим, что ненулевое значение энтропии в любом гипотетическом процессе не позволяет осуществить передачу всей информации, поэтому, когда мы говорим о голографии, как полном эксперименте в оптике, надо учитывать квантовые ограничения. Более детально это было рассмотрено совместно с Курашовым в одной из предыдущих лекций.

2. Инвариантность голограмм к обращению. К голограмме неприменимы понятия - позитивная и негативная, она инвариантна к обращению. Данное свойство обусловлено тем, что записанная в фотослое функция корреляции несет информацию об амплитудных а фазовых соот-

ношениях между объектным и опорным потоками света в виде амплитудного, фазового и поляризационного контраста. Физическая природа этого обусловлена тем, что функция корреляции инвариантна к циклической перестановке произведения операторов.

Для любых линейных операторов А справедливо следующее общее соотношение:

Sp(A⁺) = Sp(A)^*.

На основании этого тождества, эрмитовости оператора плотности и инвариантности шпура от произведения операторов относительно циклической перестановки операторов, корреляционные функции удовлетворяют следующему соотношению:

|Ф⁽ⁿ⁾(x₁…x_2n)|^*= Sp[E^(-)(x_2n)…E^(-)(x_n+1)E⁽⁺⁾(x_n)…E⁽⁺⁾(x₁)ρ]=

=Sp[ρE^(-)(x_2n)…E^(-)(x_n+1)E⁽⁺⁾(x_n)…E(+)(x₁)].

Когерентность фотонных полей предполагает внутреннюю неразличимости фотонов в объеме когерентности, поэтому при решении уравнений движения для ансамбля тождественных частиц мы используем гамильтониан, который в силу этой тождественности инвариантен к процедуре перестановки частиц.

Следствием сказанного является то, что уравнению Шредингера, системы тождественных частиц удовлетворяет любая линейная комбинация решений, отличающихся перестановками координат частиц.

Наблюдаемой динамической переменной квантовой теории для потока света является функция взаимной корреляции, являющаяся результатом суперпозиции волн, удовлетворяющих волновому уравнению. Корректная формулировка принципа неразличимости тождественных частиц означает, что все наблюдаемые динамические величины инвариантны относительно операции перестановки тождественных частиц или перестановки тождественных частиц не могут быть наблюдаемыми. Отсюда следует как инвариантность ансамбля тождественных частиц к трансляциям в четырехмерном пространстве, так и инвариантность голограмм в обращении.

3. Делимость голограмм. Следующим любопытным свойством голо-

грамм является возможность восстановления объекта по некоторой ее части. Эта особенность голограмм обусловлена тем, что информация объекта закодирована во всем объеме суперпонирующих полей и поэтому часть корреляционной функции является самой корреляционной функцией. Этим же, по-видимому, объясняется информационная избыточность голограмм. Согласно тому, что часть функции корреляции характеризует всю ее, объясняется делимость голограммы и возможность восстановления всего объекта по ее части, в связи с чем мультиплицирование голограмм можно осуществлять до ее записи делением функции взаимной корреляции полупрозрачным зеркалом на n - потоков, каждый из которых взаимодействует со своей фоторегистрирующей средой. Однако деление голограммы на части приводит к снижению контраста, что объясняется уменьшением числа единиц информации, формирующих восстановленное изображение.

Сущность этого явления можно объяснить следующими соотношениями. При ограничении числа фотонов поля излучения, степень функции взаимной корреляции его ограничена сверху, т.е. фотонное поле малой интенсивности не может обладать функцией корреляции сколь угодно высокой степени. Поскольку в функцию корреляции входят операторы уничтожения 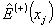, она обращается в нуль для поля с конечным числом фотонов N_max, когда n>N_mах, следовательно, такое поле не может быть когерентным во всех порядках. Таким образом, при данной плотности фотонов N_mах степень функции корреляции не может быть выше n_mах.

С другой стороны, для частично-когерентного поля излучения все функции корреляции выражаются через функцию корреляции первого порядка

Ф⁽ⁿ⁾(x₁…x_2n)=n![Ф⁽¹⁾(x₁x₂)]ⁿ

и на фотопластинка запоминается распределение интенсивности

T(x_ix_j)=h n!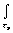[Ф⁽¹⁾(r_ir_j)]ⁿdt',

где h - квантовая эффективность фотослоя. Отсада видно, что когда мы разделяем голограмму на части, то делим n! на данное

число раз, но так как n! велико, то имеется значительный запас. Однако при большом делении рассеивающих центров на данной части голограммы может быть уже недостаточно для формирования хорошего качества восстановленного изображения. Обратим внимание на то, что n! - число рассеивающих центров, а не число фотонов, и поэтому нельзя увеличить качество восстановленного изображения за счет повышения интенсивности восстанавливающего потока света.

4. Трансляция голографической информации. Свойства распространения функции взаимной корреляции, делимость и инвариантность ее к обращению дозволяют транслировать голографическую информацию на большие расстояния. Эти особенности голографического процесса в трактовке функций взаимной корреляции дают возможность осуществления двух любопытных экспериментов. Первый из них связан с возможностью "трансляции объекта наблюдения" на большие расстояния. Из того, что функция взаимной корреляции запоминается в фоточувствительной среде, имея гипотетическую сверхширокополосную объемную регистрирующую среду, можно в полихроматическом когерентном голографическом процессе осуществить "восстановление" в ней объекта наблюдения. Эта принципиальная возможность "трансляции объекта посредством распространения функции взаимной корреляции высших порядков в полихроматическом когерентном излучении обуславливается возможность приготовления сверхширокополосного когерентного излучения и регистрирующей среды, обладающей чувствительностью во всей полосе спектра излучения.

Другим таким необычным экспериментом представляется возможность установления контактов с инопланетными цивилизациями, достигшими определенного технологического уровня, а также возможность передачи голографической информации на большие расстояния.

З а к л ю ч е н и е

В данной обзоре на основании работ Д.Габора, Р.Глаубера, Э.Вольфа, Мавделя и других ученых показано, что функция взаимной корреляции является комплексноанадитическим сигналом, удовлетворяет волновому уравнению. Не являясь волной, она ведет себя как волна и, не являясь интенсивностью, имеет ее размерность. В силу этого

представляет собой наблюдаемую динамическую переменную.

Функция взаимной корреляции, обладая инвариантностью к трансляциям в пространственно-временном объеме, при априорно заданных параметрах облучающего света переносит информацию о пространственно-временных свойствах объекта наблюдения. Закодированная а функции взаимной корреляции информация в процессе ее распространения сохраняется, в силу чего Габор назвал ее информационным инвариантом.

Сказанное позволяет сделать утверждение, что вся голографическая информация до ее записи существует в виде пространственно-временных вариаций параметров светового потока, которые описываются функцией взаимной корреляции.

До известной работы Р.Глаубера по квантовой теории процесса фотодетектирования описание процесса фоторегистрации строилось на интуитивных и эмпирических представлениях, в связи с чем голографический процесс не имел законченного физического описания.

Весьма важным для построения корректного описания голографического процесса является показанное Глаубером свойство фоточувствительных сред регистрировать усредненную за время экспозиции функцию взаимной корреляции.

Таким образом, голографический процесс является типично информационным, в котором информация о пространственно-временных свойствах объекта наблюдения посредством когерентного света с априорно заданными параметрами кодируется в виде функции взаимной корреляции. Свойства распространения функции взаимной корреляции обеспечивают перенос закодированной в ней информации потоком света. При взаимодействии его с фоточувствительной средой эта информация регистрируется в виде функции взаимной интенсивности.

Монохроматическая плоская волна является математической абстракцией, которой в мире наблюдаемых ничего не соответствует, и она, как заметил С.И.Вавилов, не переноси т энергии. Монохроматическую волну нельзя приготовить, ибо, начав это, мы уже задаем спектр ее. Исходя из соотношения неопределенностей, процесс приготовления такой волны должен длиться бесконечно долго.

С другой стороны, монохроматическая плоская волна не имеет фурье- и аналогичных ему преобразований. Всякое преобразование осуществляется в конечное время в конечной области, поэтому монохро-

матическая плоская волна после прохождения через какой-либо прибор (например, линзу) приобретает необратимые изменения и навсегда утрачивает свои идеальнее свойства. В силу этого Габором, Вольфом и Борном введено понятие комплексно-аналитического сигнала.

То обстоятельство, что функция корреляции, имея размерность интенсивности, является наблюдаемой и, не являясь волной, ведет себя как комплексно-аналитический сигнал, порождает возможность делать неправильные выводы из правильно поставленного эксперимента. Действительно, оперируя представлениями волн и допуская их наблюдаемость, мы можем получить результаты эксперимента, находящиеся в "хорошем" согласии с этими представлениями. Ситуация полностью соответствует известному афоризму Н.Бора: "Совпадение результатов эксперимента с дурацкой теорией ничего не говорит в ее пользу". В действительности согласие упрощенных волновых представлений например в оптической голографии, результатами эксперимента сохраняется с точностью до пренебрежения энергочувствительной принципиально квантовой природой фотонаблюдения. Поступая так, как это делается во многих работах по голографии, т.е. излагая волновой аспект этого процесса, "записывают" волну (полностью опуская природу фотопроцесса), а затем ее "восстанавливают", тогда как в действительности никакой "записи" и никакого "восстановления" оптической волны в голографическом процессе нет. Согласие же обеспечивается тем, что функция взаимной корреляции является комплексно-аналитическим сигналом (аналогом волны) и способностью запоминать ее фоторегистрирующей средой.

Рекомендуемая литература по данной теме следующая:

1. Gаbоr D. Новый принцип микроскопии, Nature, 161, 771, 1948.

2. Gabor D. Микроскопия на основе метода восстановления волновoго фронта. Proc.Roy.Soc, A-197, 454, 1949.

3. Gabor D. Prog. in Optics, H.P.C. том 1. 110-220, 1964.

4. Р.Глаубер. Оптическая когерентность и статистика фотонов в сб. "Квантовая оптика и квантовая радиофизика", "Мир", М., 1966.

5. Р.Глаубер. Когерентность и детектирование квантов в сб. "Когерентные состояния в квантовой теория", "Мир", М., 1972.

6. Э.Вольф, Л.Мандель. УФИ, 87.3, 491-520, 1965.

7. Дж.Клаудер, Э.Сударшан. Основы квантовой оптики, "Мир", М., 1970.

8. М.Борн, Э.Вольф. Опновы оптики, "Наука", М., 1970.

9. Дж.Гудмен. Введение в фурье оптику, "Мир", М., 1970.

10. А.Папулис. Теория систем и преобразований в оптике, "Мир", М., 1971.

11. Gаbor D. Ionrn. Sc. Instr., 8, 73-78, 16I-163, 253-255, 1975.

12. И.А.Дерюгин. Свет как носитель информации "Квантовая электроника" 2, Киев, "Наукова думка", 1967.

13. Р.Кольер и др. Оптическая голография, "Мир", М., 1973.

14. Дж.Велис, Д.Рейнольдс. Голография, Военниздат, М., 1970.

15. Дж.Строун. Введение в когерентную оптику и голографию, "Мир", М., 1967.

16. Л.М.Сороко. Основы голографии и когерентной оптики, "Наука", М., 1971.

17. И.А.Дерюгин, В.Н.Курашов. Когерентность и фазовые соотношения в квантовой оптике, изв.АН СССР, сер.физика, т.XXXVII, №10, 2032, 1973.

18. Фон Нейман. Математические основы квантовой механики, "Наука", М., 1964.

19. Gabor D. Proc, Phys.Soc, В-64, 449, 1951.

20. И.А.Дерюгин. В.Н.Курашов и др. Поляризационные эффекты в голографии, УФН, том 108, вып.4, стр.733-747, 1972.