ГОЛОГРАФИЧЕСКАЯ РЕГИСТРАЦИЯ НА ТЕРМОПЛАСТИЧНЫХ СРЕДАХ
Н.Г.Кувшинский, М.Ю.Баженов, Н.И.Соколов
В работе изложены некоторые особенности работы термопластичных сред (ТС) при регистрации и воспроизведении оптических голограмм.
Рассмотрены: спектральная область чувствительности, образование скрытого изображения, проявление, передаточные характеристики. В результате анализа делается вывод о том, что ТС могут регистрировать оптические голограммы во всей видимой и ближней ИК-области спектра и воспроизводить голограммы в реальном масштабе времени. Полоса пространственных частот передаточной характеристики определяется реологическими свойствами термопластичного слоя и управляется потенциалом поверхности, скоростью нарастания температуры и временем проявления.
В в е д е н и е
Действие света на подготовленные к регистрации голограмм ТС приводит к образованию скрытого изображения, представляющего собой источник сил, распределенный по поверхности или по поверхности и объему ТС в соответствии с распределением интенсивности света в регистрируемом изображении. Природой образования источника сил и особенностями его распределения отличаются друг от друга известные способы записи на ТС. Скрытое изображение может быть создано в результате чисто физических процессов /1,2/ или в результате фотохимических реакций /3/. Первые способы записи наиболее перспективны в применении в связи с тем, что ТС могут быть многократно использованы для записи и воспроизведения гологpaмм. Объединяет способы записи на ТС процесс проявления, заклю-чающийся в размягчении ТС, во время которого источник сил скрытого изображения деформирует ТС, и скрытое изображение преобразуется в геометрический рельеф поверхности. По этой причине информационные свойства ТС для всех способов записи будут иметь много общих особенностей, т.к. в основном определяются реологическими свойствами тонкой термопластичной пленки, находящейся на жесткой подложке. Известные информационные свойства ТС одного способа записи могут быть использованы при анализе информационных свойств ТС другого способа записи с коррекцией на особенности источника сил скрытого изображения.
i. Термопластичные среды
Далее мы рассматриваем фотопластический способ регистрации голограмм /1/. ТС при этом способе записи представляют собой тонкие прозрачные пленки, нанесенные на металлизированные стеклянные подложки и сочетающие в себе термопластичные и фотопроводниковые свойства (рис.1а) (иногда используют двухслойные пленки, в которых термопластичные и фотопроводниковые свойства разделены между слоями -рис.1б). Для подготовки ТС к регистрации голограмм их поверхность равномерно заряжают (обычно в коронном разряде) - рис.1в. При регистрации голограммы, вследствие фотопроводимости ТС на ее поверхности создается потенциальный рельеф - рис.1г, который можно рассматривать как скрытое изображение. Проявление заключается в
размягчении ТС нагревом, например, за счет джоулева тепла, выделяющегося в металлизированном подслое (рис.1д) при прохождении импульса тона, во время которого источник сил скрытого изображения деформирует ТС и скрытое изображение преобразуется в геометрический рельеф поверхности. Для стирания проявленного изображения необходимо пропустить через металлизированный подслой импульс тока большей длительности, чем импульс тока проявлений. В качестве фотопроводникового термопластичного слоя обычно используют поли- n -винилкарбазол (ПВК), реологические и электрические свойства которого определяются особенностью строения полимерной цепи. Очень большие карбазольные боковые группы сделали
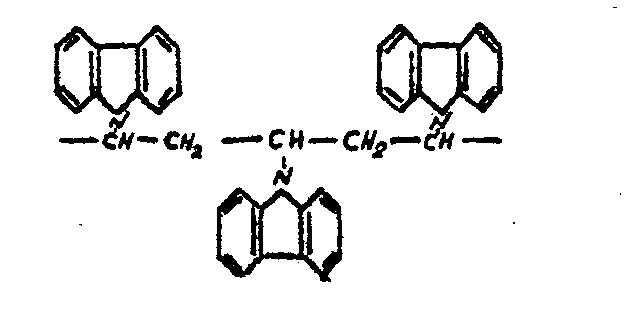
Рис.2. Химическая формула ПВК.
макромолекулу чрезвычайно жесткой и для вращения этих групп необходима высокая температура размягчения. Для снижения температуры размягчения, что требуется для качественного проявления скрытого изображения ПВК пластифицируют органическими добавками с низкой температурой плавления. В наших исследованиях в качестве пластификатора применена стабилизированная канифоль, являющаяся продуктом изомеризации и гидрирования живичной канифоли.
Фотопроводимость несенсибилизированного ПВК наблюдается в УФ области спектра. Возбуждение фототока происходит при энергиях фотонов, значительно меньших ширины запрещенной зоны (4,4 эв), и поэтому их энергии недостаточно для прямой генерации носителей тока. В связи с этим предполагают /4/, что проводимость является дырочной и дырки генерируются в результате взаимодействия экситонов с дефектами. Для смещения фотопроводимости в видимую область спектра ПВК сенсибилизируют красителями или электроно-акцепторны-
ми добавками. При сенсибилизации красителями предполагают /5/, что дырки генерируются двумя процессами при фотовозбуждении или уровней красителя, или ПВК. Наиболее эффективно расширение спектральной области проводимости происходит при введении в ПВК электроно-акцепторных добавок, с которыми молекулы ПВК образуют комплексы с переносом заряда. При введении электронно-акцепторных добавок у пленок ПВК появляется поглощение в видимой и ближней ИК-области спектра и, как показали проведенные наци исследования, характеристика фотопроводимости качественно повторяет ход кривой поглощения для спектрального диапазона, когда можно считать, что свет равномерно поглощается по толщине пленки. На рис.3 приведен из /6/ спектр поглощения пленок ПВК, сенсибилизированного 2,4,5,7-тетранитрофлюоренсном. Видно, что спектральная область поглощения
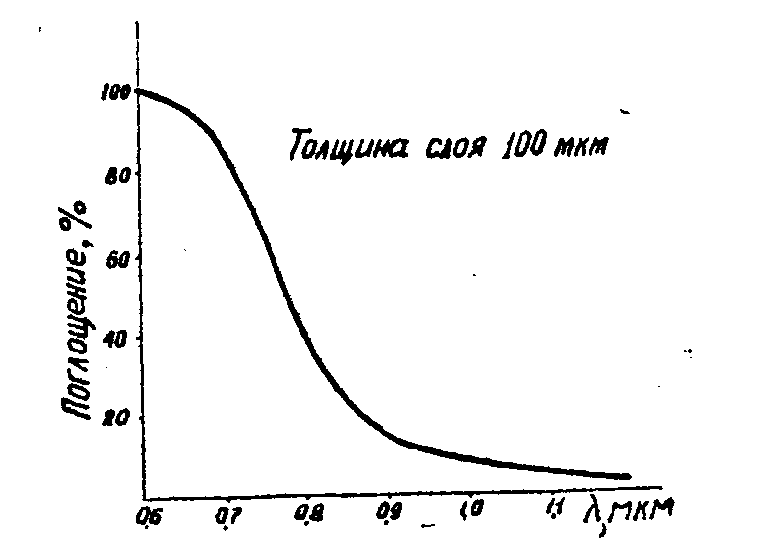
Рис.3. Спектр поглощения ТС толщиной 100 мкм.
расширена на видимую и ближнюю ИК области спектра. Пленки ПВК получают поливом из раствора на стеклянные подлодки с проводящим слоем. (Толщина пленок 0,5÷5 мкм). Проводящий слой (представляет собой тонную пленку двуокиси олова, имеющую прозрачность 85-90% и сопротивление 30-40 ом/см2) используется в качестве второго электрода при зарядке ТС и для проявления скрытого изображения. Таким образом, на заряженных ТС, представляющих собой тонкие пленки пластифицированного ПВК и сенсибилизированного электроно-
акцепторными добавками, можно создать скрытое изображение в виде потенциального рельефа в широком спектральном диапазоне от УФ до ближней ИК области.
ii. Метод оценки ТС
Проявленное изображение на ТС представляется в виде геометрического рельефа поверхностей поэтому ТС анализируются как рельефо-фазовые детекторы голограмм. Вопросы анализа информационных свойств рельефо-фазовых детекторов голограмм подробно рассмотрены в /7/. Для фазовых сдвигов Δφ(х) κ 0,6 рад. коэффициент пропускания ТС [τ(υ)] μожно представить линейной функцией фазового сдвига
τ(υ) = 1 + i Δφ(x) . (1)
При условии линейной зависимости Δφ(υ) ξт экспозиции jt зависимость (1) дает возможность считать, что в рельефо-фазовых детекторах голограмм по аналогии с амплитудными детекторами межмодуляционный шум рассеивается в направлении восстанавливающего луча и не влияет на яркость и качество восстановленного изображения. Это позволяет при определении пригодности рельефо-фазовых детекторов для регистрации голограмм ограничиться регистрацией и восстановлением голограмм плоского волнового фронта не прибегая к анализу голограмм сложных объектов. Однако, так как голограмма реального объекта представляет собой интерференционную картину большой области пространственных частот, то при анализе ТС нельзя ограничиваться определением области jt и контраста (κ)* при которых зарегистрированный волной фронт на данной несущей пространственной частоте будет линейно восстановлен. Необходимо еще измерение передаточной характеристики ТС, которая при условии
выполнения приближения (1) представляет собой зависимость высоты синусоидального рельефа на поверхности ТС (корня квадратного из дифракционной **эффективности (η)) от пространственной частоты (ν). Таким образом, пределы применения ТС для регистрации голограмм определяются из анализа двух семейств передаточных характеристик, измеренных при регистрации и восстановлении голограмм плоского волнового фронта, в первом семействе для линейной области jt при постоянном κ, во втором -для линейной области κ, при постоянной jt.
iii. Скрытое изображение
Процесс подготовки ТС к регистрации голограмм, заключающийся в осаждении на поверхность ионов в коронном разряде, является сложным процессом, во время которого может происходить удаление носителей тока из ТС или наоборот инжекция носителей тока в ТС из металлизированного подслоя, образование объемного заряда и т.д. При этом электрическое поле поверхностных зарядов может проникать на всю толщину термопластичного фотопроводникового слоя или только на его часть. В наших исследованиях в качестве термопластичного фотопроводникового слоя использовался ПВК, сенсибилизированный 2,4,7 - тринитро-9-флюореноном (0,5% к весу ПВК), пластифицированный стабилизированной канифолью, вводимой в количестве 25% к весу ПВК. При зарядке такой ТС положительным зарядом наблюдается линейная зависимость между потенциалом насыщения (vc) и толщиной слоя (d) для d < 10 мкм. Согласно /8/, можно считать, что глубина проникновения поля в случае положительного поверхностного заряда превышает рабочие толщины нашего термопластичного фотопроводникового слоя (0,5 - 5 мкм), и заряд экранирования накапливается в проводящем металлизированной подслое. Далее будут рассматриваться процессы только при положительном поверхностном заряде. В этом случае поведение ТС можно описать мо-
делью двойного электрического слоя с эффективной толщиной, равной рабочей толщине термопластичного слоя. Используемые нами ТС имеют очень слабое поглощение в видимой области спектра, поэтому при освещении ТС можно считать, что свет равномерно поглощается по ее толщине. Поглощение света приводит к генерации дополнительных носителей, н увеличению тока и уменьшению поверхностной плотности заряда. Процесс световой разрядки только в первом приближении может быть сведен к простому уменьшению поверхностной плотности заряда, т.к. при перемещении носителей в больших электрических полях может происходить захват носителей на глубокие ловушки, накопление объемного заряда и установление в слое электретного состояния. Однако, роль перечисленных выше явлений в источнике сил скрытого изображения пока не выяснена, и мы будем рассматривать скрытое изображение в виде зависимости поверхностной плотности заряда σt от координаты х вдоль поверхности.
При регистрации голограмм плоского волнового фронта распределение интенсивности света в плоскости регистрации голограмм будет синусоидальным:
j(x) = a12 + a22 - 2a1a2sinν'x. (2)
Здесь А1 и А2 - соответственно, амплитуды вектора напряженности электрического поля объектного и опорного луча, ν' определяется углом, под которым сводятся на поверхности ТС объектный и опорный лучи (ν' =2πν).
Если при регистрации голограмм ограничиться диапазоном экспозиций, соответствующих линейному участку зависимости 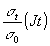 , и распределение поверхностной плотности заряда в скрытом изображении будет тоже синусоидальным.
, и распределение поверхностной плотности заряда в скрытом изображении будет тоже синусоидальным.
σt(x) = σ0 – σ0βjt = σ0 – a12 βtσ0 - a22 βtσ0 -2a1a2βtσ0sinν'x. (3)
Здесь σ0 - исходная поверхностная плотность заряда, определяемая начальным потенциалом поверхности v; β - коэффициент, характеризующий скорость изменения поверхностной плотности заряда, определяемый как тангенс угла наклона из зависимости 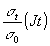 .
.
Обозначим σ0 – a12 βtσ0 - a22 βtσ0 через σ01 и через σ1 величину 2a1a2βtσ0. Величина σ01, определяет постоянную составляющую поверхностной плотности заряда после экспонирования, а σ1 - амплитуду переменной составляющей заряда. Тогда выражение (3) может быть записано в следующем простом виде:
σt(x)=σ01-σ1sinν'x. (4)
Глубина модуляции поверхностной плотности заряда при регистрации голограмм плоского волнового фронта зависит от экспозиции, и для экспозиции насыщения зависимости 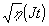 при v равном vc не превышают 5%,и, следовательно, можно приближенно считать, что для самой большой экспозиции σ1~0,05σ01. Модуляция поверхностной плотности заряда приводит к появлению переменной составляющей нормального давления в ТС, выражение для которой можно легко получить, воспользовавшись расчетом Шафферта /9/ для напряженности электрического поля в диэлектрической пленке с переменной плотностью поверхностного заряда:
при v равном vc не превышают 5%,и, следовательно, можно приближенно считать, что для самой большой экспозиции σ1~0,05σ01. Модуляция поверхностной плотности заряда приводит к появлению переменной составляющей нормального давления в ТС, выражение для которой можно легко получить, воспользовавшись расчетом Шафферта /9/ для напряженности электрического поля в диэлектрической пленке с переменной плотностью поверхностного заряда:
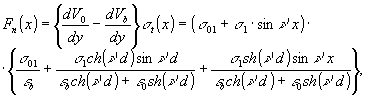 (5)
(5)
здесь v - потенциал над поверхностью ТС, vb - потенциал внутри ТС, ось у направлена перпендикулярно поверхности ТС, а ось х - параллельно. Для практически реализуемых условий εb=3; εa=1; ν'd>1 выражение (5) может быть упрощено и представлено в следующем виде:
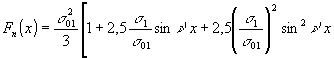 . (6)
. (6)
Так как 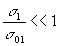 , то третьим членом в скобках в выражения (6) можно пренебречь. Тогда выражение (6) имеет вид:
, то третьим членом в скобках в выражения (6) можно пренебречь. Тогда выражение (6) имеет вид:
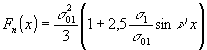 . (7)
. (7)
Таким образом, в скрытом изображении на ТС, поле электростатических сил для анализируемого диапазона jt и рабочего диапазона v, включая vс, линейно запоминает синусоидальный растр, соответствующий голограмме плоского волнового фронта.
iv. Хаотические деформации
Большая постоянная составляющая заряда в скрытом изображении изменяет гиббсовскую свободную энергию поверхности ТС вследствие электрокапиллярного эффекта, что учитывается в изменении эффективного коэффициента поверхностного натяжения (Т*)/10/
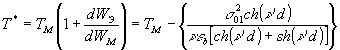 . (8)
. (8)
Здесь Тм - коэффициент поверхностного натяжения незаряженной. ТС; wэ - электростатическая энергия ТС; wм - гиббсовская свободная энергия поверхности незаряженной ТС. В связи с этим при проявлении скрытого изображения, заключающегося в размягчении ТС, наряду с регулярным рельефом, соответствующим регистрируемому изображению, будет развиваться хаотический рельеф. Хаотический рельеф является самостоятельным предметом исследования при проявлении скрытого изображения на ТС, и не только потому, что он является источником шума и от него нужно избавляться. Дело в том, что развитие хаотического рельефа, так же как и регулярного, в основном определяется реологическими свойствами заряженной ТС и для некоторых условий проявления анализа информационных свойств ТС можно делать на основе анализа свойств хаотического рельефа, что значительно упрощает эксперимент при измерении передаточных характеристик. Это предположение подтверждается экспериментально. Так, например, Урбахом /11/ было замечено, что оптимальные пространственные частоты передаточной характеристики регулярных деформаций и спектра частот хаотических деформаций практически совпадают.
На рис.4 приведены измеренные нами относительная передаточная характеристика регулярной деформации 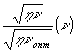 (9) (кривая (1)) и передаточная характеристика хаотических деформаций
(9) (кривая (1)) и передаточная характеристика хаотических деформаций
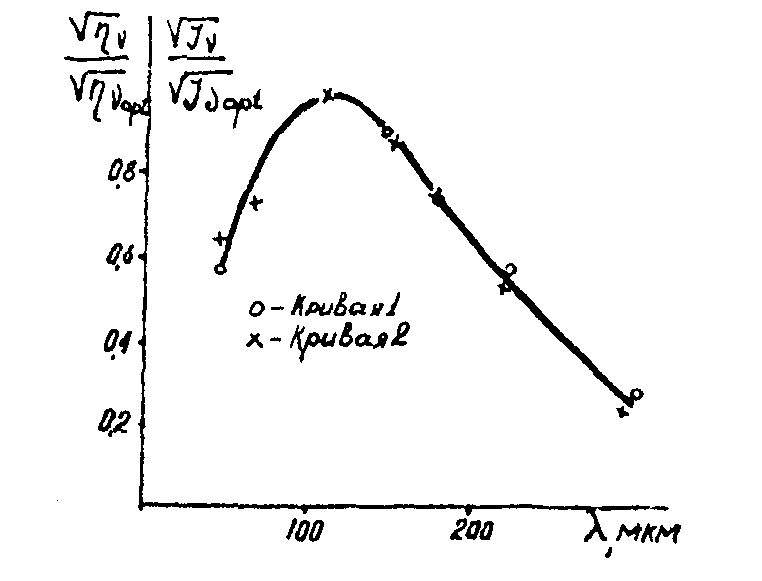
Рис.4. Передаточные характеристики.
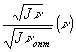 (10) (кривая (2)), измеренные на одном образце при одинаковых v и одинаковых условиях проявления. В (9) и (10) оптимальная пространственная частота соответствует максимальному значению η в зависимости
(10) (кривая (2)), измеренные на одном образце при одинаковых v и одинаковых условиях проявления. В (9) и (10) оптимальная пространственная частота соответствует максимальному значению η в зависимости 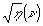 и максимальному значению интенсивности света j в дифракционной картине хаотических деформаций в зависимости
и максимальному значению интенсивности света j в дифракционной картине хаотических деформаций в зависимости 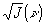 . Как видно на рис.4, передаточная характеристика ТС и передаточная характеристика хаотических деформаций для выбранных условий проявления практически совпадают.
. Как видно на рис.4, передаточная характеристика ТС и передаточная характеристика хаотических деформаций для выбранных условий проявления практически совпадают.
Рассмотрим развитие хаотических деформаций на поверхности заряженной ТС при проявлении. При этом считаем, что поверхностная плотность заряда не модулирована. Бадд /10/ предложил рассматривать хаотические деформации как сумму рельефо-фазовых синусоидальных решеток и решил задачу развития амплитуд этих решеток для случая, когда фото проводниковый термопластичный слой конечной толщины моделируется ньютоновской жидкостью, и задаче предполагалось, что амплитуды решеток развиваются по закону Δlieωit при постоянной температуре и при отсутствии релаксации и изменения поверхностной плотности заряда. Получено решение в виде зависимости ω от ν для различных v ТС.
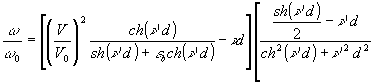 . (11)
. (11)
Здесь 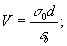
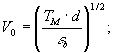 м – вязкость;
м – вязкость; 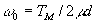 . На рис.5 приводим рассчитанные по формуле (11) зависимости относительной скорости роста амплитуды (ω/ω0) от произведения ν'd. Наличие максимума на зависимостях рис.5 означает, что и передаточные характеристики хаотических деформаций токе будут иметь максимум. Передаточные: характеристики представим в виде отношения Фурье-образа синусоидального рельефа для времени проявления t1 к Фурье-образу синусоидального рельефа в начале проявления /7/
. На рис.5 приводим рассчитанные по формуле (11) зависимости относительной скорости роста амплитуды (ω/ω0) от произведения ν'd. Наличие максимума на зависимостях рис.5 означает, что и передаточные характеристики хаотических деформаций токе будут иметь максимум. Передаточные: характеристики представим в виде отношения Фурье-образа синусоидального рельефа для времени проявления t1 к Фурье-образу синусоидального рельефа в начале проявления /7/
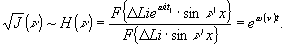 (12)
(12)
Здесь Н(ν) пропорционально 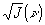 - передаточной характеристике хаотических деформаций, приведенной на рис.4.
- передаточной характеристике хаотических деформаций, приведенной на рис.4.
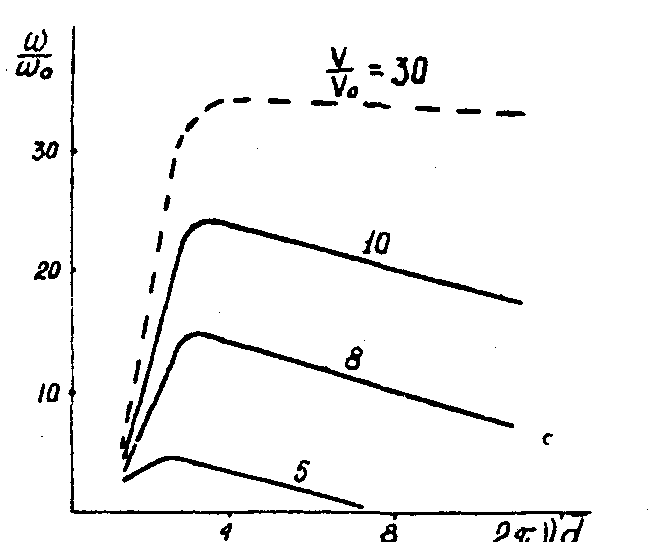
Рис.5. Зависимости 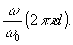 .
.
Положение максимума передаточной характеристики (значение νopt) для термопластичного слоя одной толщины, а также полоса частот хаотических деформаций, определяемая для простоты рассмотрения по максимальной пространственной частоте (ν'opt) спектра частот хаотических деформаций, зависят от v. Определим эти зависимости из (11):
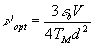 для
для 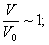
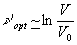 для
для 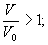 (13)
(13)
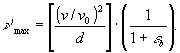 (14)
(14)
Основные выводы расчета сводятся к следующему.
1. Передаточная характеристика хаотических деформаций имеет максимум, наличие которого обусловлено влиянием толщины термопластичного слоя на развитие деформаций, период которых соизмерим с толщиной слоя.
2. Значения νopt и νmax зависят от v, что позволяет считать Тc запоминающими средами с электрически управляемыми информационными свойствами.
Результаты расчета Бадда качественно подтверждаются экспериментально. Уменьшение амплитуд составляющих спектра частот хаотических деформаций при постоянной температуре, оцениваемое по изменению интенсивности света в дифракционной картине хаотических деформаций, происходит по экспоненциальному закону с постоянными времени, такими, как при уменьшении амплитуд соответствующих частот регулярных синусоидальных рельефо-фазовых решеток /12/, т.е. хаотические деформации можно представить в виде суммы рельефо-фазовых синусоидальных решеток. Дифракционная картина хаотических деформаций имеет вид кольца, а передаточная характеристика, полученная на основе фотометрирования дифракционной картины, имеет максимум (см.рис.4, кривая 2). Экспериментально наблюдается также управление νоpt v. На рис.6 приводим из /7/ зависимость νоpt(v) для различных толщин фотопроводникового термопластичного слоя. Видно, что увеличение v приводит к увеличению νорt, причем чем меньше толщина слоя, тем в больших пределах происходит управление. Реальный процесс проявления отличается от рассмотренного Баддом. При проявлении температура термопластичного слоя меняется, и он проходит все состояния от стеклообразного до вязкотекучего. Как показали исследования, приведенные в /12/, развитие хаотических деформаций начинается еще до перехода термо-
пластического слоя в режим ньютоновского течения, и при развитии хаотических деформаций необходимо учитывать сопротивление сдвига вязкому течению.
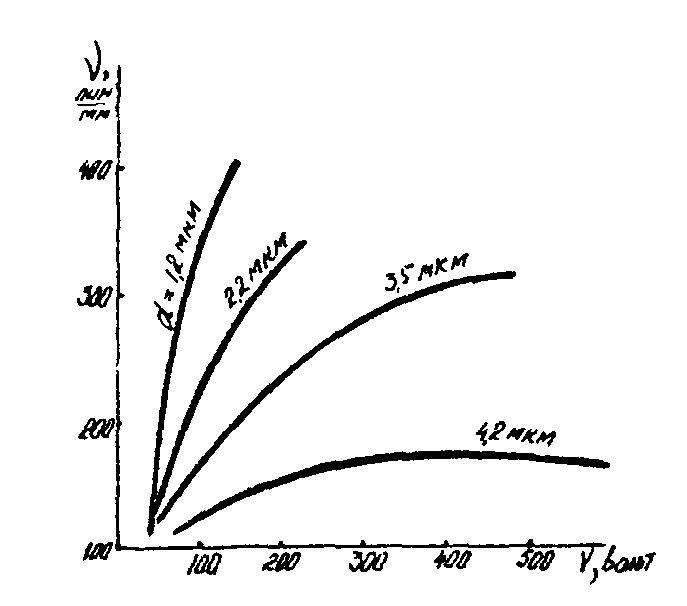
Рис.6. Зависимости νopt(v).
Кроме того, в процессе развития хаотических деформаций изменяется начальная плотность заряда вследствие деформации поверхности, увеличения ее площади и релаксации заряда в результате проводимости термопластичного слоя. На рис.7 приводим измеренные в нашей лаборатории зависимости νopt передаточной характеристики хаотических деформаций от времени проявления для трех v (кривая 1"а" - начальный v=300 вольт, кривая 2"а" - 220 вольт, кривая 3"а" - 180 вольт). Кривые 1,2,3 характеризуют изменение v, скрость нарастания температуры составляет 64 град/сек. (измерение зависимостей рис. 6-9 проведены на несветочувствительном термопластичном слое ТПН-8).
Исследование реологических свойств термопластичного слоя в диапазоне температур проявления показало /12/ что рост νоpt (кривые 1"а", 2"а") наблюдается в режиме неньютоновского течения и связан, по нашему мнению, с уменьшением напряжения сдвига по мере увеличения температуры; уменьшение νоpt связано с уменьшением v.
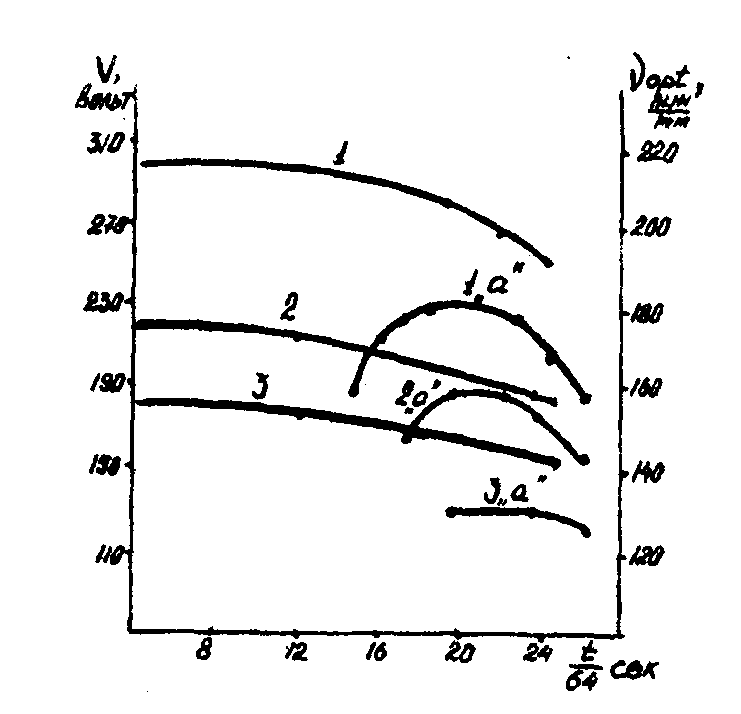
Рис.7. Зависимости v(t) - кривые 1, 2, 3 и νopt(t) - кривые 1-"a", 2"a", 3"a", соответственно, для v = 300; 220; 180 вольт.
На рис. 8 приводим измеренные в нашей лаборатории зависимости νopt от времени проявления для начального v = 300 вольт, отличающиеся скоростью нарастания температуры. Для кривой 1"а" скорость нарастания температуры 95°С/сек, для кривой 2"а" -64°С/сек, для кривой 3"a"=35°c/ceк. Кривые 1,2,3 характеризуют изменение потенциалов поверхности. Видно, что увеличение скорости нарастания температуры приводит к достижении больших значений νоpt, что связано, по нашему мнении, с уменьшением времени развития хаотических деформаций в режиме неньютоновского течения. Как показано на рис.7 (кривые 1"а" и 2"а"), режим неньютоновского течения стимулирует развитие низкочастотных составляющих в спектре частот хаотических деформаций, амплитуды которых при низких скоростях нарастания температуры еще в режиме неньютоновского течения могут достичь достаточной величины для существенного уменьшения постоянной со-
ставляющей поверхностной плотности заряда вследствие увеличения площади поверхности. Это приводит к уменьшению максимального достижимого значения νоpt для данного начального v.
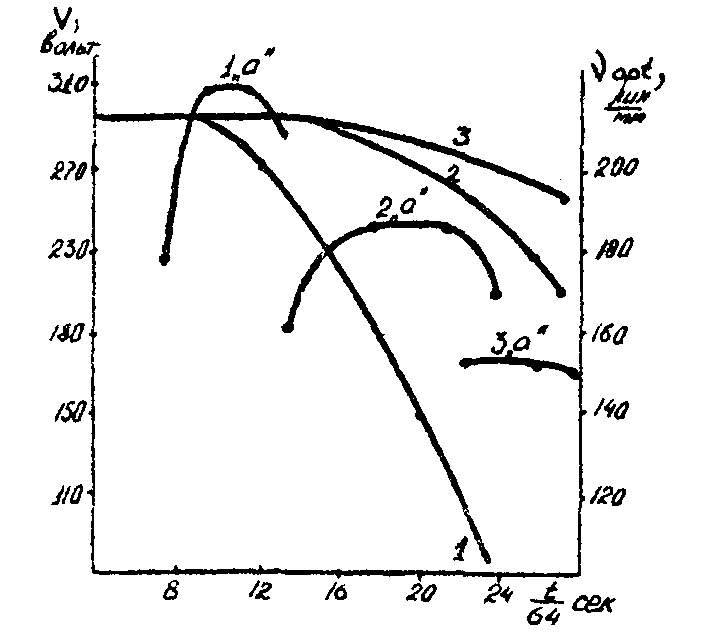
Рис.8. Зависимости v(t) (кривые 1,2,3) и νopt(t) (кривые 1"а", 2"а", 3"а"), соответственно, для трех скоростей нарастания температуры 95, 64, 35°С/сек.
На рис.9 приведены зависимости νopt∙d(v), характеризующие управление передаточными характеристиками tС для трех скоростей нарастания температуры 32°С/сек (кривая 1), 64°С/сек (кривая 2), 95°С/сек (кривая 3).
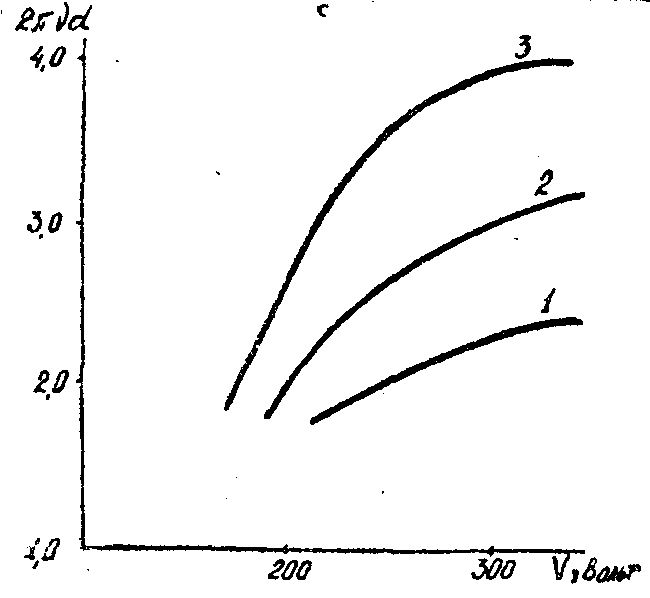
Риc.9. Зависимость 2πνd(v) для трех скоростей нарастания температуры (кривая 1-36°c/сек; 2-64°С/сек; 3-95°С/сек).
Как видно на рис.9, увеличение скорости нарастания температуры приводит к расширению области управления νopt и к увеличению тангенса угла наклона зависимости νopt∙d(v). Таким образом, исследование хаотических деформаций и оценка информационных свойств ТС по передаточным характеристикам хаотических деформаций позволяют сделать следующие выводы.
1. Хаотические деформации можно рассматривать в виде суммы рельефо-фазовых дифракционных решеток.
2. Передаточная характеристика хаотических деформаций имеет максимум, определяемый влиянием толщины термопластичного слоя на развитие деформаций, период которых соизмерим и больше толщины слоя.
3. Оптимальная пространственная частота и полоса частот зависят от потенциала поверхности и управляются им в широких пределах.
4. В реальном режиме проявления оптимальная пространственная частота передаточных характеристик изменяется во время проявления, что, по нашему мнению, связано с неньютоновским режимом течения термопластичного слоя в начале проявления и релаксацией потенциала поверхности.
5. Увеличение скорости нарастания температуры приводит к увеличению максимально достижимого значения оптимальной пространственной частоты для данного потенциала поверхности, что связано, по нашему мнению, с уменьшением времени развития хаотических деформаций в режиме неньютоновского течения.
6. Увеличение скорости нарастания температуры расширяет диапазон управления оптимальной пространственной частотой хаотических деформаций.
v. Передаточные характеристики ТС
Рассмотрим проявление регулярного рельефа на ТС, соответствующего изображению голограммы плоского волнового фронта.
Задача проявления скрытого изображения независимо от природы источника сил и модели ТС наиболее полно сформулирована в /13/,
идеи были позднее реализованы Н.Г.Находкиным с сотрудниками при решении задачи проявления скрытого изображения на ТС, моделируемой ньютоновской жидкостью при постоянной температуре для произвольного распределения источника сил по поверхности и объему ТС /14,15/. Решения в /14,15/ получены в виде передаточных характеристик, что позволяет сразу использовать результаты расчета для анализа информационных свойств ТС, сравнения с экспериментом и для постановки новых исследований. Общий анализ расчетных передаточных характеристик для различных режимов проявления и свойств ТС сделан Н.Г.Находкиным в /7/. Здесь мы остановимся на некоторых особенностях передаточной характеристики ТС для случая, когда источник сил скрытого изображения может быть представлен нормальной синусоидальной силой, приложенной к поверхности ТС (формула 17 из /7/). Анализ проводим для ν'd > 1, когда роль тангенциальных сил при деформировании ТС незначительна.
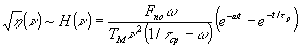 (15)
(15)
В этом выражении будем считать, что поверхностная сила получена в результате модуляции поверхностной плотности заряда, когда σ1 << σ01 и релаксация σ01 в процессе проявления отсутствует. σ1, а следовательно, и амплитуда силы fno, релаксирует с постоянной времени τр. При таком предположении под Тm следует понимать эффективный коэффициент поверхностного натяжения Т*, а ω имеет такой же смысл и значение, как в (11).
В соответствии со сделанными предположениями передаточную характеристику (15) представим в виде
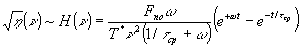 (16)
(16)
Сравним выражения для передаточных характеристик регулярных (16) и хаотических деформаций (12). Видно, что для времени проявления t > 1/ω и для отношения v/v0>1 в выражении для ω в (11) вид передаточной характеристики регулярных деформаций (16)
будет, в основном, определяться экспонентой еωt, независимо от значения τр, и вид передаточных характеристик регулярных и хаотических деформаций будет одинаковым.
Анализируемый расчет качественно подтверждается экспериментально. Для времен проявления t>1/ω вид передаточных характеристик регулярной и хаотической деформации качественно совпадает (см.рис.4, кривые 1 и 2).
Для линейного участка зависимости 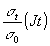 амплитуда fno в (16) линейно зависит от jt и ответ ТС при проявлении голограмм плоского волнового фронта, оцениваемый по корню квадратному из η, должен линейно зависеть от jt.
амплитуда fno в (16) линейно зависит от jt и ответ ТС при проявлении голограмм плоского волнового фронта, оцениваемый по корню квадратному из η, должен линейно зависеть от jt.
На рис.10 приведены зависимости 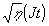 для различных v; d термопластичного фотопроводникового слоя была равна 3 мкм; пространственная частота интерференционной картины голограммы плоского волнового фронта составляла 150 лин/мм; для исследуемой области экспозиций значение σ1 не превышало 0,1σ01.
для различных v; d термопластичного фотопроводникового слоя была равна 3 мкм; пространственная частота интерференционной картины голограммы плоского волнового фронта составляла 150 лин/мм; для исследуемой области экспозиций значение σ1 не превышало 0,1σ01.
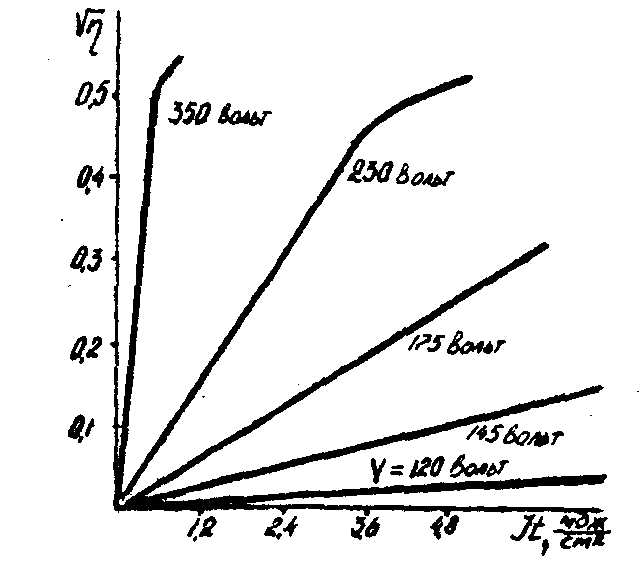
Рис.10. Зависимости 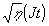
Видно, что зависимость 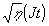 линейна для широкой области значений
линейна для широкой области значений 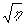 . Так, например, для v = 350 вольт зависимость
. Так, например, для v = 350 вольт зависимость 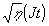 линейна вплоть до предельной η. Для времен проявления t>1/ω, ν'd>1 и v/v0>1 в (11) тангенс угла наклона зависимости
линейна вплоть до предельной η. Для времен проявления t>1/ω, ν'd>1 и v/v0>1 в (11) тангенс угла наклона зависимости 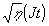 будет, в основном, определяться экспоненциальным членом е+ωt, в котором ω будет зависеть от квадрата v. Этот вывод качественно подтверждает измеренная
будет, в основном, определяться экспоненциальным членом е+ωt, в котором ω будет зависеть от квадрата v. Этот вывод качественно подтверждает измеренная
нами зависимость тангенса угла наклона линейного участка зависимостей 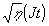 от v, которую приводим на рис.11.
от v, которую приводим на рис.11.
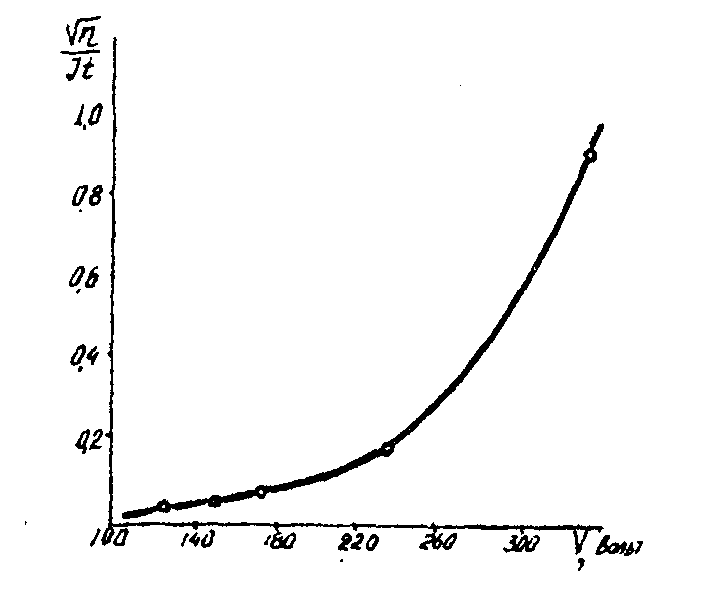
Рис.11. Зависимости 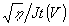 .
.
Из анализа передаточной характеристики (16) для t>1/ω и v/v0>1 следует другой важный вывод: так как форма передаточной характеристики регулярных деформаций определяется экспоненциальным членом еωt, то ν'opt и ν'max, передаточной характеристики регулярных деформаций будут управляться потенциалом поверхности аналогично управлению значениями ν'opt и ν'maх для хаотических деформаций (13 и 14). Этот вывод тоже качественно подтверждается экспериментально.
На рис.12 приводим передаточные характеристики tС d = 3мкм отличающиеся v. Видно, что увеличение v приводит к увеличению значений νopt и расширяет полосу пространственных частот.
Реальный процесс проявления отличается от рассмотренного Н.Г.Находкиным, тем, что проявление происходит при непрерывном нарастании температуры, во время которого термопластичный слой проходит все состояния от стеклообразного до вязкотекучего.
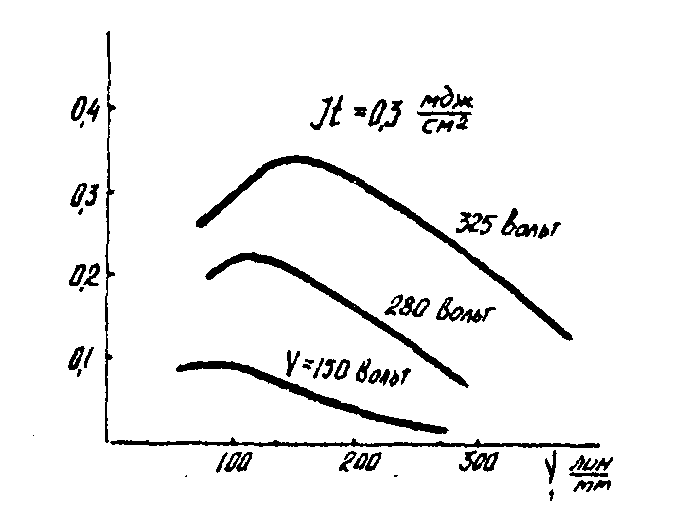
Рис.12. Передаточные характеристики для трех v.
Проведенные нами исследования реологических свойств термопластичного слоя в диапазоне температур проявления позволяет считать, что развита регулярного рельефа начинается в области перехода от стеклообразного состояния к вязкотекучему. В связи с этим, по нашему мнению, при проявлении регулярных деформаций наблюдается ряд таких же особенностей как и при проявлении хаотических деформаций. На рис.13 приводим измеренные нами передаточные характеристики ТС, полученные при проявлении голограмм плоского волнового фронта со средней скоростью нарастания температуры 1200°
С/сек, отличающиеся временем проявления; а на рис.14 приведены передаточные характеристики, полученные при проявлении голограмм плоского волнового фронта со средней скоростью нарастания температуры 2400°С/сек. (В обоих опытах толщина фотопроводникового слоя составляла 1,5 мкм, v =270 вольт и соответствовал vс). Анализ передаточных характеристик ТС, приведенных на рис.13 и 14, позволяет сделать вывод, аналогичный сделанному ранее при анализе передаточных характеристик хаотических деформаций. В процессе проявления происходит непрерывное изменение передаточных характеристик, сопровождающееся в начале проявления смещением νоpt в сторону высоких пространственных частот и расширением полосы частот. Этот эффект наблюдается тем значительнее, чем выше скорость нарастания температуры.
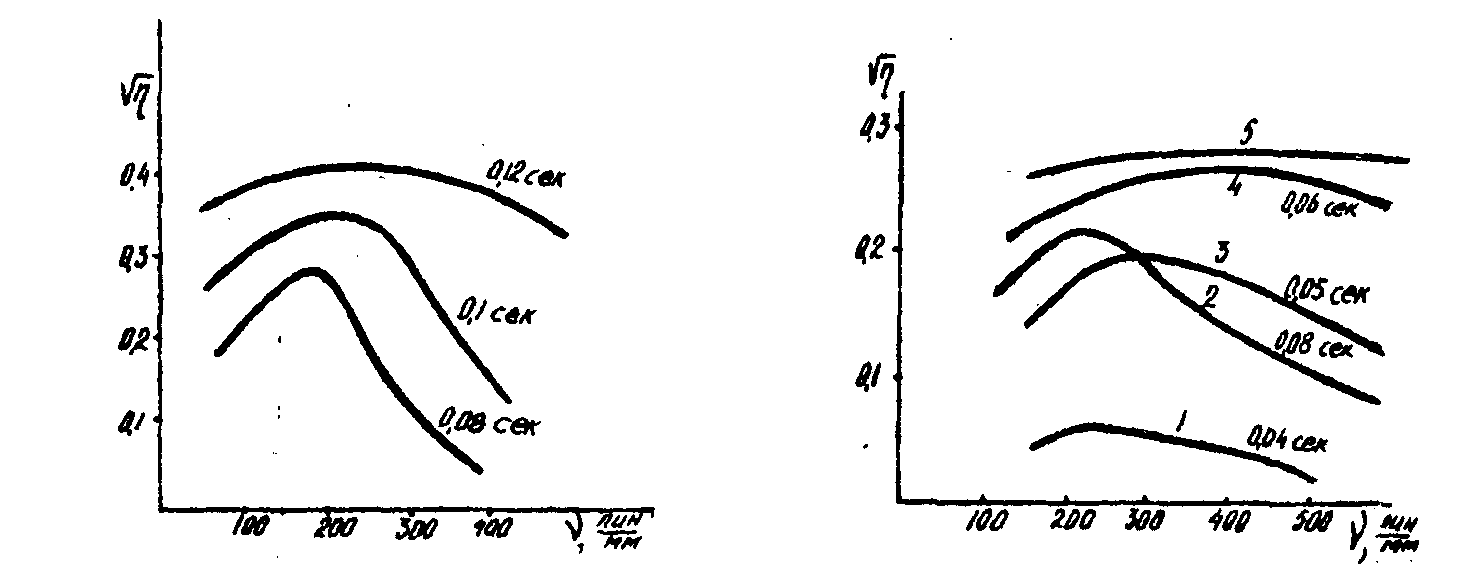
Изменение значения νоpt в процессе проявления для передаточных характеристик получается также из расчета при моделировании термопластичного слоя ньютоновской жидкостью при изотермическом процессе проявления (15) и при режиме проявления с переменной вязкостью /16/. Сравнить предсказание теории с экспериментом пока нельзя в связи с тем, что не удается осуществить режим проявления, в котором термопластичный слой мог быть моделирован ньютоновской жидкостью при постоянной температуре или в режиме изменения вязкости. В настояний момент мы все же придерживаемся изложенной ранее точки зрения и заключающейся в том, что эффект изменения передаточных характеристик связан с неньютоновским характером течения термопластичного слоя в начале проявления, т.к. эффекты изменения передаточных характеристик должны, согласно (15), вовремя разыгрываться при временах проявления t<1/ω или соизмеримых с 1/ω. Изменения передаточных характеристик на рис.15 наблюдаются для времен проявления 0,04-0,06 сек. Измеренное нами значение 1/ω для термопластичного слоя при температуре 70°
С, которую он имеет ко времени проявления 0,24 сек, значи-
тельно меньше времени 0,04 сек.
Предсказания же расчета /16/, как уже упоминалось, пока не могут быть проверены экспериментально, и самое главное-пока нет физической интерпретации вытекающим из расчета выводам.
Проведенные исследования позволяют сделать следующие выводы.
1. Предсказания теории качественно подтверждаются экспериментально:
а) передаточная характеристика имеет максимум;
б) значения оптимальной пространственной частоты и полоса частот передаточной характеристики зависят от толщины слоя и управляются потенциалом поверхности;
в) при больших временах проявления передаточные характеристики регулярных и хаотических деформаций качественно совпадают;
г) ответ ТС, оцениваемый как корень квадратный из дифракционной эффективности, линейно зависит от экспозиции для области экспозиций, когда амплитуда силы скрытого изображения линейно зависит от экспозиции;
д) чувствительность ТС, оцениваемая по тангенсу угла наклона зависимостей 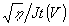 зависит от потенциала поверхности.
зависит от потенциала поверхности.
2. В реальном режиме проявления передаточная характеристика ТС непрерывно изменяется во время проявления. На начальном участке проявления происходит увеличение оптимальной пространственной частоты и расширение полосы частот, что связываем с неньютоновским режимом течения ТС. Эффект изменения оптимальной пространственной частоты и расширение полосы частот тем больше, чем выше скорость нарастания температуры при проявлении.
vi. Подавление шума
В iv и v главах мы рассмотрели процессы проявления регулярных и хаотических деформаций без учета взаимного влияния, что справедливо для небольших амплитуд регулярного рельефа. Рассмотрим результаты, проведенных нами исследований кинетики проявле-
ния голограмм плоского волнового фронта и хаотических деформаций. Опыт был поставлен следующим образом. На равномерно заряженной поверхности образца выбирались два участка, на одном из которых регистрировали голограммы плоского волнового фронта (при самой большой экспозиции глубина модуляции исходной поверхностной плотности заряда не превышала 2%, пространственная частота интерференционной картины голограммы плоского волнового фронта была приблизительно равна оптимальной пространственной частоте передаточной характеристики хаотических деформаций). Считывание результатов проявления осуществляли двумя лучами от оптического квантового генератора ЛГ-38. Один из лучей освещал участок образца, где не регистрировались голограммы плоского волнового фронта и где должны были развиваться только хаотические деформации, другой-освещал участок образца, на котором одновременно развивались хаотические и регулярные деформации. Результаты проявления наблюдали в частотной плоскости и регистрировали с помощью кинокамеры со скоростью 64 кадра/сек. (В этих исследованиях количество сенсибилизатора в образцах было уменьшено до 0,05% для того, чтобы уменьшить влияние считывающих лучей на σ01 и σ1 во время проявления). Рассмотрим рис.15. Время τ1 - соответствует началу развития хаотических деформаций на участке образца, где не регистрировались голограммы плоского волнового фронта.
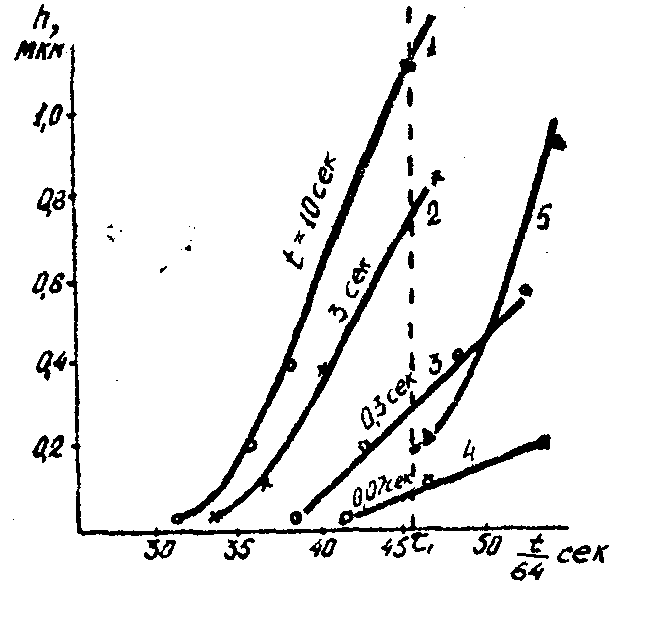
Рис.15. Зависимости h(t) – кривые 1,2,3,4; кривая 5-зависимость времени проявления хаотического рельефа от h.
Кривые 1, 2, 5, 4 представляют собой зависимости амплитуды регулярного рельефа от времени проявления для четырех экспозиций, соответственно, 10; 3; 0,3; 0,07 сек. Точки пересечения пунктирной линии, восстановленной перпендикулярно оси времени из точки τ1, с зависимостями 1, 2, 3, 4 соответствуют амплитудам регулярного рельефа, который образовался к началу развития хаотического рельефа на участке образца, где не регистрировались голограммы плоского волнового фронта. Кривая 5 представляет собой зависимость времени, соответствующего началу развития хаотических деформаций на участке образца, где регистрировались голограммы плоского волнового фронта, от высоты регулярного рельефа, который образовался к моменту времени τ1.
Анализ зависимости рис.15 позволяет сделать следующие выводы: 1) регулярный рельеф начинает развиваться раньше, чем рельеф хаотический Время проявления τ1 - время развития регулярного рельефа без хаотического; 2) на участке образца, где регистрировались голограммы плоского фронта, хаотические деформации начинают развиваться на предварительно деформированной поверхности и позже времени τ1; время, соответствующее началу проявления хаотических деформаций, тем больше, чем сильнее была деформирована поверхность к моменту времени τ1. Анализ кинограмм проявления хаотических и регулярных деформаций позволяет отметить другие особенности, которые не отражены на рис.15. Увеличение амплитуды регулярных деформаций к моменту времени τ1 приводит не только к смещению в сторону больших времен начало развития хаотических деформаций, но и изменяет их свойства. Меняется угловое распределение интенсивности света в дифракционной картине хаотических деформаций, уменьшается оптимальная пространственная частота передаточной характеристики в полоса частот. При амплитудах регулярного рельефа к моменту τ1, больших 0,5 мкм, дифракция от хаотических деформаций наблюдается практически только в направлении, перпендикулярном направлению дифракции от регулярного рельефа. На рис. 16 кривая 1 представляет собой зависимость относительного изменения оптимальной
пространственной частоты передаточной характеристики хаотических деформаций от амплитуды рельефа, образовавшегося к моменту времени τ1. Видно, что увеличение амплитуды регулярного рельефа приво-
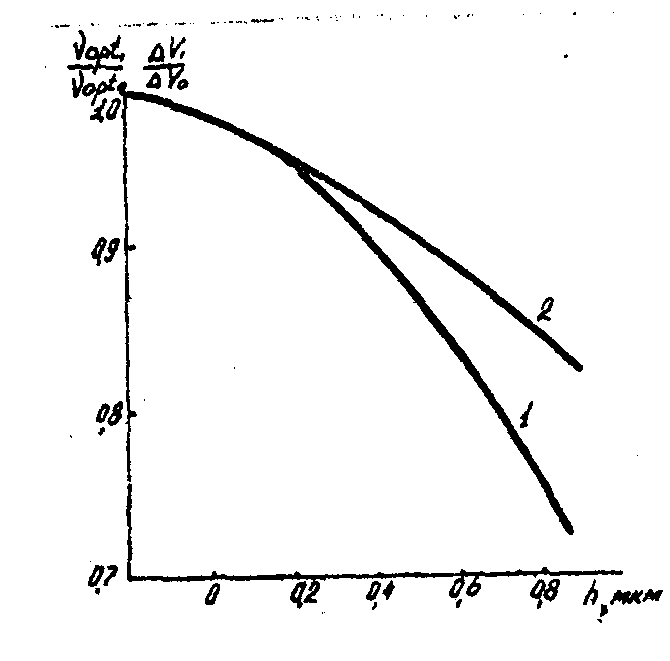
Рис.16. Зависимости 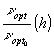 - кривая 1 и
- кривая 1 и 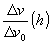 - кривая 2.
- кривая 2.
дит к уменьшению оптимальной пространственной частоты передаточной характеристики хаотических деформаций. Одной из причин наблюдаемого явления является уменьшение постоянной, соответствующей заряда σ01, вследствие деформирования поверхности ТС регулярными деформациями, что приводит к уменьшению диапазона потенциала поверхности управляющих оптимальной пространственной частотой передаточной характеристики. (На рис.16 кривая 2 характеризует относительное уменьшение диапазона потенциалов поверхности, управ-
ляющих оптимальной пространственной частотой от высоты регулярного рельефа, образовавшегося к моменту времени τ1).
Таким образом, роль специфических шумов на ТС, обусловленных хаотическими деформациями, может быть сведена к минимуму выбором времени проявления t<τ1 или увеличением амплитуды регулярного рельефа (увеличение экспозиции), который уменьшит скорость развития хаотического рельефа и изменит его свойства.
Как было показано ранее, увеличение скорости нарастания температуры, уменьшение времени проявления приводят к улучшению информационных свойств ТС, а проявление за время t<τ1 позволит получить голографические изображения, лишенные шума. Требования уменьшения времени проявления вытекают не только на основании изложенных выше соображений. При использовании голографических методов для анализа процессов в реальном масштабе времени необходимо сокращение временного интервала между регистрацией и визуализацией скрытого изображения, определяемого временем проявления. Время проявления зависит от скорости нарастания температуры и, по нашему мнению, при выбранном способе проявления ограничено конечным временем диффузии тепла от металлизированного подслоя к поверхности термопластичного слоя.
В нашей лаборатории М.Ю.Барабашом и В.А.Павловым было замечено, что при временах проявления t ~ 5∙10-4 сек и скоростях нарастания температуры, обеспечивающих разогрев термопластичного слоя за это время, развитие рельефа продолжается и после прекращения нагрева. Согласно расчету Ю.П.Гущо /17/, время установления температуры металлизированного подслоя на поверхности термопластичного слоя лежит в интервале 10-5÷10-3 сек, что качественно согласуется с описанным опытом.
В настоящей работе мы рассмотрели последовательный фотоплас-
тический способ записи, где процессы зарядки, регистрации голограмм, проявление осуществляются последовательно один за другим. Иногда процессы зарядки, регистрации и проявления совмещают. Это позволяет значительно расширить полосу пространственных частот передаточной характеристики (см.рис.14, кривую 5) и достигнуть разрешения 4500 лин/мм /18/. Одновременный режим характеризуется рядом специфических особенностей и требует отдельного рассмотрения.
В ы в о д ы
1. При анализируемом в работе фотопластическом способе записи на ТС регистрация изображения, проявление и стирание происходят в результате физических процессов, что позволяет использовать один и тот же образец для многократной регистрации голограмм.
2. tС являются рельефо-фазовыми детекторами голограмм.
3. Спектральная чувствительность ТС лежит в диапазоне длин волн 0,3÷1,3 мкм.
4. Зависимость 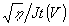 имеет протяженный линейный участок и при потенциалах насыщения простирается до предельных значений дифракционной эффективности.
имеет протяженный линейный участок и при потенциалах насыщения простирается до предельных значений дифракционной эффективности.
5. Информационные свойства ТС управляются электрическим полем в значительных пределах. Увеличение потенциала поверхности приводит к увеличению тангенса угла наклона зависимостей 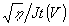 , увеличению оптимальной пространственной частоты и расширению полосы частот.
, увеличению оптимальной пространственной частоты и расширению полосы частот.
6. Результаты расчета качественно подтверждаются экспериментально.
7. Режим проявления существенным образом влияет на свойства передаточных характеристик. Увеличение скорости нарастания температуры и снижение времени проявления позволяют получать более широкополосную передаточную характеристику.
8. Влияние хаотических деформаций, возникающих на поверхности ТС при проявлении скрытого изображения может быть сведено к минимуму при уменьшении времени проявления.
9. При выбранном способе проявления ТС обеспечивают качест-
венное проявление за 10-3 сек, что позволяет использовать ТС для работы в реальном масштабе времени.
Л и т е р а т у р а
1. j.gaynor, s.aftergut. j.appl.phys., 34, 2102, 1963.
2. r.w.grundlach and c.i.claus. j.phot. sci. and eng., 14, 1963.
3. n.g.kuvshinsky, a.a.kostuk, n.g.nahkodkin, a.v.morozov, b.g.fedorovsky. experimentelle technik der physik, xx, 27, 1972.
4. h.bauser, w.klöpffer. chem.phys.lett., 7, 137, 1970.
5. s.hirosi, m.kadzuhisa. electrophotograpy, 9, 89, 1970.
6. w.s.colburn, l.m.ralson, j.c.dwyer. appl.phys.lett., 23, 3, 1973.
7. Находкин Н.Г., Кувшинский Н.Г., Почерняев И.М. Сборник "Способы записи информации на бессеребряных носителях", Киев, 5, 3-18, 1974.
8. Гренишин С.Г. Электрофотографический процесс, "Наука", 129, 1970.
9. Шафферт Р. Электрофотография , "Мир", 1968.
10. h.f.budd. j.appl.phys., 36, 1613, 1965.
11. j.g.urbach. phot.sci. and engin., 10, 287, 1966.
12. m.g.kuvshinsky, yu.m.barabash, i.v.tarshinov. inter.cong. of phot.sci., v2, sec.5, drezden, p.145, 1974.
13. Находкин Н.Г. Сборник "Способы записи информации на бессеребряных носителях", Киев, 1, 8-62, 1969.
14. Находкин Н.Г., Бутенко А.Д. Сборник "Способы записи информации на бессеребряных носителях", Киев, 2, 15, 1970.
15. Находкин Н.Г., Бутенко А.Д., Труды международного конгресса по фотографической науке , секция Е, М., стр.177-180, 1970.
16. Бутенко А.Д.. Шевляков Ю.А. Сборник "Способы записи информации на бессервбряных носителях", Киев, 4, 95-100, 1973.
17. Гущо Ю.П. Фазовая рельефография, Энергия, 106, 1974.
18. t.l.credelle, f.w.spong. rca rev., 33, 1, 1972.

