ВЛИЯНИЕ НЕЛИНЕЙНОСТИ ФАЗОЭКСПОЗИЦИОННОЙ ХАРАКТЕРИСТИКИ*) РЕГИСТРИРУЮЩЕГО МАТТЕРИАЛА НА КАЧЕСТВО ГОЛОГРАФИЧЕСКОГО ПРОЦЕССА
О.В.Рожков
На базе ранее описанной /1/ методики и модели исследуется изменение качества изображения диффузного объекта, восстанавливаемого с тонкой фазовой голограмчы, зарегистрированной в среде с нелинейным откликом; при этом основное внимание уделено резкому возрастанию интермодуляционного шума. Анализу предпослано рассмотрение вопроса о линейности "поведения" регистрирующей среды, т.е. пригодности (фазо) экспозиционной характеристики для расчета фазовых набегов, возникающих в любой точке голограммы (сложного объекта). Применение одного из голографических способов уточнения параметров фазоэкспозиционной кривой иллюстрируется на примере фоторезиста Шипли az - 1350.
Указывается, что в рассматриваемом случае получение высококонтрастного изображения гарантирует удовлетворительные линейные искажения в воспроизведении градаций (яркости) серого.
В /1/ была изложена общая методика оценки качества голографического процесса с помощью пространственной параметрической кривой "коэффициент нелинейности - дифракционная эффективность-отношение сигнал-шум" (или ее плоских проекций в координатах
"коэффициент нелинейности кн - дифракционная эффективность η и "отношение сигнал/шум ( s/n )Σ - дифракционная эффективность ηΣ"). Эта методика была проиллюстрирована на целом ряде регистрирующих материалов, причем, наиболее полно была рассмотрена тонкая фазомодулирующая среда с линейным откликом, т.е. с линейной экспозиционной кривой.
Как следует из нижней части рис.4 (см/1/), в случае такой регистрирующей среды (с линейной фазоэкспозиционной характеристикой) при разумном выборе r(>1) можно ожидать умеренный (кн≈0,5) ;спад яркостей наиболее светлых участков голографируемого (диффузного) объекта вплоть до предельно достижимых дифракционных эффективностей ηΣ=14÷20%. Åсли же ограничиться значениями ηΣ<0,1, то линейные искажения в воспроизведении градаций серого практически будут незаметны (кн>0,8).
Отношение сигнал/шум ( s/n )Σ, характеризующее контраст восстановленного изображения (диффузного) объекта, зарегистрированного в тонкой фазомодулирующей среда с линейным откликом, также весьма высоко, что иллюстрируется верхней частью рис.4 в /1/. Так, например, при дифракционной эффективности ηΣ < 10% отношение сигнал/шум ( s/n )Σ численно равно*) отношению (ηΣ/r)-1 (где r - отношение интенсивностей опорного и предметного пучков). Таким образом, для получения отличного (для зрителя) контраста (когда ( s/n ) > 102 /4/) достаточно обеспечить на стадии записи r ≥ 102 ∙ ηΣ, что при 10-процентной дифракционной эффективности потребует r ≥ 10. Удовлетворительное качество (в смысле зашумленности интермодуляционными
помехами /1/) соответствует ( s/n ) ≈ 20 /4/, т.е. обеспечивается линейной фазомодуляционной средой уже при r≥2 и ηΣ≈ 0,1. С другой стороны, получение предельно достижимых значений ( ~ 22%) дифракционной эффективности тонкой фазовой голограммы (диффузного объекта), зарегистрированной в среде с линейным откликом, несколько повышает требования к величине r. Для отличного контраста требуется r≈102, тогда как для удовлетворительного-достаточно r≈20.
В то же время известные экспериментальные данные /3/ существенно отличаются от рассчитанных по /1/ результатов в сторону резкого уменьшения контраста и почти полного исчезновения его зависимости от r (соотношения интенсивностей опорного и сигнального пучков). Хотя существует целый ряд технических (непринципиальных) причин, за счет которых можно, по крайней мере, качественно объяснить резкое ухудшение отношения сигнал/шум (например, в /5/ контраст исходного тест-объекта составлял всего лишь 1:40), однако при достаточно чистом эксперименте /3/ существенную роль может играть такая принципиальная причина, как нелинейность отклика фазомодулирующей среды./6/.
i. Описание регистрирующей среды
Как уже упоминалось, основной характеристикой регистрирующей среды является экспозиционная кривая, которая обычно снимается экспериментально (на нулевой пространственной частоте) и описывает зависимость вносимых данной средой (после экспонирования и обработки) амплитудных или фазовых*) искажений от экспозиции Е. В то же время для голографии (и некоторых других процессов - например, фотографии с пространственной поднесущей /7/) существенно наличие несущей пространственной частоты. С тем, чтобы обойти это несоответствие, обычно априори полага-
ют, что не происходит изменения формы, снятой на нулевой пространственной частоте экспозиционной кривой (т.е. поведение регистрирующей среды линейно), а по мере роста несущей частоты в большей или меньшей степени изменяется (обычно-уменьшается) чувствительность при записи синусоидального распределения интенсивности (точнее-экспозиции).
Такое изменение (обычно-падение) чувствительности характеризуется модуляционной передаточной функцией (МПФ) регистрирующего материала, которая, однако, имеет смысл только для линейного участка экспозиционной кривой.
Таким образом, регистрирующая среда может быть описана либо:
1) нелинейной экспозиционной кривой, снятой на нулевой пространственной частоте (при наличии горизонтального участка МПФ во всем рабочем диапазоне частот); либо
2) МПФ - но только для линейного участка экспозиционной кривой.
Первым способом удобно описать идеальный (бесконечно монодисперсный и бесконечно тонкий) фото (химический) материал, имеющий значительный горизонтальный участок на МПФ и крутой спад ее после νпред. Удовлетворительной иллюстрацией такой формы МПФ служат галлоидосеребряные фотоэмульсии Кодак-649 и позитивного фоторезиста Шипли Аz - 1350 /3/.
Использование второго способа описания регистрирующей среды (с помощью МПФ) удобно для такой сравнительно экзотической регистрирующей среды, как фототермопластики (на начальном участке рельефоэкспозиционной кривой), где изменением условий "обработки" можно существенно менять как полуширину (полосы частот), так и центральную (квазирезонансную) частоту МПФ /8/. Однако при таком описании входное воздействие (экспозиция) должно быть разложено на гармонические составляющие, что в целом ряде случаев оказывается затруднительным. В то же время при первом способе описания экспозиция может быть описана в произвольном виде, что, безусловно, весьма удобно.
ii. Уточнение формы экспозиционной кривой
регистрирующего материала
В целом ряде случаев (например, для фоторезистов, см. рис.2в /3/) оказывается затруднительным достаточно точное снятие экспозиционной кривой. Кроме того, всегда желательно иметь подтверждение того априорного предположения, что поведение регистрирующей среды линейно. В простейшем случае (для горизонтального участка МПФ) это означает, что снятая на нулевой пространственной частоте экспозиционная кривая достаточно пригодна для других пространственных частот (и их совокупности).
Одним из возможных путей решения этих двух вопросов (уточнения формы экспозиционной кривой и проверки линейности поведения регистрирующей среды) является сравнение зависимостей дифракционной эффективности голограммы (двух плоских волн), полученных экспериментально и теоретически. Проиллюстрируем это на примере тонкой фазомодулирующей среды (хотя подобное рассмотрение можно провести и для других типов регистрирующих сред).
Пусть фазоэкспозиционная кривая имеет вид:
где δакс - максимально достижимые фазовые искажения, δn и Е1 - смещение точки перегиба аппроксимирующей функции f, соответственно, вверх и вправо от начала координат, Е0 -константа экспозиции, такая, что δмакс-δn=f(∞)Е0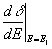 .
.
Поскольку поле двух плоских волн создает распределение экспозиции
e(x)=eср[1+cos(2πνx)], (2)
где eсред = Еr + Еs = τ(r2 + s2)- средняя'экспозиция,
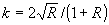 - контраст интерференционной картины,
- контраст интерференционной картины,
r = Еr/Еs =(r/s)2 отношение интеясивностей (плоских) волн,
то фазовые искажения, вносимые рассматриваемой; голограммой (пос-
ле обработки), можно представить в виде:
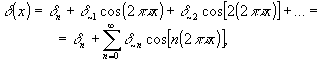 (3)
(3)
где
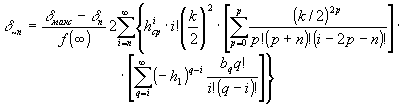 (4)
(4)
bq - коэффициент в разложении функции f в степенной ряд hср=eср/e0; h1=e1/e0 - нормированные экспозиции, Р =[2i-2n+(-1)i+n-1]/4). Обобщая модель голограммы в виде трех наложенных друг на друга субголограмм (см.рис.3в /1/) на случай бесконечного числа парциальных субголограмм (см. /6/, а также рис.3в /1/) каждая из которых представляет из себя косинусоидальную фазовую решетку с пространственной частотой (nν) θ (половинными) фазовыми искажениями δ~n, можно представить дифракционную эффективность тонкой фазовой голограммы двух плоских волн в виде
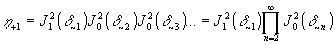 . (5)
. (5)
Совпадение формы и абсолютных значений η+1(hср; h1) с экспериментальной кривой η+1(Еcp) позволяет уточнить нормированный параметр экспозиционной кривой h1=Е1/Е0, (для чего, естественно, надо рассчитать несколько кривых η+1(hcp) при h1, близких к отношению Е1/Е0, даваемому экспозиционной кривой) и константу экспозиции Е0, которая вычисляется из соотношения масштабов на совпадающих кривых η+1(hcp) и η+1(Еcp). Таким способом были уточнены параметры рельефоэкспозиционной кривой фоторезиста Шипли Аz - 1350, обработанного в течение 20 с в проявителе А-303 при 25°С (кривая 1 на рис.2в /3/). Оказывается, что если глубина рельефа (в мкм) зависит от экспозиции Е (в мДж/см2 для λ= 0,44 мкм) как
-Δ(Ε)=0,55+0,45th(0,025Е-0,6), (6)
то расчетная дифракционная эффективность (при показателе преломления фоторезиста n ≈ 1,7 /3/) совпадает с экспериментальными кривыми η+1(Еcp), что иллюстрируется рис.1. Фирменная обработка того же фоторезиста (проявитель Аz -1350, 25°С, 20с) лишь увеличивает величину Е1 до 80мДж/cм2, что соответствует кривой 2 на рис.2 (см. /3/) и рис.7 (см. /5/).
Более уверенно о линейности поведения регистрирующей среды можно говорить при совпадении экспериментальных и расчетных зависимостей дифракционных эффективностей голограммы трех плоских волн /9/.
Поскольку линейность поведения интересует нас в основном для корректного описания регистрирующей среды при рассмотрении вопроса об интермодуляционном шуме (см. iii), то проверку линейности поведения целесообразно проводить при больших значениях (отношения интенсивности опорного пучка к сигнальному) r.
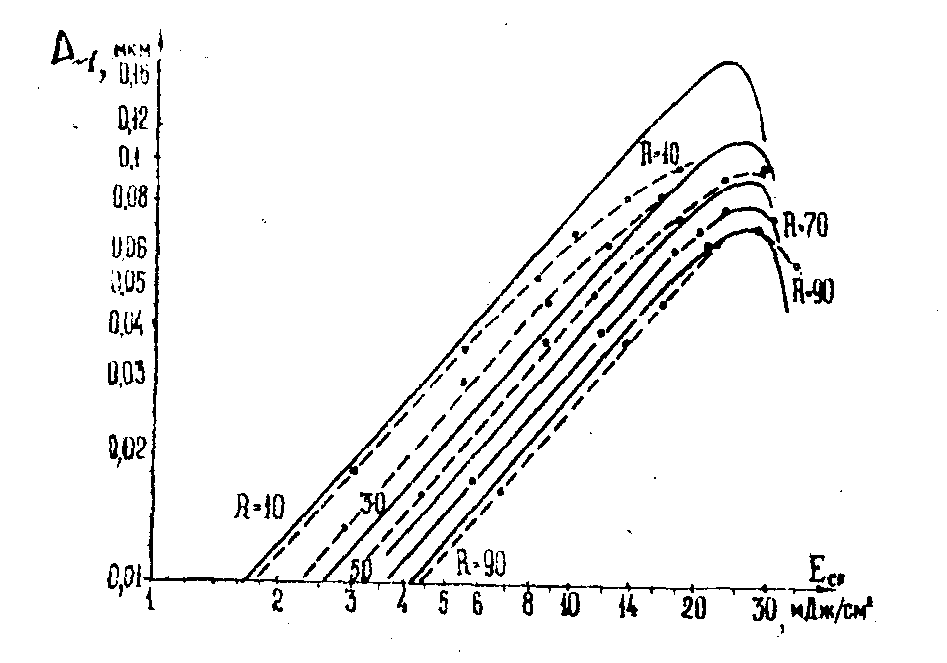
Рис.1. Экспериментальные /3/ (λ = 0,63 мкм, n = 1,7) и теоретические зависимости высоты рельефа Δ~1 основной решетки голограммы двух плоских волн, зарегистрированной в фоторезисте Шипли Аz -1350, описываемом ур.(6).
Если экспериментальная зависимость η+1(Еcp) снята при достаточно больших значениях r, то ее можно приме-
нить для непосредственного "синтезирования" фазо-экспозиционной кривой, соответствующей ненулевой (несущей) пространственной частоте, используя тот тривиальный факт, что 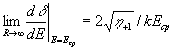 . Хотя таким образом нельзя найти начальное значение фазовых искажений δ(0)=δ(Ε)|Е=0, для фазомодулирующих сред это обычно не имеет значения.
. Хотя таким образом нельзя найти начальное значение фазовых искажений δ(0)=δ(Ε)|Е=0, для фазомодулирующих сред это обычно не имеет значения.
iii. Интермодуляционный шум тонких базовых голограмм, зарегистрировенных в среде с нелинейним откликом
Имея уточненное описание фазоэкспозиционной кривой регистрирующего материала и большую или меньшую уверенность в линейности его поведения, можно аналитически рассмотреть вопрос об интермодуляционном шуме /1/ тонкой фазовой голограммы при нелинейном отклике /6/. При этой следует четко представлять, что, как показано в /1,3/, этот вид нелинейных искажений изображения, восстанавливаемого с тонкой фазовой голограммы, является принципиально неустранимым в силу специфики данного типа голограмм, связанного с нелинейностью самой фазовой модуляции как таковой. Лишь использование третьего измерения регистркрувцей среды (толстые фазовые голограмиы) позволяет ослабить влияние интермодуляционного шума за счет "самофильграция", воникающей из-за наличия сильно выраженного эффекта Брэгга /10/.
Не лишне также напомнить, что под интермодулнциоывым шумом в /1/ и здесь подразумевается усредненное по площади причинно-обусловленное интермодуляционное изображение (духи, phantom). При этом для вычисления такого усредненного шума необходимо знание лишь статистики сигнальной волны, тогда как для расчета интермодуляционного изображения требуется ее полное описание (с учетом фазового распределения), что при современной состоянии ЭЦВМ позволяет рассчитывать интермодуляционные изображения лишь простых регулярных объектов (например, матрицы излучателей в оптических ЗУ /11/).
В неиболее общем случае суммарная экспозиция в плоскости голограммы х(х,у) может быть записана как Е(х)=Еr(х)+Еs(x)+Еrs(х), где er=τr2- экспозиция опорного пуч-
ка (τ - время экспозиции), Еs - экспозиция сигнального пучка, ers - интерференционный член. Для объекта, состоящего из М точек (см.рис.2), каждая из которых создает в плоскости голограммы поле 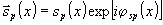 , экспозиция сигнального пучка
, экспозиция сигнального пучка
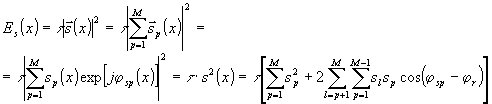 , (7)
, (7)
а интерференционный член (при опорной волне) 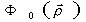 .
.
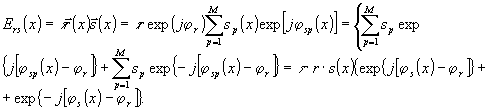 (8)
(8)
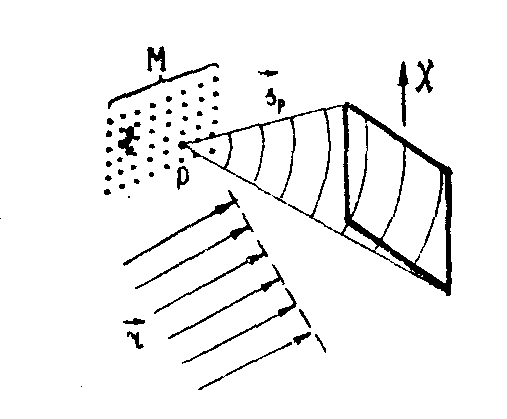
Рис. 2 .
Запись голограммы многоточечного
(в том числе и диффузного) объекта.
В результате после голографирования такого объекта и обработки тонкой регистрирующей среды, характеризуемой фазоэкспозиционной кривой (1), фазовый сдвиг, вносимый голограммой в точке с координатами Х(х, у), можно представить в виде
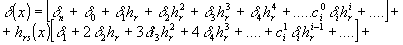
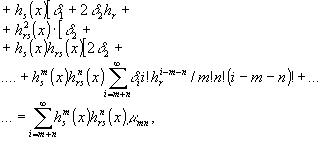 (9)
(9)
где hr=er/e0; hrs(x)=ers(x)/e0; hs(x)=es(x)/e0 - нормированные экспозиции,
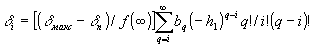 , (10)
, (10)
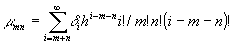 - чувствительность к нормированным экспозициям при регистрации "mn" - ной (парциально) субголограммы. На основании (10) можно выделить три составляющие фазового сдвига.
- чувствительность к нормированным экспозициям при регистрации "mn" - ной (парциально) субголограммы. На основании (10) можно выделить три составляющие фазового сдвига.
1. Постоянный для данной голограммы фазовый сдвиг (первая строка (9), соответствующая m=n=0);
2. Фазовый сдвиг, несущий информацию о предметной волне (вторая строка (9), соответствующая m=0, n=1);
3. Фазовый сдвиг, обусловленный взаимной интерференцией точек объекта друг с другом (третья и последующие строки с m>1). Тогда процесс реконструкции такой (тонкой фазовой) голограммы можно рассматривать как взаимодействие восстанавливающей волны 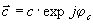 с совокупностью трех наложенных друг на друга фазовых фильтров - фильтром, вносящим постоянный фазовый сдвиг, информационной субголограммой и шумовой субголограммой (см.рис.3). Если φc=φr и шумовая субголограмма отсутствует, то информационная субголограмма с амплитудным коэффициентом про-
с совокупностью трех наложенных друг на друга фазовых фильтров - фильтром, вносящим постоянный фазовый сдвиг, информационной субголограммой и шумовой субголограммой (см.рис.3). Если φc=φr и шумовая субголограмма отсутствует, то информационная субголограмма с амплитудным коэффициентом про-
пускания
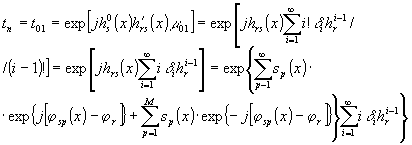 (11)
(11)
восстанавливает основную и сопряженную предметные волны.
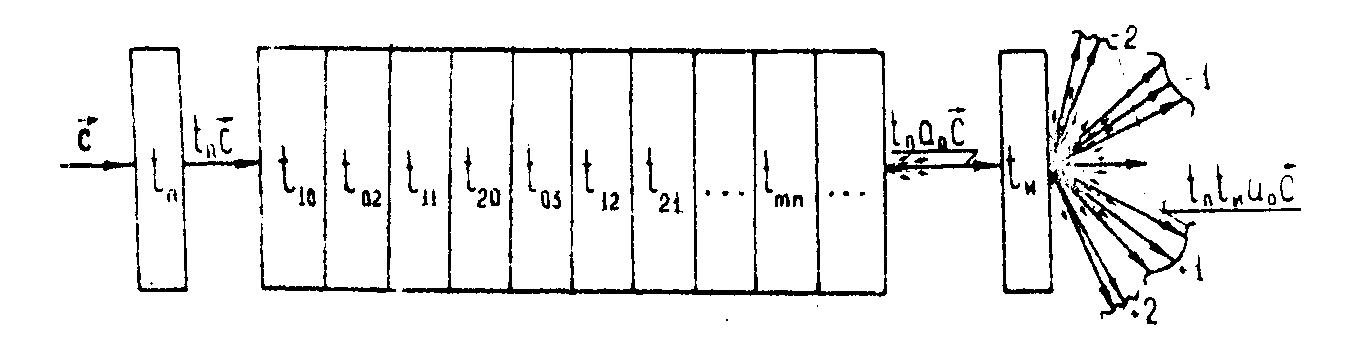
Рис.3. Модель для анализа тонкой фазовой голограммы,
зарегистрированной в среде с нелинейным откликом.
В свою очередь, шумовая субголограмма может быть представлена (как показано на рис.3) в виде набора парциальных шумовых субголограмм, т.к. ее амплитудный коэффициент пропускания
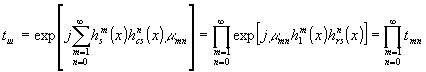 . (12)
. (12)
Наличие квадратичной составляющей (b2≠0) в отклике регистрирующей среды приводит к увеличению количества парциальных шумовых субголограмм с 1 при линейном (bq|q>1=0) отклике до 4. Кубическая составляющая индуцирует уже 8 парциальных шумовых субголограмм и т.д. (12; 17; 23; ...). В результате для модели рассматриваемой голограммы (см.рис.3) нерассеянная часть плоской волны, участвующая в восстановлении информационной субголограммы, имеет вид (см.(24) и (26) /1/):
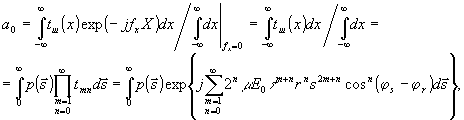 (13)
(13)
где 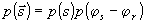 - плотность распределения вероятности сигнальной волны в плоскости голографирования. В частном случае линейного отклика (
- плотность распределения вероятности сигнальной волны в плоскости голографирования. В частном случае линейного отклика (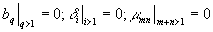 ) (13) принимает известный /1,5/ вид:
) (13) принимает известный /1,5/ вид:
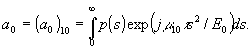 (14)
(14)
С другой стороны, поскольку мы условились понимать под интермодуляционным шумом усредненное (по площади) интермодуляционное изображение, то такое усреднение можно проводить как во всей шумовой субголограмме сразу (см.вторую строку в (13)), так и в каждой отдельной "mn" -ной парциальной шумовой субголограмме, для которой нерассеянная часть(плоской) восстанавливающей волны
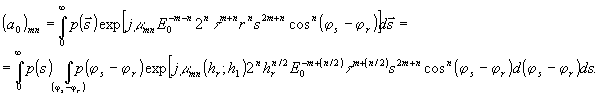 (15)
(15)
При таком представлении пропускание (по интенсивности) всего набора парциальных шумовых субголограмм, т.е. шумовой субголограммы,
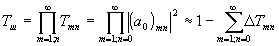 (16)
(16)
(где Δtmn=1-tmn=[l-|(a0)mn|2]<<1 - для высококонтрасткого изображения, а именно такое интересует нас), а отношение сигнал/шум /1,10/
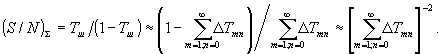 (17)
(17)
Из (17) отчетливо видно, что любая нелинейность (фазо) экспозиционной кривой вызывает ухудшение контраста восстановленного (с тонкой фазовой голограммы) изображения, поскольку каждая ΔТmn является действительным положительным числом (или нулем).
Наиболее общим методом вычисления (a0)mn является численное интегрирование, хотя часто задача может быть решена анали-
тически. Так, при релеевском распределении плотности вероятности амплитуды сигнальной волны /1,10/, когда 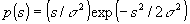 , и равновероятном распределении фазы сигнальной волны оказывается возможным провести аналитическое вычисление всех (а0)mn, за исключением (а0)mn, при m ≥ 3. При этом, если для вычисления (а0)mn первых парциальных шумовых субголограмм имеются табличные интегралы (часто содержащие специальные функции), то для вычисления (a0)mn парциальных шумовых субголограмм с более высокими номерами приходится использовать разложение косинуса и синуса в степенной ряд. Часть результатов приведено в таблице, где a mn =μ mn hrm+n /
, и равновероятном распределении фазы сигнальной волны оказывается возможным провести аналитическое вычисление всех (а0)mn, за исключением (а0)mn, при m ≥ 3. При этом, если для вычисления (а0)mn первых парциальных шумовых субголограмм имеются табличные интегралы (часто содержащие специальные функции), то для вычисления (a0)mn парциальных шумовых субголограмм с более высокими номерами приходится использовать разложение косинуса и синуса в степенной ряд. Часть результатов приведено в таблице, где a mn =μ mn hrm+n /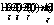 .
.
Таблица
|
m
|
n
|
(a0)mn
по (15) для диффузного
объекта
|
amn
|
|
1
|
0
|
1/(1-ja10)
|
μ10hr/r
|
|
0
1
2
|
2
1
0
|
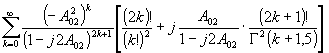
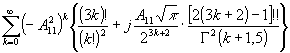
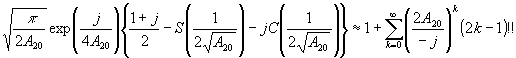
|
μ02hr2/r
μ11hr2/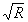
|
|
0
1
2
3
|
3
2
1
0
|
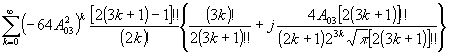
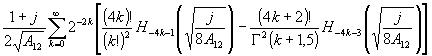
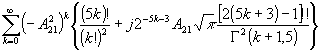
интеграл не берется
|
μ03hr2/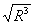
μ12hr3/r2
μ21hr3/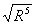
μ30hr3/r3
|
|
0
|
4
|
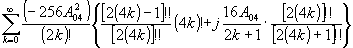
|
μ04hr4/r2
|
Существенно, что ввиду комплексности полученных выражений для
(а0)mn вычисление значений Тmn = |(a0)mn|2 можно проводить только в численном виде (при использовании ЭВМ наиболее удобен язык Фортран-4).
Для построения (плоской) параметрической кривой "отношение сигнал/шум (s/n)Σ - дифракционная эффективность ηΣ "достаточно вычислить ряд значений (s/n)Σ по (17) и (ηΣ/tn) = tШexp(-2μ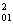 h
h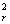 /r)i1(2μ
/r)i1(2μ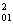 h
h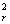 /r) для соответственно выбранных значений нормированной экспозиции опорного пучка hr = τr2/e0=er/e0 при интересующем значении r=er/<es>. В случае необходимости можно построить семейство параметрических кривых (s/n)Σ - - (ηΣ/tr) при разных значениях r.
/r) для соответственно выбранных значений нормированной экспозиции опорного пучка hr = τr2/e0=er/e0 при интересующем значении r=er/<es>. В случае необходимости можно построить семейство параметрических кривых (s/n)Σ - - (ηΣ/tr) при разных значениях r.
iv. Нелинейные искажения при воспроизведении градаций в восстановленном изображении
Как уже указывалось в /3,6/, интермодуляционный шум является наиболее чувствительным к нелинейности фазоэкспозиционной кривой тонкого регистрирующего материала. В результате анализа как теоретических (см. Ш и /6/), так и экспериментальных /3,5/ данных можно считать, что при получении высококонтрастного восстановленного изображения нелинейные искажения в передаче градаций серого (т.е. яркости) голографируемого объекта не будут заметно отличаться от таковых (см.нижнюю часть рис.4 в /1/) для тонкой регистрирующей среды с линейной фазоэкспозиционной характеристикой (хотя возможно не только уменьшение κн, но и его увеличение, т.е. уменьшение нелинейных искажений за счет частичной компенсации собственной нелинейности тонкой фазовой голограммы, возникающей /1,3/ на стадии восстановления регистрирующей среды, о чем упоминалось в /1/ при рассмотрении реального фото термопластика). В силу этого подробный анализ нелинейных искажений (в передаче градаций серого) вряд ли целесообразен, тем более, что на практике /3/ изменение формы (линеаризация) фазоэкспозиционной кривой обычно используется для получения максимального значения отношения сигнал/шум, в силу чего отсутствует возможность минимизации нелинейных искажений.
Таким образом, малейшая нелинейность фазоэкспозицхонной характеристики тонкого регистрирующего материала приводит к резкому
падению контраста восстанавливаемого с голограммы изображения диффузного объекта, тогда как нелинейные искажения в передаче градаций (яркости) серого оотаются удовлетворительными.
Литература
1. В.Б.Немтинов, О.В.Рожков. Метод оценки качества голографического процесса. Материалы iv Всесоюзной школы по голографии, Л., 191÷211, 1974.
2. Дж.Гудмен. Введение в фурье-оптику, Мир, М., 1970.
3. Нелинейные искаженна и интермодуляционный шум рельефно-фазовых голограмм, записанных на фоторезисте, ЭИ ФКА, НиПФ, №23, (реф.95), стр. 1÷13, 1974.
4. У.Дж.Хэннэн. Голографические кинофильмы, получаемые тиснением. Техника кино и телевидения, №8, 43÷51, 1973.
5. f.iwata, j.tsujiuchi. characteristics of a photoresist hologram and its replica. appl.opt., 13, 6, 1327, 1974.
6. В.Б.Немтинов, О.В.Рожков. Интермодуляционные искажения тонких фазовых голограмм, обусловленные нелинейностью отклика регистрирующей среды. В сб. "Оптическая голография и ее применение", ЛДНТП, Л., стр.96, 1974.
7. Н.Г.Власов, Г.В.Скроцкий. Фотография с пространственной несущей и голография. Материалы vi Всесоюзной школы по голографии., стр.165-175, 1974.
8. Н.Г.Находкин и др. Управляемые фазовые термопластические среды для регистрации и обработки информации. В 5 вып. сб. "Способы записи информации на бессеребояных носителях", "Высш.школа", К., стр.3-19, 1974.
9. j.a.jenny. nonlinearlties of photopolimer holographic recording materials. appl.opt., 11, 6, 1371, 1972.
10. j.upatnieks, c.leinard. efficiency and images/Image contrast of dielectric holograms. josa, 60, 3, 297, 1970.
11. В.hill. point efficiency and signal-to-background ratio in exponential holograms for optical memories. appl.opt., 11, 12, 2937, 1972.

