|
|
 |
 |

|
| |
ОЦЕНКА ПОГРЕШНОСТЕЙ ИЗНЕРЕНИЙ В ГОЛОГРАФИЧЕСКОЙ ИНТЕРФЕРОМЕТРИИ ОТРАЖАЮЩИХ ОБЪЕКТОВ
Н.Г.Власов. А.Е.Штанько
Проанализированы основные источники погрешности измерения смещений поверхности диффузно-отражакщих объектов методом голографической интерферометрии. Получены зависимости погрешности определения смещения от погрешности непосредственно измеряемых величин. Отмечено наличие систематической погрешности измерения, обусловленной усреднением интерференционной картины по апертуре регистрирующей оптической системы, получена ее зависимость от апертуры и вектора смещения, а также указан способ ее учета. Дня конкретной голографической схемы получены оценки среднеквадратичной погрешности определения смещений.
Процесс голографическвх интерференционных измерений в общем случае состоит из двух операций:
1. измерение порядковых номеров интерференционных полос (включая дробную часть номера) в точках объекта с заданными координатами, либо измерение координат центров интерференционных полос на восстановленном изображении объекта;
2. фиксация в выбранной для расчета системе координат направлений освещения и наблюдения исследуемых точек объекта, т.е. измерение углов, составляемых этими направлениями с осями координат (эта операция, в частности, может сводиться к измерению координат освещающего источника, исследуемых точек объекта и точек наблюдения и дальнейшему вычислению направляющих косинусов указанных направлений /1/).
Погрешности голографических интерференционных измерений обусловлены погрешностью, с которой выполняются измерения в каждой из отмеченных выше операций /2/. В дальнейшем изложении остано-
вимся на оценке погрешности измерения смещений поверхности диффузно отражающих объектов при различных воздействиях. Измерение смещений в голографической интерферометрии заключается в расчете трех проекций вектора смещения в исследуемых точках поверхности объекта. Рассмотрим последовательно влияние на погрешность определения смещений диффузно отражающих объектов: а) погрешности измерения порядковых номеров интерференционных полос (либо координат центров полос), б) погрешности измерения углов освещения и наблюдения исследуемого объекта.
а) Пусть среднеквадратичная ошибка измерения порядковых номеров интерференционных полос в исследуемых точках объекта равна σ ni. Связь между вектором смещения 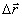 исследуемой точки и порядковыми номерами интерференционных полос n1, n2, n3, наблюдаемых в этой точке по трем различным направлениям, выражается системой из трех линейных алгебраических уравнений /1/. В матричном виде эта система имеет вид: исследуемой точки и порядковыми номерами интерференционных полос n1, n2, n3, наблюдаемых в этой точке по трем различным направлениям, выражается системой из трех линейных алгебраических уравнений /1/. В матричном виде эта система имеет вид:
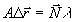 , (1) , (1)
где А - матрица коэффициентов при неизвестных данной системы уравнений, 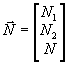 . .
Считая, что ошибки распределены по нормальному закону и, следовательно, при сложении случайных, величин их дисперсии складываются, получим, что среднеквадратичная погрешность 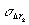 определенная К-ой проекции вектора определенная К-ой проекции вектора 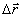 равна равна
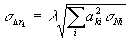 , (2) , (2)
где 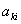 - элементы матрицы А-1 обратной по отношению к матрице А; индексом к, принимающим значения 1, 2, 3 пронумерованы оси координат х, у и z, соответственно. Считая, что - элементы матрицы А-1 обратной по отношению к матрице А; индексом к, принимающим значения 1, 2, 3 пронумерованы оси координат х, у и z, соответственно. Считая, что 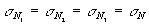 , из формулы (2) получаем , из формулы (2) получаем
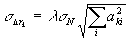 . (3) . (3)
Таким образом, сумма квадратов элементов строки матрицы А -1 определяет степень влияния погрешностей в измерении n на погрешность определения соответствующей проекции вектора 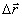 . .
Погрешность измерения порядкового номера полос обусловлена несколькими причинами, из которых наиболее существенными являются:
1. аппаратурная погрешность системы, регистрирующей положение полос или дробную часть их номера;
2. погрешность, обусловленная случайными флуктуациями интенсивности и разности фаз интерферирующих волновых полей, характерными для диффузно-когерентного излучения;
3. погрешность интерполирования порядкового номера интерференционных полос на интервал, лежащий между центрами соседних полос (такое интерполирование необходимо, так как координаты максимумов интерференционных полос, вообще говоря, не совпадают с координатами точек объекта, в которых рассчитываются перемещения).
Величина 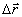 , как правило, лежит в пределах от 0,1 до нескольких десятых долей полосы. Имеется сообщение об измерении n с точностью ~ 0,01 полосы /3/. , как правило, лежит в пределах от 0,1 до нескольких десятых долей полосы. Имеется сообщение об измерении n с точностью ~ 0,01 полосы /3/.
б) Из (1) следует, что порядки интерференционных полос зависят от направления освещения 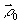 и наблюдения и наблюдения 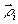 исследуемой точки объекта ( исследуемой точки объекта (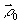 и и 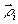 определяют элемента матрицы А). Эта зависимость имеет вид: определяют элемента матрицы А). Эта зависимость имеет вид:
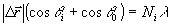 , (4) , (4)
где θ i и θ0 - углы, составляемые вектором 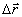 с единичными векторами с единичными векторами 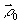 и и 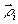 , соответственно. Дифференцируя (4) получим: , соответственно. Дифференцируя (4) получим:
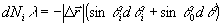 . (5) . (5)
Из (5) следует, что погрешностям измерения углов наблюдения и освещения dθi и dθ0 эквивалентна некоторая определенная погрешность dni измерения порядкового номера интерференцион-
ных полос. Воспользовавшись этим, определим влияние погрешностей измерения углов на погрешность определения проекций вектора смещения 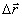 . Из (5) . Из (5)
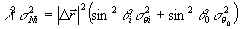 , (6) , (6)
где 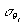 и и 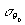 - среднеквадратичные погрешности измерения углов наблюдения и освещения, соответственно; - среднеквадратичные погрешности измерения углов наблюдения и освещения, соответственно; 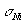 - эквивалентная им среднеквадратичная погрешность измерения порядкового номера интерференционных полос. Учитывая (1) по аналогии с (2) для среднеквадратичной погрешности - эквивалентная им среднеквадратичная погрешность измерения порядкового номера интерференционных полос. Учитывая (1) по аналогии с (2) для среднеквадратичной погрешности 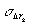 определения К-ой проекций вектора определения К-ой проекций вектора 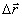 , имеем: , имеем:
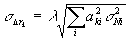 . (7) . (7)
В отличие от приводе иных в работе /2/ приближенных оценок погрешностей, учитывающих случай самого неблагоприятного расположения вектора смещения относительно направлений наблюдения и освещения, формулы (6), (7) дают точную оцзнку погрешностей для любого конкретного расположения вектора 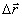 . Приближенную оценку погрешности отдельных проекций вектора смещения можно получить, принимая . Приближенную оценку погрешности отдельных проекций вектора смещения можно получить, принимая 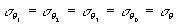 и заменяя sinθi и sinθ0 на 1. Тогда из (6,7) и заменяя sinθi и sinθ0 на 1. Тогда из (6,7)
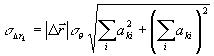 . (8) . (8)
Первое слагаемое (8) характеризует вклад, вносимый в 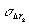 ошибками определения направлений наблюдения, второе слагаемое - ошибками определения направления освещения. ошибками определения направлений наблюдения, второе слагаемое - ошибками определения направления освещения.
В отличие от рассмотренной ранее погрешности измерения порядковых номеров интерференционных полос вклад, вносимый погрешностью определения направлений освещения и наблюдения, пропорционален модулю измеряемого вектора смещения. Основными источниками этой погрешности являются:
1. погрешность угловых или линейных измерительных инструментов;
2. конечные размеры апертуры оптической системы, с помощью которой производится наблюдение интерференционной картины на восстановленном изображении.
Последний фактор приводит к тому, что наблюдаемая интерференционная картина является суммой интерференционных картин, построенных лучами различньд направлений, попадающих во входной зрачок оптической системы. При этом в результирующей картине положение интерференционных полос будет соответствовать некоторому направлению наблвдения, в общем случае не совпадающему с центральным лучом входного зрачка оптической системы. Если при вычислении вектора смещения 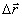 считать, что направлением наблвдения является центральный луч зрачка, то возникает систематическая ошибка измерения порядковых номеров интерференционных полос, зависящая от апертуры регистрирующей оптической системы, а также от величины и направления вектора смещения считать, что направлением наблвдения является центральный луч зрачка, то возникает систематическая ошибка измерения порядковых номеров интерференционных полос, зависящая от апертуры регистрирующей оптической системы, а также от величины и направления вектора смещения 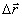 . Найдем эту зависимость. . Найдем эту зависимость.
Предположим, что изображение, восстановленное голограммой, заданной методом двойной экспозиции, наблюдают с помощью оптической системы, сфокусированной на некоторую точку 0 диффузного объекта, лежащую на оси оптической системы. Введем сферическую систему координат с началом координат в точке 0 (рис.1). Вклад в интенсивность ее изображения, определяемый излучением, проходящим через бесконечно малый элемент s апертуры с телесным углом Ψ=ξdξdη μожно выразить:
i( ξ,η)=i0Ψ+iΨcos{kΔπ[cosξ cosξ0+sin ξ sinξ0 cos( η-η0)]+φ}, (9)
где i0 - константа, пропорциональная яркости точки 0 на восстановленном изображении объекта; k - волновой вектор излучения; Δr - модуль вектора смещения; ξ, η - угловые координаты алемента s апертура; ξ0, η0 - угловые координчты вектора смещения; φ - разность фаз волновых полей, освещающих точку О в смещенном и несмещенном положениях. В формуле (9) аргумент косинуса в фигурных скобках представляет собой разность фаз волно-
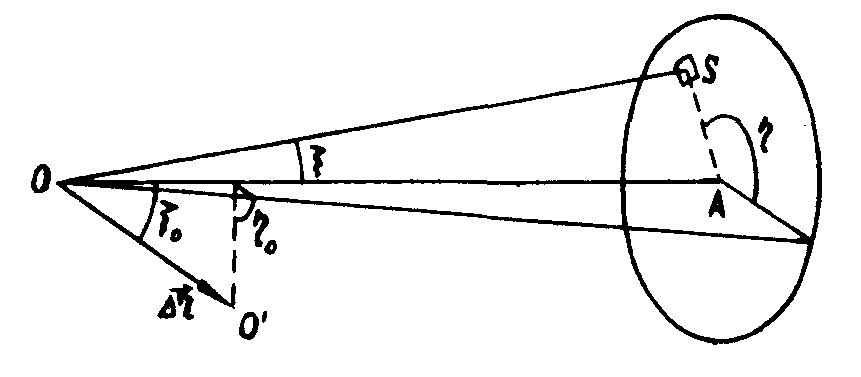
Рис.1. К рассмотрению усреднения интерференционной картины по апертуре оптической системы. ОА - ось оптической системы; О'- смещенное положение точки О; ξ , η - σгловые координаты элемента s апертуры; ξ0, η0 - угловые координаты вектора смещения 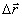 . .
вых полей, рассеянных точкой О в двух положениях в направлении, определяемом углами ξ и η . Для удобства дальнейших операций представим i(ξ, η) β виде
i( ξ,η)=i0Ψ+i0Ψ re exp{ikΔr[cosξ cosξ0+sin ξ sinξ0 cos( η-η0)]+iφ}. (10)
Как было показано в нашей предыдущей лекции на этой школе, для того чтобы учесть случайную зависимость диффузно-когерентных волновых полей от пространственных координат при описании интерференционных эффектов, целесообразно ввести усреднение по пространству. В дальнейшем под i(ξ ,η) αудем понимать интенсивность, усредненную в плоскости изображения по некоторому направлению, для которого 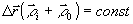 . Полная интенсивность i изображения точки o, построенного оптической системой, будет равна: . Полная интенсивность i изображения точки o, построенного оптической системой, будет равна:
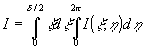 , (11) , (11)
где δ - угловая апертура оптической системы.
В ( 11) не входит взаимная интенсивность, образованная наложением волновых полей, прошедших через различные участки апертуры, т.к. при указанном выше усреднении она стремится к нулю.
Сделаем вполне оправданное для голографиче cкой интерферометрии предположение, что апертура оптической системы невелика (в противном случае контракт интерференционных полос будет низким). Тогда, заменяя в (10) cosξ на 1-ξ2/2 и используя интегральное представление функций Бесcеля /4/ из (10), (11), получим:
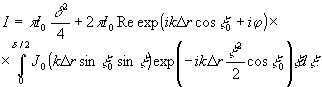 (12) (12)
Рассмотрим случай очень малых апертур. При δ→0 из (12)
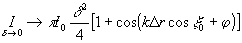 . (13) . (13)
Как видно из выражения (13), фаза интерференционной картины в рассматриваемой точке o соответствует геометрической разности хода лучей, распространяющихся по оси оптической системы. В общем случае, описываемом выражением (12), к фазе, обусловленной этой геометрической разностью хода и равной аргументу ехр, стоящей перед интегралом, добавляется некоторая дополнительная фаза α,
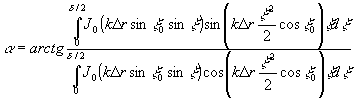 (14) (14)
которая, как следует из (14), зависит от апертуры оптической системы и вектора смещения и 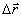 . Об этой дополнительной фазе упоминалось в нашей предыдущей лекции на этой школе, где было отмечено, что в результате усреднения интерференционной картины по направлениям наблюдения . Об этой дополнительной фазе упоминалось в нашей предыдущей лекции на этой школе, где было отмечено, что в результате усреднения интерференционной картины по направлениям наблюдения 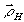 , попадающим в апертуру оптической системы, к аргументу функции взаимной корреляции добавляется величина α12. Поскольку аргумент функции взаимной корреляции представляет собой фазу наблюдаемой интерференционной картины, величина α12 равна дополнительной фазе α. Интересно отметить, что второе слагаемое выражения (12) с точностью до обозначений совпадает с выражением для трехмерного распределения комплексной амплитуды вблизи фокуса сходящейся сферической волны, приведенный, например, в /5/. Это совпадение не случайно. Действительно, второе слагаемое (12) совпадает также с выражением для функции взаимной когерентности в изображении некогерентного теплового источника. Последнее следует из того, что взаимная когерентность подчиняется тому же волновому ураанению, что и комплексная амплитуда /5/. Как отмечалось на нашей предыдущей лекции, функция взаимной когерентности для диффузно-когерентного излучения, введенная усреднением по пространству, совпадает с функцией взаимной когерентности для теплового излучения, введенной усреднением по времени. При выводе (12) учитывалась только та интенсивность, которая вносит вклад в образование интерференционной картины, т.е. учитывалась взаимная интенсивность, которая после соответствущей нормировки переходит в функцию взаимной когерентности для диффузно-когерентного излучения и, следовательно, совпадает с трехмерным распределением комплексной амплитуды вблизи фокуса. Последнее достаточно хорошо изучено и, при необходимости, может быть использовано для анализа усреднения по апертуре в голографической интерферометрии. , попадающим в апертуру оптической системы, к аргументу функции взаимной корреляции добавляется величина α12. Поскольку аргумент функции взаимной корреляции представляет собой фазу наблюдаемой интерференционной картины, величина α12 равна дополнительной фазе α. Интересно отметить, что второе слагаемое выражения (12) с точностью до обозначений совпадает с выражением для трехмерного распределения комплексной амплитуды вблизи фокуса сходящейся сферической волны, приведенный, например, в /5/. Это совпадение не случайно. Действительно, второе слагаемое (12) совпадает также с выражением для функции взаимной когерентности в изображении некогерентного теплового источника. Последнее следует из того, что взаимная когерентность подчиняется тому же волновому ураанению, что и комплексная амплитуда /5/. Как отмечалось на нашей предыдущей лекции, функция взаимной когерентности для диффузно-когерентного излучения, введенная усреднением по пространству, совпадает с функцией взаимной когерентности для теплового излучения, введенной усреднением по времени. При выводе (12) учитывалась только та интенсивность, которая вносит вклад в образование интерференционной картины, т.е. учитывалась взаимная интенсивность, которая после соответствущей нормировки переходит в функцию взаимной когерентности для диффузно-когерентного излучения и, следовательно, совпадает с трехмерным распределением комплексной амплитуды вблизи фокуса. Последнее достаточно хорошо изучено и, при необходимости, может быть использовано для анализа усреднения по апертуре в голографической интерферометрии.
Оценим величину α. Из (14) следует, что α принимает максимальное по модулю значение 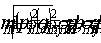 при ξ =0, т.е. когда смещение направлено вдоль оси оптической системы и α = 0 при ξ=π/2, ς.е. при смещении, перпендикулярном оптической оси. Следовательно, величина при ξ =0, т.е. когда смещение направлено вдоль оси оптической системы и α = 0 при ξ=π/2, ς.е. при смещении, перпендикулярном оптической оси. Следовательно, величина 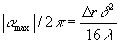 может служить оценкой погрешности измерения порядковых номеров интерференционных полос, обусловленной эффектом усреднения интерференци- может служить оценкой погрешности измерения порядковых номеров интерференционных полос, обусловленной эффектом усреднения интерференци-
онной картины по апертуре оптической системы. Эта погрешность становится заметной лишь при больших смещениях ( ~ 100 мкм) и сравнительно большой апертуре оптической системы (~0,1), однако, при точном измерении дробной части интерференционных полос, например, по методу, предложенному в /3/, эту погрешность следует учитывать и при обычных условиях. Выражение (14), в принципе, позволяет не только получить оценку указанной погрешности, но и скорректировать с ее учетом вычисленные проекции вектора 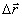 . Для этого целесообразно воспользоваться методом последовательных приближений, приняв за первое приближение значения проекций вектора . Для этого целесообразно воспользоваться методом последовательных приближений, приняв за первое приближение значения проекций вектора 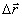 , рассчитанные по трем интерферограммам без учета α, затем, используя вычисленные по формуле (14) значения α, скорректировать порядковые номера интерференционных полос, повторить расчет и т.д. В результате, систематическая погрешность, вызванная усреднением по апертуре, будет исключена. , рассчитанные по трем интерферограммам без учета α, затем, используя вычисленные по формуле (14) значения α, скорректировать порядковые номера интерференционных полос, повторить расчет и т.д. В результате, систематическая погрешность, вызванная усреднением по апертуре, будет исключена.
Итак, в результате проведенного анализа установлена связь погрешностей определения вектора смещения 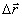 с погрешностями непосредственно измеряемых величин (формулы (3), (7) и (8)). Входящие в эти формулы элементы обратной матрицы А-1 являются функциями геометрических параметров гологоафической схемы. Для использованного в ряде работ (например, в /2,6/) расположения направлений наблюдения и освещения (рис.2) можно получить простые зависимости сумм с погрешностями непосредственно измеряемых величин (формулы (3), (7) и (8)). Входящие в эти формулы элементы обратной матрицы А-1 являются функциями геометрических параметров гологоафической схемы. Для использованного в ряде работ (например, в /2,6/) расположения направлений наблюдения и освещения (рис.2) можно получить простые зависимости сумм 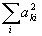 и и 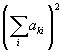 от углов β и γ, показанных на рис.2. от углов β и γ, показанных на рис.2.
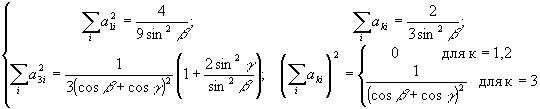 (15) (15)
Объединяя (3), (8) и (15), окончательно получим:
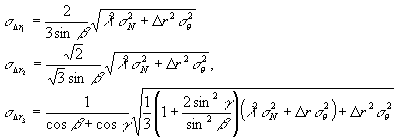 (16) (16)
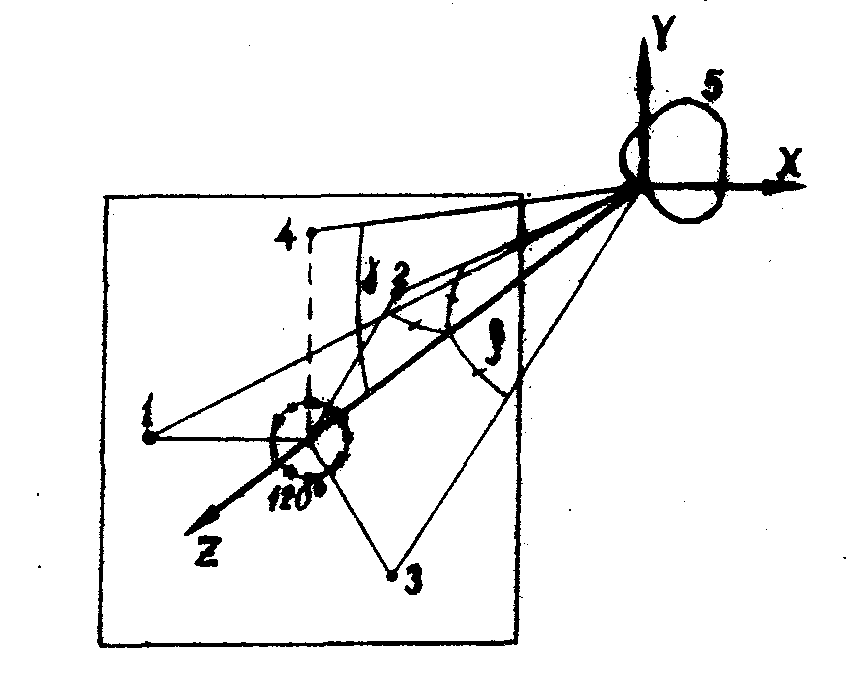
Рис.2. Расположение направлений наблюдения 1, 2, 3 исследуемого объекта 4, а также направления освещения 5 в голографической схеме.
Для реализуемых на практике схем погрешности определения первых двух проекций (на оси ОХ и ОУ), как правило, в 2-3 раза больше погрешности определения третьей проекции (на ось oz). Например, для схемы с параметрами β = 30°, γ = 0 οри смещении
Δ r=10 мкм, λ=0,6 мкм, σh=0,1, σθ=5∙10-3 среднеквадратичные погрешности составят: 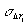 =0,11 мкм, =0,11 мкм, 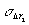 =0,14мкм, =0,14мкм, 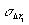 =0,04 мкм. Как видно из полученных результатов, по точноcтным характеристикам голографическая интерферометрия уступает классической (в классической интерферометрии =0,04 мкм. Как видно из полученных результатов, по точноcтным характеристикам голографическая интерферометрия уступает классической (в классической интерферометрии 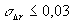 мкм для той же длины волны). Таким образом, повышение точности измерений и оценка принципиально достижимой точности в голографической интерферометрии диффузно отражающих объектов является предметом дальнейших исследований. мкм для той же длины волны). Таким образом, повышение точности измерений и оценка принципиально достижимой точности в голографической интерферометрии диффузно отражающих объектов является предметом дальнейших исследований.
Л и т е р а т у р а
1. Н.Г.Власов, А.Е.Штанько. Материалы vi Всесоюзной школы по голографии , Л., стр.259, 1974.
2. t.matsumoto, k.iwata, r.nagata. appl.opt., 12, 5, 961, 1973.
3. r.dandliker, b.ineichen, f.m.mattier. opt.communs., 9, 4, 412, 1974.
4. Джефрис, Б.Свирл c. Методы математической физики. Изд.Мир, М., вып.3, 1970.
5. М.Борн, Э.Вольф. Основы оптики, изд. Наука, М., 1973.
6. Н.Г.Власов, В.Н.Проценко, А.Е.Штанько. Современные проблемы прикладной гологрвфии . Изд.МДНТП, стр.74, 1974.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

