|
|
 |
 |

|
| |
ГОЛОГРАФИЧЕСКИЙ СИНТЕЗ ТРЕХМЕРНЫХ РЕНТГЕНОВСКИХ ИЗОБРАЖЕНИЙ
В.А.Бердоносов, В.И.Горбунов, А.К.Стоянов
Предложена теоретическая модель голографического синтеза трехмерных рентгеновских изображений. На основе модели показано, что при определенных условиях синтеза компонента мнимого изображения эквивалента полю излучающих источников с плотностью распределения, пропорциональной плотности вещества объекта. Расчетные свойства идеально синтезированных изображений совпадают с экспериментальными.
За последнее время появился ряд экспериментальных работ, посвященных голографическому синтезу 3-х мерных рентгеновских изображений /1-4/. В нашей работе дается теоретическое описание процесса синтеза и свойств восстановленных изображений.
Методика синтеза подробно описана в /1-4/ и состоит обычно из двух стадий. На первой из них получают серию плоских рентгенограмм при различных положениях источника излучения. Положения объекта и рентгеновской пленки при этом остаются неизменными. При каждой экспозиции источник смещают на один и тот же шаг. Таким образом, получают набор рентгеновских ракурсов объекта. На второй стадии синтезируют голографическую матрицу рентгенограмм. Рентгенограммы записывают на фотопластинку в последовательности их получения. Перед экспозицией каждая из них устанавливается в общем для всех снимков положения, подвижная диафрагма перед фотопластинкой сдвигается на шаг, соответствующий смещению рентгеновского источника. Опорный пучок при этом остается постоянным. Основным условием при синтезе является то, что элементы матрицы должны лежать на траектории перемещения рентгеновского источника. Независимо от траектории перемещения, восстанавливаемое мнимое изображение при наблюдении дает иллюзию объемного распределения плотности непрозрачного объекта.
Качество иллюзии зависит от числа элементов матрицы и шага смещения источника. При достаточно малом шаге и большом числе элементов (рентгенограмм) можно добиться непрерывного паралакса в горизонтальном направлении /2-3/.
Дадим теперь математическое описание процесса синтеза изображений, разбив его на следующие этапы:
1) запись рентгенограмм;
2) синтез матрицы голограмм;
3) восстановление изображения.
Рассмотрим волновое поле, восстановленное матрицей голограмм при следующих идеальных условиях:
а) сдвиг источника происходит на бесконечно малый шаг по прямой линии;
6) запись изображения рентгенограммы осуществляется на бесконечно малый участок голограммы. Такие условия получаются при предельном переходе из реальных условий синтеза /1-4/.
Реальная задача - трехмерная. Это означает, что волновое поле в плоскости 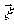 (рис.1) предмета, освещённого единичной плоской волной, определяется соотношением: (рис.1) предмета, освещённого единичной плоской волной, определяется соотношением:
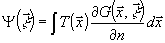 . (1) . (1)
Здесь 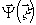 - амплитуда световой волны в плоскости голограммы; - амплитуда световой волны в плоскости голограммы;
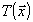
- граничное условие в предметной плоскости;
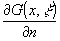
- производная по нормали 3-мерной функции Грина
уравнения Гельмгольца.
Используя параксиальные приближения, уравнения (1) обычно записываются в виде /5/
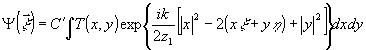 , (2) , (2)
где 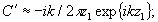
k =2π/λ - волновое число, λ - длина волны излучения, используемого при записи голограмм. Поскольку в большинстве случаев 5-мерные изображения синтезируют только с горизонтальным паралаксом, что обусловлено особенностями человеческого зрения, нас будет интересовать составляющая (2), описывающая изменения световой волны в плоскости (хoz), т.е. рассматриваем
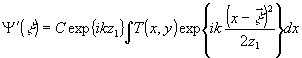 . (3) . (3)
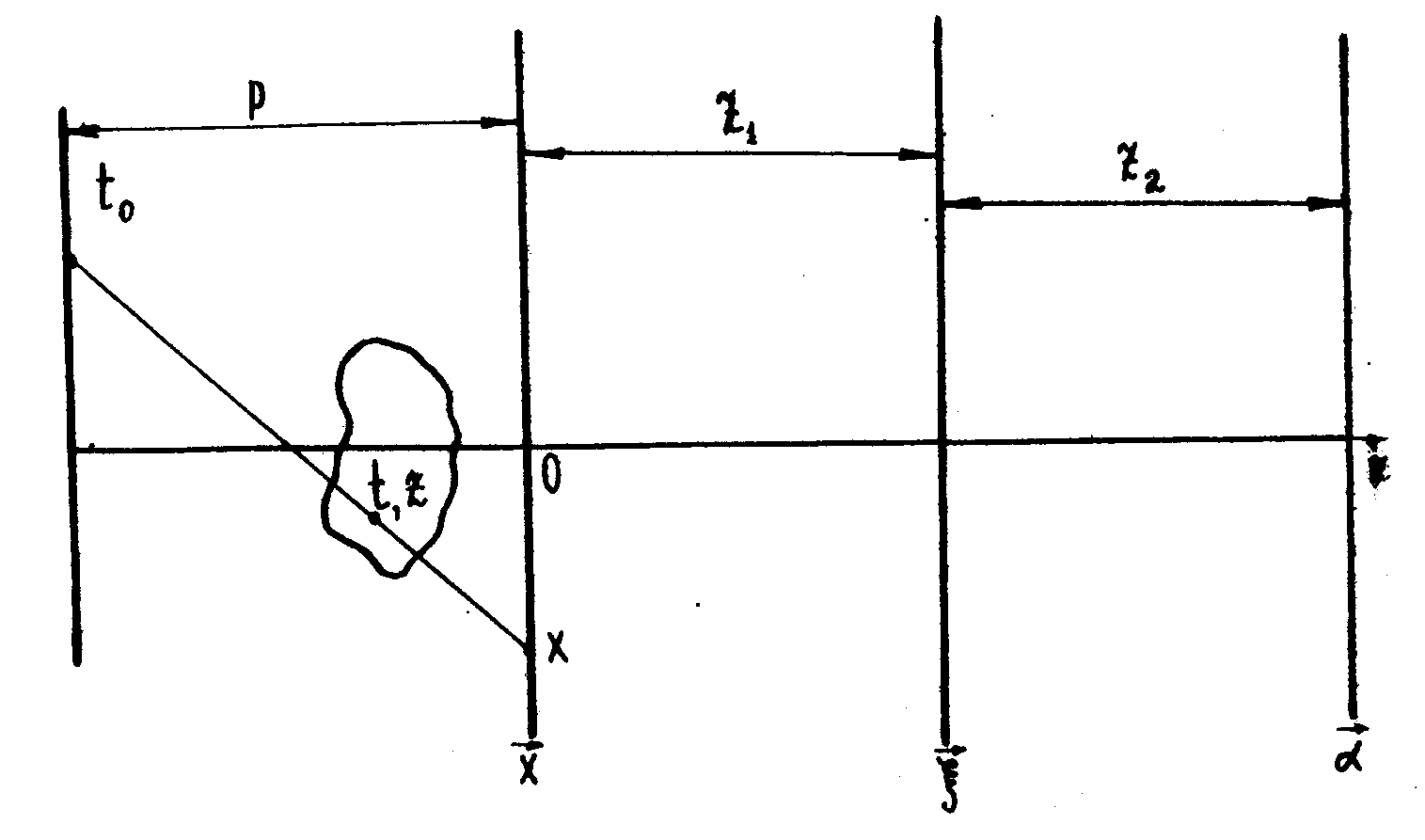
Рис.1. Система координат синтеза 3-х мерного рентгеновского изображения.
t0 - координата точечного источника рентгеновского излучения.
t,z - координаты поглощающего объекта.
p - расстояние от плоскости источника до рентгенограммы.
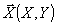 - -
координаты в плоскости рентгенограммы.
z1 - расстояние от рентгенограммы до голограммы.
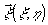 - -
координаты в плоскости голограммы.
z2 - расстояние от голограммы до плоскости наблюдения.
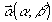 - -
плоскость наблюдения восстановленного объекта.
Таким образом, трехмерная задача сводится к плоской.
1. Запись рентгенограммы
Допустим, объект в плоскости toz имеет распределение плотности ρ(t,z). Положим, далее, что при экспонировании ракурсов предмета изготовлены рентгенограммы с малой оптической плотностью d. Тогда для коэффициента амплитудного пропускания рентгенограммы
t = τ 1/2, (4)
где Т = 10 -d - коэффициент пропускания рентгенограммы по интенсивности, можно записать два первых члена разложения в ряд:
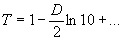 (5) (5)
Считая, что запись производится на линейном участке характеристической кривой, т.е.
d=d0 +γlge, (6)
где γ - коэффициент контрастности, e=jt - экспозиция, j - интенсивность излучения, t - время экспонирования, для Т получим следующее приближенное равенство:
t=a+b lgj. (7)
Здесь а, b - константы.
Пусть х - координата в плоскости рентгенограммы (рис.1). Тогда в точке Х интенсивность излучения, от которой зависит Т, запишется для точечного источника с координатами (t0, p) как
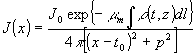 . (8) . (8)
Здесь j0 - начальная интенсивность, μm - массовый коэффициент ослабления излучения. Интегрирование в (8) ведется вдоль прямой, проходящей через точки (х,0) и (t0, р). Перейдём от линейного интеграла к интегралу по площади. Для этого воспользуемся свойствами δ - функции Дирака, определённой на плоскости [6]. Получим
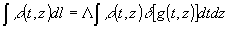 . (9) . (9)
В (9) g(t,z) - уравнение прямой через точки (t0,p) и (х,0) 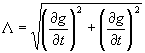 - величина, обратная плотности распределения функции р(t,z) вдоль прямой q(t,z)=0.Уравнение прямой g(t,z) есть - величина, обратная плотности распределения функции р(t,z) вдоль прямой q(t,z)=0.Уравнение прямой g(t,z) есть 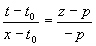 . Отсюда . Отсюда
(z -р)х-zt0+pt=0, (10)
Учитывая (8), (9), (10), для Т (x) получим:
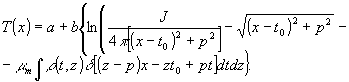 (11) (11)
Возьмём | ρ| таким, чтобы соблюдалось неравенство
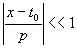 . (12) . (12)
Такое условие обычно выдерживается при радиографировании. В этом случае для ( 11) можно записать
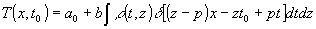 (13) (13)
a0, b - константы, получившиеся в (11) при соблюдении (12). Предположим, задан точечный объект с плотностью ρδ(t-t',z-z'). Подставляя это значение в (13), получим для пропускания рентгенограммы
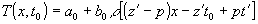 . (14) . (14)
2. Запись голограммы
Используя схему с боковым опорным пучком, можно записать результирующее поле в плоскости голограммы как
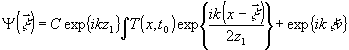 . (15) . (15)
Здесь 1-й член описывает волну, дифрагированную на рентгенограмме, 2-й член - плоскую двумерную опорную волну, падающую под малым углом v к голограмме /5/.
Пропускание элементов голограммной матрицы, соответствующее рентгенограмме объекта, полученной при положении источника (t0, р), в нашем случае определится как
i(ξ,t 0)=δ(ξ-t0)|Ψ(ξ)|2. (16)
3. Восстановление изображения
Поле, восстановленное голограммной единичной рентгенограммы, определяется соотношением, подобным (3). Граничным условием служат i(ξ,t0), т.е.
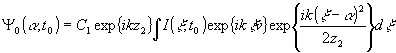 . (17) . (17)
Суммарное поле составной голограммы всех рентгенограмм, полученных при непрерывном смещении источника рентгеновского излучения, определяется, очевидно, как
 . (18) . (18)
Используя обобщённую функцию Френеля /6/, определяемую как
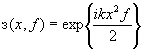 , ,
и подставляя в (16) соотношения (16), (17), (15), выделим из (18) член, описывающий восстановление мнимого изображения. Получим
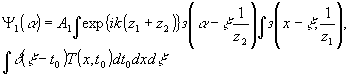 (19) (19)
При получении (19) был изменен порядок интегрирования, что допустимо, поскольку используемые нами функции интегрируемы /7/.
Рассмотрим изображение, синтезированное для точечного объекта, т.е. полагаем, что t(x,t0) берётся в виде (14). Непосредственным вычислением можно убедиться, что член с а0 обуславливает фоновую составляющую. Тогда интеграл по t0 с учётом (14) даст следующее выражение для компоненты изображения:
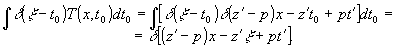 (20) (20)
В интеграле по х

сделаем замену x-ξ=x'. Тогда он преобразуется к свертке, имеющей смысл в данном случае, поскольку одним из сверточных членов является δ-функция /5,6/. Получим
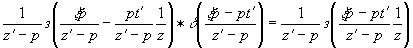 , (21) , (21)
* - символ свертки. Подставляя (20) и (21) в выражение для мнимого изображения (19), придём после недолгих вычислений к следующему результату:
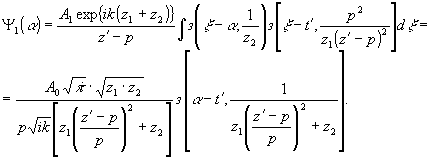 (22) (22)
Перепивем в явном виде (22)
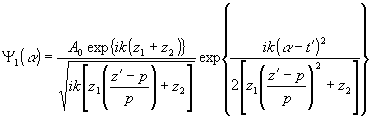 . (23) . (23)
А 0 - константа. Рассмотрим выражение
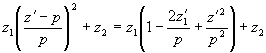 . .
Пусть условие синтеза такое, что
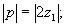 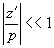 . (24) . (24)
Первое условие легко выдержать на стадии записи матрицы, второе обычно выполняется в практике радиографии и означает, что предмет расположен близко к рентгеновской плёнке. Как следует из рис.1, z1>0, р< 0, т.е. 2z1/p<0. Тогда, пренебрегая членами 2-го порядка малости, для рассматриваемого выражения получим значение z1+z2+z'. Таким образом, поле, восстановленное матрицей,
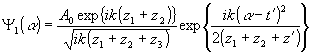 . (25) . (25)
Волна Ψ1(α) из (25) с точностью до постоянных совпадает с волной от точечного источника в двумерном случае /8/, рассматриваемой в параксиальном приближении. Следовательно, наблюдатель, находящийся в плоскости α, увидит изображение точечного светящегося источника на расстоянии |z1+z2+z'| от себя.
Допустим объектом радиографирования служили два точечных тела с координатами ( t',z') и (t",z"), причём |z'|<|z"|. Учитывая, что z'<0 и z"<0, из (25) получим, что голограмма восстановит два изображения светящегося источника, из которых один, соответствующий телу с координатой z", будет расположен ближе к наблюдателю, чем другой с координатой z'. Таким образом, приходим к выводу, что изображение псевдоскопично по отношению к выбранному началу координат. Такая ситуация равносильна наблюдению со стороны рентгеновского источника, что подтвервдается экспериментальными работами /1-4/.
Полученные результаты непосредственно обобщаются на тело с произвольной плотностью распределения вещества ρ(t,z). Для этого в (19) подставим значение коэффициента пропускания из (13). Нетрудно заметить, что промежуточные расчёты полностью совпадают с расчётами для точечного объекта, а результирующая компонента мнимого изображения описывается интегральным соотношением.
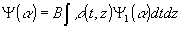 . (26) . (26)
Ψ (α) - поле, определяемое (23) или при соблюдении условий (24) выражением (25). Поскольку Ψ1(α) имеет смысл волны от точечного источника, то и Ψ(α) из (26) описывает вполне конкретную физическую ситуацию, а именно: волновое поле от совокупности изучающих источников с плотностью распределения ρ(t,z) /8/.
Следует отметить, что (26) даёт такое описание с точностью до констант, определяющих величину амплитуд восстановленной волны. Для визуального наблюдения такая точность вполне достаточна.
Свойства синтезированного кзобрааения такие же, как получались для точечного объекта. Действительно, можно записать
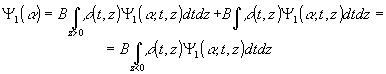
так как ρ(t,z)≡0 в полуплоскости z>0. В явном виде
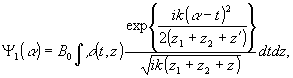 (27) (27)
что эквивалентно полю излучавших источников с плотностью ρ распространявшемуся вдоль оси (-z), т.е. эквивалентно наблюдению со стороны рентгевовского источника.
Рассмотрим теперь свойства действительного изображения. Пусть при восстановлении используется комплексно-сопряжённый пучок exp{-ikξv}. Составляющая действительного изображения в этом случае запишется следующим образом:
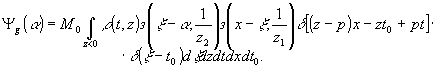 (28) (28)
Производя вычисления и упрощения, подобные применявшимся ранее, получим для (28)
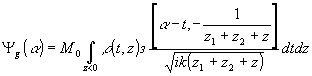 . (29) . (29)
Как и следовало ожидать, (29) описывает сходящееся волновое пoлe источников с плотностью распределения ρ (t,z). Физически это означает, что за голограммой существует область, где световые лучи, пересекаясь, образуют световую копию ρ(t,z).
Допустим, в плоскости (α ,z2), расположенной на расстоянии z2=-(z1+z') от годеграммы, при восстуновпеиии помещается фото-пластинка. Распределение амплитуды света в этой плоскости
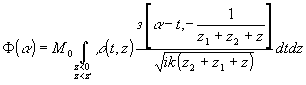 , ,
причём максимальный вклад дают точки, попавшие в плоскость сечения z2=-z1-z'. Используя тот факт, что
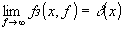 , /6/ , /6/
получим, что в основном распределение поля в плоскости сечения имеет вид:
φ 0(α,z)=m1ρ(α1z'+z 1). (30)
Иными словами, в плоскости регистрации фокусируется всё, что лежит непосредственно в ней, и размазывается, лежащее вне её. Этот результат совпадает с экспериментальными данными по голографическому томосинтезу /3,4/.
В ы в о д ы
Составная голограмма позволяет синтезировать трёхмерную световую копию внутренней структуры непрозрачного объекта по серии теневых рентгенограмм. При наблюдении мнимого изображения создаётся иллюзия объёмности предмета, а действительное изображение позволяет получить послойные снимки внутренней структуры. Глубину среза можно выбирать по собственному желанию после синтеза изображения.
На эксперименте невозможно осуществить бесконечно-малые сдвиги рентгеновского источника и, следовательно, диафрагмы при записи голограммы в силу ограниченной разрешающей способности глаза, можно взять достаточно малые конечные перемещения. Выбранная модель даёт результаты, совпадающие с экспериментальными данными, полученными в таких условиях.
Л и т е р а т у р а
1. j.d.redman, w.p.wolton, shuttleworth. nature, 58, 220, 1968.
2. t.kasahara, y.kimura, r.hioki, s.tanaka. japan.j.appl.phys., 8, 124, 1969.
3. g.groh, m.cock. appl.opt., 7, 3, 260, 1973.
4. kock, u.tiemens. opt.communs., 9, 3, 775, 1973.
5. Де Велис, Голография , Воениздат, М., 1970.
6. Сороко Л.М. Основы голографии и когерентной оптики , "Наука", М. 1971.
7. Владимиров b.c. Уравнения математической физики, "Наука", М., 1970.
8. Кошляков h.С., Глинер Э.Б., Смирнов М.М. -Уравнение в частных производных математической физики. Высшая школа, М., 1970.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

