|
|
 |
 |

|
| |
МОДЕЛИРОВАНИЕ ПРОЦЕССА ОПТИЧЕСКОЙ ФИЛЬТРАЦИИ И ОПТИМИЗАЦИЯ ПАРАМЕТРОВ ЗАПИСИ
ГОЛОГРАФИЧЕСКИХ ФИЛЬТРОВ
А.М.Беккер, Б.Г.Турухано
Рассматривается возможность моделирования процесса оптической фильтрации. Приводится постановка задачи выбора оптимальных параметров записи (соотношение интенсивностей записывающих пучков и времени экспозиции) с учетом реальных характеристик фотоматериалов и заданных параметров фильтра (селективности и дифракционной эффективности). В качестве иллюстрации рассчитываются оптимальные параметры фильтра для решения задачи распределения по размерам центрально-симметричных объектов (кружки различных радиусов, имитирующих бактериальные колонии).
1. Моделирование процесса оптической фильтрации
Будем рассматривать задачу распознавания образов в когерентно-оптическом корреляторе по схеме Вандер Люгта /1/. При предъявлении на вход коррелятора объектов, подлежащих опознаванию, распределение амплитуд светового поля в выходной плоскости становится пропорциональным значениям функции корреляции входного объекта и импульсного отклика фильтра, установленного в системе. Будем измерять интенсивность светового поля в точке корреляционной плоскости, соответствующей началу координат входной плоскости. То есть измеряется величина
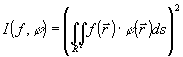 , (1) , (1)
где 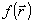 - функция пропускания входного транспаранта, а - функция пропускания входного транспаранта, а
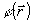
- импульсный отклик фильтра.
Предположим, что совокупность входных объектов нам известна и может быть описана в виде 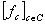 , где С - множество параметров. Задача распознавания образов состоит в выделении объектов fс , где С - множество параметров. Задача распознавания образов состоит в выделении объектов fс таких, в которых 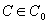 , , 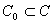 . Когерентно-оптическая система сводит эту задачу к дискриминации значений . Когерентно-оптическая система сводит эту задачу к дискриминации значений 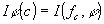 . Если известны значения функции . Если известны значения функции 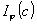 при всех при всех 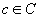 и фиксированном φ, то можно оценить пригодность фильтра с импульсным откликом и фиксированном φ, то можно оценить пригодность фильтра с импульсным откликом 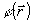 для решения данной задачи распознавания. для решения данной задачи распознавания.
Измерение значений функции 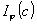 - процесс весьма трудоемкий, поэтому представляет интерес моделирование работы оптического коррелятора для нахождения значений - процесс весьма трудоемкий, поэтому представляет интерес моделирование работы оптического коррелятора для нахождения значений 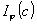 . Перейдем к методам моделирования. . Перейдем к методам моделирования.
Будем пользоваться в расчетах не импульсным откликом фильтра 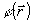 , а функцией комплексного пропускания фильтра (к.п.ф.) , а функцией комплексного пропускания фильтра (к.п.ф.) 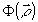 , связанной с , связанной с 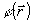 преобразованием Фурье: преобразованием Фурье:
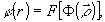 (2) (2)
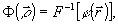 (3) (3)
где f - оператор Фурье-преобразования. Используя теорему свертки, получаем из формулы (1)
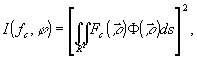 (4) (4)
где 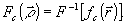
Получение голографического фильтра по Вандер Люгту сводится к записи голограммы Фурье входного транспаранта. При этом свойства полученного фильтра зависят не только от самого транспаранта, но и от параметров записи: отношения амплитуд объектного и опорного пучков - q, времени экспозиции - Т и характеристической кривой регистрирующего материала - χ.
На первом этапе моделируется процесс записи голографического фильтра, а на втором - его работа в схеме Вандер Люгта.
Опишем процесс моделирования. Пусть при записи фильтра на фотоматериале с кривой почернения χ(Е) регистрируется голограмма входного транспаранта с функцией пропускания 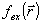 . При этом соотношение пучков равно q0, а время экспозиции Т0. Функция амплитудного пропускания фильтра в этом случае имеет вид: . При этом соотношение пучков равно q0, а время экспозиции Т0. Функция амплитудного пропускания фильтра в этом случае имеет вид:
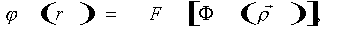 (5) (5)
где х - соответствующая координата вектора 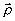 ; ; 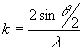 ; θ - σгол между пучками. ; θ - σгол между пучками.
Считаем, что функция χ(Е) выражает зависимость амплитудного пропускания фотоэмульсии t от величины экспозиции Е. Вычислив преобразование Фурье функции 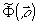 в окрестности точки kπ, οолучим импульсный отклик фильтра в окрестности точки kπ, οолучим импульсный отклик фильтра 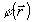 . Такой способ расчетов требует большого объема вычислений, так как функция . Такой способ расчетов требует большого объема вычислений, так как функция 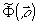 быстро осциллирует и численные методы вычисления интегралов требуют большего числа шагов для достижения нужной точности. Если предположить, что угол между опорной и предметной волнами достаточно велик, т.е. что функция быстро осциллирует и численные методы вычисления интегралов требуют большего числа шагов для достижения нужной точности. Если предположить, что угол между опорной и предметной волнами достаточно велик, т.е. что функция 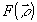 мало изменяется на достаточно большом числе периодов, можно разложить ее в ряд Фурье по cos nkπ. Коэффициенты разложения, естественно, зависят от мало изменяется на достаточно большом числе периодов, можно разложить ее в ряд Фурье по cos nkπ. Коэффициенты разложения, естественно, зависят от 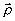 . Нас интересует поле в первом порядке дифракции плоской волны на фильтре. Оно определяется первым членом ряда, выпишем этот член: . Нас интересует поле в первом порядке дифракции плоской волны на фильтре. Оно определяется первым членом ряда, выпишем этот член:
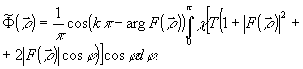 (6) (6)
Таким образом функция к.п.ф. определяется выражением:
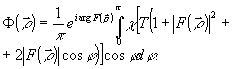 (7) (7)
Обозначим интеграл, зависящей от параметров q и Т в формуле (7), через
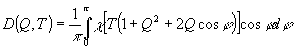 . (8) . (8)
Величина d2(q,Т) определяет дифракционную эффективность голографической решетки, записанной на фотоматериале о кривой почернения χ(Е), при соотношении пучков, равном q, за время экспозиции Т.
Перепишем формулу (7) в виде
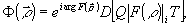 (9) (9)
где q - отношение амплитуд пучков при записи фильтра.
Для уменьшения объема вычислений целесообразно функцию d(q,t) протабулировать, вычислив ее значения в точках 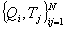 , перекрывающих достаточно широкую область изменения параметров, а для получения значений в промежуточных точках приманить интерполяцию. , перекрывающих достаточно широкую область изменения параметров, а для получения значений в промежуточных точках приманить интерполяцию.
2. Оптимизация параметров записи
Для каждой конкретной задачи распознавания образов может быть указан оптимальный вид функции iоп(с). Однако, фильтр с импульсным откликом φ, при котором iφ(с)=iоп(с), вообще говоря, реализован быть не может, поскольку выбранная схема накладывает следующие ограничения на функцию к.п.ф. - 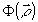 : :
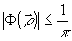 (10) (10)
(ограничение дифракционной эффективности, см. /2/),
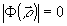 , , 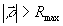 (11) (11)
(ограничение действующего размера фильтра) .
Поэтому приходится ставить задачу выбора оптимального фильтра.
Сначала введем понятие дифракционной эффективности фильтра. Для рассматриваемого случая разумным представляется такое определение :
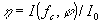 */ (12) */ (12)
где i0 - интенсивность освещающего источника.
Величина η определяет светосилу прибора и естественно потребовать, чтобы η≥ηmin. Можно найти максимальную возможную дифракционную эффективность фильтра при заданной функции 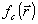 и указать вид функции к.п.ф., максимизирующей η. и указать вид функции к.п.ф., максимизирующей η.
Пусть согласованным является объект 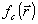 , согласно (1) и (4) , согласно (1) и (4)
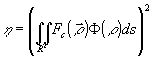 , (13) , (13)
так как 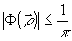 - согласно условию (10), - согласно условию (10),
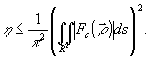 (14) (14)
Если взять 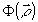 , равной , равной 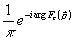 , то получим , то получим
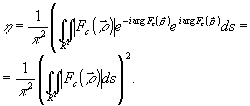 (15) (15)
То есть максимальная дифракционная эффективность фильтра равна
и такая эффективность достигается при использовании фильтра с функцией к.п.ф., равной:
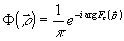 . (17) . (17)
Дадим две постановки задачи оптимизации.
1. Найти функцию 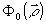 , такую, что , такую, что
а) 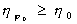 имеет экстремум на φ0 имеет экстремум на φ0,
б) 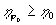 , ,
в) 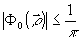 , ,
г) 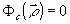 при при 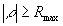 . .
2. Найти значения параметров записи фильтра такие, что
а) 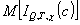 имеет экстремум в точке (q0, t0, χ0 имеет экстремум в точке (q0, t0, χ0),
б) 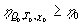 , ,
в) 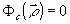 при при 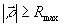 . .
Условие 1 в) в задаче 2 выполняется автоматически, так как учитывается влияние фотоматериала и, значит, 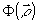 определяется значением d(q,t), которое не может превосходить величины 1/π. определяется значением d(q,t), которое не может превосходить величины 1/π.
В задачах 1) и 2) вид функционала М зависит от конкретной задачи распознавания и определяется критериями распознавания, вытекающими из общей теории распознавания образов. Задача 1) является задачей оптимального управления /3/ и может быть решена одним из существующих методов. В результате ее решения мы получаем вид функции к.п.ф., оптимизирующей функционал М при заданных ограничениях. Однако, реализация фильтра с заданной функцией к.п.ф. требует сложнейших устройств оптического вывода информации из ЭВМ, имеющих порядка 10 12 элементов разрешения. Реальнее использовать стандартный способ записи фильтра, при этом для оптимизации параметров записи нужно решать задачу 2). Она также является задачей
нелинейного программирования.
С другой стороны значение максимума (минимума) функционала при решении задачи 1), вообще говоря, больше (меньше), чем в задаче 2). Это станет очевидным, если учесть, что функция Ф q,t,χ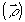 , где параметры найдены при решении задачи 2), наверняка удовлетворяет ограничениям задачи 1). Таким образом, может встретиться ситуация, при которой значение функционала М, оптимизирующего задачу 2), недостаточно велико (мало). Это означает, что стандартным процессом записи нельзя получить фильтр с нужными свойствами. В то же время значение, полученное из задачи 1), может быть достаточным для распознавания и в таком случае придется прибегать к более сложным способам изготовления фильтра. , где параметры найдены при решении задачи 2), наверняка удовлетворяет ограничениям задачи 1). Таким образом, может встретиться ситуация, при которой значение функционала М, оптимизирующего задачу 2), недостаточно велико (мало). Это означает, что стандартным процессом записи нельзя получить фильтр с нужными свойствами. В то же время значение, полученное из задачи 1), может быть достаточным для распознавания и в таком случае придется прибегать к более сложным способам изготовления фильтра.
Следует отметить, что решение задачи 2) гораздо менее трудоемко, чем решение задачи 1), так как число параметров в задаче 2) мало, в то время как в задаче 1) мы имеем дело с оптимизацией функционала от непрерывной функции.
В частном случае, если считать фотоматериал заданным, функционал М зависит только от двух параметров и простейшим способом решения является просчет значений М и η в достаточно широкой области изменения параметров.
Решение задачи 2) в одном аз частных случаев будет рассмотрено ниже.
Прежде, чем перейти к экспериментальным результатам, отметим, что на протяжении всей работы считалось, что значение функции корреляции измеряется в начале координат выходной плоскости. Это не является обязательным. Метод остается в силе и при иных способах снятия корреляционной функции. Более того, различные способы измерения выходного сигнала можно рассматривать как дополнительные параметры процесса и из этих способов может быть выбран оптимальный.
3. Экспериментальная проверка записи оптимального
фильтра
При экспериментальной проверке записи оптимального фильтра использовался фотоматериал ПЭ-633. Для учета характеристик фотоматериала функция дифракционной эффективности d(q,Т) в зависимос-
ти от соотношения амплитуд пучков и времени экспозиции табулировалась. При этом области изменения параметров были следующие:
qÎ
[0.01, 100] , lgtÎ
[0,2] . График зависимости d(q,Т) приведен на рис.1.
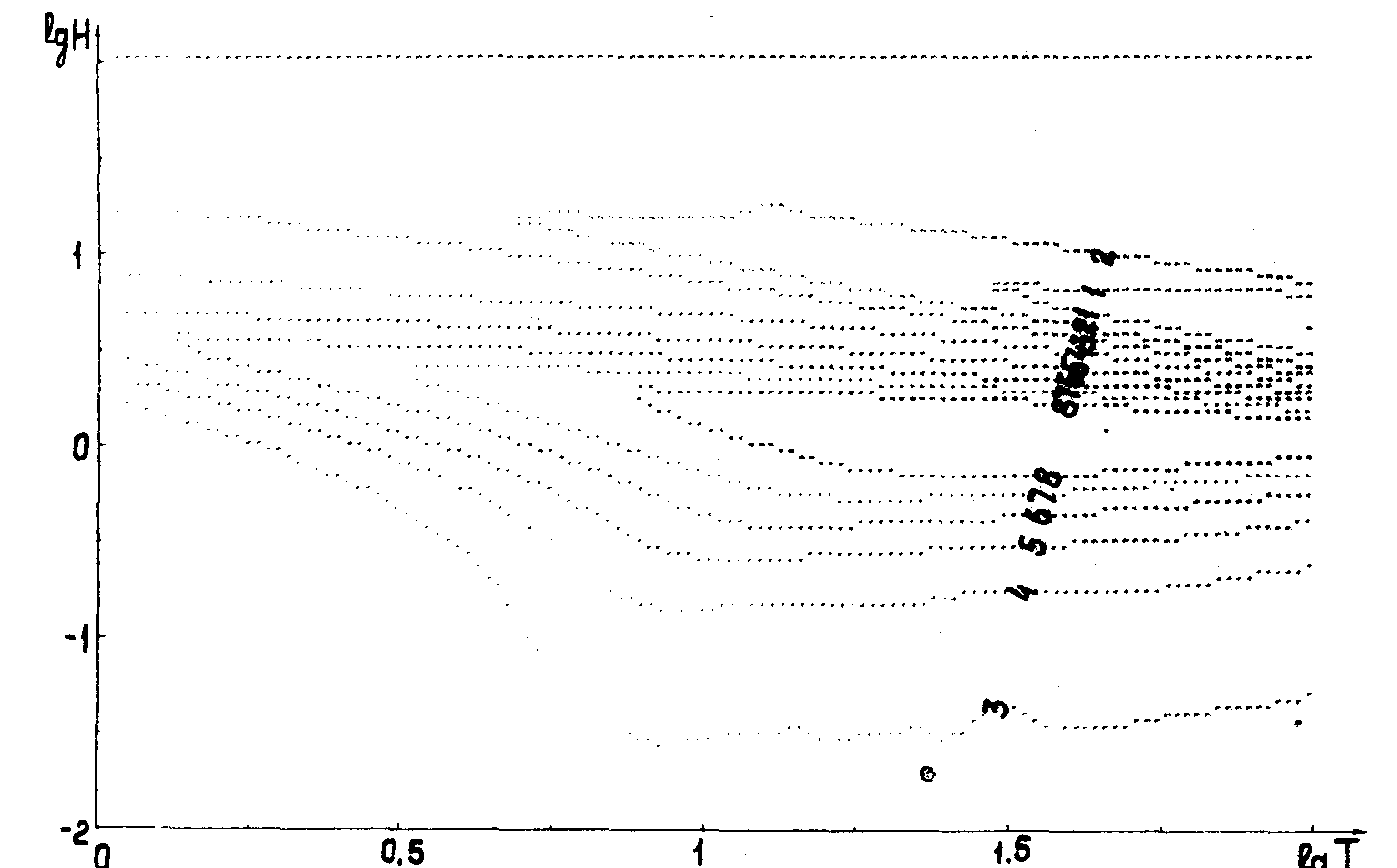
Рис.1. Проекция линий уровней дифракционной эффективности на плоскость ( lgt, lgq):
линия "9" соответствует d=0.10;
линия " 0" соответствует d=-0.04;
(остальные линии разбивают интервал [-0.04; 0.10] на 9 частей равной длины).
Далее проводилось моделирование процесса записи и работы фильтра для распознавания круглых отверстий по размерам. В качестве входного объекта использовалось отверстие радиусом 1 мм. Отношение амплитуды объектного пучка к опорному q = 10. Такое соотношение выбрано для усиления нелинейности записи фильтра. Отметим, что при линейной записи выбирается q<1. Значение времени экспозиции Т выбиралось так, чтобы величина iопt (где iоп - интенсив-
ность опорного пучка) соответствовала середине линейного участка кривой почернения фотоэмульсии ПЭ-633. После изготовления фильтра в такими параметрами записи определялась функция к.п.ф., а уже по ней рассчитывалась функция i(r) c данными параметрами записи, соответствующая корреляции входного объекта и импульсного отклика фильтра.
Отметим, что в данной задаче функция к.п.ф. центрально- cимметрична и вещественна. Следовательно, для определения 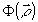 достаточно просканировать поле в первом порядке дифракции и получить значение достаточно просканировать поле в первом порядке дифракции и получить значение 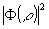 при при 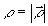 , а затем определить точки перемены знака функции к.п.ф. по реверсу контраста модуляционных полос на фильтре. На рис.2 приводится фотография фильтра в первом порядке дифракции. На рис.3 показана увеличенная зона фильтра, поясняющая реверс контраста при переходе от одного порядка к другому. , а затем определить точки перемены знака функции к.п.ф. по реверсу контраста модуляционных полос на фильтре. На рис.2 приводится фотография фильтра в первом порядке дифракции. На рис.3 показана увеличенная зона фильтра, поясняющая реверс контраста при переходе от одного порядка к другому.

Рис.2. Микрофотография поля фильтра в первом порядке дифракции плоской волны.
Результаты расчетов и измерений корреляционной функция приведены на рис.4. Первая кривая (тонкий пунктир) показывает ход корреляционной функции i(r), рассчитанной по экспериментально
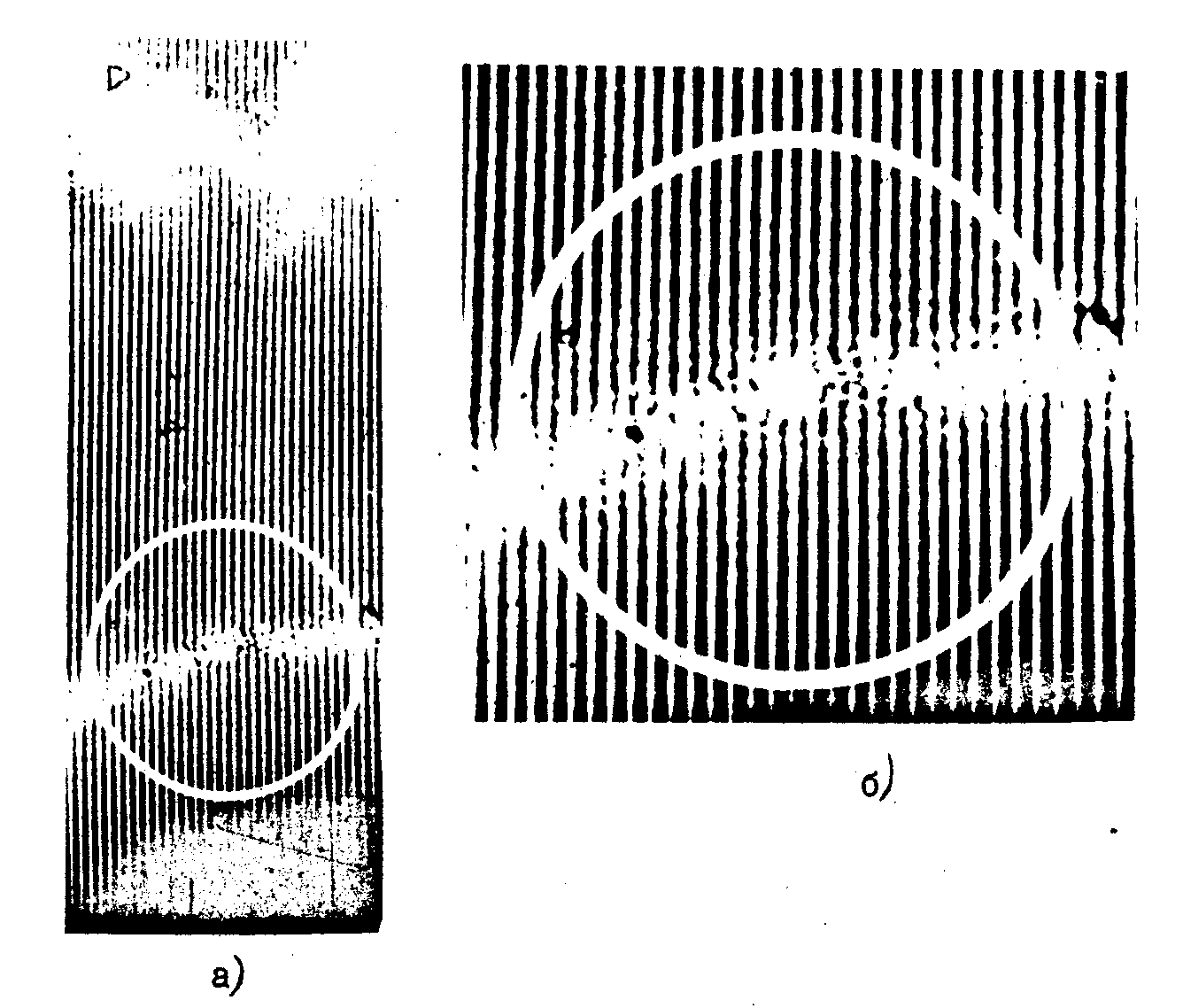
Рис.3. Микрофотография участка голографического фильтра. На увеличенном участке (б) виден реверс контраста модуляционных полос при переходе от одного порядка фильтра к другому.
измеренной функции к.п.ф. 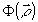 . Вторая кривая (жирный пунктир) - расчет корреляционной функции по заданным параметрам записи фильтра q и Т. Третья кривая (сплошная линия) дает экспериментальную корреляционную функцию. Видно, что все три кривые достаточно хорошо совпадают, особенно в области главного максимума. Таким образом, предложенная методика моделирования позволяет производить оценку результатов эксперимента при решении задачи оптимизации. Задача оптимизации параметров записи фильтра для распознавания центрально-симметричных отверстий по размерам решалась следующим . Вторая кривая (жирный пунктир) - расчет корреляционной функции по заданным параметрам записи фильтра q и Т. Третья кривая (сплошная линия) дает экспериментальную корреляционную функцию. Видно, что все три кривые достаточно хорошо совпадают, особенно в области главного максимума. Таким образом, предложенная методика моделирования позволяет производить оценку результатов эксперимента при решении задачи оптимизации. Задача оптимизации параметров записи фильтра для распознавания центрально-симметричных отверстий по размерам решалась следующим
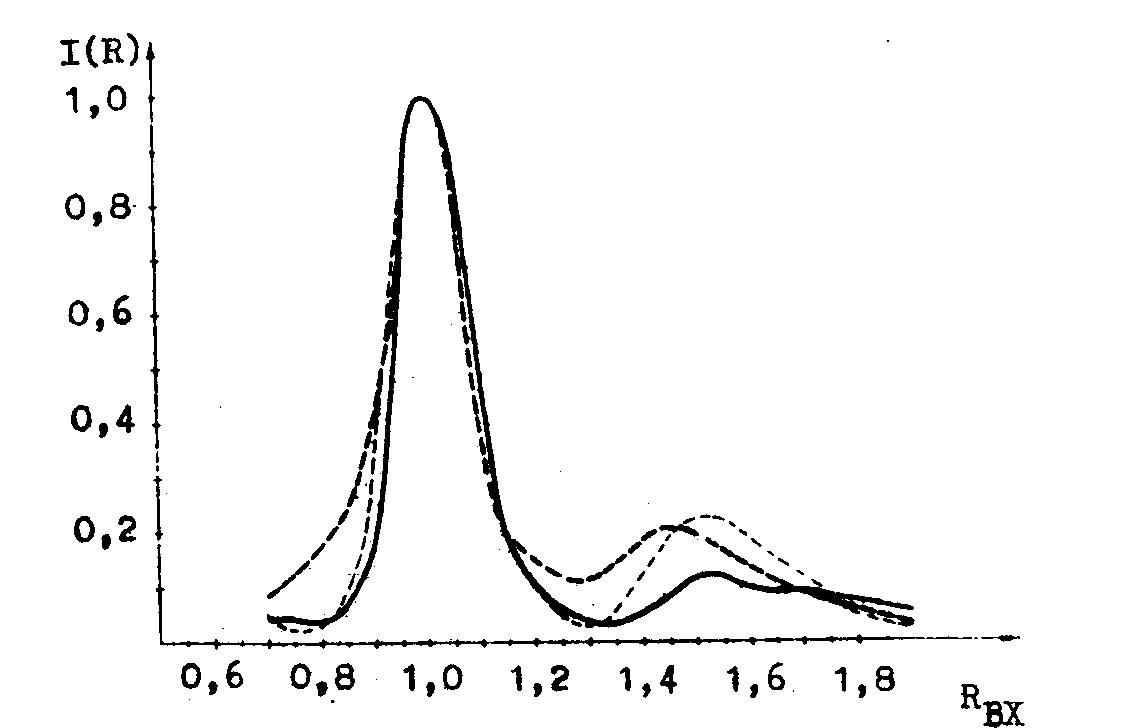
Рис.4. Кривив зависимости выходного сигнала от радиуса отверстия на входе коррелятора i(r).
образом. Строился функционал М, определяющий распознающую способность фильтра. В качестве критерия селективности фильтра принималось уменьшение корреляционного сигнала i(r) при изменении радиуса входного отверстия на 5% от согласованного, принятого за единицу:
 . (18) . (18)
Значения функционала m(q,t) выводились. ЭВМ в логарифмических координатах q и Т, т.е. значения цифр на графике являются проекциями линий уровня m(q,t) на плоскость (lgq, lgt). В тех же координатах выводилось значение дифракционной эффективности фильтра η, определяемое выражением (15). Оба графика совмещалась и из ограничения η≥0.8ηmax, находилось оптимальное значение q и Т, при котором селективность фильтра М=3,4. Рассчитанные значения М и η приведены на рис.5. Селективность возрастает с возрастанием значений цифр. Кривая а ограничивает значение ди-
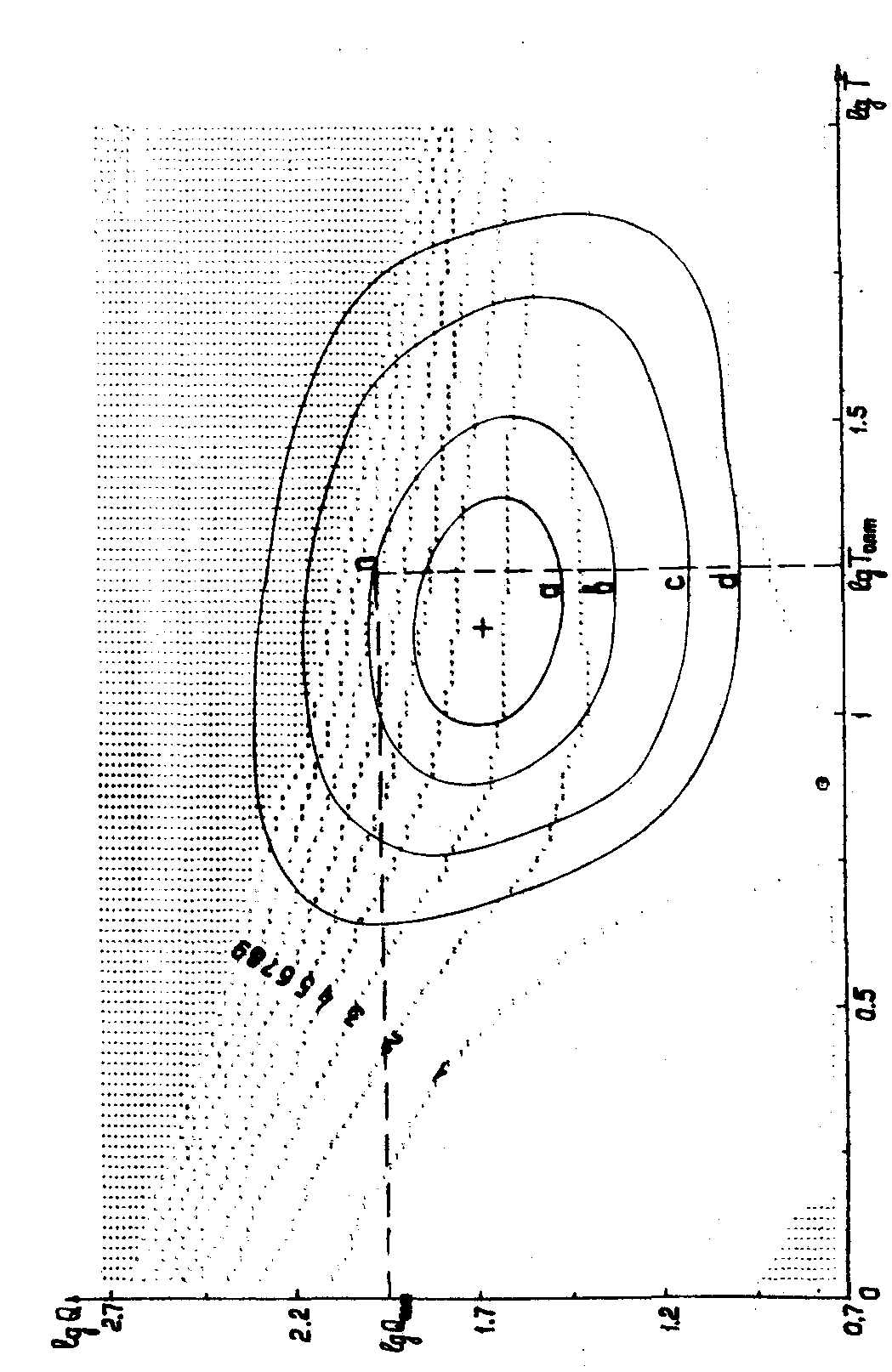
фракционной эффективности η =-0,8η+. Для выбора оптимальных условий записи находим точку внутри области ограниченной кривой "b", в которой величина М максимальна. Такой точкой является точка касания кривых "b" и "7 ". Она соответствует параметрам записи q=71 и Т=17,8, где величина Т=1 соответствует началу отсчета на характеристической кривой эмульсии.
Записанный с найденными параметрами фильтр обладал селективностью М=3,2 и дифракционной эффективностью η=0,055. Эти величины хорошо согласуются с теоретическими и являются вполне достаточными для надежного распознавания.
Резюмируя изложенное, отметим, что в задаче анализа центрально-симметричных отверстий по размерам предложенная методика моделирования процесса записи и работы голографического фильтра позволила выбрать параметры записи и экспериментально получить фильтр, обладающий максимальной селективностью при заданной величине дифракционной эффективности. При этом удалось избежать чрезвычайно трудоемкого экспериментального перебора параметров записи для получения фильтра с желаемыми свойствами. Кроме того, при экспериментальном выборе параметров нельзя гарантировать, что такие параметры будут являться оптимальными в указанном выше смысле.
Л и т е р а т у р а
1. a.b.vander lugt. ieee Тrаns., it-10, 2, 139, 1964.
2. Э.И.Крупицкий, И.С.Барбанель. Оптика и спектроскопия, xxxiii, вып.3, 571, 1970.
3. А.Фиакко, Г.Мак-Кормик. Нелинейное программирование, М., 1972.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

