Media-security

ГОЛОГРАФИЯ И ПЕРСПЕКТИВНЫЕ МЕТОДЫ УПРАВЛЕНИЯ В.К.Быховский

Обсуждается концепция интерференционного управления объектами, основанная на использовании операций над волновыми фронтами (акустическими, оптическими, "цифровыми" и т.д.). Предлагаются методы корреляционной или ассоциативной записи и выборки временных цепочек изображений, которые можно трактовать как программы управления. Кратко обсуждаются технические средства интерференционного управления, в частности, голографический управляющий процессор. Анализируются будущие аспекты интерференционного или фазового управления.

1.В в е д е н и е

В работах Ван-Хеердена /1/ в Сороко /2/ впервые было указано на возможность интерференционной обработке информации - обработка, основанной на операциях с волновыми фронтами. По сравнению с традиционной электронной обработкой данных на ЭВМ интерференционная обработка отличается многоканальностью или параллельностью, а также высокой надежностью. К основным операциям интерференционной обработки относятся корреляционная (ассоциативная) запись волнового фронта по признаку - опорной волне и корреляционное (ассоциативное) считывание волнового фронта по признаку.

В настоящей лекции рассматриваются проблемы интерференционного (фазового) управления системами (объектами). Под управлением понимается процесс удержания объекта (путем "вращения различных ручек" - параметров управления) в заданной области пространства состояний объекта. Как правило, собственно вычислительные процессору не имеют самостоятельного значения, а образуют составную часть некоторого процесса управления (не обязательно автомати-

ческого). Именно процесс управления в конечном счете обеспечивает адаптацию объекта к "его среде", т.е. является основной функцией, связанной с деятельностью человека.

Почему мы должны связывать с интерференционным управлением какие-то особые надежды и почему существующие методы управления нас не удовлетворяют? Дело в том, что использование волновых фронтов в качестве носителей информации и использование операций над волновыми фронтами, по-видимому, открывают новые возможности обработки информации и управления, недостижимые существующими методами.

Колебательные (волновые) процессы обладают присущей им пространственной и временной упорядоченностью движения, которая находит отражение в ряде явлений, не имеющих аналога в традиционных электронных схемах. К ним относятся: интерференция волн, явление многократного эха, огибание препятствий, возможность записи волн (волновых фронтов) в накопительных средах, уникально большой коэффициент разветвления при генерации и распространении волн, возможность считывания записанных ранее волновых фронтов, устойчивость волнового движения по замкнутой траектории и некоторые другие. В настоящее время только начинается использование всего комплекса явлений модуляции, усиления, записи-считывания, взаимодействия волн и т.д. для целей обработки информации и управления системами.

Таким образом, можно надеяться, что идеи, методы и технические средства голографии будут способствовать совершенствованию и развитию методов управления современными сложными объектами (транспортными системами, роботами, вычислительными и коммутационными сетями и т.д.). В данной лекции обсуждаются некоторые новые возможности управления, основанные на использовании механизмов когерентности (фазовых механизмов) в их различных проявлениях. В разделе 2 обсуждаются принципы интерференционного или голографического управления, в разделе 3 - средства голографического управления (программные, схемные и физические модели устройств управления); в разделе 4 кратко рассмотрены будущие аспекты интерференционного управления.

2. Голография и управление. Возможен ли голографический

процессор?

Как известно, всякий процесс управления включает две фундаментальные операции:

- измерение входного сигнала Х по эталону Х₀ и определение "невязки" Δ(Х, Х₀);

- выработка программы управления u(х), переключающей объект из состояния Х в состояние Х₀.

Пример. Терморегулятор измеряет текущую температуру Т по эталону Т₀, т.е. определяет невязку ΔТ =Т-Т₀ и вырабатывает управление u(Δ).

Структуру программы управления u(Δx) β общем случае можно описать как последовательность во временя сигналов-изображений:

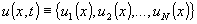. (1)

Алгоритм управления в технических системах управления имеет такую логическую структуру:

если Δ=Δ₁, то u=u₁(x,t);

если Δ=Δ₂, то u=u₂(x,t); (2)

• • •

если Δ=Δ_n, то u=u_n(x,t);

если Δ≠Δ_i, то аварийная остановка системы

(i=1,2,..., n).

Таким образом, совокупность Δ_i-Δ_i представляет собой пару причина-следствие или (что то же самое) стимул-реакция. Рассмотренный алгоритм предполагает, что в памяти система управления должны быть заранее записана программы реакции u_i(x,t) на весь спектр возможных входных сигналов {Δx_i} (стимулов). Проектирование система управления как раз и заключается в определении класса {Δx_i} входных сигналов и в разработке программ- реакций (u_i(x,t)}. Это означает, что система управления работает как обобщенный дешифратор входных сигналов. Сама программа реакции u_i может быть весьма детальной и состоять из ряда подпрограмм (ветвей), распределенных в пространстве и во времени.

Основной недостаток такого рода управляющих систем - отсутствие смысловой надежности /3/. В самом деле, если вход Δ даже незначительно отличается от соответствующего эталонного сигнала Δ_i, система управления оказывается в тупике - не может выработать соответствующую программу-реакцию и (Δ).

Пример. Подчас даже незначительная ошибка в тексте программы на языке (например, ФОРТРАН) исключает возможность наработки соответствующей машинной программы, которая представляет собой реакцию транслирующей системы на соответствующий текст-вход.

Этот недостаток еще более очевиден при анализе типичной системы управления - операционной системы ЭВМ; даже при незначительном отклонении формата входного сигнала (задания, записанного на языке управления работами) от эталонного формата операционная система оказывается в тупике.

Между тем, едва ли можно прекратить управление многими реальными объектами управления (уличным движением, посадкой самолета и т.д.). Иными словами, даже при "нестандартном" входе Δ≠Δ_i, надежная система управления должна вырабатывать "приемлемую" программу управления и (Δ). Это и означает смысловую надежность (разумеется, предполагается и соответствующая надежность технических средств системы).

Отсюда видно, что несомненный интерес представляет создание т.н. интерполирующих /3/ систем управления, способных осуществлять своеобразную интерполяцию "опорных" программ u_i(x,t) , записанных в памяти системы управления на стадии программирования, т.е. вырабатывать программу-реакцию даже на нестандартный вход. Разумеется, качество программы будет неодинаковым для различных входов и в ряде случаев, возможно, плохим. Вопрос о качестве программ должен рассматриваться в рамках охватывающей системы управления, содержащей критерий качества работы охватываемой системы.

Как видно, для реализации алгоритма управления (2) необходимо выполнят к операции:

- корреляционной (ассоциативной) записи и считывания программ;

- выделения общих частей сигналов (формирование эталонов Х);

- управляемой внешними сигналами (параметрами) выборки программ u(х,t)={u₁, u₂,…,u_n};

- формирования (синтеза) программ u(x,t) пo эталону выхода.

Математическая модель корреляционной (ассоциативной) записи, считывания и интерполяции сигналов дана в приложении.

Когерентно-оптоэлектронная техника открывает широкие возможности реализации указанных операций и создания интерполирующих систем управления.

Рассмотрим когерентно-оптоэлектронный голографический процессор /4/, предназначенный для анализа проблем и управления системами. Основа процессора - оптически перестраиваемая процессорная среда искусственного /5/ или естественного /4/ происхождения, которая может голографически накапливать ("свертывать") различные последовательности сигналов-изображений u₁, u₂,.., u_n (т.е. программы p(x,t)). Наиболее общий механизм голографической запаси временной последовательности схематически можно представить следующим образом /4,6/:

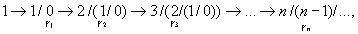(3)

где γ_i - символ голограммы (коррелограммы), записанной на i-ом такте, а символ p/q означает голограмму, полученную когерентным смешением волн р и q независимо от их сложности. Процесс голографического (ассоциативного) накопления цепочки сигналов изображений можно описать следующей символической схемой:

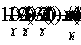
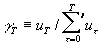(4)

(штрих у знака Σ означает когерентное суммирование волновых фронтов). Как видно, из схемы, 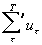является ассоциативным(опорным) признаком для записи последующего во времени изображения u_t+Δt.

Простейший случай ассоциативного накопления типа (3) описывается следующей схемой:

1→2/1→3/2→4/3→...→n/(n-1). (5)

Эта схема учитывает "зацепление" текущего изображения лишь с ближайшим по времени. Схема (3) учитывает "зацепление" текущего изображения со вcеми предшествующими по времени. Можно рассмотреть и промежуточные системы ассоциативного накопления, отличающиеся той или иной "глубиной зацепления" текущего изображения.

Оптические схемы, реализующие ассоциативную запись и считывание (см.дальше) временных цепочек по механизмам (3) и (5), представлены на рис.1^*/. На рис.2 показаны оптические схемы записи-считывания временных цепочек, ориентированные на использование объемных процессорных сред. Электромагнитная волна u_i при взаимодействии с кристаллом пространственной структуры u₀ порождает рассеянную волну u₁/u₀ ( u₁ модулирована структурой u₀); возникает интерференционное поле (u₁/u₀) и соответствующая голограмма γ₁ в кристалле. Аналогично формируется голограмма γ₂ и т.д. В упрощенном виде эта схема напоминает механизм брэгговского рассеяния волны от системы кристаллических плоскостей.

При считывании на вход процессора подается сигнал u_i(1≤i≤n). Процесс циклического порождения выходной последовательности можно представить следующей схемой /4,6/:

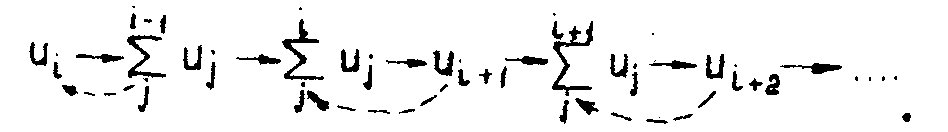
(6)

Если i=1, считывается вся первоначально записанная последовательность.

Для рассмотренных механизмов ассоциативной записи цепочек существенно, что при наложении голограмм в одном и том же объеме процессорной среды происходит не только корреляция ("зацепление") пространственных элементов одного и того же изображения (осуществляемая в традиционном голографе Габора /7/), но также и корреляция ("зацепление") сигналов-изображений, разделенных во временя. Идея голографической записи одномерных сигналов f(t) была высказана Лонге-Хиггансом /8/ (голофон Лонге-Хиггинса). Поэтому прибор, предназначенный для ассоциативной записи цепочек сигналов-изображений может быть назван голографоном /4,6/. Этот прибор реализует тип записи существенно более полный по сравнению с наложением ряда голограмм на одном и том же участке накопительной (процессорной) сре-

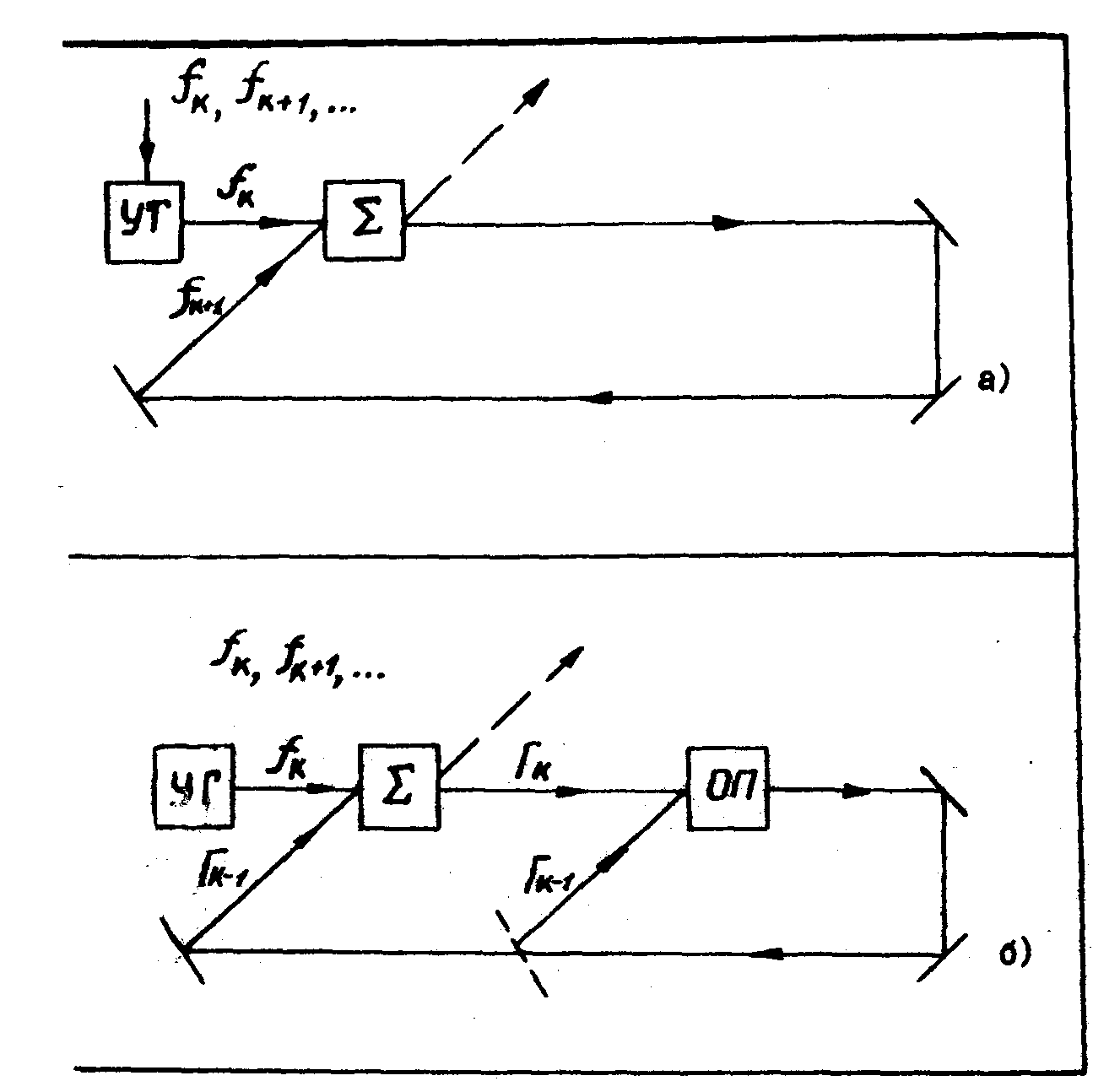
Рис.1. Оптическая схема корреляционной (ассоциативной) записи и считывания временных цепочек изображений:

а) - запись с парным зацеплением; б) - запись с многократным зацеплением.

f_k, f_k+1- элементы входной последовательности изображений; УТ - управляемый транспарант;

Σ- оперативный сумматор интерферограмм <f_kf_k+1>;

ОП - оперативная память для формирования многократно кодированной опорной волны.

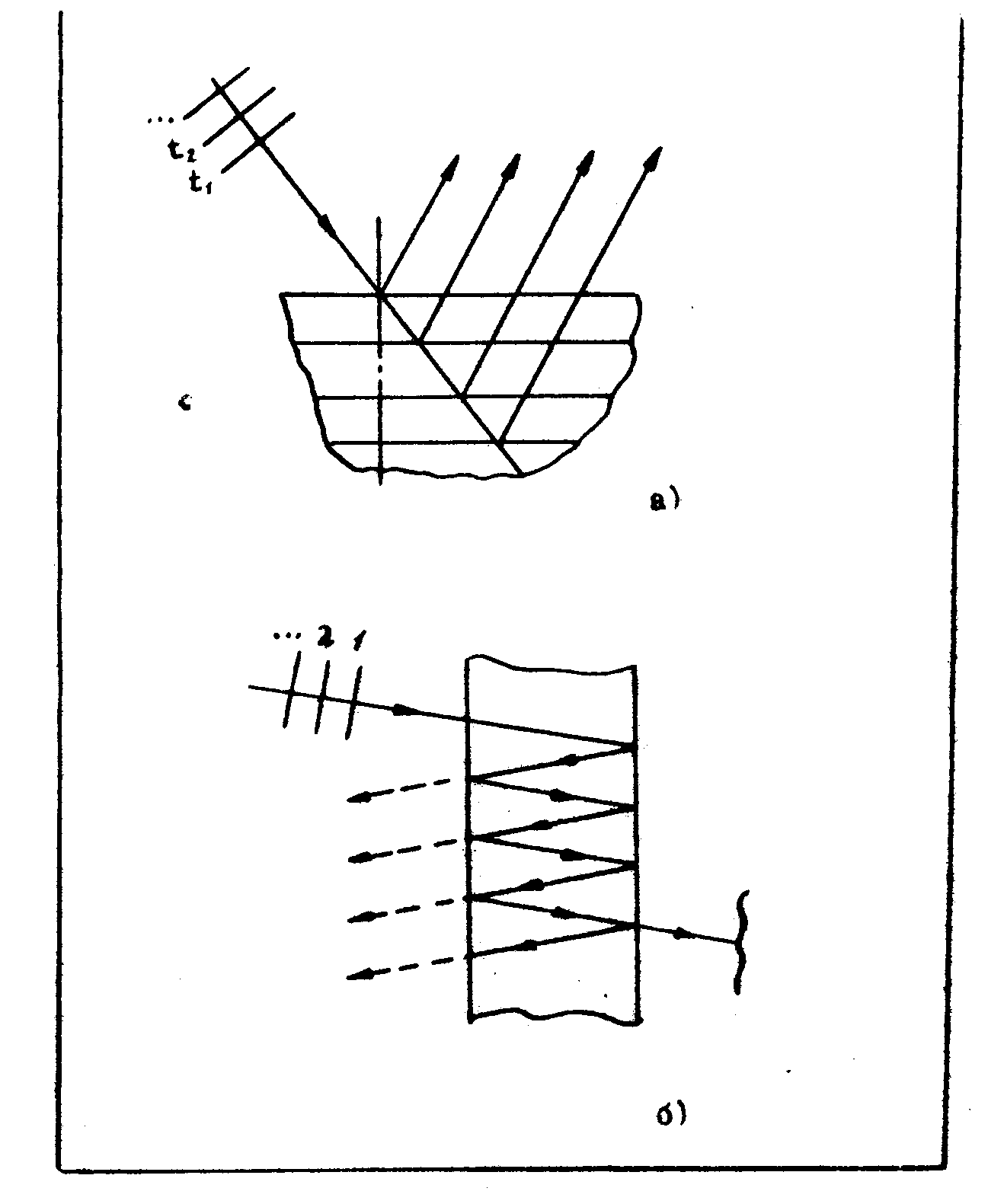
Рис.2. Схема записи и считывания временных цепочек изображений в объемных (слоистых) средах:

а) запись на основе брэгговского механизма (t₁, t₂,… - элементы входной последовательности изображений, б) запись с применением многократной линии задержки (1, 2,... - элементы входной последовательности изображений).

ды, при котором имеет место некогерентное (без корреляционного зацепления) сложение различных изображений, разделенных во времени.

Наряду с жесткой выборкой цепочки сигналов (в том порядке, в какой она была записана) возможна программно-управляемая выборка /4/. В этом случае динамически-формируемый опорный сигнал синтезируется не только с участием записанных ранее сигналов, но также и с помощью внешних программных сигналов (рис.3).

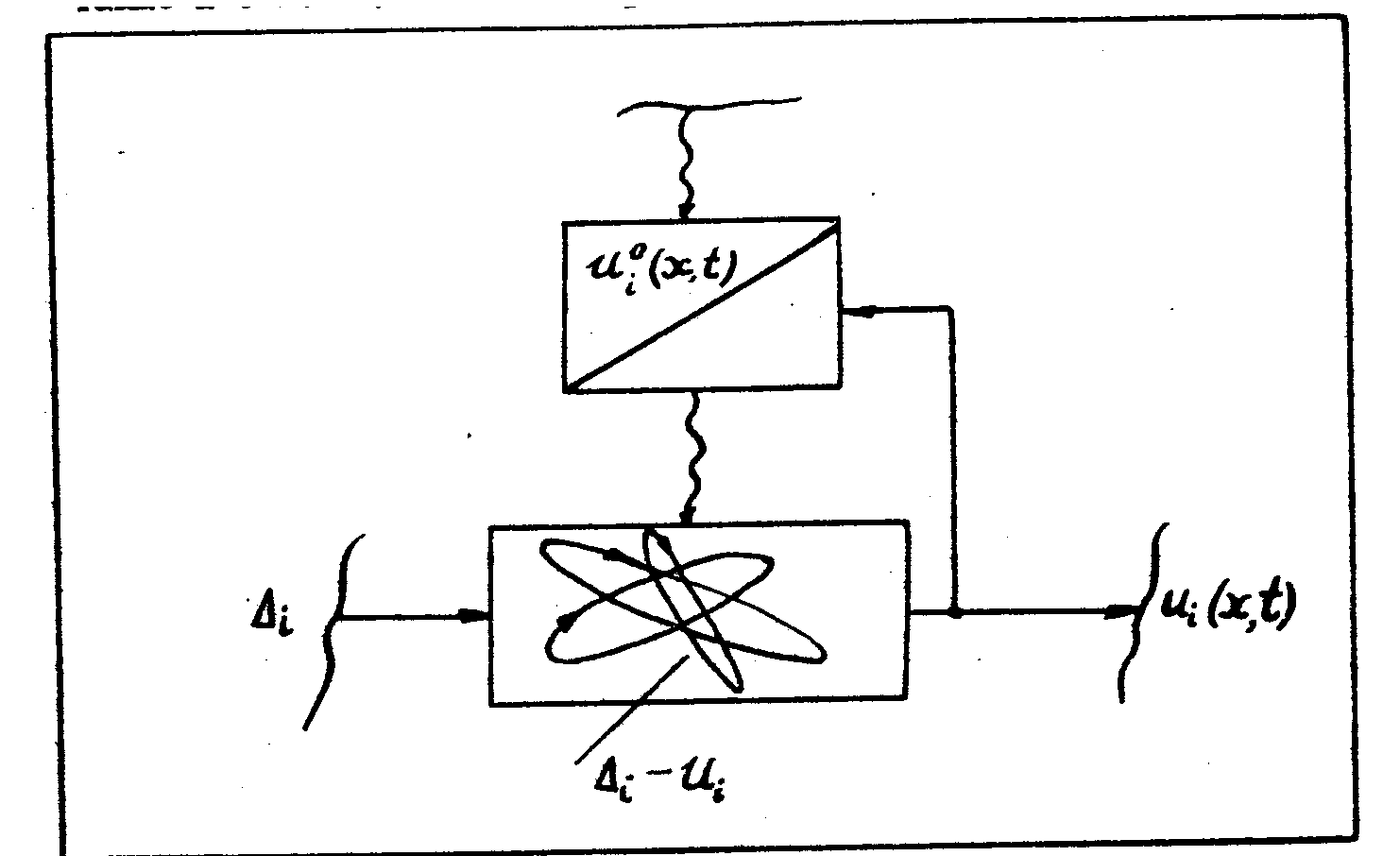
Рис.3. Схема программно-управляемого голографона:

{Δ_i-u_i} - совокупность пространственно-наложенных опорных пар; {u_i⁰}- совокупность эталонных (программных) сигналов, порождаемых охватывающей системой управления.

При восстановлении некогерентно наложенных сигналов-изображений имеет место одновременное восстановление всех сигналов, записанных в различные моменты времени. При восстановлении когерентно наложенных сигналов осуществляется упорядоченная во времени выбор-

ка записанных сигналов.

Если в процессор записаны несколько временных цепочек u₁(x,t), u₂(x,t),..., u_n(x,t), то при подаче на вход некоторого cигнала Δ осуществляется интерполяция входа Δ по системе опорных цепочек и вырабатывается синтетическая цепочка u(x,t), которая ранее не записывалась в процессор. Точная форма интерполированное цепочки определяется системой опорных цепочек, формой входного cигнала Δ, а также структурой процессора (т.е. "встроенной" схемой интерполяции int):

u(x,t)=int{Δ; u₁(x,t), u₂(x,t),..,u_n(x,t)}. (7)

Указанное свойство напоминает интерполяцию в числовых таблицах. Отличие состоит в том, что в рассматриваемых системах элементами таблицы являются опорные пары причина-следствие (или стимул-реакция). Таким образом, рассматриваемое устройство можно рассматривать как интерполятор причинно-следственных цепей.

В результате наложения ряда сигналов реализуется весьма важная логическая операция - выделение общих частей записанных сигналов. В самом деле, при наложении общие части сигналов накапливаются и усиливаются, тогда как различия вносят вклад в "суммарный фон".

Более подробно схемы реализации перечисленных выше операций и структура процессора будут рассмотрены в разделе 3, в котором даются варианты реализации голографического (ассоциативного) процессора с применением различных технических средств.

3.Технические средства голографического управления

Программные модели. С помощью ЭВМ можно построить программные модели ряда рассмотренных голо графических корреляторов - голографа Габора, голофона Лонге-Хиггинса, голографона (в том числе программно-управляемого) , а также ряда других корреляционных приборов.

Японские исследователи /9/ предложили и реализовали на ЭВМ ассоциатрон - сеть запоминающих и логических (коррелирующих) элементов с поведением, напоминающим свойства системы наложенных го-

лограмм. Асооциатрон осуществляет пространственную корреляцию различных элементов (полей) входного векторного кода и запоминает соответствующую коррелограмму (голограмму). При подаче на вход ассоциатрона некоторого поля (признака) на выходе порождается ассоциативно-связанное с данным поле. Путем замыкания обратной связи выход - опорный вход выходной сигнал может быть подан на вход в качестве опорного. Таким образом, реализуются режим записи и считывания временных цепочек (аналог голофона).

Корреляционная матричная память со свойствами, аналогичными ассоциатрону, предложена Кохоненом /10/. В памяти записываются коррелограммы "опорного" и "сигнального" векторных кодов, причем запись последовательных во времена сигналов осуществляется с пространственным наложением. С помощью обратной связи реализуется режим записи-считывания временных цепочек.

Интересную корреляционную модель мозга предложил Фукусима /11/. Модель основана на записи временных корреляций между элементами временных цепочек и на наложении соответствующих коррелограмм в одной и той же области накопительной среды. На рис.4 показан процесс записи и считывания цепочек изображений 1,2,..., 9 и А, В, .... После записи модель может работать в режиме ассоциативной (интерполирующей) выборки цепочек. Обращает на себя внимание своеобразный аффект постепенного улучшения качества выбираемых изображений, обусловленный перестройкой корреляционной матрицы на каждом такте выборки. При многократной прокрутке цепи на некотором такте может быть получен хорошо сформированный признак, по которому и осуществляется выборка соответствующей цепи. В оптической голографии такого рода временные режимы пока еще не исследованы.

В работе /12/ предложен и реализован на ЭВМ универсальный коррелятор матричного типа. Расширение возможностей достигается как за счет выбора настраиваемой ячейки корреляционной матрицы, так и за счет создания режима программного управления. Во всех вышеперечисленных моделях выбираемая последовательность полностью определялась входным сигналом и записанными ранее коррелограммами. Программно-управляемый коррелятор обеспечивает произвольную выборку с последовательностью, определяемой не только входом и содержимым памяти коррелятора, но и внешними программными сигналами, вво-

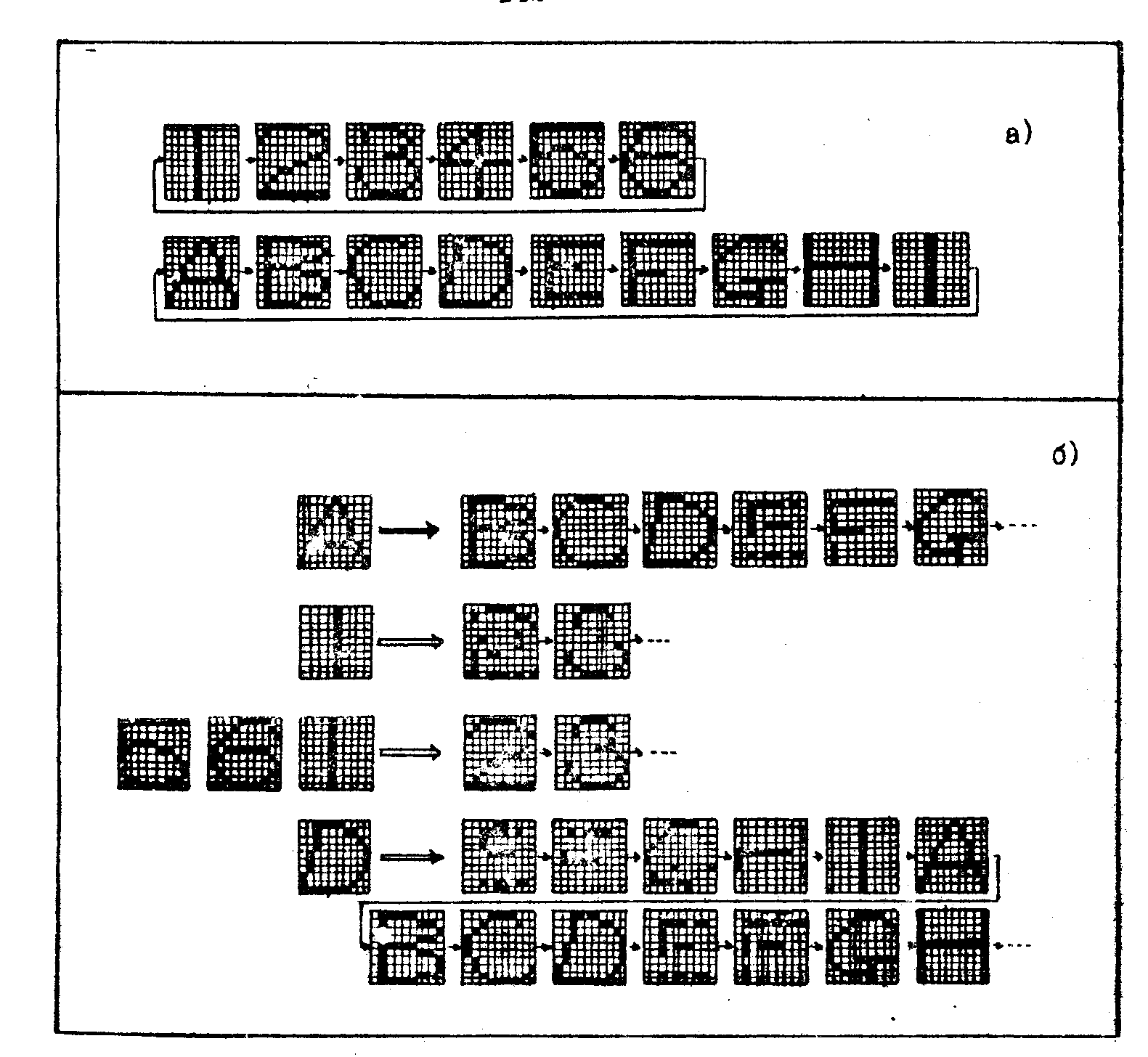
Рис.4. Результаты машинного моделирования операций записи и считывания временных цепочек в ассоциативном процессоре /11/:

а) - запись двух циклически-замкнутых последовательностей (цифр и букв);

б) - результаты считывания при возбуждении процессора различными входными изображениями и отрезками цепей.

димыми в контур обратной связи. Некоторые возможные режимы работы коррелятора представлены на рис.5.

Любой из рассмотренных корреляторов с пространственным наложением коррелограмм (голограмм) характеризуется тем, что отношение сигнал/шум зависит от степени заполнения памяти и уменьшается с заполнением памяти. В традиционных системах памяти это отношение постоянно. В работе /13/ предложен коррелятор на основе "развивавшейся" среды. Число ячеек (объем корреляционной матрицы) в этом корреляторе не постоянно, а зависит от входного потока информации: как только в некоторой ячейке матрицы отношение сигнал/щум уменьшится ниже определенного порога, запускается механизм удвоения ячейки (механизм увеличения памяти). В результате удвоения память увеличивается, степень заполнения уменьшается, и поэтому отношение сигнал/шум возрастает. В этом устройстве объем матрицы контролируется входами сигналами, т.е. запись осуществляется в "растущей" среде. Такой коррелятор можно рассматривать как модель клеточной среды, растущей под влиянием сигналов "новизны". Различные режимы работы развивающегося коррелятора представлены на рис.6(а,б,в). В случаях б и в для упрощения картины представлена выборка, соответствующая сигналам только одного уровня.

Схемные цифровые модели. Несмотря на заметные успехи в создании т.н. "синтетических" голограмм с помощью ЭВМ, сама идея расчета голограмм на ЭВМ обладает существенным недостатком: в отличие от "естественных" голограмм синтетические вычисляются поточечно, т.е. последовательно во времени. Поэтому в системах, в которых синтез голограммы должен быть осуществлен в реальном масштабе времени, метод синтетических голограмм едва ли окажется полезным (например, в системах с накоплением синтетических голограмм).

Эти недостатки устраняются в т.н. схемных цифровых голограммах /5/ - перспективной разновидности синтетических голограмм. Средой для записи таких голограмм являются цифровые микроэлектронные и оптоэлектронные фазовые решетки /5/, реализуемые на основе однородных микроэлектронных и оптоэлектронных больших интегральных схем (БИС). Такие фазовые решетки или схемные корреляционные матрицы должны обладать свойством близкодействия, т.е. способностью передавать сигнал от точки к точке. Это означает, что рассматри-

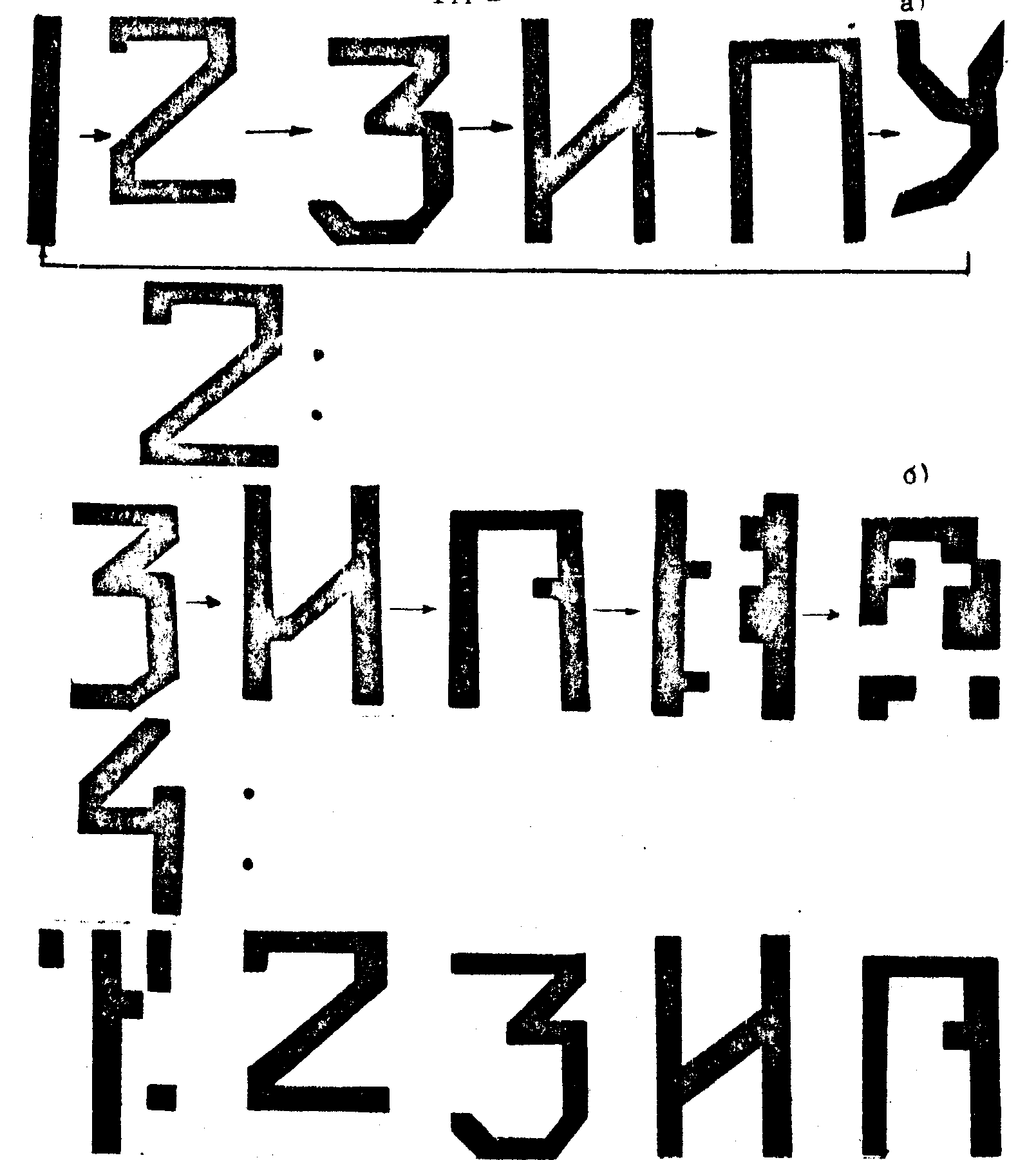
Рис.5. Результаты машинного моделирования работы программно-управляемого голографона: а) - запись последовательности изображений 1,2,3, И,П,У с парным зацеплением; б) - порождение выходных цепей при подаче использованного ранее изображения 2 и "неизвестного" изображения 4 (эффект интерполяции опорных пар).

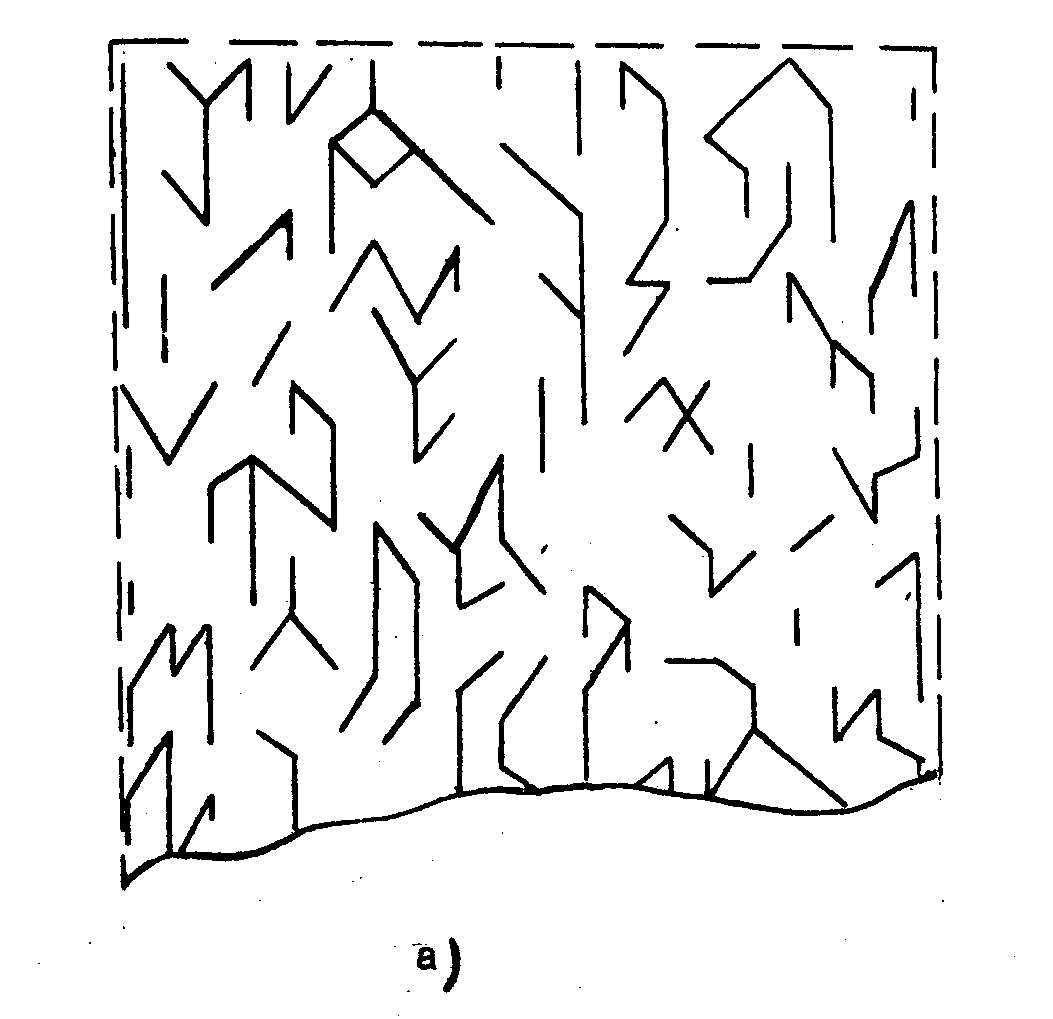
Рис.6. Результаты машинного моделирования корреляционной (ассоциативной) записи и считывания в голографоне с переменным числом ячеек ("развивающийся" процессор):

а)- пространственное распределение изменяющихся во времени (в вертикальном направлении) случайных входных сигналов 20-битного формата;

б)- аналогичная картина для выходных сигналов, демонстрирующая стохастическую структуру в пространстве в во времени;

в) пространственно-временная структура выходных сигналов, когда на вход подается последовательность одинаковых сигналов 11...1 (20 бит ), переходит в упорядоченную структуру, изменяющуюся к стационарному состоянию.

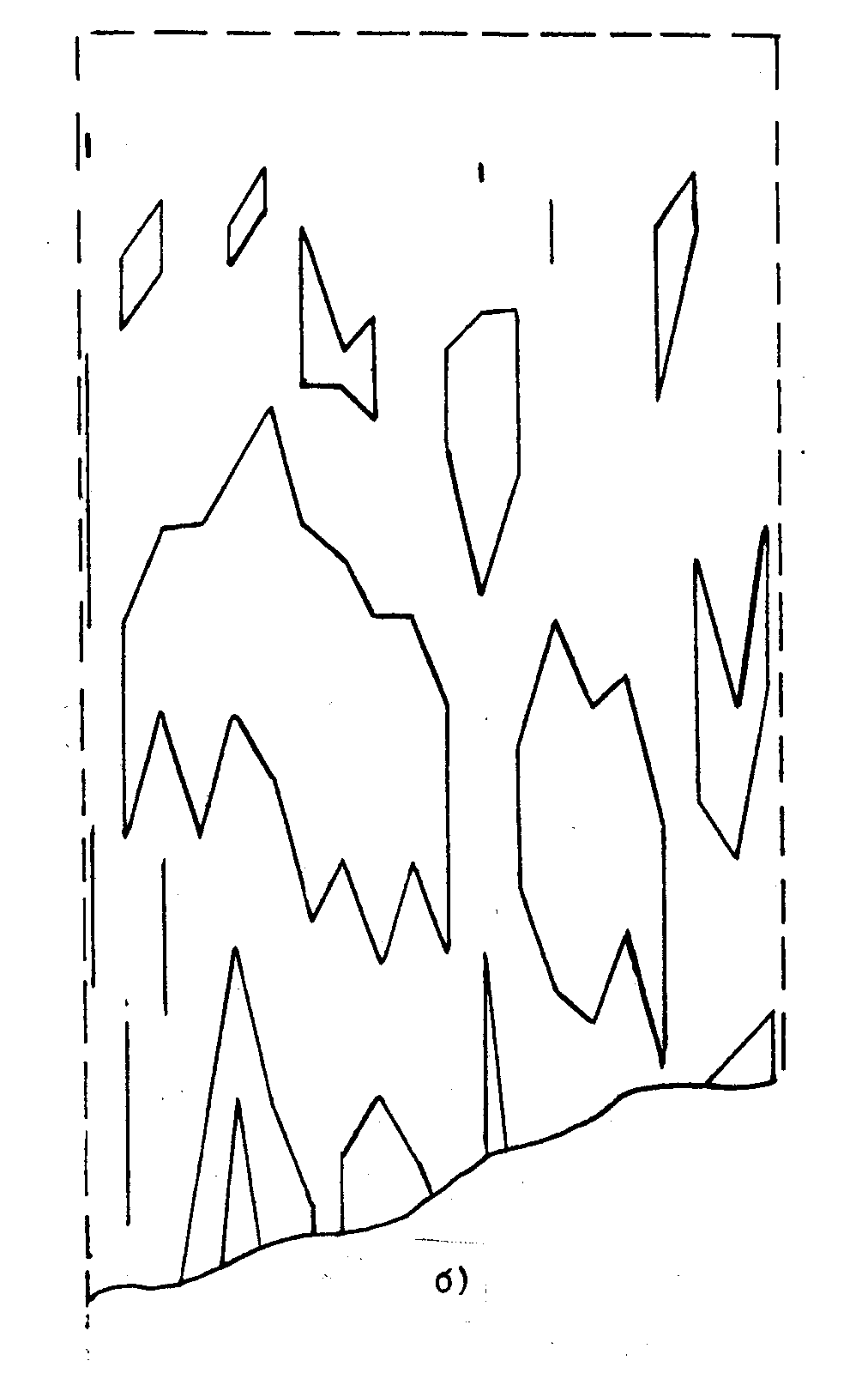
Рис.6.

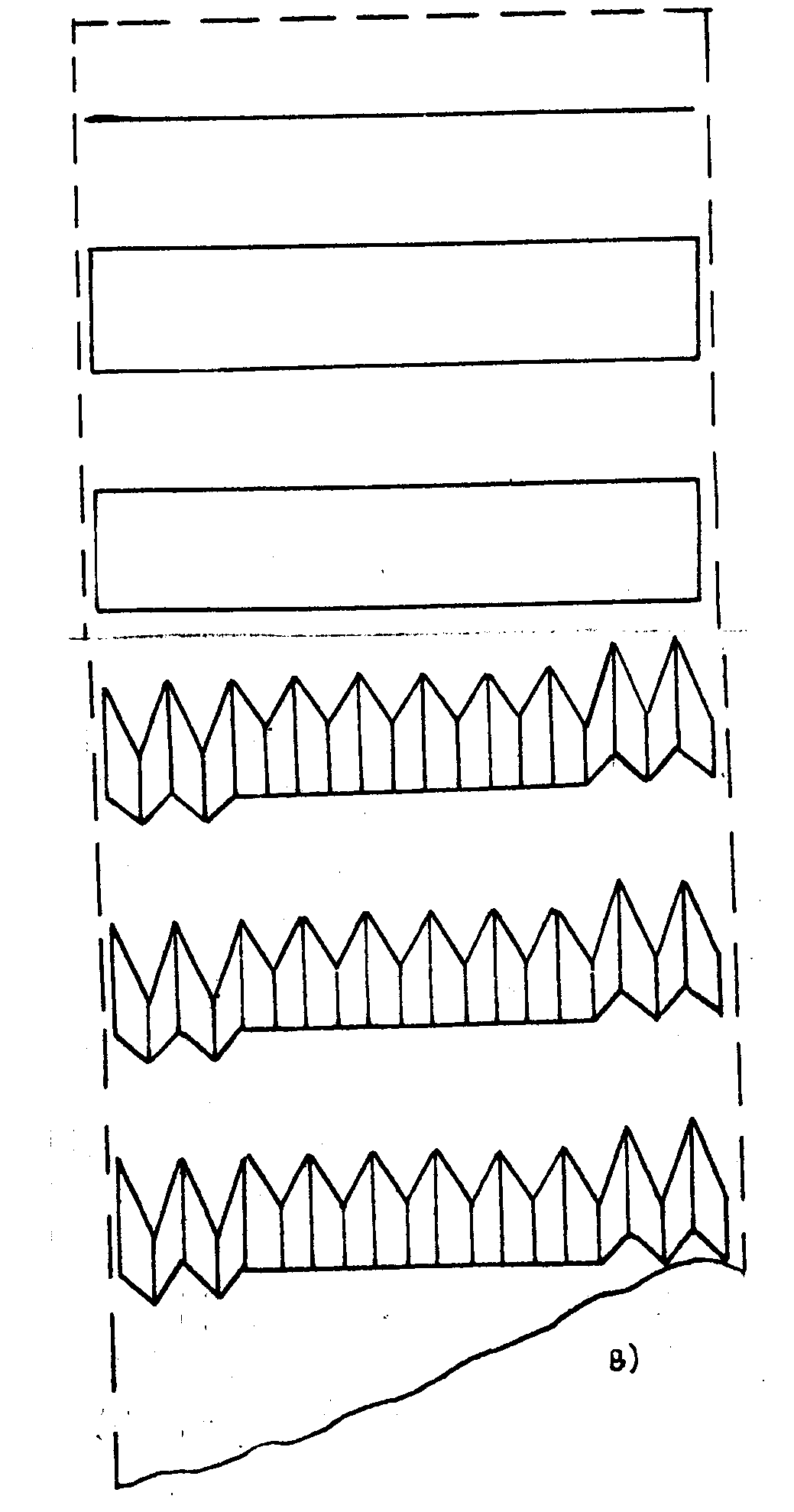
Рис.6 .

ваемые решетки удовлетворяют принципу Гюйгенса. Цифровая природа решеток обеспечивает управляемое усиление волновых фронтов, затухающих при распространении в решетке.

Микроэлектронные корреляционные матрицы снабжаются двумя входными регистрами: опорным и сигнальным. Волновые фронты, порождаемые соответствующими регистрами, интерферируют (коррелируют) в решетке, при этом закон корреляции определяется логикой, "встроенной" в каждую ячейку матрицы (решетки). В простейшем случае (распространение в решетке в двух ортогональных волн) запись корреляций осуществляется в тех ячейках матрицы, в которых с помощью 2-входовой логики совпадения регистрируется синхронный (когерентный) приход двух волновых фронтов. Для запоминания количества совпадений предусмотрена память, управляемая от выходов логической схемы. Схема ячейки и структура матрицы показаны на рис.7.

При считывании волна опроса порождается опорным регистром и, проходя по матрице, модулируется (по определенному закону) содержимым памяти каждой ячейки. Выходной регистр можно снабдить дополнительными устройствами - дискриминатором, сумматором и т.д., в функции которых входит приведение выходного сигнала к должному формату, накопление и т.д.

Путем замыкания обратной связи выходной регистр-опорный регистр реализуется режим работы типа голографон, обеспечивающий ассоциативную запись и считывание временных цепочек.

Указанные схемные цифровые корреляторы обладают многими ценными свойствами, присущими голографическим устройствам: надежностью относительно нарушений связей и самих ячеек, параллельностью работы, ассоциативностью доступа и т.д. Некоторые свойства схемных цифровых корреляторов пока еще не имеют аналога в оптических системах записи-считывания; к ним относятся режимы записи и считывания временных цепей, управляемая логика корреляции, управляемая обратная связь и т.д.

Возможности т.н. логических (цифровых) голограмм были рассмотрены недавно Сороко /20/ который обратил внимание на ряд преимуществ схемно-реализуемых логических голограмм.

Большой интерес представляют цифровые оптоэлектронные фазовые решетки (корреляционные матрицы). Это - однородные БИС с встро-

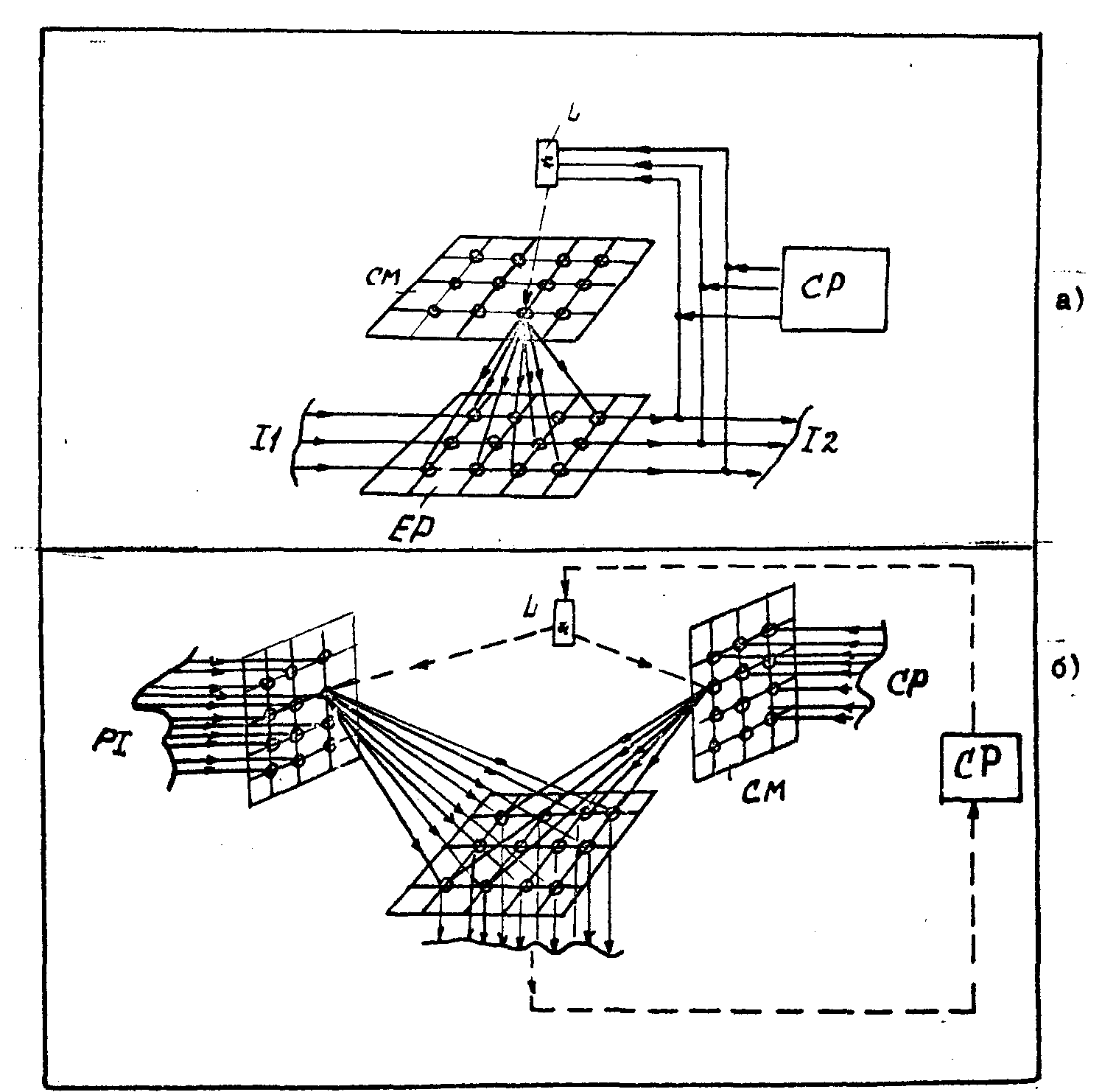
Рис.7. Блок-схемы оптоэлектронных процессоров-корреляторов с голографической управляющей памятью:

а)- процессор ЕР с электрическими входами (i 1) и выходами (i 2) и с оптической голографической управляющей памятью СМ; СР - управляющий процеccор c хранимой программой;

б) - процессор с параллельными оптическими входами и выходами для управляющей (СМ) и обрабатываемой (pi) информации и с оптической обратной связью СР для модификации программы управления вычислительным процессом.

енной фотоприемной подрешеткой и встроенной модулирующей (выводной) подрешеткой /5,12/. Иными словами, входной и выходной регистры такой матрицы распределены по всей матричной структуре, причем обеспечивается параллельный ввод и вывод информации в матрицу. Разделение формата входного регистра на опорную и сигнальную части - произвольное. Так, при записи в матрицу оптического изображения (например, буквы а) каждый оптический вход оказывается источником расходящейся (например, сферической) волны. Волны от всех каналов интерферируют (коррелируют) между собой с записью результатов корреляции подобно тому, как это имело место в микроэлектронных корреляционных БИС. "Радиус" размазывания оптического входа, целесообразно сделать регулируемым. В ряде случаев, когда высокой, надежности не требуется, можно ограничиться небольшим радиусом размазывания (например, зоной размером 2х2 ячеек). Однако, когда необходима высокая надежность, этот радиус должен быть большим (вплоть до размера всей матрицы). Таким образом, надежность (или избыточность) оказывается регулируемой. Эта возможность весьма удобна также в процессе создания и юстировки оптической схемы сопряжения оптической памяти и оптоэлектронного матричного коррелятора: размазывание входа по некоторой зоне не требует точной юстировки каждой пары окно-луч.

Выводная подрешетка может быть выполнена в виде матрицы жидкокристаллических клапанов/14/, матрицы встроенных интегральных кремниевых модуляторов /5/, гибридно-встроенных светодиодов или полупроводниковых лазерных диодов. При этом выходное изображение может быть записано (как и транспаранта) в оптическую память, отображено оператору системы или передано по оптическому каналу связи.

Физические модели. Дальнейшие перспективы реализации ассоциативных (голографических) процессоров-корреляторов связаны с использованием непрерывных сред, перестраиваемых оптическими, акустическими и др. сигналами.

Большой интерес представляют собой пьезо(сегнето)электрические кристаллы, в которых могут распространяться поверхностные (объемные) акустические волны. Входной и выходной регистры для таких сред могут быть выполнены в виде линейки (или матрицы) интеграль-

ных излучателей и приемников (например, резонаторы встречно-штыревого типа). В поляризованных сегнетоэлектриках электрические домены обладают преимущественной ориентацией и образуют своеобразную накопительную среду для записи голограмм /15/. Интерференционное поле, порождаемое входным регистром, может быть записано в результате изменения ориентации доменов под влиянием максимумов интерференционного поля. Указанные среды допускают запись голограмм с наложением и могут быть использованы для создания голографических корреляторов различного функционального назначения /15/.

Оптический ассоциативный процессор на основе перестраиваемого электрооптического материала рассмотрен в работе /4/, в которой анализируются типы инверсных (метастабильных) сред, пригодных для ассоциативной записи временных цепочек изображений. Надо полагать, однако, что создание полностью оптического ассоциативного процессора потребует серьезных и длительных исследований перестраиваемых материалов "с встроенным усилением".

4. Будущие аспекты интерференционного (фазового) управления

Рассмотренные принципы и технические средства управления в конечном счете основаны на использовании фазовой информации. В традиционных системах обработки информации и управления (например, в ЭВМ) фазовая информация, присущая естественным сигналам, теряется. Однако, поскольку большинство моделей реальных процессов обладает присущей им пространственной связностью (когерентностью) и временным упорядочением (синхронизацией), при создании моделей процессов в ЭВМ фазовую информацию приходится восстанавливать искусственно - с помощью логических схем и надлежащего программирования. В голографических системах фазовая информация учитывается уже на уровне схем (материала системы).

В связи о этим представляет интерес попытка использовать для целей обработки информации и управления фазовые эффекты, присущие естественным схемам: электронным, оптическим, акустическим и т.д. Следует учитывать, однако, что разработка соответствующего подхода находится пока еще в самой начальной стадии. Поэтому мы лишь качественно рассмотрим несколько возможностей, предоставляющих по-

тенциальный интерес для создания систем управления (автоматов) будущего.

Когерентно-электронные схемы /6/. Почему два тока в обычных электронных схемах не интерферируют? Длина свободного пробега l_с или длина когерентности в металлах или полупроводниках изменяется обычно в пределах 1-100 нм. Однако, при понижении температуры l_с увеличивается и при переходе в сверхпроводящее состояние может достигать макроскопических значений (вплоть до 1,33 м /16/). В таких когерентно-электронных схемах /6/ как амплитуда, так и фаза электронного тока (квантового тока) могут быть использованы для кодирования информации. Квантовые токи могут интерферировать; как известно, созданы образцы вакуумных и пленочных электронных интерферометров (см.,например, /16/). Для записи электронных голограмм /17/ могут быть использованы пленки некоторых сегнетополупроводников и сегнетодиэлектриков, обладающих "мягкой" (перестраиваемой) подрешеткой, находящейся в инверсном (химически преднакачанном) состоянии /4/. Запись осуществляется либо непосредственно медленными электронами, либо оптически (с оптическим возбуждением электронных состояний). В работе /17/ предложено электронно-голографическое запоминающее устройство с применением сегнетоэлектрической накопительной среды. Для считывания информации, записанной в виде решетки "переклиненных" атомов, могут быть использованы излучательные эффекты, сопровождающие перестройку решетки. Возможны и другие варианты считывания, включающие визуализацию выходного электронного изображения /17/ с применением вакуумных развертывающих систем.

Главное преимущество когерентно-электронных схем по сравнению с когерентно-оптическими заключается в том, что длина волны электронной (де-бройлевской) несущей на 3-4 порядка меньше длины волны оптической несущей. Это означает, в частности, что объемная плотность записи может быть на 9-12 порядков выше таковой в оптических накопительных системах. Еще одно преимущество когерентно-электронных цепей обусловлено возможностью прямого управления электронной волной с помощью электрических воздействий. Так, например, изменение длины волны осуществляется простым изменением управляющего напряжения.

Электромагнитные решетки как управлявшие элементы. Обычно

(оптический) резонатор служит для фазовой синхронизации излучательных процессов во многих возбужденных атомах и для пространственной селекции мод электромагнитного поля (ЭМ). Однако, резонатор может быть полезен и как своеобразное устройство управления процессами, протекающими в резонаторе. Управляющим элементом резонатора является ЭМ решетка, отражающая пространственную и временную структуру ЭМ поля в резонаторе.

Как известно, в резонаторе могут быть сформированы стоячие и бегущие ЭМ решетки. Стоячие решетки переключаются путем изменения граничных условий в резонаторе. Для этого можно применить зеркала с управляемым коэффициентом отражения или управляемые транспаранты. Бегущие ЭМ решетки создаются в результате интерференции (биений) мод с различными частотами и определенными фазами. Путей надлежащего управления фазами можно синтезировать ЭМ решетки, осуществляющие разнообразные поисковые операции (сканирование, зондирование площадей и объемов, развертку и т.д.). Решетки могут быть использованы для пространственного управления процессами, протекающими в резонаторе. В частности, для модуляции свойств поверхностей кристаллов, объемом в химических реагирущих смесей и т.д. В лазерных резонаторах управляемые внешними источниками ЭМ решетки могут служить для модуляции (управления) параметров лазерного излучения - длины волны, параметров когерентности, мощности и т.д. Использованию лазерного резонатора в качестве устройства управления процессом роста кристалла посвящен отдельный раздел.

Резонатор как схема параллельного перебора (схема оптимизации). Как известно, для отыскания оптимальных управлений применяется метод перебора состояний, контролируемый критерием качества. В современных устройствах перебора (ЭВМ) операция переборе осуществляется последовательно во времени, и поэтому число варьируемых (оптимизируемых) параметров обычно не превышает 3-6 ("проклятие размерности"). Между тем, имеется настоятельная необходимость оптимизации систем с 10⁴-10⁶ параметрами.

Схема параллельного перебора, скорость которого не зависит от числа оптимизируемых параметров, может быть основана на использовании управляемых переходных процессов в (оптическом) резонато-

ре /3/. Схема перебора показана на рис. 8. Перебор состоянии осуще-

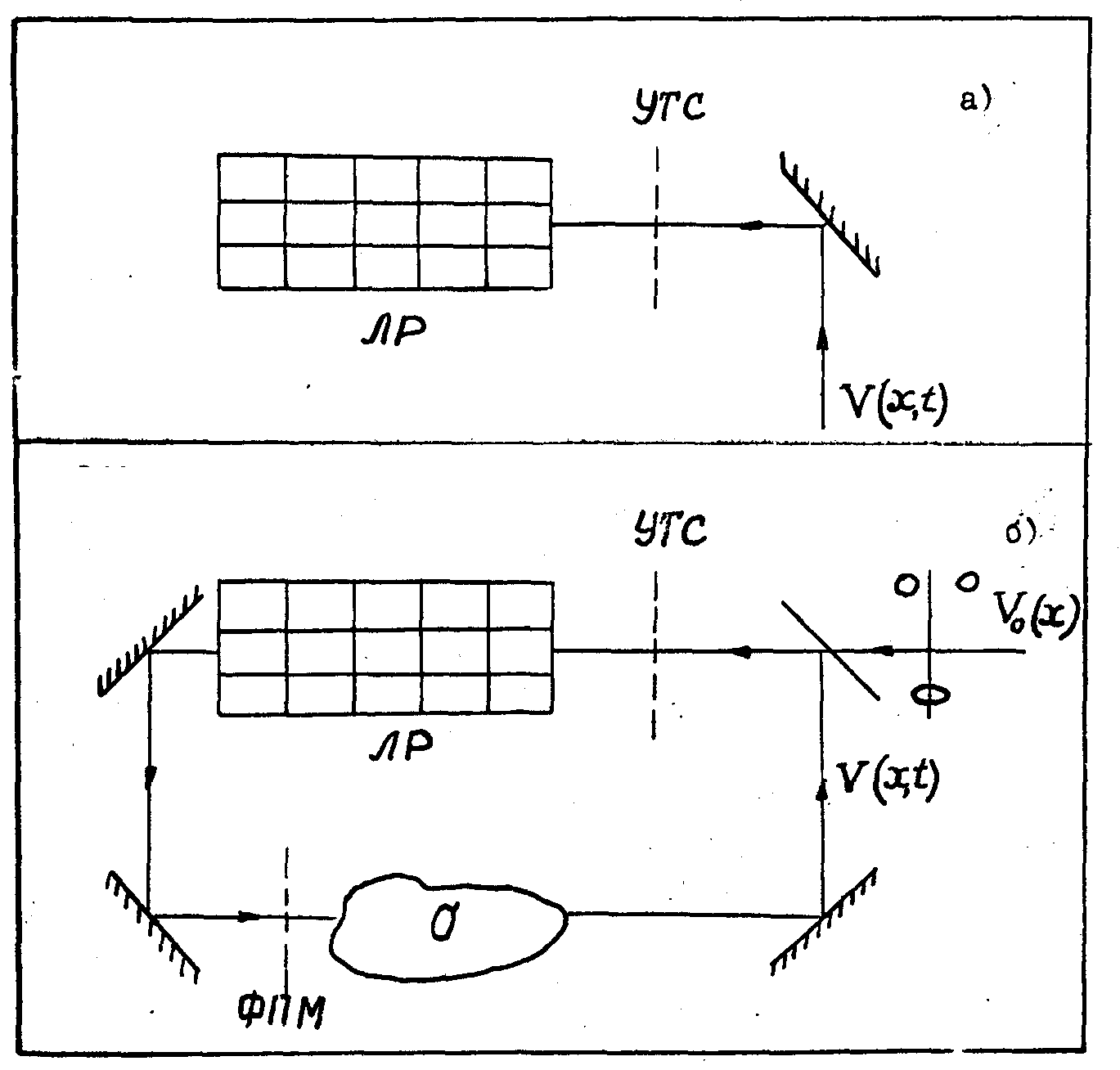
Рис.8. Схема параллельного перебора состояний (мод), выполненная на основе оптического резонатора с управляемыми граничными условиями:

а)- схема управления переходным процессом (переключения мод) путем формирования оперативных граничных условий на встроенном в резонатор УТС;

б)- схема слежения (стабилизации) за состоянием объекта δ; ЛР - лазерный резонатор; УТС - встроенный оптически-управляемый транспарант; ФПМ - встроенная в резонатор фотоприемная матрица, v₀ - изображение, кодирующее эталонное состояние объекта; v - изображение, кодирующее текущее состояние объекта.

ствляется в переходном процессе, запускаемом изменением граничных условий в резонаторе. Для формирования граничных условий, т.е. для управления переходным процессом, можно применять (вместо зеркала) управляемый транспарант. Считывание модовой структуры резонатора можно осуществить с помощью фотоприемной матрицы, встроенной в резонатор; выходы матрицы непосредственно переключают объект управления. Каждое пробное состояние объекта, генерируемое резонатором, сравнивается по выходу с эталонным состоянием, и результат сравнения ("невязка") подается на формирователь граничных условий (УТ). В результате в переходном процессе принимает участие вся замкнутая система, включающая объект управления. Переходный процесс завершится лишь при условии совпадения выходного сигнала объекта с эталонным сигналом. В этом случае граничные условия перестанут изменяться и переходный процесс (процесс перебора) прекратится. Параллельность перебора обусловлена тем, что одновременно проверяется (на соответствие граничным условиям) целый класс состояний резонатора, т.е. сравнение осуществляется по многим пространственным каналам. Важная особенность физических схем перебора в том, что в процессе перебора происходит непрерывное и "самосогласованное" изменение граничных условий в резонаторе.

К возможности фазового управления ростом кристаллов. В процессах роста кристаллов наблюдается /18/ ряд явлений пространственного и временного упорядочения, которые пока еще но имеют удовлетворительной трактовки. К ним относятся кольца Лизиганга, решетка из плавающих кристаллов /18/, селективность в процессах перекристаллизации, упорядоченная ориентация при эпитаксиальном наращивании /18/ и т.д. В чем, например, причина весьма тонкой селекции (избирательности) процесса адсорбции атомов (молекул) из газовой фазы при росте?

В одной из работ автора /19/ выдвинуто предположение о том, что избирательность может быть обусловлена передачей когерентности от растущего кристалла А атому В неупорядоченной фазы (газ, расплав, раствор и т.д.). и на зависимости сил взаимодействия А-В от фазового состояния (параметров когерентности) электронных оболочек А и В. Как хорошо известно, два атома водорода h(is) притягивается или отталкивается в зависимости от того, в каком фазовом состоя-

нии находятся их электроны. Если волновые функции атомов Н_А и Н_В в фазе, т.е. если

Ψ=Ψ_А+Ψ_В,

где Ψ_А и Ψ_В - атомные электронные волновые функции, атомы притягиваются с энергией (в макетные) 4,74 эв. Однако, если электронные волны Ψ_А и Ψ_В в противофазе, т.е. если

Ψ=Ψ_А-Ψ_В,

то атомы Н_А и Н_В отталкиваются. Это - не что иное как эффекты конструктивной (синфазной) и деструктивной (противофазной) интерференции - основа квантовой трактовки свойств химической связи. В конечном счете, управление взаимодействием А-В осуществляется весьма слабым (с энергетической точки зрения) сигналом - спиновой компонентой общей волновой функции системы, т.е. управляющий сигнал на 4-6 порядков слабее управляемого.

Если предлагаемый фазовый механизм контроля межатомных сил правильный, то существует возможность искусственного изменения параметров когерентности электронных оболочек А и В и тем самым возможность искусственного управления ростом кристалла /19/ или направлением химической реакции. Разумеется, в фазовый механизм вносят вклад все квантовые числа системы АВ (а не только спиновые). Поэтому управляющими входами, контролирующими межатомное взаимодействие, является параметры когерентности электронных состояний А и В. Возможности фазового управления становятся особенно гибкими, если одна из систем А(В) или обе находятся в когерентных супер-позиционных состояниях. Каждое такое состояние задается вектором комплексных коэффициентов {с_k} - весов стационарных состояний в суперпозиционном состоянии Ψ или матрицей плотности и тока в надлежащем базисе.

Поскольку управление параметрами когерентности отдельного атома невозможно, необходимо обеспечить излучательную связь между всеми атомами газовой фазы, возбужденными в надлежащее когерентное состояние, а также создать условия фазовой синхронизации всех пар А-В. Иными словами, процесс управляемого роста должен осуществлять-

ся в резонаторе, в котором происходит принудительная синхронизация всех элементарных актов возбуждения атомов и взаимодействия с кристаллом через связывающее (управляющее) поле излучения, формируемое о помощью внешних источников излучения с управляемыми параметрами когерентности.

Подбирая надлежащие параметры когерентности, можно обеспечить селективную адсорбцию на поверхности кристалла атомов одного определенного типа (или даже атомов в определенном электронном состоянии). Для пространственного управления адсорбцией атомов можно использовать искусственно созданную в резонаторе решетку определенной пространственной структуры.

Таким образом, возможно, что в основе механизма "узнавания" в системах атом-кристалл лежат хорошо известные фазовые (интерференционные) эффекты и возможность передачи параметров когерентности с помощью модулированных фотонов. Процесс роста должен сопровождаться когерентным излучением, модулированным структурой кристалла. Иными словами, фотоны, излученные кристаллом, должны обладать специфическим (для данного кристалла) когерентным суперпозиционным состоянием поляризации (наряду, возможно, с суперпозиционным энергетическим состоянием). Такие модулированные фотоны несут всю информацию о структуре растущего кристалла и, в принципе, могут вызвать процесс кристаллизации в удаленном от источника излучения месте.

В ы в о д ы.

1. На основе идей и методов голографии могут быть созданы не только эффективные системы памяти, но и голографические процессоры, отличающиеся повышенной надежностью и быстродействием и способные управлять реальными сложными объектами.

2. В голографическом процессоре реализуются операции ассоциативной записи цепочек изображений, сопровождающиеся автоматическим выделением общих элементов как в пределах отдельного изображения, так и в пределах всей временной цепи. При считывании некоторой цепи по входному изображение осуществляется выявление ("вычисление") связей входного изображения с записанными в процессор ранее. Таким

образом, результатом работы процессора являются неизвестные ранее (скрытые) пространственные и временные связи между элементами цепей. Процесс считывания можно также трактовать и использовать для интерполяции входного изображения по системе опорных цепочек.

3. В настоящее время разработаны и исследованы ряд реализованных на ЭВМ моделей голографических процессоров, демонстрирующих свойства выявления скрытых связей и интерполяции.

Созданы схемотехнические предпосылка для разработки цифровых голографических устройств на основе однородных микроэлектронных и оптоэлектронных корреляционных матриц - больших интегральных схем.

Предложены и разрабатывается перспективные акустические и оптические модели голографических процессоров.

4. Разработка концепции голографического (фазового) управления находится в начальной стадии. Наиболее перспективными представляются следующие направления исследований и разработок: создание интегральных когерентно-электронных (джозефсоновских) схем, использование перестраиваемых электромагнитных решеток в качестве объемных управляющих элементов, исследование логических свойств резонаторов (как устройства оптимизации), доследование возможностей когерентно-оптического управления процессом роста кристаллов (оптоэлектронных функциональных схем машин будущих поколений).

Автор благодарен Г.В.Скроцкому за разъяснение, касающееся необходимости применения процесса управления ростом ко всему коллективу атомов, а не только к элементарному акту, В.В.Аристову за обсуждения механизма голографической записи и считывания временных цепочек изображений. Автор благодарит также А.Е.Краснова и Ю.А.Грибова за полезные обсуждения.

Приложение

Рассмотрим математическую, модель операции пространственной интерполяции. Формирование каждой опорной решетки Р_ab и ее воздействие на входные сигналы удобно описывать с помощью матрицы или оператора проектирования. Так, если опорная решетка Р_ab образуется в результате взаимодействия двух "волновых фронтов" а и b, то оператор, соответствующий этой решетке ab, можно представить в виде:

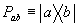, (1)

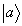где и 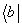- соответственно, кэт- и бра- векторы в соответствующем пространстве входных состояний (дираковские обозначения). В матричных обозначениях (1) имеет следующий вид:

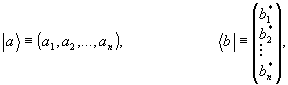(2)

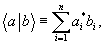
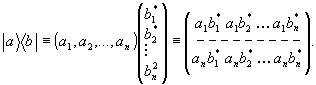
Из определения (1) следует:

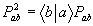, (3)

т.е. p_ab является оператором проектирования:

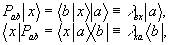(4)

где 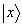- произвольный кэт-вектор, а 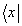- произвольный бра-вектор. Как видно, если входной вектор кэт-типа, то решетка p_ab, проектирует его на свой кэт-вектор 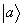, если это бра-вектор, то проекция осуществляется на бра-вектор 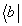. Иными словами, при полном опросе (бра- и кэт-составляющими) решетка p_ab порождает решеточные составляющие 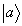и 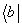с весами λ_bx и λ_xa соответ-

ственно.

Если а=b и 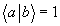, проектор Р_ab переходит в стандартный оператор проектирования Р_a с обычными свойствами:

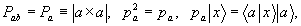
т.е. проектор Р_a - ортогональный.

Рассмотрим систему решеток типа (1):

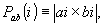i=1,2,…n (5)

и введем пространство r_n, "натянутое" на систему решеток (5):

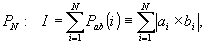(6)

здесь i - единичный оператор ("разложение единицы"). Тогда проекция произвольного вектора х (c бра- и кэт-соcтавляющими) в пространство r_n дается соотношением (вектор к преобразуется оператором r_n):

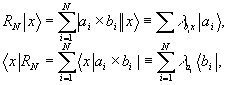(7)

где λ_αβ - соответствующие коэффициенты корреляци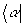и и 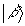(или проекции кэт-вектора 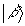) на все бра-векторы ).

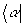Рассмотрим теперь различные частные случаи соотношения (7).

1. Пусть n =1. Тогда

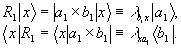(8)

Таким образом, при опросе решетки r₁ произвольным вектором х восстанавливается бра-часть 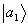(с весом 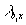) и кэт-часть 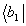(с весом ).

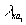Положим последовательно х=a₁ и х=b₁:

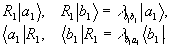(9)

Таким образом, при опросе решетки r₁ бра-вектором 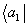"восстанавливается" (порождается) бра-вектор 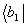; при опросе кэт-вектором 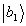восстанавливается кэт-вектор 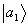. Последний вывод справедлив, если cоответcтвующие недиагональные коэффициенты корреляции λ_αβ ("проекции") равны нулю; это, как известно, имеет место при условии ортогональности соответствующих векторов.

Таким образом, если λ_αβ =δ_αβ (δ_αβ - символ Кронекера), то решетка r₁ обладает своеобразным свойством селективности, т.е. выделения коррелированного ответа.

2. Пусть n=2. Тогда:

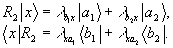(10)

Таким образом, при опросе "двойной решетка" r₂ произвольным вектором х восстанавливаются бра-част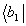и и 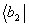и кэт-части и 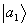(все - с соответствующими весами).

Если 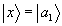и λ_αβ=δ_αβ, то

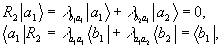(11)

т.е. реализуется эффективная система восстановления попарно-связанных в решетках r_αβ≡|α´ β| векторов.

3. Пусть n>2 и 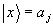. Тогда:

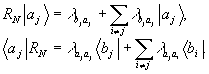(12)

Если λ_αβ=δ_αβ, то 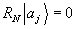и 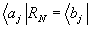, т.е. реализует-

ся эффективный механизм коррелированной записи и считывания сигналов а_i и b_i (i= 1,2,..., n) сложной структуры.

Что касается обеспечения условия λ_αβ=δ_αβ, то для этого могут быть предложены эффективные методы корреляционного "зацепления" сигналов, т.е. методы формирования коэффициентов λ_αβ. В общем случае опрос описывается общим соотношением (7) и соответствует операции интерполяции входа х по системе опор r_n.

Л и т е р а т у р а

1. p.j.van heerden. optical information storage in solids. appl. opt., 9, 387, 1963.

2. Л.М.Сороко. Интерференционная обработка информации. Усп.физ. наук, т.90, 3-29, 1966.

3. В.К.Быховский. Управление и обработка информации в асинхронных процессорных сетях. Труды финско-советского симпозиума "Мини-ЭВМ и распределенная обработка данных" (Хельсинки, 24-26 ноября 1974 г.,), т.1, 1974.

4. В.К.Быховский. Принципы построения ассоциативного оптического процессора. В кн: Проблемы голографии, вып.2, изд. МИРЭА, 165-170, 1973.

5. В.К.Быховский и др. Методы оптического ввода информации в интегральные микроэлектронные структуры. В кн: Проблемы голографии, вып.2, изд.МИРЭА, 170-175, 1973.

6. В.К.Быховский. Когерентно-электронные системы накопления и обработки информации. Вычислительные системы, вып.49, 174, 1972.

7. d.gabor. associative holographic memory. ibm j.res.dev., 13, 2, 156, 1969.

8. h.c.longuet-higgins. a holographic model of temporal recall. nature, 217, 104, 1968.

9. n.nakano. associatron- a model of associative memory. ieee trans. on syst., man and cybernetics, smc-2, 380, 1972.

10. t.cohonen. correlation matrix memory. ieee Тrans. on Соmp., c-21, 353, 1972.

11. k.fukushima. a model of associative memory of a brain. kybernetik, 6, 3, 1973.

12. В.К.Быховский и др. Параллельный оптоэлектронный процессор для анализа проблем и управления системами. Автометрия, № 2, 1975.

13. В.К.Быховский, Н.Н.Полухина. Об одной модели распределенной регуляции в биологических системах. В кн: Регуляция биохимических процессов в микроорганизмах. Пущино-на-Оке, АН СССР, Научный центр биологических исследований, 23-27, 1972.

14. w.c.stewart, l.s.cosentino. optics for в read-write holographic memory. appl.opt., 9, 2271, 1970.

15. К.И.Брицын и др. Акустоголографический процессор. Автометрия, №2, 1975.

16. Л.Солимар. Туннельный эффект в сверхпроводниках и его применение, М., Мир, 1974.

17. В.К.Быховский. Интерференционное запоминающее устройство. Бюлл. изобр., №9, 1970. Авт.свид.№264729.

18. А.В.Шубников, В.В.Парвов. Рост кристаллов. Наука, 1970.

19. В.К.Быховский. Модель управляемого роста макромолекулярных и кристаллических структур. Кристаллография, т.18, 575-579, 1973.

20. Л.М.Сороко. Опыт Юнга-Уолша и логическая голография. Материалы vi Всесоюзной школы по голографии. Л., изд.ЛИЯФ, 81-127, 1974.