КВАНТОВЫЕ ЭФФЕКТЫ В ГОЛОГРАФИИ
Б.А.Гришанин
Обсуждается возможная роль квантовой природы волновых полей в голографии. Для случая электромагнитного поля оценивается роль шума поглощения квантов и рассчитывается принципиальный предел информационной емкости голографического канала, связанный с вакуумным квантовым электромагнитным полем.
1.
Перспективы неоптической голографии
Современная голография имеет дело почти исключительно с диапазоном длин волн, ограниченным с коротковолновой стороны видимыми электромагнитными волнами. Этот диапазон непригоден для получения изображений объектов, сравнимых по масштабам с атомными структурами, имеющими порядок 1Å. Само же зарождение голографии в работах Габора было связано именно с задачами электронной микроскопии. Несмотря на фундаментальные преимущества диапазона волн λ ~ 1Å è менее, таких как электронные и рентгеновские, голография в этом диапазоне не получила широкого развития вследствие отсутствия источников, сочетающих достаточную интенсивность и когерентность.
Тем не менее, работы по голографии в этом диапазоне продолжаются. Например, в работе группы японских авторов /1/ была получена осевая электронная голограмма Фраунгофера частиц золота диаметром 100 Å на длине волны λ=0,037 Å è с помощью Нe-ne лазера были восстановлены изображения высокого качества.
Проникновение в область коротких волн происходит и с противоположного участка спектра длин волн - со стороны более длинноволнового оптического диапазона, в котором имеются источника достаточно интенсивного и высококогерентного излучения. Первые го-
лограммы в области вакуумного ультрафиолета были недавно получены группой Харриса /2/ с использованием 9-ой гармоники λ=1182 Å ëазера 10640 – Å nd: АИГ. Средняя мощность отфильтрованного излучения составляла Р = 1,5 мк вт при длительности импульсов ~ 0,5n сек с частотой следования 5n сек. В качестве фоточувствительного материала применялся полиметилметакрилат (ПММА), обеспечивающий разрешение менее длины волны. С помощью интерференции двух плоских волн были получены голографические дифракционные решетки с постоянной d = 836 А, а также голограммы Фраунгофера сферических частиц диаметрами 0,4 - 1.3 (микрон). Оптимальная экспозиция составляла Е = 100 мк да/см~ Для восстановления изображения использовались результаты промера голограммы электронным микроскопом, в соответствии с которыми изготавливалась увеличенная копия голограммы, по которой восстанавливалось изображение в видимом свете. (Предлагается также техника непосредственного расчета изображения на компьютере с помощью вычисления интеграла Френеля /3/).
В настоящее время ведется интенсивная работа по исследованию возможностей создания генераторов когерентного излечения в диапазонах вакуумного ультрафиолета, рентгеновских и даже γ-волн. Что касается первых двух диапазонов, то для них механизм генерации предполагается таким же, что и для обычных лазеров, т.е. электронные переходы в атомах. Генерация же γ-излучения связывается с переходами между ядерными энергетическими уровнями, что требует привлечения методов накачки и синхронизации, существенно, отличных от традиционных для оптических лазеров.
Если лазеры этих типов будут созданы, то, вероятнее всего, голография явится одной из первых сфер их применения. В связи с невозможностью применения обычных линз в этих диапазонах электромагнитных волн голографические методы дают единственно возможный способ получения изображений. В случае же электронной микроскопии улучшение когерентности источников также стимулировало бы применение голографических методов, поскольку они свободны от искажений, свойственных электронной микроскопии.
2.
Определение квантовых эффектов и наиболее универсальные
квантовые особенности волновых полей,
существенные для голографии
Переход к новым сферам приложения голографии естественно потребует модернизации представлений, сложившихся в традиционной оптической голографии. Одним из направлений такой модернизации является учет квантовой природы волновых полей. Но, прежде чем переходить к анализу соответствующих новых (ректоров, необходимо проанализировать содержание понятия квантового эффекта.
Последовательное определение "квантовости" состоит в отнесении к квантовым эффектам тех, для которых существенно ненулевое значение постоянной Планка ħ=
h/2π = 1,054·10-27 эрг·сек. Такая точка зрения соответствует привычному определению "квантовости" для таких явлений как:
1) волновые свойства частиц с ненулевой массой покоя, обусловленные ненулевым значением длины волны де-Бройля λ
=hc/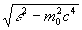 , что следует из стационарного общерелятивистского уравнения Клейна-Гордона
, что следует из стационарного общерелятивистского уравнения Клейна-Гордона
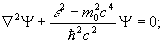 (2.1)
(2.1)
2) корпускулярный характер энергии полей частиц с нулевой массой
m0=0, как это следует из (2.1) с учетом того, что коэффициент при втором члене есть k2=ω2/с2 и потому ε=hc/λ οри λ<∞.
Вспомним, однако, о таком эффекте как запрет Паули, не позволяющий двум ферми-частицам, например электронам, находиться в одном и том же состоянии. Этот запрет следует из квантовой специфики волновой функции Ψ, которая в квантовой теории является не числовой, как в классической теории, а операторной функцией (в общем случае с несколькими компонентами). Поэтому в квантовой теории не все физические величины, связанные с полем, коммутируют, т.е. АВ≠ВА, как это имеет место при перемножении матриц. Для полей ферми-частиц:
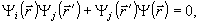 (2.2)
(2.2)
откуда и вытекает после соответствующего анализа запрет Паули. Для эффектов, связанных с этим запретом, постоянная Планка не имеет решающего значения, хотя по общепринятой классификации это явление вполне квантовое.
Существенно отметить, что хотя квантовая специфика любых эффектов всегда в конечном счете связана с проявлением перечисленных факторов (волновой характер частиц ненулевой массы, корпускулярный характер безмассовых полей, запрет Паули), их проявления настолько разнообразны и различны по результирующим эффектам, что качественный анализ этих эффектов без использования математического аппарата квантовой теории крайне затруднителен. Это в значительной степени связано с отсутствием должной базы для физической интуиции, которая может быть выработана лишь путем исследования все более расширяющегося круга квантовых явлений. Особенно продуктивно в этом отношении исследование квантовых объектов макроскопического характера.
Здесь следует отметить, что квантовая природа явлений не обязательно связана с их микроскопичностью. Это ясно из существования таких квантовых явлений, как сверхпроводимость, ферромагнетизм, квантовые свойства света. (Например, для потока лазерного излучения интенсивностью
i, условие буквальной применимости к нему классических волновых представлений:
i
c
2/ ħ
ω4>>1
выполняется лишь для потоков
i 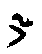 1000 вт/см2. Квантовый же характер слабых световых потоков, как это следует из опытов Вавилова, может быть обнаружен невооруженным глазом). Квантовые эффекты делятся на макроскопические и микроскопические точно так же, как и неквантовые, и при этом следует помнить, что граница между "микро" и "макро" условна и зависит от степени оснащенности иссле-
1000 вт/см2. Квантовый же характер слабых световых потоков, как это следует из опытов Вавилова, может быть обнаружен невооруженным глазом). Квантовые эффекты делятся на макроскопические и микроскопические точно так же, как и неквантовые, и при этом следует помнить, что граница между "микро" и "макро" условна и зависит от степени оснащенности иссле-
дований предельно чувствительной аппаратурой и степени нашей адаптации к масштабам.
При переходе от оптического к рентгеновскому и γ-диапазону электромагнитных волн проявляется целый спектр квантовых особенностей: поглощение, рассеяние и отражение носят существенно квантовый характер. Это в равном степени относится и к электронным волнам. Исследование этих явлений составляет предает оптики и атомной физики и реальные голографические эксперименты, естественно, должны учитывать квантовую специфику всех этих явлений. Однако здесь мы коснемся только самых универсальных квантовых закономерностей, которые с неизбежностью должны проявиться в любом голографическом эксперименте:
а) противоречивость требований большой интенсивности и высокой когерентности для источников электронных волн;
б) квантовый характер поглощения энергии электромагнитных волн;
в) роль вакуумного электромагнитного поля.
3.
Голографический канал связи и соответствующие
ему информационные характеристики
Самыми универсальными оценками роли различных эффектов в голографии являются информационные оценки, поскольку голографический эксперимент в информационном смысле реализует составной канал связи следующего вида: объект → волновой фронт → интерференционная картина → голограмма → восстановленный фронт. Отметим в связи с этим обстоятельством, что представления теории связи использовались еще Лейтом и Упатниексом для объяснения разделения изображений.
Ограничение количества информации в любом из звеньев описанного голографического канала означает, по меньшей мере, такое же ограничение для всего канала. Поэтому имеется возможность оценивать эти ограничения по наиболее "узкому" звену. Таким узким звеном в случае плохой когерентности будет звено волновой фронт → интерференционная картина. В случае регистрации голограммы с по-
мощью материала, работающего как поглотитель квантов поля (практически виреально используемые голографические регистрирующие "материалы работают именно так), можно оценить связанные с этим потери, рассчитав информационную емкость звена интерференционная картина → голограмма. Принципиальный предел для информационной емкости всего голографического канала, обусловленный не техническими ограничениями, а квантовым характером поля (наличием вакуумного шумового поля) можно получить, рассчитав информационную емкость звена, объект → волновой фронт. Некоторые из оценок такого типа даются ниже.
4.
Принципиальные пределы степени когерентности
электронных источников
Как уже отмечалось выше, электроны подчиняются запрету Паули: в одном и том же состоянии не может находиться более одной частицы. Этим они принципиально отличаются от бозе-частиц, например, фотонов, которых в каждом состоянии может быть сколько угодно. Именно это свойство фотонов используется в лазерах, где относительно "небольшое" число состояний "накачивается" большим числом порций энергии (квантов), что и обеспечивает интенсивное излучение. В случае же электронов для получения больших интенсивностей требуется иметь много состояний. Поэтому, чем больше интенсивность, тем большая для ее получения требуется полоса частот ω=Ε/ħ и, соответственно, меньшая длина когерентности l=2π/Δω. Если забыть о неизбежном электромагнитном взаимодействии электронов (кулоновское отталкивание) и рассмотреть состояния свободного электронного поля, детектируемого на некоторой апертуре s, то, подсчитывая число состояний n, соответствующих интервалу наблюдения Т и интервалу частот Δω, μожно для интенсивности потока i = n/st и длины когерентности Е получить соотношение
i
l<2k
2c.
Это ограничение, правда, не имеет практического значения: при
l~1 м
и λ
~ 1 Å èз него следует i < 1026 частиц/см2сек. Для более реальных оценок требуется учесть более конкретные условия генерации электронного потока. teм не менее, можно ожидать, что принципиальные пределы в данном случае не имеют практического значения и ограничения когерентности и интенсивности связаны лишь с техническими возможностями.
5.
Роль шумов, обусловленных поглощением квантов
Для электромагнитного поля принципиальных ограничений на когерентность и интенсивность, подобных описанным выше, не существует, т.е. интенсивность источников может, в принципе, считаться неограниченной и не зависящей от его когерентности, декретный же характер поглощения квантов является достаточно универсальным явлением для голографии, так как принцип действия подавляющего большинства регистрирующих материалов, применяемых в настоящее время, состоит именно в поглощении квантов энергии поля. К сожалению, точный расчет информационной емкости звена интерференционная картина → поглотитель квантов (голограмма) аналитически выполнить не удается. Тем не менее, составить представление о роли этого эффекта можно, рассчитав обусловленное им ограничение разрешающей способности голограммы.
Число квантов электромагнитного поля, в среднем попадающее на площадь Δs, есть
n=eΔs/ħω,
(5.1)
где Е - экспозиция, величина которой связана с чувствительностью и другими характеристиками регистрирующего материала. Для упоминавшегося в п.1 эксперимента в диапазоне вакуумного ультрафиолета в объеме разрешения материала Δ
s было n~1000, т.е. относительная флуктуация числа квантов i/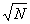 в объеме разрешения была порядка нескольких процентов. Это означает, что роль квантового характера поглощения в данном эксперименте на один - два порядка была менее существенна роли конечной разрешающем способности матери-
в объеме разрешения была порядка нескольких процентов. Это означает, что роль квантового характера поглощения в данном эксперименте на один - два порядка была менее существенна роли конечной разрешающем способности матери-
ала. Квантовое же ограничение разрешающей способности для данного эксперимента, вытекающее из (5.1), при n~1 имеет порядок 3 Å, что не представляет в данном эксперименте реального ограничения. Если же, однако, при этих расчетах подставить частоты ω рентгеновского диапазона (при той же экспозиции Е), то получим для квантового предела разрешающей способности
Δs~ħω/e≈300
Å,
что вполне ощутимо.
Резюмируя, можно сказать, что применяемые в наиболее тонких современных голографических экспериментах экспозиции и разрешающие способности регистрирующих материалов позволяют приблизиться к уровню квантовых шумов, а в рентгеновском диапазоне квантовые шумы, по-видимому, будут существенным фактором.
6.
Принципиальный квантовый предел информационной
емкости электромагнитного голографического канала
Если допустить возможность записи голограммы не только методом счета квантов, а любым способом, то никаких принципиальных ограничений на передачу информации по звеньям голографического канала от выходного волнового фронта до восстановленного не будет. Однако, даже в этом идеальном случае в силу квантового характера электромагнитного поля информационная емкость звена объект - волновой фронт ограничена вследствие некоммутативного характера физических переменных поля и вытекающего отсюда факта существования вакуумного шумового электромагнитного поля.
Объектная волна имеет в квантовом случае вид :
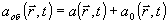 ,
,
где а есть классическая (числовая) комплексная амплитуда объектной волны, а
0 - квантовый вакуумный шум, имеющий операторный (нечисловой) характер. Если поле разложить с помощью преобразования Фурье на плоские волны, то на каждую плоскую волну вакуумного
поля будет приходиться энергия вакуумных флуктуации ħω/2. Классическая амплитуда
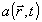 несет неискаженную голографическую информацию об объекте, которая наблюдается на фоне вакуумного шума а0
несет неискаженную голографическую информацию об объекте, которая наблюдается на фоне вакуумного шума а0.
Можнo выполнить точный расчет количества информации, которое содержится в объектной волне
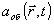 относительно
относительно 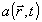 при ее наблюдении на плоской поверхности (апертуре) s в течение времени Т.
при ее наблюдении на плоской поверхности (апертуре) s в течение времени Т.
Предположим, как это всегда имеет место в голографии, что
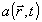 не содержит временной информации, а пространственная ограничена некоторой пространственной частотой νmax. Эти обстоятельства учитываются видом классической объектной волны
не содержит временной информации, а пространственная ограничена некоторой пространственной частотой νmax. Эти обстоятельства учитываются видом классической объектной волны
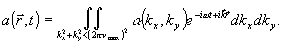
Здесь функция
α(kx, ky) описывает двумерную голографическую информацию об объекте. Если фиксировать энергию волны 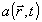 на апертуре s за время Т, положив ее плотность ε/s равной экспозиции Е, то максимум информации между аоб и а[α] дается формулой:
на апертуре s за время Т, положив ее плотность ε/s равной экспозиции Е, то максимум информации между аоб и а[α] дается формулой:
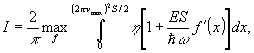 (6.1)
(6.1)
где функция
f >0 удовлетворяет условию:
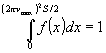 , (6.2)
, (6.2)
связанному с ограничением энергии, а
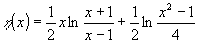
функция, называемая иногда "квантовым логарифмом".
Если выполнено условие
ρ>>1 большого отношения сигнал/шум
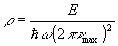 , (6.3)
, (6.3)
то из (6.1), (6.2) можно получить явное выражение
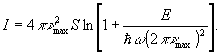 (6.4)
(6.4)
Характерной особенностью выражения (6.4) является его линейная зависимость от площади, что выражает геометрический характер информации. Произведение
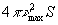 имеет смысл числа элементарных информационных каналов.
имеет смысл числа элементарных информационных каналов.
В суперквантовом пределе малого отношения сигнал/шум ρ
<<1
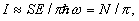
где n - среднее число квантов регистрируемого поля на всей апертуре.
7.
З а к л ю ч е н и е
Изложенные соображения и оценки показывают, что в современной оптической голографии специфические квантовые особенности волнового поля с информационной точки зрения мало существенны. По этой причине актуальность квантовой модернизации теоретических принципов голографин самым прямым образом зависит от успехов в области создания новых источников волновых полей и перспектив их использования в голографии. Остается выразить надежду на скорый прогресс в этой области и экспериментальное освоение существенно квантовой голографической информации.
Л и т е р а т у р а
1. jap.j.appl.phys., 7, 295, 1968.
2. appl.phys.lett., 25, 451, 8, 15 oct., 1974.
3. appl.phys.lett., 11, 77, 1967.

