ГРУППОВЫЕ СВОЙСТВА ГОЛОГРАММ
В.Б.Немтинов
В рамках скалярной теории дифракции исследована групповая структура интерференционного поля. Построена теоретико-групповая модель инвариантности интерференционного поля, регистрируемого на голограмме. Показано, что она позволяет с единой теоретико-групповой точки зрения не только классифицировать все имеющиеся в настоящее время разновидности голограмм, но и прогнозировать новые типы голограмм. Приведены примеры, иллюстрирующие применение модели.
В в е д е н и е
В настоящее время известно большое количество различных разновидностей голограмм. При этом в основу классификации обычно кладутся определенные физические характеристики, признаки и свойства голограмм, регистрирующих сред и схем записи.
В частности, в зависимости от структуры поля, записываемого на голограмме, различают голограммы сфокусированного изображения, голограммы Френеля и Фраунгофера и различные виды голограмм Фурье /1,2/. Выбор схемы голографирования (относительное расположение предметного и опорного пучков) приводит к понятию осевой голограммы с наклонным опорным пучком и голограммы во встречных пучках. При определенном положении интерференционной картины, регистрируемой на голограмме, относительно светочувствительного материала в зависимости от соотношения между толщиной материала и шагом интерференционной картины можно говорить о плоских и объемных голограммах. Использование регистрирующих сред с амплитудной и фазовой модуляцией позволяет выделить, соответственно,
амплитудные и фазовые голограммы /1/. В зависимости от множества точек, в которых осуществляется регистрация интерференционной картины, различают непрерывные и дискретные голограммы. Последние по способу регистрации делятся на физические и математические (машины) /3/.
Приведенный достаточно большой перечень различных типов голограмм показывает, что в настоящее время отсутствует единый подход к классификации голограмм, учитывающий математическую структуру голографической записи. Последнее, естественно, затрудняет прогнозирование новых типов голограмм и схем записи. В то же время процесс регистрации голографической информации обладает резко выраженным свойством симметрии, которое можно описать с помощью принципа взаимности /3/. Иначе говоря, при определенных условиях предметная и опорная волны могут меняться местами.
С другой стороны, при записи голограммы регистрируется интерференционная картина, которая возникает при сложении двух (или нескольких) распределений комплексной амплитуды поля (предметной и опорной волны). Идея инвариантности суммарного поля, регистрируемого на голограмме, которая лежит в основе симметрия голографической записи, наиболее полно может быть описана в рамках теории групп /4/. Применение теоретико-группового подхода в голографии интересно тем, что при этом физические идеи не упускаются из виду.
Теоретико-групповой формализм широко используется в современной физике /5,6/. Основные понятия теории групп (одного из важных разделов "неколичественной" математики) проникли во многие разделы физики и нашли применение в таких ее областях, как например, квантовая механика и кристаллография. При этом теория групп оказывается весьма полезной при систематизации широкого круга различных физических задач, связанных с теми или ввмми проявлениями симметрии (выделение кристаллографических сметем, классифякацхя уровней энергии в квавтогой механике и т.п.).
В работе в рамках скалярной теории дифракции дан теоретико-групповой анализ математической структуры голографической записи. Показано, что идея инвариантности интерференционного поля, обусловленной симметрией процесса голографической регистрации, оказы-вается полезной при систематизации имеющихся разновидностей голограмм и прогнозировании новых типов голограмм. При этом все разновидности голотрамм допускают единое рассмотрение с теоретико-групповых позиций. Приведем сначала ряд математических сведений, которые лежат в основе последующего рассмотрения.
1. Определение группы
Абстрактной группой g /4,5/ называется множество элементов g, h, r и т.д. с бинарной алгебраической операцией Ä
, заданной на атом множестве. Иначе говоря, для любой пары элементов g, hÎ
g определен третий элемент rÎ
g, так что
gÄ
h=r. (1)
В общем случае заданная операция может быть некоммутивной (некоммутивная группа) и иметь произвольную природу. Однако при этом должны выполняться следующие три аксиомы:
а) введенная операция должна быть ассоциативной, т.е. для произвольных элементов
g, h, rÎ
g
gÄ
(hÄ
r)=(gÄ
h) Ä
r=gÄ
hÄ
r. (2)
б) во множестве
g должен существовать единичный элемент e, такой что для любого gÎ
g
gÄ
e=eÄ
g=g (3)
в) кроме того, для любого элемента
gÎ
g существует обратный элемент g-1, такой, что
gÄ
g-1=g-1Ä
g=e (4)
В качестве групповой операции
Ä
может быть обычное
сложение (аддитивная группа) или умножение (мультипликативная группа) чисел, умножение матриц, операторов и т.п. Если групповая операция перестановочна, то группа называется коммутативной или абелевой.
Нетрудно видеть, что несмотря на число формальное определение с группами в той или иной мере сталкивается каждый, кто занимается математикой или ее приложениями. Рассмотрим несколько примеров групп.
Приме
p.1. Множество комплексных чисел, за исключением нуля, с обычной операцией умножения образует мультипликативную группу. В данном случае выполнение групповых аксиом очевидно. Роль единичного элемента е играет обычная единица, а обратный элемент g-1=1/g.
Пример 2.
В качестве
другого примера, результаты которого будут использованы в дальнейшем, рассмотрим аддитивную группу комплексных чисел. Элементы группы - все комплексные числа. Групповая операция Ä
- обычное слодение комплексных чис-л, обозначаемое, естественно, знаком +. В случае аддитивной группы единичный элемент е = 0 и называется нулевым элементом. Обратный элемент g-1=-g обычно называется противоположным элементом.
Пример 3. Элементы группы - множество всех комплексных чисел, по модулю равных
1. Групповая операция - обычное умножение. Общий вид элемента такой группы g=exp(iφ) , так что e=1, а g-1=exp(-jφ) . Рассмотренный пример имеет глубокий физический смысл, заключающийся в том, что множество амплитудных коэффициентов пропускания тонких фазовых голограмм образует группу.
Пример 4. Все приведенные выше примеры относятся к классу бесконечных групп. В качестве конечной грушм можно рассмотреть множество, элементами которого служат целые числа 0 и
1. Групповой операцией является сложение по модулю 2, т.е. мы складываем элементы и берем остаток от деления их суммы на 2:
0+0=0, 0+1=1+0=1, 1+1=0.
Здесь 0 является нулевым элементом группы, а
1 служит для самой себя противоположным элементом.
Пример 5. Можно привести примеры более сложных групп. Все рассмотренные выше группы являются абелевыми. Примером некоммутативной группы слунит множество невырожденных матриц порядка
n с операцией матричного умножения. В общем случае множество всех невырожденных преобразований пространства образует группу, где под произведением преобразований понимают преобразование, получающееся в результате последовательного применения (суперпозиции) преобразований. В частности, можно выделить группу вращении трехмерного пространства и т.п.
Рассмотренные примеры позволяют говорить, что понятие группы с точки зрения количества операций является более простой математической конструкцией (в группе задана только одна операция). В то же время это и более абстрактная категория, ибо на практике обычно приходится сталкиваться с множествами, в которых задано не менее двух операций (поле, векторное и гильбертово пространство и т.п.).
Однако относительная простота понятия группы приводит к тому, что теоретико-групповой формализм может играть фундаментальную роль при анализе математической структуры голографической записи. Для описания групповой структуры интерференционного поля нам понадобятся понятия подгруппы и фактор-группы.
2.
Подгруппа
Основные свойства некоторой конкретной группы можно выяснить при анализе ее внутренней структуры. Для этого широко используется понятие подгруппы.
Пусть множество g образует группу. Непустое подмножество Нc g называется подгруппой, если выполнены два условия:
а) Элемент h1Ä
h2Î
h, если h1, h2Î
h (групповая операция Ä
замкнута на множестве Н).
б) Обратный элемент h-1Î
h, если hÎ
Н (групповая операция Ä
обратима на множестве h).
Нетрудно видеть, что подгруппа представляет собой самостоятельную группу. Иначе говоря, термин "подгруппа" можно еще расшифровать как "группа, содержащаяся внутри группы".
Рассмотрим некоторые примеры подгрупп.
Пример 6. Множество вещественных чисел, за исключением нуля, образует подгруппу в группе всех комплексных чисел (за вычетом нуля) по умножению (пример 1).
Пример 7. Другой подгруппой группы всех комплексных числе по умножению является группа всех комплексных чисел по модулю равных 1 (пример 3).
Пример 8. Множество всех вещественных, целых или четных чисел образует соответствующую подгруппу в аддитивной группе комплексных чисел (пример 2).
Каждая группа имеет две особые подгруппы, которые называются несобственными. Множество, состоящее из всех элементов группы g, является подмножеством группы g и группой относительно определенной в нем бинарной операции. Поэтому группа будет одновременно своей подгруппой. С другой стороны, подмножество Е, содержащее единственный элемент е, удовлетворяет аксиомам подгруппы, так как еÄ
е = е. Следовательно, каждая группа содержит подгруппу, состоящую из единственного элемента е.
Одна из основных задач теории групп состоит в отыскании всех остальных (собственных) подгрупп данной группы
g. Применительно к голографии выявление специфики возможных подгрупп в групповой структуре интерференционного ноля позволяет исследовать различные разновидности голографической записи и выявлять возможные новые типы голограмм.
3.
Фактор-группа
Из теории групп известно, что по любой подгруппе hÌ
g можно построить, разложение исходной группы g на непересекающиеся множества (смежные классы). В аддитивной записи (групповая операция - сложение) левым смежным классом группы g по подгруппе Н, порожденный элементом gÎ
g, называется множество элементов g+Н, представляемых в виде q+h,
где
hÎ
Н. Аналогично можно ввести понятие правого смежного класса Н+g. Если левые и правые смежные классы совпадают, то подгруппа h называется нормальным делителем или инвариантной подгруппой. Иначе говоря, разложение группы g в смежные классы по нормальному делителю Н является правильным разбиением этой группы.
С помощью инвариантной подгруппы
h и группы g можно построить новую группу, элементами которой являются множества элементов g (смежные классы). При этом под суммой смежных классов g+Н и r+h (g, rÎ
g) пониматся смежный класс (g+r)+Н. Роль нулевого элемента выполняет инвариантная подгруппа Н, а противоположным элементом для смежного класса g+Н служит -g+h. Эта группа смежных классов называется фактор-группой группы g по инвариантной подгруппе Н и обозначается g/h.
Рассмотренный аппарат позволяет перейти к изучению математической структуры голографической записи.
4.
Групповая структура интeрференционного поля
В приближении скалярной теории дифракции комплексная амплитуда любого оптического возмущения (дифракционный образ), распространяющегося в свободном пространстве, удовлетворяет уравнению Гельмгольца /7,8/. На голограмме регистрируется суммарный дифракционный образ, определенный на плоскости или в некотором объеме пространства и являющийся суммой предметной gн и опорной gr волны. Причем, реализация этого процесса может носить как физический, так и машинный (дискретный) характер /3/.
В силу линейности уравнения Гельмгольца множество дифракционных образов представляет собой абелеву группу g с операцией вложения, определенной в поле комплексных чисел (пример 2). Иначе говоря, сумма дифракционных образов
gr+gн снова оказывается дифракционным образом. Нулевым элементом является дифракционный образ gº
0. Противополжным элементом для g служит элемент -g=g exp(jπ), отличающийся фазовым сдвигом π.
Структура дифракционной волны зависит от области дифракции,
в которой она рассматривается. В частности, используя для нахождения дифракционного образа интеграл Френеля-Кирхгофа, можно выделить три основные области дифракции: область геометрической тени, область дифракции Френеля и область дифракции Фраунгофера /2,7,8/. Каждое из рассмотренных подмножеств дифракционных образов в группе g в силу линейного характера описания дифрагированной волны с помощью интеграла Френеля-Кирхгофа представляет собой соответствующую подгруппу Н
c g. Физически это означает, что сумма френелевских, фраунгоферовских и теневых образов снова является соответствующим дифракционным образом.
Таким образом, в структуре группы g всех дифракционных образов можно выделить три характеристические собственные подгруппы, соответственно, Френелевских Ф, фраунгоферовских
f и теневых Т образов. Кроме того, дополнительно полезно рассмотреть собственную подгруппу f дифракционных фурье-образов /1,8/, которая очевидно является подгруппой в группе f всех фраунгоферовских образов. Рассмотренный набор собственных подгрупп в рамках скалярной теории дифракции описывает групповую структуру поля, регистрируемого на голограмме. Выделение других собственных подгрупп или в общем случае какой-либо другой произвольный способ построения подгрупп в группе всех дифракционных образов позволит глубже понять характер регистрируемого поля и структуру голографической записи.
Любая подгруппа Н абелевой группы
g инвариантна. Тогда по инвариантной подгруппе Н можно построить фактор-группу g/Н, представляющую собой разложение исходной группы g дифракционных образов на непересекающиеся смежные классы gr+h. При этом произвольный смежный класс gr+h образуется из множества элементов группы g, представляемых в виде суммы gr+gн, где grÎ
g, gнÎ
Н. Таким образом, суммарную комплексную амплитуду поля, регистрируемую на голограмме, можно рассматривать как элемент фактор-группы (некоторый смежный класс), построенной по подгруппе Н соответствующих дифракционных образов. Физически это означает, что предметная волна
gн принадлежит некоторой выбранной подгруппе Н дифракционных образов (например Т, Ф, f или
f), а опорная волна gr является в общем
случае произвольным дифракционным образом группы
g.
Такой
подход описывает математическую структуру интерференционного поля, регистрируемого на голограмме. С одной стороны, амплитудно-фазовое распределение поля в предметной волне gн на практике всегда может быть отнесено к одной из рассмотренных выше собственных подгрупп дифракционных образов Т, Ф, f, f. Иначе говоря, в качестве gн должны рассматриваться соответствующие элементы
gtÎ
t, gФÎ
Ф, g
rÎ
f
или gfÎ
f. В то же время на голограмме регистрируется интерференционная картина, которая возникает при сложении соответствующей предметной волны gн и произвольной опорной волны
gr. Такая структура полностью описывается соответствующим смежным классом gr+Н, так что на конкретной голограмме записывается определенный представитель gr+gн смежного класса.
Построение фактор-группы g/Н задает правильное разбиение группы g дифракционных образов на непересекающиеся подмножества gr+Н, которые включают в себя вое элементы группы g. В результате каждый дифракционный образ g принадлежит определенному смежному классу gr+Н (элементу фактор-группы g/h). Вид фактор-группы обусловлен структурой полк, регистрируемого на голограмме.
5.
Теоретико-групповая модель голограммы
При анализе процесса восстановления гологрзмма характеризуется некоторой, вообще говоря,комплексной функцией, зависящей от типа голограммы и класса регистрируемых объектов, вида и характера отклика регистрирующей среды, а также от условий записи и обработки. Это может быть амплитудный коэффициент пропускания в случае плоской голограммы или распределение диэлектрической проницаемости и проводимости для объемной голограммы /1/. В свою очередь, как показано выше, структура интерференционного поля, ааписываемого на гопограмме, характеризуется фактор-групповой g/h, построенной по подгруппе Н соответствующих дифракционных образов. Тогда описание математической модели обобщенной голограммы сводится к заданию некоторой функции, которая определена на фактор-группе g/Н.
Построенная модель описывает групповые свойства, присущие природе голографического процесса,и имеет общий характер. Она позволяет с единой теоретико-групповой точки зрения рассматривать все имеющиеся в настоящее время разновидности голограмм
/1/. Классификация голограмм в зависимости от характера суммарной регистрируемой волны (голограмма Френеля, Фурье, Фраунгофера, сфокусированного изображения и т.п.) и от схемы записи (осевая голограмма, голограмма с наклонным опорным пучком, голограмма во встречных пучках) задается в виде разложения исходной группы g на непересекающиеся смежные классы, являющиеся элементами фактор-группы g/Н, и выбора представителя в смежном классе. В то же время вид функции, определенной на фактор-группе, позволяет классифицировать голограммы на амплитудные и фазовые, плоские и объемные, непрерывные и дискретные. Наконец, в зависимости от физической реализации смежного класса можно говорить о физических и машинных (синтезированных на ЭВМ) голограммах.
Кроме того, такой подход позволит прогнозировать возможность получения новых типов голограмм. В частности, ниже на основе теоретико-группового анализа введено общее понятие Фурье-подобной голограммы. Отыскание новых собственных подгрупп Н в группе g всех дифракционных образов может привести к получению более универсального разбиения исходной группы g на смежные классы (построение универсальной фактор-группы g/h) и к появлению новых голографических структур.
Отправным моментом при построении групповой модели голограммы является выбор собственной подгруппы Н. Отсутствие универсальной собственной подгруппы приводит к различным разбиениям группы g дифракционных образов на смежные классы. При этом один и тот же суммарный дифракционный образ, регистрируемый на голограмме, принадлежит разным смежным классам, структура которых обусловлена соответствующей фактор-группой
g/Н.
Однако с физической точки зрения такая неоднозначность не играет существенной роли. На практике при записи голограим Френеля, Фраунгофера или Фурье естественно в качестве собственной подгруппы рассматривать соответствующую подгруппу дифракционных образов Ф, f или
f. Выбор собственной подгруппы
для голограммы сфокусированного изображения зависит от характера поля на голограмме. В качестве Н может использоваться как подгруппа Т теневых образов, так и подгруппа Ф Френелевских образов. Детальный анализ группы всех дифракционных образов
g может привести к отысканию новой собственной подгруппы, учитывающей геометрию записи голограмм сфокусированных изображений.
Известны различные критерии качества изображения, восстанавливаемого с голограммы /1/. В работе /1/ для оценки качества топографического процесса введено понятие пространственной параметрической кривой "отношение сигнал/шум-дифракционная эффективность-коэффициент нелинейности" (ОСШ-ДЭ-КН). Тогда с теоретико-групповой точки зрения в общем случае для описания процесса восстановления математическая модель голограммы представляет собой некоторую вектор-функцию, которая определена на фактор-группе, построенной по подгруппе соответствующих дифракционных образов. В частности, параметрическая кривая ОСШ-ЛЭ-КН
/9/ также должна быть задана на фактор-группе.
В заключение рассмотрим некоторые примеры, иллюстрирующие применение теоретико-групповой модели голограммы.
6.
Фурье-подобные голограммы
Известен ряд схем записи голограмм, при которых в плоскости голограммы регистрируется либо точный фурье-образ объекта, либо произведение этого фурье-образа на квадратичный фазовый множитель. При этом различают фурье-голограмму, квази-фурье-голограмму и безлинзовую фурье-голограмму /1/. В основе такой классификации голограмм лежат различные схемы записи.
Использование теоретико-группового подхода при анализе имеющихся схем фурье-голографии дает возможность с единой теоретико-групповой точки зрения систематизировать различные типы фурье-голограмм. В то же время исследование групповой структуры множества дифракционных фурье-образов позволяет ввести новое общее понятие Фурье-подобной голограммы.
Как показано выше, множество дифракционных фурье-образов
представляет собой собствечную подгруппу f в группе g (fcg) всех дифракционных образов. С помощью этой подгруппы можно построить правильное разбиение группы g на непересекающиеся смежные классы gr+f, являюицюся элементами фактор-группы g/f. Тогда с теоретико-групповой точки зрения при записи голограммы по одной из схем фурье-голографии на ней регистрируется интерференционное поле, структура которого задается соответствующим смежным классом. Конкретная интерференционная картина зависит от вида представителя gr+gf (grÎ
g,) в смежном классе.
Фурье-голограммой называется голограмма, на которой регистрируется результат интерференции двух волн с комплексными амплитудами в плоскости гологюммы, являющимися фурье-образами объекта и опорного источника /1/. Суммарное поле в плоскости голограммы складывается из плоской волны g'f (фурье-образ точечного источника) и фурье-образа g''f телеграфируемого объекта, так что
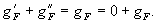 (5)
(5)
Так как сумма фурье-образов снова является фурье-образом, то на голограмме-регистрируется представитель нулевого смежного класса 0+
f=
f в фактор-группе g/f, роль которого играет исходная подгруппа f дифракционных фурье-образов. Интенсивность интерференционной картины определяется квадратом модуля |gf|2 регистрируемого представителя gfÎ
f.
Тогда описание математической модели истинной фурье-голограммы сводится к заданию амплитудного коэффициента пропускания
t0 плоской голограммы на нулевом смежном классе 0+f факторгруппы g/f, построенной по подгруппе f дифракционных фурье-образов, иначе говоря, в качестве предметного и опорного волнового фронта используется фурье-образы, а выражение для амплитудного коэффициента пропускания t0 зависит от выбора конкретного представителя в нулевом смежном классе 0+f. Если q'f представляет собой плоскую волну, то получается определение фурье-голограммы, приведенное выше.
В случае квази-фурье-голограммы регистрирующая пластинка
располагается в задней фокальной плоскости линзы, а предмет и опорный точечный источник находятся в одной и той же плоскости, не являющейся передней фокальной плоскостью линзы /1/. Во всех трех случаях (транспарант расположен вплотную к линзе, перед линзой и за линзой) структура смежного класса имеет вид:
gr+f, где элемент grÎ
g, порождающий соответствующий смежный класс, определяется схемой записи. Суммарное поле, записываемое на голограмме, задается представителем gr+gf. Однако структура эткх смежных классов такова, что квадрат модуля любого представителя совпадает с квадратом модуля соответствующего представителя из нулевого смежного класса f, так что
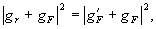 (6)
(6)
где
g'f - фурье-образ точечного источника.
Все вышеизложенное легко переносится на случай безлинэовой фурье-голограммы, при записи которой опорный источник располагается в плоскости транспаранта /1/. При этом в качестве элемента
gf рассматривается фурье-образ произведения амплитудного пропускания транспаранта и квадратичного фазового множителя.
Обобщая вышеизложенное, можно ввести понятие Фурье-подобной голограммы, заданной такой совокупностью смежных классов
gr+f, для которых выполняется равенство (6). Иначе говоря, математическое описание Фурье-подобной голограммы сводится к заданию амплитудного коэффициента пропускания t0 на некотором подмножестве снежных классов {gr+f} в фактор-группе g/f, таком, что квадрат модуля любого представителя gr+gf равен квадрату модуля соответствующего представителя из нулевого смежного класса, 0+f. Частными случаями Фурье-подобной голограммы являются истинная фурье-голограмма, квази-фурье-голограмма и безлинзовая фурье-голограмма.
С другой стороны, по-видимому, можно найти какую-то новую схему голографирования, при которой интерференционная картина, регистрируемая на голограмме, будет иметь структуру Фурье-подобного смежного класса. Очевидно, что, в принципе, таких смежных классов существует неограниченное множество. Более детальный
анализ групповой структуры фурье-подобных смежных классов позволит установить возможные конкретные схемы записи.
При этом всем Фурье-подобным голограммам в определенной мере свойственна нечувствительность восстановленного изображения к трансляциям голограммы. Это следует из общего характера структуры Фурье-подобных смежных классов.
7.
Голография бегущих волн интенсивности
В работе /10/ рассмотрены отображающие свойства бегунах волн интенсивности, которые возникают при изменении длины волны излучения, рассеянного объектом. С теоретико-групповой точки зрения это приводит к параметризации соответствующей собственной подгруппы Н.
В общем случае /10/ предметная gh и опорная gr волна характеризуются различными частотами ω и имеют вид:
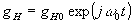 , (7)
, (7)
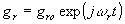 . (8)
. (8)
Распределение интенсивности в интерференционной картине можно представить в виде
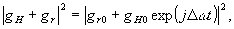 (9)
(9)
где D
ω=ω0-ωr. Очевидно, что координатные функции gh0 и gr0 являются некоторыми дифракционными образами. При этом gh0 принадлежит соответствующей собственной подгруппе Н(gh0Î
h), а gr0, вообще говоря, является произвольным элементов группы g(gr0Î
g).
Тогда на основании (9) можно ввести в рассмотрение параметрическую /4,5/ подгруппу Н
ω(gh(Δω)=gh0exp(jΔωt)Î
hω). Иначе говоря, при регистрации голограммы бегущих волн интенсивность интерференционного поля определяется параметрическим смежным классом gr0+hω, который задается представителем
gr0+gh
(Δω). (10)
8.
Голографическая интерферометрия
В качестве простого примера приценения теоретико-группового подхода рассмотрим структуру голографической записи в методе голографической интерферометрии /1/. Нетрудно видеть, что как в способе двух (или нескольких) экспозиций, так и в методе голографической интерферометрии в реальном масштабе времени, интерференционное поле характеризуется суммарным снежным классом. При сложении смежных классов в зависимости от характера опорной волны мы либо остаемся в пределах одного и того же класса, либо получаем новый смежный класс.
З а к л ю ч е н и е
Построение теоретико-групповой модели обобщенной голограммы, по сути говоря, представляет собой доказательство существования голограмм с заданными групповыми свойствами (теорема существования в голографии). При этом модель описывает возможные типы голограмм, для которых следует разрабатывать схемы записи, но не указывает конкретные пути их получения, что естественно для любой теоремы существования. В частности, проведенный выше анализ схем фурье-голографии и введение понятия Фурье-подобной голограммы наводят на мысль о существовании подобной структуры в подгруппе Ф френелевских дифракционных образов и в других собственных подгруппах.
В работе теоретико-групповой подход при исследовании структуры голограмм рассмотрен в приближении скалярной теории дифракции. Однако он может быть распространен и на более общий случай поляризационной записи /11/ путем анализа групповой структуры векторного поля. Кроме того, интерференции двух сигналов произвольного спектрального состава /12/ можно также описывать с теоретико-групповой точки зрения с помощью функций корреляции.
Л и т е р а т у р а
1. Р.Кольер, К.Беркхарт, Л.Лин. Оптическая голография, изд. "Мир", М., стр. 233. 1973.
2. Л.М.Сороко. Основы голографии и когерентной оптики, изд. "Наука", М.. стр.379, 1971.
3. Э.И.Крупицкий. Основные теоремы голографии для линейной стационарной среды. Материалы
vi Всесоюзной школы по голографии, Л., стр.128, 1974.
4. А.Г.Курош. Теория групп, изд. "Наука", М., 1967.
5. М.Хамермеш. Теория групп и ее применение к физическим проблемам, изд. "Мир", М., 1966.
6.Н.Я.Виленкин. Специальные функции и теория представлений групп, изд. "Наука", М., 1965.
7. М.Борн, Э.Вольф. Основы оптики, изд. "Наука", стр.3
46, 1973.
8. Дж.Гудмен, Введение в фурье-оптику, изд. "Мир", М., стр. 55, 1970.
9. В.Б.Немтинов, О.В.Рожков. Метод оценки качества голографического процесса. Материалы
vi Всесоюзной школы по голографии, Л., стр.192, 1974.
10. Ю.Н.Денисюк. Об отображающих свойствах бегущих волн интенсивности при записи динамических объемных голограмм. В сб. "Современное состояние и перспективы развития голографии", изд. "Наука", Л., стр.5, 1974.
11. Ш.Д. Какичашвили. Поляризованный свет в голграфии и метод поляризационной записи. Материалы
v Всесоюзной школы по голографии, Л., стр. 511, 1973.
12. Г.В.Скроцкий. Интерференция и когерентность. Материалы
vi Всесоюзной школы по голографии. Л., стр.37, 1974.

