|
|
 |
 |

|
| |
ИНТЕРФЕРОМЕТРИЧЕСКИЙ МЕТОД ЗАПИСИ И ВОССТАНОВЛЕНИЯ ИЗОБРАЖЕНИЙ В ОПТИКЕ
И.А.Дерюгин, В.Н.Курашов
Рассмотрены методы оптического восстановления изображения объекта по измерениям автокорреляционной функции излучения в дальней зоне, основанные на применениях экспоненциальной фильтрации принимаемого сигнала и некогерентного опорного источника. Дан анализ возможностей использования для этих целей интерферограмм интенсивности. Приведены оценки искажений восстановленного изображения, связанных с немонохроматичностью источника.
Решение проблемы записи и восстановления пространственного распределения комплексной амплитуды волнового поля, впервые найденное Габором /1/, основывается на явлении интерференции электромагнитного излучения; необходимым условием его эффективности является высокая пространственная и временная когерентность используемых источников. Развитие лазерной техники во многих случаях позволяет удовлетворить эти требования. Тем не менее, в последнее время заметно повысился интерес к голографии в некогерентном свете. В идейном отношении все подобные системы регистрации основаны на наблюдении автокорреляционной картины излучения объекта, что устраняет необходимость использовать когерентный источник. Ниже мы рассмотрим общие характеристики таких методов регистрации оптических полей, а также остановимся на одном перспективном методе их реализации с использованием интерферометра интенсивности.
При изложении идеи автокорреляционной записи комплексного волнового поля удобно начать с анализа обычной голографической системы. Поскольку единственной,непосредственно наблпдаекой в оптическом эксперименте, является интенсивность излучения
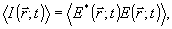 (1) (1)
усредненная за достаточно длительный по сравнению с периодом колебания отрезок времени, фазовая информация, содержащаяся в комплексной амплитуде аналитического сигнала 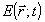 , при таком измерении безвозвратно теряется. Однако регистрация абсолютного значения фазы поля , при таком измерении безвозвратно теряется. Однако регистрация абсолютного значения фазы поля 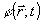 в известном смысле является излишней, так как последняя физически определена лишь с точностью до произвольной постоянной. Таким образом, существенное значение имеет только относительное фазовое распределение, т.е. разность в известном смысле является излишней, так как последняя физически определена лишь с точностью до произвольной постоянной. Таким образом, существенное значение имеет только относительное фазовое распределение, т.е. разность 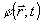 и некоторого произвольного "опорного" значения и некоторого произвольного "опорного" значения 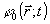 . Именно это обстоятельство использовано в голографии, где реперное значение фазы создается дополнительно введенным когерентным фоном. Суммарная интенсивность излучения, . Именно это обстоятельство использовано в голографии, где реперное значение фазы создается дополнительно введенным когерентным фоном. Суммарная интенсивность излучения,
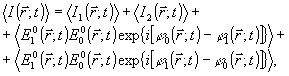 (2) (2)
содержит, очевидно, информацию о фазовом распределении поля источника 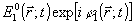 по отношению к известной фазе опорного поля по отношению к известной фазе опорного поля 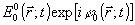 , закодированную в интерференционной картине (2). При подходящем выборе , закодированную в интерференционной картине (2). При подходящем выборе 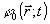 эта информация оказывается вполне достаточной для полной реконструкции излучения источника. Как следует из (2), основным объектом регистрации в голографическом процессе является корреляционная функция: эта информация оказывается вполне достаточной для полной реконструкции излучения источника. Как следует из (2), основным объектом регистрации в голографическом процессе является корреляционная функция:
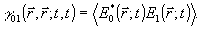 (3) (3)
Последняя, однако, не единственно возможный источник информации
об амплитудно-фазовом распределении поля. Если ограничиться излучением о гауссовой статистикой, наиболее общими характеристиками являются корреляционные функции:
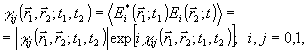 (4) (4)
описывающие статистические связи комплексных амплитуд объектного и опорного источников в различных пространственно-временных точках. В частности, основная информация об относительных фазах полей оодержится в фазе корреляционной функции 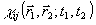 , так что для ее регистрации можно воспользоваться измерением любо! из корреляционных функций (4). будем называть такое определение амплитудно-фазового распределения поля интерферометрическим, поскольку оно непосредственно связано с наблюдением одного из возможных типов интерференционных картин, описываемых соответствующими функциями (4). Приведем два известных примера реализации интерферометрического метода. , так что для ее регистрации можно воспользоваться измерением любо! из корреляционных функций (4). будем называть такое определение амплитудно-фазового распределения поля интерферометрическим, поскольку оно непосредственно связано с наблюдением одного из возможных типов интерференционных картин, описываемых соответствующими функциями (4). Приведем два известных примера реализации интерферометрического метода.
1. Фурье-спектроскопия. Определение корреляционной функции 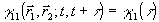 является основой известного метода спектрального анализа, называемого фурье-спектроокопией /2/. Для стационарных полей спектральная плотность является основой известного метода спектрального анализа, называемого фурье-спектроокопией /2/. Для стационарных полей спектральная плотность 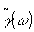 связана с связана с 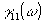 соотношением соотношением
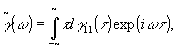 (5) (5)
так что измерение 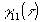 позволяет определить позволяет определить 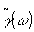 посредством выполнения обратного преобразования Фурье. Для этой цели могут быть использованы как численные методы, так и методы, основанные на оптической обработке. посредством выполнения обратного преобразования Фурье. Для этой цели могут быть использованы как численные методы, так и методы, основанные на оптической обработке.
2. Голография интенсивностей. Принцип получения гологромм в пространственно-некогерентном свете схематически изображен на рис.1. Оптическая интерферометрическая схема (в нашем случае –
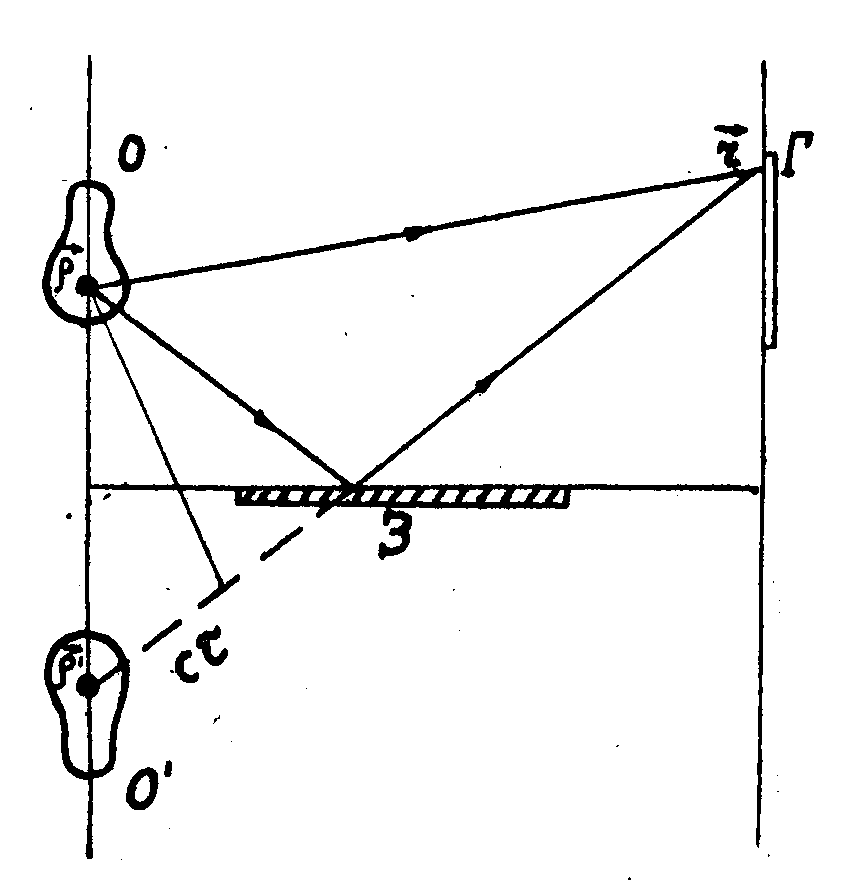
Рис.1. Принцип получения голограмм в пространственно-некогерентном свете.
зеркало Ллойда) расщепляет потов излучения на два идентичных пучка, интерферирующих на экране. Поскольку для пространственно-некогерентых объектов интерференционную картину создают лишь сопряженные точки ( 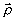 и и 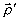 ), нетрудно показать, что распределение интенсивности в плоскости голограммы имеет вид: ), нетрудно показать, что распределение интенсивности в плоскости голограммы имеет вид:
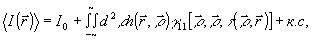 (6) (6)
где 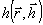 - ядро интегрального преобразования, описывающее изменение корреляционной функции при распространение излучения - ядро интегрального преобразования, описывающее изменение корреляционной функции при распространение излучения  - временная задержка, зависящая как от точки объекта - временная задержка, зависящая как от точки объекта 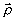 , так и от точки наблюдения , так и от точки наблюдения 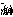 . Для монохроматически излучающих спектрально чистых объектов . Для монохроматически излучающих спектрально чистых объектов 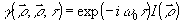
так, что 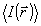 представляет ообой некогерентное наложение интерференционных картин, создаваемых каждой точкой объекта и однозначно связанных с распределением интенсивности представляет ообой некогерентное наложение интерференционных картин, создаваемых каждой точкой объекта и однозначно связанных с распределением интенсивности 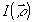 в плоскости объекта. Таким образом, в этом методе производится косвенная регистрация корреляционной функции в плоскости объекта. Таким образом, в этом методе производится косвенная регистрация корреляционной функции 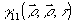 , дающая возможность восстановить , дающая возможность восстановить 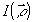 выполнением интегрального преобразования выполнением интегрального преобразования 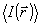 , обратного (6). , обратного (6).
Суммируя сказанное, модно сделать вывод, что измерение одной из корреляционных функций (4) позюляет получить систему восстановления определенных характеристик излучения, его пространственного или временного спектра. Однако, в общем случае не существует взаимно однозначной связи 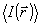 с характеристиками объекта с характеристиками объекта 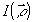 или или 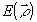 . В то же время такое соответствие имеется между . В то же время такое соответствие имеется между 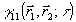 и и 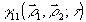 , так как последняя есть просто граничное условие для волнового уравнения, которому подчиняется корреляционная функция. Ввиду этого представляют особый интерес системы записи и восстановления оптических волновых фронтов, основанные на непосредственной регистрации , так как последняя есть просто граничное условие для волнового уравнения, которому подчиняется корреляционная функция. Ввиду этого представляют особый интерес системы записи и восстановления оптических волновых фронтов, основанные на непосредственной регистрации 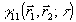 в плоскости наблюдения. Вообще говоря, для этой цели пригодна любая интерферометрическая схема, в которой пространственно-временные сдвиги можно изменять в процессе измерения. Амплитуда корреляционной функции в плоскости наблюдения. Вообще говоря, для этой цели пригодна любая интерферометрическая схема, в которой пространственно-временные сдвиги можно изменять в процессе измерения. Амплитуда корреляционной функции 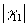 при этом непосредственно связана с видностью интерференционных полос, а ее фаза при этом непосредственно связана с видностью интерференционных полос, а ее фаза 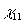 определяется их относительным сдвигом, отсчитываемым от положения полос предварительно полученной интерференционной картины для известного источника (например, точечного) /3/. В действительности, однако, такое измерение фазы определяется их относительным сдвигом, отсчитываемым от положения полос предварительно полученной интерференционной картины для известного источника (например, точечного) /3/. В действительности, однако, такое измерение фазы 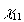 с достаточной точностью оказывается очень сложным, а иногда и вообще невозможным. В последние годы предложены новые способы операционного определения фазы корреляционной функции, применение которых в сочетании с новой техникой интерферометрии значительно расширяет возможности метода. Кратко остановимся на описании этих идей. с достаточной точностью оказывается очень сложным, а иногда и вообще невозможным. В последние годы предложены новые способы операционного определения фазы корреляционной функции, применение которых в сочетании с новой техникой интерферометрии значительно расширяет возможности метода. Кратко остановимся на описании этих идей.
1. Метод экспоненциального Фильтра /4/. Рассмотрим одномерный пространственно-однородный источник, корреляционная функция которого пропускается при регистрации через линейную систему с импульсным откликом h(х). На выходе образуется оглаженная корреляционная функция:
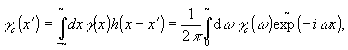 (7) (7)
спектральная плотность которой
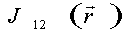 (8) (8)
где Н(ω) - передаточная функция фильтра. Выберем Н(ω) в виде
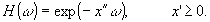 (9) (9)
Тогда, в соответствии с (7), (8),
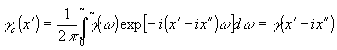 . (10) . (10)
При определенных условиях, накладываемых на спектральную плотность 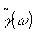 , , 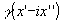 - функция, аналитическая в нижней полуплоскости комплексной плоскости /5/. Используя соотношение Коши-Римана, - функция, аналитическая в нижней полуплоскости комплексной плоскости /5/. Используя соотношение Коши-Римана,
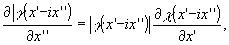 (11) (11)
найдем для этого случая
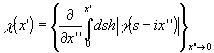 . (12) . (12)
Таким образом, для определения фазы корреляционной функции доста-
точно найти предельные значения 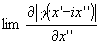 и, и, 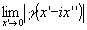 вблизи действительной оси. Практически это позволяет вместо экспоненциального фильтра с передаточной функцией (9) использовать линейный фильтр. Первые эксперименты, выполненные по этой методике /6/ показали, что основные ошибки в восстановленном изображении связаны с получением синтезированного транспаранта и носят систематический характер, так что они могут быть исклкнены применением более совершенной аппаратуры цифровой обработки результатов. вблизи действительной оси. Практически это позволяет вместо экспоненциального фильтра с передаточной функцией (9) использовать линейный фильтр. Первые эксперименты, выполненные по этой методике /6/ показали, что основные ошибки в восстановленном изображении связаны с получением синтезированного транспаранта и носят систематический характер, так что они могут быть исклкнены применением более совершенной аппаратуры цифровой обработки результатов.
2. Метод некогерентного опорного источника. Наиболее перспективный путь операционного определения фазы корреляционной функции основан на аналогии с методом регистрации фазы поля в голографии /7/. Как и в последнем случае, фазовое распределение не обязательно должно измеряться непосредственно; нелинейное преобразование произвольного вида позволяет перекодировать его в информацию другого типа. Наиболее простым является квадратичное детектирование суммы измеряемой корреляционной функции
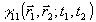
с некоторой известной "опорной" функцией 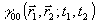 : :
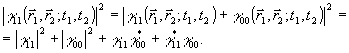 (13) (13)
Совершенно очевидно, что последние два члена в (13) содержат информацию как об амплитуде, так и о фазе комплексной функции 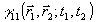 в виде своеобразной "интерференционной картины". В действительности, однако, явление интерференции в обычном смысле здесь не наблюдается, наоборот, необходимое условие получения выражения (13) есть некогерентное слоаение поля опорного источника в виде своеобразной "интерференционной картины". В действительности, однако, явление интерференции в обычном смысле здесь не наблюдается, наоборот, необходимое условие получения выражения (13) есть некогерентное слоаение поля опорного источника 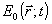 с полем объекта с полем объекта 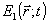 . Распределение (13) может быть использовано для определения . Распределение (13) может быть использовано для определения 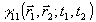 либо для измерения разности фаз либо для измерения разности фаз 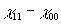 , если независимо измеряется , если независимо измеряется 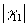 . Теоретически . Теоретически
такой метод возможен при выборе любой опорной корреляционной функции γ 00, однако практическое его осуществление требует выполнения ряда определенных условий, накладываемых процессом регистрации и расшифровки "интерферограммы" (13). Ясно, прежде всего, что наиболее удобен опорный источник, фазовое распределение которого либо мало отличается от сигнального, либо образует особенно простую пространственно-временную картину. Наиболее очевидный пример такого рода - точечный источник /8/. Действительно, полагая 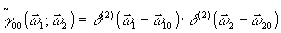 и выполнял преобразование Фурье третьего члена в (13), найдем и выполнял преобразование Фурье третьего члена в (13), найдем
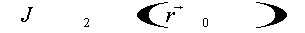
(14) где 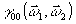 - спектр пространственных частот точечного опорного источника; - спектр пространственных частот точечного опорного источника; 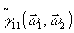 - спектр объекта. Таким образом, Фурье-преобразование транспаранта с амплитудным пропусканием (13) восстанавливает спектр сигнала, сдвинутый в частотной области на - спектр объекта. Таким образом, Фурье-преобразование транспаранта с амплитудным пропусканием (13) восстанавливает спектр сигнала, сдвинутый в частотной области на 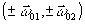 . Точечный опорный источник играет в этом методе ту же роль, что и наклонный луч в голографии Лейта и Упатниекса, однако, здесь он некогерентен с сигналом. Схематически принцип воспроизведения изображения объекта показан на рис.2. . Точечный опорный источник играет в этом методе ту же роль, что и наклонный луч в голографии Лейта и Упатниекса, однако, здесь он некогерентен с сигналом. Схематически принцип воспроизведения изображения объекта показан на рис.2.
Практическая реализация системы с некогерентным опорным источником, в принципе, может быть выполнена по любой интерферометрической схеме. Однако, некогерентность складываемых полей и квадратичность преобразования (13) делают наиболее удобным метод интерферометрии интенсивностей Хенберри-Брауна и Твисса /9/. Сигнал и опорное излучение детектируются здесь системой сканируемых фотоумножителей, полоса пропускания которых достаточно велика. Выходные токи после фильтрации перемножаются и усредняются по времена, в результате чего на выходе образуется сигнал, пропорциональный корреляционной функции токов. Нетрудно показать /10,11/, что последняя может быть записана в виде
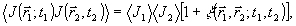 (15) (15)
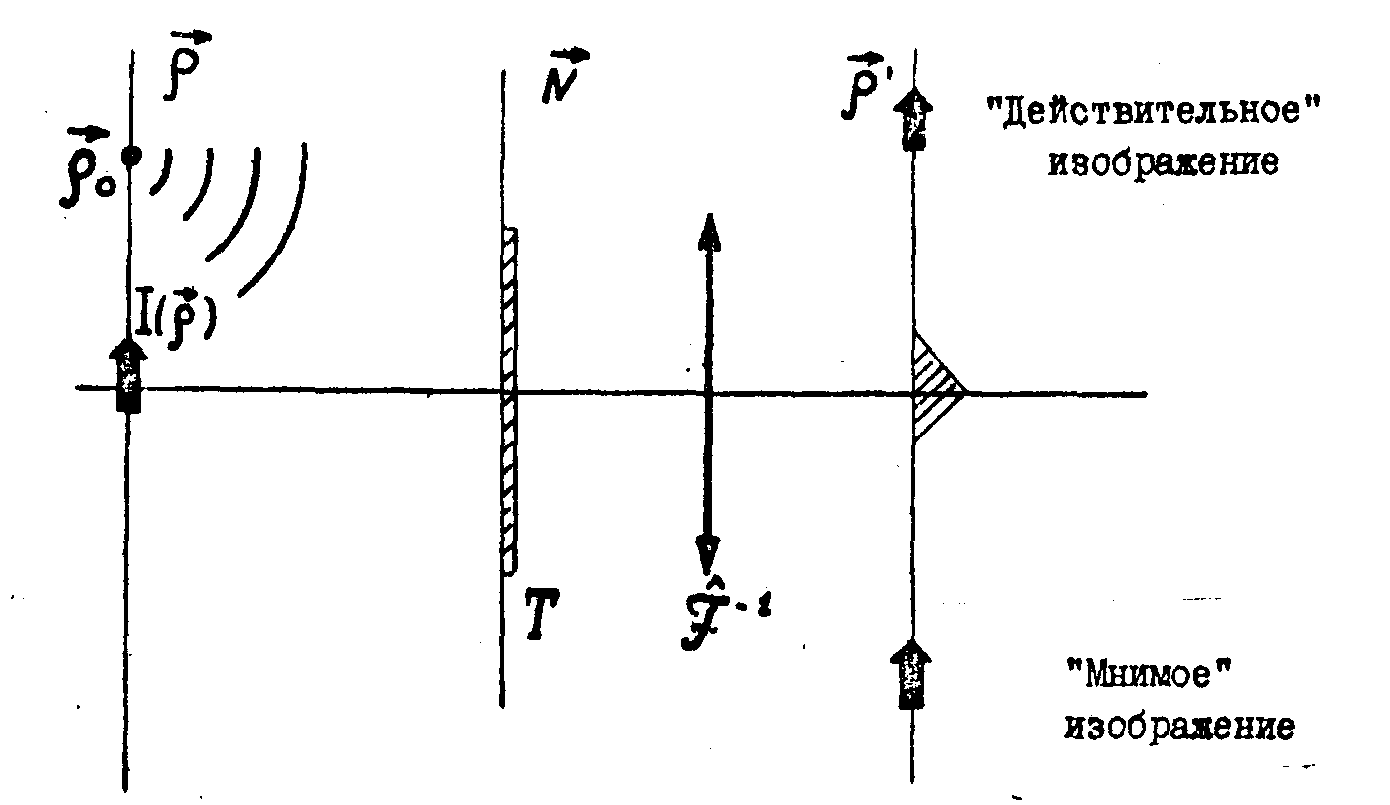
Рис.2. Принцип воспроизведения изображения объекта.
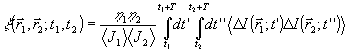 , (16) , (16)
η 1 и η2 - квантовые эффективности детектора; Т - их постоянная времени; 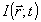 - мгновенная интенсивность оптического сигнала в точке - мгновенная интенсивность оптического сигнала в точке 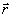 ; ; 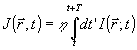 - сигнал на выходе фотоумножителя. В случае одномодового одночаототного лазера - сигнал на выходе фотоумножителя. В случае одномодового одночаототного лазера 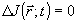 , так что , так что 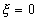 и сигнал на выходе интерферометра практически не зависит от и сигнал на выходе интерферометра практически не зависит от 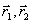 . Однако, для теплового источника . Однако, для теплового источника 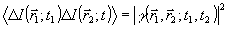 , откуда при t<<τk, где τk - время когерентности излучения, , откуда при t<<τk, где τk - время когерентности излучения,
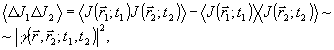 (17) (17)
т.е. образуется сигнал, пропорциональный квадрату модуля корреляционной функции, как это требуется в методе некогерентного опорного источника. Как правило, t>10-9 и, следовательно, временная когерентность излучения должна быть достаточно высокой. Ввиду этого, наиболее удобно использование так называемых пcевдотепловых полей /12/, образованных рассеянием лазерного излучения движущимся матовым стеклом. Амплитудные флуктуации в этом случае хорошо описываются гауссовым законом, хотя время корреляции и может оставаться достаточно большим ( ~10-6 сек и выше). Практическая схема метода изображена на рис.3 /13/. Запись транспаранта производилась с помощью электронно-лучевой трубки высокого разрешения, восстановление изображения - по обычной схеме оптического преобразования Фурье. Отметим, что описанный метод относительно нечувствителен к фазовым флуктуациям света, вызываемым неоднородностями среды, но может обладать рекордными чувствительностями по ин-
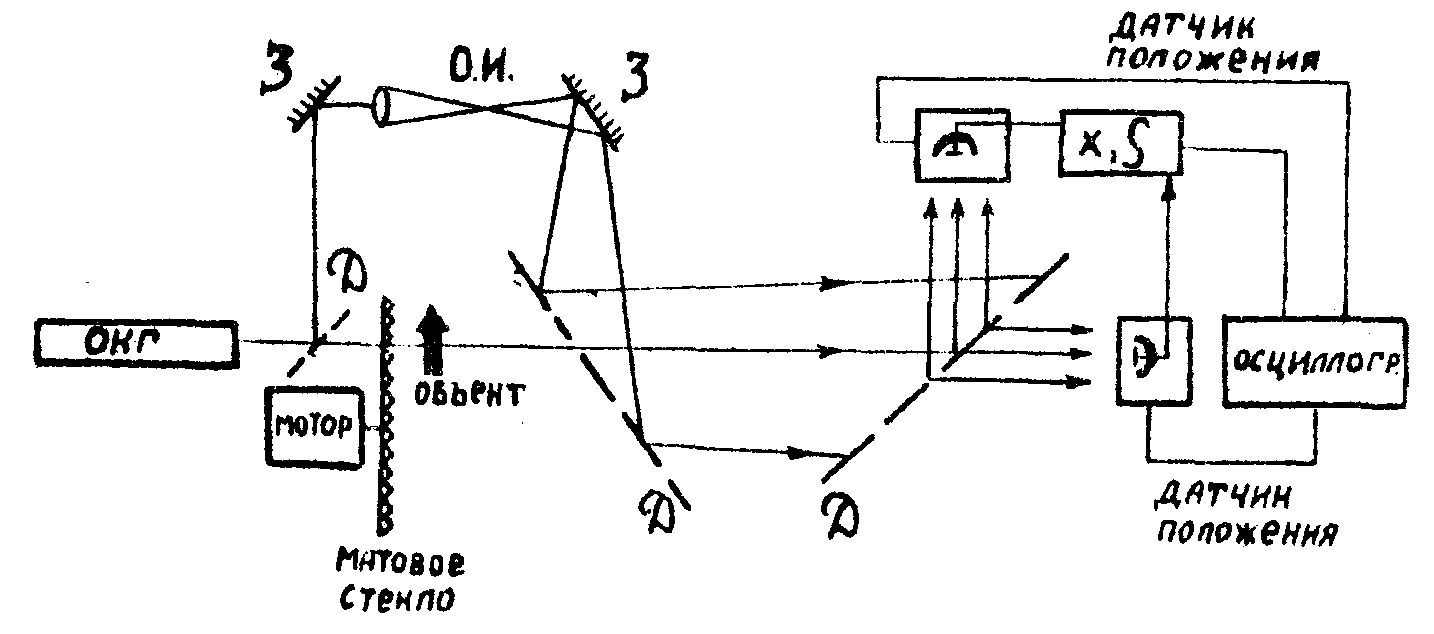
Рис.3. Схема метода.
тенсивности, поскольку интерферометр Хенберри-Брауна и Твисса способен работать в режиме счета отдельных фотонов.
Основная проблема, возникающая при реализации метода накогерентности опорного источника, связана с четырехмерностыо измеряемой функции 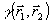 , которую не только оптически обработать, но и записать на двумерный транспарант, в принципе, невозможно. Однако, двумерность визуальной информации позволяет в некоторых случаях определить систему координат , которую не только оптически обработать, но и записать на двумерный транспарант, в принципе, невозможно. Однако, двумерность визуальной информации позволяет в некоторых случаях определить систему координат 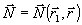 , в которых корреляционная функция , в которых корреляционная функция 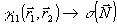 может быть записана и использована для однозначного восстановления распределения поля может быть записана и использована для однозначного восстановления распределения поля 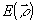 или интенсивности или интенсивности 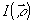 по объекту. Решение этой задачи требует знания точной связи коррелляционных функций в плоскости объекта и в плоскости наблюдения, которая может быть получена различными способами. Для наших целей наиболее удобен метод углового спектра /14-16/, позволяющий в простой форме получить необходимые результаты с учетом полихроматичности полей. по объекту. Решение этой задачи требует знания точной связи коррелляционных функций в плоскости объекта и в плоскости наблюдения, которая может быть получена различными способами. Для наших целей наиболее удобен метод углового спектра /14-16/, позволяющий в простой форме получить необходимые результаты с учетом полихроматичности полей.
Для простоты будем рассматривать скалярное приближение теории дифракции, согласно которому корреляционная функция 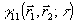 удовлетворяет уравнению удовлетворяет уравнению
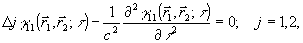 (18) (18)
при граничном условии в плоскости 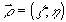
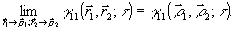 (19) (19)
Определяя временной спектр функции γ 11,
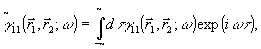 (20) (20)
получим для 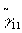 уравнение Гельмгольца: уравнение Гельмгольца:
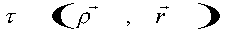 (21) (21)
где ω =ρκ. По аналогии о угловым представлением волновых полей можно записать решение (21) в виде:
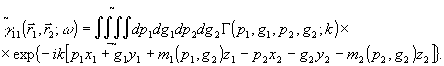 (22) (22)
Функция Г (p1, g1, p2, g2; k), зависящая от координат, имеющих смысл направляющих косинусов в разложении 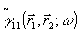 по плоским волнам, называется угловым спектром корреляционной функции и, как следует из (22), непосредственно равна фурье-преобразованию последней в плоскости источника: по плоским волнам, называется угловым спектром корреляционной функции и, как следует из (22), непосредственно равна фурье-преобразованию последней в плоскости источника:
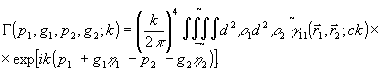 (23) (23)
Это обстоятельство облегчает вычисление 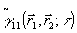 особенно для дальней зоны, когда размеры апертур источника и приемника малы по сравнению о расстоянием между ними. При этих условиях особенно для дальней зоны, когда размеры апертур источника и приемника малы по сравнению о расстоянием между ними. При этих условиях
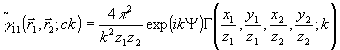 , (24) , (24)
где
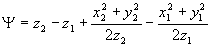 . (25) . (25)
Подставляя (24) в (20), найдем
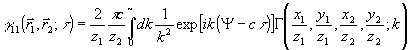 . (26) . (26)
Будем считать далее, что источник спектрально чистый, т.е.
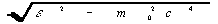 , (27) , (27)
тогда
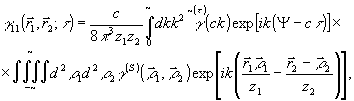 (28) (28)
где 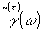 - преобразование Фурье корреляционной функции - преобразование Фурье корреляционной функции 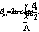 . Меняя в (28) порядок интегрирования и дифференцируя внутренний интеграл по параметру, преобразуем (28) к виду: . Меняя в (28) порядок интегрирования и дифференцируя внутренний интеграл по параметру, преобразуем (28) к виду:
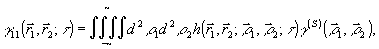 (29) (29)
где
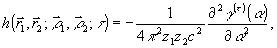 (30) (30)
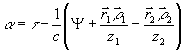 . (31) . (31)
Таким образом, ядро интегрального.преобразования (29) для полихроматического излучения не совпадает с ядром Фурье, т.е. строгое определение 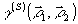 требует в общем случае знание спектрального состава излучения. Однако, для узкополосного сигнала, полагая требует в общем случае знание спектрального состава излучения. Однако, для узкополосного сигнала, полагая 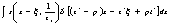 и пренебрегая величинами порядка и пренебрегая величинами порядка 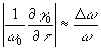 , получим: , получим:
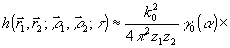 (32) (32)
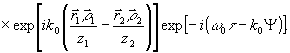
Выражение (32), по-прежнему, отличается от ядра преобразования Фурье множителем γ0(α), но, учитывая слабую зависимость последнего от аргумента, можно попытаться восстановить 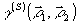 , выполняя обратное преобразование без учета такой зависимости. При этом полихроматичность поля приведет к возникновению искажений в восстановленном изображении, которые, как мы покажем ниже, в оптическом диапазоне сравнительно малы. , выполняя обратное преобразование без учета такой зависимости. При этом полихроматичность поля приведет к возникновению искажений в восстановленном изображении, которые, как мы покажем ниже, в оптическом диапазоне сравнительно малы.
Удовлетворяя условие фокусировки приемной системы в плоскость объекта, т.е. полагая 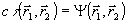 , найдем оптимальную процедуру восстановления. Предположим вначале, что источник монохроматический, или , найдем оптимальную процедуру восстановления. Предположим вначале, что источник монохроматический, или 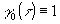 . Тогда, с учетом z1=z2=z, получим . Тогда, с учетом z1=z2=z, получим
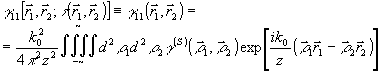 , (33) , (33)
откуда
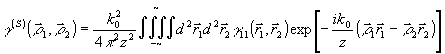 . (34) . (34)
Как уже отмечалось, не существуют оптические методы выполнения четырехмерного преобрев ования (34). Поэтому введем координаты
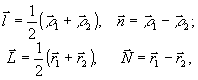 (35) (35)
определяющие среднее положение двух точек ( 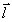 и и 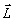 ) и расстояние между ними ( ) и расстояние между ними ( 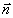 и и 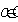 ). В этих координатах ). В этих координатах
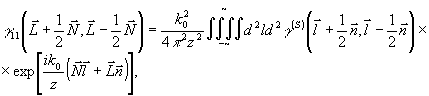 (36) (36)
т.е. функции 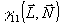 и и  , подобно (33), образуют пару преобразований Фурье. Заметим теперь, что , подобно (33), образуют пару преобразований Фурье. Заметим теперь, что 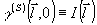 и, таким образом, зависимость от и, таким образом, зависимость от 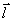 определяет распределение интенсивности по источнику. Наоборот, зависимость от определяет распределение интенсивности по источнику. Наоборот, зависимость от 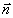 связана с когерентными свойствами излучателя. Аналогичные соотношения справедливы и для связана с когерентными свойствами излучателя. Аналогичные соотношения справедливы и для 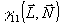 , причем, как это следует из (36), когерентность поля в плоскости наблюдения сопряжена с распределением интенсивности по объекту и наоборот. В соответствии со сказанным выше определений подлежит функция , причем, как это следует из (36), когерентность поля в плоскости наблюдения сопряжена с распределением интенсивности по объекту и наоборот. В соответствии со сказанным выше определений подлежит функция 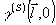 . Поэтому, выполняя преобразование, обратное (36), в координатах . Поэтому, выполняя преобразование, обратное (36), в координатах 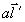 и и 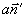 , где , где 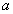 - произвольная постоянная, - произвольная постоянная,
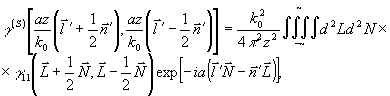 (37) (37)
и полагая 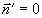 , найдем , найдем
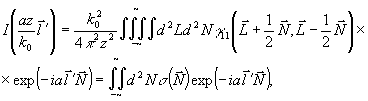 (38) (38)
где σ (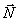 ) - функция когерентности в плоскости наблюдения, усредненная по координате ) - функция когерентности в плоскости наблюдения, усредненная по координате 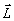 при фиксированном расстоянии между точками наблюдения: при фиксированном расстоянии между точками наблюдения:
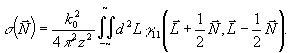 (39) (39)
Выражения (38-39) формально решают поставленную задачу, т.е.позволяют осуществить переход к двумерной функции 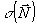 , однозначно связанной с интенсивностью , однозначно связанной с интенсивностью 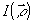 . Записывая . Записывая 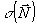 на транспаранте и освещая последний когерентным излучением о волновым вектором на транспаранте и освещая последний когерентным излучением о волновым вектором 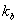 , получим преобразование (38) для значения постоянной , получим преобразование (38) для значения постоянной 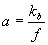 при использовании линзы с фокусным расстоянием f как элемента, выполняющего преобразование Фурье. К сожалению, экспериментальное определение при использовании линзы с фокусным расстоянием f как элемента, выполняющего преобразование Фурье. К сожалению, экспериментальное определение 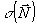 связано со значительными трудностями выполнения усреднения (39). Поэтому практически такая методика может применяться лишь в тех случаях, когда выражение (39) упрощается. Важнейшей ситуацией такого типа является случай, когда функция пространственной когерентности источника факторизуется в переменных связано со значительными трудностями выполнения усреднения (39). Поэтому практически такая методика может применяться лишь в тех случаях, когда выражение (39) упрощается. Важнейшей ситуацией такого типа является случай, когда функция пространственной когерентности источника факторизуется в переменных 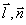 : :
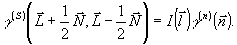 (40) (40)
Нетрудно видеть, что в этом случае факторизуется и функция 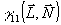 : :
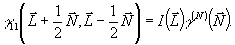 (41) (41)
причем,
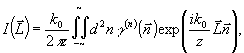 (42) (42)
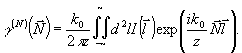 (43) (43)
Таким образом, фиксируя произвольное значение 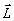 , т.е. выполняя измерение функции когерентности при определенном значения среднего расстояния между точками наблвдения, и повторяя , т.е. выполняя измерение функции когерентности при определенном значения среднего расстояния между точками наблвдения, и повторяя
описанную выше процедуру оптического восстановления транспаранта с амплитудным пропусканием 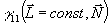 , найдем в соответствии с (43) , найдем в соответствии с (43)
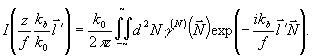 (44) (44)
Частным, но практически очень важным случаем, для которого выполняется условие факторизации (40), является проотранственно-некогерентный источник:
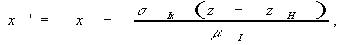 (45) (45)
Непосредственно из (44) и (45) находим:
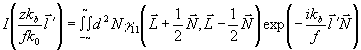 (46) (46)
при произвольном значении 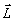 . Именно по такой методике был осуществлен эксперимент, схематически изображенный на рис.3 /13/. . Именно по такой методике был осуществлен эксперимент, схематически изображенный на рис.3 /13/.
В заключение остановимся коротко на искажениях восстановленного изображения, связанных с временной некогерентностью излучения. Для простоты будем рассматривать пространственно-некогерентный объект с корреляционной функцией (45). В плоскости наблюдения, с учетом (32), получим:
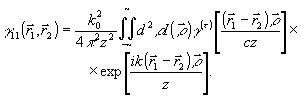 (47) (47)
Выполняя обратное преобразование Фypьe, получим в фокальной плоскости линзы изображение:
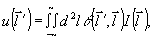 (43) (43)
где 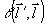 - сглаживающая функция, определяющая искажение распределения интенсивности по объекту: - сглаживающая функция, определяющая искажение распределения интенсивности по объекту:
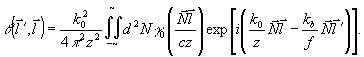 (49) (49)
Заменяя переменные интегрирования 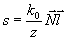 , преобразуем (49) к виду: , преобразуем (49) к виду:
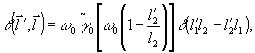 (50) (50)
где 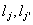 - компоненты векторов - компоненты векторов 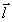 и и 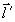 . Для монохроматического источника . Для монохроматического источника 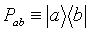 , так что подстановка (50) в (48) дает прежний результат. Если же полоса частот излучения имеет конечную ширину, сглаживающая функция (50) описывает усреднение распределения интенсивности , так что подстановка (50) в (48) дает прежний результат. Если же полоса частот излучения имеет конечную ширину, сглаживающая функция (50) описывает усреднение распределения интенсивности 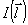 для каждой точки изображения для каждой точки изображения 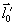 по прямой по прямой 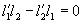 с весовой функцией с весовой функцией 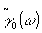 . Поскольку последняя максимальна вблизи ω=0, основной вклад в изображение точки . Поскольку последняя максимальна вблизи ω=0, основной вклад в изображение точки 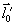 , дают точки объекта, для которых , дают точки объекта, для которых 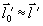 . Длина участка усреднения при этом определяется полосой частот . Длина участка усреднения при этом определяется полосой частот 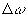 и может быть найдена из соотношений и может быть найдена из соотношений
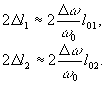 (51) (51)
Таким образом, точка объекта, находящаяся на оптической оси, не искажается при произвольном спектральном составе излучения.Для внеосевых точек искажения пропорциональны их расстоянию до оси. В оптическом диапазоне при использовании псевдотепловых источников 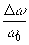 <10-6, так что практически подобные искажения можно не учитывать. Однако, при использовании интерферометрических методов в радиодиапазоне этот эффект может стать значительным. В этом случае для правильного восстановления изображения необходимо применять более сложную процедуру фильтрации. <10-6, так что практически подобные искажения можно не учитывать. Однако, при использовании интерферометрических методов в радиодиапазоне этот эффект может стать значительным. В этом случае для правильного восстановления изображения необходимо применять более сложную процедуру фильтрации.
Необходимо отметить некоторые трудности, связанные с практи -
ческим осуществлением интерферометрического метода записи изображений. Важнейшая из них - сложность записи информации. Изготовление транспаранта обычно производится о помощью электронно-лучевой трубки высокого разрешения, модулируемой сигналом интерферометра. При этом, однако, затруднен вывод информации при сохранении достаточного разрешения. Наиболее перспективными представляются системы записи, основанные на сканировании лазерного луча, позволяющие, в принципе, непосредственно решать поставленную задачу. Можно надеяться , что создание эффективных сканирующих устройств оптического диапазона с достаточным разрешением позволит сделать интерферометрический метод не только лабораторным, но и практическим средством записи и обработки информации в оптике.
Л и т е р а т у р а
1. d.gabor. proceedings of the royal society, a192, 454, 1949.
2. Г.Гебби, Р.Твисс. УФН, 99, 87, 1969.
3. j.goodman. j.of the opt.soc. of amer., 60, 506, 1970.
4. c.mehta. nuovo cimento, 36, 202, 1965.
5. e.wolf. proceedings of the physical. soc., 80, 1269, 1962.
6. d.kohler, l.mandel, j.opt.soc.amer., 63, 127, 1973.
7. c.mehta. j.opt.soc.amer., 58, 1233, 1968.
8. d.kohler, l.mandel. j.opt.soc.amer., 60, 280, 1970.
9. r.handbury brown, r.twiss. nature, 177, 27, 1956.
10. l.mandel, e.wolf. review of modern physics, 37, 231, 1965.
11. И.А.Дерюгин, В.Н.Курашов. Р.А.Абдуллаев, В.h.Настиг. Изв.АВ СССР, сер.физич., 37, 2115, 1973.
12. w.martienssen, e.spiller. amer.j.of phys., 32, 919, 1964.
13. t.beard. appl.phys.letters, 15, 227, 1969.
14. a.walther. j.opt.soc.amer., 58, 1256, 1966.
15. a.jaiswal, c.mehta. opt.communs., 5, 50, 1972.
16. a.jaiswal, g.agarwal, c.mehta. nuovo cimento, b15, 295, 1973.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

