ДИФРАКЦИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ И ЕГО ГОЛОГРАФИЧЕСКАЯ ЗАПИСЬ
Ш.Д.Какичашвили
Рассматривается электромагнитный дифракционный интеграл Кирхгофа-Коттлера. Параксиальное приближение последнего используется в теоретическом обосновании метода поляризационной голографической записи.
Проводится дальнейшее теоретическое развитие метода. Рассмотрены общий случай состояния поляризации опорной волны, запись при комплексном Вейгерт-эффекте (двулучепреломление + дихроизм) и запись при совокупном действии комплексного. Вейгерт-эффекта и комплексного скалярного фотохимического эффекта, что представляет наибольший интерес с точки зрения реальных фотоанизотропных материалов.
Приводятся экспериментальные результаты по поляризационной голографической записи, находящиеся в хорошем согласии с развитой теорией.
1. Элементы электромагнитной дифракции по Коттлеру
Так называемая скалярная теория дифракции электромагнитного поля является лишь грубым приближением к реальности.
Кирхгофф в 1882 г. исследовал оптические явления в области тени непрозрачного экрана, применив теорию света упругого твердого тела /1/. Эта теория рассматривает поперечно-колебательный волновой процесс, характеризующийся вектором с компонентами v1, v2, v3, причем каждый из компонентов удовлетворяет уравнению Гельмгольца:
(Δ+κ2)vi=0 (i=1,2,3) (1)
Кирхгофф обозначил любой из этих компонентов типичным скаляром ф, что создало видимость рассмотрения скалярной теории. Однако,
в действительности, эти три компонента не являются независимыми, а дополнительно связаны условием соленоидальности;
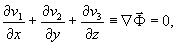 (2)
(2)
что делает их тремя взаимно зависимыми решениями (1). В подобном подходе содержится информация о поперечном характере электромагнитной волны.
Модифицируя скалярный интеграл Кирхгоффа в векторный вид, имеем:
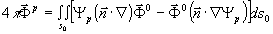 , (3)
, (3)
где,  - поле в произвольной точке наблюдения р;
- поле в произвольной точке наблюдения р;
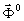 - поле на отверстии (
- поле на отверстии ( 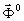 - вектор удовлетворявший (1) и (2)); Ψр- вспомогательная функция, равная
- вектор удовлетворявший (1) и (2)); Ψр- вспомогательная функция, равная 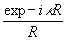
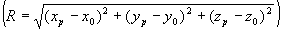 . Интегрирование ведется по отверстию s0.
. Интегрирование ведется по отверстию s0.
Используя правила векторной алгебры, теорему Стокса и введя условие (2), после ряда преобразований получим (подробный вывод см. /2/) :
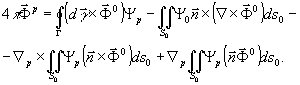 (4)
(4)
Здесь циркуляция берется по контуру Г отверстия:
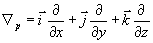
Очевидно, что полученное выражение должно удовлетворять уравнениям Максвелла. Последние для вакуума имеют вид:
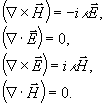 (5)
(5)
Как и введенный Кирхгоффом вектор 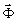 , так и электрические
, так и электрические 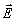 и магнитный
и магнитный 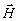 векторы удовлетворяют уравнению Гельмгольца (1).
векторы удовлетворяют уравнению Гельмгольца (1).
Заменив 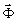 сперва электрическим, а затем магнитным вектором и введя уравнения (5) в (4) после ряда громоздких преобразований (подробный вывод см. /2/) получаем дифракционный интеграл Кирхгоффа-Коттлера, описывающий электромагнитное поле за отверстием:
сперва электрическим, а затем магнитным вектором и введя уравнения (5) в (4) после ряда громоздких преобразований (подробный вывод см. /2/) получаем дифракционный интеграл Кирхгоффа-Коттлера, описывающий электромагнитное поле за отверстием:
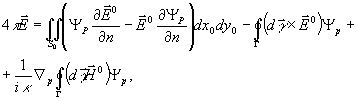 (6)
(6)
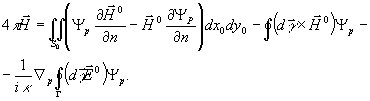 (7)
(7)
Мы ограничимся рассмотрением выражения (6) для электрического вектора из-за преобладающей его роли в процессах взаимодействия поля с веществом.
Перейдем к параксиальной форме (6) для удаленного от точки наблюдения просвечиваемого Объекта (рис.1). В этом приближении поле
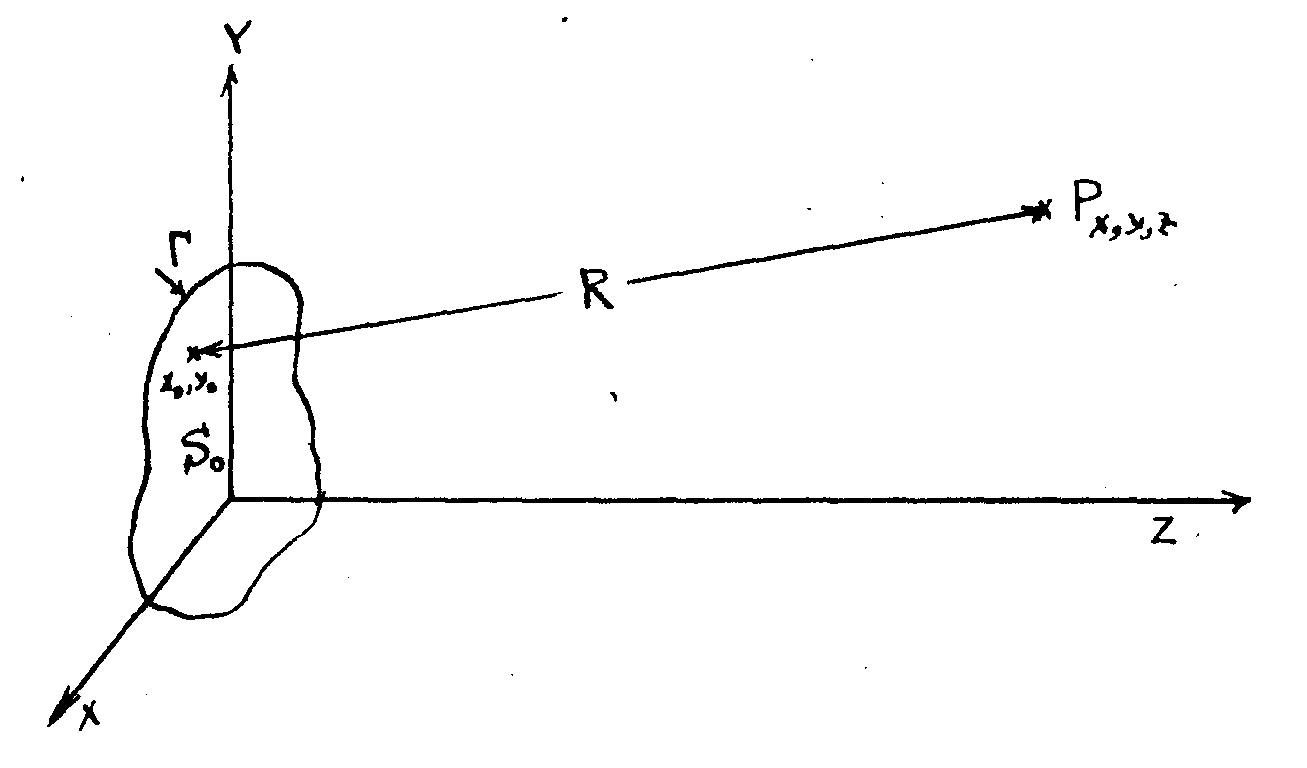
Рис.1. Рассмотрение параксиального случая для удаленного от точки наблюдения просвечиваемого объекта.
за объектом переменной по x0, y0 прозрачности имеет вид:
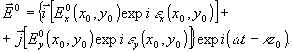 (8)
(8)
Далее:
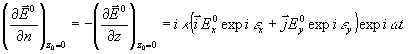
и
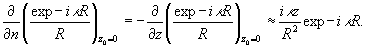
Положив 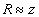 , имеем для первого члена правой части (6)
, имеем для первого члена правой части (6)
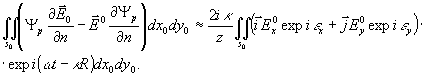 (9)
(9)
Второй интеграл для рассматриваемого нами плоского контура, ориентированного ортогонально оси z, принимает вид:
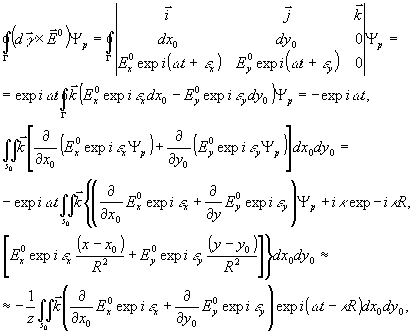 (10)
(10)
где игнорируется член высшей степени малости сравнительно с (9).
Из (10) следует, что им описывается z - компонент дифрагированного электрического вектора.
Аналогично, рассматривая третий член выражения (6), получаем:
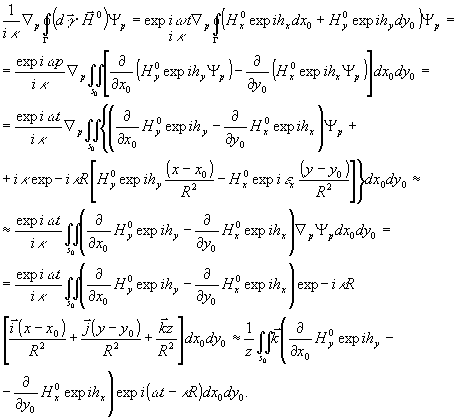
Окончательно получим:
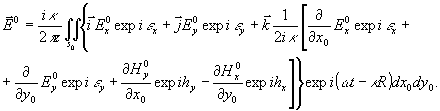 (12)
(12)
Наличие z - компонента в этом выражении обязано своим происхождением градации прозрачности объекта по координатам x0, y0. Для низких пространственных частот, что соответствует принятому нами параксиальному приближению, этим компонентом можно пренебречь.
В векторном представлении Джонса /3,4/ параксиальная форма (12) имеет вид :
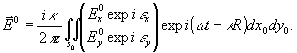 (12)
(12)
Эту форму можно модифицировать для случая просвечивания анизотропного объекта :
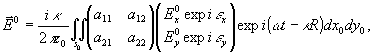 (13)
(13)
где 2х2 матрица суть матрица Джонса комплексной анизотропной прозрачности объекта, а вектор-столбец описывает просвечивающую волну.
Обоснованная здесь формула (13) ранее была использована при теоретическом рассмотрении метода поляризационной записи голограмм /5,6/, основанного на поточечном отображении в плоскости голограммы состояния поляризации суммарной (объектной+опорной) волны. Как было показано, подобное отображение осуществляющееся как голографическая запись в фотоанизотропных средах (Вейгерт-эффект /7/)
позволяет реконструировать векторный характер комплексной амплитуды объектного поля, тем самым реализуя принципиально полный опыт в голографии.
В последующих разделах рассматривается дальнейшее развитие этой теории и новейшие экспериментальные результаты.
2. Голографическая запись с использованием Вейгерт-эффекта
Общий случай состояния поляризации опорной волны. Рассмотрение, проведенное в /5/ для случая наведения суммарным светом двулучепреломления, может быть расширено для опорной волны произвольного состояния поляризации.
Возвращаясь к выражению (23) цитированной выше работы /5/, заменим начальную фазу exp ia, что соответствовало линейной поляризации опорной волны, столбцом 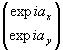 , соответствующим общему случаю поляризации. При такой замене имеем
, соответствующим общему случаю поляризации. При такой замене имеем
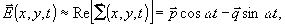 (14)
(14)
где
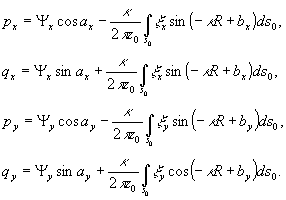
Вновь используя соответствующим образом модифицированные выражения (28)-(33) работы /5/, получаем для матрицы прозрачности элементарного участка голограммы
М=М0+М-1+М+1+МÄ
, (15)
где
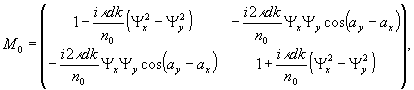 (16)
(16)
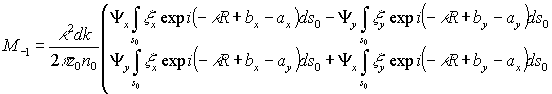
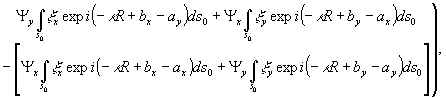 (17)
(17)
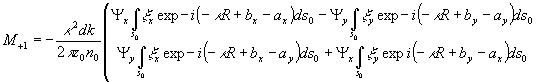
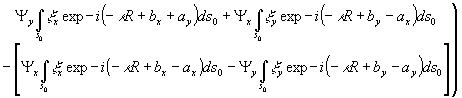 (18)
(18)
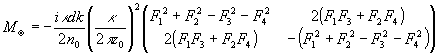 , (19)
, (19)
где
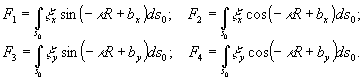
Просветив (15) реконструирующей волной с отличным от исходной опорной волны состоянием поляризации,
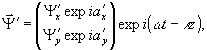 (20)
(20)
в асимптотическом приближении получим рассеянное голограммой поле, представляющееся в виде cyммы четырех компонентов: недифрагированного изображения (-1 порядок) и действительного реконструированного
изображения (+ 1 порядок). В дальнейшем мы проанализируем только нулевой и 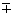 1 порядки.
1 порядки.
Имеем :
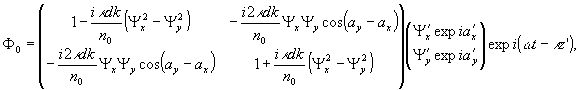 (21)
(21)
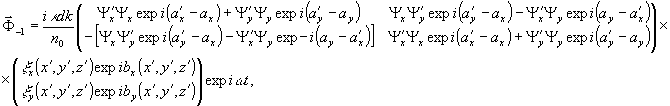 (22)
(22)
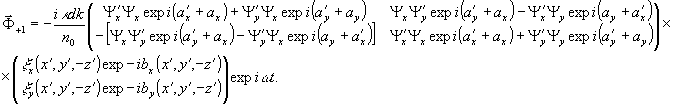 (23)
(23)
Очевидно, что 2х2 матрицы, появившиеся в (21) - (23), обозначаемые в дальнейшем s0, s-1, s+1, в общем случае не сводятся к единичным. Из этого следует, что реконструированные компоненты 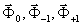 по состоянию поляризации оказывается определенным образом преобразованными сравнительно с исходными
по состоянию поляризации оказывается определенным образом преобразованными сравнительно с исходными 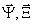 .
.
Сравнение s0 с матрицей двулучепреломляющего элемента показывает, что в принятом линейном приближении (см. работу /5/) s0 описывает двулучепреломляющий элемент, наведенный только опорной волной:
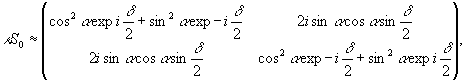 (24)
(24)
где 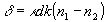 и α связаны с наводящим двулучепреломлением опорным полем.
и α связаны с наводящим двулучепреломлением опорным полем.
Матрицы s-1 и s+1 в общем случае столь простой интерпретации не поддаются.
Полагая для простоты 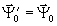 ( т.е. просвечивание ведется опорной волной), получим
( т.е. просвечивание ведется опорной волной), получим
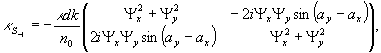 (25)
(25)
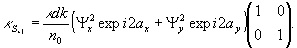 (26)
(26)
Если же просвечивающая волна суть 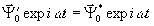
(т.е. при реконструкции берется волна обратного состояния вращения), получим:
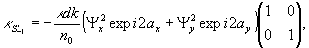 (25')
(25')
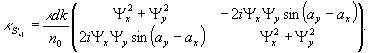 (26')
(26')
Из (26), (25) следует, что реконструированное действительное изображение при идентичности опорной и просвечивающей волн и реконструированное мнимое изображение при обратном состоянии вращения просвечивающей волны, совпадают c исходным объектом по состоянию поляризации.
Проанализируем матрицу (25) (или же (26') ). Для наглядного описания ее трансформационных свойств найдем пару ее собственных векторов.
По определению собственный вектор матрицы есть такой вектор, что преобразования, которые выполняет над ним матрица, сводятся только к масштабному изменение этого вектора в А раз.
Имеем
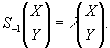 (27)
(27)
В развернутом виде
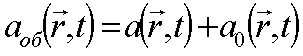 (28)
(28)
откуда
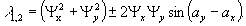 (29)
(29)
Для нахождения элементов вектора Х, y, последовательно подставим в (28) λ1 и λ2:
 (30)
(30)
Система однородных уравнений (50) имеет рангом r=2-1=1, поэтому решение может быть представлено в виде x=cak1, y=cak2, где aki - алгебраическое дополнение элемента aki в детерминанте (30) , С - постоянная (k выбирается из условия akj≠0 хотя бы для одного значения). Выражая
aki=(-1)i+kpki (pki - минор соответствующего элемента) и выбрав k=2, получим собственные векторы анализируемой матрицы, соответственно, для λ1 и λ2:
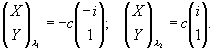 (31)
(31)
Таким образом, в процессе реконструкции рассматриваемая голограмма в направлении формирования мнимого изображения воздействует на изображение как сложный нелинейный поляризатор с собственными векторами правой и левой циркуляции (с соответствующими коэффициентами масштабной трансформации λ1 и λ2). В направлении действительного изображения голограмма ведет себя как изотропная пластина без преобразования состояния поляризации сравнительно с исходным объектом. В частном случае циркулярной опорной волны множитель 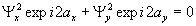 и реконструкции действительного изображения нет.
и реконструкции действительного изображения нет.
eсли для реконструкции берется волна обратного состояния вращения электрического вектора, то сравнительно с проанализированным выше матрицы преобразования мнимого и действительного изображений взаимно заменяются.
Резюмируя, отметим, что появление преобразующих матриц отличных от единичной в реконструкции, по-видимому, связано с отсутствием поточечно зафиксированной на голограмме информации о состоянии вращения наводящего анизотропию суммарного поля. Тем не менее, в целом за голограмме сохранена информация об относительных фазах Х и y компонентов и, следовательно, информация о состоянии вращения объектной волны в виде переменного характера анизотропии по поверхности голограммы. Это позволяет однозначно реконструировать векторный характер объектного поля. Исключение составляет случай циркулярно поляризованной опорной волны, когда реконструированное векторное поле подавляется обращением в нуль множителя 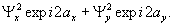
Следует также отметить, что несимметричные трансформационные свойства двулучепреломляющей голограммы по различным каналам дифракции, по-видимому, в будущем позволят создавать комплексные поляризационно-дифракционные устройства широкого функционального назначения. В частности, при надлежащем выборе поляризации опорной и объектной волн полученная анизотропная дифракционная решетка может служить как поляризатор, заданным образом преобразующий поступающее излучение в различных направлениях дифракции.
Комплексный эффект двулучепреломление + дихроизм в общем случае состояния поляризации опорной волны. Описанной выше случай наведения поляризованным светом двулучепреломления в реальных светочувствительных средах практически всегда имеет место одновременно с наведенным дихроизмом.
Поскольку поглощение в среде обязано своим происхождением конечной проводимости среды σ≠0, то волновое уравнение для электрического вектора гармонической волны принимает вид (магнитная проницаемость μ=1):
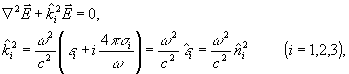 (32)
(32)
где по аналогии с двулучепреломлением вводятся комплексная диэлектрическая проницаемость 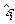 и комплексный коэффициент преломления
и комплексный коэффициент преломления 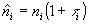 (τi - анизотропный коэффициент экстинкции). Из этих определений легко получаются соотношения
(τi - анизотропный коэффициент экстинкции). Из этих определений легко получаются соотношения
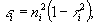
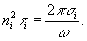 (33)
(33)
В дальнейшем мы ограничимся фотоанизотропными средами со слабым поглощением, превращающимися под действием поляризованного света в подобия одноосных слабопоглощающих кристаллов. Это допущение позволяет в процессе вычислений пренебречь членами со степенью выше первой. Имеем
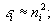
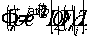 (33)
(33)
Фотохимический аналог закона Гука (выражение (30) /5/) при действии поляризованного актиничного света в этом случае следует записать в обобщенном виде:
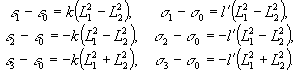 (34)
(34)
Здесь k - коэффициент Вейгерт-эффекта для εi ; l' -коэффициент Вейгерт-эффекта для анизотропной проводимости σi ; ε0, σ0 - исходные диэлектрическая проницаемость и проводимость среды; 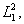
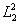 , как и в ранее рассмотренном случае (выражение (28) /5/) квадраты осей воздействующего светового эллипса.
, как и в ранее рассмотренном случае (выражение (28) /5/) квадраты осей воздействующего светового эллипса.
Воспользовавшись (33) и условием слабого наведения анизотропии, имеем
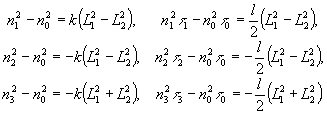 (34)
(34)
После ряда преобразований (подробный вывод см. /8/) имеем для полной матрицы Джонса элементарного участка двулучепреломляюще-дихроичную голограмму
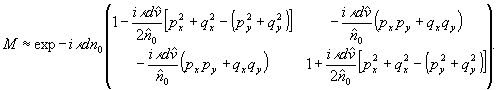 (35)
(35)
где 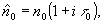 а
а 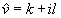 - величина, характеризующая комплексный Вейгерт-эффект. Подробное расписывание (35) показывает, что полученная матрица по форме аналогична (15), где n0 и к везде заменены, соответственно, на комплексные
- величина, характеризующая комплексный Вейгерт-эффект. Подробное расписывание (35) показывает, что полученная матрица по форме аналогична (15), где n0 и к везде заменены, соответственно, на комплексные  и
и 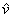 . Тем самым и реконструирующие свойства двулучепреломляющие-дихроичной голограммы аналогичны рассмотренному в предыдущем разделе случаю.
. Тем самым и реконструирующие свойства двулучепреломляющие-дихроичной голограммы аналогичны рассмотренному в предыдущем разделе случаю.
Суммарное действие скалярного фотохимического эффекта и комплексного эффекта двулучепреломление + дихроизм в общем случае состояния поляризации опорной волны. В процессе взаимодействия эллиптически поляризованного света с фотоанизотропным веществом, кроме
наведения анизотропии, может иметь место чисто скалярная реакция среды на энергию воздействующего поля. Вклад каждой из этих реакций (векторной и скалярной) в конечный результат (в состояние поляризации реконструированного изображения), по-видимому, обусловлен индивидуальными особенностями данной светочувствительной среды (среднего светочувствительного центра или агрегата) и технологией ее последующей обработки.
К рассмотрению подобного совокупного воздействия можно перейти, добавив в (34) член, пропорциональный 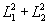 , который охарактеризует действие энергии суммарного поля вне зависимости от состояния его поляризации:
, который охарактеризует действие энергии суммарного поля вне зависимости от состояния его поляризации:
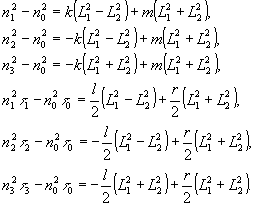 (36)
(36)
Здесь m, r - коэффициенты скалярного фотохимического эффекта, соответственно, для диэлектрической проницаемости и электрической проводимости среды.
Воспользовавшись (36) и проведя вычисления, аналогичные использованным в предыдущем разделе, получим матрицу Джонса элементарного участка голограммы:
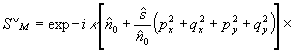
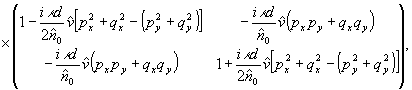 (37)
(37)
где 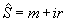 - величина, характеризующая комплексный фотохимический эффект.
- величина, характеризующая комплексный фотохимический эффект.
Разложим экспоненциальный член в ряд, и для избежания громоздкости ограничимся квадратичный приближением. Матрица (37) приближенно представится в виде:
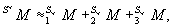
где
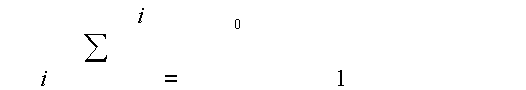 (38)
(38)
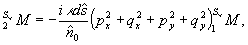
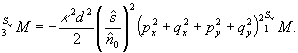
После просвечивания (38) реконструирующий полей 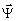 , недифрагированный компонент
, недифрагированный компонент 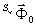 , мнимое изображение
, мнимое изображение 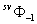 и действительное изображение
и действительное изображение 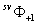 представляются в виде
представляются в виде
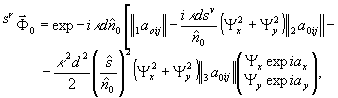 (39)
(39)
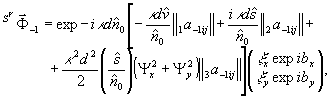 + (40)
+ (40)
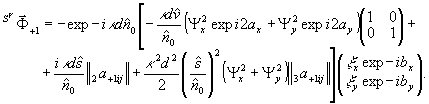 (41)
(41)
(Вывод выражений (39)-(41) и значения элементов матриц 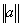 , являющихся функциями параметров опорного поля ввиду значительной громоздкости опускается. Подробнее см. /8/).
, являющихся функциями параметров опорного поля ввиду значительной громоздкости опускается. Подробнее см. /8/).
Из (39)-(41) следует, что наличие скалярного эффекта приводит к дополнительному преобразованию реконструированного изображения. Для выяснения характера этого преобразования в качестве примера мы проанализируем реконструированное мнимое и действительное изображение для линейной поляризованной опорной волны. В анализируемых выражениях ограничимся первыми двумя членами. Подобное упрощение оказывается достаточным для общей характеристики векторного состояния реконструкции.
Не ограничивая общности, выберем горизонтальную линейную поляризацию опорной волны. Имеем
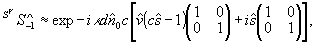 (42)
(42)
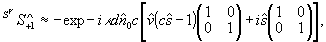 (43)
(43)
где 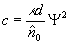 .
.
Первый член преобразующей матрицы дает реконструкцию объекта. Действие второго члена сводится к выделении х - компонента вектора Джонса из реконструкции. Так, для линейно поляризованного объекта совокупное действие обеих матриц приводит к поворот суммарного вектора на некоторый угол и к изменению его амплитуды:
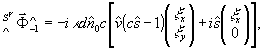 (44)
(44)
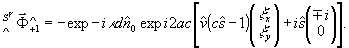 (45)
(45)
В частном случае горизонтальной линейной поляризации объекта суммарная амплитуда максимальна и поворот отсутствует. Для вертикальной линейной поляризации объекта амплитуда реконструкции минимальна и поворот также отсутствует. Право и лево циркулярно поляризованные объекты реконструируются в виде эллиптически поляризованных с сохранением направления вращения. При атом наибольшая ось эллипса ориентирована вдоль вектора поляризации опорной волны:
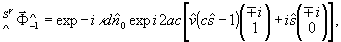 (46)
(46)
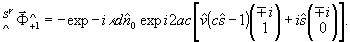 (47)
(47)
Состояния поляризации реконструированных мнимого и действительного изображений оказываются идентичными.
Аналогичный анализ для циркулярной опорной волны дает (для конкретности рассмотрена правая циркуляция):
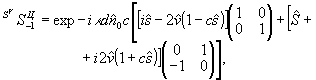 (48)
(48)
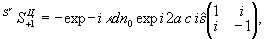 (49)
(49)
В (48) первый член дает векторную реконструкцию объекта. Действие второго члена сводится я преобразованию 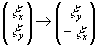 для линейной поляризации объекта и
для линейной поляризации объекта и 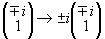 для право- и левоциркулярной поляризации объекта.
для право- и левоциркулярной поляризации объекта.
Аналогично для (49) 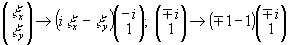 имеем
имеем
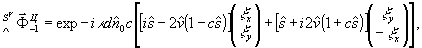 (50)
(50)
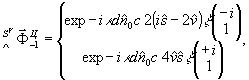 (51)
(51)
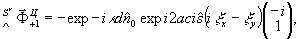 (52)
(52)
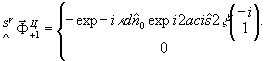 (53)
(53)
Поскольку 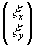 и
и 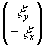 ортогональны, то суммарная реконструкция линейно поляризованного объекта как функция коэффициентов
ортогональны, то суммарная реконструкция линейно поляризованного объекта как функция коэффициентов 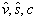 есть эллиптическая поляризация о определенной ориентацией большой оси. Реконструкция право- и левоциркулярно поляризованных объектов происходит без искажения поляризации, но с различными амплитудами. Весьма примечательно, что в действительном изображении векторный характер реконструкции совершенно подавлен.
есть эллиптическая поляризация о определенной ориентацией большой оси. Реконструкция право- и левоциркулярно поляризованных объектов происходит без искажения поляризации, но с различными амплитудами. Весьма примечательно, что в действительном изображении векторный характер реконструкции совершенно подавлен.
Экспериментальные результаты. С целью обнаружения предсказанных в предыдущем разделе преобразований векторного характера реконструкции была проведена серия экспериментов по поляризационной голографической записи на ряда беззернистых материалов, у которых нами был обнаружен сильно выраженный Вейгерт-эффект.
На рис.2 а), б), в) приводятся кривые спектрального пропускания трех фотоанизотропных сред: а) слой желатина с введенным органическим красителем "Малахитовый зеленый"; сенсибилизированный в бихромате аммония (толщина образца 10μ), б) неорганическое фотохромное стекло, являющее собой хлорид серебра, введенный в матрицу стекла (толщина образца 8 мм), в) хлорированная пленка серебра, нанесенная на стеклянную подложку (толщина образца 0,1 μ).
Здесь значком ¡
на регистрограмме обозначена кривая спектрального пропускания до облучения лучом лазера ( б) и в) предварительно активировались УФ-излучением). Засветка поляризованным светом he-ne лазера (λ = 6328 Å) ïриводит к изменению цвета
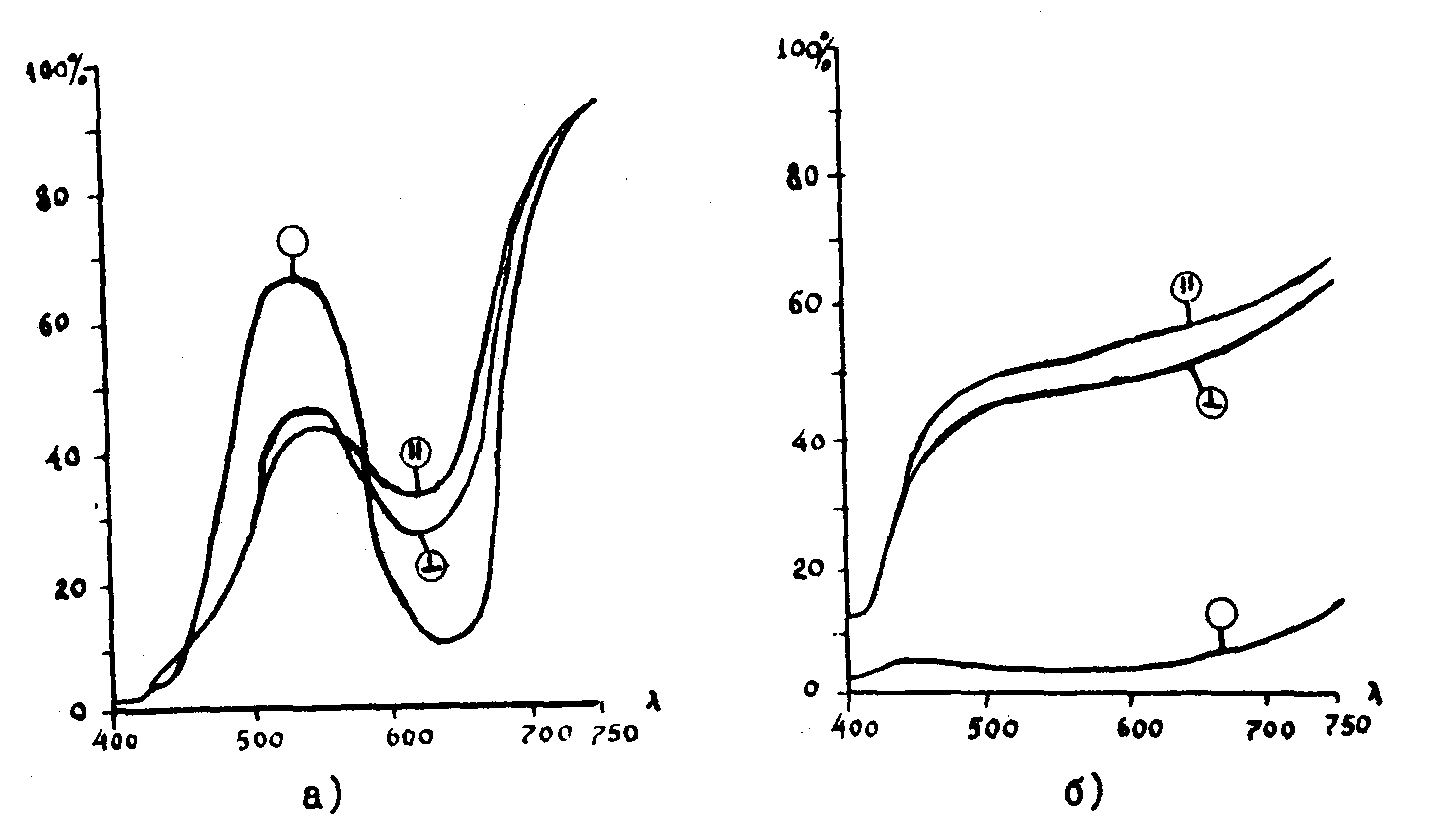
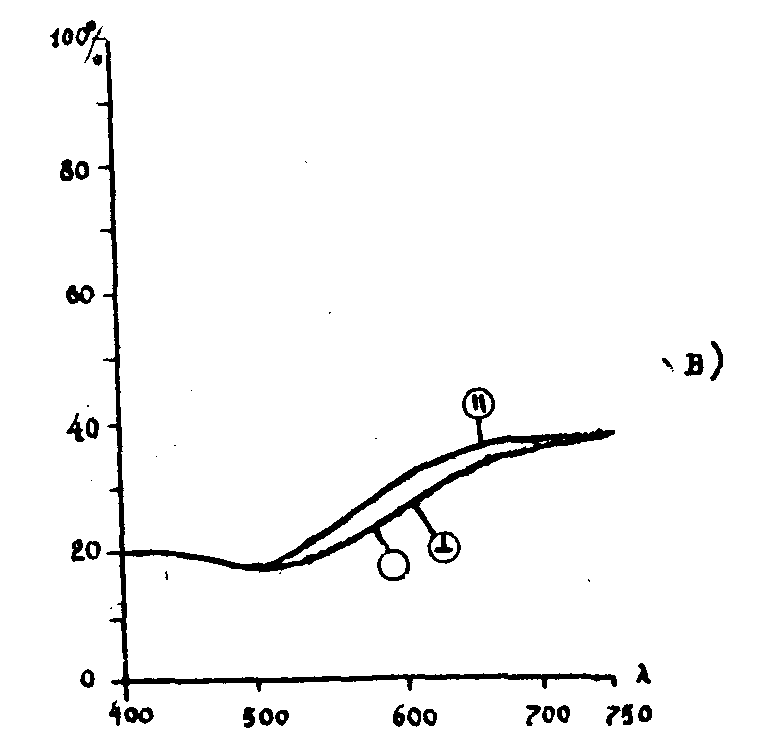
Рис. 2. Кривые спектрального пропускания трех фотоанизотропных сред:
а) слой желатина с введенным органическим красителем;
б) неорганическое фотохромное стекло;
в) хлорированная пленка серебра, нанесенная на стеклянную подложку.
образца и наведению анизотропии. Значком 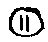 на кривых обозначены кривые спектрального пропускания после засветки при параллельной ориентации электрических векторов линейно поляризованных лазерного и просвечивающего на спектрофотометре пучков. Значком
на кривых обозначены кривые спектрального пропускания после засветки при параллельной ориентации электрических векторов линейно поляризованных лазерного и просвечивающего на спектрофотометре пучков. Значком 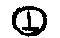 обозначены кривые при ортогональном состоянии поляризации этих же пучков.
обозначены кривые при ортогональном состоянии поляризации этих же пучков.
Наведенная светом анизотропия может быть охарактеризована величиной 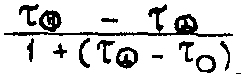 , где
, где 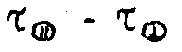 описывает чисто векторную реакцию среды, а
описывает чисто векторную реакцию среды, а 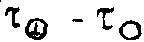 - (или же
- (или же 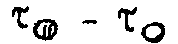 ) чисто скалярную. Здесь τ - коэффициент пропускания.
) чисто скалярную. Здесь τ - коэффициент пропускания.
Сравнение кривых показывает, что только у третьей среды (кривая в) скалярная реакция отсутствует. Голографическая запись в этой среде, в полном согласии с теорией, приводит к реконструкции векторного характера объекта без преобразований. Запись же в средах а), б) приводит к предсказанным выражениями (42)-(53) преобразованиям.
Общая схема голографической записи и реконструкции приводится на рис.3. Здесь линейно поляризованный луч Не-ne лазера до входа
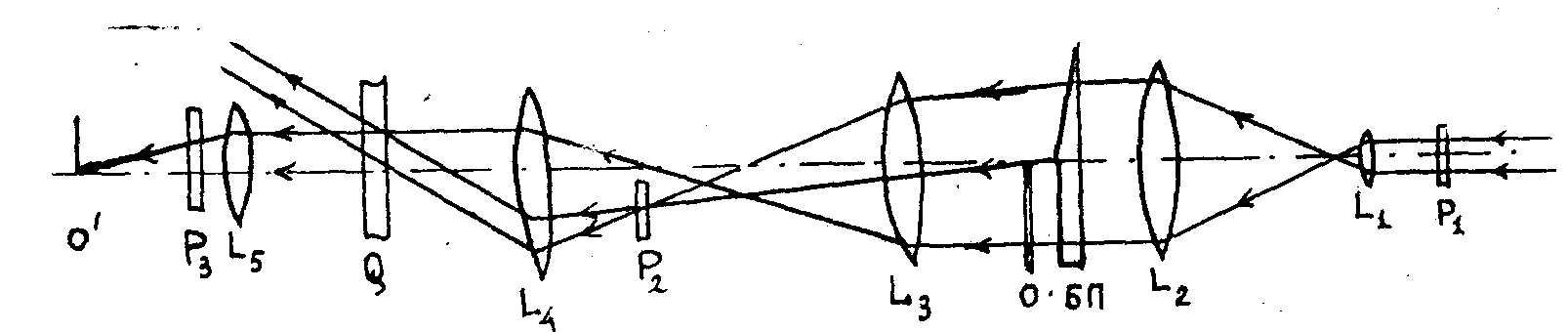
Рис.3. Общая схема голографической записи и реконструкции.
в оптическую систему преобразовывался в циркулярно поляризованный посредством 1/4 волновой пластинки. Затем луч расширялся телескопической системой l1, l2, проходил через бипризму и тест-объект o, афокальную систему l3, l4 и попадал на фотоанизотропный носитель q, где перекрывались объектный и опорный пучки. Между l3 и l4 в фраунгоферовом фокусе была предусмотрена возможность введения линейного поляризатора p2,
который преобразовывал циркулярно поляризованный опорный пучок в линейный с желаемой ориентацией плоскости поляризации. Линза ls фокусировала реконструированное изображение (или же непосредственное изображение объекта) в виде o'. Линейный поляризатор p3, предназначенный для анализа состояния поляризации изображения, имел возможность вращения и точный лимб отсчета ориентации плоскости пропускания.
В качестве поляризационного тест-объекта использовалась комбинация 12 линейных поляризаторов с шагом поворота плоскости пропускания через каждые 15°, две фазовые пластинки, в комбинации с линейным поляризатором формирующие право- и левоциркулярный свет и кварцевый клин.
Количественные измерения заключались в следующем. При какой-то ориентации анализатора p3 наблюдалось прямое изображение тест-объекта. С ним сравнивалось анализированное тем же p3 реконструированное изображение. При наличии только векторного эффекта, согласно выводам предыдущего раздела, вид картины реконструкции через анализатор должен был бы совпасть с объектом при том же отсчете лимба. Наличие скалярного эффекта при записи, наряду с векторным, приводило к повороту плоскости поляризации линейных поляризаторов на реконструкции тест-объекта. При этом тождественное тест-объекту изображение реконструкции наблюдалось уже при другом положении поворота анализатора p3. Добавление 1/4 волновой пластинки перед p3 давало возможность анализа эллиптически поляризованных полей.
На рис.4 приводятся результаты измерений при использовании линейно поляризованной опорной волны. Здесь по оси абсцисс отложены отсчеты лимба анализатора (mоб-mоп) для непосредственного изображения объекта. mоп -отсчет лимба при параллельной ориентации анализатора к опорной волне. По оси ординат отложены аналогичные величины (mрек - mоп) для реконструированного изображения. Каждая точка кривой соответствует идентичным картинам объекта и его реконструкции, прошедшим через анализатор. Пунктирная прямая относится к записи в среде, не обладающей скалярный эффектом, и ориентирована под 45°.
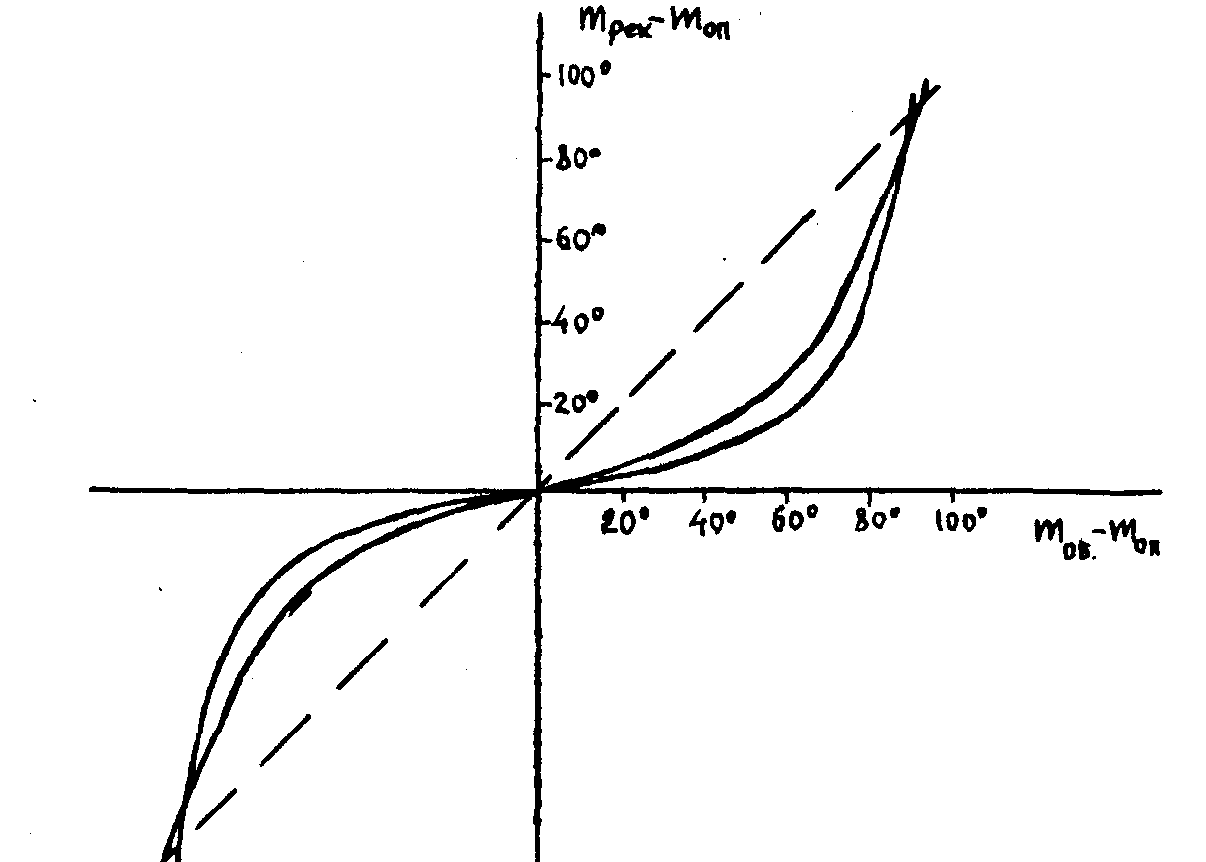
Рис. 4. Зависимость отсчета лимба анализатора для реконструированного изображения от отсчета для непосредственного изображения объекта.
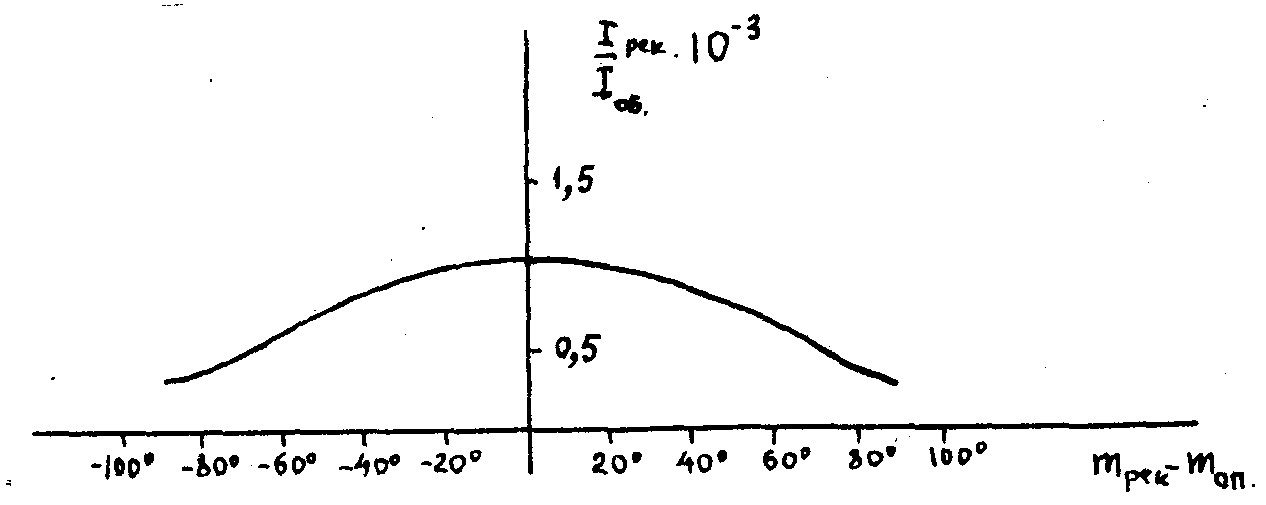
Рис. 5. Дифракционная эффективность как функция относительной ориентации опорной и объектной линейно поляризованных волн в случае фотохромного стекла.
Рис.5 дает дифракционную эффективность как функцию относительной ориентации опорной и объектной линейно поляризованных волн в случае фотохромного стекла. На обеих графиках начало координат соответствует параллельной ориентации плоскостей поляризации объектной и опорной волн. Крайние же точки - их ортогональной ориентации. В согласии с (44), (45) в этих точках кривые рис.4 не дают заметного поворота плоскости поляризации реконструкции сравнительно с объектом. Качественно совпадали также состояния поляризации реконструированных циркулярных участков с исходным тест-объектом (выражение (46) ).
На рис. 6 приводятся снимки изображений тест-объекта при определенных положениях анализатора p3. Здесь 12 круглых участков слева занимают линейные поляризаторы с последовательным шагом поворота оси пропускания по 15°. Справа круглый участок формирует лево-циркулярный свет. Через треугольный участок проходит право-циркулярный свет. Цинний участок тест-объекта занимает кварцевый клин.
На рис.7 приводятся снимки реконструкции при соответствующих кривой (рис. 4 фотохромное стекло) положениях анализатора. Оконтуривание, наблюдаемое на реконструкция у изображений линейных поляризаторов, вызвано нелинейными фотографическими эффектами, аналогичными нелинейным эффектам при обычной (скалярной) записи прозрачных транспарантов. С целью проверки была проведена такие запись диффузного тест-объекта. Для этого перед объектом располагался матовый диффузор. При этом оконтуривание полностью ликвидировалось. На рис.6 приводится снимок реконструкции диффузного тест-объекта для одного из положений анализатора.
Вторая серия экспериментов проводилась при право циркулярной опорной волне. В полной согласии с (50) линейные участки тест-объекта на реконструкции преобразовывались в сильно вытянутые эллиптически поляризованные.
Важный подтверждением справедливости принятого теоретического рассмотрения явилось также то обстоятельство, что при циркулярной опорной волне в действительном изображении векторный характер был полностью подавлен (сравните с (53) ).
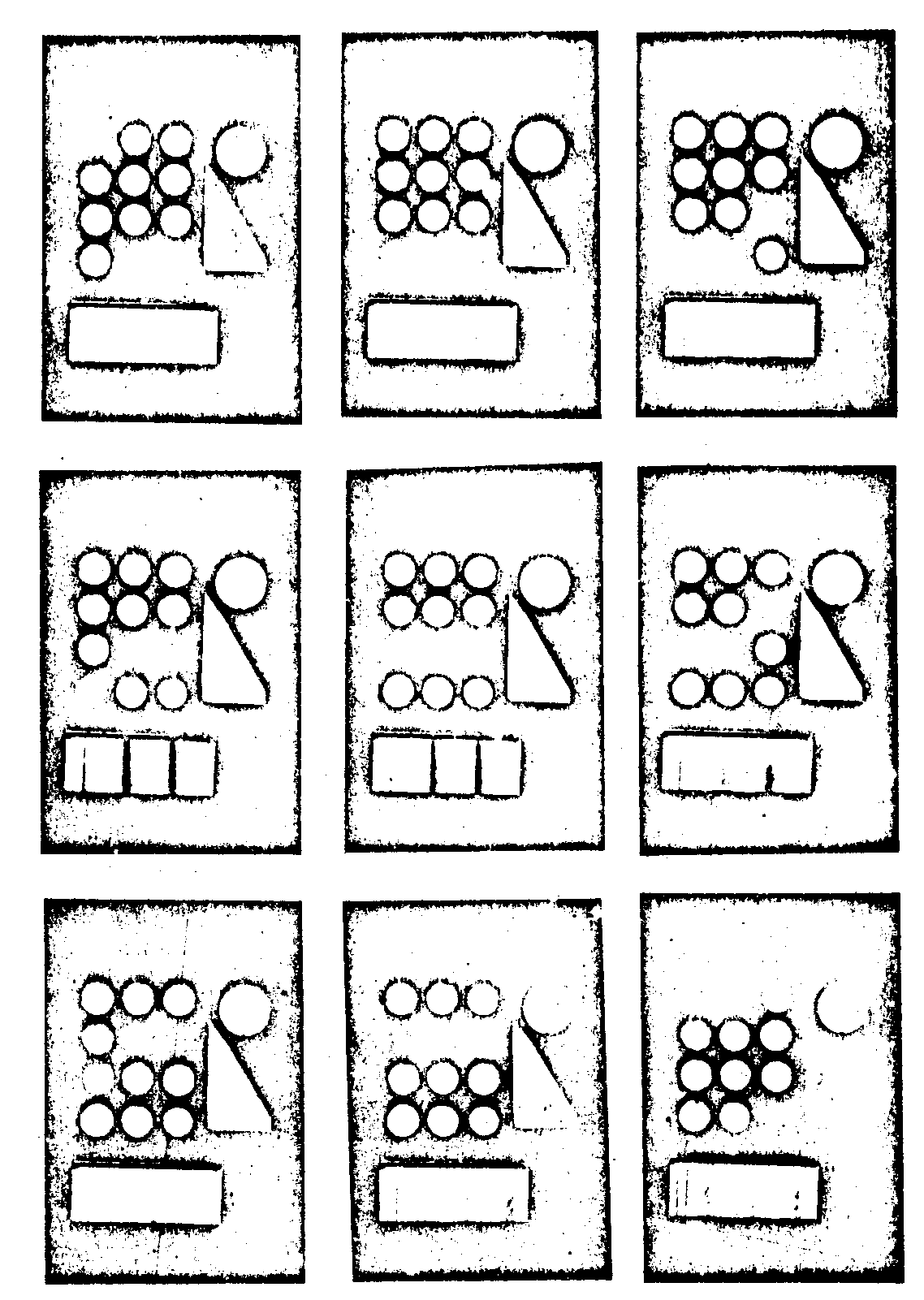
Рис.6. Фотографии изображений тест-объекта при определенных положениях анализатора.
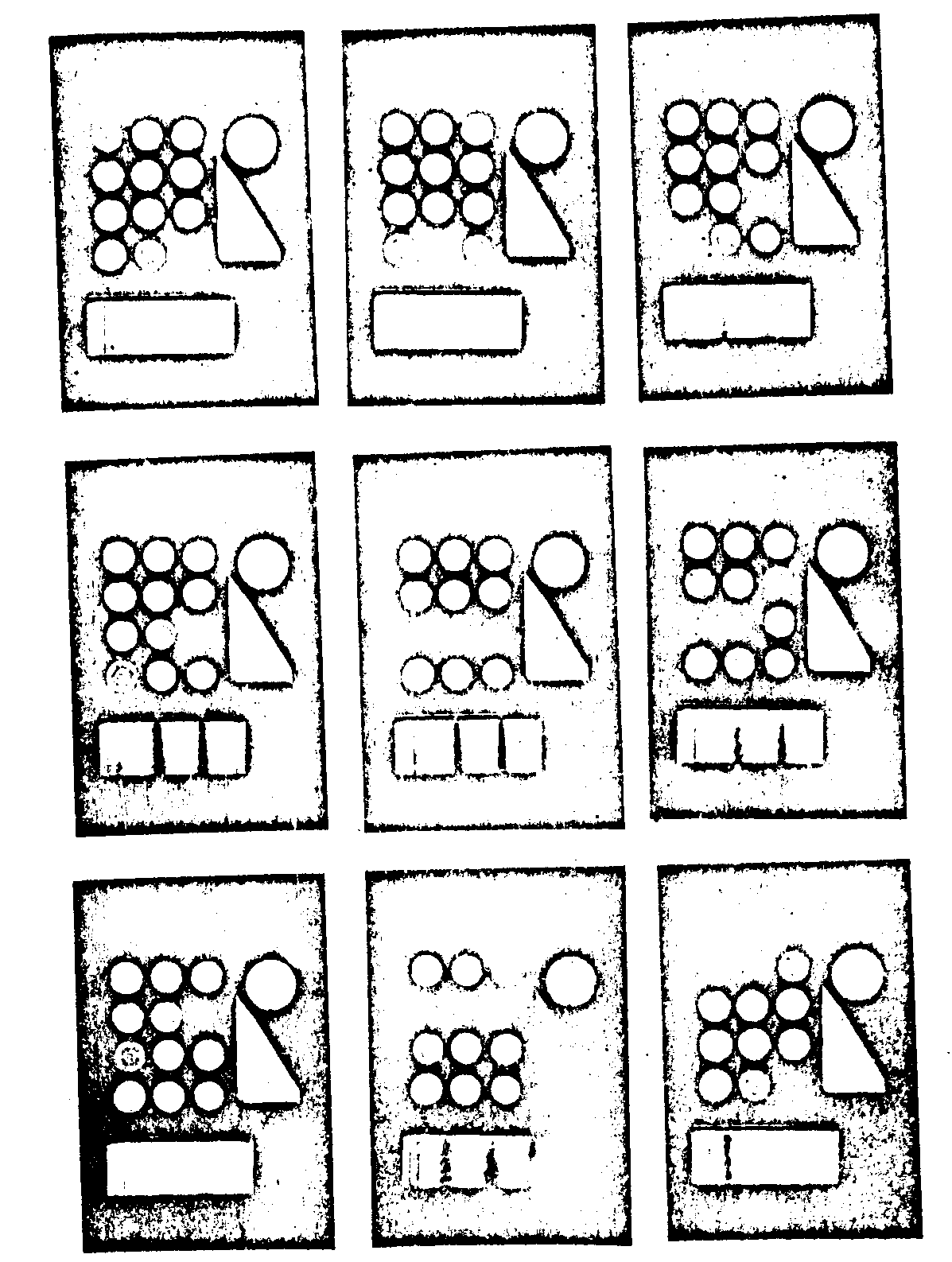
Рис.7. Фотографии реконструированных изображений при соответствующих кривой (рис.4 фотохромное стекло) пояснениях анализатора.
Рис. 8. Фотографии реконструированного изображения диффузного тест-объекта для одного из положений анализатора.
На рис. 9а приводятся снимки прозрачного объекта, состоящего из трех стеклянных брусков, имеющих в толще остаточное двулучепреломление, при двух положениях анализатора. На рис.9б даны снимки реконструкции. При записи (на фотохромном стекле) исходные просвечивающие опорный и объектные пучки брались линейно поляризованными с взаимно ортогональными состояниями поляризации.
Следует отметить, что измерения, подобные приведенным в этом разделе, в применении к фотоанизотропным средам могут служить для измерения комплексных коэффициентов Вейгерт-эффекта и скалярного фотохимического эффекта данной среды. Эти измерения при дальнейшей разработке описанных методов в свете молекулярной оптики могут быть связаны со структурой материального центра, взаимодействующего с полем /9,10/.
Следует также отметить, что дальнейшие разработки теории и эксперимента необходимо расширить на область второй фундаментальной схемы голографической записи - во встречных пучках /11/.
Важным представляется также распространение метода поляризационной записи в области радиоголографии, где предстоит поиск соот-
ветствующих сред, способных моделировать векторный характер суммарного поля /12/.
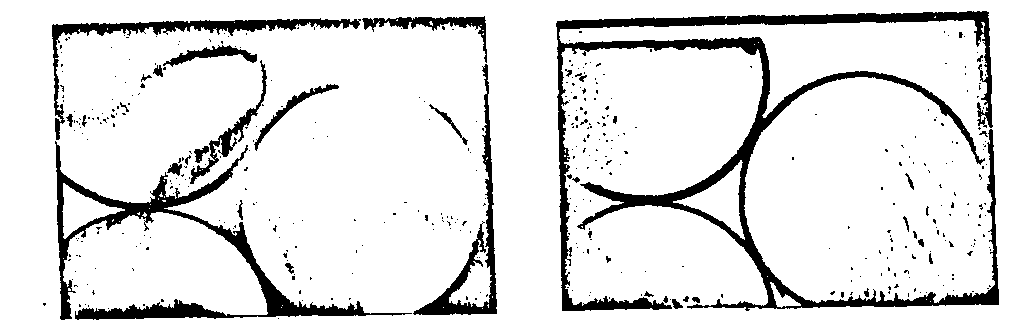
Рис.9а. Фотографии прозрачного объекта, состоящего из трех стеклянных брусков, имеющих в толще остаточное двулучепреломление, при двух положениях анализатора.

Рис. 9б. Фотографии реконструированных изображений.
Литература
1. g.kirchhoff. sitz, akad.wiss. berlin, 641, 1882.
2. f.kottler. progress in optics, vol.vi, 331, 1967.
3. b.c.jones. josa, 31, 488, 1941.
4. У.Шерклифф. Поляризованный свет. "Мир", М., 1965.
5. Ш.Д.Какичашвили. Материалы v Всесоюзной школы голографии. Л.. 511, 1973.
6. Ш.Д.Какичашвили. Квантовая электроника. №6, 1435, 1974.
7. А.weigert. verhandl.p.phys.ges., 21, 479, 1919.
8. Ш.Д.Какичашвили. Некоторые физические методы голографической записи и реконструкции. Диссертация на соискание канд.ф.-м.наук. Тбилиси, 1974.
9. Г.В.Скроцкий. Т.Г.Изюмова. Успехи физ.наук. 73, 423, 1961.
10. М.С.Соскин, С.К.Одулов, П.П.Погорецкий, Е.Н.Салькова, iЕЕЕ, 9, 630, 1973.
11. Ю.Н.Денисюк. ДАН СССР, 144, 1275, 1962.
12. Л.Д.Бахрах, А.П.Курочкин. ДАН СССР, 171, 1309, 1966.

