|
|
 |
 |

|
| |
ДИФРАКЦИОННАЯ ТЕОРИЯ ГОЛОГРАФИИ
В. В. Аристов, Г. А. Иванова
В работе рассматривается дифракционная теория голографии. Проанализированы следствия теории, показано, что восстановление изображения по плоской голограмме возможно лишь при определенных положениях восстанавливающей волны. Рассмотрена схема голографии без опорной волны. Показано, что по голограмме интенсивностей в некоторых случаях можно восстановить изображение, причем требования к стабильности при получении голограмм менее жесткие, чем в традиционной голографии. Рассмотрены некоторые применения теории к голографическим схемам.
В в е д е н и е
В последние годы разработан ряд новых голографических схем, наряду с оптической голографией появилась радиоголография, акустическая голография, получены голограммы в дальнем ультрафиолете. Достижения экспериментальной голографии заставили в ряде случаев отказаться от использования традиционного изложения процесса записи и восстановления волнового фронта, которое основано либо на аппарате геометрической оптики, либо на приближениях Френеля, Фраунгофера, Фурье физической оптики.
В 1970 году Вольф и Шевел предложили использовать скалярную теорию дифракции, основанную на разложении волнового поля по плоским волнам, для анализа процесса записи и восстановления волнового фронта /1/. Развиваемую теорию они назвали дифракционной теорией голографии (ДТГ). Это название сохранилось затем и в последующих публикациях, поэтому иы считаем целесообразным использовать его в нашей лекции. В лекции излагаются основы ди-
фракционной теории голографии, анализируются следствия, к которым приводит применение этой теории к тем схемам, в которых не выполнено приближение малости размеров голограммы и предмета по сравнению с расстоянием между ними.
2. Используемые в теории приближения
а) Мы уже отмечали, что дифракционная теория голографии является скалярной теорией. Скалярное представление волнового поля является удовлетворительным при решении многих задач и практически всегда применяется для описания голографических схем.
б) Будем считать, что объект и голограмма рассеивают слабо, так что справедливо первое борновское приближение как при нахождении волнового поля,рассеянного объектом, так и голограммой. Это приближение используется почти во всех теориях, которые описывают голографический процесс.
в) Удобно предполагать, что спектр пространственных частот волны после рассеяния на предмете ограничен. Такое приближение позволяет просто находить связь между водной, рассеянной предметом, и волной, восстановленной голограммой.
В дифракционной теории голографии отсутствуют жесткие ограничения' на размеры голограммы и предмета по сравнении с расстоянием между ними. Ниже приводится вывод основных уравнений теории из интеграла Релея-Зоммерфельда. Этот интеграл описывает дифракцию при r>>λ, где r - расстояние от источника до точки наблюдения. Ограничение такого вывода не распространяется на сам вывод, дифракционная теория справедлива при небольших значениях r, когда в дифрагированном поле присутствуют затухающие водны.
3. Основные уравнения теории
Выведем основные уравнения, описывающие дифракцию. Пусть на плоский предмет с амплитудным пропусканием Т (х, у, 0) падает плоская монохроматическая волна u0=ехр[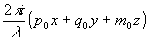 ] pиc.1. Здесь р0, q0, m0 - направляющие косинусы волны. Мы ] pиc.1. Здесь р0, q0, m0 - направляющие косинусы волны. Мы
считаем, что объект рассеивает слабо, так что вариация показателя преломления мала (Δn(x,y)<<1) и можно использовать первое борновское приближение при нахождении рассеянной волны.
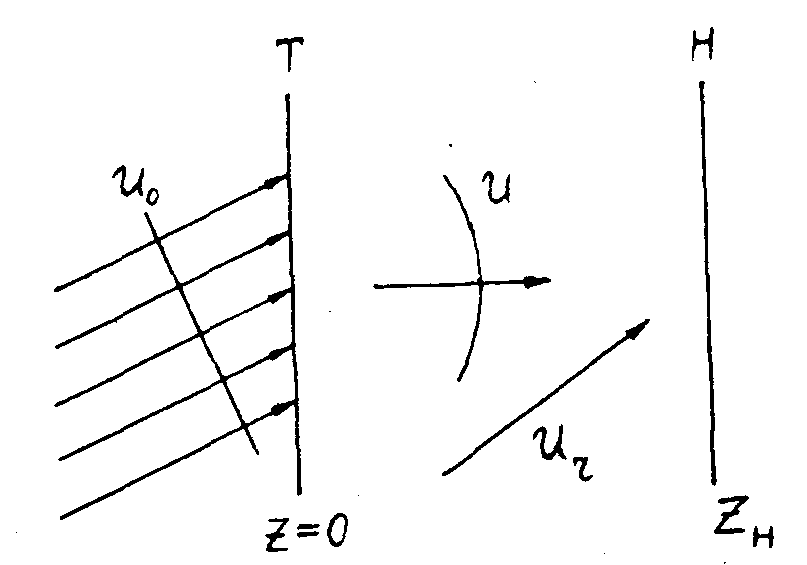
Рис.1. Схема получения голограммы.
Согласно теории Релея-Зоммерфельда, поле в плоскости z(z>>λ) описывается формулой:
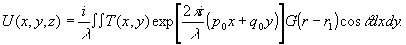 (1) (1)
Здесь g (r-r1) - функция Грина, 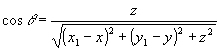 . Видно, что интеграл (i) является сверткой двух функций: . Видно, что интеграл (i) является сверткой двух функций:
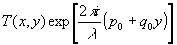
и g(r-r1)cosθ. Теперь разложим поле u(x,y,z) по плоским волнам. Для этого вычислим преобразование Фурье функции u(х,у,r). Из формулы (1) и свойств преобразований Фурье следует, что
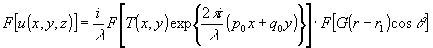 (2) (2)
В приложении 1 книги "Оптическая голография" /2/ показано , что 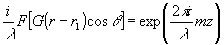 . Обозначим . Обозначим 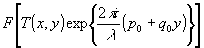 через А(p,q) тогда из (1) и (2) через А(p,q) тогда из (1) и (2)
следует, что поле u(х,у,r) в любой плоскости z за транспарантом может быть представлено в виде:
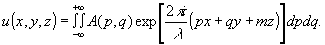 (3) (3)
Здесь 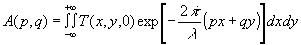 - угловой спектр волны рассеянной предметом, m= - угловой спектр волны рассеянной предметом, m=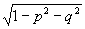 , если p2+q2≤1, и m=i , если p2+q2≤1, и m=i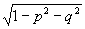 , если p2+q2>1. Волны, у которых m - действительно, называются однородными. Волны, у которых m - мнимая величина, называются затухающими, поскольку для них множитель exp , если p2+q2>1. Волны, у которых m - действительно, называются однородными. Волны, у которых m - мнимая величина, называются затухающими, поскольку для них множитель exp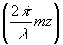 превращается в превращается в 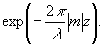 . Амплитуда затухающих волн быстро уменьшается в направлении z. Формально длину волны затухающих волн λ3 можно представить равной . Амплитуда затухающих волн быстро уменьшается в направлении z. Формально длину волны затухающих волн λ3 можно представить равной 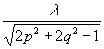 , и поэтому, если фиксировать не только однородные, но и затухающие волны, то можно получить сколь угодно высокое разрешение в монохроматическом свете частотой ω0. В обычных голографических схемах этого сделать не удается, поскольку, как правило, расстояние предмет-голограмма много больше длины волны λ. На таких расстояниях все затухающие волны имеют очень малые амплитуды, ими можно пренебречь и считать, что в формуле (3) интегрирование ведется по частотам р, q, которые лежат в круге единичного радиуса p2+q2≤1. , и поэтому, если фиксировать не только однородные, но и затухающие волны, то можно получить сколь угодно высокое разрешение в монохроматическом свете частотой ω0. В обычных голографических схемах этого сделать не удается, поскольку, как правило, расстояние предмет-голограмма много больше длины волны λ. На таких расстояниях все затухающие волны имеют очень малые амплитуды, ими можно пренебречь и считать, что в формуле (3) интегрирование ведется по частотам р, q, которые лежат в круге единичного радиуса p2+q2≤1.
Из формулы (3) следует, что спектр пространственных частот в плоскости z связан со сяектром в плоскости предмета соотношением 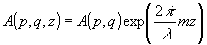 , а поле в любой плоскости z может быть записано следующим образом: , а поле в любой плоскости z может быть записано следующим образом:
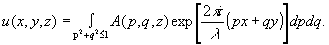 (4) (4)
Распространение волны из плоскости z=0 в плоскость z проявляется только в изменении относительных фаз различных составляющих углового спектра. Эти фазовые сдвиги возникают вследствии того, что плоские волны распространяются под различными углами и проходят различные расстояния, пока достигнут плоскости z.
Хорошей иллюстрацией, к рассматриваемой теории является дифракция на периодических структурах с периодом l>>λ. Для
квадратной решетки пропускание Т( x, у, 0) равно
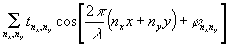 . .
Пусть p0=q0=0, то есть волна u0 падает под прямым углом на решетку, тогда спектр А(р,q) состоит из плоских волн c p=nxλ/l и q=nyλ/l, где nx и ny -целые числа. Поскольку l>>λ, то
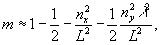
а 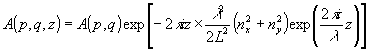 . Видно, что при . Видно, что при 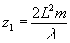 , где m - целое число, А (р,q,z)=А(р,q)exp( , где m - целое число, А (р,q,z)=А(р,q)exp(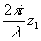 ), то есть в плоскости г, должно сформироваться изображение исходной структуры, которое носит название изображения Фурье. Этот эффект легко наблюдать экспериментально. ), то есть в плоскости г, должно сформироваться изображение исходной структуры, которое носит название изображения Фурье. Этот эффект легко наблюдать экспериментально.
Мы взяли квадратную решетку с периодом l=0,4 мм и осветили светом Не-ne лазера (p0=q0=0). На расстоянии 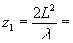 51 см наблюдалось изображение решетки. Фотография исходной структуры представлена на рис. 2а. 51 см наблюдалось изображение решетки. Фотография исходной структуры представлена на рис. 2а.
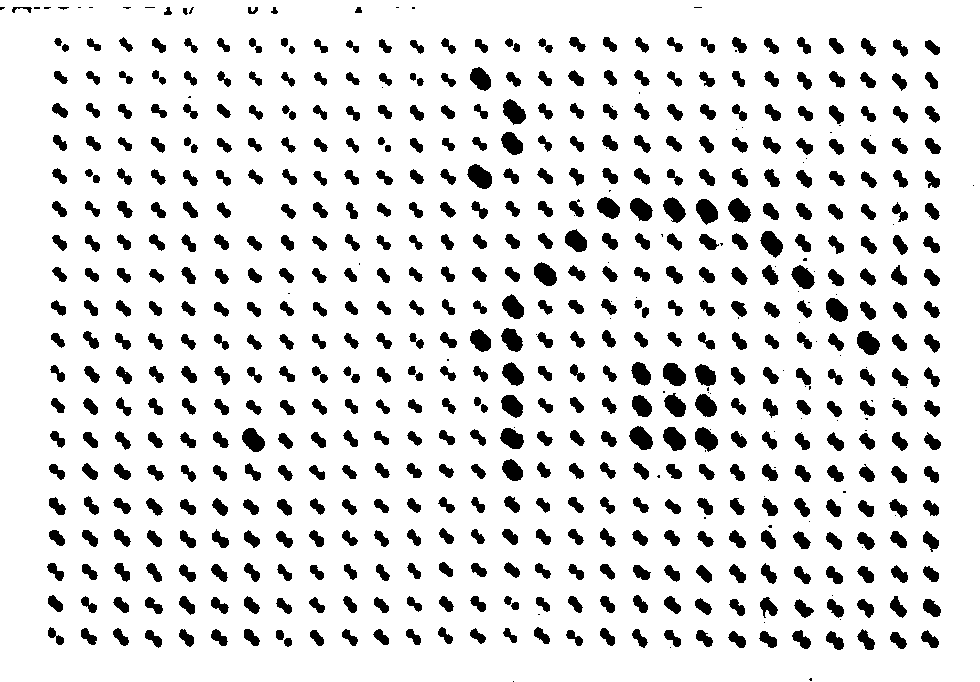
Рис.2а. Фотография дифракционной решетки, содержащей нарушения структуры.
Решетка содержала дефекты. В плоскости z1 наблюдается изображение решетки без дефектов (рис.26), поскольку в этой плоскости только периодическая часть спектра А(р,q,z) равна периодической части А(р,q).
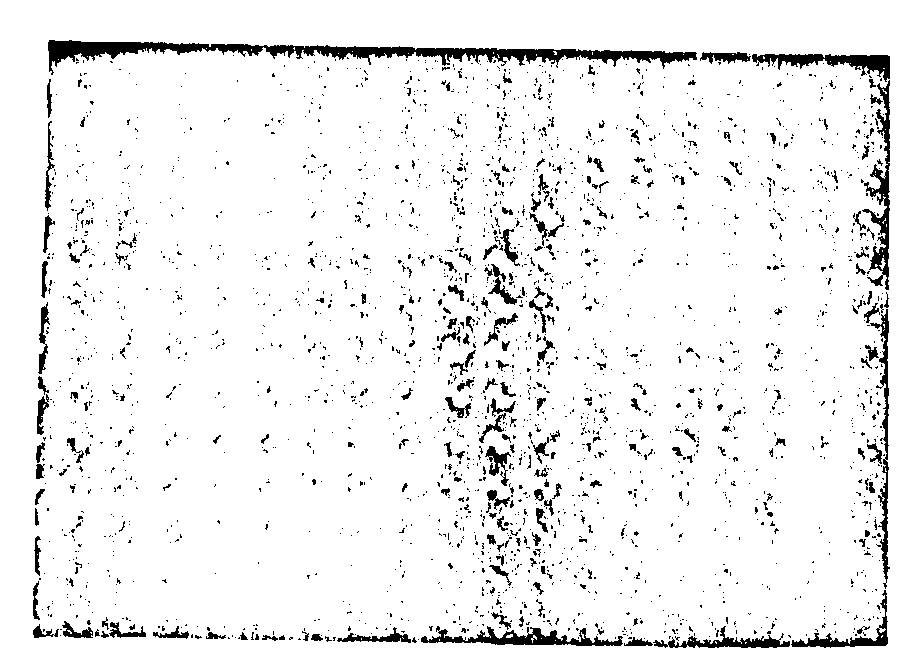
Рис.2б. Изображение Фурье решетки рис.2а.
На рис.3а приведена фотография структуры, которая представляет собой налокение двух решеток с разными периодам.
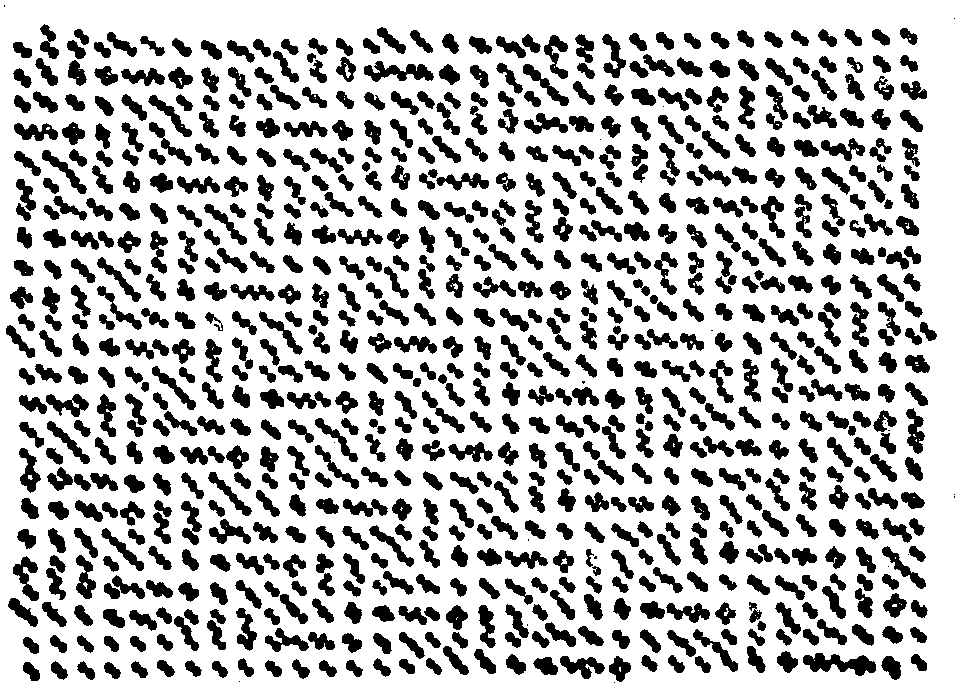
Рис.3а. Фотография транспаранта, структура которого состоит из двух одинаковых решеток с разным периодом ( l1=0,63 мм, l2=0,45мм).
Спектр такой решетки состоит из двух частей: одна часть соответ-
ствует периоду l1, другая l2(А=a1+a2). При освещении такой решетки плоской волной с p0=q0=0 на расстоянии 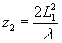 образуется изображение одной решетки, на расстоянии образуется изображение одной решетки, на расстоянии 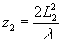 образуется изображение другой. Несфокусированные части спектра А дают в плоскостях z1 и z2 фон (рис.3б и 3в). образуется изображение другой. Несфокусированные части спектра А дают в плоскостях z1 и z2 фон (рис.3б и 3в).

Рис.36. Фотография изображения Фурье решетки с l1= 0,63 нм на расстоянии z=130 см.

Рис.3в. Фотография изображения Фурье решетки с l2=0,45 мм на расстоянии z=64 cм.
На изображениях Фурье решеток, приведенных на рис.3б и 3в, присутствует фон от несфокусированной части спектра (сравни с рис.2б). Из приведенных примеров следует, что выводы дифракционной теории хорошо подтверждаются в эксперименте i). Таким образом, волна, рассеянная предметом, может быть представлена интегралом по плоским волнам. Такое представление справедливо вплоть до таких расстояний r от предмета, которые сравнимы с длиной волны. Распространение волны описывается умножением углового спектра на величину 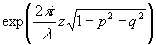 . В угловом спектре (спектре плоских волн) содержатся затухающие волны, длина волны которых в (2p2+2q2-1)1/2 раз короче, чем длина однородных волн. Рассмотрим теперь схему голографичесиого эксперимента. . В угловом спектре (спектре плоских волн) содержатся затухающие волны, длина волны которых в (2p2+2q2-1)1/2 раз короче, чем длина однородных волн. Рассмотрим теперь схему голографичесиого эксперимента.
4. Основные уравнения голографии
Пусть в плоскости z=zh (рис.1) помещена фотопластинка, и в этой плоскости поле u(x,у,zh) интерферирует с когерентной плоской волной ur=eхр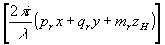 . Фотопластинка является квадратичным детектором и реагирует на распределение интенсивности волнового поля. Предположим, что амплитудное пропускание фотопластинки Тh после ее фотографической обработки пропорционально распределению интенсивности. Опуская постоянные множители и величину, описывающую равномерное почернение, запишем: . Фотопластинка является квадратичным детектором и реагирует на распределение интенсивности волнового поля. Предположим, что амплитудное пропускание фотопластинки Тh после ее фотографической обработки пропорционально распределению интенсивности. Опуская постоянные множители и величину, описывающую равномерное почернение, запишем:
Т h= Тi+ Тii+ Тiii. (5)
Здесь
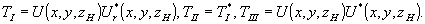
На стадии восстановления осветим голограмму плоской волной 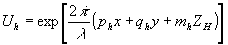 . За голограммой появятся три волны . За голограммой появятся три волны
ui, uii и uiii, которые соответствуют ti, tii и tiii. Найдем спектр волны 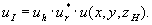 Обозначим через σix и σiy величины рh Обозначим через σix и σiy величины рh-p r и qh-qr, соответственно. Согласно теореме сдвига преобразования Фурье спектр А(р,q) поля ui равен А(р- σix , q- σiy , z h). Это означает, что поле ui плоскости z≥zh может быть представлено следующим образом:
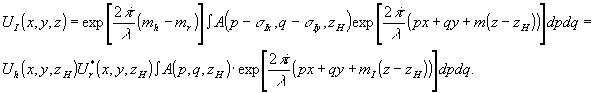 (6) (6)
Здесь mi=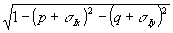 , интегрирование ведется по частотам р, q, для которых выполнено , интегрирование ведется по частотам р, q, для которых выполнено 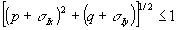 . Аналогично находим выражения для полей uii и uiii . Аналогично находим выражения для полей uii и uiii
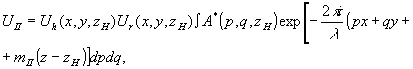 (7) (7)
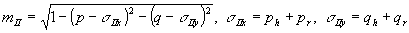 , ,
интегрирование ведется по частотам, для которых 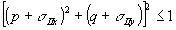 . Аналогично находим выражения для полей uii и uiii: . Аналогично находим выражения для полей uii и uiii:
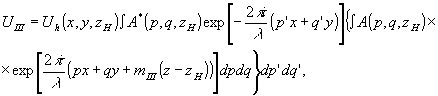 (8) (8)
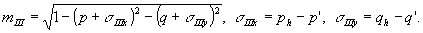
В выражении (7) интегрирование ведется по частотам, для которых
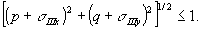
Из формул (6-8) следует, что при изменении угла падения uh на голограмму изменяются положения спектров волн ui, u ii и uiii.Так, например, если 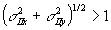 , то волна uii переносится только затухающими волнами. Эта ситуация представлена на рис.4. Область пространственных частот исходной волны , то волна uii переносится только затухающими волнами. Эта ситуация представлена на рис.4. Область пространственных частот исходной волны
u(x ,у,zh) обозначена на рисунке через Д.
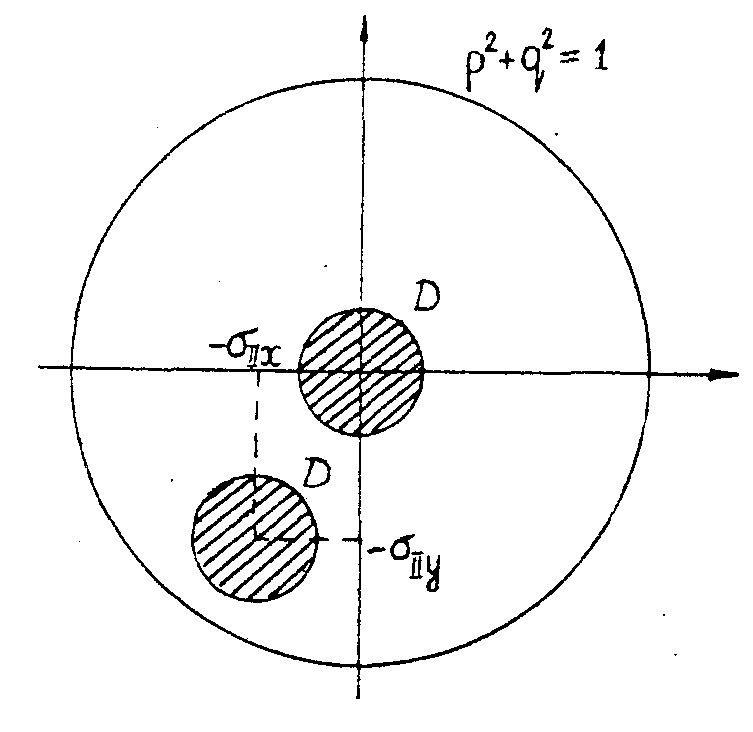
Рис.4. Сдвиг спектра частот при реконструкции изображения.
d - область спектра пространственных частот волны u(х,у,zh). Круг единичного радиуса p2+q2=1 ограничивает область однородных волн.
Эта область для волн uh сдвигается при восстановлении на величину σiix, σiiy и оказывается за пределами круга единичного радиуса при 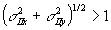 . В этом случае волна uii для расстояний (z-zh)>>λ имеет очень малую амплитуду и наблюдается всего одно изображение, восстановленное волной ui. eсли ur ≡ uh, то σi=0, σii . В этом случае волна uii для расстояний (z-zh)>>λ имеет очень малую амплитуду и наблюдается всего одно изображение, восстановленное волной ui. eсли ur ≡ uh, то σi=0, σii=(2p r, 2q r) и второго изображения не наблюдается при 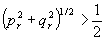 , то есть когда угол между нормалью к голограмме и опорной волной ur больше 30°. , то есть когда угол между нормалью к голограмме и опорной волной ur больше 30°.
Следует отметить, что при выводе формул, связывающих спектр восстановленного изображения с исходным спектром поля, мы рассматривали только положительное направление распространения
mi(z-zh)>0 . В принципе, все рассуждения не изменятся, когда mi(z-zh)<0, то есть когда рассматриваются отраженные волны, соответствующие ti, tii и tiii. Эти волны действительно наблюдаются наряду с проходящими. В дальнейшем мы отражен-
ные волны рассматривать не будем, поскольку все выводы, сделанные относительно проходящих волн, справедливы и для отраженных.
5. Анализ изображений, образуемых волнами ui и uii
Ниже мы будем отдельно рассматривать следующие случаи :
а) Восстанавливающая волна uh проходит в том же направлении, что и опорная при записи голограммы, или восстанавливающая волна проходит в зеркальном направлении, так что ph=pr, qh=qr, mh=±mr (рис.5а). В этом случае
σ i=0, σii=(2p r,2q r).
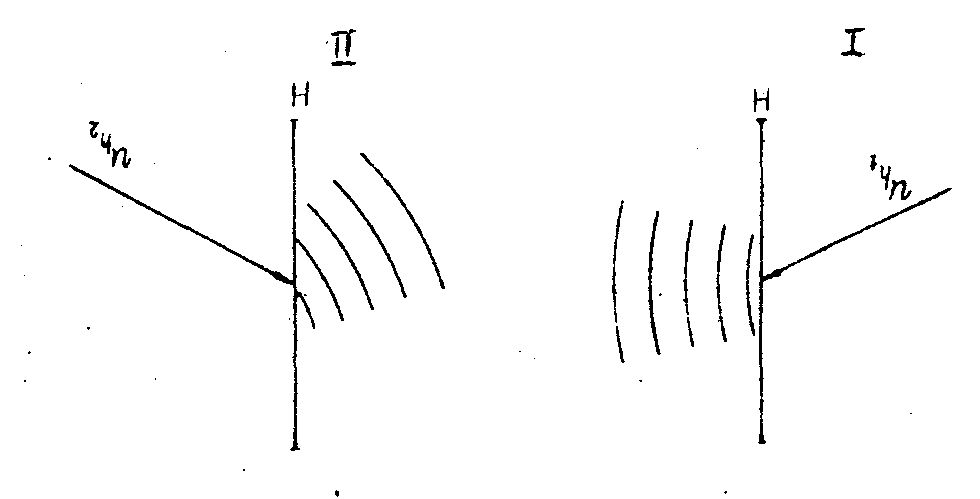
Рис.5а. Волна uh проходив в том же направлении, что и опорная при записи голограммы (i) uh1=ur , или в зеркальном направлении (ii) 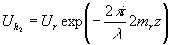 . .
б) Восстанавливающая волна проходит в сопряженном напраьле-нии к опорной волне или в зеркально-сопряженном направлении, так, что ph=-pr, qh=-qr, mh=±mr, σi=(-2p r,-2q r), σii=0 (рис.5б).
в) Восстанавливающая волна проходит в произвольном направлении σi≠0, σii≠0.
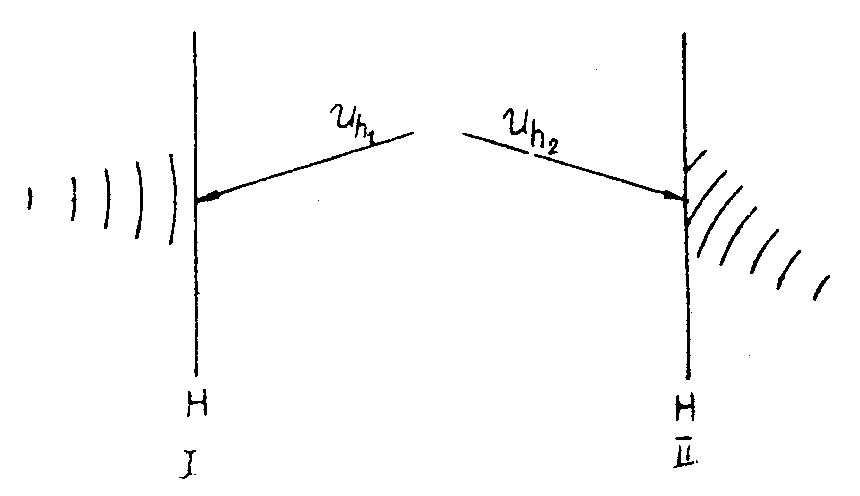
Рис.5б. Волна uh проходит в сопряженном направлении к волне ur(i) uh1=ur* или в зеркально-сопряженном направлении 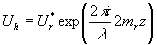 . .
Случай (а). При σi=0 волна ui в плоскости zh в точности воспроизводит волну u(х,у,zh) при записи голограммы. Из формулы (6) следует, что в плоскости z=0 обязуется мнимое изображение предмета:
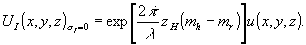
Случай (б). Из формулы (7) следует, что при σ ii=0
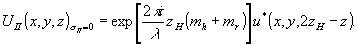
Это означает, что в плоскости z =2zh образуется действительное псевдоскопическое изображение предмета.
Случай (в). Проанализируем вначале условия образования изображения волной ui при σi≠0 . При σi≠0 угловой
спектр волны u i отличается от спектра исходной волны u(х ,у ,z ) на фазовый множитель 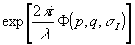 , где Ф(p,q,σi , где Ф(p,q,σi)=(z-z h)(m i-m) . Если вспомнить, что распространение волны из плоскости z=0 в плоскость z описывается только фазовым множителем 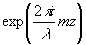 , то можно ожидать, что при τi , то можно ожидать, что при τi≠0 изображение не будет наблюдаться или будет несфокусированным. Оценим допустимую величину смещений восстанавливающей волны относительно опорной.
Будем считать, что спектр пространственных частот волны, рассеянной предметом, ограничен, так что
p3<<1, q3<<1. (9)
Это приближение выполняется, если в структуре Т(х,у, 0) нет деталей, размер которых порядка длины волны. Разложим фазовый множитель Φ(р,q,σi) в ряд по степеням р, q с точностью до членов р3, q 3. Группируя члены ряда, получим:
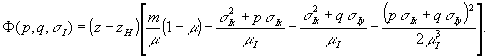 (10) (10)
Здесь μ=(1-σ -σ -σ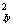 ) )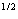 . .
Сделаем в формуле (6) замену переменных:
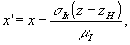 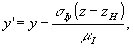 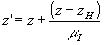 . (11) . (11)
В атом случае (6) преобразуется х следующему виду:
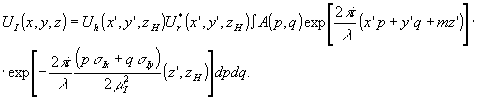 (12) (12)
Волна u i образует изображение предмета в плоскости z’=0, если фазовый множитель 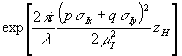 изменяет фазу, любой из плоских волн А(р,q) больше, чем на π/2: изменяет фазу, любой из плоских волн А(р,q) больше, чем на π/2:
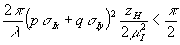 . (13) . (13)
Неравенство (1 3) выражает известное правило Релея, которое гласит, что любая оптическая система не должна искажать фазу волнового фронта больше, чем на π/2. Проведем численную оценку неравенства (13). Положим λ=0,6 мкм, p≈10-1, σy=0, z h=10 см, тогда из (13) получаем
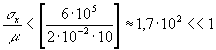 . .
Величина σx~1,7∙10 -2 соответствует отклонению реконструирующей волны от положения опорной на угол порядка 1°. Если изображение наблюдается глазом, то, поскольку разрешение глаза соответствует пространственным частотам порядка 10-2, глаз начинает фиксировать ухудшение разрешения, начиная с величин σx<1,7"10 , то есть с отклонения на 10°. Неравенство (13) выполняется либо при небольших zh, в широком интервале значений σx (для голограмм сфокусированных изображений и в схеме Денисюка), либо при σx<<1, σy<<1. Последнее неравенство можно переписать так:
ph≈+pr, qh≈+qr, mh≈±mr. (14)
Проведя аналогичные рассуждения для волны uii, мы получим, что
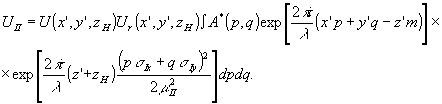 (15) (15)
Здесь 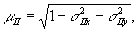
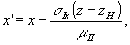 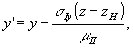 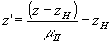 . (16) . (16)
Волна uii образует действительное изображение в плоскости z=zh(μii+1) , если выполнено неравенство (13), где σi заме-
нено на σii. В случае волны uii условие образования изображения (14) запишется:
ph≈pr, qh≈qr, mh≈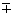 mr. (17) mr. (17)
Неравенство (14) и (16) одновременно не могут быть выполнены при достаточно больших zh. Это означает, что по плоской голограмме может восстанавливаться только одно сфокусированное изображение, при этом должно быть выполнено одно из условий (14) или (17). Отметим, что первым из условий (14) и (17) является условие Вульфа-Брэгга для восстановления изображений по трехмерной голограмме; оказывается, что как по трехмерной голограмме,так и по плоской можно восстановить всего одно хорошее изображение при определенном положении восстанавливающей волны. Для трехмерной голограммы таких положений два, для плоской - четыре.
При выполнении условий (14) - (17) волна ui (uii) образует хорошее изображение в точках, определяемых равенством (11), (16). Для волны ui изображение образуется в точках x'=x+zhσix, y'=y+z hσiy, z=z h(1-μi), для волны uii в точках x'=x-zhσiix, y'=y-z hσiiy, z=z h(1-μii). Смещение изображений точек легко представить геометрически. Пусть, например, σiy=0 . Проведем из точки q0 в плоскости транспбранта перпендикуляр на плоскость голограммы в точку q(рис.6).
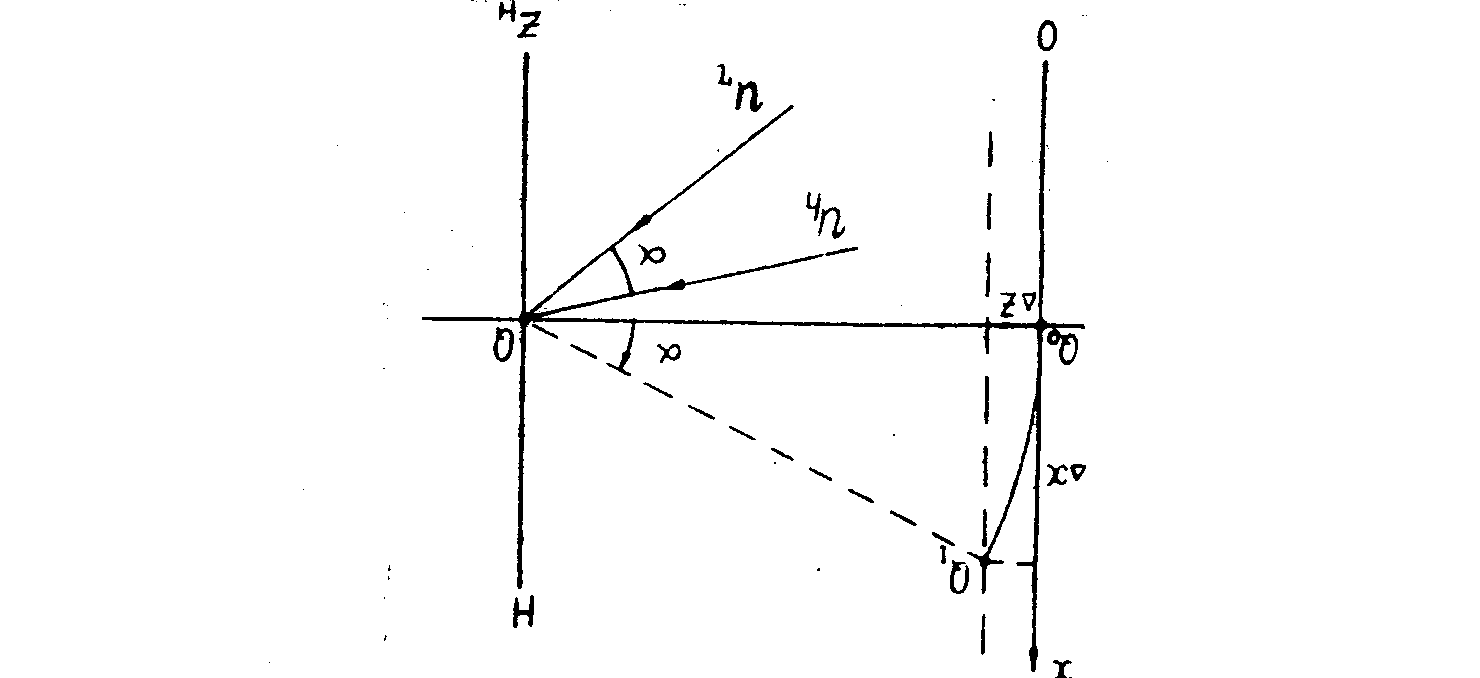
Рис.6. Схема нахождения положеняа точек в изображенля, восстановленном по голограмме. Угол между волнами ur и uh равен α.
Вектор ( σx,o, μ) направлен под углом α к линии q0o, причем sinα=σх, cosα=μ. При восстановлении изображения точка перемещается в точку q1 на расстояние Δx=zhσix=z hsinα вдоль оси x и на расстояние Δz=zh(1-cosα) вдоль оси z. Это означает, что точка q0 при изменении величины σ смещается по сфере, радиус которой равен zh, а центр лежит в точке q голограммы (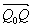 - нормаль к поверхности голограммы). Этот вывод относится также и к мнимому изображению. Из сказанного следует, что при изменении величины σi (в пределах, определяемых неравенством (13)) изображение плоских объектов геометрически не искажается. В случае трехмерных объектов изображение передается с разлыным смещением точек в различных плоскостях z. - нормаль к поверхности голограммы). Этот вывод относится также и к мнимому изображению. Из сказанного следует, что при изменении величины σi (в пределах, определяемых неравенством (13)) изображение плоских объектов геометрически не искажается. В случае трехмерных объектов изображение передается с разлыным смещением точек в различных плоскостях z.
Сделанный нами вывод о поведении изображения при σi≠0 легко проверяется в эксперименте. В начале лекции отмечалось, что для демонстрации результатов дифракционной теории удобной является схема, в которой в качестве предмета используется квадратная решетка с периодом l>>λ. Волна, рассеянная такой решеткой, состоит из дискретного спектра с p=nxλ/l, q=nyλ/l. На расстоянии z1=2l2/λ образуется изображение Фурье решетки. Поместим в плоскость фокусировки z1 фотопластинку и направим на нее опорную волну с pr=qr=0. На фотопластинке запишется голограмма с почернением th=t1+t2+t3. Здесь Т1=Тp(х,у,о), t2=t1*, Т3=|t p(x,y,o)| 2. Если каждую плоскую волну спектра А (р,q) записывать независимо от других плоской опорной волной с рr=q r=0, тогда Т3=const , Тh=t 1+ Т2=2 Тp, поскольку Т1*= Т1. Мы видим, что плоская квадратная решетка является синтезированной голограммой (Тiii=0 ), записанной плоской опорной волной pr=qr=0 в плоскости zh=z1 от транспаранта с пропусканием 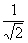 Т(х,у,о) от такой же решетки, а изображение Фурье решетки является ее гoлографическим изображением. Такая аналогия дает возможность проследить особенности голографического изображения на примере поведения изображения Фурье. Для изображения Фурье четыре условия образования изображения (14) и (17) сводятся к двум: Т(х,у,о) от такой же решетки, а изображение Фурье решетки является ее гoлографическим изображением. Такая аналогия дает возможность проследить особенности голографического изображения на примере поведения изображения Фурье. Для изображения Фурье четыре условия образования изображения (14) и (17) сводятся к двум:
ph≈0, qh≈ 0, mh≈±1, (18)
то есть изображение Фурье образуется только тогда, когда решетка-голограмма освещается волной, падающей перпендикулярно к плоскости голограммы.
Нами была взята квадратная решетка с периодом l≈0,4 мм. Освещая ее плоской монохроматической волной,мы наблюдали за изменением изображения Фурье решетки в плоскости z1=2l2/λ при вращении решетки-голограммы вокруг вертикальной оси. В таких уcловиях эксперимента σy=0 , σx=sinα, где α- угол между нормалью к транспаранту и волновым векторам волны uh. При σx≠0, σy=0 дополнительный фазовый множитель проявляется для тех плоских волн, для которых р≠0. Разрешение должно сохраняться в направлении у, а в направлении х должно ухудшаться. На рис.7 приведены фотографии восстановленных изображений при α=0°, 10° и 20°.

Рис. 7. Восстановленные изображения (изображения Фурье)
при различных положениях волны uh а) σx=p h-p r=0.

б) σx=p h-p r=0,17,

в) σx=p h-p r=0,34
Из критерия Релея (13) следует, что ухудшение изображения должно замечаться глазом, начиная с α≈2°. При угле α=10° сфокусированное изображение образуется только 4 порядкам дифракции. Из рисунка 7 видно, что, действительно, изображение при α=10° очень плохое. Это означает, что критерий (13) правильно
определяет допустимые отклонения восстанавливающей волны от тех положений, которые заданы условиями (14), (17) и (18).
Аналогичные результаты получаются и при исследовании других голографических схем. Так, например, в работе Ковальского и Полянского /6/ записывалась голограмма от двух точек. Затем она освещалась из одной точки и измерялась интенсивность "основного" изображения (образуемого волной ui при σi=0) и сопряженного (образуемого волной uii при σii=2p r, 2q r) в зависимости от апертуры голограммы. Было замечено более быстрое увеличение интенсивности основного изображения по сравнению с интенсивнoстью сопряженного при увеличении апертуры. Это свидетельствует о том, что сопряженное изображение является несфокусированным. При увеличении апертуры голограммы возрастает вклад высоких пространственных частот, для которых фазовый сдвиг при σii≠ Ф является существенным. Это приводит к более медленному росту интенсивности этой точки.
Поведение изображения при восстановлении голограммы волной, отличающейся от опорной, исследовалось с помощью других приближений теории /7/. Было показано, что возникающие фазовые искажения являются аберрациями различного типа. Эти результаты качественно согласуются с результатами, получаемыми из дифракционной теории. Из этой теории, кроме того, следует, что при регистрации на голограмме достаточно широкого спектра частот эти аберрации существенны уже при небольших смещениях реконструирующей водны. Допустимый предел этих смещений может быть установлен в каждом случае на основе критерия Релея.
Из изложенного ясно, что по плоской голограмме может быть восстановлено одно хорошее изображение при определенном положении реконструирующей волны. Условия, накладываемые на положение реконструирующей волны похожи на условия Вульфа-Брэгга для трехмерных голограмм. Отличие заключается в том, что при освещении плоской голограммы всегда возникают все дифрагированные волны
ui, uii и uiii. В случае трехмерной голограммы появляются или волны ui, или uii, или, если условия Вульфа-Брэгга не выполнены, дифрагированных волн нет совсем.
Перейдем теперь к анализу изображения, образуемого волной uii.
6. Анализ изображений, образуемых волной uii
Поле uiii образуется в результате дифракции волны uh на интерференционной картине, возникшей в результате взаимной интерференции волн, которые составляют поле u(х,y,z). Для простоты будем в дальнейшем считать, что рh=q h=0. В атом случае выражение для поля uiii можно свести к формуле (12) для поля ui, если считать, что σix=-p', σiy=-q', 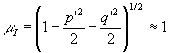 . Мы по-прежнему считаем выполненными условия (9), поэтому в рассматриваемом случае можно пренебречь дополнительным фазовым множителем 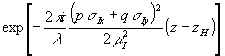 . Учитывая сказанное выше, получим . Учитывая сказанное выше, получим
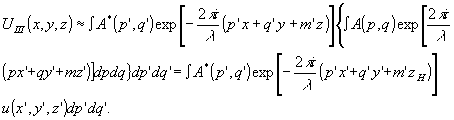 (19) (19)
Из формулы (19) видно, что поле u iii состоит из наложения полей u(х',у',z') от одинаковых транспарантов, которые смещены друг относительно друга. Эти волны имеют различную амплитуду и фазу a*(p',q')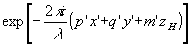 . Разрешение по предмету определяется максимальной пространственной частотой р, q и имеет порядок λ/p. Если смещения x', у', z' меньше, чем разрешение, которое обусловлено максимальной пространственной частотой, то величину u(x', у', z') можно считать приблизительно равной u(х, у, z) и вынести из-под знака интеграла. Тогда (19) перепииется следующим образом: . Разрешение по предмету определяется максимальной пространственной частотой р, q и имеет порядок λ/p. Если смещения x', у', z' меньше, чем разрешение, которое обусловлено максимальной пространственной частотой, то величину u(x', у', z') можно считать приблизительно равной u(х, у, z) и вынести из-под знака интеграла. Тогда (19) перепииется следующим образом:
uiii=u(x,y,o)u*(x,y,zh) (20)
при
pp'zh< λ. (21)
При выполнении: условия (21) поле u iii восстанавливает изображение предмета c наложением на него расфокусированного изображения из плоскости z=zh. Оценим численное значение неравенства (21). Пусть р'≈p≈10-2, λ~0,6∙10-4 см, тогда изображение восстанавливается при zh<0,6 см.
При больших значениях z, когда условие (21) не выполняется, поле uiii не восстанавливает изображение ни в какой плоскости. Следует отметить, что если z велико, то по полю uiii может быть восстановлено изображение, описываемое функцией Паттерсона /8/. Выведем условие, при котором это возможно. Пусть предмет имеет ограниченные размеры, равные Д. Согласно теореме Котельникова спектр частот А(р,q) может быть представлен суммой функций an(pn,qn) в точках отсчета рnq n, разделенных на угловую величину λ/d. При zhλ/d>d почернение фотопластинки в различных точках определяется только интенсивностью волн с различными значениями рn, q n, поскольку области, в которых интенсивности отдельных волн велики, ограничены размерами порядка размеров предмета. На таких расстояних практически отсутствует взаимная интерференция плоских волн А(рn, q n). Это означает, что в рассматриваемом случае uiii(x,y,o)~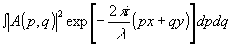 , то есть восстанавливается изображение, описываемое функцией автокорреляции-функцией Паттерcона. , то есть восстанавливается изображение, описываемое функцией автокорреляции-функцией Паттерcона.
Таким образом, при регистрации голограмы без опорной волны следует различать три области. Первая - при zh<λ/p2max, вторая при λ/p2max<z h<d 2/λ и третья при zh>d2/λ. В первой области по полю uiii удается восстановить изображение предмета, в третьей - образ, описываемый функцией Паттерсона. При регистрации плоской голограммы в промежуточной области информация о предмете теряется.
Для проверки сделанных в этом разделе выводов мы освещали решетку с периодом l≈0,4 мм слабо расходящейся когерентной волной света и регистрировали интенсивность света в различных плоскостях z за решеткой. По такой голограмме интенсивностей не удается восстановить изображение решетки, если z≠z1. Если z отличается от zh на величину порядка 1 сантиметра и меньше, то по голограмме интенсивностей восстанавливается изображение решетки. Это хорошо видно из рис.8, где представлена фотография поля |u(х,у,z)|2 в плоскости близкой z1 (рис.8а), и восстановленное изображение в поле uiii (рис.8б).

Рис.8а. Фотография голограммы интенсивностей в плоскости, близкой к zh/2.

Рис.8б. Фотография восстановленного изображения по голограмме рис.8а.
По голограмме интенсивностей, записанной в третьей зоне, действительно наблюдается изображение, описываемое функцией Паттерсона /8/.
Полученные на основе дифракционной теории голографии результаты находятся б хорошем соответствии с экспериментами по фото-
графированию в когерентном свете (по получение голограмм интенсивностей сфокусированных изображений). Внешне такая голограмма выглядит как фотография, однако, наличие интерференционной структуры сообщает фотографическому изображению основные свойства голографического. При освещении такой голограммы в квазиосевом направлении наблюдается голографическое изображение /9/. По свидетельству авторов этой работы глубина резкости таких голограмм около сантиметра, что соответствует границе 1 области для zh.
Итак, мы проанализировали поведение восстановленного по голограмме изображения в рамках дифракционной теории голографии. Мы проследили за тем, как изменяются координаты точек изображения при изменении наклона реконструирующей волны, установили, что голографическое изображение образуется только в том случае, когда опорная и реконструирующая волны не сильно отличаются друг от друга, причем восстанавливается всего одно изображение, второе оказывается несфокусированным. Это обстоятельство накладывает ограничения на увеличение, которое можно получить, используя большие голограммы, обуславливает их спектральную избирательность.
По голограмме, записанной без опорной волны, можно восстановить либо изображение предмета, либо его образ, описываемый функцией Паттерсона, если записывать голограмму в области 1 или 3, соответственно.
Свойства плоских голограмм, предсказываемые дифракционной теорией,оказываются похожими на свойства трехмерных. Это обстоятельство должно учитываться при анализе влияния толщины на свойства голограмм.
Ниже мы рассмотрим несколько примеров применения дифракционной теории голографии к анализу голографических схем.
7. Анализ некоторых голографических схем
а) Голограммы, полученные без опорной волны.
С помощью дифракционной теории голографии мы определили условия, при которых восстанавливается изображение предмета или его образ по голограмме интенсивностей. Рассмотрим теперь одно из свойств таких голограмм.
Выше отмечалось, что поле uiii образуется в результате дифракции восстанавливающей волны на интерференционной картине, возникшей в результате взаимной интерференции волн, составляющих поле u(х, у, z). Это наводит на мысль о том, что в рассматриваемой схеме можно предъявлять менее жесткие условия к стабильности установки при получении голограмм. Пусть голограмма регистрируется вблизи предмета, который во время экспозиции смещается на расстояние Δxmax. Проинтегрируем выражение для поля uiii по х и получим
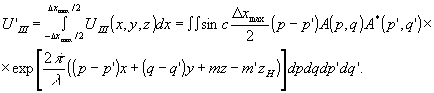 (22) (22)
Это выражение является сверткой двух функций 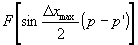 и uiii при Δx=0. При выполнении условия малости расстояния zh (условие (21) ) поле uiii восстанавливает изображение предмета в плоскости z=0. В рассматриваемом случае каждая точка в изображении размывается на величину Δxmax, поскольку и uiii при Δx=0. При выполнении условия малости расстояния zh (условие (21) ) поле uiii восстанавливает изображение предмета в плоскости z=0. В рассматриваемом случае каждая точка в изображении размывается на величину Δxmax, поскольку 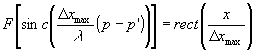 . Аналогичный результат можно получить и в случае голограммы, записываемой при больших z в 3 зоне. . Аналогичный результат можно получить и в случае голограммы, записываемой при больших z в 3 зоне.
Получена фотография образа треугольника. При получении голограммы без опорной волны в дальней зоне голограмма смещалась на 0,3 мм. Время экспозиции составляло 20 сек, сторона треугольника была равна 3 мм, z=150 мм. Несмотря на значительное перемещение предмета, его образ восстанавливается, интерферэнционных полос нет. Получена фотография при восстановлении голограммы интенсивностей сфокусированных изображений i). Лицо освещалось светом Не-ne лазера ЛГ-36А. Время экспозиции составляло 1 минуту.
Таким образом, при получении беаопорных голограмм снижаются требования к механической стабильности установки. Оказывается возможным получагь голографические изображения при значительных смещениях предмета. Разрешение оказывается равным величине перемещения. Полученные результаты показывают, что схемы безопорной
голографии могут использоваться для получения изображений в условиях, близких к условиям получении фотографических изображений.
б) Голографическая микроскопия
Идея создания голографического микроскопа заключается в следующем. Вначале с помощью электромагнитных волн, длина которых равна λ 1, записывается голограмма. Затем, освещая голограмму светом с длиной волны λ2, мы получаем увеличенное в λ2/λ1 раз изображение. Эта схема предлагалась для регистрации голограмм в той части спектра, где нет фокусирующих оптических устройств. Посмотрим, при каких условиях возможна работа такой схемы.
Легко показать, что в рассматриваемом случае даже при σ1=0 появится дополнительный фазовый множитель 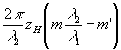 , где , где 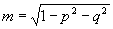 , , 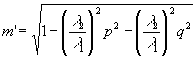 . Этот множитель мал только при небольших значения zh. Например, для того, чтобы выполнялся критерий Релея при λ2/λ1 . Этот множитель мал только при небольших значения zh. Например, для того, чтобы выполнялся критерий Релея при λ2/λ1=10 4, необходимо, чтобы zh было меньше λ2 λ2/λ1≈1 (мы считаем, что m'= 0, m≈1-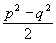 , , 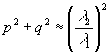 . При переходе от красного света к зеленому . При переходе от красного света к зеленому 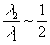 , zh<1 см, при обратном переходе (λ2/λ1≈2) условия более жестки - zh<1/8 см. Фазовые искажения можно убрать, если перед наблюдением изображения увеличить голограмму в λ2 , zh<1 см, при обратном переходе (λ2/λ1≈2) условия более жестки - zh<1/8 см. Фазовые искажения можно убрать, если перед наблюдением изображения увеличить голограмму в λ2/ λ1=М раз в этом случае должно наблюдаться беэабберационное изображение, увеличенное в М раз.
Возможность получения высокого разрешения с помощью голографического микроскопа была замечена давно /10,11/ и к настоящему времени предложены различные схемы рентгеновского голографического микроскопа /12-14/ оптического голографического микроскопа со сверхразрешением /15/. Следует отметить, что нужно осторожно относиться к оптимистическим оценкам величин достижимого в голографическом микроскопе разрешения, поскольку оно зависит не только от аббераций, но и от других, многочисленных и часто не учитываемых факторов.
Например, в схемах рентгеновской голографии кристаллов /14/, в схеме Нассенштейна /15/ предлагается регистрировать различные участки спектра пространственных частот с помощью различных опорных волн. Из изложенного выше ясно, что для того, чтобы при восста-
новлении изображения эти участки спектра интерферировали с правильным соотношением фаз, необходимо контролировать распределение фаз в опорных волнах. Для плоских опорных волн /14/ это условие означает контроль разности хода с точностью до долей длины волны. Этого обычно сделать невозможно и, следовательно, в рассматриваемых схемах не может быть достигнуто разрешение больше, чем λ 2.
В заключении этого параграфа укажем на некоторые трудности рентгеновской голографической микроскопии, которые следуют из анализа схеы на основе дифракционной теории. Рассмотрим схему голографии Фурье /11/ при λ 1=10 -8 см, zh=103 см. Из (13) следует, что для получения резрешения порядка λ1, необходимо, чтобы при восстановлении изображения выполнялось условие σ1<10 -6. Для получения разрешения порядка λ2≈10-4 см необходимо, чтобы величина σ1 была меньше, чем 10-2. Изменение температуры объекта во время получения голограммы на t° приводит к изменению спектра пространственных частот на Δp≈pαt, где α≈10-5/град - коэффициент термического расширения. Множитель m1zh изменяется при этом на р2αtzh. Это изменение должно быть меньше λ1/4 . Для получения разрешения в 1Å необходимо фиксировать пространственные частоты вплоть до p=1. Отсюда αt°zh<λ1/4 или, учитывая численное значение входящих в неравенство коэффициентов, получим, что стабильность температуры необходимо поддерживать с точностью выше, чем 2·10-7 градуса.
Таким образом, из приведенных примеров видно, что для получения высокого разрешения в голографическом микроскопе необходимо выполнить ряд жестких требований к стабильности условий при получении голограммы.
в) Схема голографии О.Н.Денисюка /16/
При записи голограмм по методу Ю.Н.Денисюка предмет располагается вблизи голограммы. Из критерия Релея (13) следует, что при zh<1 см допустимое отклонение восстанавливающей волны от опорной определяется неравенством σ1< 0,5. Следовательно, при отклонении волны uh от положения ur вплоть до углов порядка 30° мы не должны замечатъ изменения разрешения. Этот вывод
относится и к случаю изменения длины волны при восстановлении. Все это означает, что по голограммам, полученным во встречных пучках при небольших zh, могут быть восстановлены изображения в широком интервале длин волн и углов даже при очень малой толщине эмульсии. Мы видим, что свойство восстанавливать изображения в белом свете связано не только с толщиной эмульсии, но и с геометрией записи голограммы.
Из формулы (12) модно увидеть еще одну интересную особенность рассматриваемых голограмм. В плоскости z'=0 волна ui восстанавливает изображение 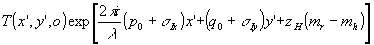 . Если предмет при записи освещался сквозь голограмму, то p0+σix . Если предмет при записи освещался сквозь голограмму, то p0+σix=p h, q 0+σiy=q h ((p 0,q 0) волновой вектор волны, освещавшей предмет, (рh,q h) -волновой вектор восстанавливающей волны). Отсюда, с точностью до постоянного фазового множителя, получаем, что 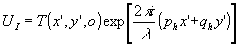 , то есть восстановленное изображение такое, каким оно видится при освещении транспаранта волной uh. Это означает, что, изменяя угол падения на голограмму восстанавливающей волны, мы получаем восстановленное изображение транспаранта при различных условиях освещения. , то есть восстановленное изображение такое, каким оно видится при освещении транспаранта волной uh. Это означает, что, изменяя угол падения на голограмму восстанавливающей волны, мы получаем восстановленное изображение транспаранта при различных условиях освещения.
Таким образом, дифракционная теория голографии позволяет просто объяснить эффект поразительного сходства в поведении изображения, восстановленного по голограмме, и поведении изображения предмета,наблюдаемого непосредственно при изменении условий освещения /17/.
8. Заключение
С момента публикации работы Вольфа и Шевега вышло несколько работ, посвященных дифракционной теории голографии. В этих работах анализировалась схема голографии Лейта-Упатниекса /1, 18-21/, рассматривалась возможность вычисления по голограиме показателя преломления объекта /22, 23/. Дифракционная теория голографии использована и в некоторых работах по анализу образования изображения в световой волне, рассеянной на ультразвуке /20/. В нашей лекции подробно проанализированы следствия дифракционной теории
голографии для случая голографии Лейта-Упатниекса, для схемы голографии без опорной волны. Приведены примеру использовчния изложенной теории, которые свидетельствуют о пользе ее применения для анализа многих голографических схем, в особенности таких, в которых не выполнено приближение малости размеров голограммы и предмета по сравнению с расстоянием между ними.
Л и т е р а т у р а
1. e.wolf, j.r.shewell. j.math.phys., 11, 2254, 1970.
2. Р.Кольер, k.Беркхарт, Л.Лин. Оптическая голография. изд. "Мир", М., стр.660, 1973.
3. j.m.cowley, А.f.Мооdiе. proc. phys.soc., В 70, 5, 1957.
4. r.p.edgar. optica acta, 16, 281, 1969.
5. Ю.Н.Денисюк, Н.М.Рамишвили, В.В.Чавчанидзе. Оптика и спектр, т.30, стр.1130, 1971.
6. Л.В.Ковальский, В.К.Полянский. Оптика и спектр, т.28, стр.338, 1970.
7. meier. josa, 55, 987, 1965.
8. В.В.Аристов, В.Л.Броуде, В.Б.Тимофеев, В.Ш.Шехтман. Квант, электроника, изд."Наумова думка", Киев, стр. 132, 1969.
9. И.С.Клименко, Е.Г.Матинян, Г.В.Скроцкий. ДАН СССР, т.211, стр.571. 1973.
10. j.t.wintrop, c.r.worthington, phys.lett., 15, 1965. phys.lett., 21, 1966.
11. Дж.Строук. Введение в когерентную оптику и голографию, изд. "Мир", М., стр.149, 1967.
12. r.dandliker, k.weiss. optics communs., 1, 323, 1970.
13. w.h.carter. josa, 60, 306, 1970.
14. w.h.carter, ho pin-chin. appl.opt., 13, 132, 1974.
15. w.h.carter. josa, 60, 1366, 1970.
16. Л.Н.Кондурова, А.И.Смирнов. ЖТФ, т.41, стр.1043 (1971).
17. sadao aoki, seishi kikuta. japan j.appl.phys., 13, 1385, 1974.
18. В.И.Зайцев, Б.К.Вайнштейн, Г.И.Косоуров, Кристаллография, т.13, стр.594 (1968).
19. Л.М.Сороко. Материалы v Всесоюзной школы по голографии, Л., стр.100, 1973.
20. Ю.Н.Денисюк, ДАН СССР, т.144, стр.1275 (1962); Оптика и спектроскопия, т.15, стр.522 (1963); Оптика и спектроскопия т.18, стр.275 (1965).
21. Ю.Н.Денисюк, В.Н.Суханов. Оптика и спектр, т.28, стр.126 (1970 г.).
22. e.wolf. optics cominuns, 1, 153, 1969.
23. e.evans. optics communs, 2, 317, 1970.
24. e.wolf. josa, 60, 18, 1970.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

