|
|
 |
 |

|
| |
ОТРАЖЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН ОТ УСИЛИВАЮЩЕЙ СРЕДЫ
А.А.Колоколов, Г.В.Скроцкий
Рассматривается отражение света от плоской поверхности полубесконечной однородной усиливающей среды и находятся коэффициенты отражения для плоских монохроматических волн. Полученные результаты показывают неприменимость принципа излучения Зоммерфельда для неограниченной усиливающей среды. На основе развитой теории дается возможное объяснение результатов измерения коэффициентов отражения света от активных сред.
Процесс отравения света является сложным явлением, особенности которого существенно зависят как от свойств отражающей среды, так и структуры падающего излучения /1/. Анализ этого явления как в случае обычных отражающих сред, так и сред с необычными свойствами проще всего выполнить, рассматривая отражения плоских монохроматических волн от полубеоконечной однородной среды. Знание коэффициентов отражения для плоских волн в рамках линейной теории позволяет исследовать отражение электромагнитных волн любой сложной структуры.
Хорошо известно, что задача нахождения коэффициентов отражения (и прохождения) плоских волн от полубеоконечной среды, при использовании только уравнений Максвелла и граничных условий на поверхности отражающей среда не имеет однозначного решения /2/. В случае, когда отражающая среда обладает конечным поглощением, к уравнениям Максвелла и обычным граничным условиям добавляют в качестве дополнительного условия принцип излучения в формулировке Зоммерфельда или Мандельштама, который определяет поведение преломленных волн на бесконечности и позволяет получить однозначное решение задачи /2,3/. Введение принципа излучения, естественно, требует определенного физического обоснования. Поэтому обычная постановка задачи об отражении плоской волны от полубесконечной среды неудобна тем, что при рассмотрения отражения от сред нового
типа (например, усиливающих) принцип излучения необходимо заново обосновывать. В связи с этим желательно выяснить, нельзя ли задачу нахождения коэффициентов отражения сформулировать таким образом, чтобы эти коэффициенты однозначно определялись без использования принципа излучения только из уравнений Максвелла и большего числа граничных условий.
Согласно работе /1/, один из возможных путей решения поставленной задачи в случае недиспергирующих сред заключается в следующем. Рассматривается отражение плоских волн от плоскопараллельного слоя однородной среды конечной толщины l. В этом случае граничных условий на двух поверхностях слоя оказывается достаточно для однозначного определения коэффициентов отражения (и прохождения). Соответствующие результаты для полубесконечной среды получаются путем предельного перехода l→∞. Этот метод позволяет уточнять условия применимости и показать физический смысл принципа излучения для процесса стационарного отражения плоских волн.
В настоящей статье на основе предельного перехода последовательно рассматривается отражение плоских волн от усиливающей среды и находятся соответствующие формулы Френеля. Эти формулы сравниваются с результатами экспериментального исследования отражения света от усиливающих сред /5,6/ и приводятся возможные объяснения наблюдаемых эффектов. Использованный нами метод позволил также получить некоторые новые результаты для отражения плоских волн от поглощающих сред. В заключении указаны некоторые, на наш взгляд, наиболее интересные задачи, возникающие при анализе отражения волн от усиливающих сред.
1. Принцип излучения Зоммерфельда и Мандельштама
Напомним некоторые особенности решения задачи об отражении плоских волн от полубесконечной поглощающей однородной и изотропной среды, существенные для исследования отражения от усиливающих сред. Как мы уже отметили, для однозначного нахождения амплитуд отраженной и преломленной волн, граничных условий, требующих непрерывности тангенциальных составляющих напряженностей электрического 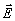 и магнитного и магнитного 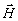 полей полей
недостаточно. Легко видеть, что этим условиям удовлетворяют две возможные преломленные волны: идущая от границы раздела под обычным углом преломления θ 2 и идущая к границе раздела под углом π-θ2 (см.рис.1) /2/. Это приводит к необходимости установить некоторое правило, позволяющее выбрать реализующуюся преломленную
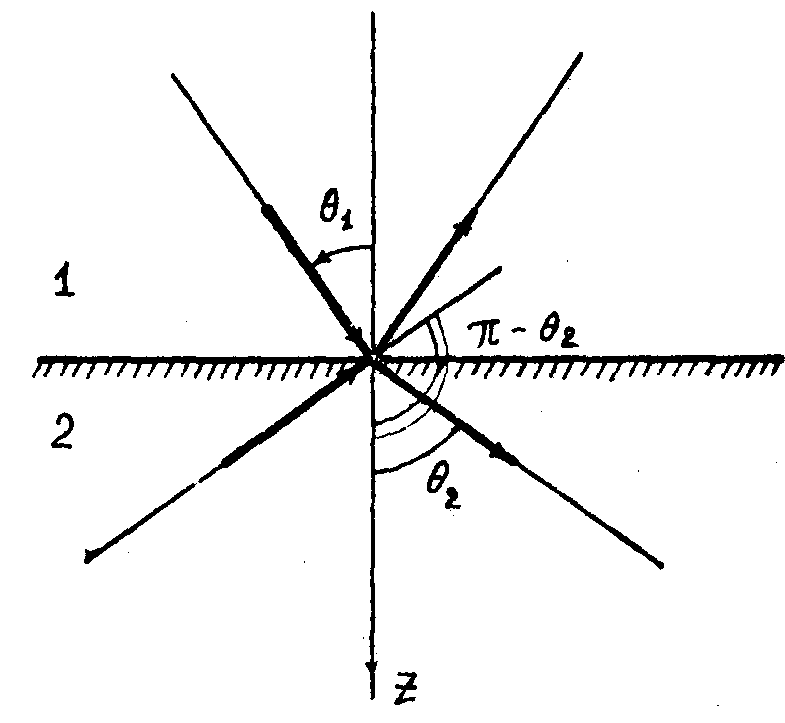
Рис.1. Четыре волны, удовлетворяющие граничным условиям на передней поверхности отражающей среды.
волну. В качестве такого правила обычно используют принцип излучения Зоммерфельда, согласно которому фазовая скорость преломленной волны в поглощающей среде должна быть направлена от границы раздала в глубь отражающей среды /3/. Иными словами, принцип излучения Зоммерфельда накладывает условие на вещественную часть волнового вектора преломленной волны rek2z> 0. Здесь k2z - нормальная составляющая волнового вектора преломленной волны. При введении принципа излучения предполагается, что в страдающей среде источники излучения (на бесконечности) отсутствуют.
Кроме того, делается неявное предположение о том, что направ-
ление скорости переноса энергии электромагнитного поля из отражающей среде определяется фазовой скоростью волны. В средах с дисперсией последнее условие выполняется не всегда . Как показано Рытовым, направление вектора Пойнтинга в диспергирующей среде определяется не фазовой, а групповой скоростью. Это обстоятельство было учтено Мандельштамом, сформулировавшим принцип выбора преломленной волны в более общей форме: поток энергии, переносимый преломленной волной, должен быть направлен от границы раздела двух сред /2/. В таком виде принцип излучения применим к любым поглощающим средам, включая и "необычные", в которых одновременно электрическая и магнитная проницаемости имеют отрицательные значения. Среда, из которой падает свет, при этом предполагается прозрачной /7/.
Принцип излучения нетрудно обобщить на случай непрозрачной отражающей среды, введя некоторый механизм диссипации энергии света, эквивалентный в определенном смысле поглощению и позволяющий исключать из рассмотрения вторую преломленную волну. Таким механизмом монет быть, например, рассеяние света на неоднородностях любой природы, не учитываемое в обычной феноменологической теории отражения.
При обосновании принципа излучения само собой разумеется, что при неограниченном росте толщины отражающего слоя l роль отраженной и преломленной на задней поверхности слоя волн стремилась к нулю. Последнее условие безусловно выполняется для однородных плоских волн в сколь угодно слабо поглощающей среде, однако, в случае усиливающей или достаточно сильно рассеивающей или поглощающей среды это условие может не выполняться. Поэтому правило отбора преломленной волны, основанное на принципе излучения Зоммерфельда или Мандельштама, в этих случаях теряет силу.
2. Принцип излучения для усиливающей среды
Для анализа отражения плоской волны от усиливающей среды применим метод, основанный на предельном переходе от отражающего слоя конечной толщины к полубесконечной среде. Для простоты будем считать, что среда, из которой падает свет, прозрачная, а отражаю-
щая среда не обладает дисперсией.
Как будет видно из дальнейшего, этот метод, эквивалентен принципу отбора, согласно которому из двух возможных преломленных волн следует выбрать такую, амплитуда которой при z→∞ стремится к нулю. Следовательно, этот принцип отбора накладывает условие на jmk2z. Поскольку принцип излучения Зоммерфельда накладывает условие на rek2z, то весьма интересно проследить, когда оба метода дают одинаковый результат, а когда - различный.
Коэффициент отражения слоя, имеющего толщину l, получаемый путем решения граничной задачи, можно записать в форме /3/
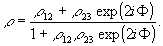 (1) (1)
Здесь ρ 12 - обычный коэффициент отражения (коэффициент Френеля) для передней поверхности слоя; Φ=k2z - набег фазы преломленной волны за один проход слоя; k2z - нормальная к поверхности слоя составляющая волнового вектора преломленной волны, re k2z > О, а ρ23 - коэффициент отражения преломленной волны от второй поверхности слоя. Если толщина слоя l>lc, где lс определяется из уравнения
|ρ 12ρ23|exp(-2j mk 2zl c)=1,
то коэффициент отражения слоя ρ является непрерывной функцией l и в формуле (1) возможен предельный переход к полубесконечной среде l→∞. для усиливающей среды jm k2z < 0 , поэтому при l→∞ величина exp(-2jmk2zl) неограниченно растет и выражение (1) принимает вид:
ρ=1/ρ 12 (2)
Подставляя в (2) соответствующие выражения для ρ12 найдем выражение для коэффициента отражения плоских волн, поляризованных перпендикулярно
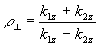 (3) (3)
и параллельно плоскости падения -
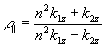 (4) (4)
Здесь n=n2/n1 - относительный показатель преломления слоя, а k1z - нормальная к поверхности слоя составляющая волнового вектора падающей волны, re k1z >0, re k2z >0 .
Формулы (3) и (4) отличаются от хорошо известных формул Френеля для пассивных сред знаком при k2z, что формально соответствует преломленной волне, распространяющейся к границе раздела под углом π-θ2, и амплитуда которой экспоненциально убывает с увеличением z. Здесь θ2 - обычный угол преломления (см. рис.1). Полученный результат становится вполне понятным, если вспомнить, что идущая к границе раздела волна возникает благодаря отражению обычной преломленной волны от второй поверхности, поэтому для усиливающего слоя достаточно большой толщины амплитуда подходящей волны на передней поверхности может оказаться во много раз больше амплитуды обычной преломленной волны.
Таким образом, при решении задачи о стационарном отражении плоских волн от неограниченной усиливающей среды в качестве преломленной волны всегда следует выбирать такую, для которой поток энергии направлен к границе раздела пассивной и активной сред. В этом случае должно реализоваться необычное преломление света, на возможность которого неоднократно указывал еще Мандельштам /2/. Обратим внимание на то, что наблюдение такого непривычного преломления возможно такие и для поглощающих сред о дисперсией, если групповая скорость преломленной волны направлена в сторону, противоположную ее фазовой. При этом, согласно принципу излучения, в формулировке Мандельштама, мы должны выбрать такую преломленную волну, групповая скорость которой направлена от границы, раздела, а ее фазовая - соответственно, к границе раздела. Такая ситуация может иметь место, например, как для упругих /8/, так и электромагнитных волн /7/.
3. Зависимость коэффициентов отражения от угла падения
Используя закон преломления и записывая относительный показатель преломления в виде n=n2/n1=n0(1-iκ), находим явную зависимость k2z от угла падения θ1:
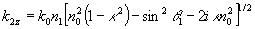 (5) (5)
Выбирая отрицательный знак в степени множителя exp(-iωt), описывающего временную зависимость полей для усиливающей среды, следует полагать κ>0. Фаза подкоренного выражения в (5) при всех значениях θ1 лежит в интервале (0,-π) и re k2z > 0. Отсюда следует, что коэффициенты отражения (3) и (4) при всех углах падения θ1 и любых значениях κ являются непрерывными функциями θ1, а их модули всегда больше единицы. Нетрудно видеть, что при κ→0 формулы (3) и (4) переходят в соответствующие формулы для прозрачной среды только в области полного отражения. Следовательно, условие непрерывности перехода, использованное в /9,10/ для выбора преломленной волны, является, вообще говоря, неверным.
Подставляя k2z из (5) в (3), получаем, что величина |ρ⊥(θ1)| достигает своего максимума, равного |n0+1/n0-1|, κ<<n0 при нормальном падении, а с увеличением θ1 она монотонно уменьшается, оставаясь все время больше единицы. Более интересна кривая зависимости |ρ||(θ1)| , имеющая один максимум при нормальном падении и второй порядка 2n02/κ|n02-1| (при равенстве θ1 углу Брюстера θb(tgθb=n 0). Следовательно, естественный свет, падающий на усиливающую среду под углом Брюстера, при стационарном отражении оказывается поляризованным в плоскости падения, в то время как естественный свет при отражении от пассивной среды под углом Брюстера, как известно, поляризуется в плоскости, перпендикулярной плоскости падения. Из формул (3) и (4) видно, что при |κ|<<1 произведение модулей коэффициентов отражения от активной и пассивной сред c одинаковыми вещественны-
ми частями показателей преломления приблизительно равно единице.
Следовательно, если при определенных условиях отражение света от пассивной среды очень мало, то в этих же условиях стационарное отражение от активной среды очень велико. Частным случаем этой общей закономерности является отражение света под углом Брюстера. На рис.2 приведены кривые зависимости модуля коэффициентов отражения от угла падения для пассивной и усиливающей страдающих сред.
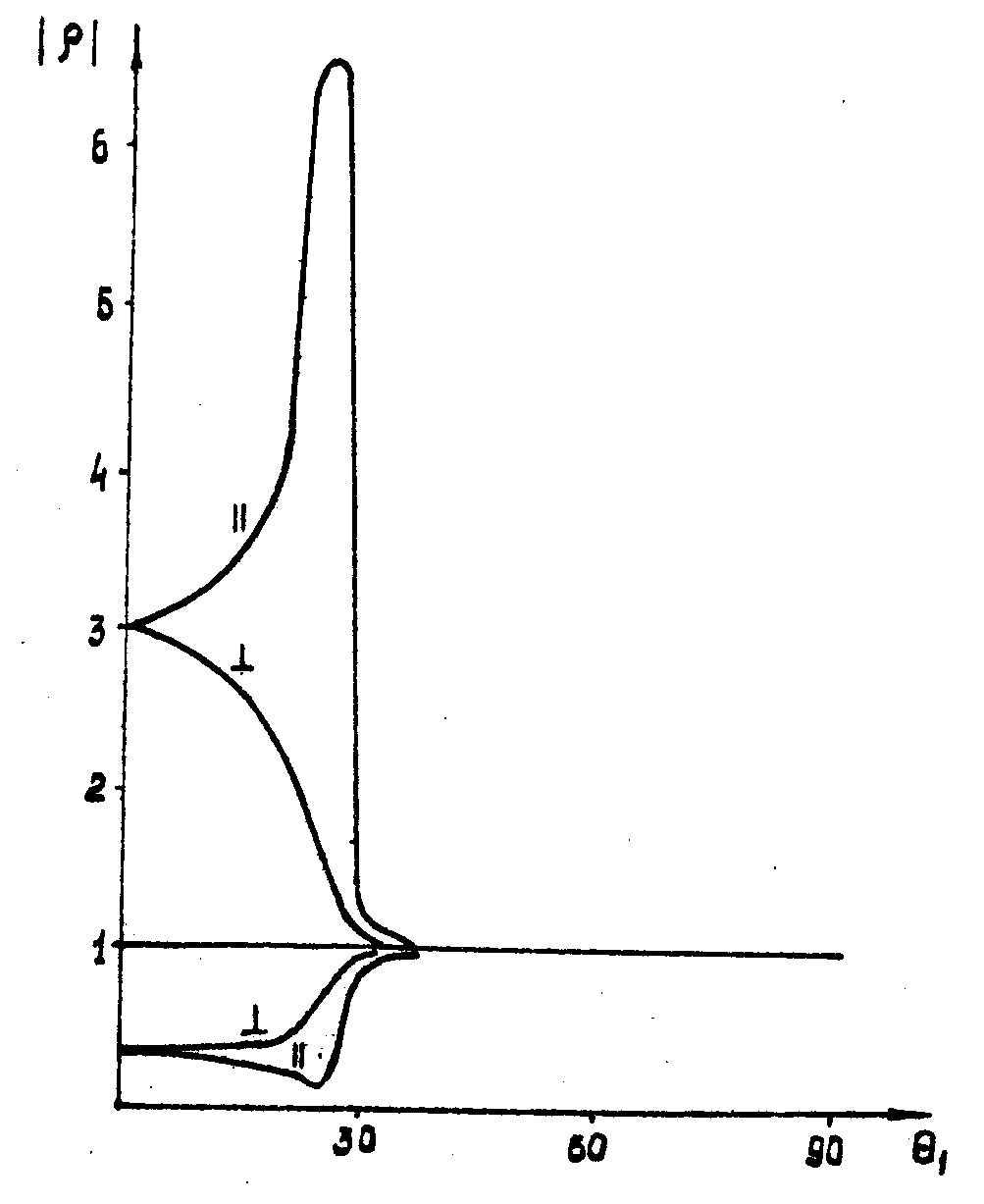
Рис.2. Зависимость модулей коэффициентов отражения от угла падения θ 1 для поглощающей (две нижние кривые) и усиливающей (две верхние кривые) отражавших сред, построенные для случая n0=0,5; κ=±0,2; θc=33°; θb=26°36 . Значки ⊥ и || обозначают перпендикулярную и параллельную поляризации падающей волна, соответственно.
4. Экспериментальное исследование отражения света
от усиливающей среды
Для экспериментального наблюдения процесса стационарного отражения необходимо, чтобы он был устойчивым. Из формулы ( 1) видно, что она переходит в (2) при условии |ρ12ρ23exp(2i Ф)|>>1, которое означает экспоненциальное нарастание любых малых возмущений поля внутри слоя. Таким образом, для усиливающего слоя достаточно большой толщины основной вклад в интенсивность отраженного света, начиная с некоторого момента времени, начинают давать усиленные возмущения и процесс отражения неизбежно приобретает нестационарный характер. Очевидно, что при предельном переходе к неограниченной усиливающей среде мы такие получаем неустойчивый режим стационарного отражения, причем этот результат не зависит ни от угла падения θ1, ни от значения n0.
Экспериментальное исследование отражения света от активных сред представляет большой практический интерес . Возможность усиления света при его отражении от активных сред была, по-видимому, впервые указана в /11/, экспериментальное измерение коэффициентов отражения для усиливающих сред проводилось в /5,6/. Эти измерения показали, что максимум коэффициентов отражения соответствует критическому углу полного отражения θc, причем величина максимума может достигать значения порядка 103 /6/.
Рассмотренная выше теория стационарного отражения плоских волн не может объяснить ни появления максимума, ни его величины. Оценка максимально возможных коэффициентов отражения для θ1=θc дает величину порядка 6 /6/, что на два порядка меньше значений, полученных экспериментально.
Коэффициент отражения света от слоя конечной толщины можно вычислять либо путем решения соответствующей граничной задачи, либо путем суммирования бесконечного числа волн, отраженных от двух поверхностей слоя. В случае поглощающей среды оба способа, как известно /1/, приводят к одинаковому результату. В случае усиливающей среды они описывают два различных режима отражения: стационарный и нестационарный, соответственно.
Для применения нестационарной теории необходимо существова -
ние сильного отражения преломленной волны на некоторой глубине в усиливающей среде. В экспериментах /5,6/ необходимое отражение может быть обусловлено неоднородностью усиливающей среды. Эта неоднородность может быть вызвана тепловым нагревом среды от излучения накачки /12/. Тогда при условии dn2/dt>0, где Т - температура, полное отражение для определенного интервала углов падения происходит на некотором расстоянии z0 от границы раздела пассивной и активной сред. В этом случае усиленная преломленная волна после отражения на глубине z0 монет дать основной вклад в интенсивность отраженного света, причем максимальное значение коэффициентов отражения экспоненциально растет с увеличением z0 /12/. К сожалению, знак производной dn2/dТ в экспериментах /5,6/ неизвестен.
Другая возможная причина сильного отражения преломленной волны связана с неоднородностью мнимой части n2. Действительно, распространение преломленной волны описывается эффективной электрической проницаемостью
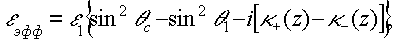 (6) (6)
где величины κ+(z) и κ-(2) описывают усиление и поглощение света в отражающей среде. κ+(0)>κ-(0) . В работах /5,6/ инверсная населенность создавалась излучением накачки, падающим нормально на поверхность раздела пассивной и активной сред. Благодаря поглощению излучения накачки величина κ+(z) экспоненциально убывает с ростом z, причем при z→∞ κ-> κ+. В результате, как следует из (6), при θ1= θc на некотором расстоянии от границы раздела εэфф обращается в нуль и преломленная волна испытывает полное отражение. Вне небольшой области, где |sin2θ1-sin 2θc| õ
κ+(0) , отражением света на не однородноcтях jmn2 можно пренебречь. Такой механизм усиления отраженного света не зависит от знака dn2/dt и, в принципе, может объяснить все основные особенности результатов экспериментов /5,6/. Для окончательного выяснения вопроса, разумеется, необходимо провести специально поставленные эксперименты.
5. Отражение плоских волн от поглощающих сред
Метод нахождения коэффициентов стационарного отражения плоских волн, описанный выше, применим, конечно, не только в случае усиливающих, но и поглощающих сред. Рассмотрим стационарное отражение от поглощающей среды с электрической проницаемостью ε=ε2' +iε2'', причем будем считать, что среда (1), из которой падает свет, также является поглощающей и имеет электрическую проницаемость ε=ε1' +iε1''. Ограничимся анализом наиболее интересного случая, когда ε1'' > ε2''.
Найдем нормальную к поверхности раздела составляющую волнового вектора преломленной волны:
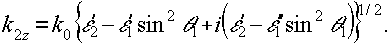 (7) (7)
Для определения k2z как однозначной функции угла падения θ1 достаточно задать фазу подкоренного выражения φ для θ1=0. Очевидно, что при нормальном падении преломленная волна должна распространяться от границы раздела, а ее амплитуда в процессе распространения - экспоненциально затухать, поэтому
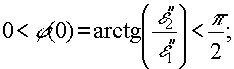 rek2z>0, jmk2z>0. rek2z>0, jmk2z>0.
В дальнейшем мы будем для определенности считать, что ε2''/ ε21'> ε2''/ ε2'. Тогда из (7) видно, что c увеличением угла падения θ1 фаза φ при некотором угле θa определяемом из уравненения
sin2 θa = ε2''/ε1'',
обращается в нуль, а затем становится отрицательной. Следовательно, в области θ1>θa j mk 2z< 0 и амплитуда преломленной волны, имеющая re k2z>0, экспоненциально растет с увеличением z. Этот экспоненциальный рост амплитуды поля не противоречит закону сохранения энергии, выражаемому уравнением
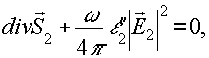 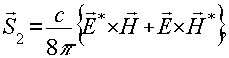
поскольку при θ1> θa затухание преломленной волны вдоль поверхности раздела сред превышает максимально возможное затухание плоских волн в отражающей среде, определяемое величиной ε''2. Иными словами, уменьшение потока энергии, переносимой преломленной волной параллельно границе раздела, происходит быстрее, чем это может быть обеспечено реальным поглощением среды (2). Поэтому в соответствии с законом сохранения энергии поток энергии, переносимой волной нормально к поверхности раздела, должен в процессе распространения увеличиваться.
Для углов падения θ1>θa вновь возникает вопрос о выборе преломленной волны. Как указывалось выше, метод предельного перехода выделяет ту преломленную волну, амплитуда которой убывает при z→∞. В соответствии с этим при θ1< θa мы должны выбрать преломленную волну, идущую от границы раздела, а при θ1>θa - преломленную волну, идущую к границе раздела. Следовательно, в области θ1<θa для коэффициентов отражения справедливы обычные формулы Френеля, а в области θ1<θa - формулы (3) и (4), в которых К27 определяется выражением (7). Отсюда следует, что при θ1>θa модуль коэффициентов отражения больше единицы. Это не противоречит, однако, закону сохранения энергии, поскольку для корректного анализа энергетического баланса необходимо рассмотреть отражение пучка и учесть краевые эффекты.
Для процесса стационарного отражения величина К 2z меняет знак при θ1=θa, поэтому в этой точке коэффициенты отражения испытывают скачок и определены неоднозначно. Этот скачок существует лишь в предельной случае полубесконечной отражающей среды. ecли отражавшая среда имеет конечную толщину l, то размер области значений углов θ1, в которой, осуществляется переход обычных формуя Френеля в формулы (3) и (4), определяется следующим выражением:
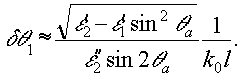
В пределе l→∞ размер переходной области обращается в нуль и коэффициенты отражения становятся разрывными функциями угла падения θ1.
Рассмотрим, теперь случай ε1''/ε1'< ε2''/ ε2', ε2''< ε1'' . Из (7) видно, что c увеличением угла θ1 от 0 до π/2 фаза φ монотонно растет, оставаясь все время в интервале (0, 3/2 π). Поэтому при всех углах падения jmК2z > 0 и коэффициенты отражения являются непрерывными функциями θ1. В этом случае при θ1> θa rek 2z<0 , т.е. преломленная волна распространяется к граница раздела.
Таким образом, при стационарном отражении плоских волн от поглощающей среды принцип излучения Зоммерфельда и Мандельштама не выполняется в области θ1>θa, что связано о особенностями распространения неоднородных волн в поглощающей среде.
З а к л ю ч е н и е
Мы ограничились здесь рассмотрением основных особенностей стационарного отражения плоских монохроматических волн от усиливающей и поглощающей сред.
В принципе все задачи, связанные c отражением электромагнитных волн от пассивных сред, могут быть обобщены на случай усиливающих. Вcе полученные здесь в применений к световым волнам результаты в равной степени относятся к отражению скалярных звуковых волн от активной по отношению к звуку среде.
Плоская монохроматическая волна является идеализацией реального пучка электромагнитных волн. Поэтому несомненный интерес представляет дальнейшее исследование отражения от усиливающих сред реальных световых пучков, в частности, сферических волн, узких световых пучков, коротких импульсов и т.п. .
Правильное понимание процессов отражения волн от усиливающих и поглощающих сред представляет большой интерес для решения многих задач квантовой электроники и особенно динамической голография.
Л и т е р а т у р а
1. В.А.Кизель. Отражение света. М., Наука, 1973.
2. Л.И.Мандельштам. Полное собрание трудов. М., изд.АН СССР, 1950; Лекции по оптике, теории относительности и квантовой механике. М., Наука, т.5, 1972.
3. А.Зоммерфельд. Оптика, М., ИЛ, 1953.
4. А.А.Колоколов. Письма в ЖЭТФ, 21, 660, 1975.
5. Б.Я.Коган, В.М.Волков, С.А.Лебедев. Письма в ЖЭТФ, 16, 144, 1972.
6. С.А.Лебедев, В.М.Волков. Б.Я.Коган. Оптика и спектроскопия, 35, 976, 1973.
7. В.Г.Веселаго. УФН, 92, 517, 1967.
8. А.Шустер. Введение в теоретическую оптику. Л.-М., ОНТИ ГТТИ, 1935.
9. Г.Н.Романов, С.С.Шакиджанов. Письма в ЖЭТФ, 16, 298, 1972.
10. Б.Б.Бойко, Н.С.Петров, И.З.Дживалдари. ЖПС, 18, 727, 1973.
11. c.j.koester. ieee j.quant.electr., ge-2, 580, 1966.
12. Б.Б.Бойко, И.З.Джилавдари, Н.С.Петров. ЖПС, 22, 545, 1975, в сб. "Квантовая электроника и лазерная спектроскопия", Минск, Наука и техника, стр.449. 1974.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

