|
|
 |
 |

|
| |
ТЕОРИЯ ГОЛОГРАФИРОВАНИЯ В МУТНЫХ СРЕДАХ
М.И.Рязанов
Рассмотрена теория интерференции волн в средах с движущимися крупномасштабными (размеры больше длины волны) рассеивателями и влияние рассеяния в мутной среде на голографирование.
1. Основная задача теории голографирования в мутных средах состоит в определении способов получения информации о предмете, если известна голограмма предмета, полученная через рассеивавшую среду и информация о свойствах самой рассеивающей среды. Вопросам получения голографического изображения через рассеивающую среду посвящен ряд работ /1-9/.
Для решения этой задачи прежде всего необходима теория интерференции волн, рассеивающихся в путной среде. Заметим, что обычно мутная среда содержит рассеивающие центры с размерами а, намного превышающими длину волны света l
(мелкомасштабные неоднородности с а <<l
не дают существенного рассеяния).
2. Формулируя теорию интерференции волн в мутной среде, удобно считать известной амплитуду рассеяния света ¦
(u
,j
) на каждом отдельном рассеивателе. Если размер рассеивателя а велик по сравнению с длиной волны, то характерной чертой амплитуды ¦
(u
,j
) является наличие острого максимума при малых углах рассеяния u
~ (l
/а). В этом случае для более подробной характеристики одноцентрового рассеяния, помимо полного сечения
s
= ò
dW
[¦
(u
,j
)]2 (1)
можно ввести так называемое "транспортное" сечение
- 179 -
s
= ò
dW
{1 - cosu
}[¦
(u
,j
)]2 (2)
характеризующее рассеяние на большие углы.
3. В слое вещества толщины l происходит многократное рассеяние света на рассеивателях. Картина рассеяния резко меняется в зависимости от толщины слоя l.
Если величина l меньше длины свободного пробега (n0s
)-1, то рассеяние вообще мало и может быть рассчитано по теории возмущений. Если l>(n0s
)-1, но меньше длины дифракционной тени a2/l
, то применимо приближение эйконала; если l>а2/ l
, но меньше транспортной длины (n0s
tr)-1, то применимо приближение многократного рассеяния. Наконец, для толщин l³
(n0s
tr)-1 влияние рассеяния полностью искажает первичную волну и рассмотрение чрезвычайно усложняется.
4. Наличие в среде рассеивателей приводит к неоднородности диэлектрических свойств среды и может быть описано введением зависящей от координат диэлектрической проницаемости:
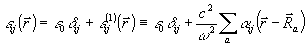 (3) (3)
где e 0
- диэлектрическая проницаемость однородной
среды без рассеивателей, суммирование проводится по координатам 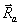 всех рассеивателей.
всех рассеивателей.
Учитывая, что величина
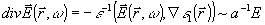 (4) (4)
мала по сравнению с (w /с)Е ,
из уравнений Максвелла можно получить уравнение для
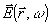 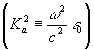 : :
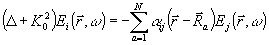 (5) (5)
Если свойства рассеивателей таковы, что поляризация волны не меняется, то a
ij = a
d
ij
- 180 -
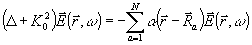 (6) (6)
Мы предполагаем решение задачи рассеяния на одном рассеивателе известным, т.е. известным решение уравнения
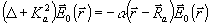 (7) (7)
Пусть до рассеяния 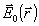 имело вид
имело вид 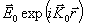 ,
тогда удобно решение (7)
представить в форме ,
тогда удобно решение (7)
представить в форме
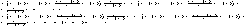 (8) (8)
где s0 является решением уравнения
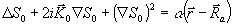 (9) (9)
5. Рассмотрим сначала слой вещества, содержащий хаотически расположенные рассеиватели, в том случае, когда его толщина мала по сравнению с длиной дифракционной тени от каждого рассеивателя,
(n0s
)-1 << l << (a2/l
) (10)
Буден. искать решение (6) в виде
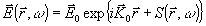 (11) (11)
откуда следует уравнение для s
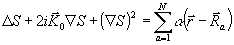 (12) (12)
Так как Ñ
s ~ а-1s, то в первом приближении можно в левой
- 181 -
части (12) пренебречь всеми слагаемыми, не содержащими К0, получив
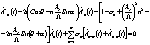
или , интегрируя по х |
|
К0:
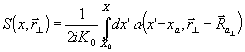 (13) (13)
Точнее говоря, при этом выводе следует учесть, что
D
s ~g
a-2s, где g
- число столкновений в слое. Поэтому приближенное решение уравнения (6) в виде
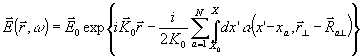 (14) (14)
теряет применимость при больших l. Область применимости (14) ограничена сверху условием (10). Таким обрезом, в области (10) меняется только фаза волны.
6. В более толстых слоях, в области
(a2/l
) << l << (n0s
)-1 (15)
можно искать решение (6) в виде
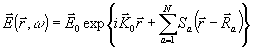 (16) (16)
откуда следует, что sа удовлетворяет уравнению
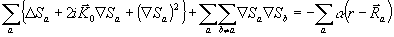 (17) (17)
- 182 -
Каждое суммирование приводит в окончательном результате к появлению
лишней степени плотности рассеивателей n0,
что позволяет опустить слагаемое с двойной суммой. После этого вследствие произвольности
координат рассеивателей (10)
сводится к сумме независимых уравнений (9)
для каждого рассеивателя. Отсюда следует, что sa(r
– 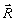 a)=s0(r
– a)=s0(r
– 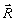 a),
т.е. решение (16)
может быть записано в виде a),
т.е. решение (16)
может быть записано в виде
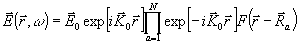 (18) (18)
где 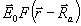 - решение задачи рассеяния на одном рассеивателе
с падающей волной
- решение задачи рассеяния на одном рассеивателе
с падающей волной 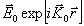 .
Приближение (18)
остается справедливым до тех пор, пока отклонение волны в слое остается калым.
В толстых слоях l ³
(n0d tr)-1
относительное изменение волнового вектора в процессе рассеяния порядка единицы
и пренебрегать двойной суммой в (17)
нельзя. Приближенное решение уравнений Максвелла в форме
(18) было развито и исследовано в /10/. Исследование
показало, что в случае, когда средний квадрат угла рассеяния во всем слое мал
по сравнению с единицей, приближенное решение
(18) дает результаты, совпадающие с результатами
решения кинетического уравнения /11/. Однако в задачах, где требуется анализ
интерференции волн в рассеивающих средах, приближение
(18) во много раз облегчает вычисления по сравнению
с методом кинетического уравнения. .
Приближение (18)
остается справедливым до тех пор, пока отклонение волны в слое остается калым.
В толстых слоях l ³
(n0d tr)-1
относительное изменение волнового вектора в процессе рассеяния порядка единицы
и пренебрегать двойной суммой в (17)
нельзя. Приближенное решение уравнений Максвелла в форме
(18) было развито и исследовано в /10/. Исследование
показало, что в случае, когда средний квадрат угла рассеяния во всем слое мал
по сравнению с единицей, приближенное решение
(18) дает результаты, совпадающие с результатами
решения кинетического уравнения /11/. Однако в задачах, где требуется анализ
интерференции волн в рассеивающих средах, приближение
(18) во много раз облегчает вычисления по сравнению
с методом кинетического уравнения.
7. В том случае, когда амплитуда
рассеяния на одном рассеивателе ¦
мала по сравнению с (n0d
)-1, для решения задачи многократного
рассеяния требуется не точный вид решения одноцентровой задачи
f(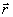 ),
а его асимптотическое поведение на далеких расстояниях, которое можно представить
в виде ),
а его асимптотическое поведение на далеких расстояниях, которое можно представить
в виде
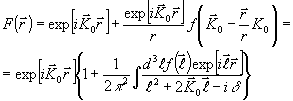 (19) (19)
- 183 -
где ¦
(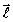 ) -
амплитуда одноцентрового рассеяния как функция разности начального и конечного
волновых векторов. Используя (19), можно
записать приближенное решение (18)
в виде ) -
амплитуда одноцентрового рассеяния как функция разности начального и конечного
волновых векторов. Используя (19), можно
записать приближенное решение (18)
в виде
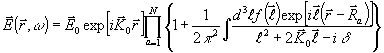 (20) (20)
Выражение (20)
можно привести к более удобному для применений виду, если учесть, что малость
элективных значений ℓ в
интеграле (?1) приводит к тому, что продольная (вдоль 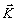 0)
компонента 0)
компонента 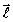 ,
ℓ| | <<
ℓ┴. Поэтому
¦ (ℓ)»
¦ (ℓ┴); ℓ2
» ℓ2┴
и в (20) можно
проинтегрировать по ℓ| |
, получив ,
ℓ| | <<
ℓ┴. Поэтому
¦ (ℓ)»
¦ (ℓ┴); ℓ2
» ℓ2┴
и в (20) можно
проинтегрировать по ℓ| |
, получив
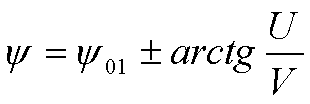 (21) (21)
где ось Х направлена вдоль К 0, q
(х)=0 при х < 0, q
(x)=1 при х > 0.
Следует отметить, что, как это следует из (19-21), при толщине слоя l, ограниченной неравенством
(a2/l
) << l << (n0s
)-1
происходит изменение фазы и амплитуды волны, в то время как при l << а2/ l
в приближений (14) изменяется только фаза волны.
8. Рассмотрим теперь случай
медленно движущихся рассеивателей, считая их скорости
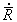 <<
с(l /a)
<< с.
В системе отсчета, скорость которой
v совпадает со скоростью рассеивателя в рассматриваемый
момент времени, можно пользоваться полученными выше формулами. В частности,
из (19) следует,
что поле рассеянной волны <<
с(l /a)
<< с.
В системе отсчета, скорость которой
v совпадает со скоростью рассеивателя в рассматриваемый
момент времени, можно пользоваться полученными выше формулами. В частности,
из (19) следует,
что поле рассеянной волны 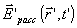 связано с полем падающей волны в той же системе отсчета
связано с полем падающей волны в той же системе отсчета
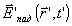 соотношением
соотношением
- 184 -
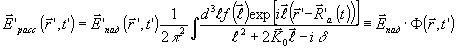 (22) (22)
Поле рассеянной волны в лабораторной системе отсчета на далеких расстояниях от рассеивателя при v << с запишется как
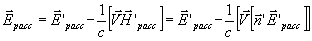
где 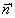 - единичный вектор направления рассеянной волны
в системе рассеивателя. Учитывая (22),
можно написать
- единичный вектор направления рассеянной волны
в системе рассеивателя. Учитывая (22),
можно написать
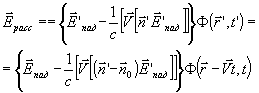 (23) (23)
(где опущены квадратичные по v слагаемые).
При (v/c)<<(l
/a) можно
пренебречь величиной (w
0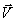 /с2)
по сравнению c /с2)
по сравнению c 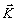 0
в знаменателе интеграла. Из (23)
следует, что при рассеянии на движущихся рассеивателях происходит изменение
поляризации даже в том случае, если на покоящемся рассеивателе поляризация не
меняется. Нетрудно оценить относительную величину изменения поляризации. В слое
толщины l
происходит ln0s
столкновений волны с рассеивателями.
Относительное изменение поляризации в каждом столкновении, как это следует из
(23), порядка (l
·v/a·c). Таким
образом, относительное изменение поляризации во всем слое составляет величину
порядка ln0s
l ·v/a·c.
С другой стороны, мы рассматриваем только не слишком толстые слои вещества
l<<(n0s tr)-1,
т.е.
ln0s l
2a-2<< 1.
Поэтому относительное изменение поляризации 0
в знаменателе интеграла. Из (23)
следует, что при рассеянии на движущихся рассеивателях происходит изменение
поляризации даже в том случае, если на покоящемся рассеивателе поляризация не
меняется. Нетрудно оценить относительную величину изменения поляризации. В слое
толщины l
происходит ln0s
столкновений волны с рассеивателями.
Относительное изменение поляризации в каждом столкновении, как это следует из
(23), порядка (l
·v/a·c). Таким
образом, относительное изменение поляризации во всем слое составляет величину
порядка ln0s
l ·v/a·c.
С другой стороны, мы рассматриваем только не слишком толстые слои вещества
l<<(n0s tr)-1,
т.е.
ln0s l
2a-2<< 1.
Поэтому относительное изменение поляризации
|
ln0s
|
l
|
· |
v |
<< |
v |
· |
a |
|
a |
c |
c |
l
|
т.е. относительной изменение поляризации мало, если
- 185 -
v/c << l
/a (24)
В реально встречающихся ситуациях это неравенство выполняется в достаточно широкой области длин волн и размеров рассеивателей. Условие (24) существенно упрощает решение задачи многократного рассеяния электромагнитных волн на движущихся рассеивателях. Оно позволяет упростить (25), пренебрегая как изменением поляризации при рассеянии, так и зависящими от скорости рассеивателя членами в знаменателе подынтегрального выражения. Поэтому, учитывая (24), можно из (23) получить приближенное выражение для электрического поля в задаче о рассеянии на движущемся рассеивателе
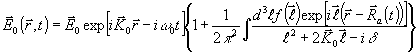 (25) (25)
отличающееся от (20)
лишь зависимостью радиуса-вектора центра инерции рассеивателя
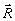 а(t)
от времени. а(t)
от времени.
В слое вещества толщины l
можно найти электрическое поле, учитывающее многократное рассеяние, аналогично
случаю покоящихся рассеивателей. Из уравнений Максвелла для электрического поля
 следует уравнение
следует уравнение
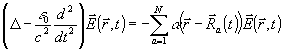 (26) (26)
Решение этого уравнения удобно искать в виде, аналогичной (16):
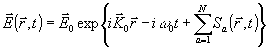 (26) (26)
Подстановка (27) в {26) приводит к уравнениям для sа:
- 186 -
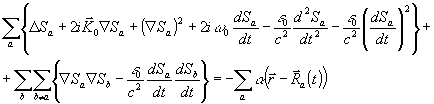
Пренебрежение двукратными суммами в этой случае приводит к
току, что, как и в случае покоящихся рассеивателей, вид sa(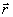 ,t)
определяется уравнением для рассеяния на одном движущемся рассеивателе с тем
же граничным условием (падающая волне вида ,t)
определяется уравнением для рассеяния на одном движущемся рассеивателе с тем
же граничным условием (падающая волне вида 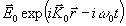 ).
Поэтому величина ).
Поэтому величина
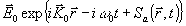
совпадает с полем в задаче однократного рассеяния (25). Учитывая это обстоятельство, можно получить
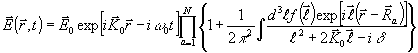 (28) (28)
Таким образом, при выполнении условия
(v/ с) << (l
/a)
решение задачи многократного рассеяния поля на движущихся рассеивателях
(28) отличается от рассеяния
(20) для случая покоящихся рассеивателей только
зависимостью 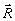 а а
от времени.
9. Пусть теперь за время голографирования каждый рассеиватель существенно пеняет свое пространственное расположение. Это означает, что радиус-вектор рассеивателя становится случайной величиной. На наблюдаемых величинах это будет сказываться таким образом, что они будут иметь различные значения в различные моменты времени. Поэтому всегда будет представлять интерес среднее по времени наблюдения значение физической величины. Рассмотрим, например,
- 187 -
интенсивность волны, проходящей в среде. Удобно для этого представить (25) в форме, аналогичной (21)
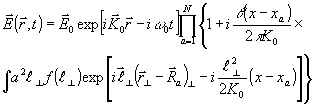 (29) (29)
Средняя по времени наблюдения интенсивность волны запишется как
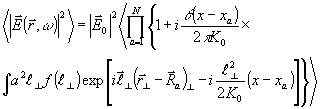
В силу хаотичности движения рассеивателей .можно считать в
первом приближении координаты каждого рассеивателя независимые .
Тогда усреднение сводится к усреднению по различным
значениям каждого радиуса-вектора 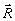 а.
Если за время наблюдения рассеиватель сдвигается на расстояния, большие по сравнению
со средники расстояниями между отдельными рассеивателями, то можно распространить
область изменения координат каждого рассеивателя на весь объем слоя. Независимость
координат рассеивателей позволяет написать а.
Если за время наблюдения рассеиватель сдвигается на расстояния, большие по сравнению
со средники расстояниями между отдельными рассеивателями, то можно распространить
область изменения координат каждого рассеивателя на весь объем слоя. Независимость
координат рассеивателей позволяет написать
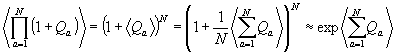 (30) (30)
с точностью до членов порядка 1/n. Для каждого отдельного рассеивателя можно заменять среднее по времени усреднением по пространственному расположению рассеивателя. Тогда, считая, что в слое между плоскостями х=0 и х=l рассеиватели распределены однородно с плотностью n0, можно получить
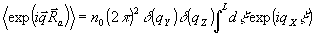 (31) (31)
Используя (31) и (30). можно получить
- 188 -
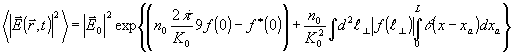 (32) (32)
Используя оптическую теорему
i(¦
*(0) - ¦
(0)) = (s
+ s
погл)k0/4p
удобно выразить мнимую часть амплитуды рассеяния вперед через полное сечение (в которое, кроме сечения рассеяния, следует включить и сечение поглощения s
погл ). Получившееся при этом слагаемое, содержащее сечение рассеяния s
, сокращается с интегралом по ℓ┴, в результате чего (32) принимает вид :
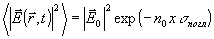 (33) (33)
При х > l следует заманить х в (33) на l.
10. Рассмотрим теперь влияние
рассеяния на интерференцию двух плоских волн. Пусть на слой вещества, ограниченный
плоскостями х=0 и х = l
падают две плоские волны, отличающиеся только тем, что волновой вектор одной
волны имеет компоненты 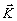 1(k0cosj
,0,k0sinj ), а
волновой вектор второй волны -
компоненты 1(k0cosj
,0,k0sinj ), а
волновой вектор второй волны -
компоненты 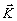 2(k0cosj
,0,-k0sinj ). (2j
- угол сбивания). Полное поле в веществе получится,
воли для каждой волны взять решение в форме
(28) и сложить их. Суммарная интенсивность
имеет вид: 2(k0cosj
,0,-k0sinj ). (2j
- угол сбивания). Полное поле в веществе получится,
воли для каждой волны взять решение в форме
(28) и сложить их. Суммарная интенсивность
имеет вид:
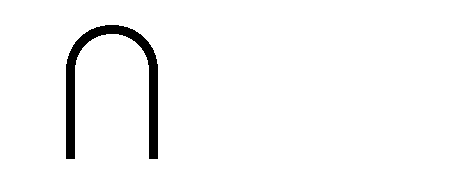 (34) (34)
- 189 -
Усреднение интенсивности с помощью (30-31) дает
<j> = 2j0exp(-n0s
поглl){1 + g
(j
,k0,a)cos(2zk0sinj
)} (35)
здесь коэффициент когерентности g
(j
,k0,а) определяется выражением
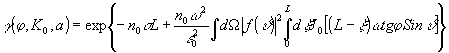 (36) (36)
где j0 - функция Бесселя. Для сферических неоднородностей
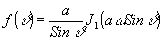 (37) (37)
Подстановка (37) в предельном случае j
>> a/l дает
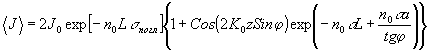 (38) (38)
в противоположном предельном случае малых углов сбивания, j
<< a/l
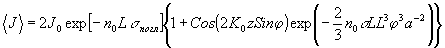 (39) (39)
Из (38)
видно, что при не очень малых углах обивания интерференционное слагаемое уменьшается
гораздо быстрее, чем полная интенсивность, заметно ослабляясь уже после одного
рассеяния на длине (n0s
)-1. в случае малых углов
сбивания, j
<< a/l интерференционное слагаемое спадает
значительно медленнее на длинах l~(a2/n0s
j 2)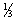 . .
Из полученных формул следует, что одним из способов передачи голографического изображения через рассеивающую среду является использования малых углов сбивания. Этот способ экспериментально осуществлен в работе /1/ .
- 190 -
Литература
1. Ю.А.Быковский. Ю.А.Зимин, Н.П.Калашников, А.И.Ларкин, М.И.Рязанов. ЖТФ, 42, 830 (1972).
2. h.kopelnik, k.pennington, j.opt.soc.am., 58, 273, 1968.
3. e.leith, j.upatnieks. j.opt.soc.am., 56, 523, 1966.
4. j.goodman, w.huntley, d.jacjson, m.lehmann, appl.phys.lett., 8, 311, 1966
5. j.goodman, d.jackson, m.lehmann, j.knots. appl.opt., 8, 1581, 1969.
6. k.stetson. j.opt.sоc.am., 57, 1060, 1967.
7. h.kopelnik. bell syst.techn.j., 44, 2451, 1965.
8. b.spits. С.r. 264b, 1449, 1967.
9. j.hamasak. appl.opt., 7, 1613, 1968.
10. Н.П.Калашников, М.И.Рязанов. ЖЭТФ, 50, 439, 1966.
11. Л.С.Долин. Ивв. ВУЗов. Радиофизика, 7, 380, 1964.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

