|
|
 |
 |

|
| |
ОСНОВНЫЕ ТЕОРЕМЫ ГОЛОГРАНИИ ДЛЯ ЛИНЕЙНОЙ стационарной СРЕДЫ
Э.И.Крупицкий
Рассматривается внешняя задача восстановления волнового поля в голографии для произвольной линейной стационарной среды (анизотропной, неоднородной, активной). Доказана теорема существования и единственности решения задачи, определяющая необходимые и достаточные условия записи поля, обеспечивающие его полное восстановление вне замкнутой поверхности регистрации. Доказана теорема дискретизации, определяющая требования к множеству точек отсчета, необходимые и достаточные для сколь угодно точного восстановления поля в любой точке внешнего пространства. При этом получен алгоритм оптимального восстановления поля по дискретным отсчетам на произвольном заданном множестве точек. Известное представление ряда Котельникова является его частным случаем. Сформулирован принцип взаимности в голографии, связанный с симметрией голограммы относительно сигнальной и опорной волн.
Введение
Голографический принцип позволяет зарегистрировать амплитудно-фазовое распределение монохроматического волнового поля на некоторой поверхности или в объеме в среде, где происходит его распространение. При этом регистрация может осуществляться на непрерывном либо дискретном множестве точек. Первый случай характерен для оптической голографии, а второй - радио и акустической. Непрерывная регистрация осуществляется путем использования физической опорной волны в среде, параметры которой меняются под действием интерференционного поля. Дискретная предусматривает использование
- 129 -
зонда (малого приемника), помещаемого в точки регистрации поля. При этом может использоваться как физическая, так и "искусственная" опорная волна (в виде опорного колебания в приемнике). В любом случае результат записи амплитудно-фазового распределения поля можно называть голограммой. Соответствующая классификация видов голограмм показана на рис.1.
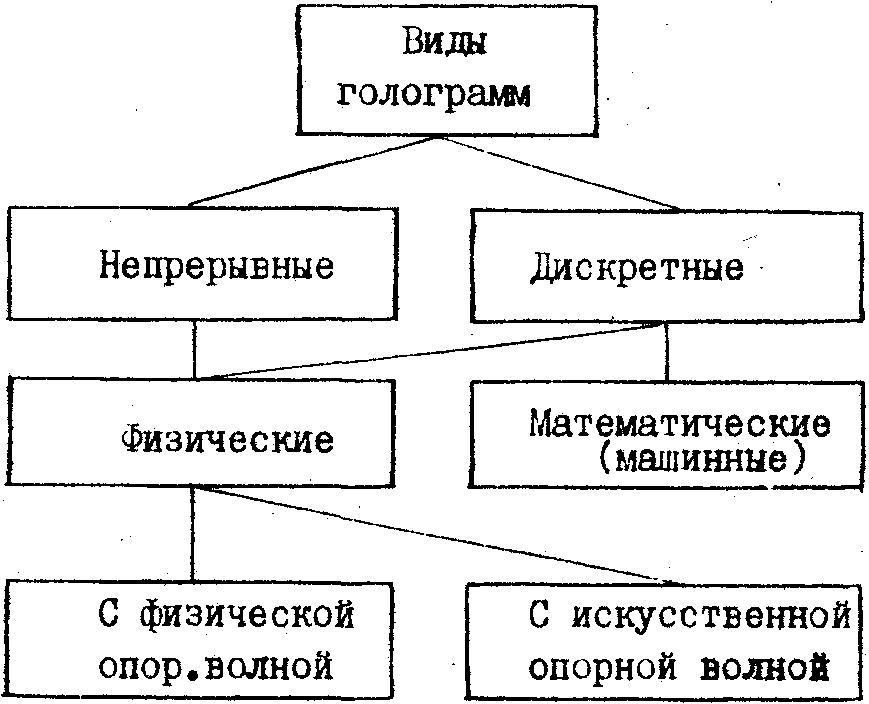
Рис.1. Классификация видов голограмм.
Принципиально голограмма содержит информацию о предметах, средах к источниках, участвовавших в формировании сигнальной и опорной волн в точках регистрации. Благодаря этому голография позволяет решать следующие две общие задачи:
- восстановление зарегистрированного волнового поля во внешней области пространства "за голограммой", где отсутствуют источники поля ("внешняя задача голографии");
- восстановление зарегистрированного волнового поля во внутренней области пространства "до голограммы" и одновременное определение при необходимости неизвестных параметров среды, рассеивающих тел или источников ("внутренняя задача голографии").
Восстановление волнового поля по голограмме может быть как
- 130 -
физическим, так и математическим (на ЭВМ). Практические методы физического восстановления хорошо разработаны для решения внешней задачи, внутренняя задача более эффективно решается с преобразованием (чаще всего масштабного характера). Примером является моделирование радио или акустического поля в оптическом диапазоне. Существенное преобразование волнового поля достигается путем восстановления вместо сигнальной волны опорной, использовавшейся при получении голограммы. Этот случай встречается, например, в голографических устройствах идентификации изображений (согласованные фильтры и т.п.), а также при коррекции индикатрисы излучения лазеров. Возможность такого преобразования основана на своеобразном "принципе взаимности", присущем голографическому способу записи волнового поля. Следует также подчеркнуть, что физическое восстановление волнового поля имеет свою специфику при использовании непрерывных и дискретных голограмм. Наконец, необходимо отметить, что процесс создания голограмм, как и процесс восстановления, может быть не только физическим, но и математическим (использование так называемых "машинных голограмм", получаемых путем расчета). На рис.2 показана классификация видов восстановления волн в голографии.
Сформулированные выше основные задачи голографии охватывают практически все многочисленные и разнообразные ее применения. Возможность их математического и "физического" решения базируется на ряде общих теорем, формулированию и доказательству которых и посвящена настоящая работа. Однако этим не ограничивается смысл основных теорем: они позволяют правильно интерпретировать практически наблюдаемые закономерности, помогают выявить и оценить источники погрешностей, появляющиеся в процессе практической реализации и т.п. Оказалось, что многие из указанных теорем можно сформулировать для весьма общего случая так называемой линейной стационарной среды без пространственной дисперсии. Эта среда может быть анизотропной, активной (гиротропной), неоднородной и обладать временной дисперсией. Линейность же ее проявляется в линейности материальных уравнений связи (линейности связи индукции и напряженности поля).
- 131 -
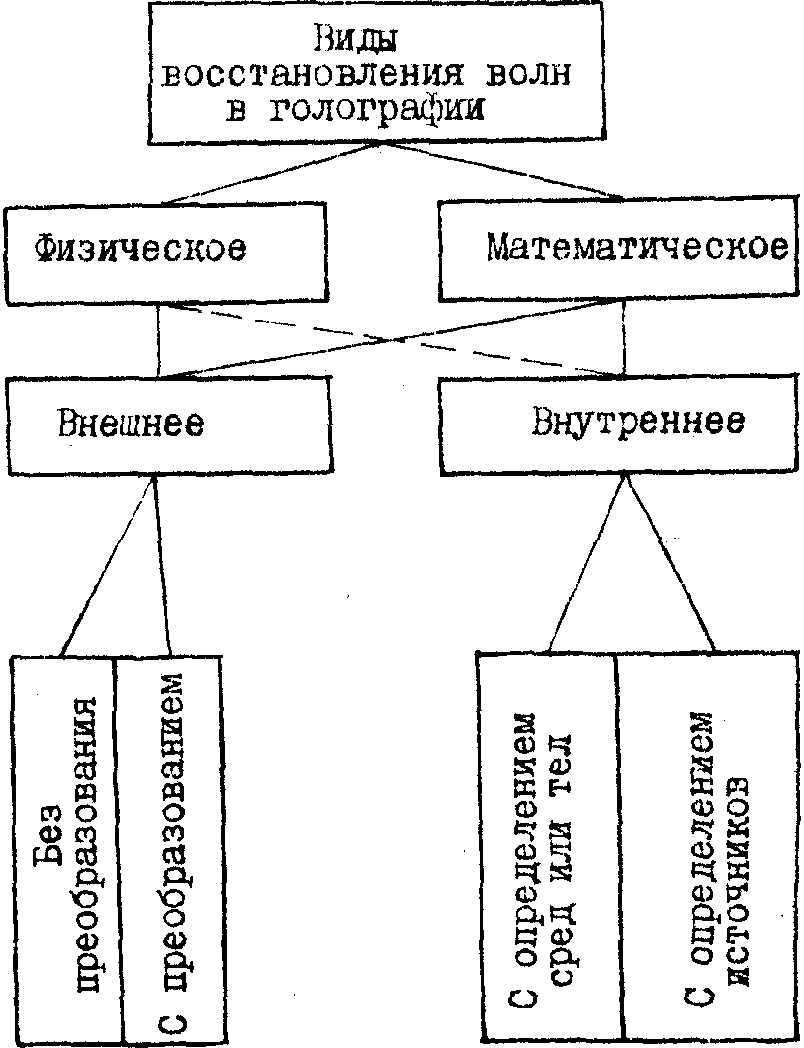
Рис.2. Классификация видов восстановления волн в голографии.
В настоящей первой части работы мы ограничимся рассмотрением только внешней задачи восстановления.
Эта задача является наиболее типичной для голографии. К ней относятся такие частные направления как получение мнимых объемных изображений предметов, голографическая интерферометрия, голографические запоминающие устройства, голографическое кодирование плоских изображений и многие другие */.
*/ Во второй части работы будет показано, что получение действительных изображений предметов в голографии является частным случаем решения внутренней задачи восстановления.
- 132 -
1. Уравнении поля в линейной среде
Приведем некоторые сведения из электродинамики, которые понадобятся нам в дальнейшей.
Уравнения Максвелла для комплексных амплитуд монохроматического поля в предположении, что временная зависимость определяется функцией exp(iw
t), имеют вид:
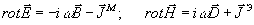 (1) (1)
где 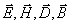 - амплитуды векторов напряженностей и индукций
электрического и магнитных полей, а
- амплитуды векторов напряженностей и индукций
электрического и магнитных полей, а 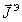 и
и 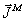 - плотности сторонних электрических и магнитных
токов, причем
- плотности сторонних электрических и магнитных
токов, причем 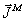 является величиной фиктивной, вводимой обычно по соображениям удобства математического
анализа.
является величиной фиктивной, вводимой обычно по соображениям удобства математического
анализа.
Для полноты системы уравнений поля к
(1) следует добавить так называемые материальные
уравнения или уравнения связи векторов 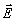 с
с 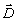 и
и 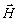 с
с 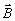 .В
случае общей линейной среды они имеют вид: .В
случае общей линейной среды они имеют вид:
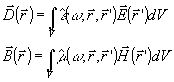 (2) (2)
где 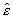 и
и 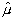 - тензоры среды. Эти уравнения являются очевидным следствием соотношений:
- тензоры среды. Эти уравнения являются очевидным следствием соотношений:
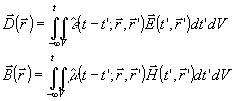 (3) (3)
которые справедливы для достаточно общей зависимости от времени.
Если ввести какую-либо систему координат, характеризуемую в каждой точке пространства
тройкой некомпланарных единичных векторов 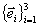 ,
то, учитывая правила умножения тензора на вектор
/1/, получим для ,
то, учитывая правила умножения тензора на вектор
/1/, получим для
- 133 -
компонент векторов соотношения:
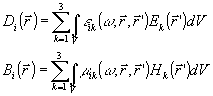 (2) (2)
Зависимость тензоров 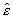 и
и 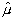 от частоты w
учитывает временную дисперсию среды. Зависимость
же от радиус-векторов
от частоты w
учитывает временную дисперсию среды. Зависимость
же от радиус-векторов 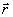 и учитывает пространственную дисперсию среды и ее неоднородность. При отсутствии
пространственной дисперсии вместо (2)
и (4) имеем:
и учитывает пространственную дисперсию среды и ее неоднородность. При отсутствии
пространственной дисперсии вместо (2)
и (4) имеем:
 (5) (5)
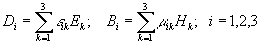 (6) (6)
В общем случае анизотропной, активной и диссипативной среды
тензоры 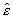 и
и 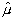 можно представить в виде
можно представить в виде
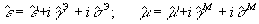 (7) (7)
где 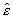 ’, ’,
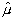 ’ -
симметричные, вещественные тензоры проницаемости; ’ -
симметричные, вещественные тензоры проницаемости; 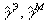 - антисимметричные, вещественные тензоры гирации, учитывающие активность среды;
- антисимметричные, вещественные тензоры гирации, учитывающие активность среды;
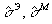 - симметричные, вещественные тензоры потерь.
- симметричные, вещественные тензоры потерь.
Таким образом, в общем случае 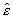 и
и 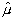 - комплексные несимметричные и неэрмитовые
тензоры, при отсутствии потерь в среде (
- комплексные несимметричные и неэрмитовые
тензоры, при отсутствии потерь в среде (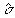 =0)
тензоры =0)
тензоры 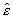 и
и 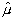 становятся эрмитовыми.
становятся эрмитовыми.
В дальнейшем нам понадобится понятие транспонированной среды,
которая характеризуется транспонированными тензорами
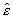 T
и T
и 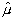 T.
Транспонирование соответствует перестановке индексов компонент, т.е.
e Тiк=e
кi,
m Тiк=m
кi
Следовательно, T.
Транспонирование соответствует перестановке индексов компонент, т.е.
e Тiк=e
кi,
m Тiк=m
кi
Следовательно, 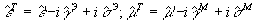 .
Изменение знака перед .
Изменение знака перед 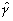 определяется тем, что тензор гирации антисимметричен. Активность среды чаще
всего
определяется тем, что тензор гирации антисимметричен. Активность среды чаще
всего
- 134 -
обусловлена постоянным магнитный полей 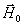 при этом транспонирование эквивалентно изменению направления
при этом транспонирование эквивалентно изменению направления 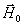 на обратное (замене
на обратное (замене 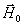 на -
на -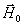 ).
Следует отметить, что у известных сред либо ).
Следует отметить, что у известных сред либо 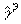 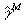 =
0, либо =
0, либо 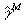 = 0; среды, одновременно являющиеся и гироэлектрическими
и гиромагнитными, пока не обнаружены /2/. Однако это не мешает нам рассматривать
общий случай
= 0; среды, одновременно являющиеся и гироэлектрическими
и гиромагнитными, пока не обнаружены /2/. Однако это не мешает нам рассматривать
общий случай 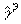 ¹ 0,
¹ 0, 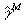 ¹ 0.
¹ 0.
При наличии поверхностей разрыва непрерывности параметров 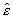 и
и 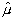 в точках этих поверхностей уравнения (1)
должны быть заменены граничными условиями:
в точках этих поверхностей уравнения (1)
должны быть заменены граничными условиями:
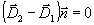 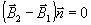 (8) (8)
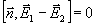 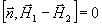 (9) (9)
где индексы соответствуют двум средам, разделенным поверхностью
разрыва, a 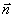 - вектор нормали, направленный во вторую среду. Если одна из сред - идеальный
проводник, электрический или магнитный, то вместо
(8) имеем:
- вектор нормали, направленный во вторую среду. Если одна из сред - идеальный
проводник, электрический или магнитный, то вместо
(8) имеем:
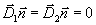 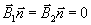 (10) (10)
а вместо (9) соответственно,
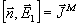 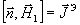 (11) (11)
где 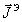 , ,
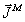 - плотности поверхностных токов.
- плотности поверхностных токов.
В дальнейшем нам понадобится обобщенная лемма Лоренца.
Лемма Лоренца для общей линейной среды может быть получена по аналогии с выводом для изотропной среды /2/.
Введем в рассмотрение вспомогательное поле 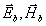 ,
порождаемое токами ,
порождаемое токами 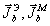 в транспонированной среде. Тогда
в транспонированной среде. Тогда
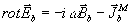 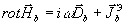 (12) (12)
где
- 135 -
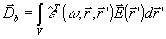 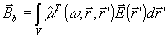 (13) (13)
В результате для точек пространства, где
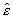 и
и 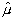 непрерывные находим:
непрерывные находим:
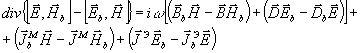 (14) (14)
Легко видеть, что при отсутствии пространственной диспероч 1, когда справедливо (5), первые две скобки обращаются в нуль и мы получаем обобщенную лемму Лоренца
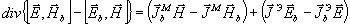 (15) (15)
справедливую для анизотропной, активной среды.
2. Существование и единственность решения внешней задачи голографии
Попытаемся сформулировать требования к голографической записи
поля в линейной среде, характеризуемой тензорами 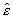 и
и 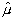 ,
которые обеспечивают существование и единственность решения внешней задачи восстановления.
Теорема существования и единственности, доказываемая виде, имеет много общего
с аналогичной теоремой, доказываемой в электродинамике, обычно, для более частного
случая линейной, однородной и изотропной среды /2/. ,
которые обеспечивают существование и единственность решения внешней задачи восстановления.
Теорема существования и единственности, доказываемая виде, имеет много общего
с аналогичной теоремой, доказываемой в электродинамике, обычно, для более частного
случая линейной, однородной и изотропной среды /2/.
Основной практический интерес представляют, на наш взгляд, следствия из этой теоремы. Для доказательства теоремы нам понадобится лемма, касающаяся полной голографической записи скалярного волнового поля.
Лемма 1
Для получения полной информации о скалярном монохроматическом волновом процессе с известной частотой М на произвольном множестве точек М необходимо и достаточно использовать два опорных
- 136 -
колебания, когерентных с волновым процессом, отличающихся между собой функциями распределения фазы на p
/2.
Доказательство .
Пусть регистрируемое и опорное колебания описываются функциями:
U(t,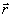 ) = A( ) = A(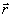 )exp[iw
t + iy ( )exp[iw
t + iy (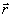 )] (16) )] (16)
U0(t,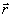 )
= A0( )
= A0(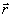 )exp[iw
t + iy 0( )exp[iw
t + iy 0(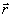 )] (17) )] (17)
Будем сначала предполагать, что регистрация осуществляется с физической волной, т.е. регистрируется интенсивность интерференционного поля:
U2 = А20 + A 2 + 2А0АСоs(y
- y
0) (18)
Для доказательства достаточности условия леммы предположим, что регистрируется интерференционное поле для двух опорных колебаний U01 и U02, когерентных с U, фаза которых отличается на величину p
/2, а амплитудные функции совпадают, т.е. А01 = А02 = А0; y
02 = ±
p
/2 Согласно (18) будем иметь пару голограмм:
|
U2 = А20 + A2 + 2А0АСоs(y
- y
01)
V2 = А20 + A2 ±
2А0АСоs(y
- y
01) |
(19) |
Рассматривая (19) как систему уравнений относительно А и y
, получим
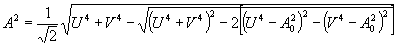 (20) (20)
y = y
01 + y 1 y
2 (21) y
2 (21)
|
где |
y
1=arcCos |
V2-A2-A20 |
y
2=arcSin |
V2-A2-A20 |
(22) |
|
±
2A0A |
±
2A0A |
Знак пересечения множеств в (21) означает, что из двух пар
- 137 -
значений углов y
1,2, определяемых (22), следует добавить к y
01 сов падающее значение. Формулы (20)-(22) однозначно определяют величины А и y
. Следовательно, условие леммы достаточно. Две записи (19) оправданно называть квадратурными голограммами; этим термином мы будем в дальнейшем пользоваться.
Обратим внимание на то, что квадратурные голограммы принципиально позволяют найти функции А и y
без каких-либо ограничений как самих функций, так и функций А и y
.
Для доказательства необходимости условия леммы допустим, что опорные колебания U01 и U02 отличаются только амплитудными функциями А01 и А02 ( y
01 = y
02 = y
0). Тогда получим голограммы:
|
U21 = А201 + A2 + 2А01АСоs(y
- y
0)
U22 = А202 + A2 + 2А02АСоs(y
- y
0) |
(23) |
Рассматривая (23) как систему уравнений, можно однозначно определить функции А и Cos(y
- y
0). Что же касается фазовой функции y
, то ее нельзя определить однозначно по известному значению косинуса. Следовательно, условие леммы и необходимо.
Лемма остается справедливой и при записи с "искусственной опорной волной" и фазовых детекторов. В этом случае измеряются величины:
U = А0АСоs(y
-y
01); V = А0АСоs(y
-y
02) (24)
Достаточно принять A01 = А02 и y
02 = y
01 ±
p
/2. Тогда
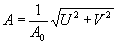 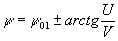 (25) (25)
Некоторые схемы получения квадратурных голограмм и их использования для физического восстановления волн приводятся в работах / 3-5/.
Предположим теперь, что источники регистрируемого поля Е ,Н расположены внутри конечной области Vвн (рис.3). Окружим эту область замкнутой поверхностью S. Среда внутри S может быть
- 138 -
неизвестной, а вне S
задана (либо в виде данных о параметрах 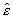 и
и 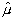 ,
либо "физически"). Как внутри, так и вне поверхности S
могут существовать поверхности разрыва непрерывности параметров ,
либо "физически"). Как внутри, так и вне поверхности S
могут существовать поверхности разрыва непрерывности параметров 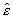 и
и  ,
в том числе границы идеально проводящих тел. Тогда имеет место следующая теорема
существования и единственности. ,
в том числе границы идеально проводящих тел. Тогда имеет место следующая теорема
существования и единственности.
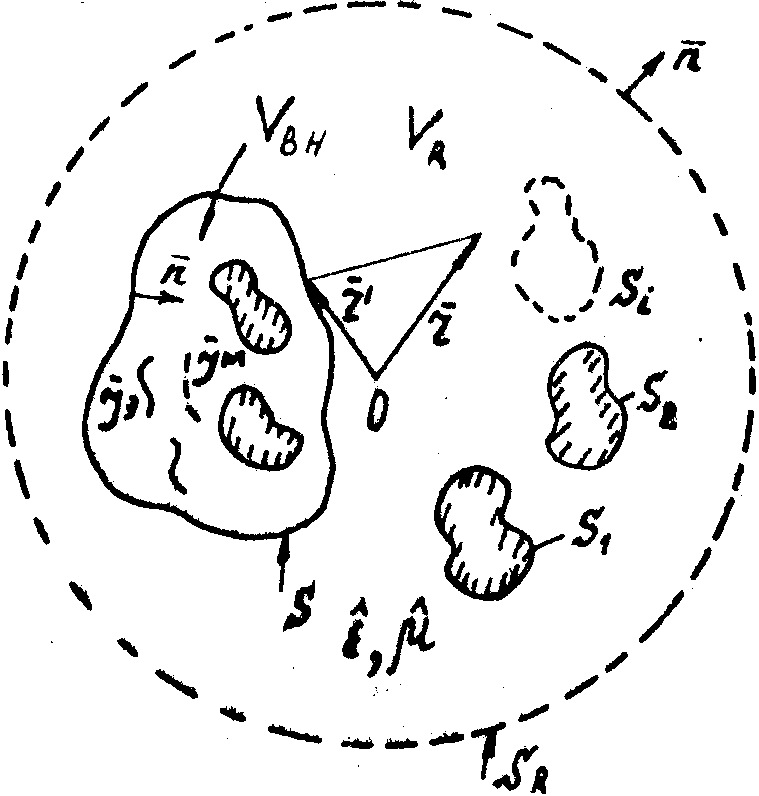
Рис.3. К Доказательству теоремы I.
Теорема 1
Для возможности полного восстановления монохроматического волнового поля в любой точке вне замкнутой поверхности S в линейной стационарной среде без пространственной дисперсии, необходимо и достаточно зарегистрировать на поверхности S две пары квадратурных голограмм.
Доказательство. Для доказательства достаточности приценки обобщенную лемму Лоренца (15) к внешнему объему V, ограниченному поверхностью S, поверхностями идеально проводящих тел Si и сферической поверхностью SR достаточно большого радиуса R (рис.3).
- 139 -
Интегрируя (15) по объему V, , получим
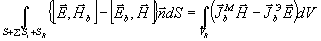 (26) (26)
где  - вектор внешней нормали к поверхности SS
= S+ S Si + SR.
По отношению к поверхности S
и Si,
взятым в отдельности, нормаль будет внутренней.
- вектор внешней нормали к поверхности SS
= S+ S Si + SR.
По отношению к поверхности S
и Si,
взятым в отдельности, нормаль будет внутренней.
Предположим теперь, что вспомогательное поле создается только
электрическим током 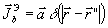 ,
т.е. элементарным диполем, расположенным в объеме VR
в точке с радиусом-вектором ,
т.е. элементарным диполем, расположенным в объеме VR
в точке с радиусом-вектором 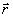 ,
и удовлетворяет на поверхности S
и тех из поверхностей Si,
которые соответствуют идеальным электрическим проводникам, граничному условию ,
и удовлетворяет на поверхности S
и тех из поверхностей Si,
которые соответствуют идеальным электрическим проводникам, граничному условию
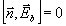 .
На поверхностях же Si,
соответствующих идеальным магнитным проводникам, пусть выполняется граничное
условие .
На поверхностях же Si,
соответствующих идеальным магнитным проводникам, пусть выполняется граничное
условие 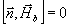 .
Кроме того, положим R®
¥ и учтем,
что в любой реальной среде поля .
Кроме того, положим R®
¥ и учтем,
что в любой реальной среде поля 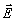 и
и 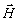 при r® ¥
убывают быстрее,
чем 1/r.
Тогда получим
при r® ¥
убывают быстрее,
чем 1/r.
Тогда получим
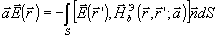 (27) (27)
где 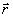 ’
- радиус-вектор точки интегрирования; ’
- радиус-вектор точки интегрирования; 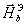 - вспомогательное магнитное поле электрического
диполя в транспонированной среде, при условии выполнения перечисленных выше
граничных условий.
- вспомогательное магнитное поле электрического
диполя в транспонированной среде, при условии выполнения перечисленных выше
граничных условий.
Полагая теперь 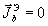 и
и 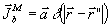 и меняя местами
и меняя местами 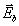 и
и 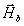 в граничных условиях, найдем
в граничных условиях, найдем
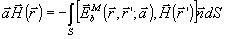 (28) (28)
Введем на поверхности S
систему координат, характеризуемую в каждой точке единичными векторами 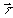 и
и 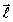 ,
касательными к поверхности S,
образующими вместе с вектором внешней нормали (вектором ,
касательными к поверхности S,
образующими вместе с вектором внешней нормали (вектором 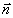 )
правовинтовую тройку. Тогда соотношения (27)
и (28) перепишутся
в виде: )
правовинтовую тройку. Тогда соотношения (27)
и (28) перепишутся
в виде:
- 140 -
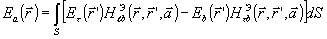 (29) (29)
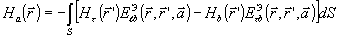 (30) (30)
где Ea
и На -
означают компоненты векторов 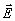 и
и  в направлении вспомогательного вектора
в направлении вспомогательного вектора 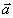 .
Придавая .
Придавая 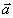 соответствующие направления, можно определить все компоненты векторов
соответствующие направления, можно определить все компоненты векторов
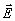 и
и  .
Соотношения
(29) и (30)
показывают, что в рассматриваемом общем случав поле в любой точке вне поверхности
S полностью определяется касательной составляющей
любого из векторов .
Соотношения
(29) и (30)
показывают, что в рассматриваемом общем случав поле в любой точке вне поверхности
S полностью определяется касательной составляющей
любого из векторов 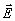 или
или  на этой поверхности. Если, например, известно поле
на этой поверхности. Если, например, известно поле 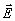 ,
то поле ,
то поле  определится из соотношения
определится из соотношения 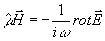 ,
в обратном случае поле ,
в обратном случае поле 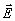 определится из соотношения
определится из соотношения 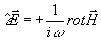 . .
Учитывая (6) можно записать эти соотношения в виде равенств:
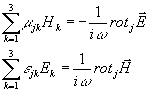 j =
1,2,3 (31) j =
1,2,3 (31)
которые представляют собой системы линейных алгебраических уравнений относительно неизвестных компонент Нк или Ек . Справа фигурируют соответствующие компоненты ротора. Далее имеем:
|
Et
= A Эt
exp[iy
Эt
] |
Eℓ = A Эℓexp[iy
Эℓ] |
(32) |
|
Ht
= AMt
exp[iy
Mt
] |
Hℓ = AMℓexp[iy
Mℓ] |
Согласно лемме 1, для определения функций АЭt
, АЭℓ, y
Эt
, y
Эℓ необходимо и достаточно зарегистрировать две пары квадратурных голограмм на поверхности S. Тоже относится и к функциям, определяющим магнитное поле. А так как достаточно определить одно из
- 141 -
касательных полей: электрическое или магнитное, то условие теоремы выполняется. Мы доказали, таким образом, достаточность условия теоремы для существования решения. Докажем теперь, что при этом обеспечивается и единственность восстановления поля вне S.
С помощью квадратурных голограмм функции АЭ ℓ,t
и y
Эℓ,t
определяются однозначно, следовательно,
однозначно определяются компоненты Еℓ,
Еt на S.
Они, в свою очередь, однозначно определяют поле
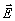 в любой точке вне S.
Действительно, допустим, что некоторому распределению Еℓ
и Еt по S
соответствует два разных поля
в любой точке вне S.
Действительно, допустим, что некоторому распределению Еℓ
и Еt по S
соответствует два разных поля 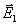 и
и 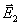 .
Оба эти поля должны удовлетворять соотношению
(29), где справа стоят одни и те же функции
Еℓ
и Еt . После вычитания справа получим нуль (в
силу линейности оператора (29),
следовательно, .
Оба эти поля должны удовлетворять соотношению
(29), где справа стоят одни и те же функции
Еℓ
и Еt . После вычитания справа получим нуль (в
силу линейности оператора (29),
следовательно, 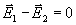 .
Индукция .
Индукция 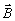 однозначно определяется через
однозначно определяется через 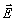 соотношением
соотношением 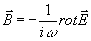 .
Вектор .
Вектор 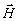 в некоторых средах неоднозначно связан с вектором
в некоторых средах неоднозначно связан с вектором 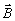 (явление гистерезиса). Однако, если напряженность поля такова, что среду можно
считать линейной, то при этом обеспечивается и однозначная связь векторов
(явление гистерезиса). Однако, если напряженность поля такова, что среду можно
считать линейной, то при этом обеспечивается и однозначная связь векторов 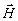 и
и 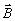 .
Те же рассуждения справедливы и в случае определения компонент Нℓ .
Те же рассуждения справедливы и в случае определения компонент Нℓ,
Нt на S.
Необходимость условия теоремы доказывается элементарно. Предположим, что регистрируется не четыре голограммы, а только три. Тогда какая-либо из функций А , y
определится неоднозначно и решение задачи восстановления не будет единственным. Отсюда и следует необходимость условия теоремы для полного восстановления.
В заключение мы поясним необходимость ограничения средами, свободными от пространственной дисперсии. Если среда обладает пространственной дисперсией, т.е. имеет место, по крайней мере, одно из соотношений (4), то формулы (15), (26)-(30) перестают быть действительны и, следовательно, условие теоремы не выполняется. Покажем это в предположении, что имеет место пространственная дисперсия электрического поля. В этом случае мы обязаны исходить из соотношения (14). При интегрировании по объему VR появится дополнительное слагаемое
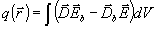 (35) (35)
- 142 -
не равное нулю и зависящее от распределения вектора 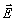 по объему VR.
В самом деле, учитывая (4),
а также тот факт, что
по объему VR.
В самом деле, учитывая (4),
а также тот факт, что 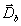 определяется в транспонированной среде, нетрудно привести
(35) к виду
определяется в транспонированной среде, нетрудно привести
(35) к виду
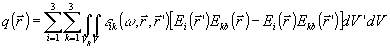 (34) (34)
Так как объемы V
и VR
не совпадают, то даже при симметрии функций e
ik
по переменным 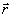 и
и 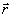 '
интегралы не равны тождественно нулю. '
интегралы не равны тождественно нулю.
Таким образом, при наличии пространственной дисперсии, строго говоря, поле должно регистрироваться не только на поверхности S, но и во всех точках объема VR.
Несмотря на это, теорема 1
может быть использована для приближенного решения внешней задачи восстановления
в голографии и при наличии пространственной дисперсии среды. Это следует из
того факта, что практически функции e ik( w
, 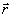 , 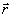 ’)
и m ik ’)
и m ik( w
, 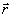 , 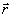 ')
быстро убывают при увеличении расстояния между точками с радиусами-векторами ')
быстро убывают при увеличении расстояния между точками с радиусами-векторами
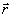 и
и 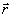 ’.
Иначе говоря, индукция в точке ’.
Иначе говоря, индукция в точке 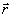 определяется напряженностью поля в этой точке и в точках, принадлежащих лишь
некоторой ее окрестности с эффективным "радиусом дисперсии". Этот радиус всегда
можно выбрать таким, чтобы влиянием точек, не принадлежащих окрестности, можно
было пренебречь. Следовательно, если точка наблюдения с радиусом вектором
определяется напряженностью поля в этой точке и в точках, принадлежащих лишь
некоторой ее окрестности с эффективным "радиусом дисперсии". Этот радиус всегда
можно выбрать таким, чтобы влиянием точек, не принадлежащих окрестности, можно
было пренебречь. Следовательно, если точка наблюдения с радиусом вектором 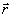 удалена от поверхности S
на расстояние большее, чем эффективный "радиус дисперсии", то значение функции
q(
удалена от поверхности S
на расстояние большее, чем эффективный "радиус дисперсии", то значение функции
q(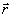 )
будет пренебрежимо малым и поле по-прежнему будет определяться лишь касательными
составляющими )
будет пренебрежимо малым и поле по-прежнему будет определяться лишь касательными
составляющими 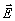 ,
либо ,
либо 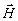 на S, т.е.
потребуется зарегистрировать две пары квадратурных голограммы на поверхности
S.
на S, т.е.
потребуется зарегистрировать две пары квадратурных голограммы на поверхности
S.
Рассмотрим теперь два следствия, вытекающие из теоремы.
Следствие 1. Для внешнего физического восстановления поля в линейной среде необходимо и достаточно восстановить во всех точках поверхности S касательную составляющую электрического или магнитного поля.
Нетрудно видеть, что именно это и осуществляется с некоторой степенью точности в любой практической схеме голографии. Для этого используется различные пространственные модуляторы поля восстанавливающего
- 143 -
источника: неоднородные слои с записью интерференционного поля, модулированные отражающие поверхности и т.п. Тот факт, что вне поверхности S возникнет полз, которое имело место при регистрации, следует из единственности решения внешней задачи восстановления. Рассматриваемое; следствие является основным теоретическим положением голографии для линейных стационарных сред.
Рассмотрим несколько подробное процесс физического восстановления на практике.
Ясно, что идеальным был бы такой способ, который позволяет непосредственно получить в каждой точке поверхности S требуемое значение амплитуды и фазы касательных составляющих поля. На практике приблизиться к такому способу удается лишь в диапазоне достаточно длинных волн (радио, акустика) путем использования решетки управляемых излучателей. Регулируя амплитуду и фазу питания излучателей и выбрав надлежащим образом их поляризацию, можно с большей степенью точности реализовать требуемое распределение касательных составляющих поля на S. Однако наибольший интерес физическое восстановление представляет для оптического диапазона, где такой способ практически не удается реализовать и приходится идти по пути использования пространственных модуляторов света. Чаще всего их роль выполняют неоднородные; слои с записью интерференционного поля, т.е. голограммы в узкой смысле этого слова. При дифракции восстанавливающей волны на таких слоях на границе возникает распределение касательных составляющих поля, которое содержит требуемое распределение в качестве полезной компоненты. Наиболее выражена эта компонента в случае толстых слоев "объемных голограмм"). Естественно, что более просто решается задача восстановления одного фазового распределения касательных составляющих. Однако, это допустимо лишь при равномерности амплитудного распределения. Этим отчасти можно объяснить широкое использование в голографии голограмм Френеля, но не Фурье.
Требования теоремы 1 на практике обычно выполняются лишь частично, что является причиной погрешностей восстановления зарегистрированного поля. Чаще всего они вызываются следующими факторами:
- игнорированием векторного характера поля;
- использованием одной топографической записи вместо пары
- 144 -
квадратурных ;
- незамкнутостыо поверхности регистрации;
- дискретностью голограммы.
Это причины принципиального характера. К ним можно еще добавить причины, обусловленные несовершенством техники записи, в частности:
- неполная когерентность и монохроматичность полей;
- несовершенство регистрирующих сред;
- дифракционные явления в модуляторе восстанавливающей волны и другие.
Следствие 2. Для математического восстановления поля 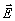 , ,
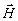 вне поверхности регистрации S
необходимо найти поля
вне поверхности регистрации S
необходимо найти поля 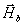 и
и 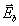 ,
создаваемые вспомогательными диполями в транспонированной
среде, а затем воспользоваться интегральными представлениями поля через касательные
составляющие на S,
которые определяются с помощью голограммы. Наиболее простые выражения для нахождения
поля ,
создаваемые вспомогательными диполями в транспонированной
среде, а затем воспользоваться интегральными представлениями поля через касательные
составляющие на S,
которые определяются с помощью голограммы. Наиболее простые выражения для нахождения
поля 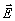 , ,
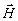 ,
имеющие вид (27), (28),
получаются в том случае, когда вспомогательные поля удовлетворяют нулевым граничным
условиям на S
и Si. Однако
при этом сами вспомогательные поля определить наиболее трудно, в особенности,
в анизотропной среде, так как приходится решать краевую задачу дифракции сферической
волны на идеально проводящих поверхностях, совпадающих с S
и Si.
Максимально просто вспомогательные поля определяются в однородном пространстве,
когда налагается лишь требование, подобное условию излучения на бесконечности,
т.е. выделяются волны, уходящие от диполя, но не сходящиеся к нему. Но зато
при этом интегральные представления для полей в точке наблюдения вне S
становятся более сложными, чем (27)
и (28). Так как теперь ,
имеющие вид (27), (28),
получаются в том случае, когда вспомогательные поля удовлетворяют нулевым граничным
условиям на S
и Si. Однако
при этом сами вспомогательные поля определить наиболее трудно, в особенности,
в анизотропной среде, так как приходится решать краевую задачу дифракции сферической
волны на идеально проводящих поверхностях, совпадающих с S
и Si.
Максимально просто вспомогательные поля определяются в однородном пространстве,
когда налагается лишь требование, подобное условию излучения на бесконечности,
т.е. выделяются волны, уходящие от диполя, но не сходящиеся к нему. Но зато
при этом интегральные представления для полей в точке наблюдения вне S
становятся более сложными, чем (27)
и (28). Так как теперь 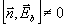 на S, то согласно
(26), получим
на S, то согласно
(26), получим
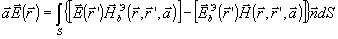 (35) (35)
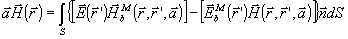 (36) (36)
где 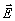 Эb Эb,
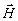 Эb Эb,
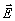 Mb Mb,
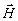 Mb Mb
- поля, создаваемые электрическим и магнитными
диполями в безграничной транспонированной среде. Важно
- 145 -
подчеркнуть, что представления
(35), (36) справедливы только в случае отсутствия
вне S идеально
проводящих тел с поверхностями Si.
Выражения (35),
(36) менее удобны, чем (27), (28),
так как в них фигурируют касательные составляющие векторов 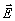 и
и 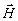 на S одновременно.
Если путем голографирования найдено распределение на
S только одного из. полей: электрического либо
магнитного, то второе может быть найдено с помощью соотношений
(31), учитывая которые, можно записать
(35) и (36)
в виде
на S одновременно.
Если путем голографирования найдено распределение на
S только одного из. полей: электрического либо
магнитного, то второе может быть найдено с помощью соотношений
(31), учитывая которые, можно записать
(35) и (36)
в виде
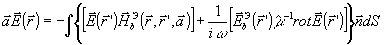 (37) (37)
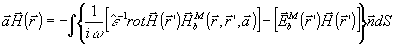 (38) (38)
где через 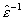 и
и 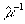 обозначены тензоры с матрицами, обратными матрицам
обозначены тензоры с матрицами, обратными матрицам
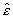 и
и 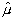 . .
Методика определения полей излучения диполей в произвольной линейной анизотропной и однородной среде изложена в работе /6/, которую можно использовать для нахождения вспомогательных полей, фигурирующих в (35)-(38).
Особый практический интерес представляет случай, когда поверхность
регистрации S
есть бесконечная плоскость и вне S
(для конкретности в правом полупространстве) среда однородна и отсутствуют идеально
проводящие тела. Этот случай наиболее близок к типичным реальным условиям голографирования.
В этом случае можно воспользоваться соотношениями
(27) и (28),
определив вспомогательные поля в предположении,
что плоскость S
есть поверхность идеального проводника: электрического или магнитного. В случае
анизотропной среды это можно сделать, используя методику, изложенную в
Ввиду громоздкости получающихся формул и необходимости
конкретизации тензоров 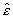 и
и 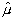 мы не .будем рассматривать здесь случай анизотропной среды и ограничимся лишь
случаем изотропной среды. Для простоты рассмотрим получение точных интегральных
представлений электрического поля. Формулы для магнитного поля легко получить
по аналогии. Пусть поверхность регистрации
S есть плоскость z=0,
а правое
мы не .будем рассматривать здесь случай анизотропной среды и ограничимся лишь
случаем изотропной среды. Для простоты рассмотрим получение точных интегральных
представлений электрического поля. Формулы для магнитного поля легко получить
по аналогии. Пусть поверхность регистрации
S есть плоскость z=0,
а правое
- 146 -
полупространство соответствует Z > 0. Тогда соотношение (29) запишется в виде
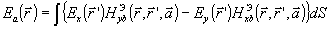 (39) (39)
где магнитное поле вспомогательного диполя, расположенного
в точке наблюдения, должно определяться на S
в предположении, что плоскость является идеальным электрическим проводником.
Поле вспомогательного электрического диполя, расположенного в точке с координатами
х,у,z.
в безграничной однородной и изотропной среде, ориентированного вдоль вектора
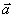 ,
определяется формулами /2/ ,
определяется формулами /2/
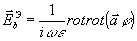 (40) (40)
где
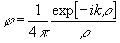 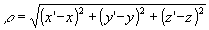
Координаты х ,у,z соответствуют точке наблюдения. Заменяя идеально проводящую плоскость изображением диполя, получим:
|
H Эxb = 0 |
H Эyb = |
¶
j
- |
при 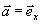
|
(41) |
|
¶
z’ |
|
|
|
H Эxb = - |
¶
j
- |
H Эyb = 0 |
при 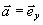
|
(42) |
|
¶
z’ |
|
|
H Эxb = |
¶
j
+ |
H Эyb = - |
¶
j
+ |
при 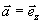
|
(43) |
|
¶
y’ |
¶
x |
Здесь обозначено
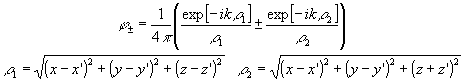 (44) (44)
При подстановке выражений (41)-(44) в (39) необходимо положить
- 147 -
Z’® 0.
В результате получаем следующие точные интегральные представления для компонент
поля 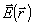 при Z > 0:
при Z > 0:
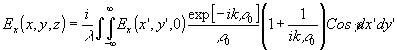 (45) (45)
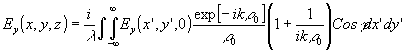 (46) (46)
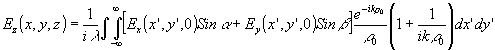 (47) (47)
где
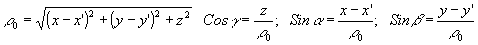
Эти соотношения можно представить и в иной эквивалентной форме
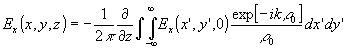 (48) (48)
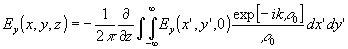 (49) (49)
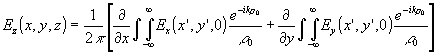 (50) (50)
При r
0 >> l
слагаемым 1/ikr
0 в (45)-(47) можно пренебречь. Если, кроме того, область D плоскости z = 0, за пределами которой можно пренебречь значениями Eх(х’,у’,0) и Ey(х’,у’,0), имеет ограниченные размеры, то в точках наблюдения, для которых
|
|
x – x‘|
|
<< 1 |
|
y – y’|
|
<< 1 |
|
r
0 |
r
0 |
будем иметь
- 148 -
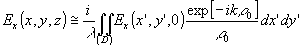 (51) (51)
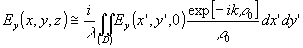 (52) (52)
Ez(x,y,z) @
0 (53)
Таким образом, при сделанных предположениях точные формулы (45)-(47) переходят в приближенные представления Гюйгенса-Кирхгофа. В оптике это соответствует рассмотрению параксиальных пучков.
Если голографическим методом найдены составляющие EX и EУ на плоскости z = 0, то по формулам (45)-(50) можно полностью рассчитать поле в любой точке z > 0.
К сожалению, расчет поля по этим формулам требует значительных затрат машинного времени. В этой связи целесообразно использовать также эквивалентные спектральные представления поля, удобные для применения алгоритма быстрого преобразования Фурье. Подставляя в (48)-(50) разложение сферической волны в интеграл Фурье
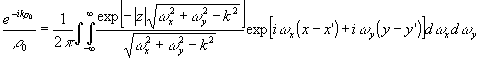 (54) (54)
и выполняя дифференцирование, получим для любой из компонент Е X, ЕУ, EZ при Z > 0 представление
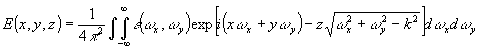 (55) (55)
где e
(w
x,w
y) - пространственно частотный спектр компоненты на плоскости z = 0, определяемый формулами
- 149 -
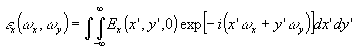 (56) (56)
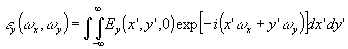 (57) (57)
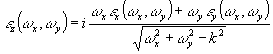 (58) (58)
Аналогичные, но более громоздкие, представления можно получить и в случае однородной анизотропной среды.
3. Дискретизация поля при голографической регистрации
При рассмотрении теоремы существования и единственности решения внешней задачи голографии мы предполагали, что используется непрерывная голографическая регистрация касательных составляющих поля на поверхности s . На практике может применяться дискретная регистрация в отдельных точках поверхности S . Такая регистрация характерна для радиоголографии и акустической голографии. В оптическом диапазоне с дискретизацией мы сталкиваемся главным образом при получении математических голограмм, синтезируемых на вычислительных машинах.
Восстановление поля по дискретным голограммам эквивалентно восстановлению по дискретным отсчетам его касательных составляющих на поверхности S и является процессом интерполяции. Этот процесс неизбежно сопровождается погрешностью, которая зависит от числа и расположения точек отсчета, а также алгоритма восстановления. Поэтому первостепенное значение имеет вопрос о сходимости интерполяционного процесса, т.е. о возможности получения сколь угодно малой погрешности аппроксимации волнового поля в любой точке пространства путем увеличения числа точек отсчета на поверхности S. Ниже мы рассмотрим теорему, которая определяет общие требования к
- 150 -
множеству точек отсчета, обеспечивающие выполнение этого условия. Одновременно мы получим оптимальный алгоритм восстановления волнового поля, обеспечивающий минимум погрешности аппроксимации при выбранном множестве точек отсчета, который включает в себя известное разложение в ряд Котельникова в качестве частного случая.
Будем в дальнейшем предполагать, что s есть неограниченная поверхность, не обязательно плоская. Можно считать, что замыкание поверхности происходит на бесконечности. Условимся для конкретности осуществлять замыкание слева.
Введем на S координаты x
,h
(рис.4) и предположим, что поле на S имеет интегрируемый с квадратом финитный пространственно-частотный спектр, отличный от нуля лишь в области Dw
. Это означает, что любая из компонент вектора E(x
,h
) может быть представлена в виде
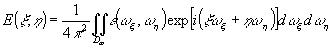 (59) (59)
В дальнейшем нам удобнее будет пользоваться более компактной записью (59)
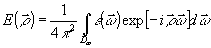 (60) (60)
где вектора  и
и 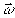 имеют компоненты {x ,h
} и {w x
,w h
}, соответственно, а
e (
имеют компоненты {x ,h
} и {w x
,w h
}, соответственно, а
e (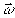 )
- пространственно-частотный спектр компоненты
поля такой, что e Î
L2(Dw
) )
- пространственно-частотный спектр компоненты
поля такой, что e Î
L2(Dw
)
Идеализация, которую мы при этом вводим, имеет тот же характер, что и широко используемая в теории сигналов.
Если S - плоскость z = 0, то согласно (55),можно написать более общее представление
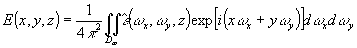 (61) (61)
где
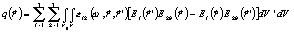 (62) (62)
- 151 -
Рис.4.
Поверхность дискретной регистрации поля.
Из (61) и (62) следует, что если спектр поля отличен от нуля только в области Dw
на плоскости z = 0, то это свойство сохраняется для любой другой плоскости z = Const, z > 0. Это легко объяснить, физически учитывая, что (61) есть разложение поля по плоским волнам. Ограниченность области Dw
соответствует ограничению углов, которые образуют направления распространения плоских волн с осью z. Эти углы, естественно, не зависят от z. Обозначим множество точек отсчета при регистрации дискретных голограмм через М. Имеет место следующая теорема.
Теорема 2
Для возможности сколь угодно точного восстановления поля в любой точке пространства вне замкнутой поверхности S, включая границу, с помощью дискретных голограмм в линейной стационарной среде без пространственной дисперсии необходимо и достаточно
- 152 -
зарегистрировать на S
две пары квадратурных голограмм, выбирая множество M
точек отсчета { k}
так, чтобы система функций k}
так, чтобы система функций
{exp[-i k k ]} ]}
была полной в пространстве L2(Dw
); для любой конечной области Dw
подобные множества точек отсчета существуют.
Доказательство. Согласно лемме
1, для однозначного определения касательных
составляющих поля 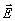 (либо
(либо 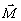 )
на поверхности S
в точках отсчета необходимо и достаточно использовать две пары дискретных квадратурных
голограмм. Таким образом, доказательство теоремы сводится по существу к доказательству
второй ее части, касающейся выбора множества точек отсчета M.
Предположим, что дискретные значения касательных составляющих поля )
на поверхности S
в точках отсчета необходимо и достаточно использовать две пары дискретных квадратурных
голограмм. Таким образом, доказательство теоремы сводится по существу к доказательству
второй ее части, касающейся выбора множества точек отсчета M.
Предположим, что дискретные значения касательных составляющих поля 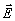 на S: Et (
на S: Et ( k)
и Eℓ( k)
и Eℓ( k)
определены по дискретным голограммам с помощью формул (20)-(22) или
(24), (25). Введем некоторое конечное подмножество
точек отсчета MN Î
М MN
® M при
N ® ¥ )
и рассмотрим достаточность условия теоремы. Для этого аппроксимируем функцию
e ( k)
определены по дискретным голограммам с помощью формул (20)-(22) или
(24), (25). Введем некоторое конечное подмножество
точек отсчета MN Î
М MN
® M при
N ® ¥ )
и рассмотрим достаточность условия теоремы. Для этого аппроксимируем функцию
e (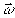 )
в области Dw
суммой )
в области Dw
суммой
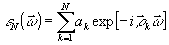 (63) (63)
определяя коэффициенты ak из условия минимума среднеквадратичной погрешности приближения, т.е.
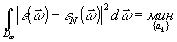 (64) (64)
Решение задачи (64) всегда существует для любого конечного N и определяется путем подстановки (63) в (64) и приравнивания нулю частных производных по всем ak*, где звездочка означает комплексное сопряжение */
В результате получаем
*/ Так как ak в общей случае комплексные, то следует дифференцировать по ak и ak*. Однако это приводит к эквивалентным системам уравнений, поэтому достаточно дифференцировать по ak*.
- 153 -
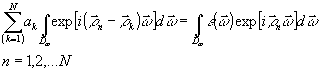 (65) (65)
Введя в рассмотрение функцию
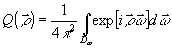 (66) (66)
и учитывая, что правые части (65) равны EfPn) , найден
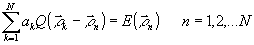 (67) (67)
Подставляя (63) в (60), получим интерполяционный многочлен
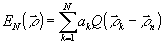 (68) (68)
где коэффициенты ak
определяются путем решения системы линейных алгебраических уравнений
(67), в общем случае комплексный. Полагая в
(68)  = =  n
и учитывая (67),
находим, что EN( n
и учитывая (67),
находим, что EN( n)
= E( n)
= E( n) n=1,2,...N. n) n=1,2,...N.
Цели система функций {exp[-i k k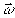 ]}
полная относительно Lk(Dw
), то при
n® ¥
суммы (65)
сходятся в средней к e
( ]}
полная относительно Lk(Dw
), то при
n® ¥
суммы (65)
сходятся в средней к e
( ),
осуществляя наилучшее приближение в метрике этого пространства. ),
осуществляя наилучшее приближение в метрике этого пространства.
Так как ядро exp[i 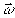 )
равномерно ограничено при всех )
равномерно ограничено при всех  и
и 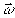 ,
то сходимость e N ,
то сходимость e N( 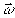 )
в среднем к e
(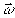 )
означает равномерную сходимость EN( )
означает равномерную сходимость EN( )
к E( )
к E( )на
всей поверхности S.
Кроме того, имеет место и наилучшее приближение в среднем EN( )на
всей поверхности S.
Кроме того, имеет место и наилучшее приближение в среднем EN( )
к E( )
к E( )
на S.
Последнее следует из (64)
и равенства Парсеваля, примененного к разности
E( )
на S.
Последнее следует из (64)
и равенства Парсеваля, примененного к разности
E( ) – EN( ) – EN( ),
a именно ),
a именно
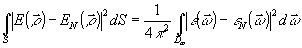 (69) (69)
В этом смысла построенный алгоритм (67), (68) восстановления
- 154 -
касательных составляющих на s
no их дискретным отсчетам на заданном множестве
точек ( k)
можно считать оптимальным, так как он обеспечивает Минимум погрешность аппроксимации. k)
можно считать оптимальным, так как он обеспечивает Минимум погрешность аппроксимации.
Аппроксимируя касательные составляющие
Et ( )
и Eℓ( )
и Eℓ( )
вектора )
вектора 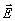 на S с помощью
рядов вида (68)
и подставляя в (29),
получим
на S с помощью
рядов вида (68)
и подставляя в (29),
получим
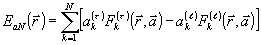 (70) (70)
где
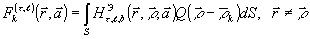 (71) (71)
Коэффициенты ak(t
,ℓ) определяются из решения систем линейных уравнений
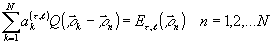 (72) (72)
Так как при 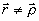 ядра HЭt
,ℓ,b
равномерно ограничены по модулю, то, учитывая равномерную сходимость EN(
ядра HЭt
,ℓ,b
равномерно ограничены по модулю, то, учитывая равномерную сходимость EN( )
к E( )
к E( ),
можно утверждать, что суммы (70)
также равномерно сходятся к Ea( ),
можно утверждать, что суммы (70)
также равномерно сходятся к Ea( )
при N® ¥
. Следовательно, многочлен
(70) позволяет путем увеличения числа точек
отсчета n
сколь угодно точно восстановить поле )
при N® ¥
. Следовательно, многочлен
(70) позволяет путем увеличения числа точек
отсчета n
сколь угодно точно восстановить поле 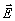 в любой точке пространства вне поверхности
S по дискретным отсчетам касательных составляющих.
Таким образом, условие достаточности доказано. Одновременно мы построили оптимальный
алгоритм внешнего восстановления поля по дискретным отсчетам, взятым на заданном
множестве точек.
в любой точке пространства вне поверхности
S по дискретным отсчетам касательных составляющих.
Таким образом, условие достаточности доказано. Одновременно мы построили оптимальный
алгоритм внешнего восстановления поля по дискретным отсчетам, взятым на заданном
множестве точек.
Необходимость условия ,теоремы доказывается проще. Предположим,
что система {exp[-i k k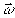 ]}
не является полной. Тогда найдется такая функция y
(w )¹
0, принадлежащая L2(Dw
), что имеют место равенства ]}
не является полной. Тогда найдется такая функция y
(w )¹
0, принадлежащая L2(Dw
), что имеют место равенства
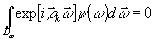 k = 1,2,… (66) k = 1,2,… (66)
- 155 -
Рассмотрим спектр 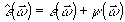 ,
которому соответствует функция ,
которому соответствует функция
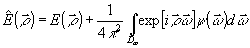 (66) (66)
В силу (73) 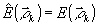 ,
k=1,2,..., т.е. функции ,
k=1,2,..., т.е. функции 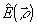 и Е(
и Е( )
совпадают в точках отсчета. В остальных точках они отличаются. Следовательно,
при отсутствии полноты по дискретный отсчетам можно восстановить две разные
функции: )
совпадают в точках отсчета. В остальных точках они отличаются. Следовательно,
при отсутствии полноты по дискретный отсчетам можно восстановить две разные
функции: 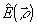 и Е(
и Е( ),
т.е. восстановление будет неоднозначный. Таким образом, полнота системы ),
т.е. восстановление будет неоднозначный. Таким образом, полнота системы
{exp[-i k k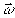 ]} ]}
необходима.
Остается доказать существование множеств { k},
обеспечивающих полноту системы при любой форме конечной области Dw
, которая может быть как односвязной, так и
многосвязной. Для этого достаточно привести хотя бы один пример соответствующего
множества. Заметим предварительно, что если система полная в некоторой области k},
обеспечивающих полноту системы при любой форме конечной области Dw
, которая может быть как односвязной, так и
многосвязной. Для этого достаточно привести хотя бы один пример соответствующего
множества. Заметим предварительно, что если система полная в некоторой области
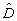 w
, включающей в себя Dw
(Dw С w
, включающей в себя Dw
(Dw С 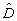 w
), то она полная и в Dw
. Выберем в качестве w
), то она полная и в Dw
. Выберем в качестве 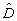 w
прямоугольник, содержащий в себе Dw
, причем w
x Î [-w
m1,w m1], w
h Î [-w
m2,w m2],
где w m1
и w m2
- максимальные пространственные частоты в спектре e
(w )
по осям x и h
. Определим
отсчетные точки координатами x r w
прямоугольник, содержащий в себе Dw
, причем w
x Î [-w
m1,w m1], w
h Î [-w
m2,w m2],
где w m1
и w m2
- максимальные пространственные частоты в спектре e
(w )
по осям x и h
. Определим
отсчетные точки координатами x r=d 1·r,
h S=d 2·S, r,S=±1; ±2,...,
где d1£
p /w m1,
d2 £ p
/w m1
- шаг дискретизации по осям x и h
. Система
функций {exp[-i(x
rw x +h
Sw h ]}
будет полной в замкнутом прямоугольнике, так как системы {exp[-ix
rw x ]}
и {exp[-ih
Sw h ]}
являются полными на отрезках [-w m1, w
m1],
[-w
m2,w
m2], соответственно. Следовательно, множество точек отсчета с координатами x
=d1r и h
=d2S обеспечивает полноту системы в области Dw
.
В заключение отметим, что дискретизация магнитного поля может быть осуществлена по аналогии.
Следствие 1. При дискретной голографической регистрации поля на поверхности s математическое восстановление его в любой точке пространства вне этой поверхности может быть осуществлено двумя способами: 1) компоненты поля восстанавливаются во всех
- 156 -
точках поверхности S по дискретным отсчетам с помощью формул (67) и (68), а затем используется интегральное представление (29); 2) поле в произвольной точке вне S определяется по формулам (70)-(72) непосредственно через отсчеты, сделанные; на поверхности регистрации, для восстановления же поля в произвольных точках поверхности s используются формулы (67), (68). Хотя выше мы отметили представление (29), фактически для внешнего восстановления поля по дискретным отсчетам могут быть использованы любые его интегральные представления через касательные составляющие на поверхности регистрации: (29), (37), (45)-(47) и т.п.
Рассмотрим применение сформулированных выше способов восстановления в наиболее важном для практики случае плоской поверхности s и однородного и изотропного полупространства. В этом случае при восстановлении по первому способу целесообразнее определять не компоненты поля ЕХ(х’,у’,0), Ey(x’,y’,0) по дискретным отсчетам, а их спектры по формулам
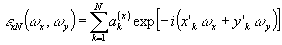 (75) (75)
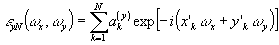 (76) (76)
где в соответствии с (67) коэффициенты а(x)k, а(y)k определяются из решения систем
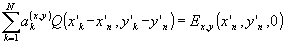 ; n=1,2,...N
(77) ; n=1,2,...N
(77)
причем
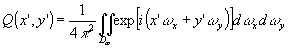 (78) (78)
Подставляя рассчитанные по (75)-(78) функции e
xN и e
yN в (55) и (58) к применяя алгоритм быстрого преобразования Фурье, можно вычислить все три компоненты поля Еx, Еy, E z в любой точке
- 157 -
правого полупространства, включая и плоскость регистрации z = 0. Аналитические выражения функции Q(х’,у’) могут быть получены для многих областей Dw
Формулы (70)-(72) для восстановления поля по второму способу проще всего получить, подставляя спектральные функции (75), (76) в (61), (62) и учитывая (58). В результате будем иметь при Z ³
0
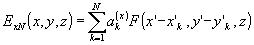 (79) (79)
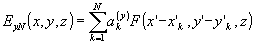 (80) (80)
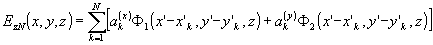 (81) (81)
где
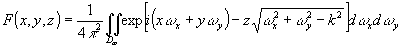 (82) (82)
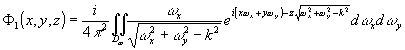 (83) (83)
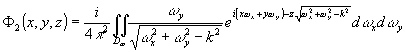 (84) (84)
Коэффициенты a(x,y)k по-прежнему определяются решением системы (77).
Функции F, Ф1, и Ф2 связаны дифференциальными соотношениями
|
¶
Ф1 |
=- |
¶
F |
|
¶
Ф2 |
=- |
¶
F |
(85) |
|
¶
z |
¶
x |
¶
z |
¶
y |
Наличие корня квадратного в показателе степени в (84) существенно затрудняет получение аналитических выражений для этих функций. Если, однако, Dw
есть круг радиуса Rw
, то имеем:
- 158 -
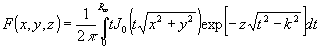 (86) (86)
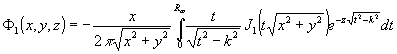 (87) (87)
Ф 1(x.,y,z) = Ф1(x,y,z)
где J0(х), J1(x) - функции Бесселя.
Второй способ восстановления особенно удобен в тех случаях,
когда удается получить простыв аналитические выражения для функций F,
Ф1,
и Ф2.
В некоторых частных случаях можно для этого воспользоваться приближенными представлениями
интегралов (82)-(87). Так,
например, при w 2x+ w
2y£ k 2,
что часто выполняется на практике, полагая 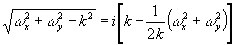 ,
нетрудно выразить эти функции через интегралы Френеля, если область Dw
состоит из прямоугольников. При вычислении
на ЭВМ можно также использовать алгоритм быстрого преобразования Фурье. ,
нетрудно выразить эти функции через интегралы Френеля, если область Dw
состоит из прямоугольников. При вычислении
на ЭВМ можно также использовать алгоритм быстрого преобразования Фурье.
Следствие 2.
Физическое восстановление поля по дискретным отсчетам касательных составляющих
может быть осуществлено путем создания на поверхности S
интерполяционных распределений составляющих поля 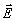 или
или  ,
найденных по формулам типа (67), (68).
В случай плоской поверхности s
процесс интерполяции (68) легко
реализуется средствами аналоговой оптики. Схема, выполняющая эту операцию для
одной поляризации, показана на рис.5. При необходимости восстановления двух
поляризаций (ЕХ
и ЕУ)
можно поместить две подобные схемы в плечи интерферометра. ,
найденных по формулам типа (67), (68).
В случай плоской поверхности s
процесс интерполяции (68) легко
реализуется средствами аналоговой оптики. Схема, выполняющая эту операцию для
одной поляризации, показана на рис.5. При необходимости восстановления двух
поляризаций (ЕХ
и ЕУ)
можно поместить две подобные схемы в плечи интерферометра.
Схема рис.5 работает следующим образом.
Во входной плоскости Р 1 устанавливается транспарант, пропускающий свет лишь в отдельных точках с координатами x’k, y’k (для простоты мы не учитываем здесь элементарных масштабных преобразований, которые могут потребоваться на практике). Пропускание транспаранта в точке (x’k,y’k) должно быть сделано равным a(x)k или a(y)k, где a(x)k, a(y)k определяются путем решения систем (77).
- 159 -
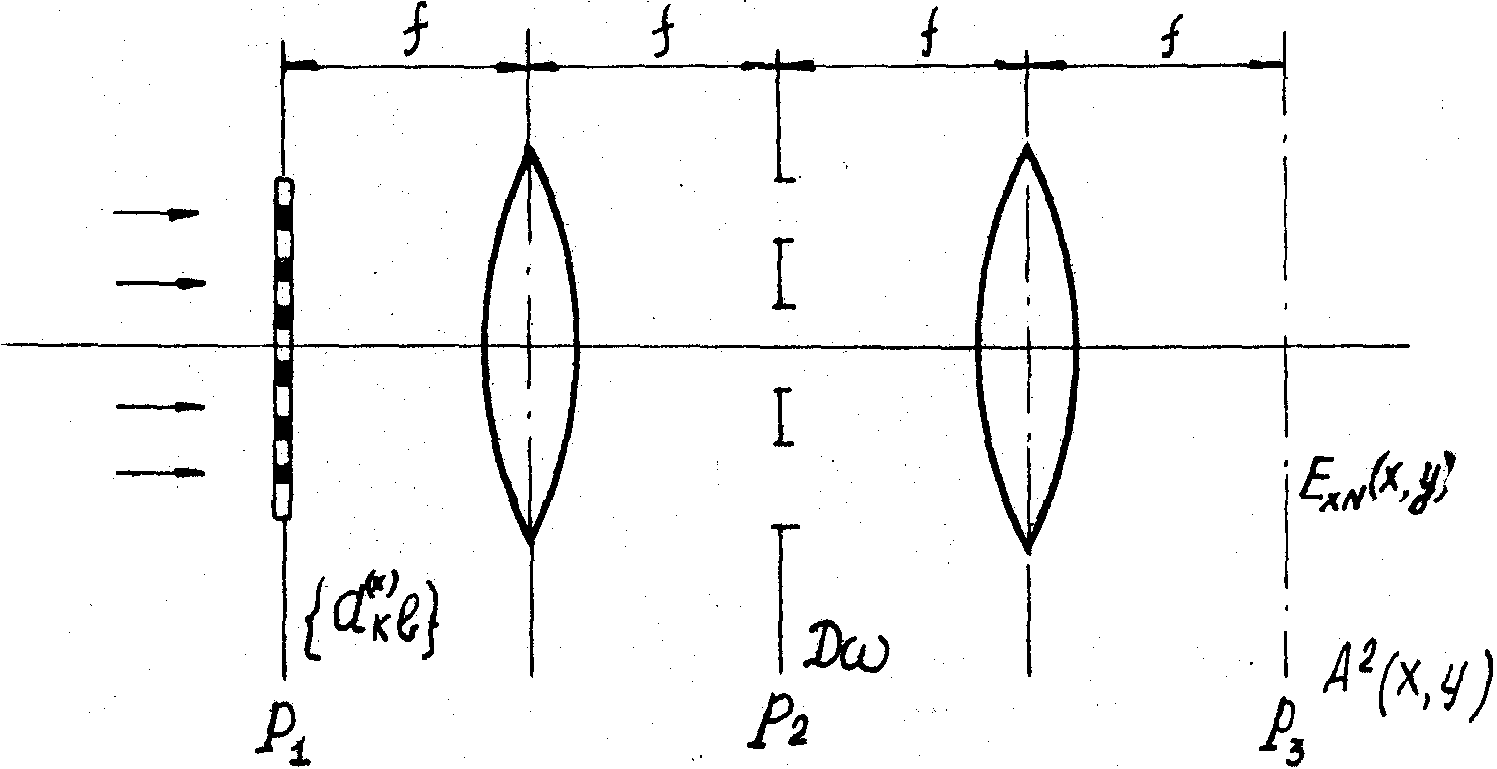
Рис.5. Схема оптимального восстановления поля по дискретным отсчетам.
Диафрагма, размещенная в частотной плоскости Р 2,
имеет отверстие, форма и размер которого соответствуют области Dw
. Таким образом, схема реализует функции
Q( - - k).
Если когерентный линейно поляризованный свет освещает весь входной транспарант,
то в выходной плоскости P3
распределение амплитуды будет пропорционально ExN( k).
Если когерентный линейно поляризованный свет освещает весь входной транспарант,
то в выходной плоскости P3
распределение амплитуды будет пропорционально ExN( )
или EyN( )
или EyN( ).
В результате за плоскостью Р3
восстановится поле, соответствующее зарегистрированной волне. Если поле в выходной
плоскости зарегистрировать голографическим методом, то получим непрерывную голограмму,
оптимальную с точки зрения минимума погрешности интерполяции поля на плоскости
регистрации S
для фиксированного множества точек отсчета. ).
В результате за плоскостью Р3
восстановится поле, соответствующее зарегистрированной волне. Если поле в выходной
плоскости зарегистрировать голографическим методом, то получим непрерывную голограмму,
оптимальную с точки зрения минимума погрешности интерполяции поля на плоскости
регистрации S
для фиксированного множества точек отсчета.
Замечание 1.
Теорема 2
может быть доказана и для случая конечной замкнутой поверхности
S, если ввести на
S периодические координаты и рассматривать
функцию E( )
как периодическую )
как периодическую
- 160 -
функцию с финитным спектром.
Замечание 2.
Нетрудно указать один широкий класс множеств точек отсчета (вообще неравноотстоящих),
обеспечивающий полноту системы {exp[-i  rS),
r,S = 0, ±1. ±2,..., относительно пространства
L2(Dw
), где Dw
- прямоугольник со сторонами [-w
m1,w m1], [¾
w m2,w
m2]. Этот класс определяется условиями rS),
r,S = 0, ±1. ±2,..., относительно пространства
L2(Dw
), где Dw
- прямоугольник со сторонами [-w
m1,w m1], [¾
w m2,w
m2]. Этот класс определяется условиями
|
x
0 = h
0 = 0 ж x
-r = -x
r; h
-S = -h
S |
(88) |
|
 ; ;
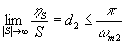
|
|
d1 > 0; d2 > 0 |
Дискретизация, определяемая условиями (68), является асимптотически равномерной с шагами d1 и d2 по осям x
и h
соответственно.
В частном случае равномерной дискретизации с d1=p
/w m1
и d2=p
/w m2
функция Q( )
обладает свойством )
обладает свойством
|
Q( k
- k
-  n)
= n)
=
|
w
m1w
m2 |
d
kn |
|
p
2 |
где d
kn - символ Кронекера.
В результате вместо системы (67) получаем равенства
|
ak = |
p
2 |
E( k) k)
|
|
w
m1w
m2 |
а многочлен (68) обращается в известный ряд Котельникова для функций двух переменных. Таким образом, полученное нами представление (67), (68) является обобщением ряда Котельникова на случай произвольной формы области Dw
и неравномерной дискретизации.
Замечание 3.
Алгоритмы восстановления поля по дискретным отсчетам
(68), (70) оптимальны при фиксированной системе
точек отсчета { k}.
Дальнейшая оптимизация возможна путей специального выбора этой системы (способа
размещения точек отсчета). Этот вопрос затрагивался в ряде работ (например,
/7/). В случае роспределения с "полосовым спектром"
можно уменьшить частоту дискретизации /8/. k}.
Дальнейшая оптимизация возможна путей специального выбора этой системы (способа
размещения точек отсчета). Этот вопрос затрагивался в ряде работ (например,
/7/). В случае роспределения с "полосовым спектром"
можно уменьшить частоту дискретизации /8/.
- 161 -
Замечание 4.
Развитый выше аппарат интерполяции может быть, в частности, использован для
восстановления интенсивности интерференционного поля
(18) по дискретным отсчетам. В данной случае
спектральная область Dw
состоит из трех площадок, покрытых двойной
штриховкой на рис.6. Для упрощения вычисления функции Q( k)
целесообразно использовать область k)
целесообразно использовать область 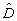 w
,É Dw ,
состоящую из трех прямоугольников (рис.6). w
,É Dw ,
состоящую из трех прямоугольников (рис.6).
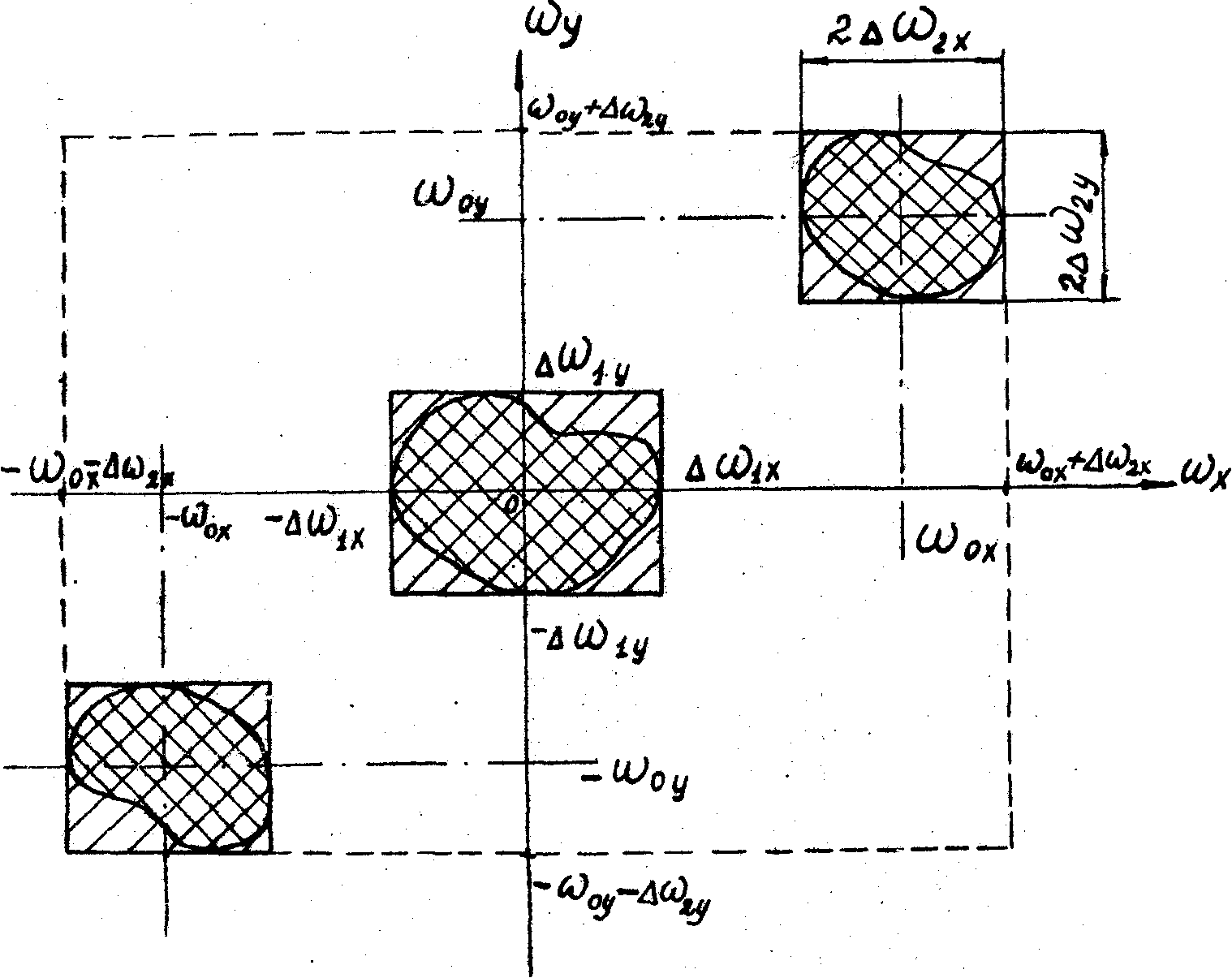
Рис.6. Частотная область спектра интенсивности интерференционного поля.
- 162 -
Учитывая (66), находим
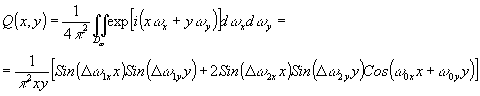 (89) (89)
Подставляя это выражение в
(77),можно вычислить коэффициенты a(x,y)k,
по которым определяется поле в любой точке внешнего пространства, включая плоскость
регистрации. Следует отметить, что интерполяция рядом Котельникова соответствует
в данном случае использованию области 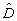 (k)w
в виде прямоугольника со сторонами (k)w
в виде прямоугольника со сторонами
[-w
0x - D
w
2x,w
0x + D
w
2x ] и [-w
0y - D
w
2y,w
0y + D
w
2y] т.е.
|
Q(x,y) = |
1 |
Sin(w
0x + D
w
2x)x·Sin(w
0y + D
w
2y) |
(90) |
|
p
2xy |
При этом шаги дискретизации должны удовлетворять условиям:
|
d1 = |
p
|
d2 = |
p
|
|
w
0x + D
w
2x |
w
0y + D
w
2y |
Использование функций (90)
проще с точки зрения вычислений, но дает худшую сходимость процесса интерполяции,
так как совершенно не учитывает формы области Dw
(обращения в нуль спектра внутри прямоугольника
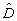 (k)w
). (k)w
).
4. Принцип взаимности в голографии
Предположим, что голографическая запись поля осуществляется с физической опорной волной. Согласно (18), интенсивность скалярного интерференционного поля симметрично зависит от распределений амплитуды как сигнальной, так и опорной волн в точках регистрации. Эта тривиальная закономерность носит, на самом деле, весьма общий характер и приводит к своеобразному принципу взаимности в голографии,
- 163 -
который можно сформулировать в виде леммы.
Лемма 2
Голографическая запись монохроматического волнового поля 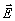 1, 1,
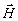 1,
с когерентной опорной волной 1,
с когерентной опорной волной 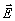 2, 2,
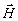 2
в произвольной линейной среде является одновременно голографической записью
поля 2
в произвольной линейной среде является одновременно голографической записью
поля 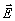 2, 2,
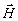 2
с опорной волной 2
с опорной волной 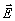 1, 1,
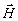 1. 1.
Доказательство . Прежде всего, ясно, что если лемма справедлива для непрерывной записи, то она справедлива и для дискретной записи (и наоборот). Поэтому не требуется различать эти два случая. Согласно теореме 1, полная голографическая запись поля в линейной среде включает в себя в общем случае четыре голограммы - квадратурные записи касательных компонент Еt
, Еℓ на поверхности регистрации. Эти записи определяются величинами:
|
V2t
= |
E1t
+ E2t
|
2; U2t
= |
E1t
+ E2t
exp[±
ip
/2]|
2; |
(91) |
|
V2ℓ = |
E1ℓ + E2ℓ|
2; U2ℓ = |
E1ℓ + E2ℓexp[±
ip
/2]|
2; |
Из (91) видно, что регистрируемые величины V2 и U2 одинаково зависят от компонент первого и второго полей, откуда и следует справедливость леммы.
Следствие 1.
Для полного физического, либо математического восстановления поля 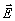 1, 1,
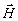 1 ( 1 (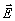 2, 2,
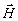 2),
записанного на поверхности S
с опорной волной 2),
записанного на поверхности S
с опорной волной 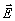 2, 2,
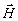 2 ( 2 (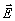 1, 1,
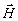 1),
необходимо и достаточно задать на этой поверхности касательные составляющие
поля 1),
необходимо и достаточно задать на этой поверхности касательные составляющие
поля 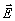 2, 2,
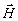 2 ( 2 (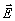 1, 1,
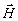 2).
Это замечательное свойство голограмм уже давно нашло практическое применение
в ряде задач и устройств. Можно, например, указать следующие его приложения:
ассоциативная голографическая память Габора, согласованные голографические фильтры
для идентификации изображений, коррекция индикатрисы излучения лазеров, коррекция
объективов с .помощью голографических фильтров и другие. 2).
Это замечательное свойство голограмм уже давно нашло практическое применение
в ряде задач и устройств. Можно, например, указать следующие его приложения:
ассоциативная голографическая память Габора, согласованные голографические фильтры
для идентификации изображений, коррекция индикатрисы излучения лазеров, коррекция
объективов с .помощью голографических фильтров и другие.
Во всех этих приложениях с помощью голограмм восстанавливается не сигнальная, а опорная волна путем освещения голограммы
- 164 -
сигнальной волной.
3аключение
Сформулированные и доказанные выше лемм и теоремы являются общим и строгим обоснованием приложений голографии, касающихся внешней задачи восстановления волновых полей. Помимо чисто методологического значения, они представляют и практический интерес с точки зрения выявления и оценки погрешностей реальных схем и методов голографии. Самостоятельный интерес могут представить алгоритмы оптимального восстановления поля по дискретным отсчетам, приведенные в работе, а также обобщение основных положений и формул на случай произвольных линейных сред.
Литература
1. Н.Е.Кочин. Векторное исчисление и начало тензорного исчисления. Изд. АН СССР, 1951.
2. Г.Т.Марков, А.Ф.Чаплин. Возбуждение электромагнитных волн, Изд. "Энергия", 1967.
3. D.Gabor, W.P.Goss. JOSA, v.56, n 7, 849, 1966,
4. G.A.Deachamps. Proc.IEEE, v.55, N 4, 570, 1967.
5. Э.И.Крупицкий, И.С.Барбанель. Оптика и спектроскопия, т.25, вып.1, 125 (1973).
6. Ф.В.Бункин. ХЭТФ. т.32, вып.2, 338 (1957).
7. Н.К.Игнатьев. Изд. вузов, "Радиотехника", т.4, вып.6, 68(1980)
8. В.М.Гинзбург, Г.Г.Левин, С.П.Толпина. ЖВМ и МФ, т.12, № 4, 1070 (1972).
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

