|
|
 |
 |

|
| |
"ОПЫТ" ЮНГА-УОЛША И ЛОГИЧЕСКАЯ ГОЛОГРАФИЯ
Л.М.Сороко
Рассматривается "опыт" Юнга-Уолша по интерференции двух узких пространственных сигналов, заданных аналоговым образом или в цифровой форме. Излагаются принципы построения и схемная реализация логической голограммы на терминалах электрической цепи, прохождение сигнала через которую задается некоторыми логическими правилами. Описывается стадия получения логической голограммы, а также стадия восстановления. Показывается, что система хранения информации в форме логической голограммы обладает предельно высокой устойчивостью и свойством ассоциативности, аналогично тем, которые имеет классическая голограмма.
Введение
Явление интерференции, сущность которого подробно излагалась на предыдущих Школах по голографии /1-5/, широко использует во многих разделах физики и техники. Наиболее ярким примером технического применения интерференции является сама голография - новый раздел прикладной оптики и квантовой электроники. Углубленная разработка процесса интерференции привела в последнее время к построению принципиально новых приборов, интерферометров интенсивности, а также к созданию завершенной теории когерентности полей /10/.
Согласно квантовой механике, интерферировать могут не только электромагнитное или акустическое поле, но также и частицы. Последовательное использование явления интерференция частиц при постановке опыта и анализе его результатов всегда оказывалось плодотворным.
- 82 -
Простейший пример использования явления интерференции в ядерной физике - это метод привязки неизвестного поля рассеяния к известной компоненте, в частности, к полю кулоновского рассеяния частиц. Совсем недавно появились оригинальные проекты экспериментов с, элементарными частицами /11-13/, сущность которых базируется на смелом использовании явления интерференции между частицами.
В данной лекции мы снова возвращаемся к явлению интерференции для того, чтобы показать, что интерферировать могут не только поля и частицы, но также аналоговые сигналы и даже сигналы, заданные в цифровой форме. Речь будет идти о так называемой логической голограмме, свойства которой являются своеобразным аналогом фундаментальных свойств классической голограммы. Эти свойства открывают перед исследователей, новые методы построения эффективных и предельно надежных систем записи цифровой информации или аналоговых сигналов.
i. Опыт Юнга и голограмма Фурье
Как известно /14/, первый опыт по интерференции света был осуществлен Юнгом (рис.1). В его установке свет от точечного монохроматического источника s проходил через два маленьких отверстия s1 и s2, сделанных в экране Э. Расстояние d между точками s1 и s2 было мало. Эти отверстия становились фактически источниками вторичного монохроматического излучения, которое создавало картину интерференции в области пересечения световых пучков от каждого отверстия на втором экране Ф. Можно показать, что расстояние "а" между соседними максимумами картины интерференции равно
a = fl
/d (1)
где l
- длина волны света; f - расстояние между первым и вторым экранами. Видно, что при фиксированных значениях f и l
величины а и d связаны однозначно. Одна из этих величин сохраняет информацию о значении другой. На существовании однозначного соотношения между шагом интерференционной картины и расстоянием между отверстиями в экране основана голограмма Фурье.
- 83 -
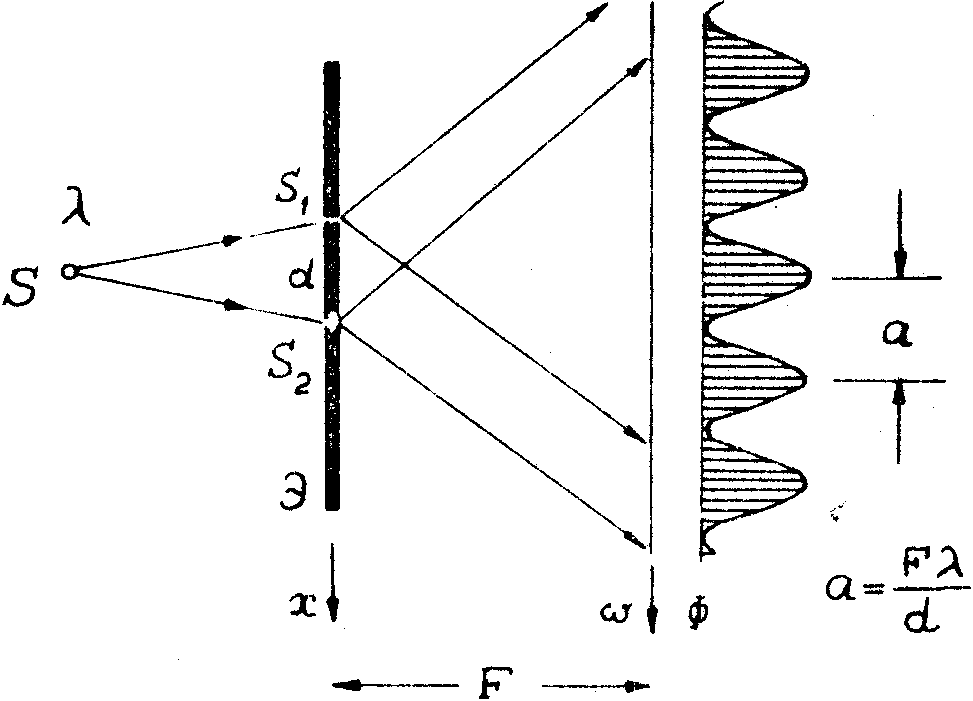
Рис.1. Схема опыта Юнга в оптике.
В современной схеме получения голограммы Фурье /15/ /
(рис.2) плоскую волну монохроматического света от лазера расщепляют на две части.
Первая из них проходит непосредственно через транспарант u(х),
голограмму Фурье которого необходимо получить. Вторую часть превращают с помощью
линзы Л0
в расходящуюся сферическую волну v(х)
с фокусом в плоскости Х.
Линза Л осуществляет преобразование Фурье. В плоскости экрана Ф происходит наложение
двух волновых полей: фурье-образа u(w
) транспаранта u(x)
в Фурье-образа v(w
) точечного источника v(х).
Последний создает в плоскости экрана Ф плоскую волну света, фронт которой образует
угол q =х0/ ¦
Л с плоскостью экрана Ф, где ¦
Л - фокусное расстояние линзы преобразования Фурье Л. Если исходный
транспарант u(х)
разбить мысленно на совокупность элементарных участков малых размеров, то волна
света от каждого элементарного участка проинтерферирует с плоской опорной волной
v(w ) я даст
свою систему интерференциониых полос. Шаг и ориентация этих полос однозначно
связаны с координатой 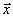 (х,у)
элементарного участка. При наличия пространственной когерентности у волны света
за транспарантом u(x} (х,у)
элементарного участка. При наличия пространственной когерентности у волны света
за транспарантом u(x}
- 84 -
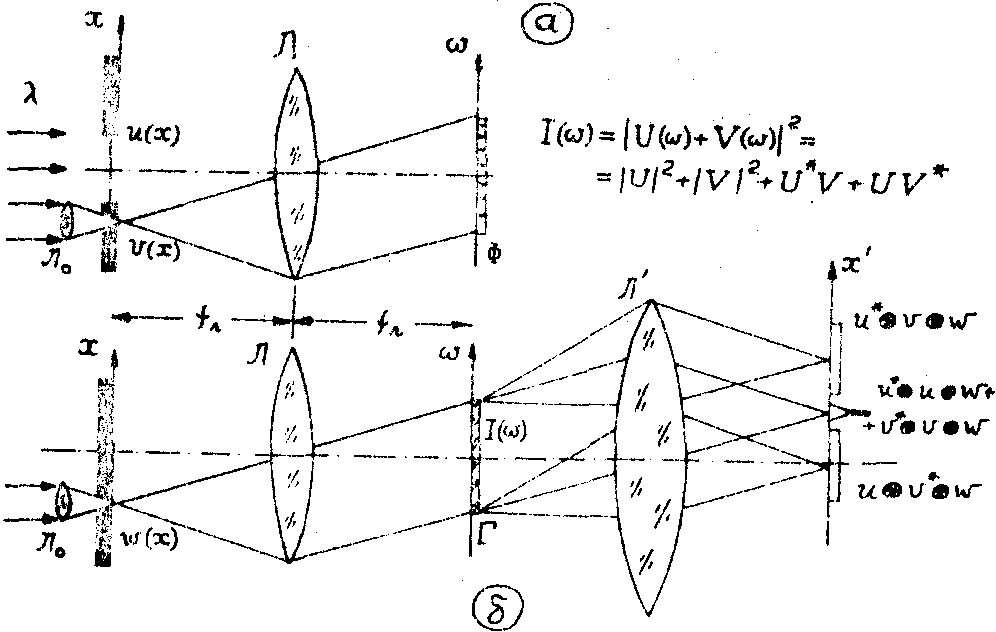
Рис.2: а) Схема получения голограммы Фурье транспаранта u(х) с использованием точечного опорного источника.
б) Стадия восстановления для голограммы Фурье, схема получения которой дана на рис.2а.
в плоскости экрана Ф произойдет когерентное сложение интерференционных картин от всех элементарных участков транспаранта u(х).
Распределение интенсивности света на голограмме Фурье имеет вид /19/:
i(w
) = |
u(w
) + v(w
)|
2 = |
u|
2 + |
v|
2 + u*v + uv* (2)
Если на стадии восстановления голограмму Фурье поместить в плоскости w
и направить на нее освещающую волну w(х), то в плоскости x за линзой обратного преобразования Фурье Л возникнет поле, состоящее из трех пространственно разделенных компонент:
|
r1 = u(x)Ä
v*(x)Ä
w(x) |
Нижняя |
(3) |
|
r2 = u*(x)Ä
u(x)Ä
w(x) +
+ v*(x)Ä
v(x)Ä
w(x) |
Центральная |
|
r3 = u*(x)Ä
v(x)Ä
w(x) |
Верхняя |
- 85 -
Обычно опорная и освещающая волны имеют вид:
v(x) = w(x) = d
(x – x0) (4)
Тогда компоненты восстановленного поля равны:
|
r1 = u(x) |
|
(5) |
|
r2 = u*(x)Ä
u(x)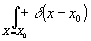
|
|
|
r3 = u*(x)
|
|
Из-за наличия компонент r2(х) и r3(х), которые отсутствовали в исходной предметной волна u(х), возникают ограничения на допустимую ширину окна для транспаранта u(х) и на положение Х0 опорного источника v(х).
Система получения голограммы Фурье, описанная выше, характеризуется двумя существенными особенностями. Во-первых, поле, регистрируемое на голограмме Фурье, является интегральным образом исходного поля u(х). Поэтому голограмма Фурье обладает свойством нелокализуемости. Каждая точка транспаранта посылает свет во все точки голограммы, а каждая точка голограммы, в свою очередь, получает свет от всех точек транспаранта. Благодаря этому система хранения данных о поле u(х) оказывается предельно устойчивой или к порче или к потере части голограммы. Во-вторых, на голограмме регистрируют распределение интенсивности, которое на математическом языке равно квадрату абсолютного значения поля в каждой точке голограммы. Вследствие этого возникает своеобразный эффект взаимного зацепления полей u(w
) и v(w
). Так как эти два поля алгебраически перемножаются в скрытом изображении голограммы, то возникает свойство ассоциативности голограммы. А именно, при определенных условиях опорная волна может быть заменена на предметную волну, так что предметная волна восстановит опорную волну. Это, по существу, означает свойство равноправности опорной и предметной волны. Для того, чтобы получить это свойство, необходимо и достаточно, чтобы автосвертки как опорной, так и предметной волн равнялись дельта-функции.
- 86 -
2. Дискретный аналог голограммы Фурье
Нелокализуемость зарегистрированной информации в голограмме Фурье и свойство ассоциативности голограммы играют фундаментальное значение, обусловившее широкое применение голограммы Фурье. Естественно возникает вопрос о том, нельзя ли придать эти свойства электрическим цепям, например, интегральным схемам, или аналоговым вычислительным устройствам. А если можно, то как это осуществить технически.
Для того, чтобы ответить на эти вопросы и облегчить ход мысли у читателя, возьмем схему получения голограммы Фурье в несколько ином вида, сохранив обе главных характеристики голограммы Фурье -нелокализуемооть информации и свойство ассоциативности. Для этого, вместо системы из свободного пространства и линзы преобразования Фурье, возьмем некоторый преобразующий элемент (ПР.ЭЛ) (рис.3), назначение которого заключается в том, чтобы превратить исходный
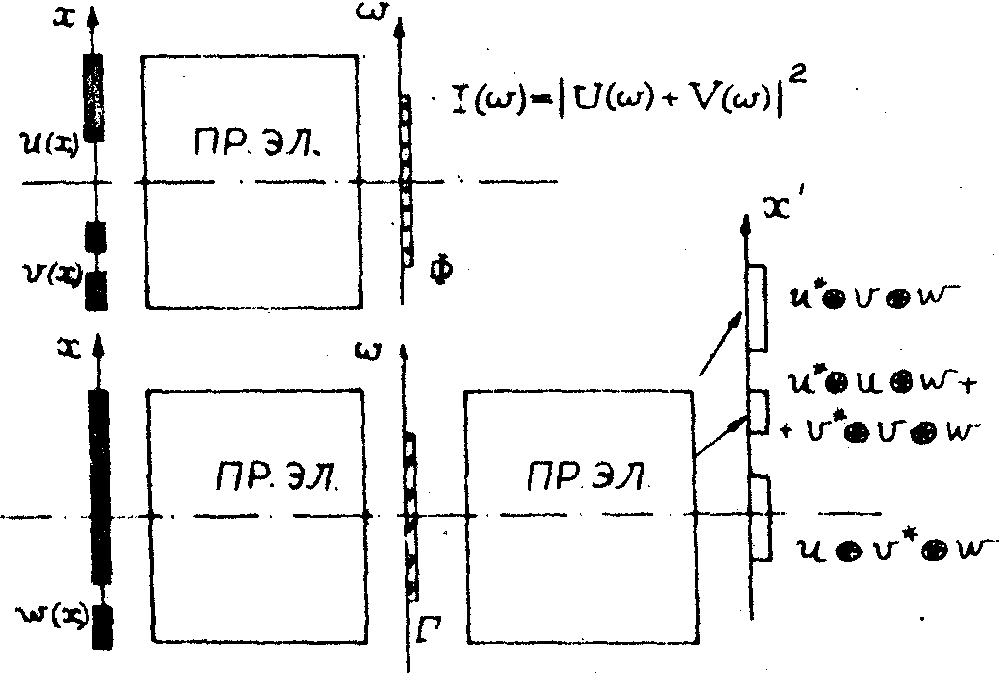
Рис. 5. Модифицированная схема голографии Фурье с использованием преобразующего элемента ПР.ЭЛ. На стадии получения голограммы используют один преобразующий элемент. На стадии восстановления используют два преобразующих элемента.
- 87 -
сигнал u(х) в некоторый интегральный образ u(w
), но так, чтобы обратное преобразование от образа u(w
) к исходному сигналу u(х) могло быть выполнено при помощи такого же преобразующего элемента.
Каждый элемент w
экрана Ф преобразует амплитуду поля u(w
) в квадрат абсолютного значения этого поля:
u(w
) ®
|u(w
)|2 (6)
Если ввести еще опорный сигнал it (х ), то на "голограмме" в плоскости Ф сформируется картина распределения интенсивности;
i(w
) = |
u(w
) + v(w
)|
2 (7)
где u(w
) - интегральный образ входного сигнала u(х), а v(w
) - интегральный образ опорного сигнала v(x).
На стадии восстановления должны произойти те же процессы, что и в классической голографии Фурье. А именно, в выходной плоскости x должны появиться три компоненты:
|
r1 = uÄ
v*Ä
w |
(3) |
|
r2 = u*Ä
uÄ
w + v*Ä
vÄ
w |
|
r3 = u*Ä
vÄ
w |
Теперь совершим переход от непрерывных сигналов u(x), v(x) и w(x) к сигналам, которые имеют вид дискретной последовательности. Одновременно с этим перейдем от математики функций классического анализа к математике решетчатых функций. Напомним, что решетчатой функцией называют вещественную или комплексно-значную функцию, которая задана на последовательности эквидистантно расположенных точек n. В промежутке между этими точками решетчатая функция не определена. Решетчатые функции широко используют в теории дискретных автоматических систем управления /16/, а также в теории матриц /17/ и в комбинаторной математике /18/.
Нам требуются решетчатые функции, заданные на конечной последовательности n точек:
Х = О, 1, 2, ..., n-1 (9)
- 88 -
Здесь
n = pn (10)
р - простое число, р ³
2, n - положительное целое число, n ³
1. Чаще всего будет рассматриваться случай р = 2.
Если исходная функция u(х) задана на последовательности точек (9,10), то ее образ u(w
) отображается на последовательности точек
w
= О, 1, 2, .... n-1 (11)
число которых также равно n.
Дискретным аналогом системы получения голограммы Фурье является схема, приведенная на рис.4. Здесь имеется входной терминал, содержащий n клемм. Исходная функция u(х) так же, как и опорный сигнал v(х), задана в виде электрических полей, постоянных или переменных, или же в виде цепочки цифр. Поступив в преобразующую
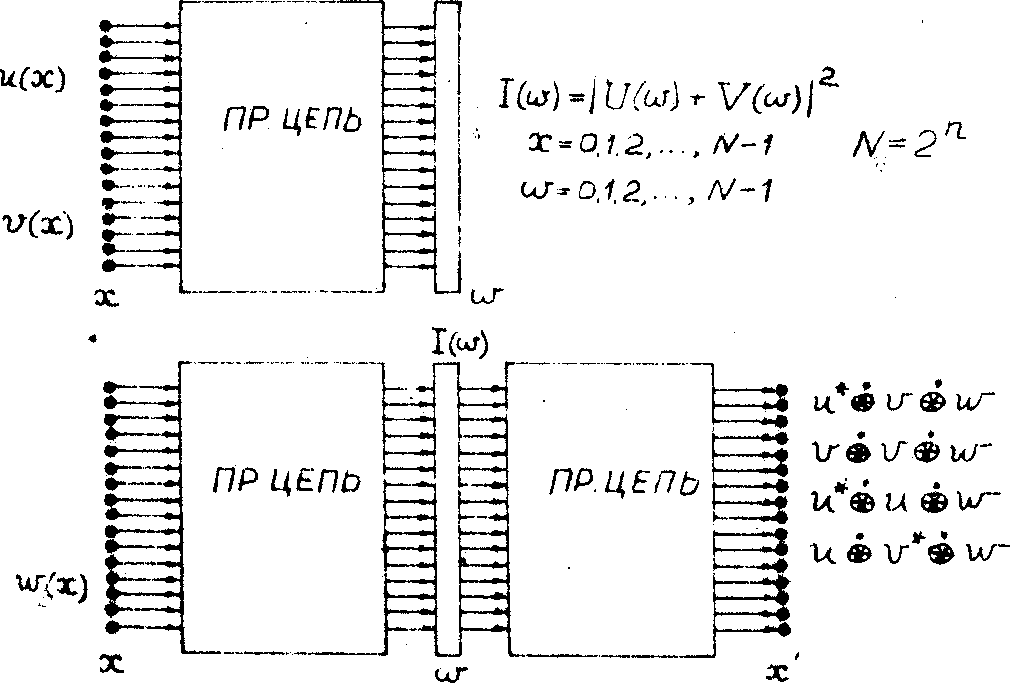
Рис. 4. Дискретный аналог голографии Фурье. Входной терминал состоит из n клемм. Каждая клемма сигнала на входных терминах преобразующей цепи связана со всеми компонентами входного сигнала. Последовательность цифр, получаемая на выходе, называется логической голограммой.
- 89 -
цепь, эти сигналы преобразуются по определенному алгоритму. Каждая компонента входного сигнала на выходном терминале но связана со всеми компонентами входного сигнала. Иначе говоря, выходная последовательность является дискретным интегральным образом входной последовательности. На следующей стадии выполняют возведение в квадрат абсолютного значения каждой компоненты выходной последовательности. Полученную в результате этих операций последовательность цифр называют логической голограммой .
На стадии восстановления с помощью тех же преобразующих цепей получаем три группы восстановленных сигналов:
Существенное отличие (12)
от (8) или
(5) состоит в том, что вместо арифметической
свертки Ä теперь стоит логическая свертка 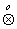 . .
Анализ показывает, что дискретным интегральным преобразованием, которое удовлетворяет приведенным выше условиям, является дискретное преобразование Уолша.
3. Логическое сложение и логическое умножение
Для решетчатых функций существует класс дискретных логических операций. Это - логическое сложение, логическое вычитание, логическое умножение, логический сдвиг, логическая свертка и, наконец, логическое дифференцирование.
Логическое сложение и логическое умножение для р
= 2 - это операции, которые заданы на элементах
a и b ,
принимающих только два значения: 0
или 1. Логическое
сложение обозначается Å ,
логическое умножение  .
По определению .
По определению
|
a
Å
b
= 1 - d
(a
,b
) |
(13) |
|
a  b
= a ·b b
= a ·b
|
где решетчатая дельта-функция равна
- 90 -
d
(a
,b
) = 1 - sgn|
a
- b
|
(14)
a sgn - решетчатая знаковая функция:
|
sgn x = |
|
+1, x > 0 |
(15) |
|
0, x = 0 |
|
-1, x < 0 |
Эти две логические операции можно определить с помощью следующих таблиц ;
|
Å
|
a
b
|
0 |
1 |

|
a
b
|
0 |
1 |
|
0
1 |
0
1 |
1
0 |
0
1 |
0
0 |
0
1 |
Любое число Х из последовательности
Х = 0, 1, ..., n-1 (16)
где n=2n, n - положительное целое число можно представить в исчислении с основанием 2:
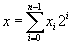 (17) (17)
где xi приникает только одно из двух значений: 0 или 1. Тогда, по определению, логическая сумма двух чисел x и у, второе из которых в двоичном представлении имеет вид
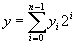 (17) (17)
равна
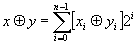 (17) (17)
Аналогично определяется логическое умножение
- 91 -
х у= у= 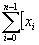  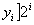 (20) (20)
Пример : 13 Å
6 = 11. Действительно, записав слагаемые в двоичном представлении и произведя логическое сложение в каждом разряде, получим
|
Å
|
[01101] |
|
|
[00110] |
|
| |
[01011] |
®
11 |
Пример : 13  6 =4. Аналогично находим
6 =4. Аналогично находим
|

|
[01101] |
|
|
[00110] |
|
| |
[00100] |
®
4 |
Благодаря свойству ассоциативности операции логического сложения можно найти логическую сумму конечного числа слагаемых:
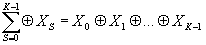 (21) (21)
На рис.5 даны примеры логического сдвига линейной решетчатой функции ¦
(х) =х для n=16 при различных значениях величины логического сдвига а.
Можно показать, что при логическом сложении чисел х с фиксированным числом а из той же последовательности (16) исходная последовательность чисел (16) преобразуется сама в себя. Это свойство логического сложения позволяет определить операцию логического сдвига, а также логической свертки.
4. Логическая свертка
Если на последовательности точек х вида (16) заданы две решетчатые функции ¦
(х) и g(x), то по определению, логической сверткой этих двух функций называется решетчатая функция
- 92 -
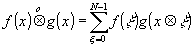 (22) (22)
В отличие от арифметической свертки или арифметической корреляции, где сдвигу на величину x
подвергается вторая функция в прямой, арифметическом смысле, при получении логической свертки двух функций одну из них подвергают логическому сдвигу, получающиеся при атом компоненты новой последовательности перемножают алгебраически с компонентами первой последовательности и, наконец, находят арифметическую сумму для каждого логического сдвига x
.
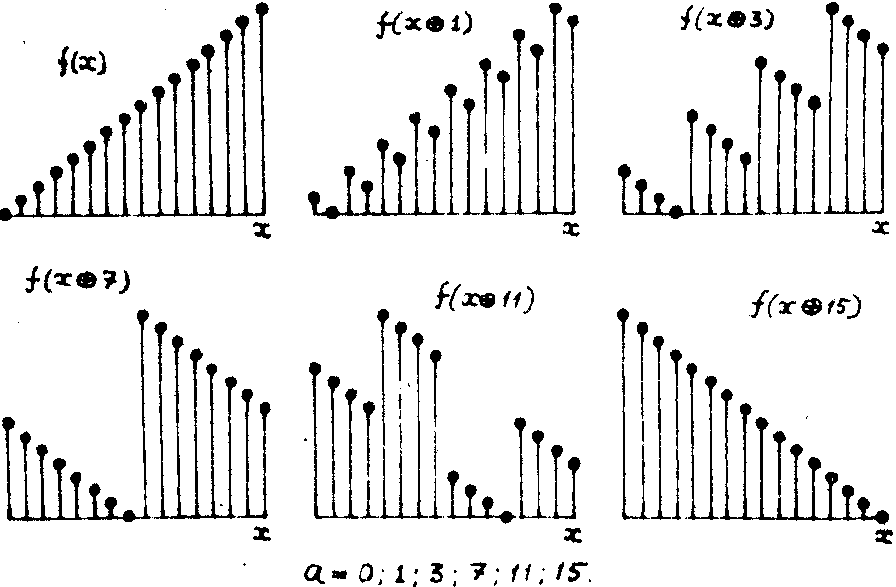
Рис.5. Логический сдвиг линейной решетчатой функции ¦
(х)=х при n=16 для различных значений логического сдвига а.
Если последовательность х содержит числа
Х = 0, 1, ..., рn-1 (23)
где р - простое число, р ³
2, n - положительное целое число, то каждый элемент этой последовательности можно записать в исчислении
- 93 -
с основанием
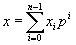 (24) (24)
Для таких последовательностей можно ввести следующие логические операции /21/:
1) логическое сложение по модулю р:
х у = у =  , zdi
= xiÅ yi, modp (25) , zdi
= xiÅ yi, modp (25)
2) логическое вычитание по модулю;
х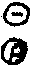 у= у= 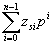 , zsi
= xi , zsi
= xi уi уi, modp (26)
3) логическое умножение по модулю ;
х 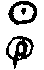 у= у= 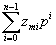 , zmi
= xi , zmi
= xi уi уi, modp (27)
Для p=3 таблицы поразрядного логического сложения, логического вычитания и логического умножения имеют вид:
| |
a
b
|
0 |
1 |
2 |
|
a
b
|
0 |
1 |
2 |
|
a
b
|
0 |
1 |
2 |
|

|
0
1
2 |
0
1
2 |
1
2
0 |
2
0
1 |

|
0
1
2 |
0
2
1 |
1
0
2 |
2
1
0 |
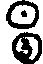
|
0
1
2 |
0
0
0 |
0
1
2 |
0
2
1 |
Операцию логического деления в общем случае определить невозможно. И только если числа р и поразрядные компоненты yi второго числа у имеют общий наибольший делитель, равный 1 для всех i=0, 1, ..., n-1, то число x можно логически разделить на число у. По определению,
4) логическое частное по модулю р чисел х и у равно
- 94 -
х 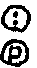 у= у=  , zdi
= xi , zdi
= xi  уi уi, modp (28)
На рис.6 дан пример логической свертки двух функций ¦
(х) и g(x) для n=16 и p=2.
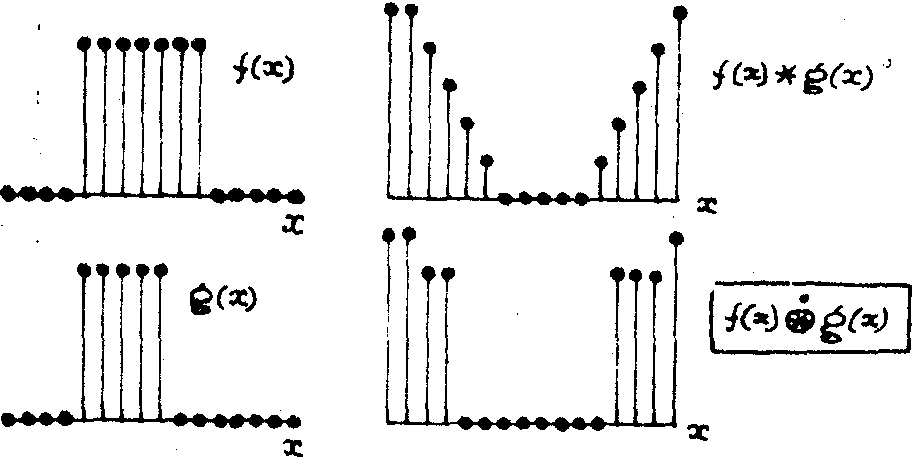
Рис. 6. Логическая свертка двух решетчатых функций ¦
(х ) и g(x) для n=16 и р=2.
5. Дискретные функции Уолша
Дискретные функции Уолша /22-28/ в классе решетчатых функций являются аналогом гармонических функций в классическом анализе. Подобно комплексной экспоненте, абсолютное значение которой равно единице, функции Уолша, будучи вещественными, принимают только два значения: +1 или -1. На массиве точек х, образующих последовательность (16), можно построить n дискретных функций Уолша. Индексом функций Уолша служит число k, принимающее значения 0£
К£
n-1. Если числа х и k записаны в двоичном представлении:
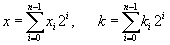 (29) (29)
- 95 -
где Х i=0 или 1, ki=0 или 1 для всех 0 £
i £
n-1, то последовательность функций Уолша в явном виде определяется так:
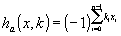 (30) (30)
Заданные в таком виде функции Уолша называют адамаровски упорядоченными. Их можно построить иначе с помощью кронекеровской степени матрицы Адамара для n=2:
которая в этом процессе построения выполняет роль затравочного "гена". На рис.7 приведены исходная матрица - ген, а также ее кронекеровские степени - вторая (n=2, n=4), третья (n=3, n=8) и четвертая (n=4, n=l6). В получающейся матрице дискретные функции Уолша с индексом k расположены в (к+1)-ой строке. На рис.7 значения функции, равные +1, обозначены темными полями, а значения (-1) - светлыми полями.

Рис.7. Схема получения адамаровски упорядоченных функций Уолша с помощью кронекеровских степеней (2,3 и 4; матрицы Адамара для n=2 (матрица - ген).
- 96 -
Дискретные функции Уолша характеризуют также другим индексом-секвентой s, которая равна числу изменений знака функции на всем массиве точек х. Так, например, функция Уолша с n=16 индексом 1, которая расположена на второй строке матрицы с n=4, n=16 (рис.7), имеет s=15. Значение секвенты s однозначно определяется индексом k, называемым волновым числом. Секвенту s можно рассматривать как аналог частоты u
экспоненциальных комплексных функций классического анализа.
Функции Уолша, расположенные в порядке возрастания секвенты s, от s=0 до s = n-1, называют секвентивно-упорядоченными функциями Уолша, которые в явном виде можно записать так:
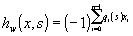 (31) (31)
где
|
q0(s) = sn-1; q1(s) = sn-1Å
sn-2; |
(32) |
|
q2(s) = sn-2Å
sn-3; ...; qn-1(s) = s1Å
s2 |
Индексы q i(s) , представленные в инвертированном порядке qn-i-1(s), равны компонентам кода Грея секвенты s.
Рассмотрим на примере построение функций Уолша для n=3, n=8.
Адамаровски-упорядоченные функции Уолша.
Составляем таблицу значений показателя степени в (30);
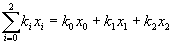 (33) (33)
где х=[х 2,х1,x 0] и k[k2,k1,k0] - числа х и k в двоичном представлении. Число х так же, как и число k, принимает 8 значений. Поэтому размер матрицы показателей степени в (30) равен 8х8. Эта матрица определяет значения всех восьми функций Уолша для восьми точек k. Там, где показатель степени равен четному числу, функция ha(x,k) равна +1, а там. где показатель степени равен нечетному числу, функция hа(x,k) равна -1.
- 97 -
Матрица показателей степени для адамаровски-упорядоченных функций Уолша
|
x[x2,x1,x0]]
k[k2,k1,k0] |
0
000 |
1
001 |
2
010 |
3
011 |
4
100 |
5
101 |
6
110 |
7
111 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
2 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
3 |
0 |
1 |
1 |
0 |
1 |
1 |
2 |
0 |
1 |
1 |
2 |
|
4 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
5 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
2 |
1 |
2 |
|
6 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
2 |
2 |
|
7 |
1 |
1 |
1 |
0 |
1 |
1 |
2 |
1 |
2 |
2 |
3 |
Матрица значений функций Уолша в адамаровском представлении для n=8
|
К |
x
ha(x,k) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0 |
ha(x,0) |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|
1 |
ha(x,1) |
+ |
- |
+ |
- |
+ |
- |
+ |
- |
|
2 |
ha(x,2) |
+ |
+ |
- |
- |
+ |
+ |
- |
- |
|
3 |
ha(x,3) |
+ |
- |
- |
+ |
+ |
- |
- |
+ |
|
4 |
ha(x,4) |
+ |
+ |
+ |
+ |
- |
- |
- |
- |
|
5 |
ha(x,5) |
+ |
- |
+ |
- |
- |
+ |
- |
+ |
|
6 |
ha(x,6) |
+ |
+ |
- |
- |
- |
- |
+ |
+ |
|
7 |
ha(x,7) |
+ |
- |
- |
+ |
- |
+ |
+ |
- |
2. Секвентивно-упорядоченные функции Уолша. Составляем матрицу значений показателя степени
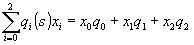 (34) (34)
- 98 -
где g(s) - код Грея числа s, q(s)=g(s), где знак тильда обозначает операцию инверсии двоичных индексов. Сначала находим матрицу показателей степени для секвентивно-упорядочённых функций Уолша.
|
s |
s2,s1,s0 |
g(s) |
q(s) |
x[x2,x2,x0]
hw(x,s) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
|
|
0 |
000 |
000 |
000 |
hw(x,0) |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
001 |
001 |
100 |
hw(x,1) |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
2 |
010 |
011 |
110 |
hw(x,2) |
0 |
0 |
1 |
1 |
1 |
1 |
2 |
2 |
|
3 |
011 |
010 |
010 |
hw(x,5) |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
4 |
100 |
110 |
011 |
hw(x,4) |
0 |
1 |
1 |
2 |
0 |
1 |
1 |
2 |
|
5 |
101 |
111 |
111 |
hw(x,5) |
0 |
1 |
1 |
2 |
1 |
2 |
2 |
3 |
|
6 |
110 |
101 |
101 |
hw(x,6) |
0 |
1 |
0 |
1 |
1 |
2 |
1 |
2 |
|
7 |
111 |
100 |
001 |
hw(x,7) |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
Затем строим матрицу значений функций Уолша в секвентивно--упорядоченном представлении для n = 8.
|
s |
x
hw(x,s) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
g(s) |
q(s) |
|
0 |
hw(x,0) |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
0 |
0 |
|
1 |
hw(x,1) |
+ |
+ |
+ |
+ |
- |
- |
- |
- |
1 |
4 |
|
2 |
hw(x,2) |
+ |
+ |
- |
- |
- |
- |
+ |
+ |
3 |
6 |
|
3 |
hw(x,3) |
+ |
+ |
- |
- |
+ |
+ |
- |
- |
2 |
2 |
|
4 |
hw(x,4) |
+ |
— |
- |
+ |
+ |
- |
- |
+ |
6 |
3 |
|
5 |
hw(x,5) |
+ |
- |
- |
+ |
- |
+ |
+ |
- |
7 |
7 |
|
6 |
hw(x,6) |
+ |
- |
+ |
- |
- |
+ |
- |
+ |
5 |
5 |
|
7 |
hw(x,7) |
+ |
- |
+ |
— |
+ |
— |
+ |
— |
4 |
1 |
Функции Уолша обладают следующими свойствами:
1. Функции Уолша h(х,k) симметричны к индексам х и k:
- 99 -
h(x,k) = h(k,x) (35)
2. Функции Уолша h(х,k) взаимно ортогональны:
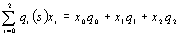 (36) (36)
3. Функции Уолша h(х,k) образуют полную симметрию:
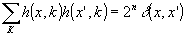 (37) (37)
Последнее свойство означает, что не существует решетчатой функции, не равной тождественно нулю, которая была бы ортогональна всем функциям Уолша.
4. Функции Уолша являются мультипликативными. Это значит, что при умножении двух функций Уолша с индексами k и k’ получается вновь функция Уолша, индекс которой равен логической сумме индексов k и k’ функций Уолша сомножителей:
h(x,k)h(x,k’) = h(x,kÅ
k’) (38)
6. Дискретное преобразование Уолша
Дискретным преобразованием Уолша называется переход от исходной решетчатой функции ¦
(x), заданной на последовательности точек х (16), к уолш-образу wa(w
), который равен
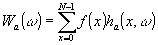 (39) (39)
Например, если исходная функция ¦
(х) задана в четырех точках своими компонентами
¦
(0), ¦
(1), ¦
(2), ¦
(3) (40)
то компоненты уолш-образа этой функции равны :
|
wa(0) = ¦
(0) + ¦
(1) + ¦
(2) + ¦
(3)
wa(1) = ¦
(0) - ¦
(1) + ¦
(2) - ¦
(3)
wa(2) = ¦
(0) + ¦
(1) - ¦
(2) - ¦
(3)
wa(3) = ¦
(0) - ¦
(1) - ¦
(2) + ¦
(3) |
(40) |
- 100 -
Знаки перед компонентами функции ¦
(х ) образуют матрицу Адамара;
|
h4 = |
|
+
+
+
+ |
+
-
+
- |
+
+
-
- |
+
-
-
+ |
|
Обратное преобразование Уолша, по определению, равно :
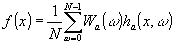 (42) (42)
Если использовать функции Уолша остаточного класса р /29,30/ заданные на последовательности точек х (23),
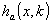  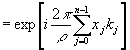 (43) (43)
где xj и kj - компоненты чисел х и k в исчислении с основанием р, то можно ввести прямое преобразование Уолша остаточного класса р:
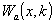  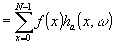  (44) (44)
и обратное преобразование Уолша остаточного класса :
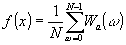  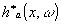  (44) (44)
7. Гомоморфное преобразование Уолша
Построенные выше дискретные преобразования Уолша решетчатых функций обладают существенным информационном свойством. А именно, любое из них имеет обратное преобразование, возвращающее нас к исходной функции. Это свойство позволяет рассматривать дискретный образ решетчатой функции как полноценный информационный эквивалент самой решетчатой функции. Дискретные преобразования решетчатых функций , которые всегда имеют однозначное обратное преобразование, называют изоморфными. Наряду с этим существует класс дискретных
- 101 -
преобразований решетчатых функций, с помощью которых можно сделать переход только в одном направлении, от исходной функции к ее образу, и нельзя сделать обратный переход, чтобы вновь получить исходную функцию. Такие преобразования называют гомоморфными преобразованиями .
При гомоморфном преобразовании всегда теряется часть исходной информации. Нечто подобное происходит при фильтрации сигналов, когда из сигналов выбрасывают нежелательные частотные компоненты, которые безвозвратно исчезают.
Типичным примером идущих только в одном направлении преобразований является гомоморфное преобразование Уолша /21/, которое по определению, называется переходом от исходной решетчатой функции ¦
(х), заданной на массиве точек х (16), к гомоморфному уолш—образу:
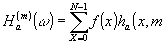  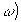 (46) (46)
где m - показатель
гомоморфности преобразования, w
- координата обратного пространства, a
m w
- логическое произведение чисел m
и w . w
- логическое произведение чисел m
и w .
Чтобы уяснить различие между изоморфным преобразованием Уолша и гомоморфным преобразованием Уолша, рассмотрим пример n=4. В этом случае исходная решетчатая функция ¦
(х ) имеет четыре компоненты (40) и изоморфный уолш-образ имеет компоненты, приведенные в (41).
Если показатель гомоморфности m=0, то
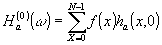 (47) (47)
Компоненты гомоморфного уолш-образа для m=0 равны
|
h(0)a(0) = ¦
(0) + ¦
(1) + ¦
(2) + ¦
(3)
h(0)a(1) = h(0)a(0)
h(0)a(2) = h(0)a(0)
h(0)a(3) = h(0)a(0) |
(48) |
- 102 -
Если показатель гомоморфности равен m=1, то
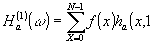  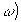 (49) (49)
Используя второй столбец таблицы логического умножения чисел m и w
для n = 4
|
m
w
|
0 |
1 |
2 |
3 |
|
0
1
2
3 |
0
0
0
0 |
0
1
0
1 |
0
0
2
2 |
0
1
2
3 |
находим
|
h(1)a(0) = ¦
(0) + ¦
(1) + ¦
(2) + ¦
(3)
h(1)a(1) = ¦
(0) - ¦
(1) + ¦
(2) - ¦
(3)
h(1)a(2) = h(1)a(0)
h(1)a(3) = h(1)a(1) |
(50) |
Для m = 2
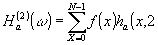  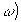 (51) (51)
Его компоненты равны
|
h(2)a(0) = ¦
(0) + ¦
(1) + ¦
(2) + ¦
(3)
h(2)a(1) = h(2)a(0)
h(2)a(2) = ¦
(0) + ¦
(1) - ¦
(2) - ¦
(3)
h(1)a(3) = h(2)a(2) |
(52) |
Наконец, для показателя гомоморфности m = 3 получаем
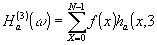  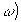 (53) (53)
- 103 -
или
|
h(3)a(0) = ¦
(0) + ¦
(1) + ¦
(2) + ¦
(3)
h(3)a(1) = ¦
(0) - ¦
(1) + ¦
(2) - ¦
(3)
h(3)a(2) = ¦
(0) + ¦
(1) - ¦
(2) - ¦
(3)
h(3)a(3) = ¦
(0) - ¦
(1) - ¦
(2) + ¦
(3) |
(52) |
Здесь 3 w
=w и гомоморфный
уолш-образ с показателем гомоморфности m=3,
а в общем случае для m=n-1,
равен изоморфному уолш-образу. w
=w и гомоморфный
уолш-образ с показателем гомоморфности m=3,
а в общем случае для m=n-1,
равен изоморфному уолш-образу.
Знаки перед компонентами функции ¦
(х) для различных показателей гомоморфности m образуют четыре различных матрицы, которые приведены в таблице для n=4. Матрица изоморфного преобразования обведена рамкой.
|
m = 0 |
m = 2 |
m = 1 |
m = 3 |
|
m0 = 0 |
m0 = 1 |
|
m1 = 0 |
m1 = 1 |
m1 = 0 |
m1 = 1 |
|
+ + + +
+ + + +
+ + + +
+ + + + |
+ + + +
+ + + +
+ + - -
+ + - - |
+ + + +
+ - + -
+ + + +
+ - + - |
+ + + +
+ - + -
+ + - -
+ - - + |
Аналогично строят гомоморфные преобразования Уолиа для более
высоких значений n. Так,
например, таблица логических произведений m w
для n = 8
имеет вид: w
для n = 8
имеет вид:
- 104 -
|
m
w
|
0 |
i |
2 |
3 |
4 |
5 |
6 |
7 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
2 |
0 |
0 |
2 |
2 |
0 |
0 |
2 |
2 |
|
3 |
0 |
1 |
2 |
3 |
0 |
1 |
2 |
3 |
|
4 |
0 |
0 |
0 |
0 |
4 |
4 |
4 |
4 |
|
5 |
0 |
1 |
0 |
1 |
4 |
5 |
4 |
5 |
|
6 |
0 |
0 |
2 |
2 |
4 |
4 |
6 |
6 |
|
7 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Гомоморфное преобразование Уолша так же, как и изоморфное преобразование Уолша, можно ввести для любого остаточного класса р. А именно:
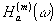  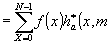 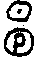 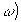  (55)
(55)
где 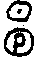
- оператор логического умножения по модулю
р, а * - знак
комплексного сопряжения.
8. Электрическая схема, выполняющая гомоморфное преобразование Уолша
Рассмотрим теперь схему электрической цепи, содержащую резисторы, сумматоры и ключи /21/ (рис.8) и функционирующую по логике алгоритма быстрого преобразования Уолша /22,31/. Покажем, что с помощью этой схемы можно осуществить любое гомоморфное преобразование Уолша для n = 2n = 4.
На четыре входных клеммы подаются четыре аналоговых сигнала, образующих четыре компоненты решетчатой функции ¦
(x):
¦
(0), ¦
(1), ¦
(2) и ¦
(3)
Резисторные элементы цепи позволяют производить арифметическое сложение и вычитание сигналов, поданных на вход схемы, в соответствии с положением ключей в этой схеме. Так, например, сигнал на
- 105 -
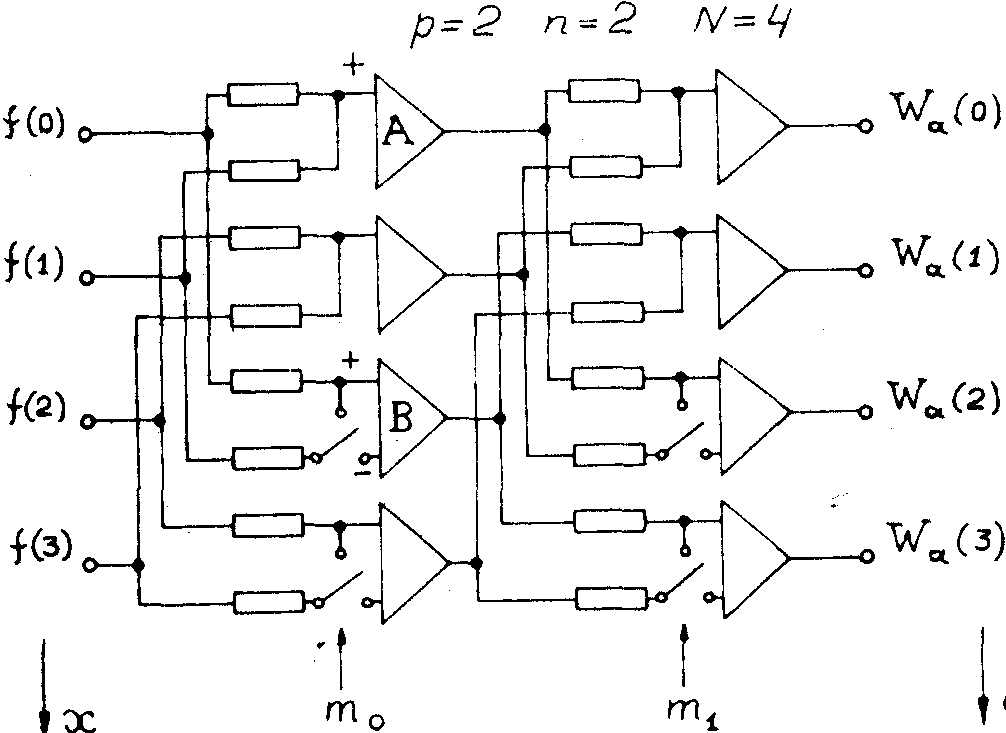
Рис.8. Схема электрической цепи, которая функционирует по логике алгоритма быстрого преобразования Уолша (см. текст).
выходе усилителя А равен
¦
(0) + ¦
(1)
Соответственно, сигнал на выходе усилителя В равен сумме
¦
(0) + ¦
(1)
для положения ключа вверх m0=0 и разности
¦
(0) - ¦
(1)
для положения ключа вниз m0 = 1. Во втором столбце резисторов, сумматоров и ключей производятся аналогичные преобразования сигналов, поступающих с выхода первого столбца. Здесь положение управляющих ключей определяется индексом m1, который, так же, как и индекс m0, может переводить схему из положения m1=0,когда она производит сложение входных сигналов, в положение m1=1, когда она производит вычитание входных сигналов.
— 106 —
Всего имеется четыре возможных комбинации положений ключей в этих двух столбцах:
m0 = 0, m0 = 0, m0 = 1, m0 = 1
m1 = 0, m1 = 1, m1 = 0, m1 = 1
Если теперь индексы положений ключей m0 и m1 приравнять значениям компонент числа m в двоичном представлении;
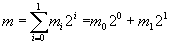 (56) (56)
то m=0, 1, 2 или 3. Видно, что в зависимости от значения показателя гомоморфности m приведенная на рис.8 электрическая схема производит одно из четырех различных гомоморфных преобразований Уолша (46).
9. Стадия получения логической голограммы
Рассмотрим стадию получения логической голограммы (рис.9). В качестве входных сигналов возьмем дельта-образный предметный сигнал u(x)=a
d
(x-x0) и дельта-образный опорный сигнал v(х).
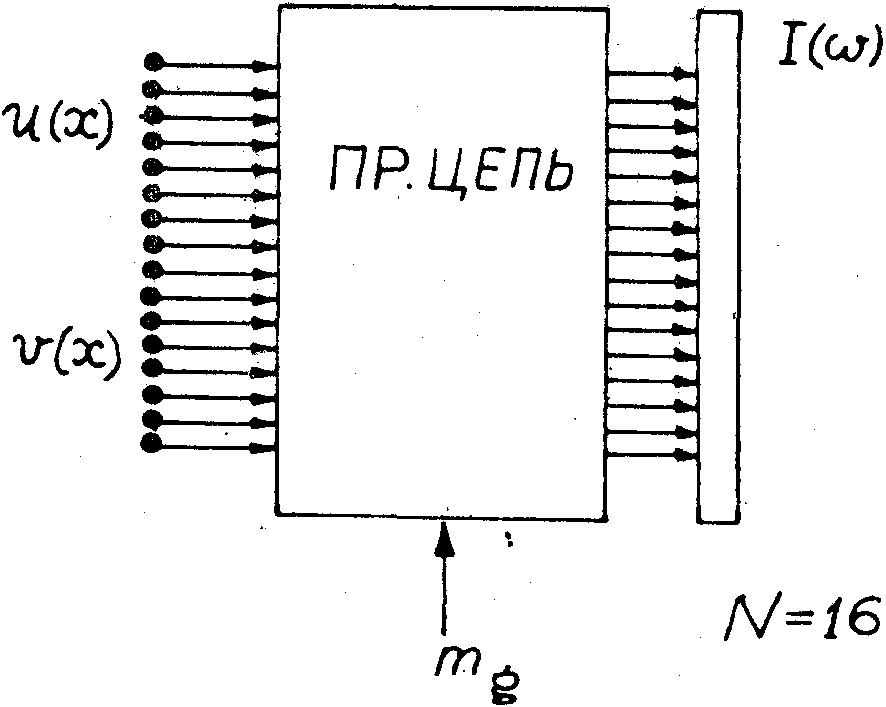
Рис.9. Схема получения логической голограммы для n=16 (см. текст)
- 107 -
Как и в классической голографии, интенсивность опорного сигнала выше интенсивности предметного сигнала (a
< 1).
Преобразующая цепь, осуществляющая дискретное гомоморфное преобразование Уолша, имеет структуру, близкую к цепи, приведенной на рис.8. Единственное различие между ними заключается в том, что число столбцов равно четырём ( n=4), а не двум (n=2), как на рис.8. В общем случае число столбцов равно n=log2n, т.е. числу двоичных разрядов в показателе гомоморфности mg на стадии получения логической голограммы. На выходе преобразующей цепи отобразятся компоненты гомоморфного уолш-образа, каадая из которых затем возводится в квадрат. Полная цепочка преобразований, выполняемых на стадии получения логической голограимы, имеет вид:
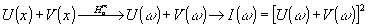 (57) (57)
Если на преобразующую цепь подать наивысший показатель гомоморфности mg = 15, то мы получим то, что можно назвать "опытом" Юнга-Уолша. Подобно опыту Юнга с двумя узкими отверстиями картина интерференции содержит эквидистантные полосы. Добавление имени Уолша означает, что система является дискретной и все преобразования с цифровыми или аналоговыми сигналами ведутся по дискретным логическим алгоритмам. В нашем случае входной сигнал (рис.10), равный
¦
(x) = d
(x) + a
·d
(x – x0), a
= 1/2, x0 = 1 (58)
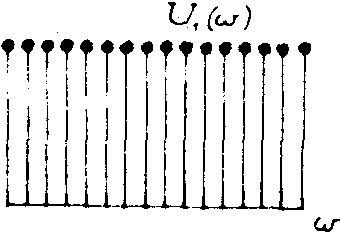
преобразуется в изоморфный Уолш-образ. Первая компонента, соответственно, описывается постоянной функцией u1(w
}=1(w
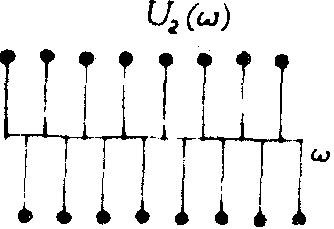
) (рис.10б). Вторая компонента имеет вид (рис.10в):
|
u2(w
= четные) = +1/2
u2(w
= нечетные) = -1/2 |
(59) |
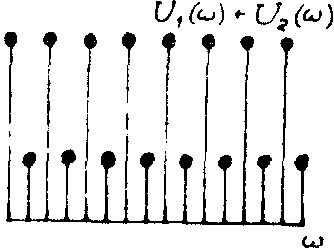
Сумма этих двух компонент показана на рис.10г. После возведения в квадрат получится сигнал i(w
), приведенный на рис.10д.
- 108 -
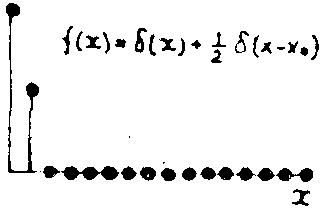 
а) б)
в) г)

д)
Рис.10.
а) Решетчатая функция ¦
(х), описывающая простейший входной сигнал, который состоит из двух дельта-функций, при Ха=1.
б) Изоморфный Уолш-образ первой компоненты d
(х) входного сигнала (рис.а).
в) Изоморфный Уолш-образ второй компоненты d
(х-х 0) входного сигнала (рис.а).
г) Изоморфный Уолш-образ входного сигнала, состоящего из двух дельта-функций (рис.а).
д) Вид логической голограммы для входного сигнала, показанного на рис.а .
- 109 -
10. Стадия восстановления сигнала
Восстановление сигнала, записанного в виде логической голограммы i(w
), осуществляется с помощью системы, схема которой приведена на рис.11. Она содержит две преобразующих цепи. На вход первой из них подается восстанавливающий сигнал w(x). Сигнал с выхода первой цепи поступает на логическую голограмму. При этом здесь происходит алгебраическое перемножение образа восстанавливающего сигнала w(w
) со значением интенсивности i(w
) логической голограммы. Полученный таким образом сигнал поступает на вторую цепь. Каждая из этих цепей осуществляет гомоморфное преобразование Уолша с одним и тем же показателем гомоморфности mz на стадии восстановления. На выходном терминале второй цепи z отобразится восстановленный сигнал r(z).
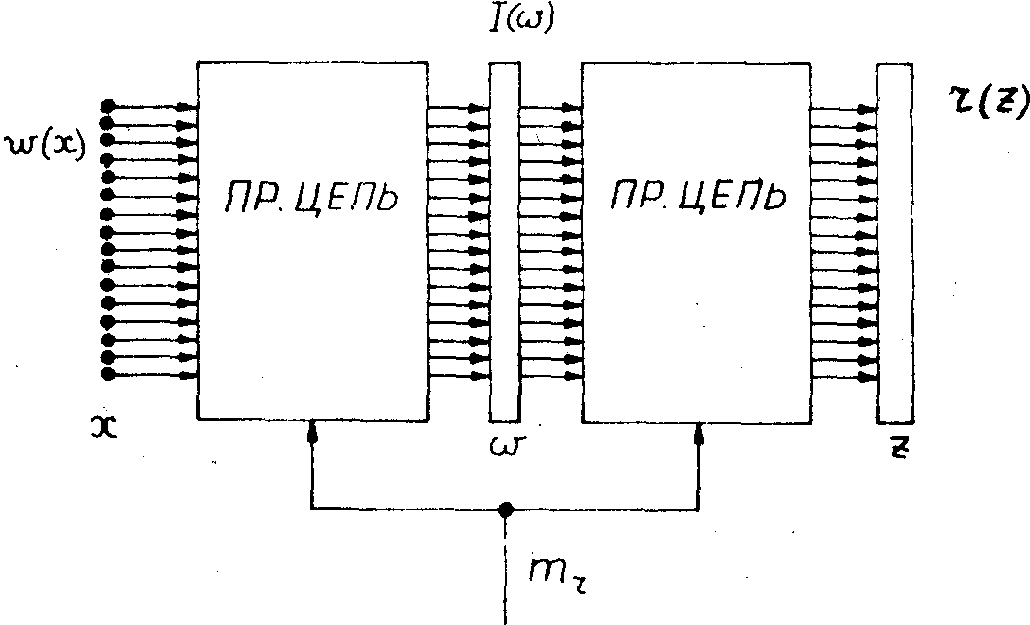
Рис.11. Стадия восстановления сигнала в вида решетчатой функции с помощью логической голограммы для n=16 (см. текст).
Если ключи в обеих преобразующих цепях поставить в положение, соответствующее mr=15, и взять w(х) = d
(х), то получится восстановленный сигнал r(z), который для рассматриваемого примера с входным сигналом (58) будет иметь вид, показанный на рис.12.
- 110 -
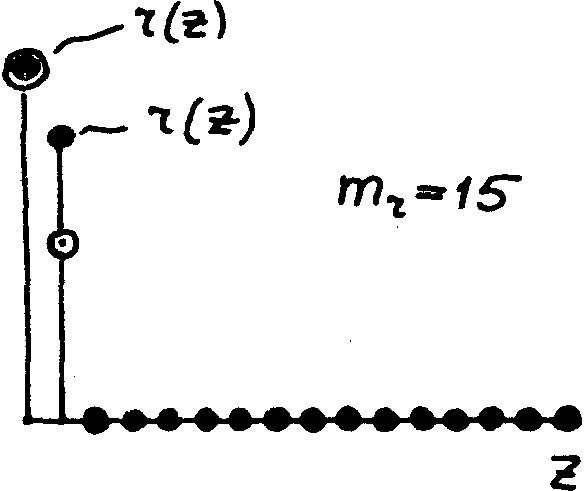
Рис.12. Восстановленный сигнал, полученный с помощью цепи, приведенной на рис.11, для логической голограммы двух дельта-функций (рис.10д).
Видно, что исходный сигнал восстановлен полностью, если не считать того, что соотношение между предметным и опорным сигналами нарушилось. Вместо a
= 1/2 получилось a
’= 4/5. Это результат нелинейного преобразования, каким является возведение в квадрат поля-образа на стадии получения логической голограммы. Аналогичные искажения имеют место в классической голограмме.
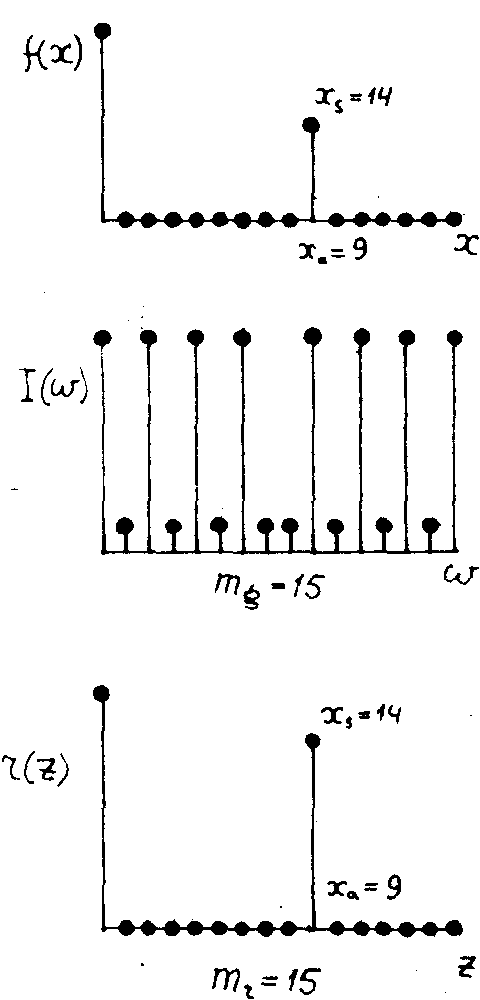
Если расстояние между узкими сигналами u(х) и v(х) уменьшить и взять, например, Ха = 9 (рис.13), то шаг интерференционной картины в логической голограмме возрастет, а число волн на логической голограмме уменьшится. Все происходит точно так же, как в опыте Юнга. Отличие опыта Юнга-Уолша от опыта Юнга состоит в том, что все сигналы являются дискретными, а преобразующее пространство заполнено электрической цепью.
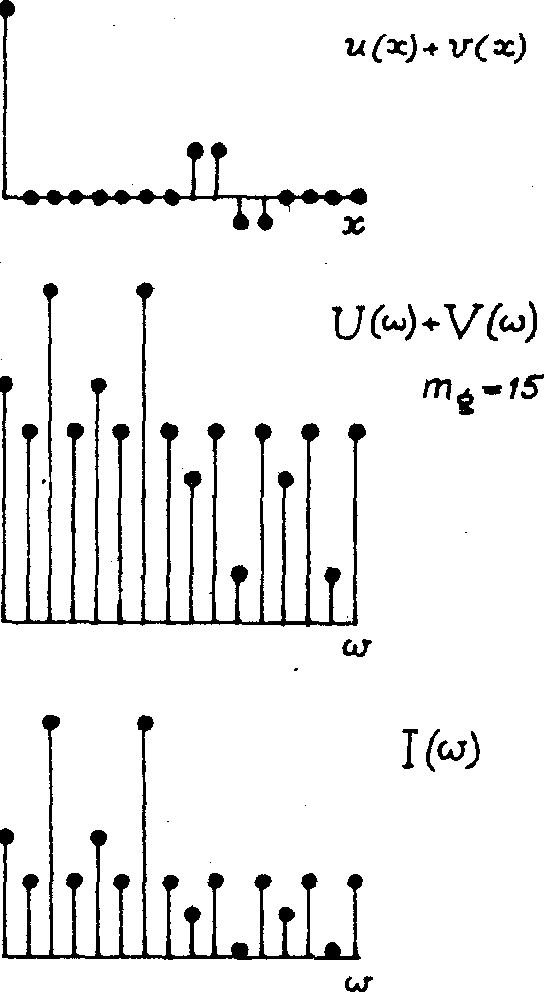
Если, наконец, взять предметный сигнал более сложной формы (рис. 14), то при восстановлении (рис.15) возникнет побочная компонента, которая в исходном сигнале отсутствовала. Это - результат тех же нелинейных искажений.
- 111 -
|
|
а)
б)
в) |
|
|
Рис.13
Стадии получения и восстановления в логической голографии для входного сигнала, состоящего из двух дельта-функций, при Ха =9:
а) входной сигнал;
б) логическая голограмма;
в) восстановленный сигнал. |
|
Рис.14.
Входной сигнал более сложной формы, чем на рис.10а и рис.13.а. |
- 112 -
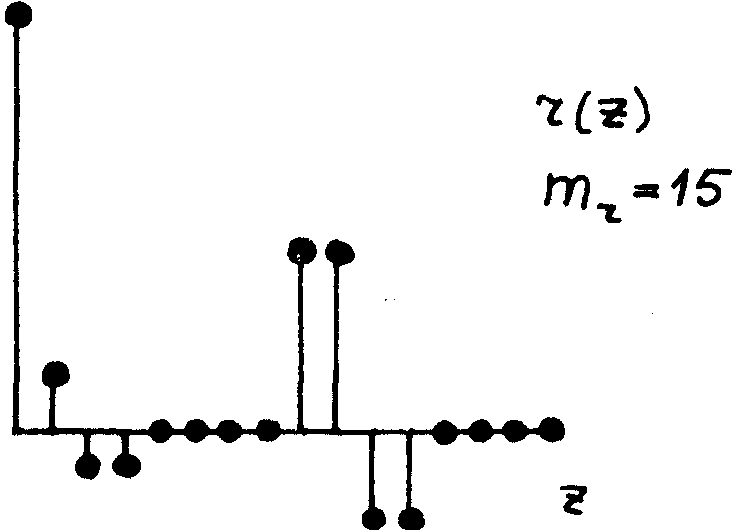
Рис.15. Восстановленный сигнал, соответствующий входному сигналу на рис.14.
11. Влияние показателя гомоморфности
Управляя ключами преобразующей цепи, можно выполнить преобразование Уолша с любым показателем гомоморфности. Сначала проанализируем влияние показателя гомоморфности на стадии восстановления. На рис.16 приведена структура логической голограммы для сигнала из рис.14 при максимально возможном показателе гомоморфности mg = 15. Как видно из рис.17а, при восстановлении с показателем гомоморфности mr = 15 восстановленный сигнал r(x) содержит исходный сигнал u(х) без искажений. Теперь возьмем показатель гомоморфности на стадии восстановления, равный mr = 11. Восстановленный сигнал имеет вид, показанный на рис.17б. Видно, что появились искажения. В нашем случае - это своеобразный эффект "эха". Чтобы понять причину эффекта удвоения со сдвигом, необходимо учесть то, что преобразующая схема с показателем гомоморфности mr = 11 пропускает компоненты с индексами x и w
, которые равны
0, 1, 2, 3; 0, 1, 2, 3; 8, 9, 10, 11; 8, 9, 10, 11.
Полностью пропущены компоненты
- 113 -
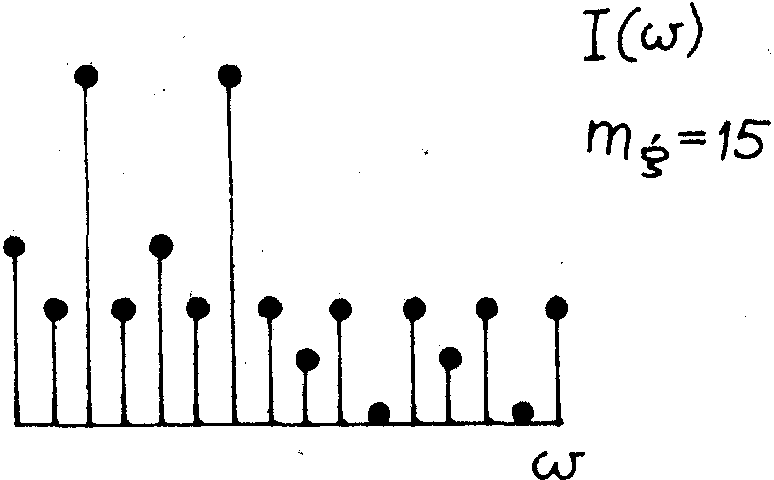
Рис.16. Структура логической голограммы сигнала, приведенного на рио.14, при показателе гомоморфности mgmax = 15.
|
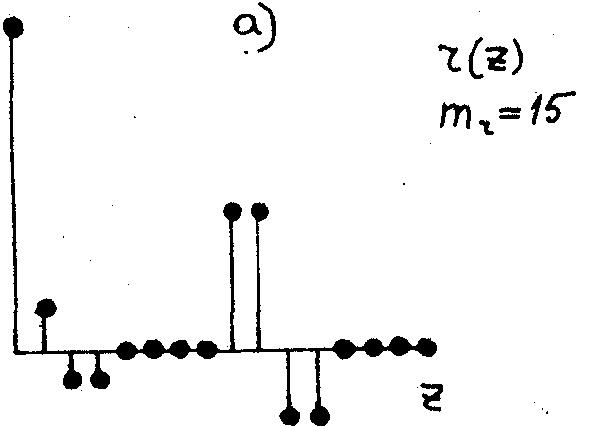
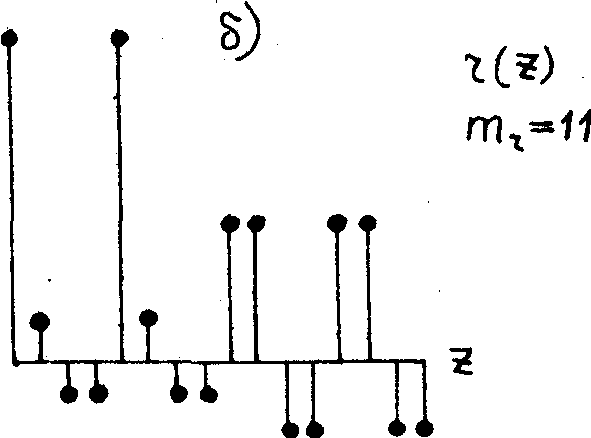
|
Рис.17
Восстановленный сигнал при разных значениях показателей гоморфности на стадии восстановления:
а) показатель гоморфности на стадии восстановления mr = 15;
б) mr = 11 |
|
|
- 114 -
4, 5, 6. 7; 12, 13, 14, 15
Такой пропуск некоторых компонент как раз приводит к тем искажениям, которые видны на рис.17б.
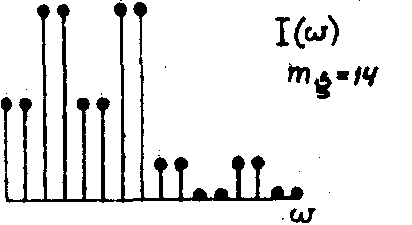
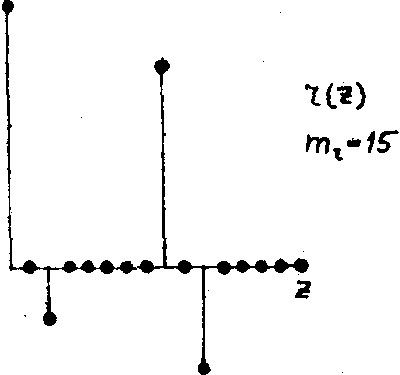
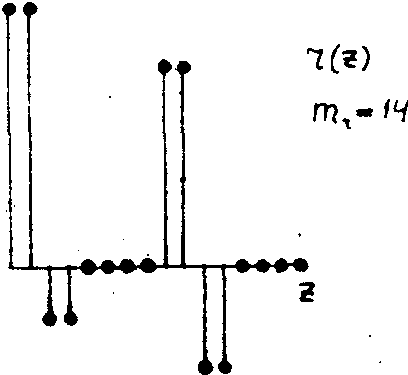
Рассмотрим теперь влияние показателя гомоморфности на стадии получения логической голограммы. Возьмем такой же сигнал (рис.14) и получим логическую голограмму, когда цепь работает с показателем гомоморфнооти mg = 14. Если учесть, что преобразующая цепь с mg = 14 пропускает w
-компоненты только с четными индексами в порядке
0, 0, 2, 2, 4, 4, 6, 6, 8, 8, 10, 10, 12, 12. 14, 14
а все нечетные компоненты блокируются, то неудивительно, что новая логическая голограмма (рис.18а) вдвое беднее той логической голограммы (рис.16), которая была получена при максимально возможном показателе гомоморфности mg. Все нечетные w
-компоненты выброшены, и их места заполнили четные компоненты, расположенные слева. Если теперь восстановить сигнал при показателе гомоморфности на стадии восстановления mr = 15, то получится сигнал, показанный на рис.18б. Наконец, если стадию восстановления провести с mr = 14, то получится сигнал, приведенный на рис.18в. Искажения в результате удвоения со сдвигом приводят в данном частном случае к увеличению числа пиков с двух до четырех. Чисто случайно искаженный сигнал совпадает с исходным сигналом на рис.14.
Используя эффект пропуска определенных ..компонент с изменением показателя гомоморфности на стадии восстановления, можно вести процесс гомоморфной фильтрации с отбором только желательных компонент логической голограммы или записанного на ней сигнала. При этом в отличие от классической голографии, функционирующей по схеме согласованной фильтрации, гомоморфный фильтр не содержит поглощающих масок, а переход от одной программы гомоморфной фильтрации к другой осуществляется с временами, типичными для совершения одного переключения в электрической схеме. Все эти свойства логической голограммы имеют принципиальное значение.
- 115 -
|
|
Рис.18.
Влияние показателя гоморфности на стадии получения логической голограммы:
а) структура логической голограммы при mr = 14;
б) восстановленный сигнал для mr=15;
в) восстановленный сигнал для mr= 14 (см. текст).
|
12. Логическая голограмма. как устойчивая форма записи информации
Как известно, классическая голограмма Фурье обладает предельно высокой устойчивостью к потере какой-либо части голограммы. Даже небольшой фрагмент голограммы воссоздает полностью все изображение. И единственное, что происходит - это ухудшается разрешающая способность в изображении и ослабляется эффект объемности.
Убедимся в том, что аналогичный эффект наблюдается у логической голограммы. Возьмем логическую голограмму на рис.10д и "отобьем" у нее фрагмент, например, правую половину. При восстановлении получится сигнал, который имеет структуру "размытой" дельта-функции (рис.19). Если такой фрагмент "отбить" от исходного сигнала
- 116 -
u (х), то, очевидно, информация об этом сигнале была бы полностью потеряна. Естественно, такая устойчивость записи информации о сигнале в форме логической голограммы вызвана тем, что информация о сигнале в ней имеет нелокализуемую структуру.
Рис.19. Устойчивость логической голограммы как интегральной формы записи исходного сигнала:
а) исходная логическая голограмма (рис.10д);
б) фрагменты логической голограммы, i1(w
), i2(w
)
в) сигналы восстановленной по фрагментам (б) логической голограммы.
- 117 -
13. Ассоциативность логической голограммы
Ассоциативностью логической голограммы называют симметрию к взаимной замене двух волн, предметной и опорной, участвующих на стадии получения голограммы в процессе восстановления. Так, например, если голограмму осветить предметной волной, то восстановится опорная волна. Чтобы убедиться в этом, рассмотрим структуру голограммы, образованной при интерференции полей а и r. Распределение интенсивности равно:
i = |
а|
2 + |
r |
2 + a *r + аr* (60)
Если голограмму i осветить волной а, то поле, восстановленное за голограммой, имеет вид
а i = аа*а + аr*r + аа*r + аar * (61)
Если
|
a|
2 @
const и |
r|
2 @
const (62)
то
а i ®
a + r + r*aa (63)
Видно, что волна а восстанавливает волну r и искаженную комплексно-сопряженную волну r*.
Если же голограмму i осветить волной r, то поле за голограммой имеет вид
ri = r а*а + rr*r + r а*r + аrr* (64)
или с учетом (62)
ri ®
r + a + a*rr (65)
Теперь волна r восстанавливает волну а и искаженную комплексно--сопряженную волну а*.
- 118 -
Тем же свойством ассоциативности обладает логическая голограмма. Убедимся в этом на примере. Возьмем два сигнала u(х) и v(x) (рис.20). Логическая голограмма для mg = 15 имеет вид i(w
) (рис.20б). Если в качестве освещающей волны w(х) взять первый сигнал u(x) (рис.20в), то на стадии восстановления появится сигнал r(z) (рис.20г), который своей правой частью похож на сигнал v(х). Строгого совпадения не получилось потому, что |
u(w
)|
2 не равна постоянной решетчатой функции (рис.20д).
Аналогичный аффект ассоциативности будет получен, если на стадии восстановления использовать в качестве освещающего сигнала w(x) второй сигнал v(х) (рис.21а). Появится сигнал r(z), который (рис.21б) своей левой частью похож на сигнал u(х ). Явные, хотя и небольшие искажения, вызваны тем, что |
v(w
)|
2 неравно постоянной величине (рис.21в).
Полная ассоциативность в логической голограмме будет достигнута только в том случае , если логическая автосвертка сигнала u(х) так же, как и сигнала v(х),равна дельта-функции или весьма близка. к ней.
14. Теория логической голограммы
До сих пор в рассмотренных выше примерах не затрагивался вопрос о том, каким образом работает реальная преобразующая цепь и каковы сигналы, которые могут быть в ней преобразованы. Фактически здесь имеется много возможностей, как с постоянными, так и с переменными электрическими сигналами. Разберем систему, приведенную в работе /21/, в которой используются несущая, зависящая от времени, в виде функции Уолша.
Пусть сигналы u(x) и v(x), описываемые решетчатыми функциями, размещены вдоль координаты х без перекрытия и пусть р=2. Эти сигналы осуществляют модуляцию несущей Уолша:
a(t) = ha(t,m) (66)
где t - время, a m - волновое число. Сигнал на входе преобразующей цепи имеет вид:
- 119 -
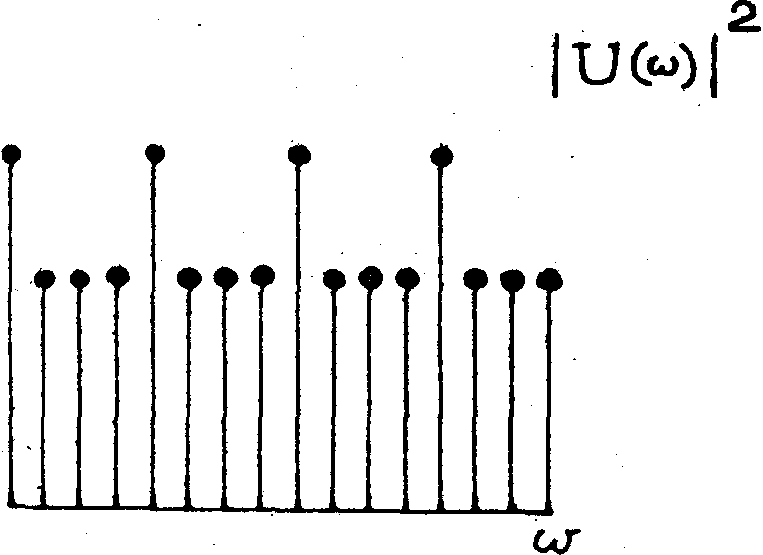
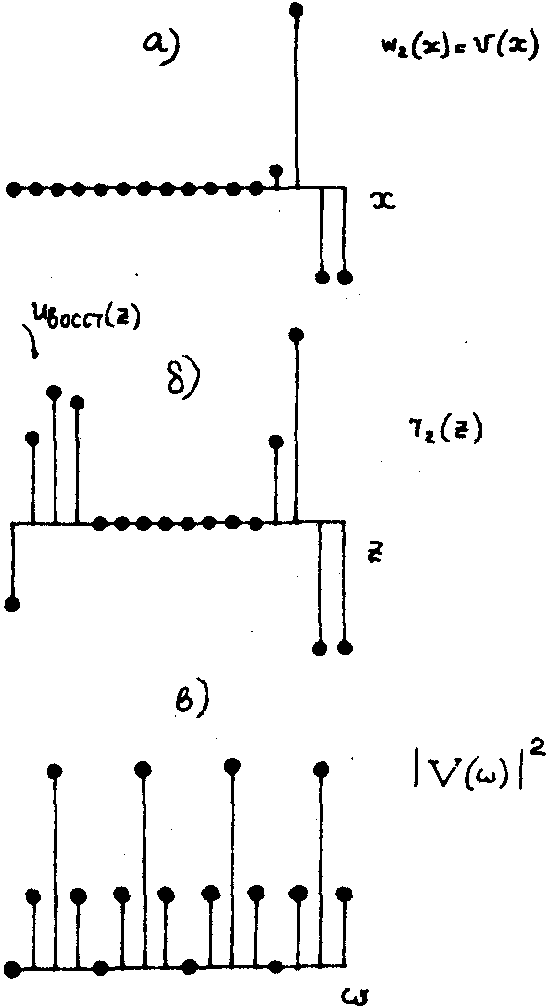
Рис.20. Свойство ассоциативности логической голограммы:
а) исходные сигналы, u(х ) - предметный сигнал и v(x) - опорный сигналы; б) логическая голограмма для mg = 15; в) освещающий сигнал равен предметному сигналу u(х); г) восстановленный сигнал, когда в качестве освещавшего сигнала выбран предметный сигнал u(х); д) квадрат модуля изоморфного уолш-образа предметного сигнала.
- 120 -
|
|
Рис.21.
Стадия восстановления с использованием в качестве освещающего сигнала опорного сигнал v(x):
а) освещающий сигнал;
б) восстановленный сигнал;
в) квадрат модуля изоморфного уолш-образа опорного сигнала.
|
Ф( x,t) = [u(х) + v(х)]hа(t,mg) (67)
Этот сигнал подвергается в цепи гомоморфному преобразованию Уолша. Сигнал, возникающий на гребенке w
, имеет амплитуду, которая равна
Ф (w
) = u(w
;mg) + v(w
;mg) (68)
где u(w
;mg) и v(w
;mg) - гомоморфные уолш-образы с показателем гомоморфности mg. На логической голограмме зарегистрируется распределение интенсивности вида
- 121 -
i(w
) = |u(w
,mg) + v(w
,mg)|
2 = |
u|
2 + |
v|
2 + u*v + uv* (69)
Фикцию i(w
) можно представить в виде
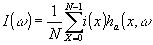  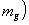 (70) (70)
где
|
i(x) = u*(x)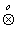 u(x)
+ v*(x) u(x)
+ v*(x)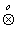 v(x)
+ v(x)
+
+ u*(x)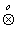 v(x)
+ v*(x) v(x)
+ v*(x)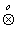 u(x) u(x)
|
(71) |
Здесь значок 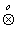 обозначает операцию логической свертки, рассмотренную выше.
обозначает операцию логической свертки, рассмотренную выше.
На стадии восстановления логическая голограмма "освещается" волной w(х), гомоморфный уолш-образ которой равен
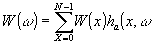  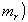 (72) (72)
где mr - показатель гомоморфности преобразующих цепей на стадии восстановления.
Если "освещающий" сигнал равен дельта-функции, то дополнительных преобразующих цепей перед логической голограммой не требуется, поскольку в этой случае w(w
) = const.
В общем случае восстановленный сигнал равен
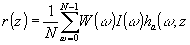  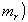 (73) (73)
Если u(x) = w(x) = d
(х), то
r(z) = d (z) + v*(z)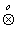 v(z)
+ v(z) + v*(z) (74) v(z)
+ v(z) + v*(z) (74)
- 122 -
Если р > 2, то восстановленный сигнал равен
Здесь
|
u’(z) = u[z (mr (mr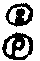 mg)] mg)]
v’(z) = v[z (mr (mr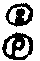 mg)] mg)]
|
(76)
|
а 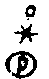 обозначает
логическую корреляцию по модулю р ® обозначает
логическую корреляцию по модулю р ®
¦ (x)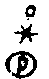 g(x)
= g(x)
= 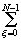 ¦
(x )g(x ¦
(x )g(x x
) (77) x
) (77)
а 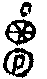
- логическую свертку по модулю р
®
¦ (x) g(x)
= g(x)
= 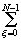 ¦
(x )g(x ¦
(x )g(x x
) (77) x
) (77)
Сигналы u’(z)
и v’(z) b (76)
отличаются от сигналов u(z)
и v(z) для
mg ¹ mr
тем, что они смещены друг относительно друга и растянуты по оси z
в отношении mg  mr. Аналогичный процесс волнового
увеличения происходит в классической голограмме, если длина волны на стадии
получения голограммы отличается от длины волны излучения на стадии восстановления.
mr. Аналогичный процесс волнового
увеличения происходит в классической голограмме, если длина волны на стадии
получения голограммы отличается от длины волны излучения на стадии восстановления.
Если w(x) = u(x) = d
(x), то
|
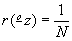  [d
(z) + v’*(z) [d
(z) + v’*(z) v’(z)
+ v’(z)
+
+ u’(z) + v’*(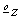 ) )
|
(75) |
Знак ( 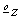 )
обозначает, что оси z
и z’= )
обозначает, что оси z
и z’=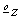 отличаются друг от друга тем, что одна из них является логически обратной другой
по
отличаются друг от друга тем, что одна из них является логически обратной другой
по
- 123 -
модулю р . Аналогом этого преобразования в мире по модулю р является простое обращение z®
z’=-z в обычном пространстве. Последнее означает только то, что изображение, получающееся в классической голографии Фурье, является перевернутым.
15. Мультипликативность функций Уолша
Как в опыте Юнга, так и при получении классической голограммы Фурье, сначала происходит сложение полей, а потом образуется картина распределения интенсивности суммарного поля. Происходит цепочка преобразований i
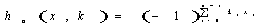 (80) (80)
где 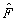 - оператор преобразования Фурье, а
- оператор преобразования Фурье, а
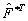 -
эрмитовски сопряженное f. -
эрмитовски сопряженное f.
Поскольку ядром преобразования Фурье является комплексная экспонента,
при умножении двух операторов 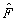 возникает оператор, ядро которого также является комплексной экспонентой. Именно
его позволяет получить на стадии восстановления исходный сигнал, подвергнутый
линейному преобразованию (автосвертка), несмотря на то, что на стадии получения
голограммы происходил нелинейный процесс возведения в квадрат суммарного поля.
возникает оператор, ядро которого также является комплексной экспонентой. Именно
его позволяет получить на стадии восстановления исходный сигнал, подвергнутый
линейному преобразованию (автосвертка), несмотря на то, что на стадии получения
голограммы происходил нелинейный процесс возведения в квадрат суммарного поля.
Подобная цепочка преобразований имеет место для логической голограммы. А именно, на стадии получения
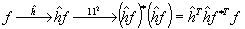 (81) (81)
Благодаря свойству мультипликативности функций Уолша, являющихся ядром преобразования Уолша, при умножении двух операторов получится оператор, ядро которого равно функции Уолша. Тогда на стадии восстановления получается сигнал, который равен логической автосвертке исходной функции
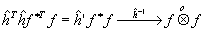 (82) (82)
- 124 -
Видно, что возведение в квадрат суммарного сигнала не препятствует стадии восстановления по той причине, что ядро преобразования Уолша, т.е. сами Функции Уолта обладают свойством мультипликативности. А именно, при умножении двух функций Уолша получается функция Уолша с индексом, который равен логической сумме индексов функций-сомножителей.
Для того, чтобы автосвертка не вносила искажений в восстановленном предметном сигнале, достаточно предметный и опорный сигналы разнести друг от друга на такое расстояние, чтобы свертка между опорным сигналом и предметным сигналом не перекрывалась с остальными компонентам свертки,
Таким образом, именно свойство мультипликативности функций Уолша лежит в основе всей системы построения логической голограммы, подобно тому, как мультипликативность комплексных экспонент позволяет восстановить предметную волну в классической голографии Фурье .
Отсутствие этого свойства мультипликативности у многих других ортогональных преобразований полностью исключает их использование в логических цепях, типа цепей для получения логической голограммы, и для восстановления сигналов. Например, не годится для этого дискретное преобразование Лежандра. Как известно, произведение двух решетчатых функций Лежандра не равно одной функции, а сводится к линейной комбинации из функций Лежандра.
16. Заключение
Появление логической голографии, о которой на vi школе по голографии говорится впервые, есть результат бурного развития как классической голографии, так и ведущихся интенсивных исследований в области решетчатых функций /23-28/, Последние, кед известно, тесно связаны с алгебраической теорией кодирования /32/ и широким фронтом работ по использованию функций Уолша и других несинусоидальных ортогональных базисов во многих разделах физики /33-37/ и техники.
Существенным преимуществом решетчатых функций и технических устройств, функционирующих по быстрым алгоритмам дискретной логики /21-31/, является то, что они хорошо подходят для непосредственного
- 125 -
сочленения с электронно-вычислительными машинами, а также для реализации при помощи логических интегральных схем. Простота последних определяется тем, что в них должны происходить только операции сложения и вычитания, а также чередование этих двух операций при помощи управляющих ключей.
В заключение следует подчеркнуть, что разработанные в физике разные системы измерений, построенные по логике интегрального или мультиплексного считывания информации / 33/ и приспособленные для работы при высоких уровнях помех и дрейфа регистрирующих блоков, открыты для дальнейшего усовершенствования с учетом свойств логической голограммы. Последняя может дополнительно увеличить степень иммунитета этих систем к потере рекорда или к высокому уровню шума в каналах регистрации, а кроме этого придаст системам полезное свойство ассоциативности.
Автор признателен Я.А.Смородинскому за полезные дискуссии.
Литература
1. Л.М.Сороко. Материалы i Всесоюзной школы по голографии, Л-д, стр.43, 1971.
2. Л.М.Сороко Материалы i Всесоюзной школы по голографии, Л-д, стр.73, 1971.
3. Л.М.Сороко. Материалы ii Всесоюзной школы по голографии, Л-д, стр.40, 1972.
4. Л.М.Сороко. Материалы v Всесоюзной школы по голографии, Л-д, стр.40, 1973.
5. Л.М.Сороко. Материалы v Всесоюзной школы по голографии, Л-д, стр.100, 1973.
6. Р.Хэнбери Браун. Измерение угловых диаметров звезд. УФК, 108, №3, 529-547, 1972.
7. Б.Бэрн. Интерферометрия с большими базами. УФН, 101, №3, 537-552, 1970.
8. М.Райл. Кембриджский одномильный радиотелескоп. УФН, 98, № 2, 383-392, 1969.
9. К.Келлерамн. Межконтинентальная радиоастрономия. УФН, 103, № 3, 591-611, 19753.
- 126 -
10. j.perlna. coherence of light. van hostrand. london, 1971.
11. Г.И.Копылов, М.И.Подгорецкий. Корреляция тождественных частиц, испускаемых высоковозбужденными ядрами. Сообщение ОИЯИ, Р4-5927, 1971.
12. В.Л.Любошиц. М.И.Подгорецний. Симметризация волновых функций тождественных частиц и принцип интерференции квантово-механических амплитуд. Сообщение ОИЯИ, Р2-5809, 1971.
13. Г.И.Копылов. Когерентность мезонов, испускаемых некогерентным образом. Сообщение ОИЯИ, p2-7120, 1973.
14. М.Борн и Э.Вольф. Основы оптики. "Наука", стр.292, 1970.
15. Л.М.Сороко. Основы голографии и когерентной оптики. "Наука", 1971.
16. Я.В.Цыпкин. Теория линейных амплитудных систем. Физматгиз, М., 1963.
17. jennifer wallis. hadamard matrices. lecture notes in mathematics. no 292, springer, pp. 273-489, 1972.
18. М.Холл. Комбинаторика. "МИР", Москва, 1970.
19. Р.Кольер, К.Беркхарт, Л.Лин. Оптическая голография, "МИР", стр.429-469, 1975.
20. t.h.prank, "implementation of dyadic correlation". ieee trans. ЕmС-13, pp. 111-117, 1971.
21. y.morita, y.sajwrai. "holography by walsh wave". cm. /28/; pp.122-126.
22. h.p.harmuth. transmission of information by orthogonal functions, berlin, springer, 2-nd edition, 1971.
23. С.А.base (ed.). 1970 proo. applications of walsh functions. washington, d.c. , ad 707431, 1970.
24. p.d.linee (ed.). "1971 proceedings of ths symposium theory and applications of walsh functions." the hatfield polytechnic, hatfield, u.k., 1971.
25. r.w.zeak, a.e.showalter (ed.). 1971 proc. applications of walsh functions, washington, d.c., ad-727-000, 1971.
26. r.w.zeek, a.e.showalter (ed.). 1972 proc. applications of walsh functions, washington, d.o., ad-744, 650, 1972.
27. p.d.lines, r.barrett (ed.). 1973 proceedings of the colloquim theory and applications of walsh functions and other non-sinusoidal functions. the hotfield polytecblic, hatfield, u.k., 1973.
- 127 -
28. r.w.zeek, e.a.showalter (ad.). 1973 proceedings applications of walsh functions, washington, d.c, ad-763-000, 1973.
29. h.e.chrestenson. a glass of generalized walsh functions. pacific. j.math., 5, 17-31, 1955.
30. r.g.selfridge. generalized walsh transform, pacific j.math., 5, 451-480, 1955.
31. Л.М.Сороко, Т.А.Стриж. Спектральные преобразования на цифровых вычислительных машинах. Сообщение ОИНИ, pio-6702, Дубна, 1972.
32. Э.Берленэмп. Алгебраическая теория кодирования, "МИР", 1971.
33. Л.М.Сороко. Мультиплексные системы регистрации частиц. ПТЭ, № 5, стр.17-19, 1973.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

