|
|
 |
 |

|
| |
СТРОГАЯ ТЕОРИЯ ОБЪЕМНЫХ ГОЛОГРАФИЧЕСНИХ РЕШЕТОК И ПЕРСПЕКТИВЫ ЕЕ РАЗВИТИЯ
Э.И.Крупицкий, Б.К.Чернов
Задача дифракции монохроматической световой волны на объемной голографической решетке, представляющей собой плоский слой с периодическим изменением коэффициента преломления, формулируется в виде дифференциальных и интегральных уравнений. Обсуждаются методы строгого решения. Приводятся известные результаты строгого решения методом характеристических волн и новые результаты, относящиеся к слою, модулированному в поперечном направлении. Дается строгое решение задачи дифракции для общего случая методом связанных волн. Указываются перспективные направления дальнейшего развития строгой теории.
Объемные голографические решетки представляют собой плоский слой о периодическим изменением коэффициента преломления, в общем случае комплексного. Задача дифракции монохроматической световой волны формулируется в виде дифференциальных и интегральных уравнений. Обсуждаются методы строгого решения. Приводятся известные результаты строгого решения и новые результаты, относящиеся к слою, модулированному в поперечном и произвольном направлениях. Обсуждается пути дальнейшего развития строгой теории.
Введение
Развитие строгой теории объемных голографических решеток имеет большое практическое значение для голографии и ряда смежных областей (ультразвуковая модуляция света, частотная фильтрация света и др.).
- 47 -
Строгая теория позволяет анализировать процесс дифракции света на таких решетках без каких-либо ограничений на параметры (глубину модуляции, углы падения и частоту дифрагирующей волны, толщину слоя и т.п.), а также оценивать качество и границы применимости более простых и легко обозримых приближенных решений.
С практической точки зрения основной интерес представляет двухмерная модельная задача дифракции плоской монохроматической волны света на неограниченном плоском слое произвольной толщины (рис.1. ) с периодически модулированным коэффициентом диэлектрической проницаемости:
e
2(x,z) = e
c[1 - g
y
(kx х – kzz)] (1)
где e
с - средняя проницаемость среды слоя; g
- индекс модуляции; kx=k·cosa
; kz=k·sina
; k=2p
/l
; L
- период решетки; a
- угол наклона "слоев" к оси z. Функция y
(t) предполагается четной, 2p
-периодической и дважды непрерывно дифференцируемой, макс. |
y
(t)|
=1.
Зависимость (1) соответствует голографическому методу записи решетки путем интерференции двух когерентных плоских волн, распространяющихся в плоскости x0z. В общем случае e
с является

Рис.1 .
Дифракция плоской волны на периодически неоднородном слое.
- 48 -
несимметричным тензором (запись в анизотропной среде с потерями, например, в кристалле). Однако, ввиду неразработанности строгой теории для случая анизотропной среда, мы ограничим рассмотрение случаем изотропных сред с потерями, когда e
с является скалярной величиной, вообще говоря, комплексной. Всюду в дальнейшей мы будем предполагать, что рассматривается упомянутая выше двумерная задача дифракции плоской монохроматической волны.
Для строгого решения этой задачи было предложено три метода: метод характеристических волн, метод связанных волн и метод интегральных уравнений. Все эти три метода будут в дальнейшем рассмотрены подробно. Здесь же отметим, что сущность метода характеристических волн состоит в отыскании поля в модулированном слое в виде суперпозиции характеристических решений волнового уравнения ос периодическим волновым числом для безграничной среды. Эти решения являются аналогом собственных волн в металлическом волноводе (так называемых "мод"). Наиболее последовательное изложение этого метода дано в работах /1-3/ применительно к задаче дифракции света на ультразвуковых волнах.
На основе этого метода в работах /4,5/ сделан численный расчет дифракционной эффективности объемной диэлектрической решетки с чисто продольной синусоидальной модуляцией (kz=0). Тем же методом в /6/ получено строгое решение задачи для случая произвольной периодической модуляции комплексной проницаемости вдоль слоя. При этом автор ограничился частным случаем e
1= e
2 (случай решетки в безграничной иммерсионной среде).
Авторами настоящей работы методом характеристических волн получено строгое решение задачи для диэлектрического слоя с чисто поперечной синусоидальной модуляцией (kx=0). Это решение приводится ниже.
В работах /2,6/ рассматривается случай дифракции Н-волн, когда вектор электрического поля нормален к плоскости падения. Случай Е-волн, когда вектор электрического поля лежит в плоскости падения, более сложен. Общая постановка задачи для этого случая дана в работах /1,4,7/.
В методе связанных волн решение внутри модулированной среды ищется в виде ряда с переменными коэффициентами, для которых получается
- 49 -
бесконечная система дифференциально-разностных уравнений. Как показано в /8/, метод особенно удобен для получения простых приближенных решений при дифракции, близкой к брэгговской. В более строгой постановке метод использовался в работах /9,10/.
В работе /9/ рассматривалась дифракция Н-волн на ультразвуковых волнах (продольная синусоидальная модуляция среды), а в /10/ на голографической решетке с синусоидальной модуляцией общего вида.
Решения были получены не для слоя, а для модулированного полупространства в пренебрежении отражением света от границы и потому не могут считаться вполне строгими.
В настоящей работе приводится строгое решение задачи дифракции ни слое для наиболее общего случая .
В методе интегральных уравнений поле внутри модулированного няни определяется путем решения некоторого интегрального уравнения второго рода. Применительно к случаю дифракции света на ультразвуковых волнах точное уравнение было получено в работе /11/. Его решение отыскивалось в форме двойного ряда экспоненциальных функций. Хотя выбранная форма решения и позволяет построить строгое решение, в работе /11/ оно не было получено ввиду серьезных вычислительных трудностей.
Ниже приводится другой вывод интегральных уравнений, позволяющий получать интегральные уравнения, отличные от приведенного в /11/ и представляющие определенный интерес.
1. Дифференциальные и интегральные уравнения задачи и методы решения
Комплексные амплитуды векторов электромагнитных волн в любой точке (кроме границ раздела сред) удовлетворяют уравнениям Максвелла
rot = -iw
m 0 = -iw
m 0 ;
rot ;
rot = iw
e = iw
e  (2) (2)
где
|
e
= |
|
e
1; z < 0; z > d |
|
e
2 = e
c(1-g
y
); 0 < z < d |
- 50 -
На границах раздела сред они заменяются граничными условиями:
|
Е1х = Е2х; Е1у = Е2у; Н1х = Н2х; Н1у = Н2у; при z=0 |
(4) |
|
Е2х = Е3х; Е2у = Е3у; Н2х = Н3х; Н2у = Н3у; при z=d |
где цифровой индекс соответствует номеру среды (рис.1).
Запишем уравнения (2) в декартовой системе координат, учитывая, что поля и параметры среды не зависят от координаты у.
|
¶
Еу |
=iw
m
0hx; |
¶
hy |
= -iw
e
ex; |
(5) |
|
¶
z |
¶
z |
|
¶
ex |
- |
¶
ez |
=-iw
m
0hy; |
¶
hx |
- |
¶
hz |
=iw
e
ey; |
|
¶
z |
¶
x |
¶
z |
¶
x |
|
¶
ey |
=iw
m
0hz; |
¶
hy |
=iw
e
ez; |
|
¶
ex |
¶
x |
Любая падающая волна может быть представлена как сумма волн, одна из которых имеет Н y=0 (Н-волна), а другая Еy=0 (e -волна). Поэтому общую задачу дифракции всегда можно разбить на две частные: задачу дифракции Н-волны и задачу дифракции e-волны. В силу изотропности сред в процессе дифракции тип волны сохраняется.
Случай Н-волн. При этом отличны от нуля лишь компоненты Еу , Нх и Нz. Следовательно, вместо (5) получим:
|
¶
Еу |
=iw
m
0hx; |
¶
ey |
= -iw
m
0hz; |
(6) |
|
¶
z |
¶
z |
|
¶
hx |
- |
¶
hz |
=iw
e
ey; |
|
¶
z |
¶
x |
Откуда находим волновое уравнение для Е y:
D
ey + k2ey = 0 (7)
- 51 -
где
|
k2 = w
2m
0e
= |
|
k21 ; при z < 0; z > d/ |
|
k22 = k2c(1 - g
y
); при 0 < z < d |
k21 = w
2m
0e
1; k2c = w
2m
0e
c/
Граничные условия для Еу будут ;
|
Е1у = Е2у ; |
¶
Е1у |
= |
¶
e2y |
при z = 0 |
(8) |
|
¶
z |
¶
z |
|
Е2у = Е3у ; |
¶
Е2у |
= |
¶
e3y |
при z = d |
|
¶
z |
¶
z |
Компоненты Нх и Нz выражаются через Еу, согласно (6).
Случай Е-волн . При этом отличны от нуля только компоненты Н y, Ех и Еz. В результате получаем
|
¶
Ну |
=iw
e
Еz; |
¶
hy |
= -iw
e
ex; |
(9) |
|
¶
х |
¶
z |
|
¶
ex |
- |
¶
ez |
= -iw
m
0hy; |
|
¶
z |
¶
x |
Отсюда находим, что Ну должно удовлетворять уравнению
|
¶
|
|
1 |
¶
hy |
|
+ |
¶
|
|
1 |
¶
hy |
|
+ hy = 0 |
(10) |
|
¶
x |
k2 |
¶
x |
¶
z |
k2 |
¶
z |
или
|
D
hy + k2hy - |
2 |
¶
k |
- |
2 |
¶
k |
¶
hy |
= 0 |
(11) |
|
k |
¶
x |
k |
¶
z |
¶
z |
и граничным условиях
|
h 1у = h2у; |
1 |
¶
h 1у |
= |
1 |
¶
h2y |
при z = 0 |
|
|
k21 |
¶
z |
k22 |
¶
z |
- 52 -
|
h 2у = h3у; |
1 |
¶
h2 у |
= |
1 |
¶
h3y |
при z = в |
(12) |
|
k22 |
¶
z |
k21 |
¶
z |
Уравнение (11)
можно свести к волновому уравнению вида (7),
но с модифицированным волновым числом  положив hу
= ku.
положив hу
= ku.
Таким образом, для решения задачи дифракции плоской волны на голографической решетке необходимо построить решение волнового уравнения
D u +  2
(x,z)·u =0 (13) 2
(x,z)·u =0 (13)
где
|
 2
(x,z) = 2
(x,z) =
|
|
k2(x,z ) в случае Н-волн |
(14) |
|
 2(x,z 2(x,z
)
в случае Е-волн
|
Для Н-волн u = Еу, а для Е-волн u = Ну/k.
Решение должно строиться отдельно для трех областей: z<0,
z>d и 0<z<d;
причем, в первых двух областях  2(x,z)
= k1. На границах z=0
и z=d решения
должны быть "сшиты" с помощью граничных условий
(8) или (12).
Подставляя Н = ku
в (11), нетрудно
показать, что 2(x,z)
= k1. На границах z=0
и z=d решения
должны быть "сшиты" с помощью граничных условий
(8) или (12).
Подставляя Н = ku
в (11), нетрудно
показать, что
|
 2(x,z)
= k2(x,z) + 2(x,z)
= k2(x,z) +
|
D
k(x,z) |
- |
2|
gradk(x,z)|
2 |
(15) |
|
k(x,z) |
k2(x,z) |
Если e 2(x,z)
меняется только по одной из координат x
или z, то
выражение для  2
несколько упрощается: 2
несколько упрощается:
|
 2(x)
= k2 + 2(x)
= k2 +
|
1 |
d2k |
- |
2 |
· |
dk |
2 |
(16) |
|
k |
dx2 |
k2 |
dx |
|
и
|
 2(z)
= k2 + 2(z)
= k2 +
|
1 |
d2k |
- |
2 |
· |
dk |
2 |
(17) |
|
k |
dz2 |
k2 |
dz |
|
Из (15) - (17)
следует, что даже при чисто синусоидальной модуляции слоя  2(x,z)
будет содержать бесконечное число гармоник того же периода. Это усложняет решение
задачи дифракции Е-волн. 2(x,z)
будет содержать бесконечное число гармоник того же периода. Это усложняет решение
задачи дифракции Е-волн.
- 53 -
Если, однако функция y
(t) выражается бесконечным рядом Фурье, что, например, имеет место при учете нелинейности записи решетки, то практически не будет разницы в решении задач дифракции Н- и Е-волн.
Следует отметить, что разделение переменных в дифференциальных уравнениях задачи можно осуществить при условии, что e
2 зависит только от одной переменной Х или z (продольная, либо поперечная модуляция).
Так как сами решения практически всегда зависят от двух переменных Х и z, то при наложении граничных условий при z = 0 и z=d получаем функциональные уравнения, которые должны удовлетворяться на всей оси Х. При решении эти функциональные уравнения всегда сводят к системам алгебраических уравнений. Наиболее просто это удается сделать в случаях чисто продольной или поперечной модуляции.
Остановимся вкратце на возможных методах решения сформулированных выше задач.
Вне слоя (области z < 0 и z > d) волновое число постоянно и решения волновых уравнений строятся элементарно. Здесь ваяно только выбрать такую форму решения, которая обеспечит выполнение граничных условий. Для этого необходимо учитывать структуру решении внутри слоя. Построение точного решения для области 0 < z < d, соответствующей неоднородному слою, представляет основную трудность.
Для решения задачи могут быть использованы следующие методы:
- метод сеток (прямое численное решение на ЭВМ);
- итерационный метод;
- методы, основанные на сведении уравнения в частных производных к обыкновенным уравнениям с последующим их решением.
Первый метод практически не реализуем современными вычислительными средствами, ввиду быстрого изменения искомой функции. Второй метод также неудовлетворителен, так как приводит к вычислении громоздких интегралов. При численном их решении возникают те же трудности, что и в первом методе, а при аналитическом - получаются крайне громоздкие выражения. Кроме того, вызывает трудности оценка сходимости процесса итераций.
Поэтому данный метод представляет интерес в основном для
- 54 -
получения простых приближенных решений при малом индексе модуляции.
Наибольший эффект дают методы третьего типа, которые и получили распространение в работах по теории голографических решеток. Встречаются две разновидности этих методов, отмечавшиеся во введении: метод характеристических волн и метод связанных волн. В методе характеристических волн волновое уравнение сводится к двум обыкновенным уравнениям второго порядка известным способом разделения переменных. При этом одно из них оказывается уравнением Хилла или Матье. Характеристические решения этого уравнения определяются путем разложения в ряды по экспоненциальным функциям, то есть используется проекционный метод их построения. В результате определяются характеристические волны, которые могут существовать независимо в безграничной модулированной среде. Поле внутри слоя строится в виде суммы этих волн с неопределенными коэффициентами, которые отыскиваются затем с помощью граничных условий. Наиболее просто этим методом решается задача дифракции на поперечно модулированном слое с синусоидальной модуляцией.
В методе связанных волн, как отмечалось ранее, решение волнового уравнения ищется сначала в виде ряда с неизвестными, медленно меняющимися коэффициентами. Подстановка ряда в исходное уравнение сводит его к бесконечной системе обыкновенных дифференциально-разностных уравнений, которая решается затем известными методами.
Строгое решение рассматриваемых задач этим методом в литературе не приводилось.
В дальнейшем мы рассмотрим строгое решение задач дифракции методами характеристических и связанных волн.
Ввиду известной структуры решения для безграничной модулированной среды можно было бы сразу использовать разложение в двойной ряд по экспоненциальным функциям. Однако, ввиду неопределенности части показателей экспонент, это не дает никаких преимуществ по сравнению с отмеченными выше методами.
Сформулируем теперь рассматриваемую задачу в форме интегральных
уравнений, используя метод вспомогательных источников /12/. Исходим из уравнений
(2), (3) и положим  ,
где ,
где  - поле падающей волны,
- поле падающей волны,  - вторичное поле, вызванное наличием в пространстве
неоднородного диэлектрического слоя. Падающее поле во
- вторичное поле, вызванное наличием в пространстве
неоднородного диэлектрического слоя. Падающее поле во
- 55 -
всем пространстве удовлетворяет уравнениям
 (18) (18)
Вычитая (18) из (2), получим
 (19) (19)
откуда следует, что вторичное поле возбуждается поляризационными
токами, имеющими плотность  .
Введем в рассмотрение вспомогательный электрический диполь, расположенный в
точке с радиусом-вектором .
Введем в рассмотрение вспомогательный электрический диполь, расположенный в
точке с радиусом-вектором  и ориентированный вдоль некоторого вектора
и ориентированный вдоль некоторого вектора  .
Пусть поле диполя удовлетворяет уравнениям .
Пусть поле диполя удовлетворяет уравнениям
 (20) (20)
В зависимости от выбора e b
и граничных условий для  , ,
 можно получать различные интегральные уравнения.
можно получать различные интегральные уравнения.
Пока что мы потребуем лишь того, чтобы вне слоя e
b= e 1
и касательные составляющие и
и  оставались непрерывными при прохождении границ слоя.
оставались непрерывными при прохождении границ слоя.
Применяя к (19) и (20) стандартную методику /12/, получим лемму Лоренца в виде
 (21) (21)
Предположим на время, что диэлектрический слой имеет конечную протяженность по всем осям, и проведем поверхность sS
как показано на рис.2. Эта поверхность разграничивает два объема: внешний v1 и внутренний v2.
Проинтегрируем (19) по суммарному объему vS
= v1+v2. Тогда получим:
- 56 -
 (22) (22)
где  - внутренняя нормаль к поверхности sS
.
- внутренняя нормаль к поверхности sS
.

Рис.2.
Области интегрирования при выводе уравнения (23).
Интеграл по внутренней поверхности равен нулю в силу непрерывности касательных составляющих вторичного и вспомогательного полей на границе диэлектрического слоя.
Увеличивая неограниченно радиус внешней поверхности s2
и, требуя выполнения условий излучения для вторичного и вспомогательного полей,
найдем, что интеграл по s2
также равен нулю. В результате приходим к интегральному уравнению второго рода
для  : :
 (23) (23)
- 57 -
Рассмотрим теперь два случая:
1) e b = e
1 при 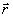 Î
v1 и
2) e b = e
с Î
v1 и
2) e b = e
с при 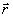 Î
v1. Î
v1.
В первом случае вспомогательное поле диполя определяется в однородном безграничном пространстве, что дает /12/
 (24) (24)
где k1=w
2m 0e
1, r=| 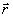 - -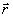 ’|
. Подставляя
(24) в (23)
и учитывая, что ’|
. Подставляя
(24) в (23)
и учитывая, что  ,
окончательно находим ,
окончательно находим
 (25) (25)
Здесь операция "ротор" действует в точке наблюдения
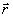 ,
а объем v1
может считаться неограниченным по осям x
и y. Это интегральное
уравнение эквивалентно интегро-дифференциальному уравнению, полученному в работе
/11/ другим методом. В этом легко убедиться, используя тождество ,
а объем v1
может считаться неограниченным по осям x
и y. Это интегральное
уравнение эквивалентно интегро-дифференциальному уравнению, полученному в работе
/11/ другим методом. В этом легко убедиться, используя тождество

где  - произвольный вектор.
- произвольный вектор.
Во втором случае, учитывая
(1) и полагая  получим уравнение
получим уравнение
 (26) (26)
где
 (27) (27)
является полем дифракции падающей волны  на однородном слое с
на однородном слое с
- 58 -
проницаемостью e c.
Интегральный член в (26)
дает добавку, обусловленную модуляцией слоя. Вспомогательное поле определяется
в данном случае в пространстве, содержащем однородный слой с проницаемостью
e c.
От векторных интегральных уравнений (25), (26)
легко перейти к системе двух скалярных, придавая
вектору  последовательно ориентацию вдоль осей Х и z.
последовательно ориентацию вдоль осей Х и z.
Решение уравнений достаточно определить при z = 0 и z = d. После этого поле в любой точке вне слоя можно определить с помощью интегралов Кирхгофа.
Для решения интегральных уравнений (25) и (26) можно использовать три вида методов: сеточный, проекционный и итерационный. Однако так же как и в случае дифференциальных уравнений, сеточный метод трудно реализуем ввиду быстрой осцилляции полей. Итерационный метод в данном случае использовать удобнее, чем в случае дифференциальных уравнений, так как решение автоматически удовлетворяет граничным условиям.
Особенно заманчивым представляется решение этим методом уравнения (26) при малых индексах модуляции у • Однако и здесь возникает проблема многократного вычисления громоздких интегралов и отсутствует оценка сходимости процесса. Наиболее приемлемым методом представляется проекционный, основанный на отыскании решения в виде ряда по некоторой системе функций. Именно такой метод и был использован в работе /11/, где анализировался случай чисто продольной синусоидальной модуляции. Решение было задано в виде двойного ряда экспоненциальных функций, который получается и в случае метода характеристических волн. Поэтому никаких особых преимуществ оно не могло дать по сравнению с упомянутым методом.
Попытки использования других функций для разложения решений пока не известны. В связи с изложенным, в дальнейшем мы ограничимся рассмотрением строгих решений только дифференциальных уравнений задачи.
2. Метод характеристических волн
Рассмотрим сначала общую методику нахождения характеристических волн для безграничной модулированной среды. Затем мы применим ее в решении двух частных задач дифракции: дифракция на слое с чисто
- 59 -
продольной либо поперечной модуляцией. Общий случай дифракции на слое с "наклонной" модуляцией пока езде не исследован, хотя путь решения намечен в работе /3/.
Выберем систему координат хОу так, чтобы a
= 0 (рис.3).

Рис.3.
Безграничная периодически модулированная среда
Согласно (1) будем иметь
e
(х) = e
с[1 - g
y
(Кх)], К = 2p
/L
(28)
Согласно (13) задача сводится к построению характеристических решений волнового уравнения
D u +  2(x)u
= 0 (29) 2(x)u
= 0 (29)
где  2(х)=k2(x)=k2c[1-g
y (kх)] в случае
Н-волн и 2(х)=k2(x)=k2c[1-g
y (kх)] в случае
Н-волн и  2(х)= 2(х)= 2(х)
в случае e-волн. 2(х)
в случае e-волн.
Так как y (t)
четная, периодическая с периодом 2p
функция, то во всех случаях будет справедливо
разложение  2
в ряд Фурье: 2
в ряд Фурье:
 (30) (30)
- 60 -
В случае Н-волн имеем  , ,
 (31) (31)
В случае же Е-волн
 (32) (32)
где  определяется с учетом (16)
и (28).
определяется с учетом (16)
и (28).
Заметим, что только в случае Н-волн ряд (30) может иметь конечное число членов. В простейшем случае синусоидальной модуляции y
(t)=cost и будем иметь s
0=1; s
1=- g
/2; s
m=0; m ³
2 для Н-волн. Для Е-волн при этом ряд Фурье будет бесконечным, так как, согласно (16) получим
|
 2(x)=k2c(1-g
coskx)+ 2(x)=k2c(1-g
coskx)+
|
g
k2coskx |
- |
3g
2k2sinkx |
|
2(1-g
coskx) |
4(1-g
coskx)2 |
Будем искать функцию u(x,z) в виде
u(x,z) = x(x)·z(z) (33)
Подставляя (33) в (29) и разделяя переменные, получим два обыкновенных дифференциальных уравнения:
z” + p2z = 0 (34)
 (35) (35)
где р 2 - постоянная разделения.
Общее решение (34) можно записать в виде
z(z) = aexp(ipz) + a’exp(-ipz) (36)
Преобразуем уравнение (35), введя обозначения
- 61 -
 (37) (37)
Тогда получим
x” + [a – 2qq(2x
)]x(x
) (38)
то есть уравнение Хилла в канонической форме /13/. В частном случае Н-волн и чисто синусоидальной модуляции оно переходит в уравнение Матье:
x"(x
) + (a – 2qcos2x
)x(x
) = 0 (39)
В соответствии с теорией Флоке /13/ линейно независимые решения уравнения (38) можно построить в виде
x1(x
) = exp(m
x
)j
(x
); x2(x
) = x1(-x
) (40)
где j
(x
) - периодическая функция с периодом p
, а m
- характеристический показатель, определяемый параметрами a, q, s
m m³
2 (вообще комплексный). Функция j
(x
) может быть представлена сходящимся рядом Фурье:
 (41) (41)
Если вещественная часть m
равна нули (m
- чисто мнимое), то решения (40) принято называть устойчивыми, если не равна нулю -- неустойчивыми. Если функция q(2x
) задана, то плоскость (a,q)
- 62 -
для уравнения (38) можно разделить на области устойчивости и неустойчивости. Области устойчивости заключены между характеристическими кривыми, соответствующими периодическим решениям уравнения (38) с периодом p
и 2p
.
Подставляя (40) и (41) в (38), получим бесконечную однородную систему линейных алгебраических уравнений относительно коэффициентов С2r:
 (42) (42)
Приравнивая нулю определитель системы, получим характеристическое уравнение для определения параметров m
и а. (Напомним, что а, согласно (37),зависит от неопределенного параметра разделения р2). Так как уравнение одно, то либо m
, либо а должно быть задано. Если задается m
, то для а получаем бесконечное счетное множество значений аn - собственные числа уравнения Хилла (Матье) и постоянные p2n. Если же задается величина а, то m
определяется однозначно решением характеристического уравнения, Как будет видно из дальнейшего изложения, в зависимости от геометрии задачи оказывается целесообразным выбрать определенным образом либо показатель m
, либо постоянную разделения p2, то есть параметр а.
Методика решения системы (42) и характеристического уравнения подробно рассмотрена в /13/ и мы не будем на ней останавливаться.
Учитывая изложенное выше, можно представить характеристические волны в виде
|
un(x,z) = exp(±
ipnz)x1,2n(kx/2) = |
(43) |
|
= exp(±
ipnz ±
m
nkx/2)j
n(±
kx/2) |
Подставляя (41) в (43), получим
- 63 -
 (44) (44)
Суперпозицией характеристических волн можно представить любое решение волнового уравнения (29). Выбор той или иной линейной комбинации характеристических волн диктуется характером возбуждения волн в неоднородной среде и удобством удовлетворения граничных условий.
Так, например, в случае чисто продольной модуляции (слой ограничен по оси z) общее решение уравнения (29) целесообразно строить в виде
 (45) (45)
где xn(x
) - любое из линейно независимых решений уравнения Хилла (Матье), соответствующее одному и тому же показателю m
. Если слой модулирован поперечно, то есть ограничен по оси Х, то следует выбрать комбинацию
 (46} (46}
Ниже будет показано, что при этом удается ограничиться одним частным решением, задав единственный параметр р .
Дифракция на слое с продольной модуляцией
Рассмотрим подробно дифракцию Н-волны, падающей под углом q
0 на слой
с продольной модуляцией (рис.4). Решение волнового уравнения
(29), где  2(х)=
k2(x),
будем искать в виде (45),
то есть 2(х)=
k2(x),
будем искать в виде (45),
то есть
 (47) (47)
где С 2r(n) - коэффициенты решения уравнения Хилла, соответствующие
- 64 -
собственному числу а n.

Рис.4.
Дифракция на продольно-модулированном слое.
Так как зависимость падающей волны от x определяется множителем exp(-ik1x·sinq
0), то целесообразно выбрать
|
m
= i2· |
k1 |
·sinq
0 = i· |
2L
|
·sinq
0 |
(48) |
|
k |
l
1 |
Поскольку m
чисто мнимое, то решения уравнения Хилла будут устойчивыми, в общем случае почти периодическими */. По заданному определяются множества собственных чисел an и коэффициентов С2r(n). Согласно (37), постоянные разделения рn определяются, в свою очередь, через an по формуле
 (49) (49)
Решение в области z<0 будем искать в виде суммы падающей и отраженной волн:
u1(x,z) = exp[-ik1(xsinq
0 + zcosq
0)] + u отр(x,z) (50)
*/ Имеется в виду класс почти периодических функций Бора.
- 65 -
Для возможности удовлетворения граничного условия при z=0 для всех хÎ
(-¥
,¥
) структура функции uomp(x,0) должна быть такой же как у u2(x,0) то есть учитывая (47) и (48), полагаем
 (51) (51)
Подставляя (51)
в уравнение (29)
с волновым числом  2=k21,
соответствующим области z<0,
находим требуемую зависимость uoтp
от координаты z. 2=k21,
соответствующим области z<0,
находим требуемую зависимость uoтp
от координаты z.
В результате получаем :
 (52) (52)
где  . .
Точно так же определяем структуру поля в области z>d в виде
 (53) (53)
В рассматриваемом случае дифракции Н-волн u(x,z)=ey. Поэтому, используя граничные условия (8) и разложения (47), (50), (52) и (53), получим следующие бесконечные системы линейных алгебраических уравнений относительно неопределенных коэффициентов an, А’n, b r, d r:
 (54) (54)
 (55) (55)
 (56) (56)
- 66 -
 (57) (57)
Здесь всюду r= 0;±1;±2;...; d
0,0=1, d
r,0=0 при r¹
0. Коэффициенты br и dr легко исключаются и тогда получаем систему для определения Аn и А’n:
 (58) (58)
 (59) (59)
r = 0; ±1; ±
2; ...
Практически, при расчетах на ЭЦВМ решают "усеченную", конечную систему, порядок которой определяется требуемой точностью вычислений. Правомерность такого подхода обоснована, например, в работе /4/.
Задача дифракции Е-волны решается аналогично. Основное отличие заключается в граничных условиях, которые, согласно (12), приобретают вид:
|
k1u1 =k2(x)u2; |
1 |
¶
u1 |
= |
1 |
¶
u2 |
при z = 0 |
(60) |
|
k1 |
¶
z |
k2(x) |
¶
z |
|
|
k1(x)u2 =k1u3; |
1 |
¶
u2 |
= |
1 |
¶
u3 |
при z =d |
(61) |
|
k2(x) |
¶
z |
k1 |
¶
z |
Трудности, связанные с появлением в граничных условиях множителей k2(x) и k-12(х), легко преодолеваются путем разложения этих множителей в ряда Фурье. После перегруппирования членов получающихся рядов придем к системе, аналогичной (58), (59), но с другими коэффициентами /4/.
Важно такие помнить, что в случае Е-волн в уравнении Хилла
(38) фигурируют коэффициенты
s m,
определяемые разложением в ряд Фурье квадрата модифицированного волнового числа
 2.
Поэтому даже при чисто синусоидальной модуляции приходится решать уравнение
Хилла, а не Матье. 2.
Поэтому даже при чисто синусоидальной модуляции приходится решать уравнение
Хилла, а не Матье.
- 67 -
Для иллюстрации изложенной выше теории приведем некоторые результаты численных расчетов, полученные в /4,5/. На рис.5 показана зависимость амплитуды минус первого порядка дифракции d-1 от угла падения q
0 для Н-волк и синусоидально модулированного диэлектрического слоя толщиной d=60 мкм и 100 мкм при g
=6,67·10-3, e
1=1, e
c= 2,25 и l
1 = 0,63 мкм, L
= 1,46. Для приведенных значений l
1 и L
угол Брэгга q
0 = 12,5° и как, видно из рис.5, при этом угле падения волны возможен полный переход энергии в минус первый порядок дифракции. Однако такое явление наблюдается только при определенном сочетании значений g
и d.

Рис.5.
Зависимость относительной амплитуды дифрагировавшей волны минус первого порядка от угла падения волны.
Кривая 1 - d = 60 мкм; кривая 2 - d = 100 мкм.
Дифракция на слое с поперечной модуляцией
Геометрия задачи показана на рис. 6. Рассмотрим сначала случай Н-волн. Ввиду однородности слоя по координате Х отраженная и
- 68 -
прошедшая водны так же, как и падающая, будут плоскими. Распространяться они будут под теми же углами, что и в случае немодулированного слоя. Отличие будет заключаться в величине коэффициентов отражения и прохождения. Поэтому решение уравнения (29) для областей z<0 и z>d запишется в виде
u1(x,z) = exp[-ik1(xsinq
0 + zcosq
0)] +
+ bexp[-ik1(xsinq
0 - zcosq
0)] (62)
u3(x,z) = dexp[-ik1(xsinq
0 + zcosq
0)] (63)

Рис.6.
Дифракция на поперечно модулированном слое.
Зависимость решений u1 и u3 от координаты x на границах z=0, z=d целиком определяется функцией exp(-ik1xsinq
0). Следовательно, решение для области 0<z<d нужно выбрать с такой же
- 69 -
зависимостью. Это можно сделать используя комбинацию (46), в которой следует поменять местами x и z, учитывая различие в рисунках 3 и 6, то есть
 (64) (64)
Для получения требуемой зависимости от х при фиксированном z достаточно положить все рn=k 1sin q
0 и выбрать знак минус перед pn. Но, как отмечалось ранее, выбор pn однозначно определяет собственное число an и характеристический показатель m
и решений уравнения Хилла.
Следовательно, в решении (64) все функции x1n и x2n будут совпадать и мы получим
 (65) (65)
где x1,2 - линейно независимые решения уравнения Хилла (Матъе), соответствующие собственному числу
a=(2/k)2(s
0k2c – p2)=(2/k)2(s
0k2c – k21sin2q
0) (66)
Наложение граничных условий (8) с учетом того, что Еу(x,z)=u(x,z), приводит к системе уравнений относительно коэффициентов А, А’, В и Д:
|
ax1(0) + a’x2(0) – b = 1 |
(67) |
|
|
ax1(h) + a’x2(h) – dexp(-irh) = 0 |
|
|
ax’1(0) + a’x’2(0) – bir = -ir |
|
|
ax’1(h) + a’x’2(h) + direxp9-irh) = 0 |
|
где h = |
1 |
kd = |
p
d |
r = |
2k1 |
cosq
0 = 2n1 |
L
|
·cosq 0 
|
|
2 |
L
|
k |
l
0 |
- 70 -
- показатель преломления среды, окружающей неоднородный слой, l
0 - длина волны в пустоте. Решая систему (67), получим
|
a = |
2irv2(h) |
a’ = |
2irv1(h) |
(68) |
|
D
|
D
|
|
|
b = |
v1(0)v2(h) – v1(h)v2(0) |
(69) |
|
D
|
|
|
d = |
2ir |
[x1(h)x’2(h) – x2(h)x’1(h)exp(irh) |
(70) |
|
D
|
где
|
v1 = x’1 + irx1 |
v2 = x’2 + irx2 |
|
|
D
=[x’2(0) – irx2(0)]v1(h) - [x’1(0)–irx1(0)]v2(h) |
Так как x2(x
)=x1(-x
), то решение задачи сводится фактически к построению одного решения уравнения Хилла (Матье), соответствующего заданным параметрам a, q, s
m. В случае дифракции Е-волн ход решения остается прежним, изменяется лишь вид граничных условий. В соответствии с (12) и с учетом, что hy=ku, находим граничные условия:
|
k1u1=k2(z)u2 |
1 |
¶
u1 |
= |
1 |
¶
(k2u2) |
при z=0 |
(71) |
|
k1 |
¶
z |
k22(z) |
¶
z |
|
|
k2(z)u2=k1u3 |
1 |
¶
(k2u2) |
= |
1 |
¶
u3 |
при z=d |
(72) |
|
k22(z) |
¶
z |
k1 |
¶
z |
В результате вместо (67) получаем систему уравнений:
a·k2(0)x1(0) + a’k2(0) – b = 1;
a·k2x1(h) + a’k2(d)x2(h) – d·exp(-irh) = 0;
- 71 -
 (73) (73)
Система (73)
аналогична (67)
и отличается лишь величиной коэффициентов при неизвестных А, А, В и Д. Поэтому
ее решение можно сразу записать, учитывая (68)-(70). Решение уравнения Хилла
Х1( x
) должно в данном случае строиться в предположении,
что коэффициенты s m
определяются формулами (32),
где  2(z)
определяется выражением (17). 2(z)
определяется выражением (17).
Используя описанную выше теорию, авторы провели численные расчеты дифракции Н-волны на синусоидально модулированной диэлектрической решетке для значений g
= 0,13 и 0,26.
На рис.7, 8 и 9 этим значениям соответствуют кривые 2 и 3, соответственно. Там же для сравнения нанесены кривые, соответствующие немодулированному слою (g
= 0, кривая 1). На рис.7 показана зависимость дифракционной эффективности отражательной решетки h
=|
В|
2 от отношения d/L
для угла падения q
0=45°, соответствующего выполнению условия Брэгга l
с =2L
Соsq
при e
1=1, e
c=1.
Из рисунка следует, что эффективность, близкую к 100%, можно получить при сколь угодно малых g
, но достаточно большой относительной толщине слоя d/L
.
На рис.8 и 9 представлены зависимости h
от угла падения волны
- 72 -

Рис.7. Зависимость h
от относительной толщины слоя d/L
для различных глубин модуляции.

Рис.8. Зависимость h
от угла падения волны для различных глубин модуляции.
- 73 -
q
0 и отношения L
/l
с дkz слоя, удовлетворяющего приведенным выше условиям и имеющего относительную толщину d/L
=9,5. Эти рисунки характеризуют угловую и частотную селективность решетки.

Рис.9. Зависимость h
от d/L
для различных глубин модуляции.
В заключение отметим, что при условиях дифракции, близких к условию Брэгга, наблюдается хорошее совпадение результатов точного анализа с приближенными данными, полученными в работе /8/.
3. Метод связанных волн
Рассмотрим построение строгого решения задачи дифракции плоской волны на наклонно модулированном слое (рис.1). Как было показано в разделе 1, необходимо найти решение уравнения (13) для трех областей: z < 0, z > d и 0<z<d и "сшить" их граничными условиями.
Для квадрата волнового числа  2(x,z)
можно записать разложение в ряд Фурье, аналогичный
(30), 2(x,z)
можно записать разложение в ряд Фурье, аналогичный
(30),
- 74 -
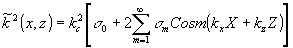 (74) (74)
где s
m определяются для Н-волн соотношениями (31), а для Е-волн - формулой

Таким образом, волновая функция внутри слоя u2(x,z) должна удовлетворять уравнению
 (75) (75)
а вне слоя уравнению
D
u1,3 + k21u1,3 = 0 (76)
Граничные условия определяются выражениями (8) и (12), где Еy=u, а Нy =ku.
Будем искать решение (75) в виде ряда
 (77) (77)
положив kcsinq
= k1sinq
0.
Подставляя (77) в (75) и выполняя преобразования, получим систему связанных дифференциальных уравнений относительно переменных коэффициентов Аn(z):
 (78) (78)
- 75 -
Из (78) следует, что коэффициенты Аn(х) связаны между собой, причем степень связи определяется величинами s
m, m ³
1. Она исчезает только при переходе к однородному слою. Поэтому (77) можно трактовать как суперпозицию связанных волн. В отличие от характеристических волн, они не могут существовать независимо в безграничной модулированной среде.
Вводя новую переменную t=k2cz и учитывая, что kx=k·cosa
, kz=ksina
, представим уравнение (78) в более удобной форме:
 (79) (79)
где  ,
l с ,
l с
- длина волны в среде со средней проницаемостью e
с,  . .
Уравнение (79) несколько упрощается лишь в случае дифракции Н-волн на слое с синусоидальной модуляцией. При этом s
0=1; s
1=- g
/2 и s
m=0, m ³
2. Поэтому
 (80) (80)
Фиксируя в (77) переменную z, легко видеть, что структура решения внутри слоя подобна (51) с тем отличием, что вместо k фигурирует kx. Следовательно, решения в областях z<0 и z>d необходимо брать в виде, подобном (50), (52) и (53), а именно:
 (81) (81)
 (82) (82)
- 76 -
где
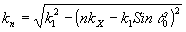
Предположим, что дифрагирует Н-волна. Подставляя (77), (81) и (82) в граничные условия (8), приходим к следующей системе соотношений между Вn; d n; a n(0), a n(d ), А’n(0) и a’n(d):
|
bn = an(0) – d
n,0 |
(83) |
|
|
dn = an(d)exp(ij
n) |
|
|
bnkn = a
nan(0) – ia’n(0) + d
n,0k1cosq
0 |
|
|
dnkn = -[a
nan(d) – ia’n(d)]exp(ij
n) |
Где a
n=nkz+kccosq
, j
n=(a
n+kn)d.
Соотношения (83)
позволяют определить коэффициенты отражения Вn
и прохождения dn
по граничным значениям функций an(z)
и их производных a’n(z). Одновременно
они позволяют задать граничные условия на функции  ,
которым должны быть подчинены решения системы
(79). ,
которым должны быть подчинены решения системы
(79).
Исключая из (83) коэффициенты Вn и dn, получим
|
(kn - a n) n(0)
+ ikc n(0)
+ ikc ’n(0)
= d n,0(kn +
k1cosq 0) ’n(0)
= d n,0(kn +
k1cosq 0)
|
(84) |
|
(kn + a
n) n(kcd)
- ikc n(kcd)
- ikc ’n(kcd)
= 0; ’n(kcd)
= 0;
n= 0; ±
1; ±
2; … |
Таким образом, точные граничные условия для функций  n(t)
являются смешанными. n(t)
являются смешанными.
Система (79) имеет постоянные коэффициенты. В соответствии с общей теорией /14/ ее частные решения следует искать в виде an=g
nexp(iW
t). Подставляя в (79), получим однородную систему алгебраических уравнений относительно g
n. Приравнивая нулю определитель системы, найдем характеристическое уравнение
- 77 -
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
=0 |
(85) |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
… |
s
m |
… |
… |
s
2 |
s
1 |
d-1 |
s
1 |
s
2 |
… |
… |
s
m |
… |
… |
… |
|
… |
… |
s
m |
… |
… |
s
2 |
s
1 |
d0 |
s
1 |
s
2 |
… |
… |
s
m |
… |
… |
|
… |
… |
… |
s
m |
… |
… |
s
2 |
s
1 |
d1 |
s
1 |
s
2 |
… |
… |
s
m |
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
где
dn = -{W
2 - 2W
(cosq
- (l
c/L
)nsina
) + [1 - s
0 +
+ (l
c/L
)2n2 – 2n(l
c/L
)sin(q
+ a
)]}
Корни уравнения обозначим W
k и будем
предполагать, что среди них нет кратных. Каждому корню W
k
соответствует частное решение  n(t)=ankexp(iW
kt), n = 0; ±1; ±2,
…, где аnk
определяются стандартным методом /14/. Общее решение запишется в виде n(t)=ankexp(iW
kt), n = 0; ±1; ±2,
…, где аnk
определяются стандартным методом /14/. Общее решение запишется в виде
 (86) (86)
где неопределенные множители Ск должны быть найдены
из граничных условий (84).
Рассмотрим подробнее этот вопрос, учитывая, что практически должна решаться
"усеченная система" дифференциальных уравнений. Пусть для конкретности n
= 0; ± 1; ±2,
… ±n, то есть "усеченная система"
имеет 2n+1
уравнение. Легко видеть, что соответствующее характеристическое уравнение будет
иметь точно 2(2n+1)
корней W k,
так как dn
являются полиномами второй степени относительно W
. Следовательно,
число неизвестных ck
также будет равно 2(2n+1).
Для каждой функции  n
имеем по два граничных условия (84),
всего их будет 2(2n+1)
и они однозначно определяют все неизвестные ck. n
имеем по два граничных условия (84),
всего их будет 2(2n+1)
и они однозначно определяют все неизвестные ck.
Для определения ck нужно подставить (66) в (84) и решить получающуюся неоднородную линейную систему алгебраических уравнений.
Другим перспективный методом решения системы (79) является численный метод сеток. Этот метод позволяет сразу же перейти от
- 78 -
системы дифференциальных уравнений, взятой вместе с граничными
условиями, к системе линейных алгебраических уравнений относительно значений
 n(ti),
взятых в узлах сетки {ti}. n(ti),
взятых в узлах сетки {ti}.
Учитывая медленность изменения функций  n(t)
на интервале [0,kc,d], можно
рассчитывать на быструю сходимость в обоих описанных выше методах. n(t)
на интервале [0,kc,d], можно
рассчитывать на быструю сходимость в обоих описанных выше методах.
Случай дифракции Н-волн усложняется за счет граничных условий, которые в общем случае принимают вид, аналогичный (71), (72).
|
k1u1=k2(x,z)u2 |
1 |
¶
u1 |
= |
1 |
¶
(k2u2) |
при z=0 |
(71) |
|
k1 |
¶
z |
k22(x,z) |
¶
z |
|
|
k2(x,z)u2=k1u3 |
1 |
¶
(k2u2) |
= |
1 |
¶
u3 |
при z=d |
(72) |
|
k22(x,z) |
¶
z |
k1 |
¶
z |
Для получения систем соотношений вида
(85) и (84)
достаточно разложить в ряды Фурье Функции  и
и  осуществить перегруппировку членов получающихся двойных сумм. В отличие от
(84) в граничных условиях появляются суммы,
которые связывают граничные условия функций an(t)
между собой. В целом же ход решения задачи остается прежним.
осуществить перегруппировку членов получающихся двойных сумм. В отличие от
(84) в граничных условиях появляются суммы,
которые связывают граничные условия функций an(t)
между собой. В целом же ход решения задачи остается прежним.
Заключение
В работе сделана попытка систематизировать методы строгого решения задачи дифракции плоской монохроматической волны света на объемных голографических решетках, представляющих собой плоские периодически модулированные слои. В настоящее время наиболее раз~ виты два метода: метод характеристических волн и метод связанных волн.
Метод характеристических волн применялся только s частном случае продольной модуляции. В настоящей работе он распространен на другой частный случай поперечной модуляции слоя. Результаты численных расчетов по этому методу являются пока единственными строгими решениями рассматриваемой задачи.
Метод связанных волн позволяет, как известно, просто получать
- 79 -
приближенные решения. Однако, как показано в настоящей работе, он может быть использован и для строгого решения общей задачи дифракции плоской волны на объемной голографической решетке. В работе выведены все необходимые для этого соотношения.
Наименее развит в настоящее время метод интегральных уравнений, хотя он обладает некоторыми преимуществами перед методом дифференциальных уравнений.
В работе предложен простой общий способ вывода интегральных уравнений задачи, получена новая форма уравнения и обсуждены различные методы решения.
Строгую теорию голографических решеток целесообразно развивать дальше по следующим направлениям:
- применение метода характеристических волн к слою с произвольной "наклонной" модуляцией;
- получение численных результатов по строгой теории методом связанных волн;
- более широкое исследование случая дифракции Е-волн, чем это сделано до настоящего времени;
- исследование влияния нелинейности процесса записи решеток и разработка теории оптимизации режима записи по различным критериям;
- вывод уточненных приближенных решений на основе строгой теории и оценка погрешностей путем сопоставления с результатами расчета по строгой теории;
- исследование и разработка метода интегральных уравнений;
- распространение строгих решений на анизотропные среды. Перечисленные направления отнюдь не исчерпывают всех задач,
представляющих практический интерес. В связи с бурный развитием
голографии круг задач непрерывно расширяется.
Литература
1. e.h.wagner. zq.f.phys., 141, 604. 1955.
2. r.s.chu, Т.tamil-. ieee trans.microwave theory and technique, mtt-18, 486, 1970.
3. r.s.chu, t.tamir, С.eng. proc.iee (g.Б.), 119, 797, 1972.
- 80 -
4. c.b.burckhardt. j.opt.soc.amer., 56, 1502, 1966.
5. c.b.burckhardt. j.opt.soc.amer., 57, 601, 1967.
6. f. С.kasper. j.opt.soc.amer., 63, 37, 1973.
7. g.yeh, k.f.cassey, z.a.kaprielian. ieee irens., microwave theory and technique, mtt-13, 297, 1965.
8. h.kogelnik. bell syst.techn.j., 48, 2909, 1969.
9. w.r.klein, В.d.cook. ieee trans.sonics and ultrasonics su-14, 123, 1967.
10. Н.М.Померанцев. Квантовая электроника, вып.5 (11), 118, 1972.
11. a.b.bhatia, w.j.noble. proc.roy.soc., a 220, 356, 1953.
12. Г.Т.Марков, А.Ф.Чаплин. Возбуждение электромагнитных волн, М.Л. "Энергия", 1967.
13. Н.В.Мак-Лахлан. Теория и приложения функций Матье, М., ИЛ, 1951.
14. В.В.Степанов. Курс дифференциальных уравнений, М.-Л., ГИТТЛ, 1950.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

