|
|
 |
 |

|
| |
ЗАПИСЬ ФАЗОВЫХ ГОЛОГРАММ В ПОЛУПРОВОДНИКОВЫХ КРИСТАЛЛАХ
С.Г.Одулов, М.С.Соскин
В работе рассмотрены физические процессы, приводящие к изменению показателя преломления полупроводниковых кристаллов под действием света, а также приведен обзор экспериментальных результатов по записи фазовых голограмм в этих соединениях.
i. Введение
Анализ современного состояния голографии показывает, что из трех ее основных компонентов (методы, источники излучения, регистрирующие среды) более всего развиты методы. Слабее обстоит дело с источниками излучения - лазерами, особенно с твердотельными лазерами для импульсной голографии быстро протекающих процессов. Наиболее отсталым участком являются среды для регистрации голограмм. Пока в подавляющем большинстве случаев используются фотоматериалы. В то же время для все большего круга задач голографии, квантовой электроники и оптики требуются голографические элементы типа решеток, корректоров, расщепителей, зонных пластинок и т.п., способные работать в ноле мощных лазерных пучков, обладающие высокой дифракционной эффективностью, в ряде случаев быстродействием и цикличностью записи.
Актуальной задачей также является создание голографических систем оперативной и полуоперативной памяти для вычислительной техники. Светочувствительный материал в таких системах должен обладать высокой светочувствительностью, большим разрешением и выдерживать более 1012 циклов срабатывания.
- 533 -
Полупроводниковые кристаллы гак класс регистрирующих сред, в принципе, отвечают всем требованиям, указанны выше. Так, в них в результате электронных переходов возможна запись объемных фазовых решеток с дифракционной эффективностью до 100% и разрешением свыше 104 лин/мм. Многие кристаллы обладает высокой лучевой стойкостью. За счет легирования кристаллов, либо использования смешанных полупроводников переменного состава можно управлять их спектральной чувствительностью во всем оптическом диапазоне, подгоняя ее к спектру излучения записывающих источников.
Одной из наиболее привлекательных особенностей полупроводниковых кристаллов является огромный диапазон времен фотоэлектрических процессов. Это позволяет надеяться на создание эффективных голографических устройств как с долговременной памятью, так и для записи и считывания в реальном времени со скоростью 109 операций в секунду и более.
В большинстве случаев элементарные процессы обратимы, так что возможна циклическая запись. Наконец, немаловажно, что производство большинства основных полупроводниковых кристаллов (кремний, германий, кристаллы a2b6 и др.) достаточно налажено и не очень дорого. Ожидаемые параметры регистрирующих сред на полупроводниках подсуммированы в таблице i.
Систематические исследования голограмм на полупроводниках начаты в самое последнее время. Так, в монография /1/ и в наиболее полном обзоре /2/ сведения о них полностью отсутствуют. Цель настоящей лекции - рассмотрение основных физических процессов голографической записи фазовых решеток в полупроводниках и диэлектриках, изложение современных теоретических представлений и анализ экспериментальных результатов. Рассмотрены также свойства голографических элементов для осуществления энергообмена между интерферирующими пучками, что важно для ряда применений.
ii. Теория записи фазовых голографических решеток в неметаллических кристаллах
1. Механизм записи
Практически все процессы записи в неметаллических кристаллах
- 534 -
связаны с электронными переходами. В результате поглощения на частоте записывающего излучения происходят переходы электронов в более высокие энергетические состояния. Как известно, возможны переходы зона - зонные с образованием пары электрон-дырка, примесь-зона с образованием свободных носителей одного знака и т.д. Возможны более сложные ситуации при наличии в кристалле прицесей нескольких сортов, когда воздействие света приводит к изменению валентности примесей /3/. Наиболее актуальные случаи показаны на рис.1.
 
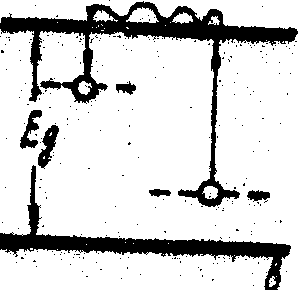
Рис.1.
Пусть на кристалл воздействует голографическое интерференционное поле. Так как число фотопереходов пропорционально локальной интенсивности света (в линейном случае при отсутствии насыщения), то и концентрация созданных неравновесных состояний будет той же функцией координат. Возникающие свободные носители будут диффундировать в области минимальной освещенности, стремясь распределиться равномерно , а также рекомбинировать с носителями противоположного знака, либо захватываться на ловушках.
При неизменности параметров записывающего поля через некоторое время установится стационарное распределение носителей в кристалле,
- 535 -
которое приведет к локальной модуляции показателя преломления среды, т.в. к записи голографической решетки. Возможны следующие основные механизмы изменения показателя преломления кристаллов в результате взаимодействия со светом .
1. Возникновение и пространственное перераспределение свободных носителей.
2. Изменение поляризации решетки при освобождении, либо захвате носителя.
5. Возникновение электрических полей в результате перераспределения объемного заряда.
4. Нагрев решетки при безызлучательных переходах.
5. Фотохимия, фотодиссоциация и др. механизмы необратимой записи.
Рассмотрим основные особенности отдельных механизмов записи.
1. Запись на свободных носителях. Свободные носители дают вклад в показатель преломления /4/ */:
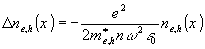 (1) (1)
Здесь D
n(х) - пространственное распределение добавки к показателю преломления, возникающей под действием света; e, me,h* - заряд и эффективная масса носителей; w
- частота света; e
0 - диэлектрическая постоянная вакуума; nе,h(х) - пространственное распределение свободных носителей (электронов или дырок) в кристалле. При концентрации электронов nе »
1018 см-3, D
n »
10 -5¸
10 -4, что вполне достаточно для образования эффективной решетки. Столь большие концентрации электронов в зоне проводимости можно создать в импульсном режиме, применяя лазеры с модуляцией добротности, либо с синхронизацией типов колебаний.
* / При концентрациях примеси в кристаллах n ³
1014 длина свободного пробега электронов оказывается существенно меньшей, чем постоянная голографической решетки, что оправдывает применение этой формулы.
- 536 -
Из соотношения (1) видно, что изменение показателя преломления тем выше, чем больше концентрация носителей и чем меньше эффективная масса и частота излучения. Это дает критерии выбора того или иного полупроводникового кристалла для записи излучением заданного лазера.
В настоящее время запись голограмм с использованием этого механизма осуществлена в кристаллах кремния /5/, селенида кадмия /6/ при помощи лазеров на ионах неодима (l
= 1,06 мкм) и сульфида кадмия /7/, окиси цинка /8/ при помощи ОКГ на рубине (l
=0,69 мкм).
2. Поляризационный механизм. В сильно поляризующихся средах уход электрона с примесного уровня изменяет не только заряд, но и дипольный момент центра, что приводит к локальному изменению показателя преломления:
D
n р(х) = ¦
pnt(x)n3 (2)
где nt(х) - концентрация освобожденных ловушек, ¦
- злектро-оптический коэффициент, р - изменение поляризации при перезарядке примеси, n - показатель преломления.
Предполагается, что данный механизм может быть ответственным за запись голограмм в сегнетоэлектриках и в широкозонных полупроводниках /9/, однако прямые доказательства его проявления пока отсутствуют. Из соотношения (2) видно, что наиболее отчетливо этот механизм должен проявляться в сильно легированных кристаллах.
3. Диффузионный механизм. Наличие значительного градиента концентрации носителей приводит к тепловой диффузии электронов в области с меньшей освещенностью. В результате возникает неравновесный объемный заряд и соответствующее поле Е можно найти из уравнения Максвелла:
dive = -(n е - nt)e (3)
Вследствие электрооптического эффекта поле вызывает модуляцию
- 537 -
показателя преломления:
D
ne = ¦
n3e(x) (4)
Оценки показывают, что наводимые электрические поля могут достигать сотен вольт на сантиметр, что дает изменения показателя преломления в четвертой и пятом знаке.
4. Тепловой механизм.
Если носители возбуждаются в глубину зоны проводимости, то они за малое время
10" сек "скатываются" на дно зоны, отдавая
избыточную энергию матрице, т.е. нагревая ее. Возникает локальный нагрев кристалла
и соответствующее изменение D nt
~ Т(х).
В случае пироэлектрических кристаллов эффект зависит от скорости тепловыделения
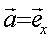 /10/ D nt ~
/10/ D nt ~ 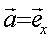 . .
Экспериментально голографические решетки вследствие тепловыделения наблюдались в кристаллах окиси цинка /8/ при двухфотонном поглощении света. По всей видимости, такие решетки можно записывать в большинстве веществ, в которых наблюдалась тепловая самофокусировка или самодефокусировка света, т.к. наводимые изменения показателя преломления D
n »
10-5¸
10-4 вполне достаточны для наблюдения дифракции.
5. Все вышеперечисленные процессы являются обратимыми и пригодны для циклической записи. Для создания стационарных голографических решеток нужно использовать необратимые явления (фотохимия, фотодиссоциация, фотоиндуцированное разрушение решетки и др.). Теория таких процессов в большинстве случаев отсутствует. Укажем лишь, что возникающее D
n(х) ~ ik(х), где k - определяется числом фотонов, участвующих в элементарном акте фотоперехода.
Наводимые изменения D
n вследствие химических превращений могут быть очень большими, вплоть до 10-1. Таким образом, голограммы с эффективностью в десятки процентов в этом случае можно записывать в пленках толщиной в десятки микрон.
К этому же разделу отнесем вещества, позволяющие запись рельефных отражательных голограмм вследствие нарушения поверхности под действием излучения.
В настоящее время известно большое количество полупроводниковых
- 538 -
соединений, в которых возможна необратимая запись /11,12/. Наибольшей светочувствительностью, по всей видимости, обладают слоистые полупроводники /13/.
Из приведенных соотношении следует, что во всех случаях, кроме диффузионного механизма, возникающая голографическая решетка не сдвинута по отношению к интерференционному полю. При записи по диффузионному механизму на средах с линейным электрооптическим эффектом в согласии с (3) решетка смещена на l/4. Под действием мощного импульсного излучения могут проявляться все механизмы изменения показателя преломления:
D
n = D
ne + D
n р + D
ne,h + D
nt + ...
Однако для каждого конкретного кристалла, при возбуждении каким-либо конкретным лазером, определяющим является один, в редких случаях два механизма. В следующем параграфе мы рассмотрим способы теоретического расчета изменения показателя преломления, а затем перейдем к подробному анализу экспериментальных результатов.
2. Расчет стационарных решеток
Чтобы рассчитать изменение показателя преломления под действием света, как следует из формул (1¸
4), необходимо знать концентрацию электронов в зоне проводимости и концентрацию заполненных ловушек в запрещенной зоне, величину наведенных электрических полей, количество выделившегося тепла и скорость тепловыделёния.
Рассмотрим простейшую модель полупроводника с одним типом примесных центров, которые могут находиться в нейтральной, либо ионизованном состоянии, отдавая электрон в зону проводимости (рис.1). Предполагается, что в любой момент времени концентрация электронов и дырок много меньше полной концентрации примеси n, так что отсутствует насыщение поглощения. Схема записи показана на рис.2.
Полная система уравнений долина включать в себя диффузионное уравнение, уравнения непрерывности для электронов и дырок и
- 539 -
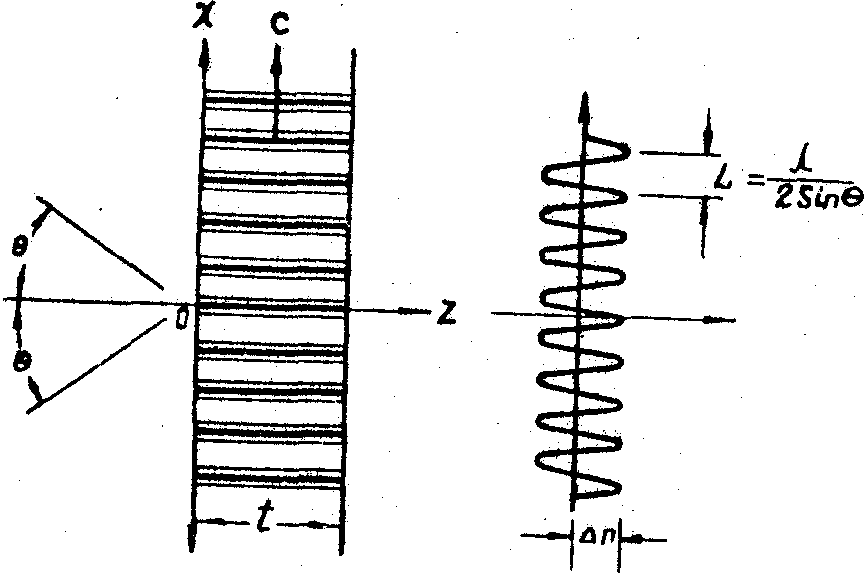
Рис.2.
уравнение Максвелла для возникающих полей /14/:
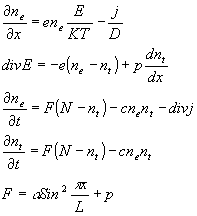 (5) (5)
Здесь nе и nt - концентрации электронов и дырок, соответственно, n - общая концентрация активных центров, a
и b
- вероятности
- 540 -
фото- и термопереходов в зону проводимости, с - вероятность бимолекулярной рекомбинации, р - изменение поляризации при ионизации примеси, j - электронный ток, е- заряд электронов, К - постоянная Больцмана.
Вероятности переходов являются параметрами среды и считаются не зависящими ни от интенсивности света, ни от возникающих электрических полей. Наконец, рассматривается одномерная задача, т.е. не учитываются эффекты, связанные с дифракцией записывающихся пучков на возникающей решетке, изменением i по мере проникновения в среду и др.
Решение системы уравнений (5) дает необходимые данные для расчета показателя преломления вследствие первых трех механизмов, т.к. позволяет найти концентрацию электронов в зоне проводимости, концентрацию положительно заряженных донорных центров и определить наводимое электрическое поле.
Даже при рассмотренных упрощениях решение системы уравнений
чрезвычайно сложно. Проанализируем стационарный случай, когда 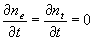 ,
j=0. Распределение свободных электронов существенно
зависит от интенсивности излучения. ,
j=0. Распределение свободных электронов существенно
зависит от интенсивности излучения.
При малых i:
 (6) (6)
При больших i:
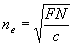 (7) (7)
Видно, что в общем случае стационарное распределение отличается от исходного (5) и не является синусоидальным, хотя по-прежнему максимумы nе(х) находятся в максимумах светового поля.
Из диффузионного уравнения по известному ne(х) находится поле, которое описывается еще более сложной функцией:
- 541 -
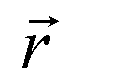 (8) (8)
где
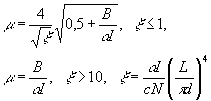
Ход e
(х) показан на рис.3. Максимумы поля смещены более, чем на l/4. Соответственно смещено и распределение D
n(x).
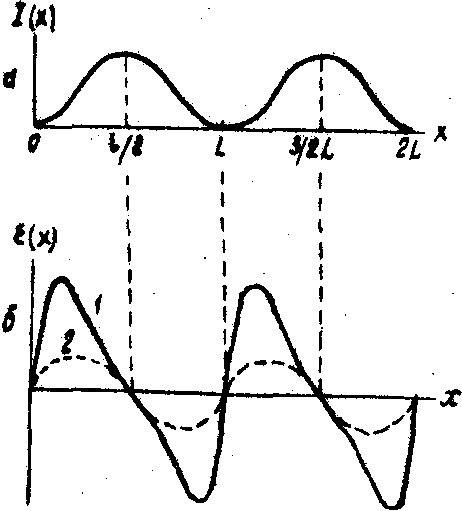
Рис.3.
Подробный анализ решения системы уравнении (5) с точки зрения голографических приложений проведен в работе /14/.
Расчет изменения показателя преломления вследствие тепло выделения основан на решении уравнения теплопроводности с периодическими начальными условиями. Подробное изложение метода приведено в
- 542 -
работах /15,16/.
3. Процессы стирания решеток
При выключении записывающего излучения возникшее распределение зарядов становится неравновесным и начинает распадаться за счет рекомбинации, либо диффузии. Тепловые решетки релаксируют за счет тепловой диффузии, приводящей к выравниванию температуры кристалла.
Процессы распада решетки можно отличить на практике, т.к. они по-разному проявляются при изменении постоянной решетки. Диффузионный ток пропорционален градиенту концентрации. При одном и том же максимальном значении концентрации градиент будет расти по мере уменьшения постоянной решетки. Расчет показывает, что время стирания решетки в этом случае уменьшается пропорционально 1/l2.
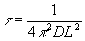
В случае рекомбинационного стирания поток пропорционален концентрации электронов и дырок и не зависит от постоянной решетки вообще.
Следует ответить, что в большинстве случаев стирание не является чисто экспоненциальный. Для случая нелинейной рекомбинации, в частности, время стирания определяется концентрацией электронов в зоне проводимости и убывает по мере роста концентрации. Из решения системы уравнений (5) в последнее время получены как различные предельные случаи, так и общий с учетом возможного равного вклада обоих процессов /17/.
Несколько более сложный случай представляет стирание решетки в присутствии больших наведенных полей, например, в сегнетоэлектриках, либо полупроводниках с большим внутренним сопротивлением. Стирание становится возможным только при условии заброса электронов в зону проводимости, либо теплом, либо светом подходящей частоты, лучше всего излучением ультрафиолетового диапазона. Темновое стирание решетки в полупроводниках с одним типом примеси определяется временем максвелловской релаксации и может 'изменяться в широких пределах вплоть до долей секунды.
- 543 -
iii. Экспериментальные результаты
1. Фазовые динамические голограммы в полупроводниковых кристаллах но свободных носителях
В данном раздел рассмотрены данные по записи голограмм с наиболее короткими веснами жизни из известных до настоящего времени. В случае, если диэлектрическая постоянная следит за изменением интенсивности возбуждающе света безынерционно, энергообмен между записывающими пучками невозможен. Этот вывод является предельно общим и независимо получен при исследовании взаимодействий в плазме, в нелинейной оптике и в голографии /18-20/.
Однако запрет энергообмена снимается, если использовать тонкий слой регистрирующей среды. Тогда, как обычно, дифракция на тонкой фазовой решетке приводит к появлению большого числа внешних порядков, что облегчает экспериментальные исследования. Поэтому наиболее простой и удобный путь исследования сред с динамической записью - это наблюдение самодифракции записывающих пучков на ими же созданной решетке. При этом необходимо, чтобы фактор Клейна - q удовлетворял следующему неравенству:

Первые работы по записи и считыванию фазовых решеток полупроводниковых кристаллах были выполнены в 1969-1970 г.г. /5/. Использовались кристаллы кремния и излучение гигантского импульса лазера на АИГ: nd3+ с l
= 1,06 мкм. Это соответствует энергии кванта 1,16 эв, что на 0,05 эв выше края собственного поглощения при Т - 300°k /5/. Импульс имел длительность t
= 7 нсек и мощность Р = 6 Мвт (энергия 0,02 дж), что приводило к возникновению высокой концентрации свободных носителей (nе = 1018 см-3). Так как время рекомбинации составляло сотни наносекунд, то ясно, что здесь возникала фазовая решетка по 1-му механизму с глубиной модуляции показателя преломления »
10-4. При толщине образца 1¸
1,6 мм это давало глубину штриха решетки 0,1¸
0,4 мк, т.е. ~ 0,1l
.
- 544 -
Схема записи и считывания показана на рис.4 . Угол между пучками составлял 0,01 - 0,05 радиан (30¸
2,5°). При атом фактор Клейна q=1¸
5, была исследована зависимость качества восстановленного изображения от толщины образца, плотности энергии лазерных пучков, угла q
и времени задержки uD
восстанавливающего пучка.
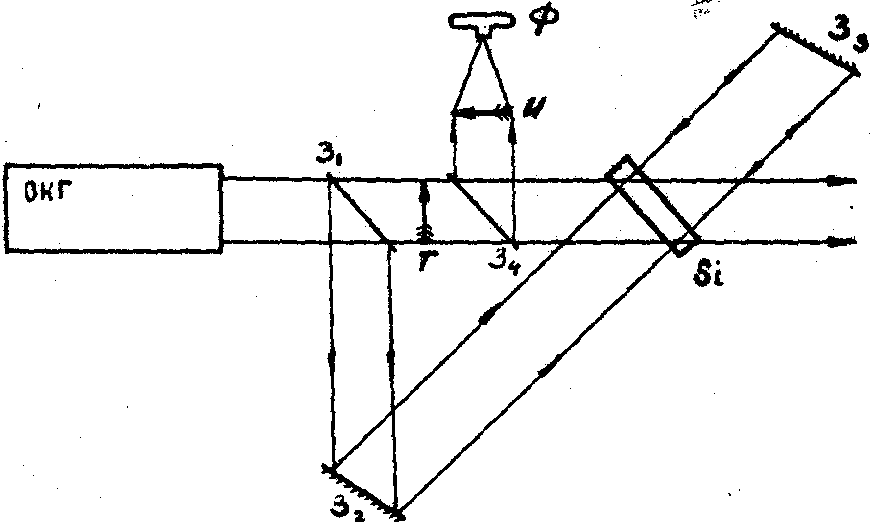
Рис. 4.
Оптимальная толщина образца оказалась, как и следовало ожидать, приблизительно равной a
0-1, где a
0 - коэффициент поглощения в см-1. В данном случае a
0 = 10-1 см-1 и zоpt = 1¸
1,6 мм. При z<a
0-1 - слабая решетка, при z>a
0-1 сильно поглощается восстанавливающий пучок и восстановленное изображение. Необходимый поток составлял »
10 мдж/см2, что соответствует числу поглощенных Фотонов 1018 см-3 и согласуется с указанной выше концентрацией свободных-носителей. По оптической схеме (рис.5) исследовалось влияние задержки на качество изображения. Видно, что эффективность падает с ростом как D
t, так и q
. Это показывает, что есть достаточно быстрый стирающий механизм временами »
10-8 сек. Расчет в
- 545 -

Рис.5.
согласии с экспериментом показал, что роль стирающего механизма играет тепловая диффузия свободных носителей в минимумы интерференционной картины, тогда как рекомбинация происходит на порядок медленнее.
Таким образом, возможна запись динамической голограммы в ИК-области спектра с временами стирания 25 мсек за счет диффузии.
Мы исследовали запись динамических решеток в кристаллах кремния с примесью фосфора (10 16 см-3, удельное сопротивление 4W
/см) в аналогичных условиях. Источником возбуждения служил лазер на стекле с nd3+, работавший в режиме моноимпульсного излучения (энергия в импульсе до 0,1 дж, длительность импульса 20·10-9 сек) либо в режиме ультракоротких импульсов облучения (энергия в импульсе 0,007 дж, длительность 12·10-12 сек).
В режиме моноимпульсного возбуждения получена дифракционная эффективность до 10%. Если учесть достаточно большое поглощение
- 546 -
возбуждающего света в образце (прозрачность кристаллов составляла »
30%), дифракционная эффективность в действительности составляет около 30%, т.е. практически достигается максимум первого порядка дифракции. Подтверждением этому служит зависимость дифракционной эффективности от интенсивности накачки, приведенная на рис.6. Угол схождения лучей в данном случае составляет 40', однако самодифракция наблюдалась и при угле схождения 5° (100 штр/мм).
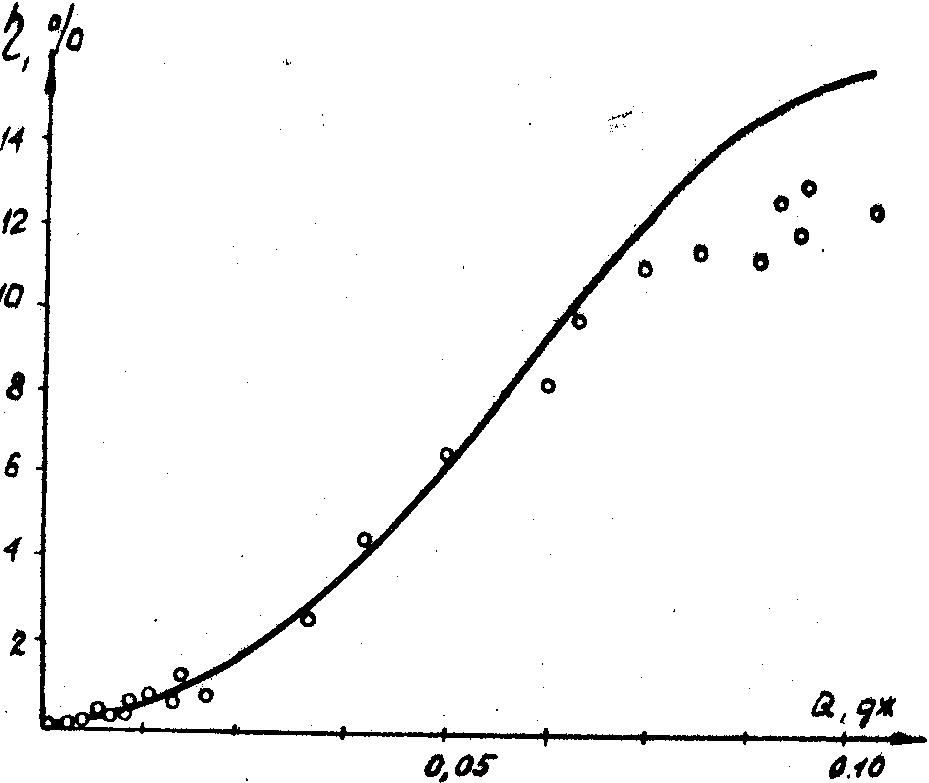
Рис.6.
Самодифракция наблюдалась также и при возбуждении ультракороткими импульсами, как цугом, так и отдельным импульсом. Дифракционная эффективность составляла единицы процентов.
Как видно, достижение высоких эффективное той при записи в кристаллах кремния ограничено большим собственным поглощением. По-видимому, большие эффективности можно получать, если использовать кристаллы с двухфотонныы поглощением света.
Исследовалась запись топографических решеток в кристаллах сульфида кадмия /7/. Возбуждение производилось моноимпульсным
- 547 -
излучением ОКГ на рубине (мощность излучения до 50 Мвт/см2). Коэффициент двухфотонного поглощения для длины волны возбуждения составляет 0,02 см-1/Мвт·см2.
В пучок излучения вкосилась бипризма, после которой два пучка сходились под углом 10' на кристалле толщиной в 1 мм (q
= 3·10-2). Наблюдались высшие порядки дифракции вплоть до ±8. Дифракционная эффективность по +1 порядку дифракции составляла 10¸
12%. Вероятно, это значение не является предельным.
По известному значению h
можно оценить наводимые изменения показателя преломления, пользуясь известной формулой
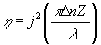
отсюда
D
n »
10-5
Временные характеристик излучения исследовались с разрешением до 1 нсек. Типичные формы записывающего и дифрагировавшего импульсов показаны на рис.7. В 1-м случае импульс дифрагировавшего
 
 
Рис.7.
- 548 -
света имел очень крутой фронт нарастания и несколько затянутый задний фронт, который, однако, всегда был круче заднего фронта лазерного импульса. Время жизни решетки оказывается рекордно малым и не превышает 5 нсек. Для кристаллов второго типа видно, что время стирания порядка длительности импульса.
С целью выяснения причины такого различия была изучена фотопроводимость образцов обоих типов, которая решающим образом зависела от концентраций дефектов и примесей (рис.8). Для кристаллов 1-го типа концентрация свободных электронов следит за импульсом лазера, а для второго типа она остается неизменной в течение сотен наносекунд после импульса, т.е. картина относительна записи решетки за времена t< t
- времени релаксации /21/.
Динамические голографические решетки, возникающие при двухфотонном возбуждении, также получены в кристаллах cdse /6/ и zno /8/.
Приведенные результаты по записи голограмм на свободных носителях являются, несомненно, лишь началом целого ряда исследований
 
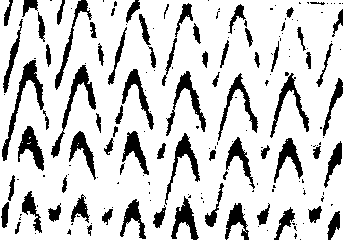 
Рис. 8. Микроинтерферограмма рельефных голографических решеток на поверхности кристаллов.
- 549 -
и достаточно ярко демонстрируют перспективность полупроводниковых кристаллов для записи динамических голограмм.
2. Фазовые стационарные решетки в неметаллических кристаллах
Экспериментальных данных по записи голограмм за счет появления стационарного электрического поля в результате диффузии немного. Известно, что такие поля создаются в сегнетоэлектрических кристаллах linro3, batio3, sbn, ktn, ba2nanℓ5o12 и т.д. (обзорная работа по записи голограмм в этих кристаллах опубликована в трудах v школы). Чисто голографические характеристики практически не исследовались. Так, например, зависимость h
от постоянной решетки известна только для batio3. В широком интервале изменение h
~ l-2. При очень малых периодах зависимость h
от l отсутствует. Такая зависимость получена при предельно больших плотностях мощности аргонового лазера в десятки вт/см2. Непосредственно из теории следует, что при больших ih
= h
0/l2, т.е. качественно в данном случае характер зависимости объясняется.
В случае промежуточных ih
=¦
(i) или слабо зависит от i.
Сам факт записи высококачественных голограмм от различных объектов и транспарантов в linℓo3 свидетельствуют о том, что слабо зависит от l. В противном случае происходило бы подчеркивание высоких частот и появлялось бы окунтурирование, которого нет на опыте.
Зависимость h
= ¦ (i) по
теории должна быть вначале линейной (при малых
i). Затем она становится корневой и насыщается.
На рис.9 показана
зависимость h
= ¦ для кристалла
batio3.
При больших i
возникает насыщение. В общем случае любая фазовая голограмма, будь то тонкая
либо объемная, может удовлетворять условию идеальности 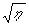 ~
i /1/ только при малых
i, где можно ограничиться первым членом разложения
функции Бесселя, либо ~
i /1/ только при малых
i, где можно ограничиться первым членом разложения
функции Бесселя, либо 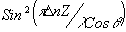 .
Если материал позволяет получать высокие эффективности, то характеристика становится
осциллирующей, что и наблюдалось на эксперименте для
linℓО3 .
Если материал позволяет получать высокие эффективности, то характеристика становится
осциллирующей, что и наблюдалось на эксперименте для
linℓО3
/22/.
Теория дает также зависимость h
~ ¦
(Т). Однако такие
- 550 -
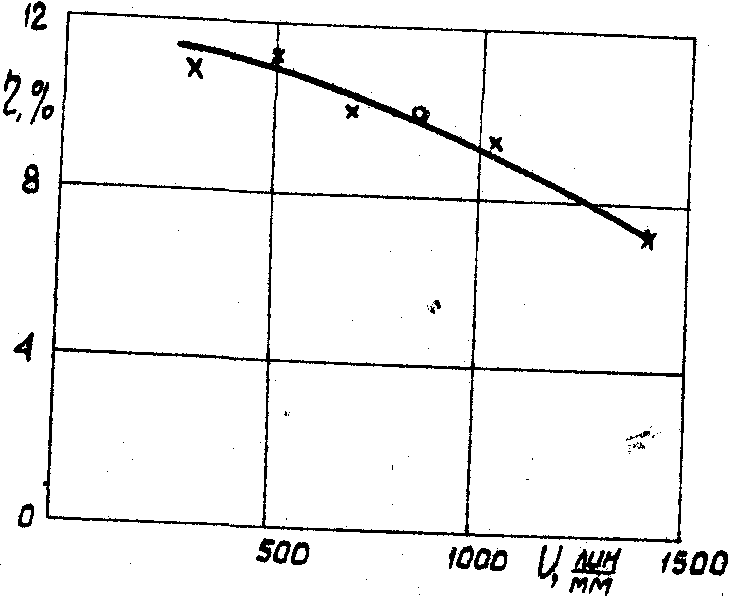
Рис.9.
эксперименты при охлаждении пока не проводились. Сравнение было проведено по "optical domage" и получено хорошее согласие. В широкой области Т:
D
n ~ a·exp[hu
/kt]
т.е. D
n растет по мере уменьшения Т. При низких Т° зависимость D
n=¦
(t) ослабляется, а затем исчезает вовсе. Таким образом, открывается неиспользованная возможность влиять на свойства записываемой голограммы за счет Изменения температуры. При этом изменятся и кинетические характеристики голограммы, т.к. будет уменьшаться или расти проводимость. Многие вещества, в которых при комнатной температуре невозможна эффективная запись за счет диффузионных полай при понижении Т могут оказаться пригодными для записи. Более того, во многих средах точка перехода в сёгнетоэлектрическую фазу лежит в области Т от азотной до комнатной, и можно на несколько порядков повысить чувствительность записи за счет охлаждения.
- 551 -
В заключении этого раздела отметим, что стационарные решетки можно "закреплять", т.е. делать нестираемыми восстанавливающим излучением. Для этого, как показал впервые Амоди, достаточно погреть кристалл до температуры Т »
100°С, когда начинается диффузия ионов /23/.
Другой вариант - считывание излучения с длиной волны в области прозрачности голографической среды при отсутствии многофотонных переходов.
Ряд широкозонных полупроводниковых кристаллов с достаточно низкой проводимостью может оказаться пригодным для записи голограмм по этой схеме. Обязательным условием для выбора конкретного соединения здесь является наличие электрооптического эффекта.
3. Тепловой механизм, записи
Закономерности тепловой записи достаточно хорошо изучены на примере жидких сред, таких как поглощающие растворы самопросветляющихся жидкостей /15/ и нелинейные преобразователи типа cs2, ccℓ4 /24/. По оценкам работы /15/ в случае твердых тел данный механизм записи значительно менее эффективен.
Последние исследования показали возможность тепловой записи в полупроводниковых кристаллах. Так, в кристалле zno при двухфотонном возбуждении моноимпульсным лазером на стекле с nd3+ возникала не только голографическая решетка на свободных носителях, описанная в предыдущем разделе, но также и тепловая решётка с существенно отличающимся временем жизни /8/.
Дифракционная эффективность такой решетки составляла доли процента (примерно на порядок меньше, чем решетки на свободных носителях). Время стирания, напротив, было существенно больше, чем время стирания решетки на свободных носителях (20 нсек и > 100 мксек, соответственно).
Интересным возможный вариантов тепловой регистрации голограмм является запись пироэлектрических полей в электрооптических кристаллах. Голографические эксперименты в этой области пока отсутствуют. Однако пироэлектрический эффект в таких кристаллах, как ниобат лития, успешно используется в настоящие время для оптического детектирования пикосекундных импульсов /10/. Так как изменение наводимого
- 552 -
поля (а следовательно, и показателя преломления при записи фазовой голограммы) пропорционально временной производной от температуры, этот процесс является очень малоинерционным и представляет интерес с точки зрения динамической голографии в режиме ультракоротких импульсов.
4. Необратимая эаписъ
Под действием мощного когерентного излучения во многих полупроводниковых материалах происходят необратимые изменения (Фотодиссоциация, поверхностные или объемные разрушения). Эти явления также могут быть использованы для записи голограмм. Наиболее подходящим классом полупроводниковых материалов для осуществления записи рубиновым лазером оказались так называемые "слоистые полупроводники".
Если поместить такое вещество в интерференционное поле на его поверхности образуется рельеф, причем глубина отдельной бороздки сравнима с длиной волны записывающего света. Исследовались кристаллы bij3, zes, zese, а также стеклообразные сплавы системы германий-селен, обогащенные селеном.
Образцы имели ряд плоскопараллельных пластинок размером 10 xl0x0,l мм3 с зеркальной поверхностью. Все перечисленные соединения обладают существенным поглощением на длине волны рубинового лазера l
= 6943 Å. Çапись производилась как моноимпульсным излучением, так и излучением в режиме свободной генерации. Соотношение интенсивностей двух записывающих пучков составляло 1:4 угол между пучками изменялся в пределах 5¸
60°. Исследования записанных решеток производились при помощи микрофотометра МИИ-4.
На рис. 8 показан вид голографических решеток разной пространственной частоты, записанные на кристаллах zes и zese. При плотностях облучения порядка 10-2 дж/см2 дифракционная эффективность составляла 0,5¸
1%, а форма штриха бала близка к синусоидальной. Для кристалла bij3 и стекол zеse синусоидальный профиль штриха сохранялся также и при повышении плотности облучения более, чем на порядок, в то время как для zes и zese
- 553 -
при больших экспозициях форма штриха заметно отличалась от синусоидальной. В оптимальных по экспозиции условиях удается записать решетки с эффективностью более 10%. Специальное напыление решеток тонкой пленкой золота позволило увеличить дифракционную эффективность до 50%.
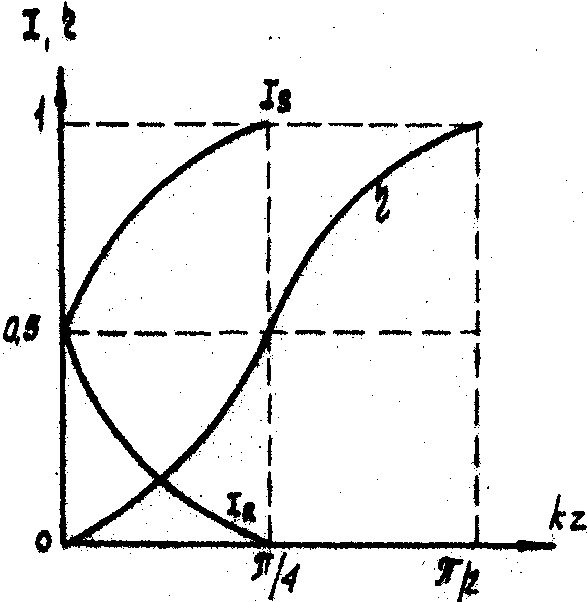
Рис. 10.
При фиксированной плотности облучения был получен ряд голографических решеток с различным числом штрихов на миллиметр. На рис.10 показана зависимость дифракционной эффективности от пространственной частоты, определенная на длине волны гелий-неонового лазера (l
= 6528 Å). Óменьшение дифракционной эффективности с ростом пространственной частоты связано как с наличной дефектов структуры кристаллов, так и с изменением условий тепловыделения. Эта характеристика может быть улучшена за счет применения более совершенной технологии изготовления кристаллов и за счет сокращения длительности записывающих импульсов.
- 554 -
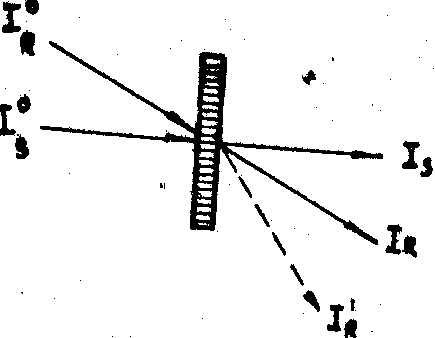
Рис.11.
iv. Энергообмен в процессе записи динамических голограмм
В ряде случаев, например, при коррекции волнового фронта излучения и обработке информации, возникает задача перераспределения энергии взаимодействующих когерентных пучков. Широкий диапазон времен стирания голограмм в полупроводниковых кристаллах дает возможность использовать записанные на них голограммы для обработки информации в реальном времени, для создания элементов оперативной памяти и т.д. Однако практическая реализация таких устройств сталкивается с некоторыми принципиальными трудностями. Так, уже отмечалось, что в нелинейной, чисто фазовой среде, показатель преломления которой безынерционно следит за изменением интенсивности в интерференционной картине n(х)=n0(x)+n2|
e|
2. Дифракция не приводит к энергообмену между двумя записывающими волнами /20/. Иными словами, если на безынерционную нелинейную среду падают две
- 565 -
волны - объектная и опорная, то несмотря на то, что решетка может записаться с большой эффективностью, на выходе интенсивности двух волн будут такими же, как и на выходе.
Как считать информацию, усилив выходящий объективный пучок так, чтобы преобразование стало энергетически выгодным? Для этого нудно сдвинуть записанную голограмму относительно интерференционной картины на некоторый фазовый угол за время, меньшее характерного времени изменения падающих пучков. Оптимальный угол рассогласования составляет Ф = p
/2, т.е. решетки должны быть смещены друг относительно друга на l/4 /25/. Тогда интенсивности, выходных пучков ir и is задаются выражениями:
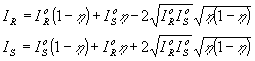
в которых есть новый интерференционный член с Ф . При Ф=90° эти выражения дают чистую синусоиду с общей амплитудой (ior + ios) и сдвигом, зависящим от соотношения интенсивностей двух пучков. Таким образом, при любом исходном соотношении интенсивности пучков и отличной от нуля дифракционной эффективности голограммы возможно полное суммирование интенсивности двух пучков на входе в одном объектном на выходе (рис.11).
Фазовый сдвиг решетки по отношению к интерференционной картине существенно влияет на энергообмен и в случае тонкой фазовой голограммы. Проведенный нами расчет показал, что при Ф = p
/2 отношение m интенсивности нулевых порядков дифракции (рис.11) следующим образом связано с отношением интенсивности интерферирующих пучков:
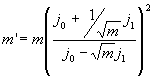
Здесь j0 и j1 - функции Бесселя нулевого и первого порядков. При выполнении условия
j0 = 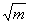 j1 j1
- 556 -
один из нулевых порядков полностью гасится, а его энергия перекачивается в нулевой порядок второго пучка, интенсивность которого i's при этом составляет:
i's @
0,3(i0r + i0s)2
Это больше интенсивности i0 падающего пучка в k£
0,3(1+m)2/m раз. Возрастает и "дифракционная эффективность" h
:
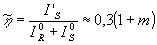
Гак, при равной интенсивности пучков
(m = 1) 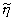 =60%,
что почти в два раза превышает максимальное значение h
=34% для одного
пучка найдено. Зависимость основных характеристик перекачки энергии от соотношения
интенсивности пучков */. =60%,
что почти в два раза превышает максимальное значение h
=34% для одного
пучка найдено. Зависимость основных характеристик перекачки энергии от соотношения
интенсивности пучков */.
Проведенный анализ показывает, что тонкие фазовые решетки в ряде случаев весьма эффективно осуществляют энергообмен пучков. (В работе /26/ это свойство использовано для измерения малых линейных перемещений). Отметим также, что амплитудные решетки как тонкие, так и объемные не обладают способностью перекачивать энергию интерферирующих пучков.
Эксперимент, или как создать смещенные решетки?
Существуют механизмы записи, при которых такие решетки возникают автоматически. Таков диффузионный механизм записи, где возникающее электрическое поле пропорционально производной от пространственного распределения электронов. Если ne(х) близко к синусоиде,
*/ Необходимо отметить, что оптимальная перекачка достигается при меньшей глубине модуляции показателя преломления, чем это следует из условия максимума функции Бесселя первого порядка. Здесь имеется аналогия с объемными решетками, где для достижения полной перекачки в случае двух пучков требуется вдвое меньшая глубина модуляции решетки, чем для достижения 100%-ной эффективности в случае одного пучка.
- 557 -
то поле при малой интенсивности будет пропорционально cos(p
x/l), а при большой интенсивности более сложной функции, первый член Фурье - разложения которой также будет acos(p
x/l). Отсюда следует, что записываемая голографическая решетка смещена на четверть периода относительно интерференционной картины.
Экспериментально такие решетки получены пока только в сегнетоэлектриках linbo3 и доказательство сдвинутости решетки - это перераспределение интенсивности проходящих пучков при записи голограммы. По всей вероятности удастся и в полупроводниках реализовать запись на этом механизме, что даст возможность использовать их для голографии в реальной времени без дополнительных ухищрений.
Большинство же известных механизмов дают решетки несдвинутые. Здесь нужно сдвиг создавать искусственно, либо механически, перемещая решетку, либо интерференционную картину, внося разность фаз между пучками. Все механизмы записи, как бы быстры они не были, имеют конечное время релаксации. Если сдвиг происходит за времена, меньшие этого характерного времени жизни решетки, результирующая голограмма окажется смещенной относительно интерференциальной решетки и мы получим желаемый эффект.
Оригинальное решение задачи создания смещенной решетки предложено Ю.Н.Денисюком /27/. Неподвижная регистрирующая среда освещается интерференционной картиной двух пучков с различающимися частотами. При этом максимум и минимум интерференционного поля равномерно смещаются со скоростью v, определяемой частотным рассогласованием записывающих пучков D
w
:
v = lD
w
/p
В зависимости от инерционности механизма D
w
выбирается таким, чтобы за время, порядка половины времени релаксации решетки происходило смещение ее на четверть периода.
Получение сдвинутых тепловых решеток за счет смещение активной среды при записи предложено в работе /20/. В работе /20/ приведен теоретический расчет параметров голографической решетки в движущемся регистрирующем слое и результирующего энергообмена.
- 558 -
v. Перспективы
1. Несколько заключительных замечаний
До сих пор речь шла, в основной, о записи синусоидальной решетки.
В соответствии с теорией /10/ для идеальной регистрирующей среды должно быть
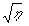 ~ 1, т.е.
h ~ i2.
Как обстоит дело в нашем случае? Как мы видели, для фазовых решеток h
= sin2(p
D nz/l cosq
) в случае объемных и
h = j2(p
D nz/l cosq
) в случае тонких решеток. И в том и в другом
случаях зависимость осциллирующая. Поэтому реально можно говорить о хорошей
передаточной функции при относительно малых D
n. Тогда
h ~ D n2
и все определяется механизмом записи. Так, для
si при записи решетки свободных носителей за
счет однофотонного поглощения D
n ~ i и h
~ i2, т.е. удовлетворяет требованию
идеальной среды.
~ 1, т.е.
h ~ i2.
Как обстоит дело в нашем случае? Как мы видели, для фазовых решеток h
= sin2(p
D nz/l cosq
) в случае объемных и
h = j2(p
D nz/l cosq
) в случае тонких решеток. И в том и в другом
случаях зависимость осциллирующая. Поэтому реально можно говорить о хорошей
передаточной функции при относительно малых D
n. Тогда
h ~ D n2
и все определяется механизмом записи. Так, для
si при записи решетки свободных носителей за
счет однофотонного поглощения D
n ~ i и h
~ i2, т.е. удовлетворяет требованию
идеальной среды.
Для cds1, cdse,
zno, когда поглощение двухфотонное D
n~ i2, a 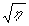 ~ i2. Наконец, при диффузионном
механизме и в теории, и на эксперименте D n
~
~ i2. Наконец, при диффузионном
механизме и в теории, и на эксперименте D n
~ 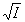 и
и 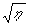 ~
~ 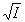 , а
с ростом интенсивности зависимость еще слабее.
Как видно, есть весь набор вариантов, и в каждом конкретном случае можно выбирать
характер зависимости h от
i. , а
с ростом интенсивности зависимость еще слабее.
Как видно, есть весь набор вариантов, и в каждом конкретном случае можно выбирать
характер зависимости h от
i.
Важной зависимостью является также h
= ¦
(l}. Для получения высококачественных изображений нужен материал, для которого h
¹
¦
(l}. Однако, если мы имеем дело с зависимостями типа h
~ (1/l)n, это может быть использовано для автоматического, дифференцирования изображения по пространственной координате.
Литература
1. Р.Кольер, Ц.Берхарт, Л.Лин, "Оптическая голография", Мир, М., 1973.
2. j.bordogna et al. rsa review, v.33, 225, 1973.
3. С.А.Казанский, А.И.Рыскин, в сб. "Оптическая и электрооптическая обработка информации", изд. "Наука", М., стр.104, 1974.
4. Р.Фейнман, Р.Лкйтон и М.Сендис. Фейнмановские лекции по физике
- 559 -
стр.65, изд. Мир, М., 1966.
5. l.woerdman. phys.res.rep., n 7, supl. 1971.
6. j.j.vaithus. phys.stat.solid., v.22, 1974.
7. Л.Л.Борщ и др. Письма в ДЭТГ, т.18, 679, 1973.
8. j.j.vert, r.j.collins. j.appl.phys., v.44, n 12, 5455, 1973.
9. w.d.jonston. j.appl.phys., v.14, n 8, 3279, 1970.
10. a.m.glass, d.h.auston. appl.phys., v.20, n 10, 398, 1972.
11. Ф.Хофф, И.Хонат, Б.Стадник. Материалы v Всесоюзной школы по голографии, Л., стр.557, 1973.
12. В.Н.Синдов, Материалы v Всесоюзной школы по голографии, Л., стр.491, 1973.
13. Д.И.Блецкан и др. Заявка на изобретение 2625/1886848 от 29/vi-1973
14. М.Ф.Дейген и др., ФТТ, 16, 1895, 1974.
15. h.eichler et al. zs angew phys., v.31, 1, 1971.
16. П.П.Погорецкий, Е.И.Салькова, М.С.Соскин, УФЖ, 19, № 10, 1974.
17. М.Ф.Дейген и др. Тезисы докладов vii Всесоюзной конференции КИНО. изд. МГУ, М., 1974.
18. В.П.Силин, А.А.Рухадзе. Электромагнитные свойства плазмы и плазмоподобных сред, изд. Наука, М., 1961.
19. Б.Я.Зельдович. Краткие сообщения по физике, изд.ФИАН, М., стр.20, вып.5, 1970.
20. Ю.А.Ананьев. Квантовая электроника, изд. "Сов.радио", 1, 1669, 1974.
21. А.А.Борщ и др. Тезисы докладов vii Всесоюзной конференции КИНО, изд. МГУ, М., стр.425, 1974.
22. j..amodei et al. appl.opt., v.11, n 2, 390, 1972.
23. j.j.amodei at al. appl.phys.lett., v.18, n 12, 540, 1971.
24. r.q.harrison et al. appl.phys.lett., v.13, 253, 1968.
25. d..l.staebler, j.j.amadei. j.appl.phys., v.43, n 3, 1042, 1972.
26. Б.Г.Турухано, Н.Турухано. Труды iii Всесоюзной школы по голографии, изд. ЛИЯФ, Л., 1973.
27. Ю.Н.Денисюк. ЖТФ, т.44, вып.1, 131, 1974.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

