|
|
 |
 |

|
| |
ИНТЕРФЕРЕНЦИЯ И КОГЕРЕНТНОСТЬ
Г.В.Скроцкий
Рассматривается интерференция двух сигналов произвольного спектрального состава. В виде примера исследуется случай квазимонохроматического излучения. Особое внимание уделяется анализу ситуации, в которой время когерентности меньше времени задержи между этими сигналами.
Полное описание явления интерференции стационарных оптических полей произвольного спектрального состава модно сделать в рамках классической теории. Полученные таким образом результаты совпадут с результатами строгого квантового описания, если пользоваться представлением об аналитическом комплексном сигнале v(t), частотный спектр которого содержит только положительные частоты.
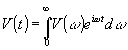 (1) (1)
Примем, что v(t) есть интересующая нас составляющая электрического поля электромагнитной волны.
Функция корреляции Г 12( t
) двух стационарных сигналов v1(t) и v2(t) не зависит от начала отсчета времени. Она определяется соотношением
Г 12( t
) = <v 1(t)v +2(t+ t
)> (2)
- 38 -
где угловые скобки <....> обозначают усреднение по времени за промежуток времени q
, больший по сравнении с периодом средней частоты сигнала.
В случае v2(t)=v1(t), получаем функцию автокорреляции Г11( t
)=<v 1(t)v 2(t+ t
)>. Для t
=0, Г11(0)=< |
v 1(t) |
2> является мерой средней интенсивности сигнала. Для сигналов оптического диапазона его можно считать бесконечным. Введем нормированную функцию корреляции g
12( t
), которая оказывается удобной мерой когерентности сигнала
|
g
12(t
)= |
Г 12(t
) |
(3) |
|
[Г 11(0)Г22(0)]½ |
Рассмотрим случай, когда такой стационарный сигнал проходит через интерферометр, т.е. каким-либо образом разделяется на два сигнала, которые затем попадают на одно и то же приемное устройство. Если время запаздывания одного из них по отношению к другому обозначить через Т , то сигнал, падающий на приемное устройство имеет вид:
v(t) = v1(t) + v2(t + t) (4)
Вычислим функцию корреляции Г(t
) этого сигнала. Согласно (2):
Г(t
) = <[v1(t) + v2(t+t)][v+1(t+t) + v+2(t+t+t
)]>
или
Г(t
) = Г 11( t
) + Г22( t
) + Г12( t
+ t ) + Г21( t
- t) (5)
Вводя нормированные функции корреляции, получим
<j>g
(t
) = <j1>g
11(t
) + <j2>g
22(t
) +
+ 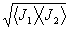 {g
12(t + t) + g
21(t - t)}, (6) {g
12(t + t) + g
21(t - t)}, (6)
- 39 -
Последнее выражение описывает изменение интенсивности, возникающее при сложении двух стационарных сигналов. Член в квадратных скобках определяет характер этих изменений в зависимости от постоянной времени принимающего суммарный сигнал устройства. Если постоянная времени этого устройства, т.е. время, за которое происходит усреднение, мала по сравнению со средним периодом изменения последнего члена, то наблюдаются биения. В этом случае приемник не может разрешить структуру спектра сигнала и позволяет наблюдать только его в целом. Если же она достаточно велика, происходит их усреднение и член в квадратных скобках выпадает. В этом, последнем случае, могут наблюдаться изменения в спектре сигнала, который, если постоянная времени приемника достаточно велика, может быть достаточно детально с его помощью исследован. Биения и интерференция - два различных проявления одного и того же явления. Сделанные выводы относятся, в равной мере, как к случаю временных, так и пространственных частот.
Между спектральной плотностью сигналов v1(w
)v2+(w
) и функцией корреляции существует простая зависимость. Ее можно установить, подставив в выражение (3) спектральные разложения v1(t) и v2(t). Согласно (1)
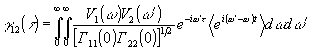
Но функция
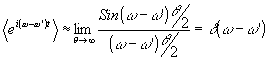
есть d
-функция Дирака, поэтому
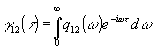 (7) (7)
где
- 40 -
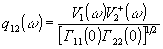 (8) (8)
нормированная спектральная перекрестная плотность сигналов. Вещественная функция
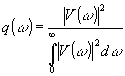 (9) (9)
описывает контур спектра исходного сигнала. Для квазимонохроматического сигнала q(w
) описывает контур спектральной линии. Согласно (7), он связан с функцией корреляции выражением
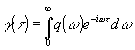 (10) (10)
Комплексную функцию g
(t
) всегда можно представить в виде
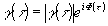 (11) (11)
где |
g
(t
)|
ее модуль, a Ф(t
) - фаза. Легко видеть, что
 (12) (12)
Переходя в (6), согласно (7), к спектральному представлению и воспользовавшись (12), получим важное соотношение:
<j>q(w
) = <j1>q11(w
) + <j2>q22(w
) +
+ 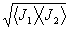 [q12(w
)e-iw t + q12+eiw
t] (13) [q12(w
)e-iw t + q12+eiw
t] (13)
Оно позволяет найти спектр суммарного сигнала.
При объяснении явления интерференции обычно ограничиваются
- 41 -
рассмотрением выражения (6) для случая t
=0, когда g
(0)=g
11(0)=g
22(0)=1 и
<j> = <j1> + <j2> +2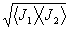 |
g 12 |
g 12 (Т)|
cosФ(Т) (14)
так как
g
12 (Т) + g
21(-Т) = g
12(Т) + g
12+(Т) = 2|
g
12(Т)|
cosФ(Т)
Видность картины интерференции
|
В = |
<j>max - <j>min |
(15) |
|
<j>max + <j>min |
в случае, когда оба сигнала имеют одинаковую интенсивность, равна модулю функции корреляции |
g
12(Т)|
. Фазу функции корреляции Ф(Т) можно определить по положению полос интерференции. Со времен Реллея считалось, что |g
(t
)| и Ф(t
) — независимые характеристики явления. Можно показать, что для аналитических сигналов вида (1) они связаны дисперсионными соотношениями и каждая из них определяет другую.
Для строго монохроматического света g
12( t
)=1. В общем случае (14) можно представить в виде суммы двух членов:
<j> = [<j1> + <j2> +2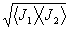 cosФ(Т)]|
g 12(Т)|
+
+ [<j1> + <j2>]{1 - |
g
12(t)|
} (16)
соответствующих двум крайним случаям: когерентного |
g
12(т)|
=1 и некогерентного |
g
12(Т)|=0 света.
Определение (3) функции g
12(t ) можно записать в форме
|
g
12(t
)= |
<v1(t)v2+(t + t
)> |
· |
<v1(t)v2+(t)> |
|
<v1(t)v2+(t)> |
[<|
v1(t)|
2><|
v2+(t)|
2>]½ |
- 42 -
Если складываемые сигналы v1(t) и v2(t) одинаковым образом зависят от времени,
|
g
12= |
<v1(t)v1+(t+t
)> |
· |
g
12(0)=g
11(t
)g
12(0) |
(17) |
|
<|
v1(t)|
2> |
При этом равны нормированные спектральные плотности сигналов q11(w
)=q22(w
) и, согласно (17), q12(w
) вещественно и равно:
q12(w
) = q11(w
)g
12(w
) (18)
Световые пучки, удовлетворяющие этим условиям, называются спектрально чистыми. Спектрально чистые излучения создают протяженные источники некогерентного света. Примером спектрально чистого излучения является также излучение черного тела.
Для спектрально чистых пучков выражения (6) и (13) могут быть записаны в виде
<j>g (t
)=[<j1>+<j2>]g
11(t )+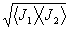 g
12(0){g 11(t
+t)+g 11(t
-t)}(19) g
12(0){g 11(t
+t)+g 11(t
-t)}(19)
и
|
<j>q(w
)=[<j1>+<j2>]q11(w
){1+2 |
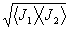
|
g
12(0)cosw
t} |
(20) |
|
<j1>+<j2> |
Пусть складываемые сигналы квазимонохроматичны, т.е. ширина их спектра мала: D
w
<<w
o, где w
o — оптическая частота, около которой центрировано излучение. Если при этом разность хода ct<c/D
w
=ct
c, т.е. время задержки Т меньше времени когерентности сигнала t
С=1/D
w
, то во всем интервале частот, в котором g
11( w
) ¹
0, можно заменить cosw
t на cosw
0Т. Интегрируя (20) от 0 до ¥
по w
и учитывая, что q(w
) и q11(w
) - нормированные спектральные плотности, получим:
<j> = <j1>+<j2> +2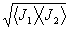 g
12(0)cosw 0t (21) g
12(0)cosw 0t (21)
- 43 -
Сравнивая с (20),
находим, что q(w
)=q(w ). Это
хорошо известное выражение описывает интерференцию двух частично-когерентных
световых пучков. Спектральный состав суммарного излучения в случае Т<t
С остается неизменный, а его интенсивность модулирована с периодом
2p /w
0. С классической точки зрения это
соответствует случаю, когда волновые цуги еще перекрываются. Новая ситуация
возникает, если время задержки Т сделать больше t
С, т.е. оптическая разность хода между квазимонохроматичесими сигналами
больше длины когерентности Сt С.
В этом случае, при интегрировании выражения
(20) по w от
0 до ¥ ,
быстро осциллирующий множитель cosw
t обращается в нуль, так как можно считать,
что q11(w
) мало изменяется на интервале 1/t,
a 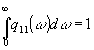 .
Отсюда следует, как очевидное в этом случае, равенство .
Отсюда следует, как очевидное в этом случае, равенство
<j> = <j1> + <j2> (22)
Свидетельствующее об отсутствии интерференции и новое важное соотношение
|
q(w
)=q11(w
){1+2 |
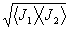
|
|
g
12(0)|
cosw
t} |
(23) |
|
<j1>+<j2> |
Таким образом, когда разность хода между сигналами больше времени когерентности t
С, интерференция, как и следует ожидать, отсутствует, средняя суммарная интенсивность постоянна и не зависит от Т. Спектральная же плотность интенсивности q(w
) испытывает биения с глубиной модуляции К.
|
К = |
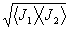
|
g
12(0)cosw
t |
(24) |
|
<j1>+<j2> |
Эта спектральная модуляция сохраняется при сколь угодна большой разности хода СТ и имеет своим нижним пределом t
=t
С.
Временная или пространственная картина интерференции не может рассматриваться сама по себе независимо от условий и способа ее
- 44 -
детектирования. Наблюдаемый результат сложения двух и более сигналов существенным образом зависит от временных и пространственных характеристик приемника излучения.
Если достоянная времени детектора излучения t
=2p
/d
w
=2p
q/w
0, (где q его добротность) больше времени запаздывания сигнала v2(t+Т) по отношению к сигналу v1(t), т.е. второй сигнал поступает в него еще до того, как закончился переходный процесс действия первого сигнала, то он, разумеется, реагирует на оба сигнала. Такой, достаточно добротный детектор q=w
0/d
w
вырезает из спектра сигнала узкую полосу частот d
w
<<D
w
, т.е. монохроматизует проходящее через него излучение, увеличивая тем самым длину м время его когерентности.
Это явление впервые экспериментально наблюдалось Алфордом и Годдом /1/. Недавно оно наблюдалось в белом свете при разности хода 10,7м /2/ (большей не допускало помещение, в котором была расположена установка). Было показано, что спектр суммарного сигнала, наблюдаемый на выходе интерферометра, промодулирован с частотой, равной средней частоте w
0 пропускания применяемого для анализа явления фильтра. При этом условие интерференции D
w
Т<1 заменяется условием d
w
t<1, где d
w
полоса пропускания интерферометра. Детальный квантовомеханический анализ этого явления показывает, что это явление является, по существу, эффектом второго порядка по степени когерентности, но эффектом первого порядка по параметру вырождения /3,4/, можно считать, что применяемый дли анализа спектра узкополосный резонансный фильтр ограничивает ширину спектра и увеличивает эффективную длину когерентности.
Изложенная выше элементарная теория явления интерференции может быть обобщена на сличай сигналов с произвольным спектральным составом. Она без существенных изменений может быть перенесена на сигналы, обладающие спектром пространственных частот. В этом случае возникновение корреляций между сигналами при произвольно большой разности хода, обусловленное введением узкополосного фильтра пространственных частот, открывает возможность
- 45 -
постановки принципиально новых экспериментов, в частности, в голографии.
Литература
1. w.p.alford, a.gold. am.j.phys., 26, 481 (1958).
2. claude delisle et michel brochu, canad.j.phys., 50, 1993 (1972).
3. m.p.givens. j.opt.soc.am., 51, 1030, 1032 (1961).
4. l.mandel. j.opt.soc.am., 52, 1335 (1962).
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

