Media-security

ГОЛОГРАФИЯ КАК РАЗДЕЛ РАДИОФИЗИКИ

А.И.Ларкин

На примере решения задач фазового детектирования в радиофизике к выявления фазовой информации в оптике рассматривается физический смысл аналогии в описании радиофизических к оптических явлений. Обсуждается адекватность такого описания и пределы его применимости в голографии. Приводятся радиотехнические аналоги основных схем голографии.

В настоящее время в специальной голографической литературе широко используется радиофизический язык - язык теории колебаний /1-3/. На возможности и целесообразность радиофизического подхода к оптическим явлениям впервые обратил внимание С.М.Рытов /4/. При таком подходе вопросы образования оптических изображений выступают как частный случай общих колебательных закономерностей. В последней время высказываются предположения (например, в /5/) о включении таких представлений в учебники и учебные программы. Связано это не только с тем обстоятельством, что на основе общей радиофизической подготовки проще усвоить основные идеи когерентной оптики и голографии при таком изложении, но также и с тем, что такое описание наряду с обычным, использующим понятия интерференции и дифракции, способствует более полному описанию различных свойств и проявлений голографического метода /6/ - таких как разрешающая способность, информативная емкость, влияние неидеальности фоторегистратора и источника излучения, фильтрация и улучшение качества изображений, распознавание образов и др.

Наиболее близкая к голографии радиофизическая задача-задача выявления информации из фазовомодулированного колебания, т.е. задача фазового детектирования. В простейшем случае слабой модуляции чистым типом спектр фазовомодулированного колебания состоит

- 488 -

из трех компонентов

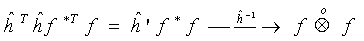
и от спектра амплитудно-модулированного колебания

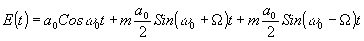
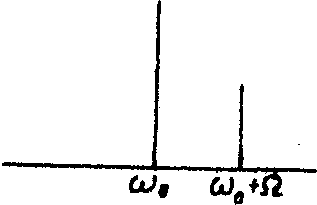
отличается только взаимным фазовым сдвигом несущей по отношению к боковым (рис.1а,б). Для выявления фазовой информации перед квадратичным детектором необходим дискриминатор, осуществляющий одно из следующих преобразований спектра и соответствующего изменения векторной диаграммы: подавление несущей (рис.2а), подавление боковой составляющей (рис.2б), поворот фазы несущей на 90°

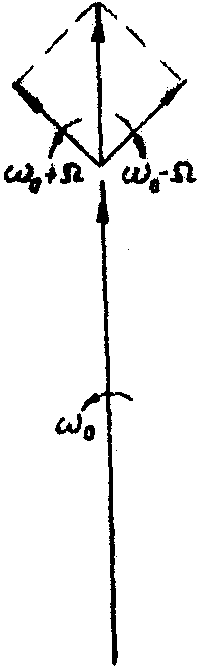
а) б)

Рис.1. Векторные диаграммы модулированных колебаний:

а) амплитудная модуляция;

б) фазовая модуляция ,

- 489 -

(рис.2в). Как видно из векторных диаграмм, преобразованное колебание оказывается модулированным по амплитуде, причем в последнем случае характер амплитудной модуляции точно соответствует исходной фазовой модуляции.

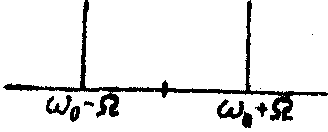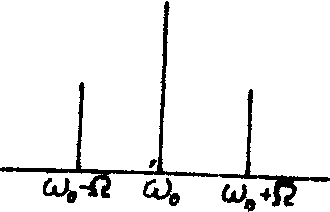
а) б) в)

Рис.2. Методы фазовой дискриминации в радиотехнике:

а) подавление несущей;

б) подавление боковой;

в) поворот несущей на p /д .

В оптике чистую фазовую модуляцию можно осуществить, пропустив плоскую волну через синусоидальную фазовую дифракционную

- 490 -

решетку. Распределение поля в фокальной плоскости, стоящей за решеткой линзы, определяется преобразованием Фурье:

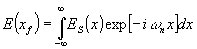
где w _n=kx¦ /¦ - пространственная частота.

Следовательно, распределение интенсивности света в фокальной плоскости соответствует распределению спектральной плотности в спектре модулированного колебания. В соответствии с этим методы фазового контрастирования в оптике можно интерпретировать аналогично методом фазового детектирования в радиодиапазоне (рис.3). Метод темного поля (рис.3а) соответствует подавлению несущей в спектре. Метод Тендера с экраном Фуко, перекрывающим фокальную полуплоскость (рис.3б), соответствует подавлению боковой составляющей. Метод фазового контраста с использованием четвертьволновой пластинки в фокальной плоскости (рис.3в) эквивалентен повороту фазы несущей на 90°. Как и в радиодиапазоне, каждый из этих

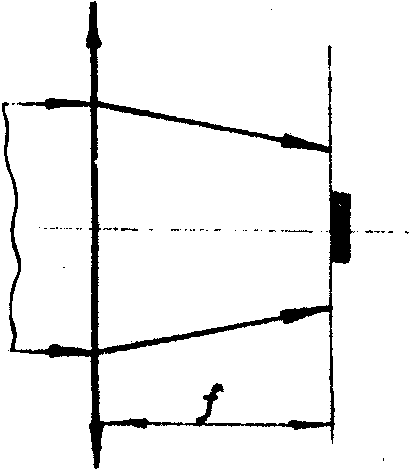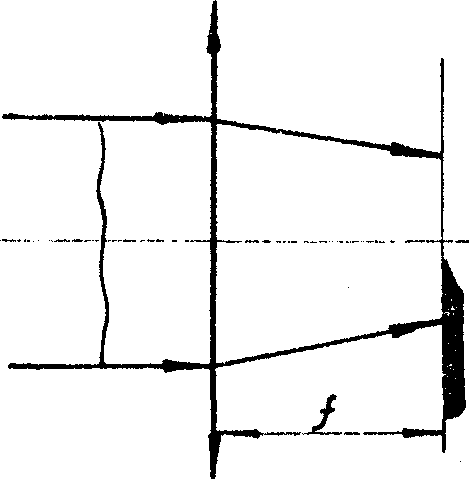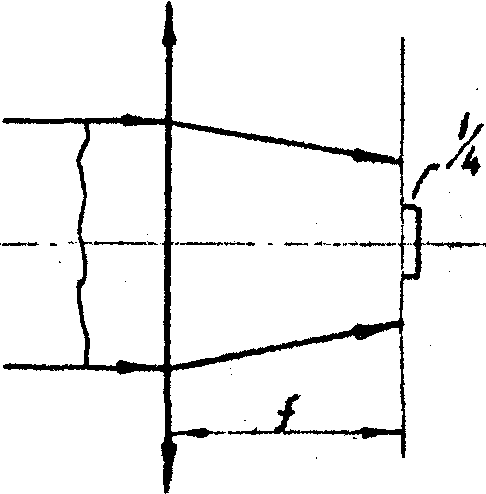
а) б) в)

Рис.3. Методы фазовой демодуляции в оптике:

а) метод темного поля;

б) метод Теплера;

в) метод фазового контраста.

- 491 -

оптических методов приводит к возможности обнаружения на квадратичном детекторе фазовой информации, т.е. фазовое детектирование в оптике достигается аналогичными преобразованиями спектра.

Наряду с перечисленными методами с целью фазовой модуляции в радиотехнике применима развитая Е.Г.Момотом /7/ идея синхронного детектирования. Можно сказать, что в общем случае квадратичного детектирования гетеродинированного сигнала сохраняется информация о фазовой модуляции. Действительно, если к фазовомодулированноиу колебанию вида exp[i(w ₀t+y (t))] линейно добавить синусоидальное колебание гетеродинного генератора exp[iw _rt], после квадратичного детектирования получки

i(t) = {exp[i(w ₀t + y (t))] + exp[iw _rt]}² =

=2+exp{i[(w ₀-w _r)t+y (t)]}+exp{-i[(w ₀-w _r)t+y (t)]}=

= 2 + 2cos[(w ₀-w _r)t+y (t)]

т.e. ток на выходе квадратичного детектора содержит информацию о характере фазовой модуляции. В частном случае, когда частота гетеродина совпадает с несущей частотой в спектре модулированного колебания, что реализуется в схеме синхронного детектирования

i(t) = 2[1 + cosy (t)]

Аналогично рассмотренным случаям можно представить оптическую схему, в которой осуществляется такое же преобразование фазовомодулированного колебания. Линейная добавка синусоидального колебания гетеродина в оптической схеме должна соответствовать интерференции исходного модулированного колебания с плоской опорной волной. Такая интерференция осуществляется в схеме голографии Лейта-Упатниекса, причем направление распространения опорной волны можно рассматривать как пространственную частоту гетеродина. В частной случае совпадения частоты гетеродина с частотой несущей в спектре схема Лейта-Упатниекса преобразуется в схему голографии

- 492 -

Габора с совпадающими направлениями распространения предметной и опорной волн.

Наряду с очевидными и удобными аналогиями, такими как время -координата, частота - пространственная частота, амплитудный детектор - фоторегистратор, спектроанализатор - линза, полоса пропускания - апертура и т.д., имеются ограничения, связанные с различной физической природой понятий "частота" и "пространственная частота". Очевидно, что в большинстве случаев Фурье-спектр в оптике оказывается двумерный, что требует соответствующих двумерных преобразований. Пространственная инвариантность спектрального преобразования в оптике оказывается паточной, т.к. сопровождается изменениями азы в спектральных составляющих и ограничена апертурой оптической системы. Наличие третьего измерения - вдоль оптической оси системы приводит к появлению эффектов, не имеющих аналогов в радиотехнике. К ним можно отнести возможность изменения масштаба Фурье-спектра и осуществление фазовой демодуляции посредством расфокусировки. Принципиальная ограниченность пространственной частоты сверху и наличие третьего измерения используются в голографии Денисюка, в схеме которой реализуется предельная величина разницы несущей и гетеродинной частот. Можно предположить, что невозможность радиофизического истолкования уникальных свойств этой схемы связана с отсутствием радиофизической аналогии предельной разности частот.

Различие физической природы радиофизической и пространственной частоты позволяет тем не менее, непосредственно переходить от пространственной частоты к "истинной" фазе в оптике, не вводя понятия "пространственной" фазы. Такой переход оказывается возможным благодаря существованию непосредственной связи направления волнового вектора с градиентом фазы в той же точке пространства, что определяется уравнением Эйконала /8/. Распределение пространственных частот в спектре определяется градиентом истинной фазы световой волны и связанным с ним изменением формы волнового фронта.

- 493 -

Литература

1. Дж.Гудмен. Введение в Фурье-оптику. М., 1970.

2. О.Нейл. Введение в статистическую оптику. М., 1966.

5. Дж.Строук. Введение в когерентную оптику и голографию. М., 1967.

4. С.М.Рытов. УФН, 41, вып.4. 425, 1950.

5. Э.Гехт. УФН, iii, вып.2, 1973.

6. И.П.Мазанько. Радиотехника и электроника, Хiii, 3, 530, 1968.

7. Е.Г.Момот. Проблемы и техника синхронного радиоприема, 1961.

8. Л.Д.Ландау, Е.М.Лифшиц. Теория поля. М., 1967.