|
|
 |
 |

|
| |
ЭЛЕМЕНТЫ ОБЩЕЙ ТЕОРИИ И МЕТОДЫ АКУСТООПТИЧЕСКОЙ ГОЛОГРАФИИ
В.Я.Телешевский
Рассматриваются свойства акустооптического взаимодействия, основанного на дифракции оптическою излучения. В приближении слабого взаимодействия исследуется процесс переноса пространственных и временных спектров взаимодействующих полей в спектр рассеянного излучения. Определяются информационные и изображающие свойства взаимодействия, а также разрешающая способность дифракционного процесса при визуализации акустических полей. Свойства рассеянного на звуке оптического излучения позволяют осуществить полное оптическое восстановление структуры акустических полей. Описаны методы оптического восстановления: дифракционные и гетеродинные. Приводятся экспериментальные результаты.
Введение
Непосредственное взаимодействие света с ультразвуковыми волнами можно рассматривать как голографический процесс, в котором запись акустической голограммы и ее оптическое восстановление совмещены во времени и пространстве. Акустическое поле объемных или поверхностных волн, возбуждаемое в оптически прозрачной среде, образует пространственно-временную структуру, действующую как фазовая оптическая голограмма источника звука. Процесс распространения акустических волн является одновременно процессом записи голограммы . Акустическое поле, выполняющее функции динамической голограммы, содержит пространственную и временную информацию об источнике звука, в том числе о возбуждающем сигнале, облучаемом объекте и т.д.
- 401 -
Дифракция света на акустическом поле приводит к частичному или полному восстановлению этой информации.
Акустооптическое взаимодействие широко используется при визуализации и оптическом исследовании ультразвуковых полей, в оптической обработке информации, технике модуляции световых потоков и других областях /1/. Несмотря на разнообразие схем и технических приемов, общим для всех этих методов является перенос информации, содержащейся в акустическом поле, в световое поле рассеянного на звуке оптического излучения. Такая особенность, характерная для акустооптических методов, доказывает целесообразность их голографической трактовки.
Голографический подход к акустооптическому взаимодействию представляет интерес по следующим соображениям. Во-первых, он позволяет исследовать разнообразные методы, основанные на этом взаимодействии, с единых позиций когерентной оптики. Во-вторых, открывается возможность широкого привлечения аналогий с классической оптической голографией. В-третьих, при подобном подходе акустическое поле рассматривается как оптический элемент с определенными изображающими свойствами. Тем самым существенно расширяются представления о свойствах и областях применения акустооптики.
Некоторые вопросы акустооптической голографии, в частности, изображающие свойства брэгговской дифракции, изложены в ряде работ /2-5/ и отражены в лекции /6/. В данной работе, являющейся продолжением /6/ излагаются теория и методы акустооптической голографии, основанной на дифракции света.
i. Слабое акустооптическое взаимодействие
i.i. Общее решение для поля и спектра рассеянного излучения уетодомтеории возцущедий
Акустооптическое взаимодействие представляет собой процесс
рассеяния светового поля на вариациях оптической неоднородности среды, ,
создаваемых акустическими волнами. Рассмотрим общий случай взаимодействия произвольных
оптического Е0( ,t)
и акустического s( ,t)
и акустического s( ,t)
полей в изотропной,
оптически прозрачной среде (рис.1). ,t)
полей в изотропной,
оптически прозрачной среде (рис.1).
- 402 -
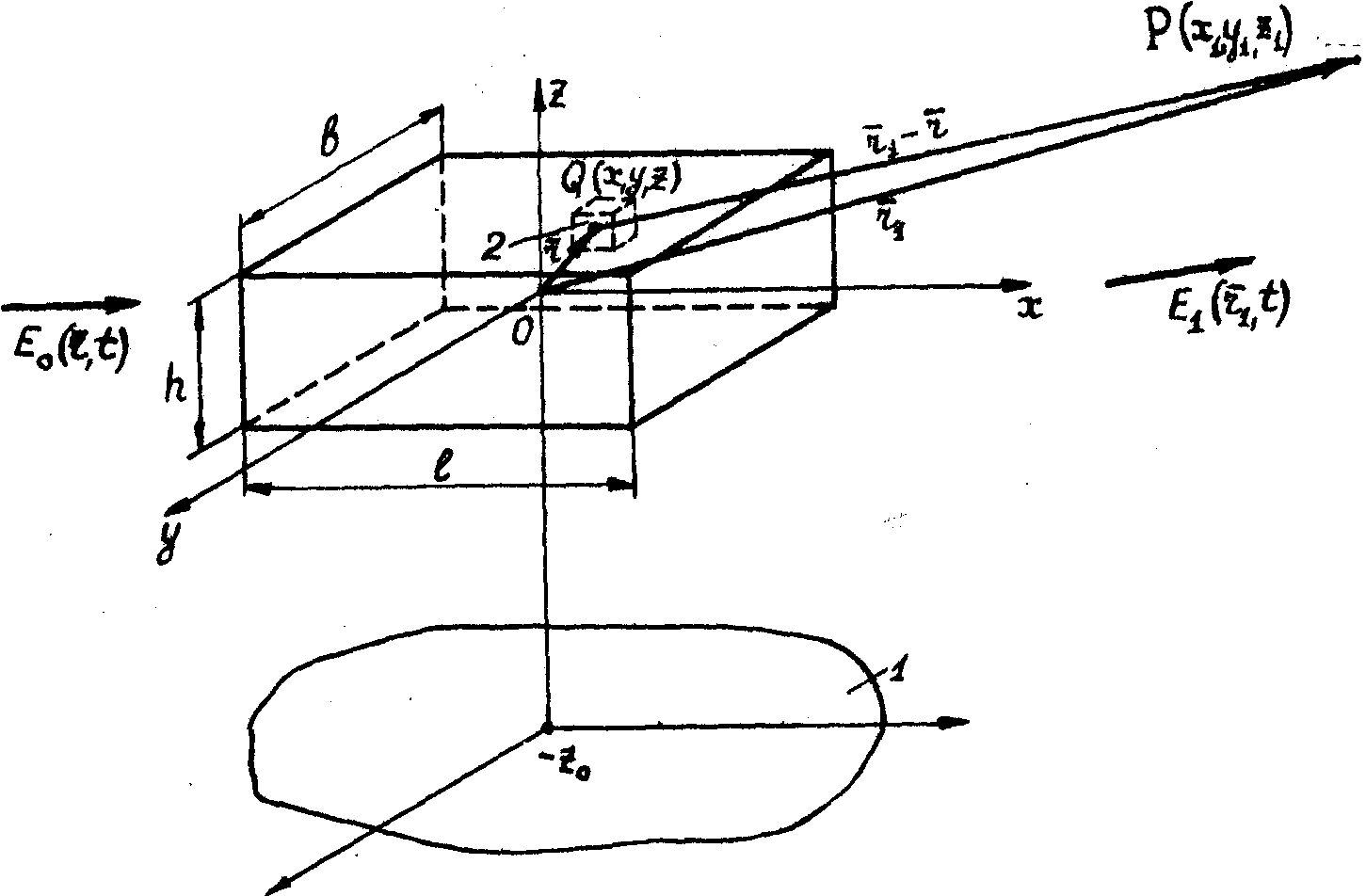
Рис.1. Схема акустооптического взаимодействия:
1 - источник акустического
поля s( ,t);
2 - элементарный объем зоны взаимодействия
dv=dx·dy·dz; q(x,y,z) - точка в зоне взаимодействия;
p(x1,y1,z1) -
точка наблюдения в рассеянном световом поле; Е0 ,t);
2 - элементарный объем зоны взаимодействия
dv=dx·dy·dz; q(x,y,z) - точка в зоне взаимодействия;
p(x1,y1,z1) -
точка наблюдения в рассеянном световом поле; Е0(  ,t)
- падающее световое ::оле; Е1(  ,t)
- рассеянное световое поле;
 -
радиус-вектор точки взаимодействия; -
радиус-вектор точки взаимодействия; 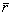 1
- радиус-вектор точки наблюдения;
lbh=v - объем зоны взаимодействия. 1
- радиус-вектор точки наблюдения;
lbh=v - объем зоны взаимодействия.
- 403 -
Акустическое поле s( ,t),
возбуждаемое в полупространстве z ³
-z0, образует в среде сложное распределение
показателя оптического преломления. В приближении линейной акустики это распределение
описывается выражением: ,t),
возбуждаемое в полупространстве z ³
-z0, образует в среде сложное распределение
показателя оптического преломления. В приближении линейной акустики это распределение
описывается выражением:
n( ,t) = n0
+ D n( ,t) = n0
+ D n( ,t)
= n0[1 + d n( ,t)
= n0[1 + d n( ,t)]
(1) ,t)]
(1)
где n0 -
показатель преломления среды, не возмущенной звуком, d
n( ,t)
= D n( ,t)
= D n( ,t)/n0
= cs( ,t)/n0
= cs( ,t) -
относительное изменение показателя преломления, С
- константа акустооптического взаимодействия.
Зона взаимодействия представляет собой объем
v= ℓbh, в пределах которого распределение
показателя преломления удовлетворяет условию ,t) -
относительное изменение показателя преломления, С
- константа акустооптического взаимодействия.
Зона взаимодействия представляет собой объем
v= ℓbh, в пределах которого распределение
показателя преломления удовлетворяет условию
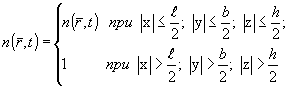 (2) (2)
где ℓ, b, h - размеры зоны в направлениях осей х, у, z, соответственно. При малой величине d
n (порядка 10-5–10-6), когда рассеянное световое поле значительно меньше падающего, имеет место слабое взаимодействие. В этом случае задача рассеяния света звуком может рассматриваться в первом борновском приближении теории возмущений /7,8/. в соответствии с этим приближением световое поле на выходе из зоны взаимодействия представляется суммой падающего и рассеянного излучений:
e( 1,t)
= e0( 1,t)
= e0( 1,t)
+ e1( 1,t)
+ e1( 1,t) (3) 1,t) (3)
где e1( ,t)
<< e0( ,t)
<< e0( 1,t) 1,t)
Волновое уравнение, описывающее распространение поля'
e( 1,t), имеет
вид: 1,t), имеет
вид:
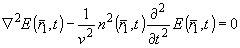 (4) (4)
- 404 -
где v - скорость света в вакууме.
При подстановке равенств (2) и (3) и последующем отбрасывании членов второго и более порядков малости (4) приводится к неоднородному волновому уравнению:
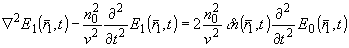 (5) (5)
В общем случае взаимодействующие поля полихроматичны. Тогда каждое из полей света и звука выражается через функции спектральной плотности временных частот посредством обратного преобразования Фурье:
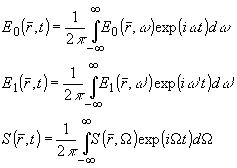 (6) (6)
где Е 0(  , w
), e 1(  , w
'), s(  , W
) - временные частотные спектры падающего и
рассеянного световых полей и акустического поля, соответственно; w
, w ', W
- временные оптические и акустические частоты,
соответственно. Так как оптические частоты много больше акустических
(W /w <10-8),
взаимодействие можно рассматривать в бриллюэновском квазистатическом приближении
/7/, предполагая акустическую волну неподвижной
в процессе рассеяния. В этом случае временные зависимости от акустических частот
восстанавливаются в окончательном результате после решения уравнения
(5). Подставляя в (5)
выражения (6)
для оптических полей, получаем
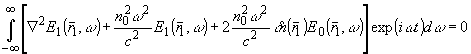 (7) (7)
Очевидно, что (7) имеет место, если каждая спектральная составляющая оптического поля удовлетворяет неоднородному уравнению Гельмгольца:
- 405 -
Ñ 2e1( 1,w
) + k2e1( 1,w
) + k2e1( 1,w
) = -2k2d n( 1,w
) = -2k2d n( 1)e0( 1)e0( 1,w
) (8) 1,w
) (8)
где k = n0w
/v - оптическое волновое число.
Решение уравнения (8) записывается по аналогии с известным из электродинамики уравнением запаздывающих потенциалов /8/:
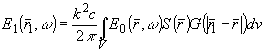 (9) (9)
где 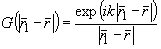 - сферическая функция Грина.
- сферическая функция Грина.
Подставляя в (9) спектральные представления (6), получаем выражение для рассеянного светового поля:
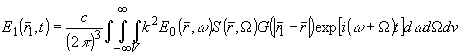 (10) (10)
Полученное выражение является достаточно общин и позволяет проанализировать основные закономерности переноса временных и пространственных спектров взаимодействующих полей в спектр рассеянного излучения.
Спектральные плотности e0( ,w
), s( ,w
), s( ,W
) взаимодействующих полей и функция Грина
g(| ,W
) взаимодействующих полей и функция Грина
g(|  1- 1- |
) являются трехмерными пространственными функциями
и выражаются через собственные пространственные спектры обратными преобразованиями
Фурье /9/: |
) являются трехмерными пространственными функциями
и выражаются через собственные пространственные спектры обратными преобразованиями
Фурье /9/:
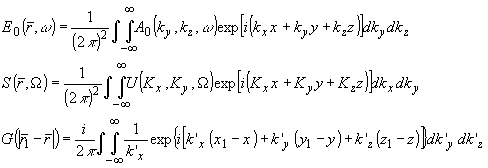 (11) (11)
- 406 -
где kx, ky, kz - пространственные частоты падающего излучения, удовлетворяющие условиям k2x+k2y+k2z = k2, k2y+k2z £
k2; k - оптическое волновое число; Кx, Кy, Кz - пространственные частоты акустического поля, удовлетворяющие условиям К2x+К2y+ К2z = k 2; k 2x+k 2y £
k 2; К - акустическое волновое число; k'x, k'y, k'z - пространственные частоты рассеянного оптического излучения, удовлетворяющие условиям k'2x+k'2y+k'2z = k2; k'2x+k'2y £
k2. Ввиду малости соотношения оптических и акустических частот, волновые числа падающего и рассеянного оптических полей принимаются равными.
Подставляя в (10) соотношения (11), после соответствующей перестановки получаем
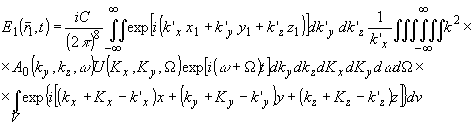 (12) (12)
Спектральная плотность рассеянного излучения,
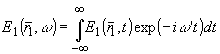
являющаяся преобразованием Фурье поля (12), после интегрирования и преобразований приводится к выражению:
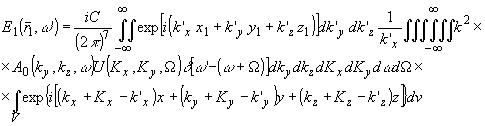 (13) (13)
Спектральная плотность e1( 1,w
') выражается через собственный пространственный
спектр обратным преобразованием Фурье: 1,w
') выражается через собственный пространственный
спектр обратным преобразованием Фурье:
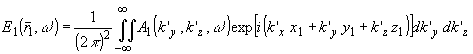 (14) (14)
- 407 -
Сравнивая (13) и (14), получаем выражение для пространственно-временного спектра рассеянного излучения:
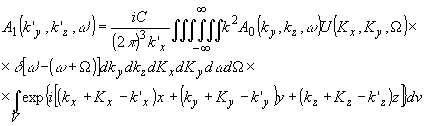 (15) (15)
Спектр (15) представляет собой сложную интегральную функцию, зависящую как от пространственно-временных спектров взаимодействующих оптического:и акустического полей, так и от размеров зоны взаимодействия.
i.2. Перенос временных и пространственных спектров взаимодействующих полей в спектр рассеянного излучения
Рассмотрим процесс переноса временных спектров взаимодействующих полей. В этом случае достаточно проанализировать спектральную плотность рассеянного излучения в виде преобразования Фурье выражения (10):
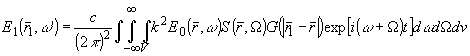 (16) (16)
Выражение (16)
определяет условия переноса временных спектров e1( ,w
) и s( ,w
) и s( ,W
) во временной спектр e1( ,W
) во временной спектр e1( ,w
') рассеянного излучения в общем случае полихроматических
взаимодействующих полей. Выделим три важных частных случая взаимодействия:
1) монохроматической световой волны с полихроматической
акустической; 2)
полихроматической световой волны с монохроматической акустической;
3) монохроматических световой и акустической
волн. ,w
') рассеянного излучения в общем случае полихроматических
взаимодействующих полей. Выделим три важных частных случая взаимодействия:
1) монохроматической световой волны с полихроматической
акустической; 2)
полихроматической световой волны с монохроматической акустической;
3) монохроматических световой и акустической
волн.
В первом случае спектр световой волны с частотой w
0 равен
e0( ,w
) = 2p e0( ,w
) = 2p e0( )d
(w - w 0) (17) )d
(w - w 0) (17)
- 408 -
и (16) после преобразований приводится к виду:
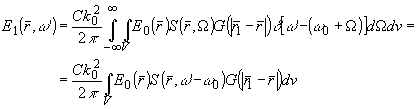 (18) (18)
где k0 = n0w
0/v.
Очевидно, что временной спектр акустического поля полностью
переносится в спектр рассеянного излучения на несущей частоте w
0. Например,
если акустическое поле имеет прямоугольный временной спектр
s( ,W
)=s( ,W
)=s( )rect(W
/W 0)
в полосе частот (-W
0/2 + W 0/2), то
в соответствии с (18)
спектр рассеянного излучения, )rect(W
/W 0)
в полосе частот (-W
0/2 + W 0/2), то
в соответствии с (18)
спектр рассеянного излучения,
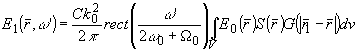
также является прямоугольным в полосе частот (w
0+W
0/2,w
0+W
/2) со смещенной центральной частотой на величину w
0. Свойство переноса временного спектра акустического поля или возбуждающего его электрического сигнала в спектр рассеянного излучения на оптической несущей w
0 лежит в основе разнообразных методов акустооптической обработки сигналов /1/.
Второй случай соответствует монохроматической акустической волне с частотой w
0, спектр которой равен:
s( ,W
) = p [s( ,W
) = p [s( )d
(W - W 0)
+ s*( )d
(W - W 0)
+ s*( )d
(W + W 0)]
(19) )d
(W + W 0)]
(19)
В этом случае спектр рассеянного излучения содержит две комплексно-сопряженные составляющие, являющиеся +1 и –1 порядками дифракции:
 (20) (20)
- 409 -
При этом спектр падающего оптического излучения в рассеянном спектре не воспроизводится.
В третьем случав спектр рассеянного излучения
e1( ,w
') получается подстановкой
(17) и (19)
в (16) и содержит
две монохроматические составляющие с частотами
(w 0+W
0) и (w
0 ,w
') получается подстановкой
(17) и (19)
в (16) и содержит
две монохроматические составляющие с частотами
(w 0+W
0) и (w
0- W
0):
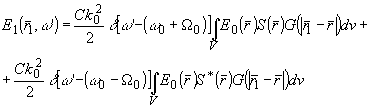 (21) (21)
Преобразование частоты при акустооптическом взаимодействии обусловлено, законом 'сохранения энергии в процессе рассеяния фотонов на фононах / 10/. Как следует из (16), частота рассеянного излучения w
' связана с частотами взаимодействующих полей дельта-функцией d
[w
'-(w
+W
)]. Это означает, что для любых частотных составляющих w
и W
спектров оптического и акустического полей составляющая w
' рассеянного излучения определяется из закона сохранения энергии hw
' = hw
+hW
- для случая поглощения и hw
'= hw
-hW
- для случая рождения фонона, где h=h/2p
, h - постоянная Планка. Таким образом, фотон-фононное взаимодействие при монохроматическом освещении обуславливает временную когерентность частотно-смещенных световых пучков, рассеянных на звуке. Это свойство взаимодействия позволяет широко использовать в акустооптической голографии интерференционные методы.
Перенос пространственных спектров исследуем для случая взаимодействия монохроматических оптического и акустического полей. Этот случай наиболее распространен в голографии. Подстановка (17) и (19) в (11) приводит в соответствии с (12) - (14) к следующему выражению для пространственно-временного спектра (15) рассеянного излучения:
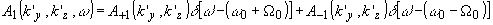
где a+1(k'y,kz) и a-1(k'y,k'z) – пространственные спектры +1 и -1
- 410 -
дифракционных порядков, соответственно,
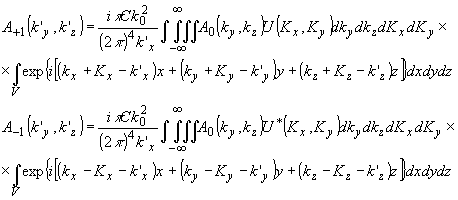 (22) (22)
Выражения (22) описывают спектры пространственных частот световых полей в +1 и -1 дифракционных порядках. Само пространственное распределение в этих порядках в соответствии с (10) равно:
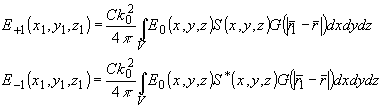 (23) (23)
В (22) входят объемные интегралы от экспоненциальных функций. Это обстоятельство указывает на то, что пространственные спектры рассеянного излучения существенным образом зависят от размеров зоны взаимодействия. Рассмотрим три основных случая: 1) размеры зоны взаимодействия не ограничены - дифракция света на толстой акустической решетке; 2) размер зоны взаимодействия в направлении света равен нулю - дифракция на тонкой акустической решетке; 3) промежуточный случай.
В случае неограниченной зоны взаимодействия объемные интегралы в (22) сводятся к трехмерным дельта-функциям:
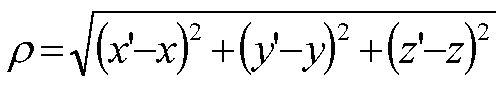
- 411 -
 (24) (24)
Физически (24)
означает, что фотон-фононное взаимодействие строго подчиняется закону сохранения
импульса /10/: h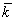 '=h '=h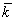 +h +h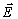 - для +1
дифракционного порядка, h
- для +1
дифракционного порядка, h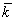 '=h '=h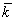 +h +h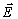 - для -i
порядка. Дифракция света на акустических волнах удовлетворяет условию брэгговского
рассеяния sinФВ=±
k/2k0, где знаки
"+" и "-"
соответствуют +1
и -` порядкам
дифракции.
- для -i
порядка. Дифракция света на акустических волнах удовлетворяет условию брэгговского
рассеяния sinФВ=±
k/2k0, где знаки
"+" и "-"
соответствуют +1
и -` порядкам
дифракции.
Подстановка (24) в (22) приводит к выражениям для пространственных спектров +1 и -1 порядков брэгговской дифракции:
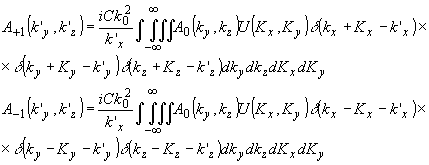 (25) (25)
Так как углы брэгговского рассеяния малы, а исследуемый спектр наблюдается в дальней зоне дифракции, то допустимо принять k'x»
k0 k2y+k2z £
k20, k'2y+k'2z £
k20. В этом случае справедливы также приближения:
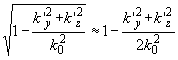
и 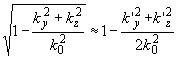
Тогда после соответствующих преобразований пространственный спектр +1 порядка приводится к виду:
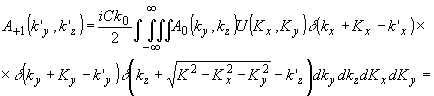
- 412 -
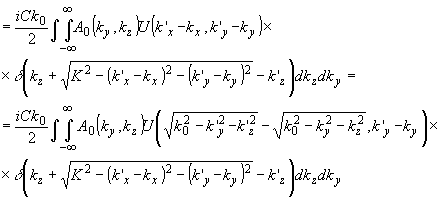 (26) (26)
Используя указанные приближения, можно записать
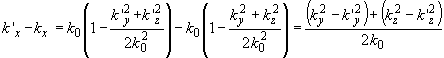
и
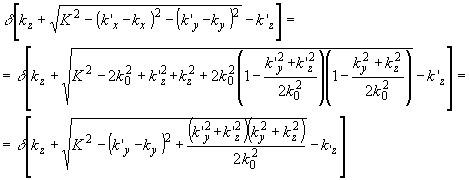
Принимая, что акустическое поле не сильно расходится в направлении
у и справедливы условия 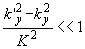 ,
получаем приближенные выражения: ,
получаем приближенные выражения:
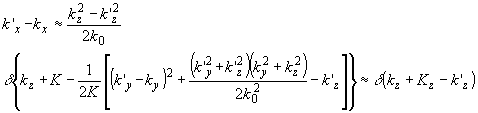 (27) (27)
Подстановка (27) в (26) приводит к выражению для спектра +1 порядка
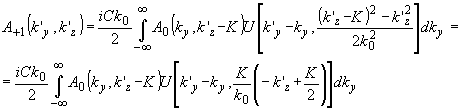 (28) (28)
- 413 -
Аналогично из (25) получаем выражение для спектра -1 порядка:
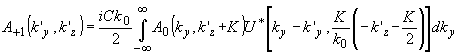 (29) (29)
Как следует из (28) и (29), перенос пространственных спектров взаимодействующих полей в дифракционные порядки осуществляется при брагговской дифракции сложным образом. Результирующий спектр по пространственным частотам k'у представляет собой свертку взаимодействующих спектров, а по пространственным частотам k'z - их произведение. В одном из сомножителей этого произведения - в акустическом спектре - пространственные частоты по оси х заменяются на пространственные частоты по оси z с соответствующим сдвигом и изменением масштаба. Физически это означает, что рассеянное световое поле в дифракционных порядках по каждому из своих измерений различным образом отображает взаимодействующие поля: вдоль оси у оно является результатом перемножения распределений амплитуд взаимодействующих оптического и акустического полей, вдоль оси z - результатом свертки распределений акустического поля в направлении х и оптического поля в направлении z.
Несложно установить условия, при которых возможна полная передача спектра акустического поля в рассеянное излучение. Такая передача осуществима, если разрешается интеграл свертки спектров взаимодействующих полей по пространственной частоте kу. Для этого необходимо, чтобы спектр освещения содержал дельта-Функции от этой частоты, т.е. имел вил А0(k у,kz)=a0(kz)d
(kу). В этом случае акустическое поле освещается цилиндрической световой волной и спектры рассеянного светового поля в +1 и -1 порядках описываются выражениями:
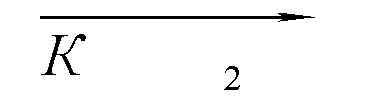 (30) (30)
В частном случае при взаимодействии акустического поля со световой
- 414 -
волной, имеющей спектр a0(ky,kz)=a0d
(ky), спектр рассеянного излучения в порядках пропорционален акустическому:
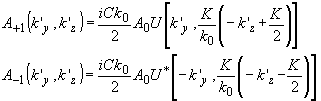 (31) (31)
Как следует из (50) - (31), при брэгговской дифракции акустический спектр переносится в оптический с заменой пространственных частот kx,ky на частоты k'z, k'y. Акустические пространственные частоты по оси у переносятся в оптический спектр с пропорциональным увеличением в К0/К раз, акустические частоты по оси х заменяются ортогональными им оптическими частотами по оси z с соответствующим изменением масштаба и сдвигом. Из этого вытекает, что акустическое поле изображается в порядках с соответствующей трансформацией, включающей сдвиг, поворот и изменение масштаба. Геометрический анализ изображающих свойств брэгговской дифракции приводится в разделе ii.
Взаимодействие на бесконечно тонком акустическом слое соответствует
дифракции Рамана-Ната /1,7/. Этот случай широко распространен в акустооптической
обработке информации и голографии при дифракции света на объемных и поверхностных
ультразвуковых волнах /1,6/. При бесконечно малой глубина акустического поля
l ® 0,
и распределение в поле равно
s( )=s(у,z)d
(x). Объемные интегралы (23),
описывающие пространственное распределение света в дифракционных порядках, с
точностью до множителя сводятся к обычным двухмерным интегралам Френеля-Кирхгофа,
соответствующим дифракции света на плоских объектах (рис.2). Для
+1 порядка )=s(у,z)d
(x). Объемные интегралы (23),
описывающие пространственное распределение света в дифракционных порядках, с
точностью до множителя сводятся к обычным двухмерным интегралам Френеля-Кирхгофа,
соответствующим дифракции света на плоских объектах (рис.2). Для
+1 порядка
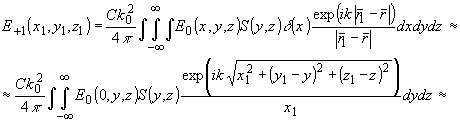
- 415 -
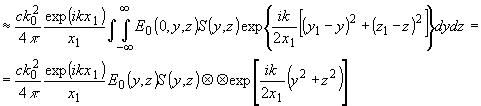
(32)
Аналогично для -1 порядка
 (33) (33)
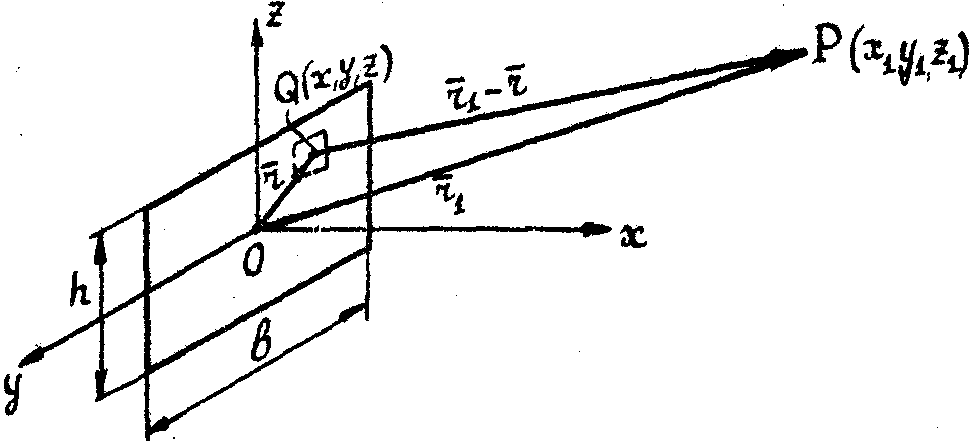
Рис.2. Схема акустооптического взаимодействия для случая дифракции
Ранана-Ната: b´
h - апертура зоны взаимодействия;
q(x,y,z)- точка в зоне взаимодействия;
Р(x1,y1,z1)
- точка наблюдения в рассеянном световом поле;
e0( ) -
падающее световое поле; Е1 ) -
падающее световое поле; Е1(  )
- рассеянное световое поле;  - радиус-вектор точки взаимодействия;
- радиус-вектор точки взаимодействия; 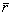 1
- радиус-вектор точки наблюдения. 1
- радиус-вектор точки наблюдения.
- 416 -
Из (32) - (33) видно, что световое поле в дифракционных порядках соответствует двумерной свертке произведений взаимодействующих полей с функцией Френеля (Ä
- символ операции свертки). Пространственный спектр плоского акустического поля равен:
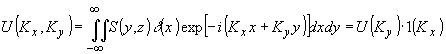 (34) (34)
Физически (34) означает, что импульс фонона, движущегося в плоской акустическом слое, не определен в направлении света /11/. Пространственный спектр светового поля в +1 порядке определяется подстановкой (34) в (22) и равен:
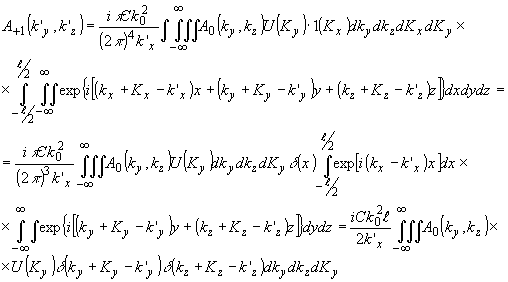 (35) (35)
Аналогично определяется пространственный спектр -1 порядка:
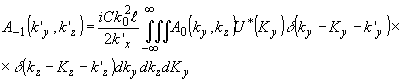 (36) (36)
Преобразования (35) и (36) приводят к выражениям для дифракционных спектров:
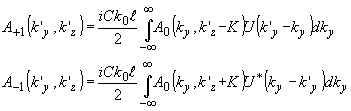 (37) (37)
- 417 -
Очевидно, что при раман-натовской дифракции, границы которой определены соответствующими критериями /1,7,11/ перенос пространственных частот Кх акустического поля в направлении света в рассеянное излучение полностью отсутствует, а сохраняется лишь передача пространственных частот в перпендикулярном направлении, т.е. частот Кy. Это означает, что раман-натовская дифракция обладает определенной избирательностью по отношению к структуре акустического поля. Это свойство дифракции может быть использовано как при оптическом исследовании акустических полей, так и в задачах метрологии и оптической обработки информации.
Дифракции типа Брэгга и Рамана-Ната, соответствующие бесконечно большой и бесконечно малой апертуре акустического поля, являются физическими идеализациями и в литературе рассматриваются как два предельных случая акустооптического взаимодействия. Очевидно, что в реальных условиях апертуры взаимодействующих полей имеют конечные размеры. Такой ситуации соответствует промежуточный случай дифракции. В этом случае дифракционные спектры (22) приводятся к выражениям:
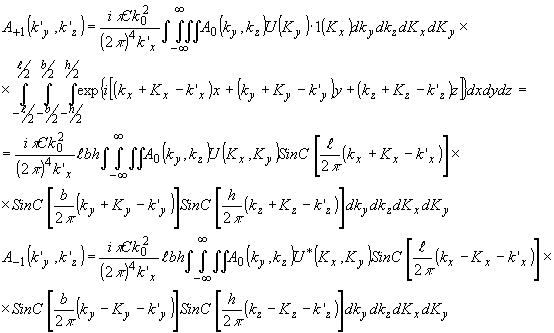 (38) (38)
- 418 -
Появление функций типа sinc (Функций отсчетов) в подынтегральных выражениях указывает на то, что каждой спектральной составляющей акустического поля в отличие от брэгговской дифракции соответствует не одна пространственная частота в рассеянном излучении, а некоторое распределение частот, максимум которого совпадает с частотой брэгговской дифракции. Размывание пространственных частот означает изменение свойств передачи спектра акустического поля в оптический дифракционный спектр, в частности, изменение разрешающей способности акустооптического взаимодействия по различным направлениям. Таким образом, размеры зоны взаимодействия, определяемые апертурами полей света и звука, существенным образом влияют на информационные свойства этого процесса.
1.3. Информационные свойства взаимодействия. Теорема Котельникова для спектров. Связь между апертурами света и звука
Взаимодействующие ноля -
оптическое Е0( )
и акустическое s( )
и акустическое s( )
- ограничены, соответственно, апертурами b´
h и ℓ´
b (рис.1). Следовательно, поля Е0( )
- ограничены, соответственно, апертурами b´
h и ℓ´
b (рис.1). Следовательно, поля Е0( )
и s( )
и s( )
являются финитными функциями, спектры которых могут быть представлены набором
выборочных значений в соответствии с теоремой Котельникова
/12/. Пространственный спектр
a0(ky,kz)
оптического поля e0( )
являются финитными функциями, спектры которых могут быть представлены набором
выборочных значений в соответствии с теоремой Котельникова
/12/. Пространственный спектр
a0(ky,kz)
оптического поля e0( ),
согласно теореме выборки Котельникова, представляется двойным рядом: ),
согласно теореме выборки Котельникова, представляется двойным рядом:
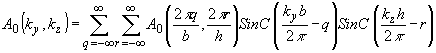 (39) (39)
пространственный спектр u(kx,ky) акустического поля - двойным рядом:
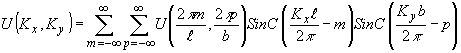 (40) (40)
Каждое из выборочных значений оптического (39) и акустического (40) спектров представляет собой плоскую волну неограниченной апертуры
- 419 -
соответствующей пространственной частоты. Следовательно, каждое отсчетное значение оптического спектра взаимодействует с отсчетным значением акустического спектра, подчиняясь условиям брэгговской дифракции (24). Из сказанного вытекает важное условие акустооптического взаимодействия: для полной передачи спектра акустического поля в рассеянное излучение необходимо, чтобы число отсчетов оптического спектра (39) было равно числу отсчетов акустического спектра (40). Соблюдение этого условия зависит от выбора апертур взаимодействующих полей.
Определим связь между апертурами, исследуя выборочную спектральную функцию рассеянного излучения. Подставляя (40) в'(38), получаем выражение для выборочной спектральной функции a+1(k'y,k'z) светового поля в +1 порядке:
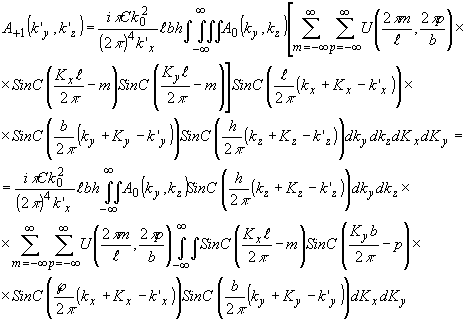 (41) (41)
При этом ищется такая выборочная спектральная функция А 0(k у,kz) освещающего светового поля, число отсчетов которой равно числу отсчетов акустической спектральной функции u(Кx,k y). Используем свойство ортогональности функций отсчетов /13/:
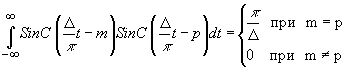 (42) (42)
где p
/D
- норма функций отсчетов относительно веса 1. Тогда
- 420-
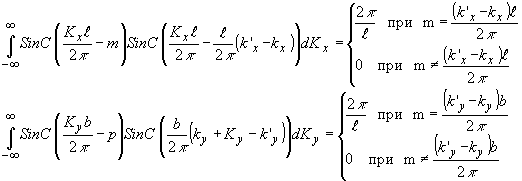
и (41) приводится к виду:
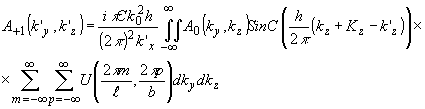 (43) (43)
Отметим, что в точках отсчета акустического спектра удовлетворяются условия :
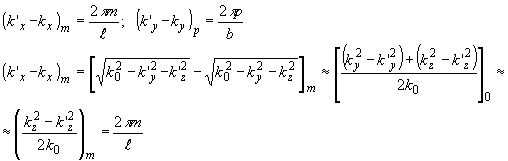 (44) (44)
С учетом ( 44) спектр (43) приводится к виду:
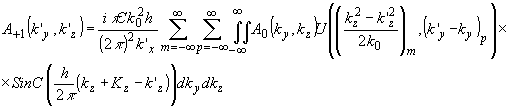 (45) (45)
Используя фильтрующее свойство Функции отсчетов
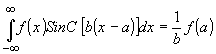
- 421 -
преобразуем (45) к виду, аналогичному (28),
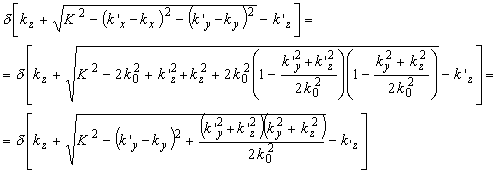 (46) (46)
Так как интервал отсчетов акустического спектра в направлении
света, т.е. по частотам Кх ,
равен 2p .ℓ,
то 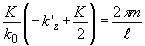 ,
откуда ,
откуда 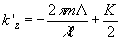 .
Тогда (46)
приводится к виду: .
Тогда (46)
приводится к виду:
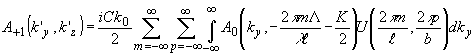 (46) (46)
Аналогичным образом выводится выражение для выборочной спектральной функция светового поля в -1 порядке:
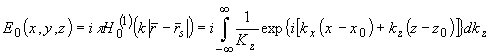 (47) (47)
Как уже указывалось в разделе i.2, полная передача акустического спектра в рассеянное излучение имеет место при освещении цилиндрической волной. В этой случае спектр освещающей волны А0(k у,kz)=ba0(mD
kz)sinc(bky/2p
) и фильтрующее свойство функции отсчетов обеспечивает решение интеграла свертки по пространственной частоте ky в (47) и (48):
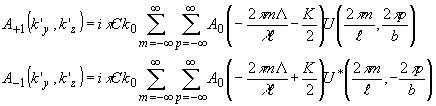 (46) (46)
Выражения (49) описывают выборочные спектральные функции световых полей в +1 и -1 дифракционных порядках, представляющие собой
- 422 -
произведения выборочных спектральных функций освещающего оптического
и акустического полей. При этом спектры (49)
соответствуют условиям полной передачи отсчетов акустического спектра в рассеянное
излучение. Нетрудно установить, что для полной передачи отсчетов акустического
спектра u(2p
m/ℓ,2p p/b)
оптический спектр освещающей волны должен иметь один отсчет по пространственной
частоте kу
и набор отсчетов по частоте kz.
При этой интервал отсчетов спектра 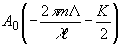 по оси пространственных частот kz,
т.е. в направлении звука, равен D
kz=2p
L /ℓl .
Этот интервал определяется апертурой h
освещающего пучка в направлении звука D
kz=2p /h. Сравнение
двух последних выражений показывает, что условием полной передачи отсчетов акустического
поля является их равенство, из которого следует
по оси пространственных частот kz,
т.е. в направлении звука, равен D
kz=2p
L /ℓl .
Этот интервал определяется апертурой h
освещающего пучка в направлении звука D
kz=2p /h. Сравнение
двух последних выражений показывает, что условием полной передачи отсчетов акустического
поля является их равенство, из которого следует
h = ℓl
/L
= ℓ/m (50)
где m=L
/l
- масштабный коэффициент, равный отношению длин волн взаимодействующих полей. Таким образом, условие полной передачи спектра акустического поля в рассеянное излучение сводится к следующему: апертура освещающего светового пучка в направлении звука меньше апертуры акустического поля в направлении света в число раз, равное отношению длин волн акустического и оптического взаимодействующих полей.
В общем случае апертура свата в направлении звука и апертура
звука в направлении света связаны между собой соотношением неопределенности.
Как известно /12,13/ ,
этому соотношению удовлетворяют финитные функции. Для двухмерного оптического
сигнала e0(y,z)
прямоугольной апертуры с энергией 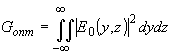 соотношение неопределенности выводится из неравенства
/13/:
соотношение неопределенности выводится из неравенства
/13/:
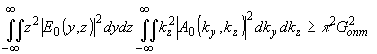 (51) (51)
Апертуру освещающего поля e0(y,z) в направлении звука dh=h и ширину спектра Аа(ky,kz) по частоте kz dkz=2kz.max определим
- 423 -
как величины среднеквадратичного уклонения квадратов модулей поля Е 0(y,z) и спектра А0(k у,kz):
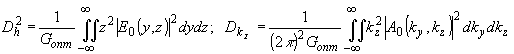 (52) (52)
Тогда подстановка (52)
в (51) приводит
к соотношению dh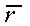 ³
1/2 или hkzmax³
1/4. Аналогичные рассуждения приведем
для акустического поля s(x,y)
прямоугольной апертуры с энергией ³
1/2 или hkzmax³
1/4. Аналогичные рассуждения приведем
для акустического поля s(x,y)
прямоугольной апертуры с энергией 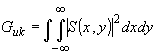 .
В этом случае соотношение неопределенности выводится из неравенства: .
В этом случае соотношение неопределенности выводится из неравенства:
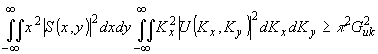 (53) (53)
Определяя апертуру акустического поля
s(x,y) в направлении
света dℓ
= ℓ и ширину спектра
u(kx,ky) по частоте kx,
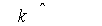 получаем: получаем:
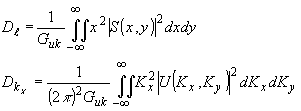 (54) (54)
Подстановкой (54)
в (53) получаем
dℓ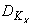 ³
1/2 или ℓkx.max³
1/4. ³
1/2 или ℓkx.max³
1/4.
В теории финитных функций /12/ доказывается теорема для обобщенного соотношения неопределенности, согласно которой для финитной функции с конечной и равной 1 полной энергией при условии, что в полосе частот -W
£
w
£
W
ее спектра сосредоточена энергия d2, а в интервале –t £
t £
t - энергия b
2, соотношение неопределенности записывается в виде неравенства W
t ³
Ф(a
,b
), где Ф(a
,b
) - функция, подлежащая определению. Полагая, что энергии финитных полей света и звука определяются одинаковыми величинами d2, а анергии их финитных спектров - величинами b
2, соотношение неопределенности записываем, соответственно, для оптического и
- 424 -
акустического полей в виде ℓК x.max = Ф(a
,b
); hkz.max=Ф0( a
, b
), откуда следует
ℓkx max = hkz max (54)
Из соотношения (54 ) вытекают три ванных следствия, определяющие информационные свойства взаимодействия:
1) условие полной порэдачк акустического спектра в дифракционные порядки:
h = ℓ/m, kz max = mkx max (55a)
в этом случае для передачи акустического спектра шириной kx max необходимо использовать освещение световой волной в М раз более широкий спектром;
2) условие избыточной передачи акустического спектра в дифракционные порядки:
h < ℓ/m, kz max > mkx max (55б)
избыточное расширение оптического спектра не приводит к улучшению изображающих свойств;
3) условие неполной передачи акустического спектра в дифракционные порядки:
h > ℓ/m, kz max < mkx max (55a)
Сужение оптического спектра или увеличение апертуры освещающей волны за пределы условия (50) приводит к ухудшению качества изображения в дифракционных порядках.
Частным случаем неполной передачи акустического спектра является передача в дифракционные порядки одного отсчета этого спектра. Это свойство дифракции, характеризующее ее избирательность, имеет существенное .значение в акустооптической обработке информации и метрологии. Благодаря этому свойству удается получать периодические изображения акустических полей сложной структуры и
- 425 -
осуществлять необходимую фильтрацию и селекцию спектральных составляющих этих полей /14,15/. В случае передачи одного отсчета ширина оптического спектра долина быть меньше величины, соответствующей одному интервалу отсчета акустического спектра, т.е. kz max = 2p
m/l
. Тогда из (54) следует h > ℓ·s/2m, где s - число отсчетов акустического спектра в полосе 2kx max. Таким образом, для передачи одного отсчета апертура освещающего поля долина быть в s/2 раз больше апертуры по условию (50). В известной литературе по дифракции света на ультразвуке /1,7/ рассматриваются, как правило, коллимированные световые пучки, для которых условие избирательности дифракционного процесса выполняется автоматически (h®
¥
). Опишем процесс передачи m1-го акустического отсчета в дифракционный спектр. Пусть спектр освещения содержит один отсчет по частоте kу и один m1-ый отсчет по частоте kz:
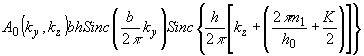 (56) (56)
где h0 = ℓ/m.
Тогда, подставляя (56) в (43), после преобразований с использованием свойств ортогональности и фильтрующего свойства функций отсчетов получаем
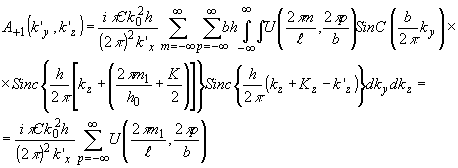 (57) (57)
Кик следует из (57), в спектр дифракционного порядка передается один m1-ый отсчет акустического поля по частоте Кх.
Передача акустического спектра по частоте требует одного отсчета освещающей волны. Это связано с тем, что вдоль оси взаимодействующие поля имеют общую апертуру b. Таким образом, цилиндрическая и, в частном случае, плоская световая волна обеспечивает полную передачу спектра акустического поля по частота Ку.
- 426 -
ii. Акустическое поле как оптический элемент
Акустическое поле, возбуждаемое в прозрачной для света среде, является оптическим дифрагирующим элементом. Основное свойство этого элемента заключается в переносе пространственно-временных спектров взаимодействующих полей в оптические дифракционные порядки. Это свойство различным образом используется в оптической обработке информации (корреляция, спектральный анализ, генерация сложных сигналов и т.д. /1/), метрологии (электрическое воспроизведение пространственно-временных оптических структур /14,15/, для модуляции световых потоков - амплитудной, фазовой, частотной, поляризационной - и визуализации акустических ползи). Во всех этих случаях акустооптический модулятор действует в оптико-электронной системе как оптический элемент с определенными изображающими свойствами, совмещающий в себе функции нескольких элементов и даме целых систем классической оптики. Возможность объединения разнородных функций в одном оптическом динамическом элементе является важной особенностью акустооптики и позволяет рассматривать ее как одно из направлений интегральной оптики.
В данном раздела лекции рассматриваются изображающие свойства акустооптического взаимодействия. Подобно классической оптике и голографии изображающие свойства взаимодействия определяются из волновой теории и сводятся к геометрическим правилам построения изображений для точечных источников взаимодействующих полей.
ii.1. Изображающие свойства взаимодействия
Как было установлено в разделе i.2, изображение акустического поля формируется в дифракционных порядках При освещении поля цилиндрической световой волной. Это означает, что точечному акустическому источнику соответствует точечное изображение в порядках при условии освещения зоны взаимодействия волной, создаваемой линейным световым источником (рис.3). Установим геометрическую связь между координатами источников света и звука и их дифракционным изображением.
- 427 -
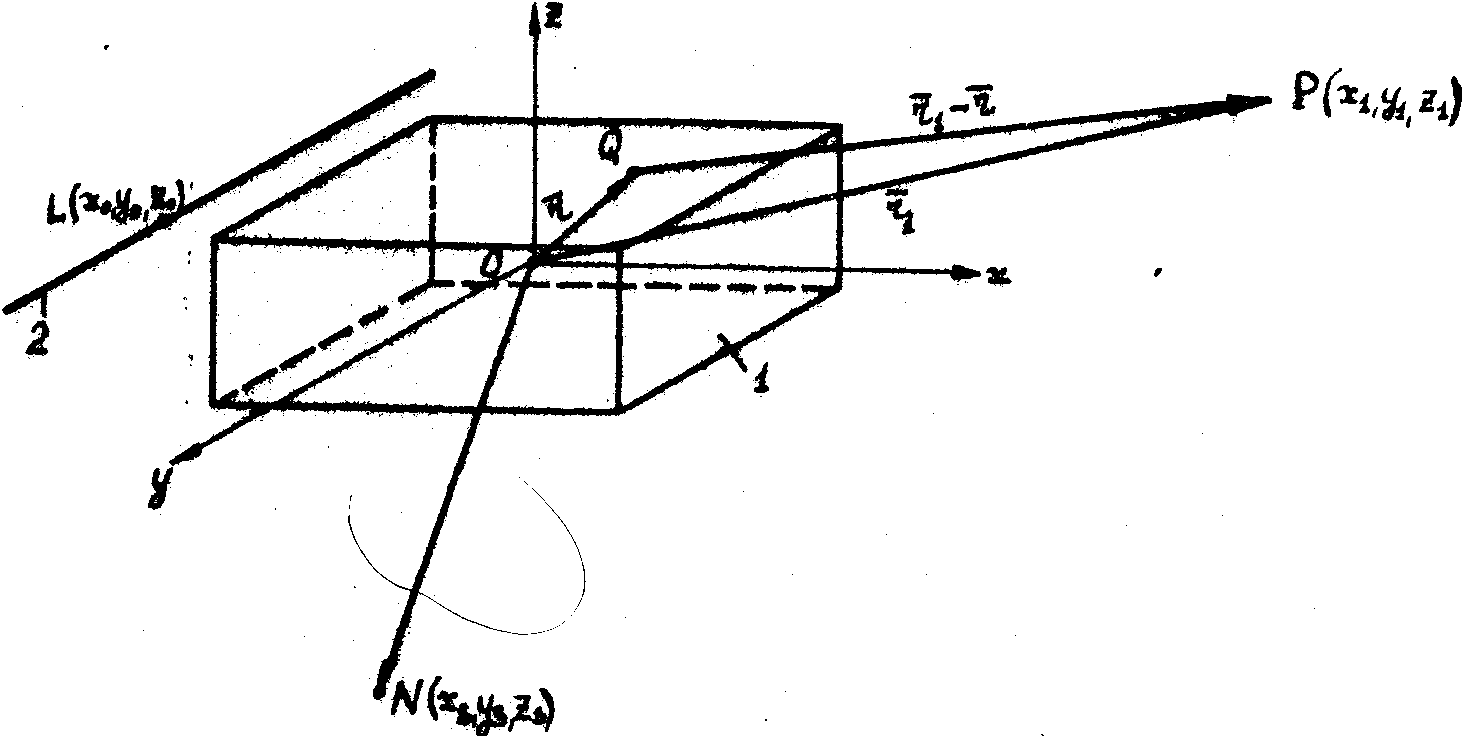
Рис.3. Схема акустооптического взаимодействия:
1 - зона взаимодействия;
2 - линейный оптический источник;
n(xs,ys,zs) -
точечный акустический источник; l(x0,y0,z0)
- точечный оптический источник;
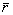 -
радиус-вектор точки взаимодействия; -
радиус-вектор точки взаимодействия; 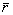 s
- радиус-вектор акустического источника; s
- радиус-вектор акустического источника; 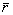 0
- радиус-вектор оптического источника; 0
- радиус-вектор оптического источника;
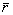 1 -
радиус-вектор точки наблюдения p(x1,y1,) 1 -
радиус-вектор точки наблюдения p(x1,y1,)
Акустическое поле точечного источника n описывается сферической функцией Грина:
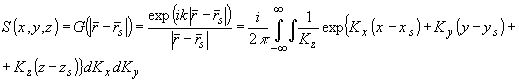 (58) (58)
- 428 -
поле линейного оптического источника - функцией Ганкеля:
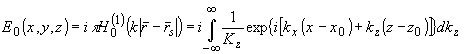 (59) (59)
Тогда, подставляя выражения (58), (59) для взаимодействующих полей и выражение (11) для функции Грина в (23), после преобразований получаем
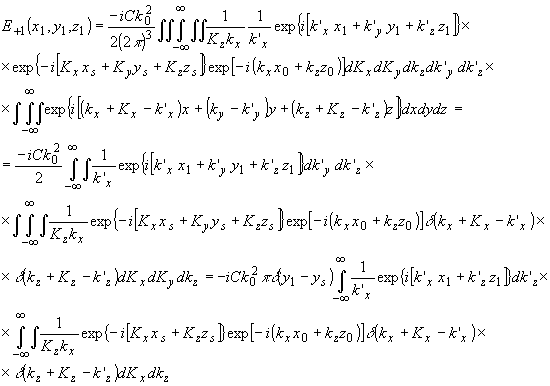 (60) (60)
Выражение (60) описывает световое поле в точке наблюдения p(x1,y1,z1) , создаваемое точечным изображением в +1 дифракционном порядке. Аналогично для -1 порядка
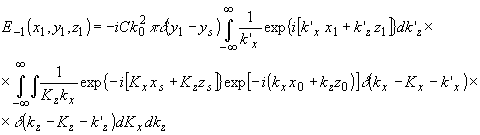 (61) (61)
Из (60) - (61) следует, что для каждого акустического источника с координатой уs рассеяние света происходит в плоскости, проходящей
- 429 -
через эту точку параллельно х z. Таким образом, зона взаимодействия может быть разбита на бесконечно тонкие слои, параллельные плоскости xz /5/, и для каждого слоя, проходящего через точку акустического источника, рассеяние решается как плоская задача. Учитывая, что k'y<<k 0, влиянием рассеянного поля каждого слоя на соседний можно пренебречь. Тогда для слоя, проходящего через точку n(хs,уs,z s) параллельно пл. xz, при условии, что точки l и Р лежат в плоскости этого слоя (y0=уs; у1=y s), имеем (60) и (61) Определим координаты источников рассеянных волн (60) и (61). Для световой волны (60), рассеянной в +1 порядок,
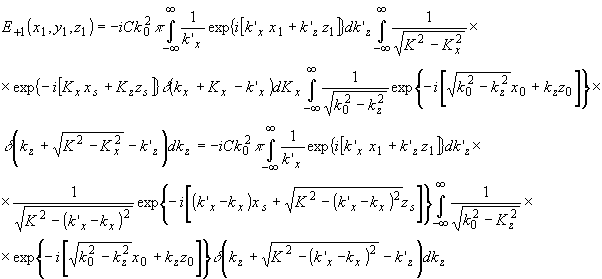 (62) (62)
Так как зона взаимодействия не ограничена, пространственные частоты по осям к и у удовлетворяют условиям брэгговского рассеяния (24). Тогда из векторных диаграмм брэгговской дифракции (рис.4) следуют зависимости
|
kx = k'xcos2 Фb + k'zsin2ФВ |
(63) |
|
kz = k'zcos2 Фb - k'xsin2ФВ |
- для +1 порядка и
|
kx = k'xcos2 Фb - k'zsin2ФВ |
(63) |
|
kz = k'zcos2 Фb + k'xsin2ФВ |
- для -1 порядка.
- 430 -
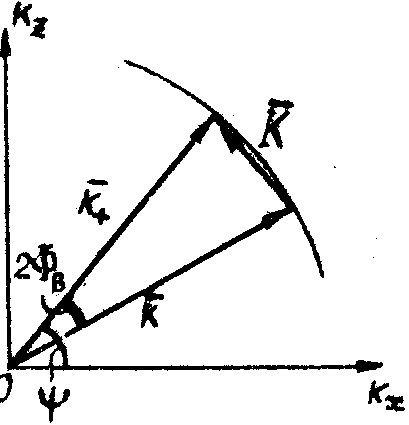 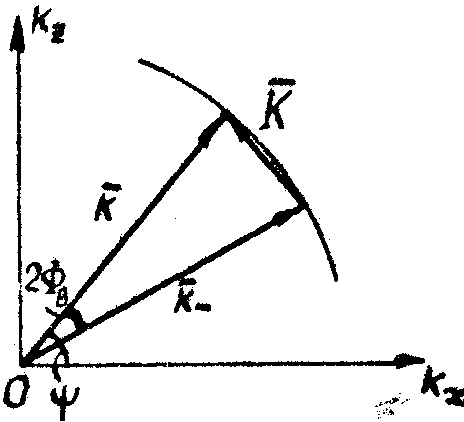
Рис.4. Векторные диаграммы брэгговской дифракции:
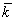 - -
вектор падающей световой волны;
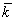 '± '±
- вектор рассеянной световой волны;
К - вектор акустической волны; y
- угол дифракции; ФВ - угол Брэгга.
Подставляя (63) в (62), получаем
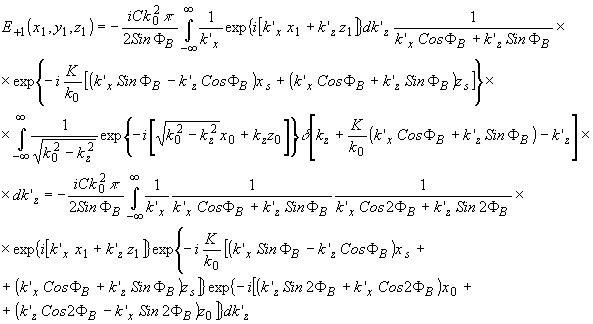 (62) (62)
- 431 -
В приближении параксиальной оптики, учитывая, что брагговские углы малы и Со sФВ »
Соs2ФВ »
1, sinФВ»
sin2ФВ<<1, получаем для k'x »
k0
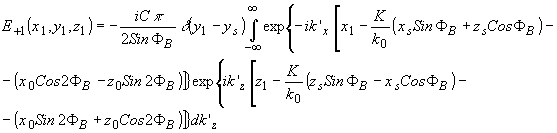 (66) (66)
Световая волна ( 66) в +1 порядке является цилиндрической световой волной вида
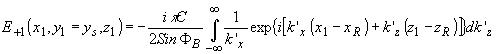
выходящей из точечного источника с координатами xryr=yszr, равными
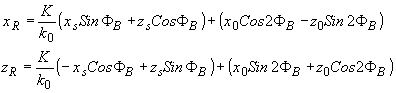 (67) (67)
Точка с координатами ( xr,zr) является изображением акустического точечного источника в +1 порядке.
Аналогично подстановкой (64) в (61) после преобразований получаем выражение для световой волны рассеянной в -1 порядок,
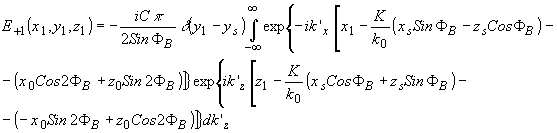 (68) (68)
Последняя также является цилиндрической волной, выходящей из точки с координатами х r, уr=y s,z r.
- 432 -
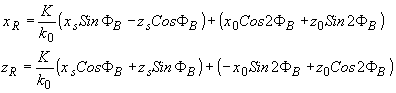 (67) (67)
Выражения (67) и (69) определяют координаты точечных изображений в +1 и -1 порядках через координаты точечных источников света и звука. Из этих выражений легко выводятся геометрические правила построения изображений при брэгговской дифракции /2-6/ (рис.5).
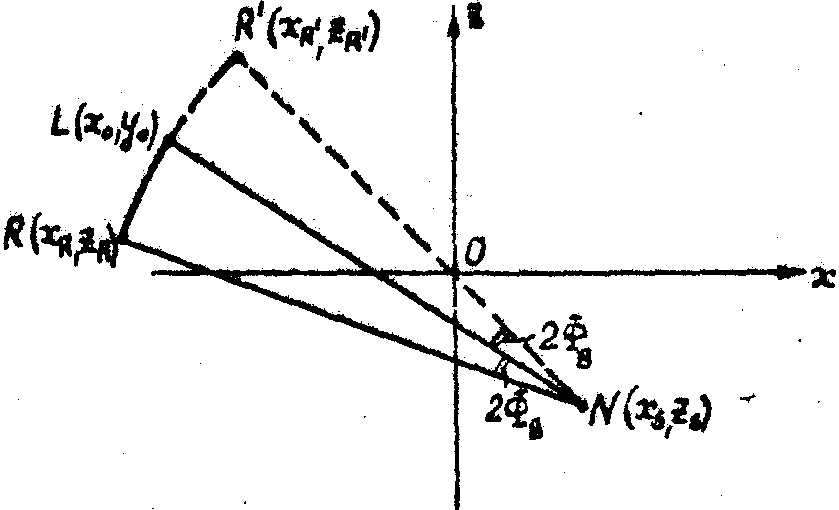
Рис.5. Схема построения изображений точечных источников:
n - точечный акустический источник с координатами хs,z s; l - точечный оптический источник с координатами x0,z0; r - точечное изображение в +1 порядке с координатами xr,zr; r'- точечное изображение в -1 порядке с координатами х'r,z'r.
В аналитической геометрии угол j
между прямыми ln и rn определяется выражением tgj
=(k2-k1)/(1+k1k2), где k1 и k2 - угловые
- 433 -
коэффициенты прямых ln и rn. Уравнения прямых ln и rn в плоскости xz, соответственно, равны:
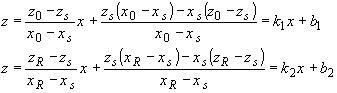 (70) (70)
а их угловые коэффициенты – k1=(z0-zs)/(x0-xs);
k2=(zr-zs)/(xr-xs)
Тогда угол j
определяется выражением
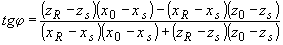
которое с учетом (67) приводится к виду tgj
=tg2ФВ. Длины отрезков ln и rn, соответственно, равны
|
(ln)2 = (x0-xs)2+(z0-zs)2; (rn)2 = (xr-xs)2+(zr-zs)2 = |
|
|
= [(x0-xs)cos2 ФВ-(z0-zs)sin2ФВ]2 + |
|
|
+ [(x0-xs)sin2 ФВ+(z0-zs)cos2ФВ]2 = (x0-xs)2+(z0-zs)2 |
Таким образом, отрезки ln = rn. Следовательно, точка изображения в +1 порядке определяется простым поворотом отрезка ln на угол 2Фb против часовой стрелки. Нетрудно показать, что для -1 порядка tgj
=-tg2ФВ и точка r' изображения определяется поворотом отрезка ln на угол 2Фb по часовой стрелке. Таким образом, изображающее правило при брэгговской дифракции сводится к следующему: для построения точки изображения иообходимо точку оптического источника перенести по дуге окружности, проведенной из точки акустического источника, как-из центра, радиусом, равным расстоянию между оптическим и акустическим источниками, на угол 2ФВ против часовой стрелки для изображения в +1 порядке и на угол 2ФВ по часовой стрелке - для изображения в -1 порядке.
На рис.6 представлена схема построения изображения фронта акустической волны, включающего три акустических источника - точки n°
, n', n". Нетрудно установить, что изображение в +1 порядке повернуто относительно Фронта n'n" на угол — ФВ+p
/2, а изображение в
- 434 -
-1 порядке
- на угол (ФВ-p
/2). При этом в обоих порядках изображения
уменьшены в кратное число раз, равное отношению длин волн взаимодействующих
полей: 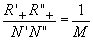 , ,
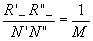
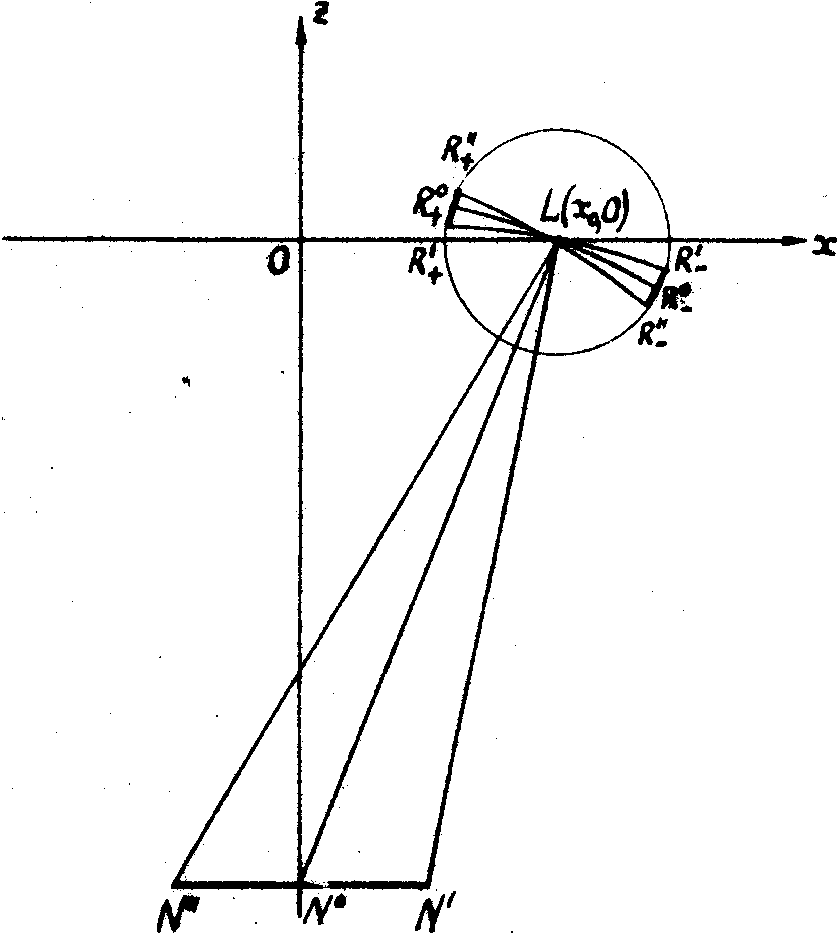
Рис. 6. Схема восстановления акустического фронта при брэгговской дифракции:
n°
, n', n" - точки фронта акустической волны; r°
+; r'+; r"+ - соответствующие им точки изображения в +1 порядке; r°
-; r'-, r"- - соответствующие им точки изображения в -1i порядке; l - точка оптического источника с координатами (х0,0).
- 435 -
Как следует из (67), (69), каждой течке акустического поля при заданных координатах оптического источника в брэгговском дифракционном процессе соответствует единственная определенная точка изображения. Это означает, что брэгговская дифракция обеспечивает полное восстановление акустического поля в оптических дифракционных порядках. Таким образом, двумерное сканирование оптическим источником по акустическому полю позволяет осуществить его оптическое восстановление. Методы оптического восстановления рассматриваются в разделе iii лекции.
Наблюдаемая в дифракционных порядках точка акустического поля может быть однозначно определена по координатам точки источника света и оптического изображения. С этой целью для координат точки акустического поля (хs,z s) перестановкой в (67) и (69) получаем системы уравнений:
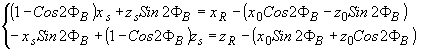 (71) (71)
- для +1 порядка и
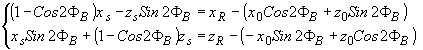 (72) (72)
- для -1 порядка.
Решение систем этих уравнений позволяет выразить координаты восстанавливаемой точки акустического поля через координаты точек оптического источника и изображения:
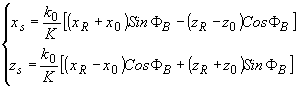 (73) (73)
- для +1 порядка и
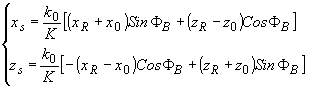 (74) (74)
- 436 -
- для -1 порядка.
Измерения координат оптических точек (х 0,z 0) и (xr,zr) обеспечивают однозначное определение наблюдаемой точки акустического поля.
ii.2. Разрешающая способность
При брэгговской дифракции, соответствующей бесконечно протяженной зоне взаимодействия, имеет место точное соответствие между каждой точкой акустического поля и ее оптическим изображением, т.е. разрешаются вое точки акустического поля. Ограничение апертур света и звука приводит к размыванию изображения точечного акустического источника и тем самым к снижению разрешающей способности акустооптического изображающего процесса. В этом случае световое поле, рассеянное в +1 дифракционный порядок при взаимодействии точечных оптического и акустического источников, описывается в соответствии с (60) выражением
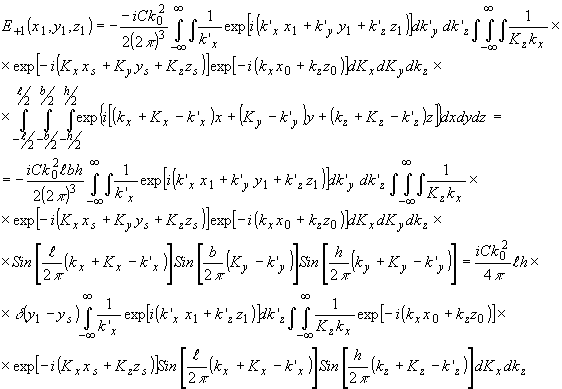 (75) (75)
Аналогично для светового поля, рассеянного в -1 порядок
- 437 -
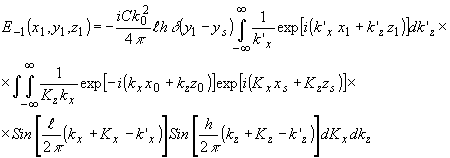 (76) (76)
При анализе разрешающей способности дифракционного изображающего процесса возможны два случая: 1) оценка разрешающей способности в зависимости от апертуры звука при бесконочной апертуре света; 2) оценка разрешающей способности в зависимости от апертур света и звука. Первое условие означает, что световой поток, формирующий оптический источник, пространственно не ограничен и источник можно принять точечным. В этом случае исследуется зависимость разрешающей способности от толщины акустического слоя, т.е. при постепенном переходе от дифракции Брэгга к дифракции Рамана-Ната. Этот случай принципиально важен для акустооптической голографии и обработки информации. Во втором случае ограниченным принимается не только сам акустический слой, но и световой поток, формирующий оптический источник. В этом случае оптический источник нельзя принимать точечным, а необходимо рассматривать его как протяженный.
Для оценки разрешающей способности акустооптического взаимодействия используем критерий Рэлея, широко распространенный в классической оптике. Критерий Рэлея устанавливает предельный интервал между точками объекта, изображения которых разрешаются визуально. Как отмечается в /12/, критерий Рэлея определяет класс тех сигналов, которые для данной системы их передачи и преобразования могут считаться функциями с финитным спектром. Поскольку взаимодействующие поля в акустооптическом изображающем процессе удовлетворяют условиям финитности, применение критерия Рэлея представляется целесообразным.
Определим разрешающую способность для первого случая, когда ограничение накладывается только на апертуру звука. В Этом случае (75) сводится к выражению:
- 438 -
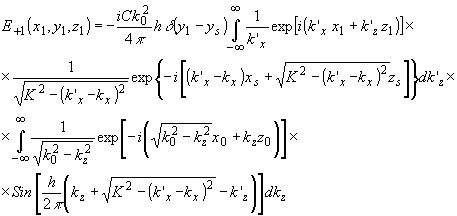 (77) (77)
Известно, что спектр ограниченной функции пропорционален свертке спектра неограниченной функции с функцией отсчетов. Для акустического поля s(x,z) в слое толщиной ℓ пространственный спектр по частоте Кx равен:
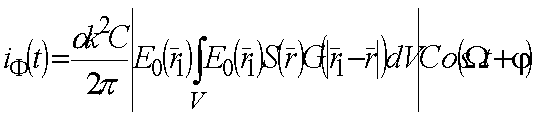
Это означает, что каждая спектральная составляющая распределяется по закону функции sinс(ℓКх/2p
). В результате окружность, являющаяся геометрическим местом концов волновых векторов акустического спектра точечного источника и полученная при пересечении сферы радиуса К с плоскостью пространственных частот (kx,kz), размывается в область, границы которой определяются функцией sinс(ℓКх/2p
) (рис.7).
Ограничение апертуры звука в направлении света эквивалентно
неопределенности импульса фонона в этом направлении,
что приводит к размыванию точки А, являющейся концом вектора 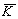 ,
в линию (рис.7). При этом акустические векторы, концы которых лежат на этой
линии, определяют составляющие акустического спектра, амплитуды которых изменяются
по закону sinс(ℓКх/2p
). Нетрудно установить, что смещенные окружности
2 и 3
являются геометрическими местами концов волновых векторов нулевой амплитуды.
При определении разрешающей способности взаимодействия ограничимся по аналогии
с классической оптикой распределением волновых ректоров акустического ,
в линию (рис.7). При этом акустические векторы, концы которых лежат на этой
линии, определяют составляющие акустического спектра, амплитуды которых изменяются
по закону sinс(ℓКх/2p
). Нетрудно установить, что смещенные окружности
2 и 3
являются геометрическими местами концов волновых векторов нулевой амплитуды.
При определении разрешающей способности взаимодействия ограничимся по аналогии
с классической оптикой распределением волновых ректоров акустического
- 439 -
спектра в продолах первых нулей Функции sinс(ℓКх/2p
), что соответствует размыканию точки L
в отрезок длиной 4p
/ℓ
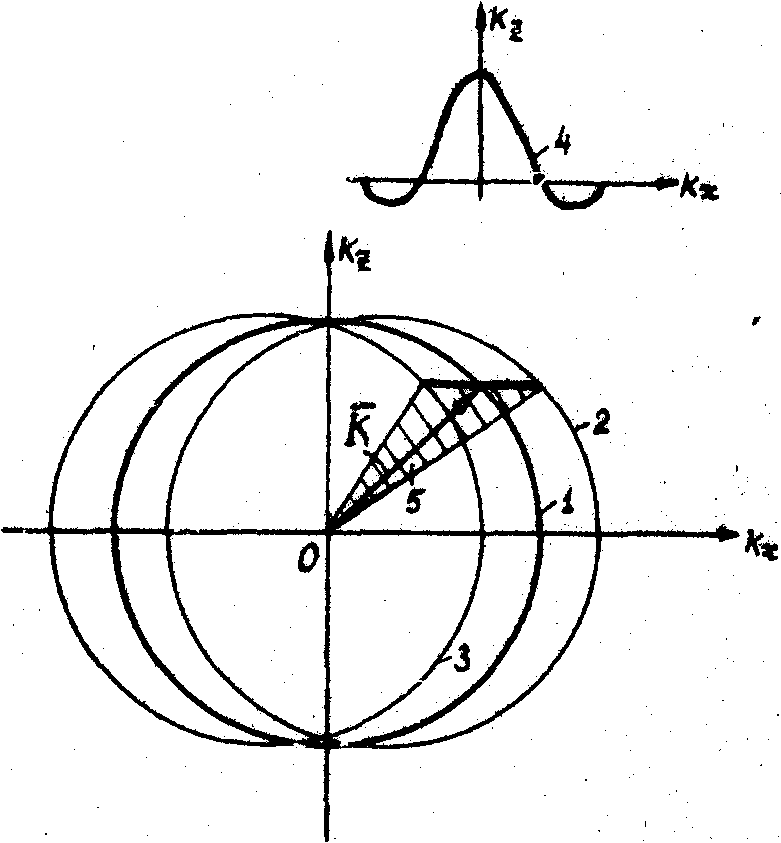
Рис.7. Сфера волновых векторов акустического спектра точечного источника при ограничении апертуры звука в направлении света:
1 - сфера волновых векторов
при неограниченной апертуре; 2 -
сфера волновых векторов, соответствующая первому положительному нулю функции
sinс(ℓКх/2p
); 3 - сфера волновых векторов, соответствующая
первому отрицательному нулю функции sinс(ℓКх/2p
); 4 - распределение
sinс(ℓКх/2p
) для волнового вектора 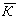 ;
5 - область размытия волнового вектора ;
5 - область размытия волнового вектора 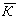 (заштрихована),
(заштрихована),
- 440 -
Координаты изображения точечного акустического источника при ограниченной апертуре звука определяются из (77) в соответствии с векторными диаграммами, представленными на рис.8.
Каждая составляющая спектра акустического поля ограниченной
апертуры представляет собой плоскую волну, рассеяние на которой должно удовлетворять
брэгговскому условие. Рассмотрим составляющую
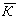 0
этого спектра в виде вектора, конец которого лежит на смещенной окружности.
При этом диаграмма на рис.8а соответствует случаю смещения волновой сферы на
величину +D , а диаграмма на рис.8б - смещению
сферы на -D
. Физически это означает, что в направлении
вектора 0
этого спектра в виде вектора, конец которого лежит на смещенной окружности.
При этом диаграмма на рис.8а соответствует случаю смещения волновой сферы на
величину +D , а диаграмма на рис.8б - смещению
сферы на -D
. Физически это означает, что в направлении
вектора 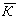 0
в акустическом поле распространяется волна, амплитуда которой составляет величину
sinс(ℓD
/2p ) от амплитуды
волны с вектором 0
в акустическом поле распространяется волна, амплитуда которой составляет величину
sinс(ℓD
/2p ) от амплитуды
волны с вектором 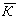 ;
конец которого лежит на основной несмещенной волновой сфере. При D
=2p r/ℓ,
где r - целое
число, функция sinс(ℓD
/2p ). Первые
нули этой функции соответствуют значениям r=
+1 (рис.8а) и r
= -i (рис.8б). ;
конец которого лежит на основной несмещенной волновой сфере. При D
=2p r/ℓ,
где r - целое
число, функция sinс(ℓD
/2p ). Первые
нули этой функции соответствуют значениям r=
+1 (рис.8а) и r
= -i (рис.8б).
Световая волна, рассеянная на акустической волне с вектором
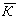 0,
определяется из построения, аналогичного рис.4. Через начало и конец вектора 0,
определяется из построения, аналогичного рис.4. Через начало и конец вектора
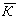 0
проводится окружность радиуса К,
и падающей световой волне с вектором 0
проводится окружность радиуса К,
и падающей световой волне с вектором 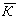 соответствует световая волна с вектором
соответствует световая волна с вектором 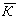 ',
дифрагировавшая в +1
порядок. Угол ФВ является измененным брэгговским углом, удовлетворяющим
условию ',
дифрагировавшая в +1
порядок. Угол ФВ является измененным брэгговским углом, удовлетворяющим
условию
sin 2Ф'В = k0/2k0
Определим рассеянное световое поле e+1(x1,y1,z1) для произвольной величины D
смещения волновой сферы. Из геометрии рис.8 следует :
|
kx = k'xcos Ф'b + k'zsin2Ф'b |
(78) |
|
kz = -k'xsin Ф'b + k'zcos2Ф'b |
Выразим соотношения (78)
через брэгговокий угол Фb.
Так как К << k0 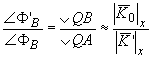 ,
где | ,
где | 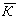 0|
x и
| 0|
x и
| 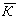 '|
x - проекции векторов '|
x - проекции векторов 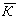 0
и 0
и 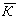 '
на ось х.
Величина | '
на ось х.
Величина | 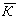 0|
x определяется из системы уравнений: 0|
x определяется из системы уравнений:
- 441 -
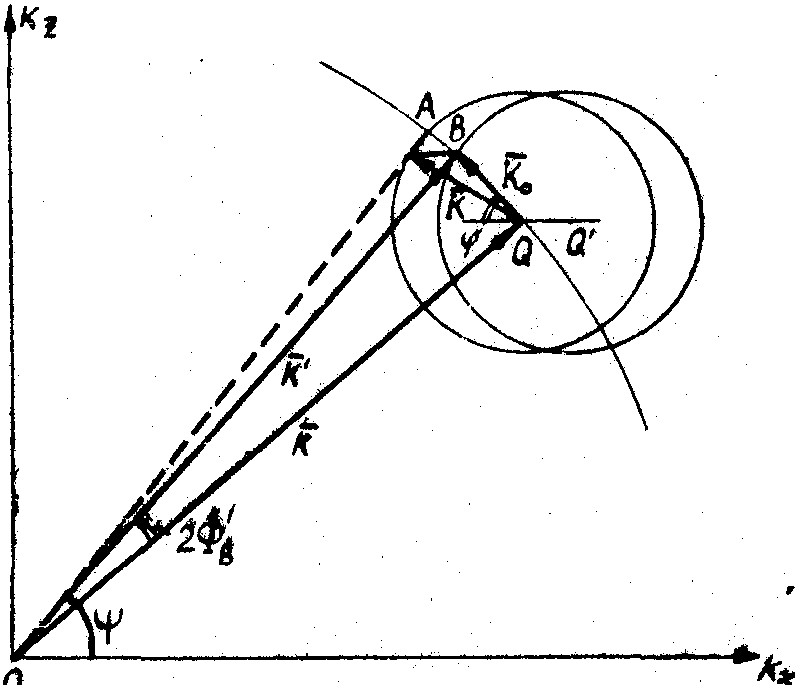 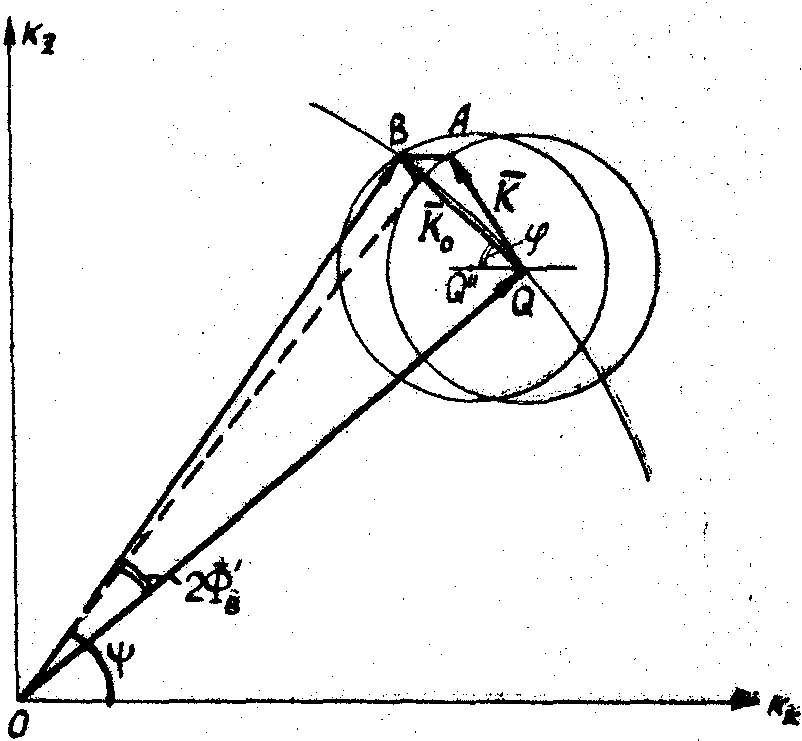
а) б)
Рис. 8. Векторные диаграммы дифракции на акустическом поле ограниченной апертуры:
а - векторная диаграмма для волновой сферы, смещенной на величину +D
;
б - векторная диаграмма для волновой сферы, смещенной на величину -D
;
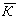 0 0
- составляющая спектра акустического поля ограниченной апертуры; 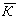 - составляющая спектра акустического поля неограниченной
апертуры;
- составляющая спектра акустического поля неограниченной
апертуры; 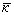 -вектор падающей световой волны,
-вектор падающей световой волны, 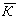 '
- вектор световой волны, рассеянной в
+1 порядок;
y - угол дифракции. '
- вектор световой волны, рассеянной в
+1 порядок;
y - угол дифракции.
- 442 -
|
(kx-D
)2 + k2z = k2 |
|
kz = -kxtgj
|
где первое уравнение описывает смещенную окружность, а второе - прямую, проходящую через точки q и b. Система приводится к квадратное уравнению
k2x(1 + tg2j
) – 2kxD
+ (D
2-k2) = 0
решение которого дает величину |
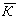 0|
x: 0|
x:
Учитывая, что j
=90°
-(y
-ФВ), а siny
=k'z/k0, после преобразований получаем
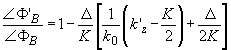 (79) (79)
Принимая
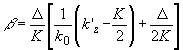 (80) (80)
приходим к выражению для измененного брэгговского угла Ф' b = Фb(1- b
) . Подстановка полученных выражений в (78) приводит к следующим соотношениям:
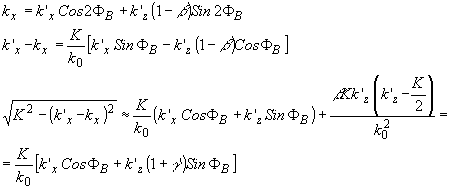 (81) (81)
при выводе которых использовалось параксиальное приближение (k'x»
k0) и допущения Сos2D
ФВ »
1, cos2ФВ >> b
sin22ФВ. При этом коэффициент g
=2b
(k'z-k/2)/k.
- 443 -
Световое поле, рассеянное в +1 дифракционный порядок, определяется подстановкой (81) в (77):
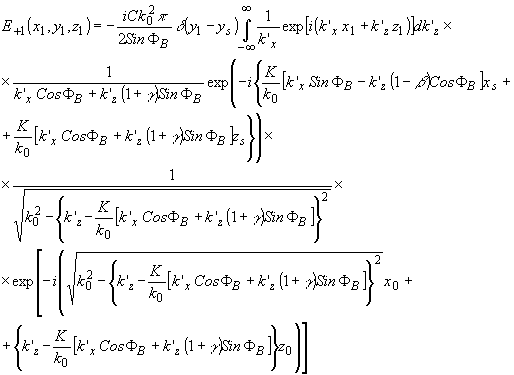 (82) (82)
и после преобразований
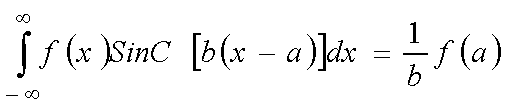
(82) в параксиальном приближении приводится к выражению
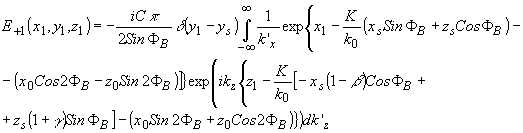 (83) (83)
Коэффициенты b
и g
являются функциями пространственной частоты k'z рассеянного излучения. При b
= 0 и g
= 0 выражение
- 444 -
(83) приводится к (66). Это означает, что максимум распределения света в размытом изображении точечного акустического источника совпадает с координатами (67) точечного источника при неограниченной апертуре звука. При b
¹
0 световое поле (83), равное
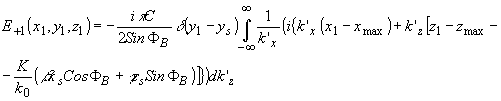 (84) (84)
где xmax = хr, z max = z r, не является цилиндрической волной, т.е. излучается не точечные источником, а некоторой областью, являющейся размытым изображением акустического источника. Границы размытия области определим как расстояние между двумя точками изображения, амплитуда света в которых равна нулю.
Векторы рассеянного излучения нулевой амплитуды соответствуют величине D
=2rp
/ℓ. Предельные значения коэффициентов b
и g
для D
=2p
r/ℓ определяются диапазоном изменения пространственных частот k'z. Согласно теореме Котельникова и (49), акустическому спектру в диапазоне частот ±kmax соответствует спектр рассеянного излучения в диапазоне частот ±k'max, где k'max= mkx max +k/2. Как следует из (84), ограничение апертуры звука в направлении света (оси х) приводит к размыванию -изображения точечного источника в направлении звука (оси z). Расстояния от точки изображения с максимальной амплитудой до первого z01 и второго z02 нуля амплитудного распределения в изображении, равные D
z1=zr-z01 и D
z2= zr-z02, в соответствии с (83)-(84) определяются выражением:
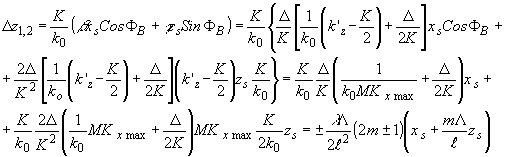 (85) (85)
- 445 -
где D
= 2p
/ℓ, m = L
/l
, m - число отсчетов в интервале Кхmax. Расстояние между нулевыми точками изображения, определяющее размер изображения в направлении оси z, равно
Очевидно, что при брэгговспой дифракции ( ℓ ®
¥
, d=0) имеет место полное разрешение всех точек акустического поля. При рамановской дифракции (ℓ = 0, d ®
¥
) отдельные акустические точки не разрешаются. Из (86) также следует, что разрешающая способность взаимодействия неравномерна по акустическому полю, так как зависит от координат источников.
Определим разрешающую способность акустооптического взаимодействия в двух ортогональных направлениях - света и звука - в случае точечного оптического источника (рис.9а,б). По критерию Рэлея изображения акустических точек n' и n" разрешаются, если координата максимума изображения zr' одной акустической точки n' совпадает с координатой zr"min минимума изображения другой точки n", т.е. zr' = zr"-D
z2. При определении разрешающей способности в направлении света (рис.9а) полагаем z0=0, z's=z"s=-zs, x"s=x's+D
xs. Тогда в соответствии с (66) и (84) получаем
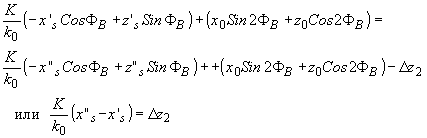
откуда
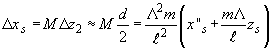 (87) (87)
Таким образом, предел разрешения взаимодействия в направлении света в m/2 раз больше размера изображения акустического точечного источника в направлении звука.
При определении разрешающей способности в направлении звука принимаем z0=0; x's=x"s=xs, z"s=z's+D
zs, (рис.9б). Тогда из
-446-
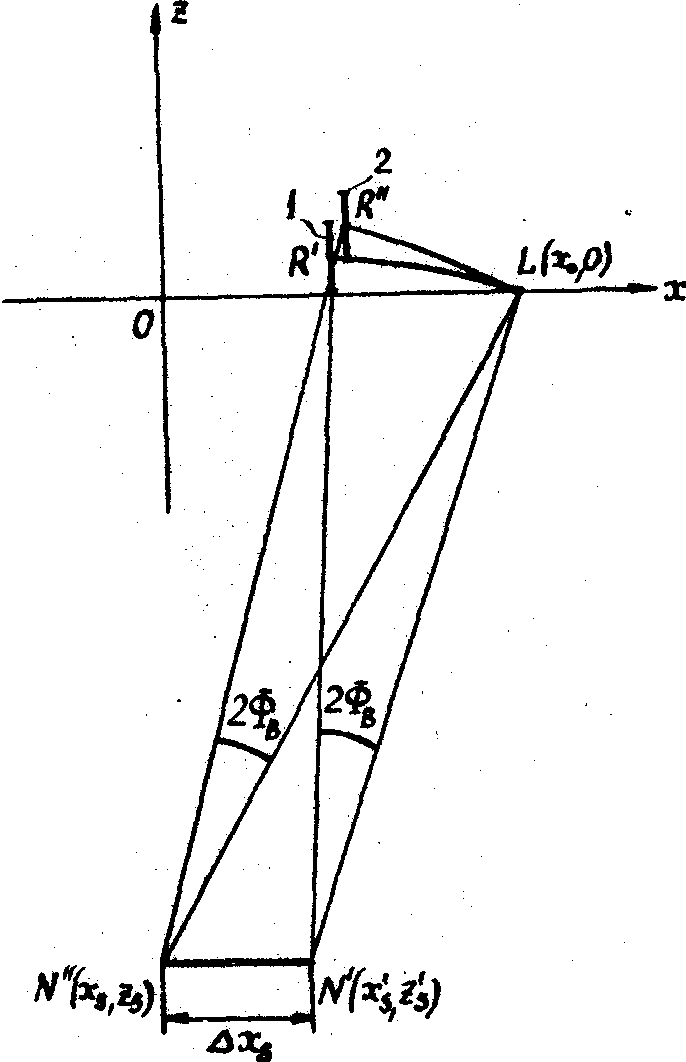 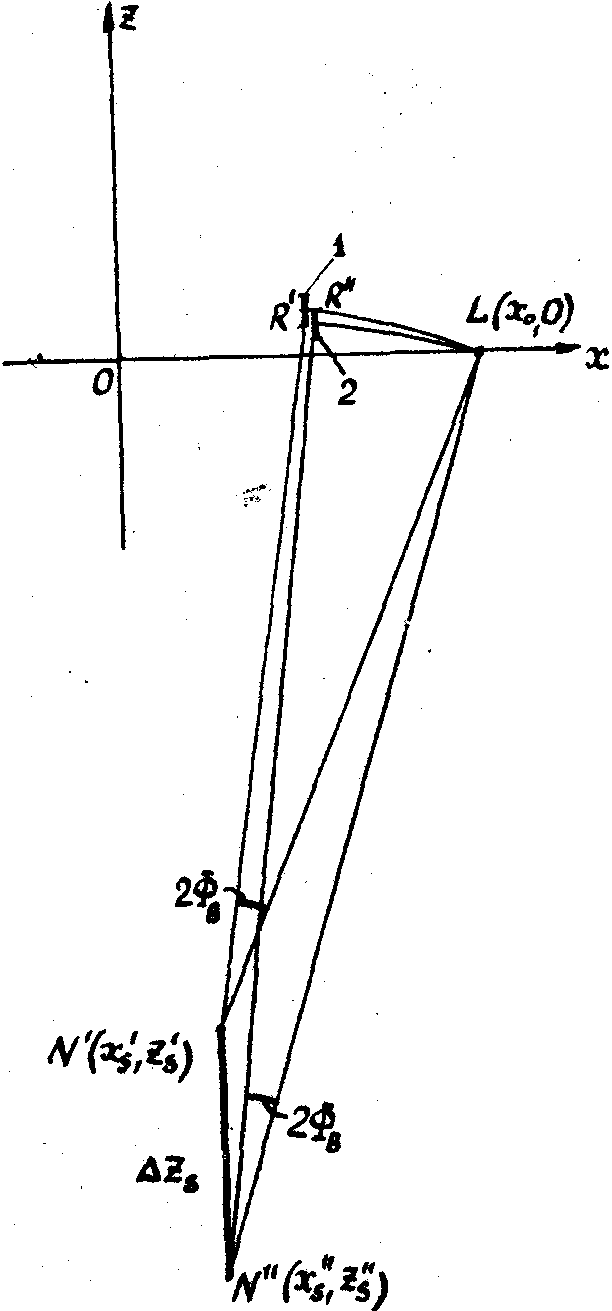
а) б)
Рис.9. Определение разрешающей способности акустооптического взаимодействия:
а - определение разрешающей способности в направлении света; б - определение разрешающей способности в направлении звука; n', n" - акустические точечные источники; l - оптический точечный источник; 1,2 - изображения акустических источников n' и n"; r', r" - точки макйимумов распределения света в изображениях 1 и 2.
- 447 -
равенства
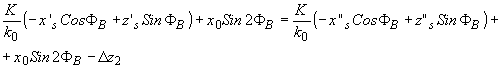
получаем 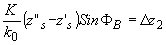 или D z2=k2D
zs/2k20.
Окончательно предел разрешения в направлении звука
или D z2=k2D
zs/2k20.
Окончательно предел разрешения в направлении звука
D
zs = 2m2D
z2 »
m2d = 2mD
xs (88)
Таким образом, разрешающая способность взаимодействия в направлении звука в 2М раз ниже разрешающей способности в направлении света.
Влияние протяженного оптического источника на разрешающую способность иллюстрируется на рис.10. В этом случае оптический источник l представляется набором точечных источников, распределенных вдоль отрезка l1l2. Размывание оптического источника имеет место при ограничении апертур оптических элементов, формирующих этот источник. Принимая x's=x"s, z's=z"s=-zs, получаем
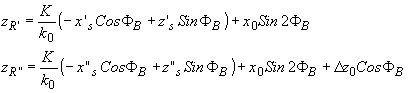
откуда zr"-zr'=D
z0cosФb »
D
z 0. Тогда размер изображения точечного акустического источника
d пр = d + D
z0 (89)
Как следует из (89), при наличии протяженного источника, предел разрешения возрастает на величину, равную размеру этого источника.
iii. Оптические методы восстановления акустических полей
Перенос пространственно-временных спектров взаимодействующих полей в спектр рассеянного изучения позволяет осуществлять оптическое восстановление акустических полой. Это обстоятельство имеет
- 448 -
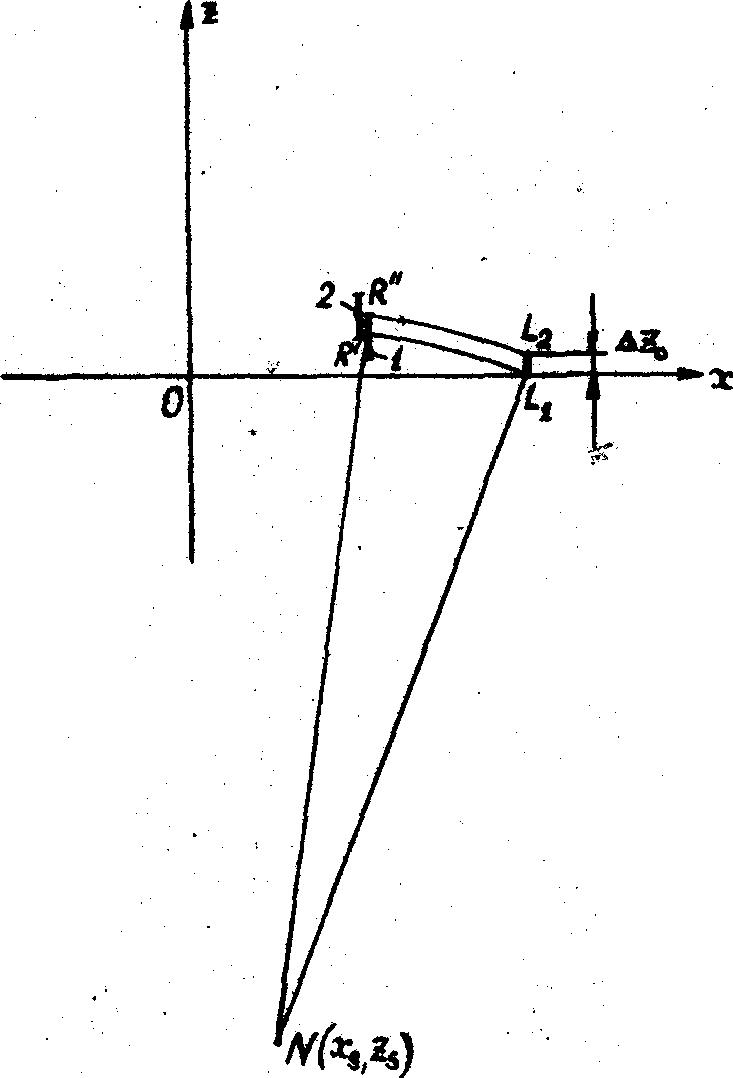
Рис.10. Определение разрешающей способности акустооптического взаимодействия в случае протяженного оптического источника :
n - акустический точечный источник с координатами (хs,z s); l - оптический протяженный источник; D
z0 - линейный размер протяженного источника; 1,2- изображения акустического точечного источника, соответственно, для точек l1 и l2 оптического источника l.
- 449 -
существенное значение для визуализации и оптического исследования акустических полей. Возможны две разновидности методов оптического восстановления: дифракционные и гетеродинные методы. Дифракционные методы основаны на визуальной или фотоэлектрической регистрации световых полей в порядках спектра дифракции. В гетеродинных методах применяется фотоэлектрическое детектирование поля интерференции дифракционных порядков с опорной световой волной, частота которой отлична от частоты света в порядках.
iii.1. Дифракционные методы
Выше были рассмотрены изображающие свойства дифракционного процесса. При брэгговской дифракции и освещении точечным источником в порядках восстанавливается изображение акустического поля. При ограничении зоны взаимодействия и изменении фронта освещающей волны разрешающая способность процесса снижается. Однако дифракция остается эффективным способом оптического зондирования акустических полей, позволяющим восстановить распределение интенсивности звука в различных сечениях поля по распределению интенсивности света в дифракционных порядках /16-18/.
Рассмотрим оптическое зондирование для случая дифракции Рамана-Ната при освещении плоской световой волной (рис.11). Световой зонд 1 щелевидной формы пересекает поле 2 гармонической ультразвуковой волны, возбуждаемой излучателем 3. Ширина зонда в направлении звука мала и составляет несколько длин акустических волн. В перпендикулярном направлении (ось у0) зонд перекрывает ширину звукового поля. Поскольку размер по оси z много меньше размера по оси у0, считаем такой пучок "узким". Плоскость х0у0 является средней плоскостью зонда. Акустическое поле в пределах зонда описывается функцией пропускания:
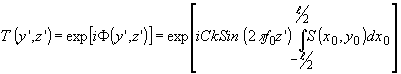 (90) (90)
где ¦
0=1/ L
- пространственная частота акустической волны, л- длина акустической волны. Спектр дифракции света на акустическом поле в фокальной плоскости цилиндрической линзы 4 описываются одномерным
- 450 -
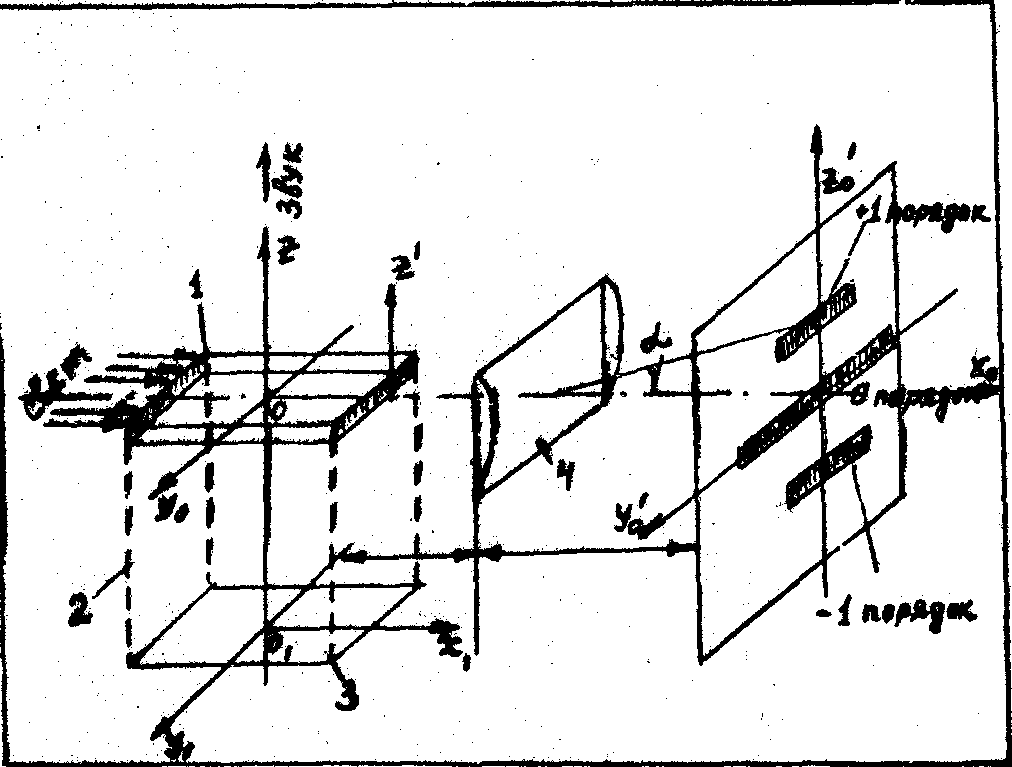
Рис.11 . Схема оптического зондирования дифракционным методом:
1 - световой зонд; 2 - акустическое поле; 3 – излучатель; Л - линза.
преобразование Фурье:
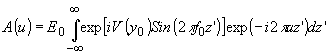 (91) (91)
где u=z'0/l
А -
пространственная частота спектра, f –
фокусное расстояние
линзы 4, 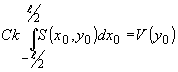 .
Используя разложение .
Используя разложение
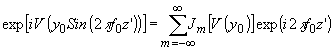
где jm[v(y0)] - бесселева функция 1 рода m-ого порядка. получаем в (91)
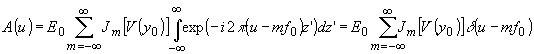
- 451 -
а переходя к координатному представлению спектра в фокальной плоскости линзы,
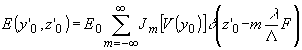 (92) (92)
Амплитудное распределение света вдоль спектральной линии m-го порядка определяется функцией jm[v(y0)] и описывается выражением
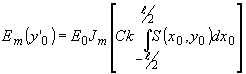 (93) (93)
При слабом взаимодействии для первого дифракционного порядка j1[v(у0)]=b 1v(y 0), где b1 - коэффициент пропорциональности (b1 »
0,5 в диапазоне v = 0¸
1,0) и
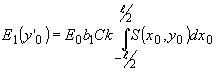 (94) (94)
Распределение интенсивности света в первом порядке вдоль оси у '0 равно:
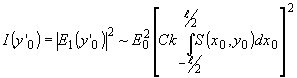 (95) (95)
Рассмотрим связь между акустическим полем в зондируемом сечении и интенсивностью света в +1 или -1 дифракционной порядке для случая плоского излучателя 3. Во френелевской зоне акустического поля распределение света в зондируемом сечении описывается двухмерной сверткой поля s(x1,yi) на излучателе 3 с функцией Френеля:
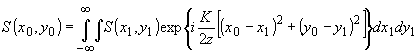
а амплитуда света в первом порядке в соответствии с (94)—
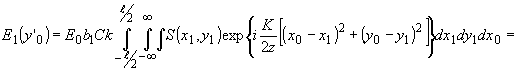
- 452 -
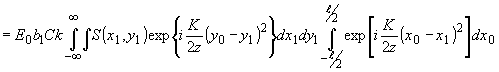 (96) (96)
Для вычисления (96) примем, что
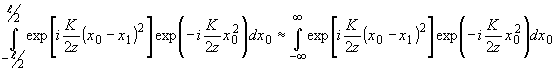
Тогда
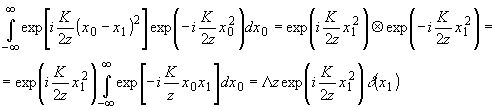 (97) (97)
Подставляя (97) в (96) и производя интегрирование, получаем с точностью до постоянного множителя выражение для амплитуды света в первом дифракционном порядке:
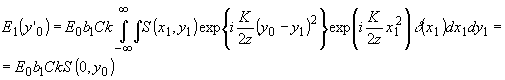 (98) (98)
Интенсивность света в этом порядке, согласно (95), пропорциональна интенсивности акустического поля Ш(0,у0) вдоль оси у0.
В дальней зоне акустическое поле соответствует двухмерному преобразованию Фурье поля s(x1,y1) на излучателе 3:
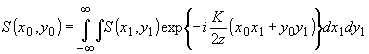
Амплитудное распределение света в 1 порядке при зондировании в этой зоне в соответствии с (94) равно:
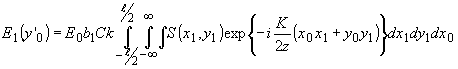
- 453 -
Изменяя порядок интегрирования и интегрируя по х 0, получаем
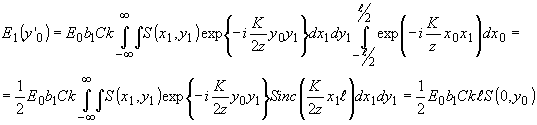
Распределение интенсивности света в первом порядке пропорционально интенсивности звука i(0,у0), распределенной вдоль оси у0 зондируемого сечения
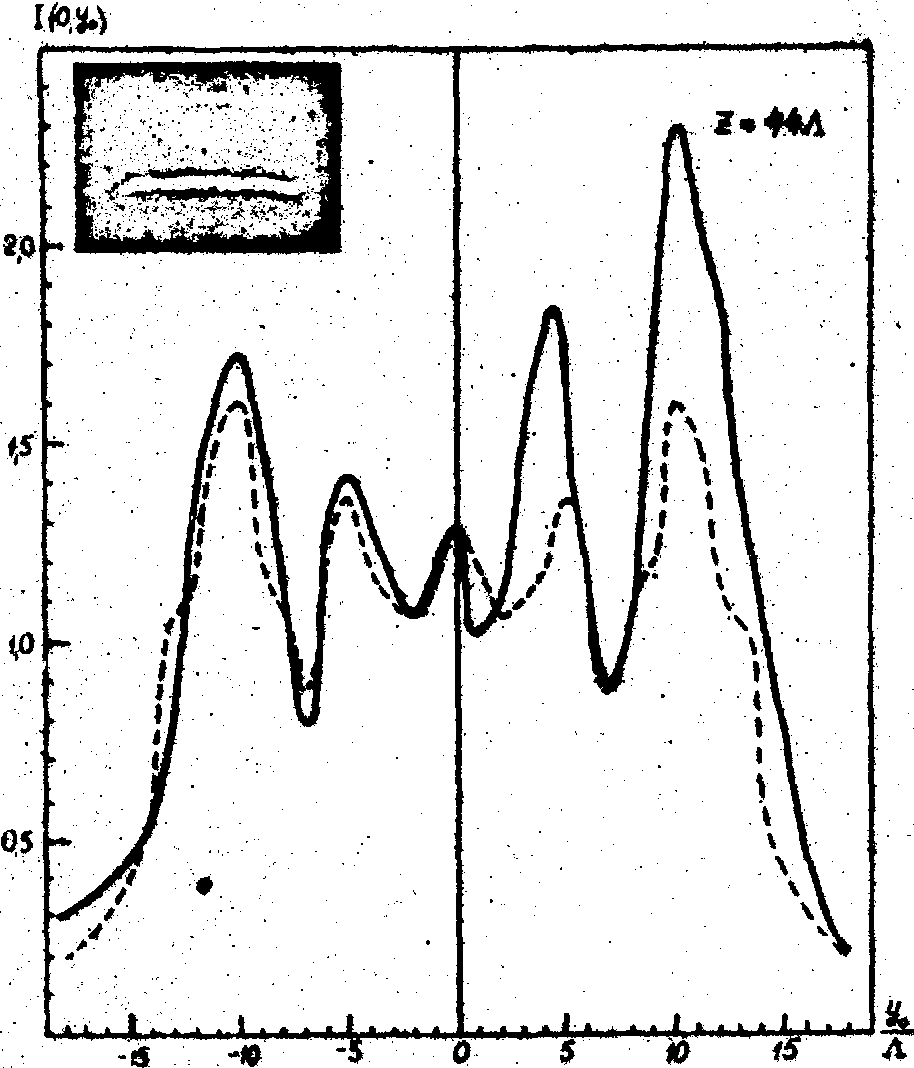
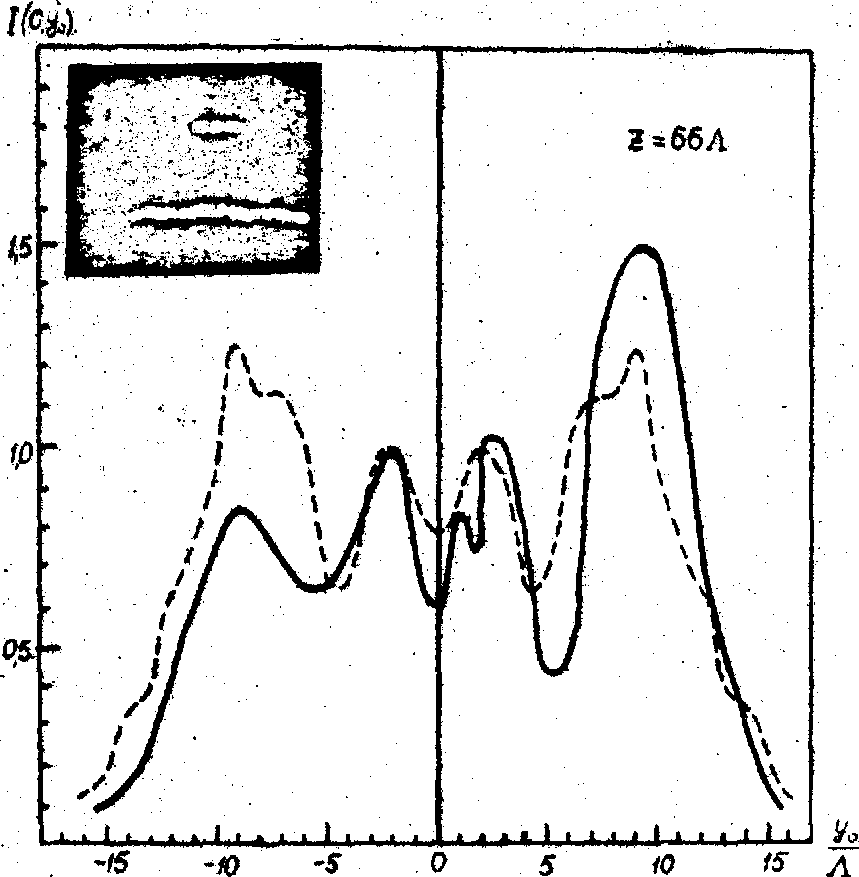
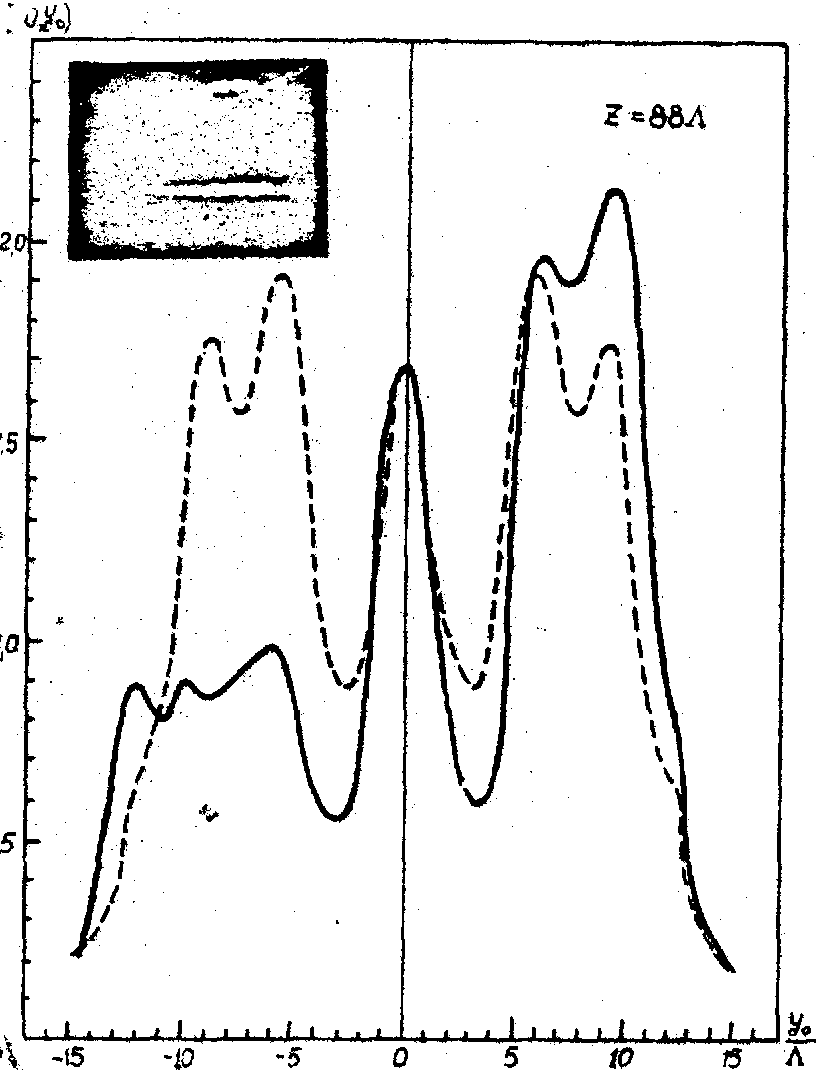
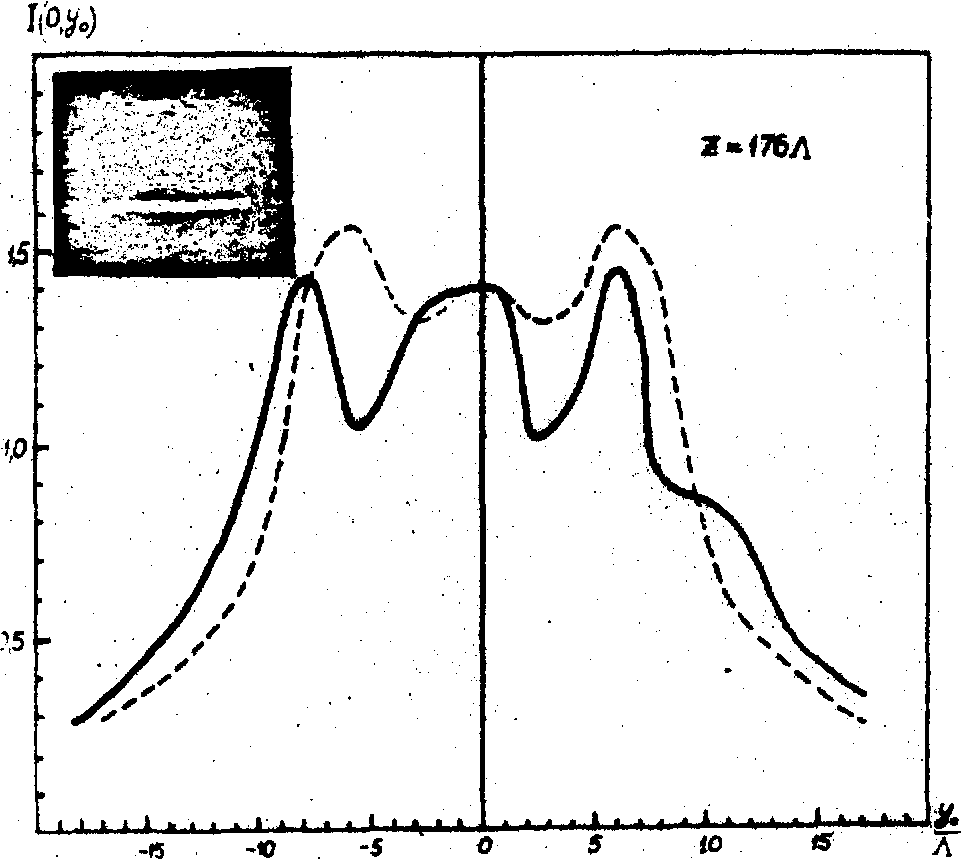
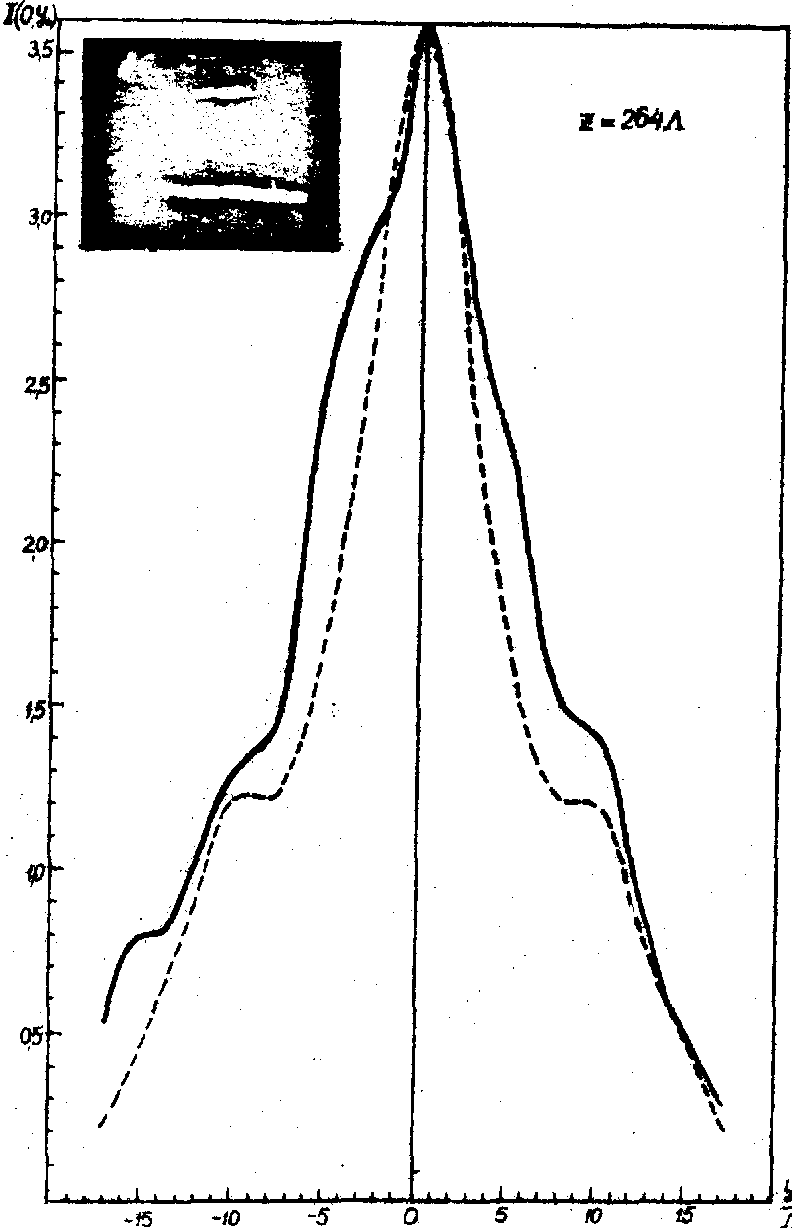
Таким образом, дифракция Рамана-Ната плоской световой волны на акустическом поле позволяет восстановить распределение интенсивностей звука и диаграмму направленности излучателя посредством измерения интенсивности света в дифракционных порядках как в ближней так и дальней зонах поля. На рис. 12 представлены результаты зондирования поля плоского излучателя звука, полученные фотометрированием интенсивности +1 порядка при просвечивании поля в различных сечениях щелевидным монохроматическим световым пучком /18/. Выбирая форму зонда и осуществляя сканирование исследуемого поля можно восстановить как линейное /17/, так и угловое /18/ распределение интенсивности звука, а также синтезировать изображение акустического поля /19/.
iii.2. Гетеродинные методы
В основу гетеродинных методов акустооптической голографии положено явление частотного сдвига дифрагированных световых пучков, Дифракционный порядок, несущий информацию об акустическом поле, интерферирует с опорной световой волной отличной частоты, и посредством фотосмешения двух оптических полей выделяется сигнал разностной частоты, амплитуда и фаза которого связана с амплитудой и фазой акустического поля. Особенность акустооптического взаимодействия заключается в том, что в качестве опорной световой волны может использоваться нулевой дифракционный порядок, содержащийся в спектре.
- 454 -
а) б)
в)
Рис.12.
- 455 -
г) д)
Рис.12.
- 456 -
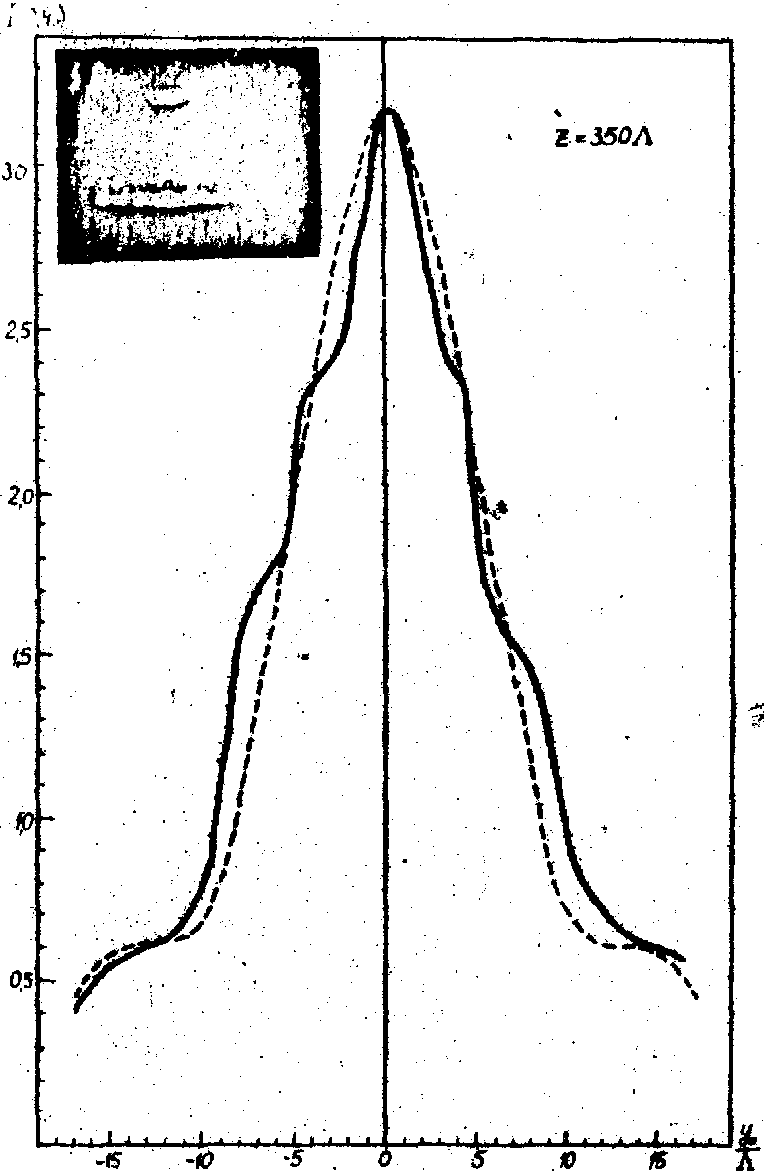
Рис. 12. Распределение интенсивности акустического поля излучателя размеров 6,8х6,8 мм2 (пьеэокерамика, частота 6,4 мггц, L
»
0,2 мм) при различных расстояниях оптического зонда от излучателя: а) z = 44L
; б) z = 66L
; в) z = 88L
; г) z = 176L
; д) z = 264L
; e)z = 350 L
. Сплошными линиями обозначены распределения, полученные фотометрированием +1 порядка. Пунктирными линиями обозначены теоретические распределения. Справа от графиков представлены фотографии дифракционных спектров (0 и +1 порядки).
При слабом взаимодействии дифракционные порядки (23) имеют различные оптические частоты:
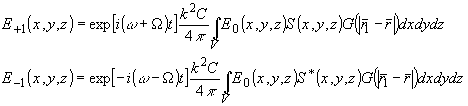 (99) (99)
Интерференция нулевого и +1 порядков приводит к выражению:
- 457 -
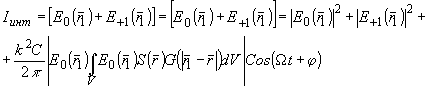 (100) (100)
где j
- фаза переменной составляющей интенсивности.
В результате фотосмешения фотодетектор выделяет сигнал разностной частоты :
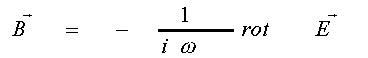
где a
- константа фотопреобразования. Осуществляя сканирование акустического поля световым зондом с гетеродинным преобразованием информации, содержащейся в первом порядке, можно восстановить распределение амплитуд и фаз в акустическом поле посредством измерения амплитуды и фазы фотоэлектрического сигнала /20-23/. В /20-21/ гетеродинный метод использован для оптического исследования акустических полей в случае брэгговской дифракции при освещении точечным источником, в /22/ - для формирования акустической голограммы поверхностных волн. В /23/ описывается метод оптического исследования акустических полей в случае дифракции Рамана-Ната при освещении поля плоской световой волной.
Особенность метода оптического зондирования /23/ заключается в фотоэлектрической регистрации поля интерференции 0 и +1 порядков во френелевской зоне оптической дифракции, где порядки перекрываются (рис.13). Акустическое поле 1, возбуждаемое излучателем 2, освещается пучком 3 лазера 4. В зоне перекрытия 0 и +1 порядков устанавливается диафрагма 5 с фотоприемником 6 и избирательным усилителем 7. В соответствии с (92)
e(0) = e0exp(-iw
t)j0[v(y0)];
e(+1) = -ie0exp(-i(w
+W
)t)j1[v(y0)]
и принимая при слабом взаимодействии j0[v(y0)]»
1, j[v(y0)]»
b1v(y0), в поле интерференции получаем
- 458 -
i инт = [e(0)+e(+1)][e*0+e20[b1ckℓ(0,y0]2-
-2e20b1ckℓs(0,y0)sinW
t
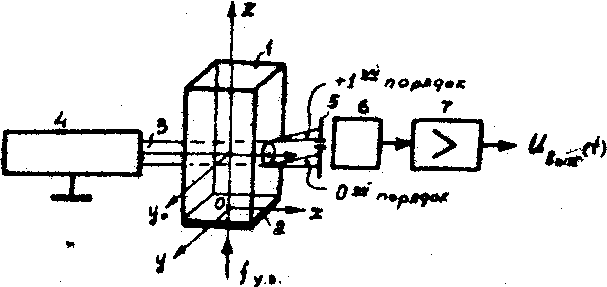
Рис. 13. Схема оптического зондирования гетеродинным методом:
1 - акустическое поле; 2 - излучатель; 3 - световой зонд; 4 - лазер; 5 - диафрагма; 6 - фотоприемник; 7 - усилитель.
Переменная составляющая интенсивности преобразуется в фототок iФ(t)=2a
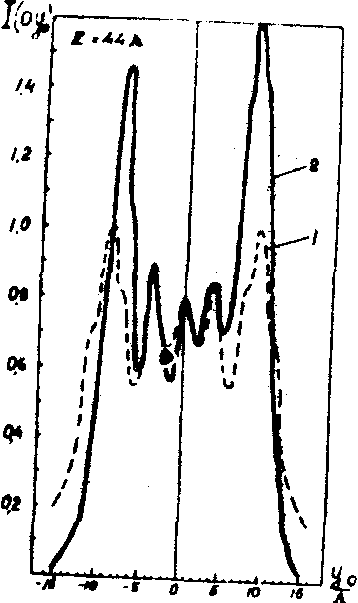
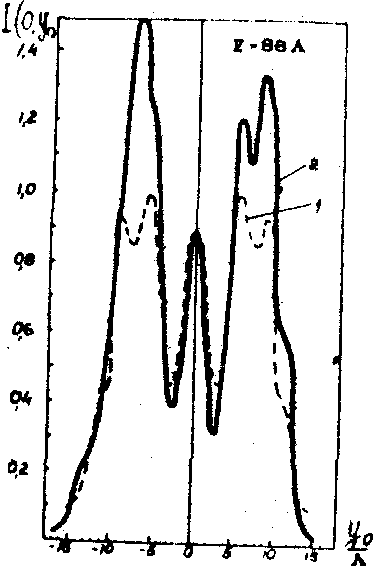
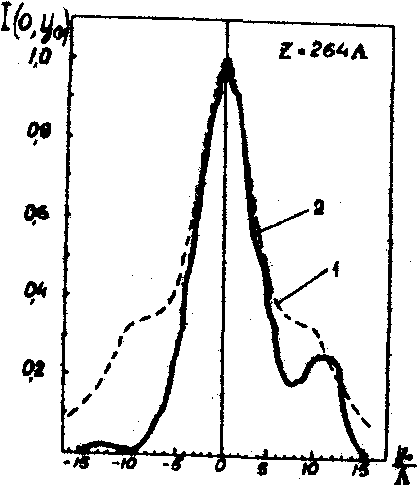
e20b1ckℓs(0,y0), пропорциональный распределению амплитуд акустического поля в точке (0,у0) зондируемого сечения поля. На рис.14а-е приведены нормированные кривые распределения интенсивности i(0,у0) акустического поля в плоскости (y,z) на различных расстояниях от излучателя. На рис.14a-в - распределения интенсивности, измеренные гетеродинным методом (кривые 2) сравниваются с теоретически рассчитанными (кривые 1). На рис.14г-е - результаты измерений гетеродинным методом (кривые 2) сравниваются с распределениями интенсивности, измеренными дифракционным методом (кривые 1). Гетеродинный метод обладает повышенной чувствительностью, помехоустойчивостью и пригоден для измерений параметров
- 459 -
акустических полей в широком диапазоне частот.
а) б)
в) г)
Рис.14.
- 460 -
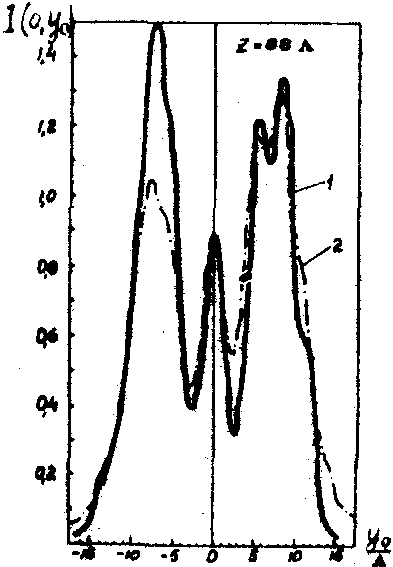 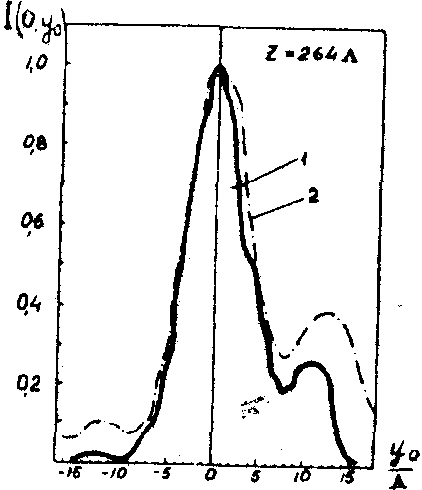
д) е)
Рис.14. Распределение интенсивности акустического поля излучателя размером 6,8х6,8 мм 2 (пьезокерамика, частота 6,4 мггц, L
»
0,2 мм) при различных расстояниях оптического зонда от излучателя:
а) z = 44L
; б) z = 88L
; в) z = 264L
.
На рис.14а-в: 1 - теоретическая кривая; 2 - кривая, построенная по измерениям гетеродинным методом.
г) z = 44L
; д) z = 88L
; е) z = 264L
.
На рис.14г-е: 1 - кривая, построенная по измерениям гетеродинным методом; 2 - кривая, построенная по измерениям дифракционным методом.
- 461 -
Литература
1. Физическая акустика. Под ред. У.Мэзона, т.vii, гл.5, Мир, М.,1974.
2. a.korpel. ieee trans.snics ultrason., su-15, 3, 153, 1968.
3. a.korpel. optical imaging of ultrasonics fields by acoustic bragg diffraction, bronder-offset n.-y., rotterdam, 1969.
4. w.h.carter. josa,. 60, 10, 1366, 1970.
5. З.И.Фейзуллин. Изв. ВУЗОВ. Радиофизика, 15, 5, 713, 1972.
6. В.И.Телешевский. Материалы iv Всесоюзной школы по голографии, Ленинград, стр.286, 1973.
7. С.М.Рытов. Изв. АН СССР, сер.физич., 2, 222, 1937.
8. Ф.М.Морс, Г.Фешбах. Методы теоретической физики, т.1, Изд.ИЛ, 1958.
9. e.wolf. opt.commun., 1, 4, 153, 1969.
10. Р.Пантел, Г.Путхоф. Основы квантовой электроники. Мир, М., 1972.
11. В.Н.Парыгин, Л.Е.Чирков. Радиотехника и электроника, 18, 4, 703, 1973.
12. Я.И.Хургин, В.П.Яковлев. Финитные функции в физике и технике. Наука. М., 1971.
13. А.Папулис. Теория систем и преобразований в оптике. Мир, М., 1971.
14. В.И.Телешевский. Измерительная техника, 3, 30 (1973); 9, 26 (1973); 7, 78 (1974).
15. w.l.teleechewski. feingeratetechnik, 2, 65, 1974.
16. m.o.gohen, e.i.gorden. b.s.t.j., 44, 693, 1965.
17. r.w.dixon, e.i.gordon. b.s.t.j., 46, 367, 1967.
18. В.И.Телешевский, Н.Т.Азаров. Проблемы голографии, вып.1, 167, М., 1973; дефектоскопия, 1, 49, 1974.
19. ueda mitsuhiro, sato takuso. bell.tokyo ihst.techn., 92, 21, 1969
20. j.lianry, h.keyani, g.wade. j.appl.phys., 43, 6, 2502, 1972.
21. a.korpel, l.w.keebler, m.ahmed. jasa, 51, 5, 1582, 1972.
22. w.l.whitman. appl.opt., 9, 6, 1375. 1970.
23. В.И.Телешевский, А.Ф.Левитес. Дефектоскопия, 5, 30, 1974.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

