|
|
 |
 |

|
| |
НЕКОТОРЫЕ ТЕНДЕНЦИИ И ЗАДАЧИ РАЗВИТИЯ КОГЕРЕНТНЫХ ОПТИЧЕСКИХ ВЫЧИСЛИТЕЛЬНЫХ УСТРОЙСТВ
Б.Е.Хайкин
Рассмотрены основные тенденции развития оптических вычислительных машин и устройств. Описан разработанный метод спектрального кодирования, повышающий точность вычислений при выполнении интегральных преобразований. Приведены результаты разработки методов вычислений, использующих достоинства когерентного света, в частности, описаны табличный и вероятностный методы вычислений.
В последние годы получили развитие исследования по применению возможностей когерентного света при разработке вычислительных устройств и машин. Причем, основное внимание уделялось разработке оптических запоминающих устройств и устройств распознавали? образов на основе согласованной фильтрации . Был выполнен ряд работ по исследованию структур оптических вычислительных устройств и машин, как чисто оптических, так и гибридных /1/, использующих возможности когерентного света в сочетании с электронными устройствами. Появлялись сообщения о создании полностью оптических вычислительных машин /2/, которые однако не подтверждались практическим выпуском машин.
Как уже отмечалось ранее /3/, сочетание ряда достоинств когерентного света (высокая плотность параллельных каналов, возможности выполнения интегральных преобразований и создания голографических ЗУ большого объема) открывают хорошие перспективы для нового этапа в развитии вычислительной техники. Однако, на сегодняшний день не решено много задач, связанных с созданием оптических вычислительных машин и устройств и даже нельзя признать
- 336 -
достаточно успешными результаты по созданию распознающих устройств на основе согласованной фильтрации и практическому выпуску голографических запоминающих устройств.
Следует отметить, что создание оптических вычислительных машин и устройств представляет из себя комплексную проблему, требующую разрешения ряда физических, технологических и математических вопросов. В практических приложениях, использующих возможности когерентного света, характерно увлечение отдельными идеями без достаточной технологической проработки и глубокого анализа ограничений по сравнению с традиционными методами.
Можно привести пример разработки устройств распознавания образов с комплексно-сопряженными фильтрами на основе известной работы Ван Дёр Люгта /4/.
К числу таких ограничений можно отнести отсутствии инвариантности к повороту и масштабу распознаваемых изображений, отсутствие инвариантности к изменений контраста изображений, необходимость нормирования изображений. Серьезным ограниченней является предположение о равномерном распределении спектра помехи, что не имеет места при распознавании сходных объектов. При большой числе распознаваемых образов возникает ограничение , связанной с введением порога распознавания. Перечисленные ограничения, пока их не удастся разредить оптическими методами, потребовали введения в устройства, использующие принцип согласованной фильтрации сложных электронных схем для окончательной обработки результатов.
Анализ современного развития оптических вычислительных машин показывает, что одними из основных ограничений в настоящее время являются отсутствие технологически отработанных реверсивных сред для оперативных и полуоперативных запоминающих устройств, сравнительно малая точность вычислений при интегральных: операциях над матричными кодами, ограничения операций согласованной фильтрации, упомянутые выше, недостаточно,; развитие математического аппарата, описывающего операции и структуры вычислительных устройств.
В настоящей лекции рассмотрены пути решения отдельных трудностей, возникающих при создании оптических вычислительных машин. В частности, рассмотрены вопросы кодирования информации с
- 337 -
целью повышения точности вычислений, развития табличного и вероятностного методов вычислений в сочетании со спектральными кодами.
К этой же проблематике относятся вопросы разработки схем согласованной фильтрации с учетом инвариантности поворота /5,6/ применения методом машинной голографии для улучшения качества астронегативов /7/ и разработки ассоциативных запоминающих устройств с использованием в качестве кодов решетчатых структур /8/, рассмотренные на 6-ой Всесоюзной школе по физическим основам голографии.
Перейдем к проблеме кодирования информации, которая является одной из наиболее сложных и специфичных в оптических вычислительных машинах. Сложность этой проблемы определяется необходимостью выполнения различных по характеру и физической сущности операций, требованиями одновременной обработки чисел и команд, выполнением операций над аналоговыми и дискретными величинами. Можно выделить основные формальные требования, которым доданы удовлетворять коды в оптических и гибридных вычислительных устройствах.
1. Возможность выполнения над кодом дискретных и аналоговых ;'образований, а также совмещение дискретных и аналоговых преобразований. Для дискретного кода типа А(х,у)=(аij)m,n с aij=1,0 характерна точность, определяемая числом разрядов в одном числе а1, а2,..., аq, входящим в матричный код А(х,у), т.е. каждое число определяется 2q различными состояниями. При аналоговых преобразованиях, описываемых преобразованием Фурье и умножением комплексных функций А(х,у), т.е.
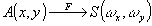
и 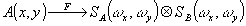
и т.п., точность вычислений определяется точностью представлений аналоговых величин в оптике. При выполнении над дискретным кодом А (х,у) преобразования Фурье точность преобразования определится числом различных градаций элементов sij спектра sa(w
x,w
y), что намного меньше точности
- 338 -
дискретного кода, определяемой величиной 2 q.
Первое Формальное требование, предъявляемое к кодам в obМ, может быть выражено
условием соответствия точности представления дискретного числа а1, а2, ...,аq,
и числа различимых состояний значений спектра для преобразования 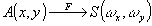 ,
т.е. ,
т.е.
2q(a1,a2,...,aq) º
r
(sij) (1)
где r
- число различных состоянии кода.
2. Равномерность различных состоянии аналоговой величины ri, при выполнении над ней интегральных преобразований так, чтобы выполнялось условие:
|
ri·r*i = pmax для всех i |
(2) |
|
rk·r*i = pmin для всех k¹
i |
т.е. аналоговая величина должна принимать q
различных состояний, удовлетворяющих условию
(2). Примером этого условия может быть операция
согласованной фильтрации, применяемая и когерентные оптических системах распознавания
образов и ассоциативного поиска. Операция согласованной
фильтрации состоит в поиске среди набора матричных кодов А1,А2,..., Аn
( или образов) такого образа
ai, для которого 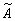 i· i·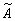 *i
соответствует максимуму корреляционной функции,
а *i
соответствует максимуму корреляционной функции,
а 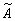 *i
комплексно-сопряженный спектр образа ai. *i
комплексно-сопряженный спектр образа ai.
3. Максимальное использование информационных свойств среды записи информации при выполнении остальных требований к кодам, т.е.
nmax = f(d
,r
,d) (3)
где nmax - различимое число кодов ai, размещаемых на участке запоминающей среды с размерами d
, разрешением r
лин/мм и различным числом градаций для каждой точки - d. Требование (3) сводится к получению максимального числа различимых кодов на
- 339 -
участке среды d
в зависимости от свойств среды.
4. Обеспечение избыточности при выполнении операций над кодами в ОВМ и при различных искажениях в ОВМ, т.е. для кодов в ОВМ должно выполняться требование (4), которое можно представить в виде
|
2q(a1,a2,...,aq) º
r
(sij) |
(4) |
|
ri·r*i = pmax, rk·r*i = pmin |
При искажении |
|
nmax = f(d
,r
,d) |
Кода (j
- D
j
) = na
|
т.е. требование сводится к выполнению ранее сформулированных условий при искажениях кода, не превышающих некоторой величины na
.
Нужно учесть, что по аналогии с электронными вычислительными машинами первоначально в когерентной оптике использовались коды, имеющие вид оптического изображения (двоичные коды, в которых каждый элемент а ij имеют вид прозрачного (0) или непрозрачного (1) квадрата). Несложно показать, что такие коды не удовлетворит сформулированные ранее условиям.
Простейший физическим аналогом кода, удовлетворяющего требованиям
(1-4), является группа кодов, соответствующая
набору резонаторов с сосредоточенными параметрами
l и С, имеющих различные резонансные частоты
¦ 0=1/2p
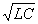 .
Размещении этих резонаторов в поле f
и изменении частоты колебаний поля будут возбуждаться соответствующие элементы,
причем можно обеспечить выполнение ранее сформулированных условий. В когерентной
оптике нужно осуществить переход к пространственным частотам. При операциях
над комплексными функциями деление на плоскость изображения и плоскость спектра
является условным. Основным является разделение на компоненты комплексного,
а не действительного пространства.
Для комплексного пространства вводятся два матричных кода, соответствующих распределению
амплитуд и фаз (или действительной и мнимой части). Физически такой код можно
представить в виде набора векторов, характеризующихся различными распределениями
амплитуд, пропорциональными длине вектора, и фаз, пропорциональных .
Размещении этих резонаторов в поле f
и изменении частоты колебаний поля будут возбуждаться соответствующие элементы,
причем можно обеспечить выполнение ранее сформулированных условий. В когерентной
оптике нужно осуществить переход к пространственным частотам. При операциях
над комплексными функциями деление на плоскость изображения и плоскость спектра
является условным. Основным является разделение на компоненты комплексного,
а не действительного пространства.
Для комплексного пространства вводятся два матричных кода, соответствующих распределению
амплитуд и фаз (или действительной и мнимой части). Физически такой код можно
представить в виде набора векторов, характеризующихся различными распределениями
амплитуд, пропорциональными длине вектора, и фаз, пропорциональных
- 340 -
углу наклона вектора (рис.1). Метод кодирования в спектральной плоскости сводится к разбиению спектрального пространства между n кодами так, чтобы удовлетворялась требования условий (1-4).
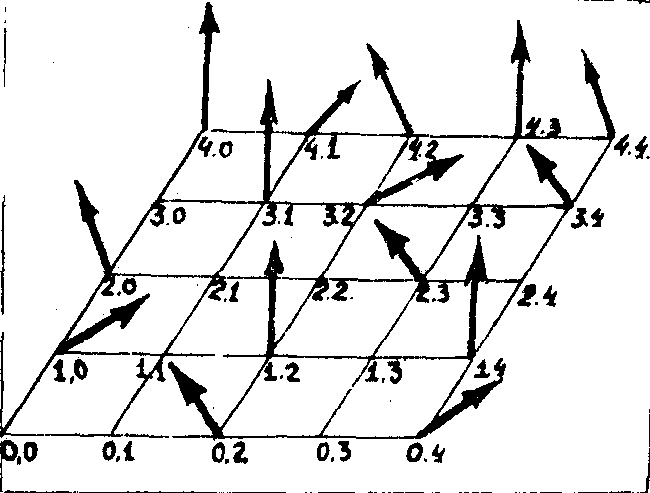
Рис.1. Векторное представление спектральных кодов.
Так как информационная емкость действительного изображения может быть представлена в виде n2q , где n2 - число разрешимых элементов, а q - число различимых градаций каждого элемента, то для комплексной плоскости информационная емкость может быть представлена в виде mn2q, где m - число различимых фаз.
Рассмотренные коды можно назвать спектральными кодами и использовать их при выполнении вычислений в ОВМ, т.е. спектральные коды a
1, a
2,..., a
n должны соответствовать числам С1,С2,..., Сn, причем точность вычислений определится числом кодов n. За счет выбора геометрических размеров спектрального кода и соотношения между n2, q и m можно получать различное число различимых кодов, т.е. фактически управлять точностью вычислений. Спектральное представление кодов хорошо сочетается с табличным методом вычислений, в котором процесс вычислений сводится к информационному поиску но признаку a
i.
Различные типы кодов для ОВМ могут формироваться как в процессе вычислении на ОВМ, так и в результате предварительного
- 341 -
синтеза на ЭВМ. В частности, синтез спектральных кодов можно осуществить машинным способом, т.е. первоначально осуществить машинным способом разбиения спектрального пространства на n кодов, а затем выполнить операцию формирования транспаранта, отображающего спектральный код. Для записи комплексного спектра в виде транспаранта выполняется амплитудное и фазовое кодирование, т.е. с помощью действительных параметре в транспаранта -геометрических форм и плотности передаются амплитуда и фаза спектра. Эта операция может быть осуществлена посредством формирования голограммы интенсивности за счет сложения спектра с опорной волной. Известны методы кодирования комплексных функций при выводе из ЭВМ на основе представления амплитуды в виде размера или интенсивности геометрических фигур, вычерчиваемых выводным устройством ЭВМ, а фазы - посредством использования свойств дифракционных решеток со смещенными щелями вызывать деформацию волнового фронта, т.е. сдвиг фаз /8/. Если для идеальной дифракционной решетки сдвиг фаз между соседними щелями составляет 2p
, то разность хода лучей между смещенной и соседней щелью в первом дифракционном порядке составляет a
и 2p
mp/d, где d - период идеальной решетки, порядок спектра, р - величина смешения периода идеальной решетки. После вычисления на ЭВМ комплексной функции a
(w
x,w
у) в виде набора ряда комплексных величин в выборочных точках a
(n/D
х,m/D
y) осуществляется вычерчивание функции, которая представляется набором элементарных ячеек, каждая из которых отображает комплексный параметр в виде полоски, высота которой пропорциональна амплитуде, а смещение - фазе.
На рис.2 приведены отдельные типы спектральных двоичных кодов, синтезированных на ЭВМ, описанным выше способом (на рис.2-а приведены значения этих кодов).
Так как между амплитудными и фазовыми распределениями существует зависимость, определяемая дифракционными эффектами, что приводит к уменьшению информационной емкости, необходимо определить закономерности образования новых спектральных кодов. Решение этого вопроса можно осуществить на основе машинного
- 342 -
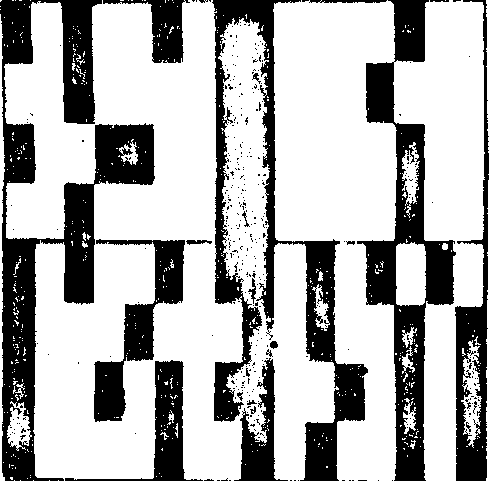 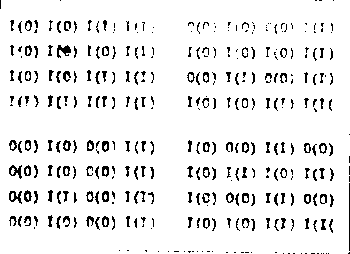
а)
Рис.2. Примеры спектральных кодов, синтезированных на ЭВМ.
моделирования. Для случая применения дифракционной синусоидальной решетки в качестве спектрального кода (рис.3) в плоскости Р 1 располагается дифракционная решетка, описываемая уравнением
t = 2 + exp[+jℓx] + exp[-jℓx] (5)
и ограниченная апертурой
|
pa(r) = |
|
1 |
r|
< a |
(6) |
|
0 |
r|
> a |
При размещении в плоскости Р 1 синусоидальной решетки, ограниченной апертурой Ра и освещении плоскости Р1 пучком коллимированного света, на выходе получим
2pa + paexp[+jℓx] + paexp[-jℓx] (7)
- 343 -
После первого преобразования Фурье (плоскость Р 2) можно записать
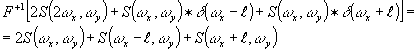 (8) (8)
где
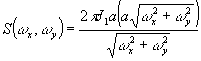 (9) (9)
Если изготовить фильтр, имеющий вид маски (в плоскости Р 2)
pb·s*(w
x-ℓ,w
y)exp[-jcw
x) (10)
ограничивающей комплексно-сопряженный спектр дифракционной решетки апертурой Ра , где
|
pb = |
|
1 |
r|
< b |
|
|
0 |
r|
> b |
a exp[-jcw
x] - функция, описывающая опорный пучок, то в результате фильтрации на выходе плоскости Р2 получим
s(w
x-ℓ,w
y)s*(w
x-ℓ,w
y)pbexp[-jcw
x) (11)
На ЭВМ исследовалась модель кодирования на основе спектральных кодов, заданных в виде набора дифракционных решеток (рис.3а), соответствующих десятичному кодированию информации; значения 0, 1,2,....9 задаются частотой, порядки - поворотом решетки. Очевидно, что для передачи числового диапазона в 1010 требуется 100 кодов.
В частотной плоскости дифракционной решетки были взяты два вектора А 1 и А2, расположенные симметрично относительно центральной оси. В результате моделирования на ЭВМ показано,
- 344 -
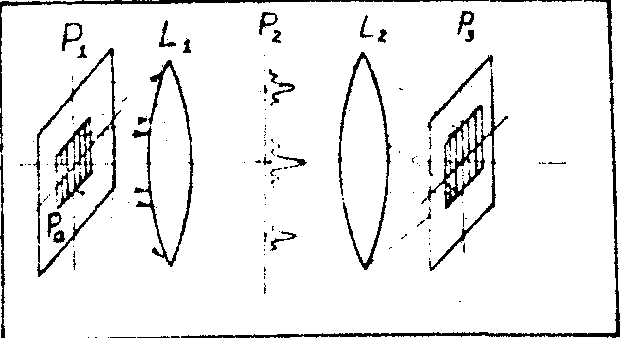 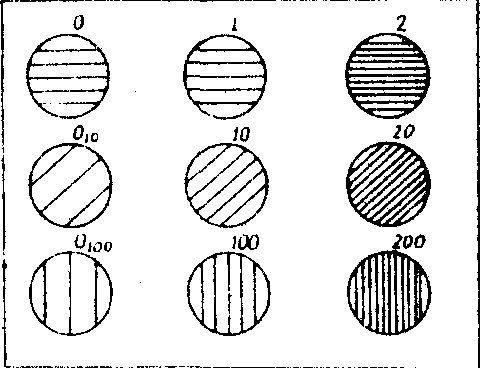
Рис.3. Рис.3а.
Схема фильтрации с Кодирование на основе
дифракционными решетками дифракционных решеток
что если код задан парой векторов, то для получения новых кодов необходимо:
- линейно изменять модуль вектора,
- нелинейно изменять фазы вектора,
- нелинейно изменять фазу и любым способом изменять модуль.
При линейной изменении фазы, новых кодов не возникает и происходит только сдвиг изображения. Несложно показать, что этот вывод распространяется на любое число векторов, больше двух. При наличии одного вектора в результате преобразования Фурье получается постоянная освещенность, т.е. фактически это соответствует точечному источнику.
На рис.4 и 5 приведены примеры параллельной и последовательной фильтрации для кода, соответствующего десятичному числу n . Точность фильтрации, т.е. величина порога составляет 1/10 от максимума для десятиразрядного числа, т.е. n = 1010. Рассмотрим основы метода табличных вычислений в ОВМ, применение которого обусловлено двумя основными обстоятельствами: большими объемами памяти оптических ЗУ и возможностью, выполнения интегральных операций, операций над понятиями (ассоциативный поиск, декорреляция памяти и т.п.).
В общем случае метод табличных вычислений основан на определении значений функции ¦
(х), заданной в виде таблицы и
- 345 -
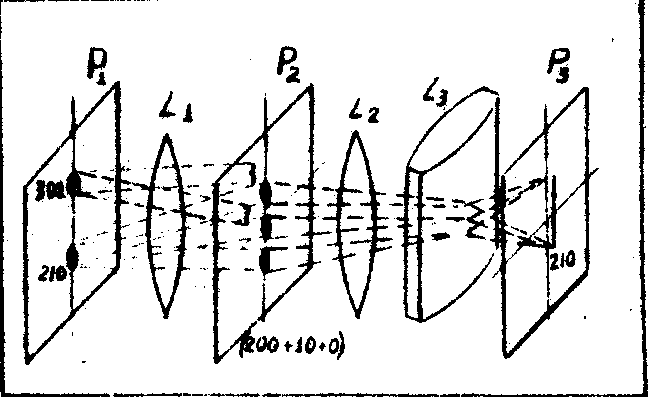
Рис.4. Схема параллельной фильтрации кода 210.
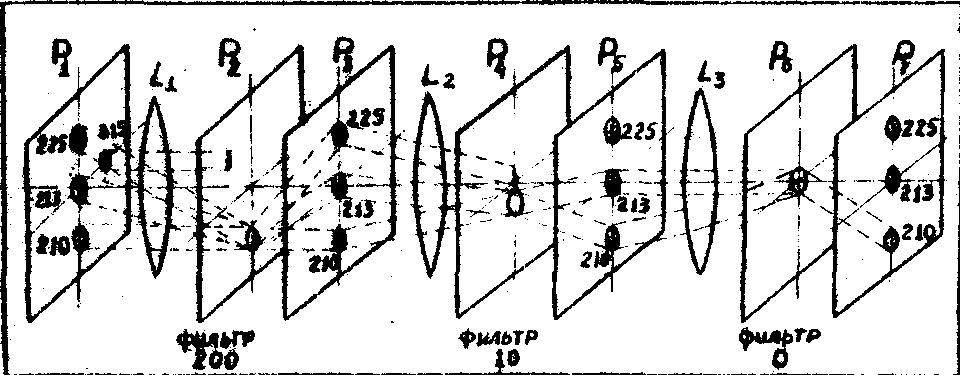
Рис.5-Схеыа последовательной фильтрации кода 210.
интерполяционных коэффициентов, позволяющих определить функции для значений аргумента, которые расположены между двумя соседними значениями таблицы. В простейшем случае интерполирующая функция может быть представлена в виде многочлена
j
(x) = d0 + d1x + ... + dnxn (12)
В методах интерполирования было показано, что для функции ¦
(х) или ее (n+1) табличных значений x0, х1, x 2,...,x n всегда существует единственный многочлен n-ой степени ¦
(х) так, что
- 346 -
выполняется равенство
¦
(x к) = j
(xк,) > к = 0,1,2,...,n.
Наиболее простое приближение достигается по методу наименьших квадратов, в котором действительной функции ¦
(x) сопоставляется функция
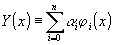
где j
i(x) - известные функции. Выбор (n+1) коэффициентов осуществляется на основе минимизации среднеквадратичной ошибки
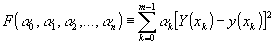 (13) (13)
для заданного множества m(m > n+1) значений аргумента х=xк. Значения коэффициентов находятся на основе решения системы линейных уравнений, т.е.
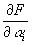 =0, (i
= 0,1,2,...,n) =0, (i
= 0,1,2,...,n)
На основе вычисления различных функций первоначально создается набор таблиц (табличные значения функций, вычисления по различным формулам, результаты решения стандартных задач), которые записываются в оптические памяти. Объем информации при кодировании записи определяется на основе оценки плотности записи и числа символов кодирования. При двоичном кодировании и выборе 64 символов (буквы, цифры, знаки), т.е. 26 бит = 64 один печатный лист информации потребует 26·4·10 4 = 2,5·10 6 бит. Традиционная форма записи таблиц с интерполяционными членами требует выполнения вычислений для получения точных значений функций, т.е. ту структуру обработки информации на основе табличных методов и интерполяционных коэффициентов включается блок вычислений на основе различных интерполяционных формул, что несложно в гибридных вычислительных структурах, объединяющих дискретные и оптические
- 347 -
блоки, но нежелательно в оптических вычислительных машинах.
Достаточно простой, с точки зрения внешнего представления кодов и системы кодирования, является запись всех значений суммы для различных слагаемых, но в этом случае значительно возрастает объем информации, требуемый для записи таблиц. Целесообразно осуществить такой выбор таблицы, чтобы ее размеры не были безграничны, например, выполняя табличную операцию над небольшим числом разрядов.
Рассмотрим табличный метод сложения для таблицы с разрядными значениями кодов слагаемых. Тогда, при разрядности чисел с n = 40, т.е. для кода с 240 после первого такта выбора табличных значений частных слагаемых получаются четыре суммы и требуется еще два такта сложения. Для хранения таблицы с m = 210 = 1024 требуется хранить 1024 значений частных сумм.
В таблице приведен объемы памяти, необходимые для хранения табличный значений при различных m, а также необходимое число тактов при 50-ти разрядной сетке.
Таблица
|
7 |
8 |
9 |
10 |
16 |
25 |
|
объем ЗУ |
128 |
256 |
512 |
1024 |
64·103 |
32·106 |
|
число тактов |
7 |
6 |
5 |
4 |
3 |
2 |
Из таблицы видно, что дальнейшее увеличение разрядности таблицы нецелесообразно, так как следующее значение m может быть только 50, что требует 250 бит, но незначительно влияет на время выполнения операции сложения.
В табличном методе к вопросам функциональной полноты добавляется задача обработки результатов табличных вычислений (учет интерполяционных коэффициентов и расчет погрешностей). Нужно также учесть ограничения табличного метода, связанного с трудностью создания таблиц для многопараметрических функций.
Вероятностный метод обработки информации в ОВМ основан на
- 348 -
использовании метода статистических испытаний /9/ .
Предпосылкой метода статистических испытаний является использование связи между вероятностными характеристиками случайных процессов и математическими величинами, описывающими решения различных типов задач (решение систем уравнений, краевых задач для дифференциальных, уравнений, задач массового обслуживания, вычисление интегралов и т.п.). В методе статистических испытаний происходит замена вычислений по сложным аналитическим выражениям вычислениями соответствующих им вероятностей или математических ожиданий. Естественно, что этот метод применим к задачам, характеризующимся марковскими процессами, при этом точность вычислений определяется вероятностным характером процессов, не очень велика и оценивается в процессе решения задачи, причем, удлиняя время решения, можно увеличить точность решения,
Рассмотрим пример вычисления интеграла на основе метола статистических испытаний. Известно, что случайная величина h
принимает значения х в некоторой области r, находящейся на оси Ох. Закон распределения h
можно задать плотностью вероятности ¦
(х) в r. Определим вероятность попадания h
в r, ограниченный границами в пределах а и b (рис.6), т.е. нужно определить вероятность
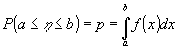 (14) (14)
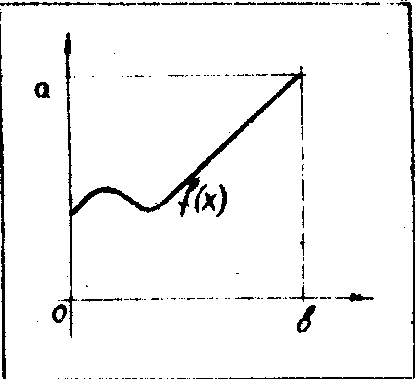
Рис.6. График функции ¦
(х).
- 349 -
Значение (14) можно найти методом статистических испытаний, сущность которого заключается в том, что из совокупности случайных чисел со знаком распределения вероятностей ¦
(х) берется число xi, которое сравнивается с границами интервала r (т.е. a £
хi < b). Число попаданий хi в интервал r равно m, а частота попадания р=m/n. Искомая вероятность определяется на основе закона больших чисел
limp(|
m/n - p|
< e
) = 1 (15)
При достаточно большом n
оценка р заменяется частотой m/n, т.е.
p » 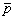 .
Величина m/n
представляет из себя приближенное решение интеграла
(14). Точность вычислений интеграла определится
количеством испытаний. Очевидно, что для равенства
(15) точность равна
e с надежностью
получения этой точности a ,
если для |
р - .
Величина m/n
представляет из себя приближенное решение интеграла
(14). Точность вычислений интеграла определится
количеством испытаний. Очевидно, что для равенства
(15) точность равна
e с надежностью
получения этой точности a ,
если для |
р - 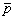 |
< e , то
справедливо |
< e , то
справедливо
p(| p - 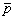 |
< e ) = a |
< e ) = a
Оценка точности основана на неравенстве Чебышева
p(| p - 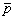 |
< e ) ³ 1
- |
< e ) ³ 1
- 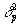 /e
2 (16) /e
2 (16)
где 
- среднеквадратичная ошибка
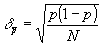
В результате преобразований (15) и (16) получим
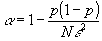 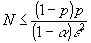 (17) (17)
Например, при a
= 0,05 и e
= 0,601 n = 50.000.
Следует отметить простоту метода (выбор случайной величины - сравнение - счет числа попаданий), и достаточно широкие вычислительные возможности метода (решение систем линейных уравнений,
- 350 -
нахождение собственных значений для эллиптических дифференциальных операторов, вычисление многомерных интегралов, задачи рассеяния нейтронов и расчета атомных реакторов, задачи массового обслуживания, задачи моделирования систем облучения, задачи управления со случайными сигналами на входе, краевые задачи для дифференциальных уравнений). Недостатком метода статистических испытаний, как уже отмечалось, является сравнительно малая точность вычислений, но в ряде случаев она и не требуется, кроме того, удлиняя время решения, можно получить требуемую точность вычислений.
Синтез, матриц случайных чисел для оптических вычислительных устройств может быть выполнен на основе машинного синтеза матричных случайных кодов с заданным законом распределения (рис.7), полученные наборы двумерных случайных чисел проверяются одним из известных методов и результат может либо записываться в оптические запоминающие устройства, либо оперативно использоваться при вычислениях. Потенциально большие объемы памяти позволяют создать достаточно обширный набор случайных кодов с различными законами распределения.
Равновероятное 20% заполнение 40% 60%

Нормальное 20% заполнение 40% 60%

Рис.7. Результат машинного синтеза случайных матричных кодов с равновероятным (Р) и нормальным(Н) законами распределения
- 351 -
Отличительной особенностью метода табличных вычислений в сочетании со спектральными кодами, а также метода вероятностных вычислений является возможность получения достаточно высокой точности вычислений при использовании интегральных операций, точность которых невелика. Использование спектральных кодов позволяет решить проблему поиска на основе комплексно-сопряженных фильтров в системах оптической памяти большого объема.
Литература
1. Б.Е.Хайкин. Материалы iv Всесоюзной школы по голографии, Л., 166, 1973.
2. electronics, 7, 29/iii, 81, 1971.
3. Б.Е.Хайкин, В.С.Хитрова. Проблемы голографии, М., вып.ii, 6, 1973.
4. a.vander lt. ieee trans., it-10, 2, n4, 139, 1964.
5. Э.Г.Аветисов. Материалы vi Всесоюзной школы по голографии, Л., стр.287. 1974.
6 . Р.А.Саргсян, В.С.Хитрова. Лекция на vi Всесоюзной школе по голографии, 1974.
7. Ф.М.Шавердян. Материалы vi Всесоюзной школы по голографии, Л., стр.325, 1974.
8. Б.Е.Хайкин. Материалы iii Всесоюзной школы по голографии. Л., стр.168, 1972.
9. Ю.А.Шрейдер, Н.П.Бусленко. Метод статистических испытаний, Фm, 1961.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

