Image processing
a.w.lohmann
fed. rep. of germany
1. introduction
the three lectures cover the subjects of "synthetic holograms", "holography through fog", and "matched filtering and other Image correlation methods".
after brief reviews (with references) the usefulness of the three subjects will be discussed. we are more optimistic than others, especially on the third subject.
vth international school on holography, novosibirsk, january 1973.
- 16 -
2.synthetic holograms
2.1 fundamentals
definition: an ordinary hologram is produced by means of an interference experiment. a synthetic hologram is produced by means of a computer and an automatic drawing machine (plotter).
pour survey articles [1,2,3,4] teach the fundamentals of "computer holography", or "digital holography", as this field is sometimes called.
are synthetic holograms useful? we will now give two general answers. more specific answers will follow when the applications of computer holography are discussed. a unique feature of computer holography is that the object does not have to exist. it is enough, if the synthetic object is defined in mathematical terms. hence, synthetic holograms are preferable over ordinary holograms, when it is difficult to produce the object (for example a speckle-free diffuser, an accurate interferometric prototype, an accurate spatial filter like for "deblurring", the input data mask of a page composer for holographic memories).
we can classify a synthetic hologram as a hybrid data processing subsystem. "hybrid" means that the production is performed by a digital computer (very flexible, but expensive to operate). later, the synthetic hologram is used as a part of an optical analog computer (for example for matched filtering or deblurring). we benefit from the advantages of both technologies, because the flexible digital step is performed only once, but the inflexible, cheap and fast analog step is often repeated in suitable applications.
- 17 -
2.2 simulation studies
the production of ordinary holograms can be simulated by making a synthetic hologram. this simulation process is a valuable exercise for students, much better than the ordinary holographic recording process. for making a computer hologram one has to understand maxwell's equations and the sampling theorem very well, because the digital computer does not understand anything. its brain is empty. however, the recording of an ordinary hologram can be done by following a simple recipe, that does not teach anything about diffraction or fourier mathematics. a more advanced simulation project is the investigation of diffusers with pseudo-random phase distributions.
2.3 display
suppose the structure of a molecule has been computed by analyzing x-ray diffractograms. now the knowledge of this 3d-structure shall be transferred into the human brain. we could synthesize a hologram with the large-scale model of the molecule as the non-existing object. that allows us to perceive the 3d-structure with parallax and all other 3d clues including color. this method is straight forward. but so far, it is too expensive. other 3d display methods (like stereo) are not as good but considerably cheaper.
2.4 spatial filtering for Image processing
spatial filtering is one of the best explored and best described areas of holography. every ordinary holographic filter can also be synthesized. some filters can be produced only synthetically, expecially if accuracy is demanded. the choice between ordinary holograms and synthetic holograms as filters depends on the arguments given in chapter 2.1. the choice will be different for different applications. how easy it is to make synthetical
- 18 -
spactial filters is demonstrated by the fact that only three papers [5] cover the field almost completely, while perhaps twenty times more literature had to be produced in order to cover the area of spatial filtering with ordinary holograms. those three papers covered as much as phase contrast, hilbert transform, first and second order differentiation, shearing, deblurring, matched filtering, gradient correlation, and code translation.
2.5 synthetic interferometric prototypes
when testing interferometrically a large telescope, one needs for comparison a wavefront that is shaped as if it had been reflected from a perfect telescope (=prototype). if that perfect telescope does not exist, we may replace it by a synthetic hologram, that can produce for us every desired prototype wave, including aspheric and asymmetric waves. the accuracy depends on the cleverness of the scientist and on the amount of money he is allowed to spend. an accuracy of a twentieth of a wavelength has been obtained in several laboratories on three different continents. many thousands of dollars have been saved by this test method. publications on this subject did appear for example in "applied optics", "optics and laser technology", and in "optik".
2.6 holographic data storage
the first question is if holographic data storage is useful in comparison to magnetic data storage. the answer is a "yes" with three "if's". the first "if" means that we optical scientists have to improve the holographic memories, especially the materials, the page composer, and the error rate. the second "if" requires that we teach the big bosses and the systems engineers somewhat about optics. and finally, holographic memories could be used much sooner, "if" the systems engineers would learn how to use sometimes very large read-only memories instead of medium large read-and write memories.
- 19 -
the second question is, if the holograms for memories should be made by diffraction or by digital computation. in my opinion, the digital or synthetic production is often better, because the input information remains in the clean digital world. the dirty analog world (page composer) is noisy, expensive, and somewhat slow. however, this problem depends also on the format requirements of the systems designers. small page sizes are favourable for synthetical holograms, while large pages (more than 104 bits) are probably cheaper to produce by diffraction experiments. that depends on the core size of the digital computer.
the third question is based on the assumption, that a synthetic hologram is better than an ordinary hologram. this assumption is not always valid, of course, depending on the format of the memory system. but once it has been decided to use synthetic holograms, the question is if the fringes on the hologram should have a sinusoidal profile (like oridnary holograms) or a square-wave profile. the latter case is also called a "binary hologram" because the transmittance can be only "one" or "zero", nothing in between (grey). these binary holograms have more light efficiency and less photographic noise than ordinary grey holograms. the reasons were explained in references [4] and [6]. recently, my co-worker t.strand verified the signal-to-noice advantage of binary, versus ordinary holograms. his results will probably appear in the spie journal "optical engineering" in the special issue on Image processing (april 1974). signal-to-noise advantages by a factor of 10: 1 are feasible. that is not surprising because zweig, higgins and macadam demonstrated more than 10 years ago, that the storage density (bits/area) of photographic material is maximal for binary pattern.
a final comment in favour of synthetic holograms as data storage elements. when computing these holograms, we simulate an ideal speckle-free diffuser, .that does not exist in reality. despite of all these advantages of synthetic holograms all (except one) 20 or 30 systems in existance use ordinary grey holograms.
- 20 -
2.7 Image communications technology
this field is now in a state of intensive development, as can be seen for example in the journal "computer graphics and Image processing" (academic press, new york and london). holograms are attractive as an encoded form of an Image signal, because holograms are burst-error insensitive. synthetic holograms in binary form have the additional advantage of leading to pulse modulation, which is often better in terms of signal-to-noise than analog modulation (here amplitude modulation for grey holograms). these brief comments are amplified in reference £4'j .
3. holography through fog
the basic idea is as following. when fog is between the object and the receiver (for example a hologram) most light rays will be scattered. those rays are bad for the Image quality. but a few rays are lucky. they will go through the fog without hitting a droplet. a hologram is a very smart receiver, because it can distinguish between the lucky and the unlucky rays. the unlucky rays will be doppler-shifted, if the fog droplets move, as they normally do. hence the unlucky rays cannot interfere with the reference wave. only the lucky rays will produce interference fringes on the hologram. when reconstructing an Image we use only the light that has been diffracted by the interference fringes on the hologram. therefore, the Image does not suffer from the fog [7].
this doppler explanation is very interesting, because it might become the basis of more holographic experiments in the future. we may consider the holographic recording-process as a heterodyne receiver process. the monochromatic reference wave is the local oscillator (frequency 1015 hertz), that is "mixed" (=interference) with the object wave. if the "time constant" (=exposure time) of the receiver is one second, only object frequencies in the range from (1015-1) hertz to (1015+l) hertz will be recorded.
- 21 –
hence, the "heterodyne selectivity" is 1015 (as good as mőssbauer, a million times better than hf technology). but our holographic heterodyne receiver is much more impressive than a mőssbauer apparatus, because a holographic plate (for example 10 x 10 cm2 of high resolution material with 10-3 mm resolution length) contains not only one single super-high-selectivity heterodyne receiver, but 1010 such receivers, as many as there are resolution elements on the photographic plate. these phantastic qualities should lead to phantastic applications, if the holographers have enough imagination.
since the publication of reference [7] the same authors have performed some theoretical signal-to-noise studies in order to understand the performance limits of holography through fog. furthermore, some newer experiments were more realistic. for example, it is possible to send both the object wave and the reference wave through the fog. details will be discussed in future papers in "applied optics".
4. matched filtering and other Image correlation methods
4.1 coherent matched filtering
very often we want to measure the similarity of two images. a quantitative definition of "similarity" is the correlation. the most populary method for measuring Image correlations is coherent matched filtering.
the invention of the holographic matched filters by a.vander lugt is one of the most brilliant optical achievements in recent years, in my opinion. blinded by the brilliance of coherent matched filtering most optical scientists apparently did not believe that this marvelous method could be further improved. however, for many applications improvements are very desirable. for example, it is necessary to have the input object in the form of a photographic transparency (or similar), because the object (outdoor scene, oscilloscope pattern, etc.) is often incoherent. then an incoherent-to-coherent conversion process is necessary which is either slow or
- 22 -
difficult and expensive. for this reason many optical scientists believe that optical matched filtering is not very useful.
we want to destroy the fairy tale that coherent light is necessary for matched filtering. we start by describing briefly coherent matched filtering, especially its disadvantages. thereafter we will outline some modified correlation methods that avoid some of those disadvantages.
the purpose of matched filtering is to find the reference signal ur(x) that might exist in the object signal
uo(x) = S
ur(x-xm)+n(x)
here, n(x) is the noise and xm are the locations
of the signals we want to detect. the first step in building a coherent matched
filter system is to get one example ur of the reference signal. this
is not always easy (see chapter 4.2). next a fourier hologram of ur(x)has
to be made, because the conjugate term 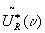 of that hologram is the desired filter function
of that hologram is the desired filter function
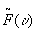 =
=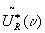 =
=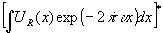
this process is problematic, because the fourier hologram has a very intensive center peak and very weak fringes in the outer parts. the photographic recording material is often not capable of recording both the center peak and the weak outer regions due to a limited dynamic range. another problem with these fourier holograms is their low light efficiency, usually less than 1%. these two disadvantages can be avoided if a diffuser (=phase randomizer) is placed upon ur(x) when recording the hologram. strictly spoken, that is forbidden in the tontext of matched filtering. if one does it anyway (as r.j.bieringer recently did, see "appl. opt.") the correlation output contains many speckle peaks, that are hot always easy to distinguish from signal peaks.
now we assume the holographic filter is ready. we have to place it into the optical system with an lateral adjustment accuracy as fine as the Image of the point source seen in the fourier plane when no object is in the input station. an accuracy of 3m
m. is typical. that is possible, of course, but either slowly or expensively to do.
- 23 -
after this lateriai adjustment is accomplished the system is ready to accept the input object in the form of a photographic transparency. in some applications a special step is necessary to convert the original object into a transparency. again, that process is either slow or expensive.
how large can the object be? that depends mainly on the tilt angle of the reference wave in the hologram recording process. a large angle assures that the useless zeroth order in the output plane is far away from the output signal in the area of the conjugate twin Image. this constraint means that the object size cannot be bigger than typically about one tenth of the object field for which the lens is well corrected. this waste can be avoided by replacing the fourier hologram by an equivalent kinoform, which has only the conjugate Image as output. but to make a kinoform is an order of magnitude more difficult.
4.2 synthetic matched filters
one of the problems mentioned in chapter 4.1 was, that the reference signal ur(x) might not exist. an example might illustrate this possitility. we want to read letters. there may be 32 different letters. should we produce 32 different matched filters, that are used for 32 different similarity measurements on every unknown input letter? no, that would be a waste of labour. since 32 is 25, only 5 binary measurements should be enough to identify one out of 32 letters. how can we do that? at first, we measure with a suitable spatial filter if our unknown letter contains a vertical line. this particular matched filter has been made with a vertical line as reference object ur(x). next, we look with a second matched filter for a horizontal line in the unknown letter. then we search in 3 more steps for left-tilted lines, right-tilted lines, and courved lines (part of a circle). if the 32 letters were designed properly, these five measurements should be sufficient for identifying the unknown letter. however, letters were designed long before matched filtering had been invented, hence wrong for us. therefore the problem is not quite so simple. in other-words, those live elements (streight lines with four different orientations, a piece of a circle) might not be "orthogonal" in the "pseudogeometric
- 24 -
five-dimensional picture domain". in that domain-each of the 32 letters is represented by a vector. given those 32 vectors we would like to know a set of five arthogonal basis vectors. each basis vector represents a picture element such as a horizontal line etc. there are of course infinitly many different sets of five orthogonal basis vectors. in most of these vector sets one or more of these basic vectors will be complex (amplitude and phase), or if not complex then perhaps real but not only positive. at least the desirable feature of having only "one" and "zero" transmittance values (=binary) for those basic vectors in the real (x,y) domain is an unlikely event to occur. it might be possible to find a set of five such simple binary vector pattern, but only at the expense of considerable computer time and based on the development of a complicated algorithm, that does not yet exist as far as i know. that algorithm is not complicated when complex Image elements are allowed. but the constraint of having to find real and binary Image elements is something that we gladly avoid. that is possible by constructing in the computer the five Image elements as complex pattern and then by making five corresponding computer holograms, which are binary fourier holograms, to be used as five basic matched filters. it would be difficult to make these five basic filters by means of ordinary holographic recording, because the construction of those five phase-and-amplitude objects is difficult.
4.3 incoherent matched filtering
for comparison we describe at first the theory of coherent matched filtering by means of the following equations:
object 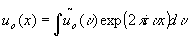
first fourier transform by the first lens 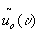 .
.
multiplication by the filter 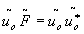
second transform 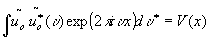
- 25 -
if the object ur(x) contains the reference signal ur(x-xm) at x=xm the output u
(x) will contain a peak at x=xm, because the integrand is then real and non-negative,
if uo = ur(x-xm)
then 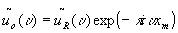
then 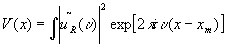
the general equation for the output 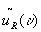 can be re-shaped into a correlation integral by inserting
can be re-shaped into a correlation integral by inserting
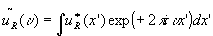
and by using 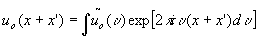
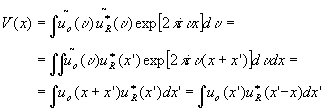
it will be very useful later on to derive this last equation
once more. we assume coherent Image forming system with a filter 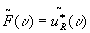 .
at first we put a point source in the center of the object plane. the corresponding
Image will be a conjugate inverted reference signal, as described symbolically:
.
at first we put a point source in the center of the object plane. the corresponding
Image will be a conjugate inverted reference signal, as described symbolically:
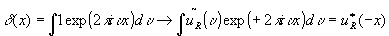
now we shift the point source laterally:
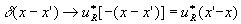
this step was based on the assumption that our Image forming system is space invariant. next we amplify the input by a factor, which will we call uo(x') for convenience. the output will be amplified by the same factor if the system is homoqeneous for complex light amplitudes. that is true for
uo(x')d
(x-x') ®
uo(x) u*r(x'-x)
the case of coherent object illumination.
- 26 -
mow we let many point sources uo(x')d
(x-x'), uo(x")d
(x-x") etc. send their waves from the object to the Image plane. all object point sources together form the object, and all point source responses together form the correlation of object and reference signal in the Image plane.
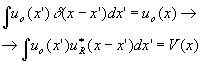
this last integration step is justified because our coherent optical system is additive for complex amplitudes. the combination of additive and homogenous is called linear.
in summary we can state that a space-invariant and linear system
with a filter 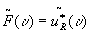 responds to
the input uo(x) with the correlation
responds to
the input uo(x) with the correlation 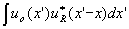 as output. now we make the transition to incoherent matched filtering. the light
is still monochromatic, but now spatially incoherent. otherwise the optical
setup is the same as before. the same fourier hologram with the complex transmittance
as output. now we make the transition to incoherent matched filtering. the light
is still monochromatic, but now spatially incoherent. otherwise the optical
setup is the same as before. the same fourier hologram with the complex transmittance
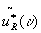 is in the frequency domain.
this system with incoherent light is still space-invariant, of course. it is
also linear, but now for intensities, not complex amplitudes. we now describe
the performance by beginning with a point-like intensity in the center of the
input plane. the output intensity is what we see when reconstructing a fourier
hologram. however, for the purpose of matched filtering we are interested only
in the conjugate Image:
is in the frequency domain.
this system with incoherent light is still space-invariant, of course. it is
also linear, but now for intensities, not complex amplitudes. we now describe
the performance by beginning with a point-like intensity in the center of the
input plane. the output intensity is what we see when reconstructing a fourier
hologram. however, for the purpose of matched filtering we are interested only
in the conjugate Image:
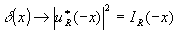
next, we shift the point source:
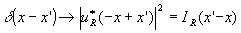
now we amplify the point source intensity by a factor 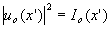
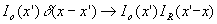
- 27 -
finally, we let many point sources radiate simultaneously, but incoherently:
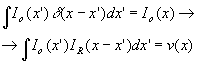
the result is the correlation of object intensity and
reference intensity distribution. we can re-shape this equation into the filter
form by inserting first 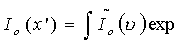 ,
then by using
,
then by using 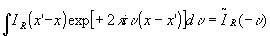 :
: 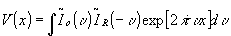 .
.
apparantly 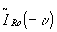 the incoherent filter function, also called "optical transfer function otf".
because ir(x) is real as intensity, the otf obeys the symmetry relation
the incoherent filter function, also called "optical transfer function otf".
because ir(x) is real as intensity, the otf obeys the symmetry relation
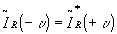 .
.
the otf is related to the coherent filter function 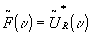 by means of an autocorrelation integral, that is sometimes called duffieux formula
by means of an autocorrelation integral, that is sometimes called duffieux formula
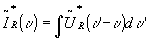
now let us briefly summarize what we got so far in this chapter. the same optical setup and the same fourier hologram can be used for coherent and for incoherent-matched filtering. the output intensities are:
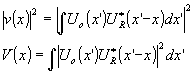
the two output intensities are very closely related in the special case of binary objects (black and white, not gray) because "one" and "zero" are the only two numbers which are the same as their square numbers. for binary objects and references it is u = u* = |
u|
2. in that case we get v(x)=v(x). in other words, the output intensities are alike, except for a quadratic process. these results are know already since 1968 [8], but they found only little attention, with one major exception [9].
maloney used a light pattern on an oscilloscope as object, for incoherent matched filtering.
- 28 -
hence he avoided the need for changing an electronic signal
into a coherent optical input signal. the conversion of an electronic
signal into an incoherent optical input signal (for example on an oscilloscope)
is much simpler, quicker and cheaper. but there are two more significant advantages
of incoherent versus coherent matched filtering. the laterial position of the
holographic filter is completely uncritical in the incoherent case. this can
be formally deduced from the duffieox formula, where a shift of 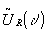 into
into 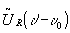 does not influence the
otf autocorrelation integral. furthermore, we can afford to place a diffuser
exp[ij (x)] on top of the reference signal ur(x),
when making the holographic filter. that diffuser dous not change the output
intensity v(x) since it is | ur·exp[ij
]| 2 = |
ur| 2 = ir(x).
but we gain two practical advantages due to the diffuser. we avoid now the photographic
dynamic range problem, and we improve the holographic light efficiency by an
order of magnitude.
does not influence the
otf autocorrelation integral. furthermore, we can afford to place a diffuser
exp[ij (x)] on top of the reference signal ur(x),
when making the holographic filter. that diffuser dous not change the output
intensity v(x) since it is | ur·exp[ij
]| 2 = |
ur| 2 = ir(x).
but we gain two practical advantages due to the diffuser. we avoid now the photographic
dynamic range problem, and we improve the holographic light efficiency by an
order of magnitude.
4.4 shift-invariant matched filtering
this method [10] has some features in common with the previous method. it loses some advantages, but it gains others instead.
in common is: position of reference uncritical;
no dynamic range problems.
new features are: the input position is unimportant, the input may move during the correlation measurement. the reference signal can be used directly (without be transformed into a hologram). white light may be used, which guarantees a speckle-free output.
lost feature: the input has to be illuminated by spatially coherent light.
the theory goes like this:
input at lateral location x0 u0(x-x0)
first fourier transform: 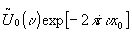
through moving diffuser: 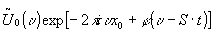
- 29 -
time average (complex amplitude): 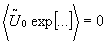
time average (intensity): 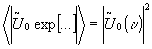
we now consider this time average intensity 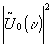 as our "secondary input". notice, the location x0 of the "primary
input" u0(x-x0) has no influence on the secondary font,
which is now spatially incoherent. the plane of this "secondary input", where
the diffuser moves laterally, is the "object plane" of an incoherent matched
filtering systems ,is described in the previous chapter 4.3. there the complex
amplitude transmittance of the filter was the fourier transform of the reference
signal. here now, everything is just in the opposite fourier domain due to the
shift-invariant pre-processing step from u0(x-x0) to
as our "secondary input". notice, the location x0 of the "primary
input" u0(x-x0) has no influence on the secondary font,
which is now spatially incoherent. the plane of this "secondary input", where
the diffuser moves laterally, is the "object plane" of an incoherent matched
filtering systems ,is described in the previous chapter 4.3. there the complex
amplitude transmittance of the filter was the fourier transform of the reference
signal. here now, everything is just in the opposite fourier domain due to the
shift-invariant pre-processing step from u0(x-x0) to 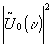 .
hence the reference signal is now
.
hence the reference signal is now 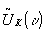 and its fourier transform ur(-x). this means that the secondary input
and its fourier transform ur(-x). this means that the secondary input
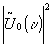 exists in the object domain.
one fourier step later we set up the reference signal ur(-x+xr).
exists in the object domain.
one fourier step later we set up the reference signal ur(-x+xr).
and one more fourier step (three fourier steps from the primary
input u0(x-x0)) we observe the intensity correlation of
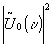 and
and 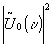 :
:
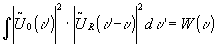
notice, the output input intensity w(u
) does not know anything about the location, of the primary input u0, and about the location xr of the reference signal ur. this independance of x0 and xr means that we have no lateral adjustment problems. both u0 and ur might move during the measurement. we do not have to produce a hologram from the reference signal ur. furthermore, the peak of the cross correlation signal w(u
) is always at the fixed point (u
= 0), where we position our photoelectric receiver. no holographic twin images or zero-order beams exist, that would restrict the usable size of the input plane. why did this method remain so unpopulary? perhaps because conservative scientists refuse to digest more than two fourier inversions in one meal?
- 30 -
4.5 fresnel correlation
in the previous chapter we achieved to correlate the fraunhofer
diffraction pattern 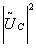 and
and 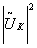 of object and reference. in order to do justice to fresnel, who was the first
to explore diffraction at a finite distance, we might try to correlate
now the fresnel diffraction pattern
of object and reference. in order to do justice to fresnel, who was the first
to explore diffraction at a finite distance, we might try to correlate
now the fresnel diffraction pattern 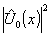 and
and 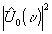 observed at distances
z behind the object and reference, respectively [11].
observed at distances
z behind the object and reference, respectively [11].
the definitions are:
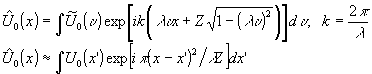
basically, the total system consists of two fresnel diffraction
systems in sequence. the first system starts with pointasource, has somewhere
the object u0(x) and at a distance z behind the object the diffraction
amplitude 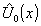 .
.
collimator lenses have been used [11], but they are not essential. that diffraction amplitude is multiplied by a moving diffuser exp[ij
(x-s·t)]. the time averages are:
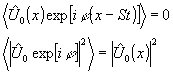
every point intensity d
(x-x’) of
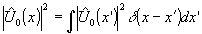 acts as
point source for the second fresnel diffraction system with ur(-x)
as diffraction object. for example the point source d
(x-x') at the exit of the first fresnel system (=entrance of second fresnel
system = diffuser plane) produces at the final output plane at a distance z
behind ur(-x) the intensity
acts as
point source for the second fresnel diffraction system with ur(-x)
as diffraction object. for example the point source d
(x-x') at the exit of the first fresnel system (=entrance of second fresnel
system = diffuser plane) produces at the final output plane at a distance z
behind ur(-x) the intensity 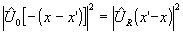 .
the lateral shift x' of the output pattern is due to the tilt angle of the wave
that comes from d (x-x') to ur(-x).
.
the lateral shift x' of the output pattern is due to the tilt angle of the wave
that comes from d (x-x') to ur(-x).
all output intensities together yield the fresnel diffraction
intensity correlation: 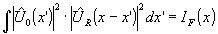
- 31 -
the advantages and disadvantages of this method are similar to those of the fraunhofer diffraction correlation method. but there are some differences. in the fresnel method the lateral locations of the object signal k, and of the reference signal 1<i, do influence the lateral location of the output signal. but these locations are not as critical as in coherent matched filtering, where the method breaks down completely when the filter is moved by a few microns.
on the other hand, the fraunhofer method (chapter 4.4) can tolerate only one input object at a time. the fresnel method is capable of handling many input objects side by side, similarly as in matched filtering. the reference [11] contains a special trick for simplifying the lateral adjustment problem.
4.6 comparison of several correlation methods
first we want to write down in mathematical terms, which type of correlation is measured by the various methods. then we will show in table form, which of the disadvantages of coherent matched filtering have been overcome by the newer methods.
a. coherent matched filtering
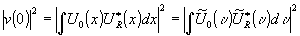
b. incoherent matched filtering
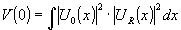
c. shift-invariant fraunhofer correlation
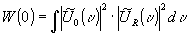
d. fresnel correlation
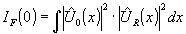
two other methods
Ā,
 are like a, b but with computer generated holographic filters.
are like a, b but with computer generated holographic filters.
- 32 -
comparison of several correlation methods
the problem solved by method
|
a |
a |
b |
b |
c |
d |
|
coherent illumination |
|
|
+ |
+ |
|
|
|
object field limited |
(+) |
(+) |
(+) |
(+) |
|
(+) |
|
object must exist |
|
+ |
|
+ |
|
|
|
object position critical |
|
|
|
|
+ |
|
|
reference position critical |
|
|
+ |
+ |
+ |
(+) |
|
dynamic range |
|
|
+ |
+ |
+ |
+ |
- 33 -
references
1. t.s.huang "digital holography" proc. ieee 59, 1335-1347 (1971).
2. a.w.lohmann "how to make computer holograms", in spie seminar proceedings, vol. 25, p. 43-49 (1971).
3. r.j.collier, c.b.burckhardt, l.h.liu "optical holography", chapter 19, new york 1971.
4. a.w. lohmann "computer holography and communications theory" in ieee-nerem 73 record on "signal processing", boston 1973.
5. b.r.brown, a.w.lohmann, d.p.paris and h.w.werlich appl.opt. 5, 967 (1966); 6, 1139 (1967); 7, 651 (1968), "computer generated spatial filters".
6. a.w.lohmann, h.w.werlich, appl. opt. 10, 2743 (1971); 11, 2996 (1972) "spatial pulse modulation in optics".
7. a.w.lohmann, c.a.shuman. opt. comm. 7, 93 (1973).
8. s.lowenthal, a.werts, c.r.acad, franc. b 266, 542 (1968).
9. w.t.maloney, appl. opt. 10, 2554 (1971).
10. j.d.armitage, a.w.lohmann, appl. opt. 4, 461 (1965).
11. m. de, a.w.lohmann, appl. opt. 6, 2171 (1967).

